数字电子技术 第2章 卡诺图化简法
- 格式:ppt
- 大小:1.05 MB
- 文档页数:36




![数字电子技术基础_第四版_阎石_课后答案[1-6章]](https://uimg.taocdn.com/6d6addfe6294dd88d0d26bcb.webp)

第7章组合逻辑电路教学重点1.掌握组合逻辑电路的分析方法和步骤,能分析简单逻辑电路的逻辑功能。
2.了解组合逻辑电路设计的基本方法和步骤。
3.熟知编码器的基本功能和常见类型,了解二进制编码器、二-十进制编码器的基本功能和真值表。
4.理解优先编码器的工作特点,掌握二-十进制优先编码器74LS147的引脚功能及应用方法,了解74LS138的扩展应用。
5.理解译码器的基本功能,熟悉常见类型;了解半导体数码管的基本结构和工作原理。
6.了解二进制译码器、二-十进制译码器的基本功能和真值表,了解典型的译码显示电路。
教学难点1.掌握组合逻辑电路的分析。
2.组合逻辑电路的设计。
3.集成电路74LS138的扩展及应用。
4.功能电路的搭建。
学时分配7.1 组合逻辑电路的基本知识7.1.1 组合逻辑电路的分析方法组合逻辑电路的分析,是指基于逻辑电路图,分析明确该电路的基本功能的过程。
组合逻辑电路的分析一般可按如图所示步骤进行。
例:分析如图所示三人表决器电路的逻辑功能。
解:第一步 根据电路逐级写出逻辑表达式AB Y =1BC Y =2AC Y =3 321Y Y Y Y ⋅⋅=AC BC AB ⋅⋅= 第二步 化简逻辑表达式AC BC AB Y ⋅⋅=AC BC AB ++=第三步 根据化简后的逻辑表达式列出真值表如表。
第四步 根据所示真值表,三输入中至少有两个或以上的输入为1时,输出才为1,否则输出为0,可知此电路为一少数服从多数的三人表决器。
7.1.2 组合逻辑电路的设计方法与组合逻辑电路的分析相反,逻辑电路的设计是根据给定的逻辑功能要求,设计出实现该功能的逻辑电路。
组合逻辑电路的设计可按下列步骤进行。
例:某写字楼控制室有3个报警灯:L 0(火警)、 L 1(盗警)和L 2(一般业务),按事态轻重缓急要求,有多个警报同时出现时,在同一时间只能有一个信号通过,首先接通的是火警信号,其次为盗警信号,最后是日常一般业务信号。



卡诺图化简法20分钟教案逻辑函数的卡诺图化简逻辑函数的卡诺图化简是《数字电⼦技术基础》第⼆章第5⼩节的内容。
《数电》是电类专业的⼀门基础课,⽽卡诺图化简是学习数字电路设计的⼀个基本⼯具,在数字电路的逻辑变量简化中起到重要的作⽤。
那么我们先了解⼀下,什么是卡诺图?⼀、卡诺图由来数字电路中的逻辑函数往往不是最简的表达形式,⽽在使⽤代数法对逻辑函数化简时,会遇到很多困难:1、逻辑代数与普通代数的公式易混淆,化简过程要求对所有公式熟练掌握,加⼤了计算难度;2、代数法化简⽆⼀套完善的⽅法可循,它依赖于⼈的经验和灵活性,运算效率低;3、代数化简⽅法技巧强,较难掌握。
特别是对于判断代数化简后的逻辑表达式是否为最简式,具有⼀定困难。
所以对于⾃变量较少的逻辑函数,我们寻求了⼀种简单有效的化简⽅式——卡诺图化简法⼜称为图形化简法。
该⽅法简单、直观、容易掌握,因⽽在逻辑设计中得到⼴泛应⽤。
卡诺图是贝尔实验室的电信⼯程师,莫⾥斯?卡诺在1953年发明的。
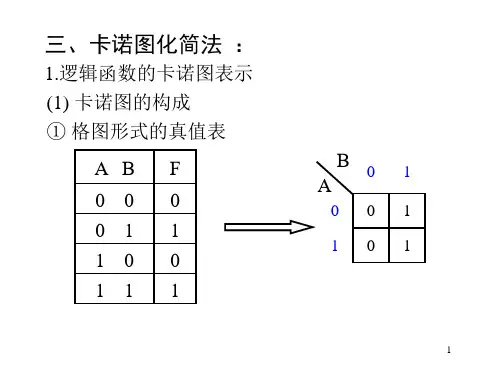
卡诺图简称K图,它是真值表的变形,将真值表按⼀定规则画成的最⼩项⽅块图。
⼆、⽤卡诺图表⽰逻辑函数1、卡诺图的定义⼏何相邻:将n变量的全部最⼩项都⽤⼩⽅块表⽰,并使具有逻辑相邻的最⼩项在⼏何位置上也相邻地排列起来,这样所得到的图形叫n变量的卡诺图。
逻辑相邻:如果两个最⼩项只有⼀个变量互为反变量,那么,就称这两个最⼩项在逻辑上相邻。
⼏种典型的卡诺图:1)两变量卡诺图每个2变量的最⼩项有两个最⼩项与它相邻2)三变量卡诺图每个3变量的最⼩项有3个最⼩项与它相邻3)四变量卡诺图每个4变量的最⼩项有4个最⼩项与它相邻最左列的最⼩项与最右列的相应最⼩项也是相邻的最上⾯⼀⾏的最⼩项与最下⾯⼀⾏的相应最⼩项也是相邻的2、卡诺图的特点各⼩⽅格对应于各变量不同的组合,⽽且上下左右在⼏何上相邻的⽅格内只有⼀个因⼦有差别,这个重要特点成为卡诺图化简逻辑函数的主要依据。
3、已知逻辑函数画卡诺图当逻辑函数为最⼩项表达式时,在卡诺图中找出和表达式中最⼩项对应的⼩⽅格填上1,其余的⼩⽅格填上0(有时也可⽤空格表⽰),就可以得到相应的卡诺图。

利用卡诺图化简逻辑函数的方法称为卡诺图化简法或图形化简法。
化简时依据的基本原理就是具有相邻性的最小项可以合并,并消去不同的因子。
由于在卡诺图上几何位置相邻与逻辑上的相邻性是一致的,因而从卡诺图上能直观地找出那些具有相邻性的最小项并将其合并化简。
1.合并最小项的规则(1)若两个最小项相邻,则可合并为一项并消去一对因子。
合并后的结果中只剩下公共因子。
(2)若四个最小项相邻并排列成一个矩形组,则可合并为一项并消去两对因子。
合并后的结果中只包含公共因子。
(3)若八个最小项相邻并且排列成一个矩形组,则可合并为一项并消去三对因子。
合并后的结果中只包含公共因子。
l下图给出了最小项相邻的几种情况最小项相邻的几种情况图(a)(b)两个最小项相邻(c)(d)四个最小项相邻(e)八个最小项相邻至此,可以归纳出合并最小项的一般规则:如果有个最小项相邻(n=1,2,…)并排列成一个矩形组,则它们可以合并为一项,并消去n对因子。
合并后的结果中仅包含这些最小项的公共因子。
2.卡诺图化简法的步骤用卡诺图化简逻辑函数时可按如下步骤进行:(1)将函数化为最小项之和的形式。
(2)画出表示该逻辑函数的卡诺图。
(3)找出可以合并的最小项。
(4)选取化简后的乘积项。
选取的原则:n这些乘积项应包含函数式中所有的最小项(应覆盖卡诺图中所以的1)n所用的乘积项数目最少,即可合并的最小项组成的矩形组数目最少n每个乘积项包含因子最少,即各可合并的最小项矩形组中应包含尽量多的最小项例1:用卡诺图化简法将式化简为最简与—或函数式解:首先画出表示函数y的卡诺图,如图通过合并最小项,得出结果,左图:右图:注:l在填写y的卡诺图时,并不一定要将y化为最小项之和的形式。
l需要找出可以何并的最小项,将可能合并的最小项用线圈出,有时存在多种可能合并最小项的方案,所以有时一个逻辑函数的化简结果不是唯一的。
例2:用卡诺图法将化为最简与—或逻辑式解:首先画出y的卡诺图,然后把可能合并的最小项圈出,并按照前面所述的原则选择化简与—或式中的乘积项最后得到结果l补充说明:在以上的两个例子中,我们都是通过合并卡诺图中的1来求得化简结果的。
第2章习题解答题2-1 用真值表证明下列恒等式。
(1) ()A B C AB AC ⊕=⊕(2) ()()()()()A B A C B C A B A C ''+++=++ (3) ()0A B A B A B '⊕==⊕⊕解:将输入变量所有的取值逐一代入公式两边计算,然后将计算结果列成真值表。
如果两边的真值表相同,则等式成立。
(1)证明()A B C AB AC ⊕=⊕表JT2-1(2) 证明 ()()()()()A B A C B C A B A C ''+++=++表JT2-2(3) 证明()0A B A B A B '⊕==⊕⊕表JT2-3题2-2 证明下列逻辑等式(证明方法不限)。
(1)()()BC D D B C AD B B D '''++++=+(2) A C A B BC A C D A BC ''''''''+++=+(3) ()ABCD A B C D AB BC CD A D '''''''''+=+++ (4) ()()()A C B D B D AB BC '''+++=+解:在实际应用中,除非逻辑式很简单、而且逻辑变量数很少的情况下,一般不宜用列真值表的方法。
对多变量、复杂的逻辑等式、通常采用公式推演或公式推演与画卡诺图相结合的方法去证明。
如果有条件使用Multisim 等EDA 软件进行证明,则更简单、便捷。
(1)()()()()BC D D B C AD B BC D B C AD B BC D AB D AC D BB BC B D'''''++++=++++''''=+++++=+(2)()A C A B BC A C D A C A B BC A BC BC A BC ''''''''''''''+++=++=+=+(3)()()()()()()()()()()()AB BC CD A D AB BC CD A D A B B C C D A D A B A C BC AC AD C D ABCD A B C D '''''''''''''+++=''''''''''=++++=++++''''=+ (4)()()()()()()A C B D B D A C B BD BD A C B AB BC ''''''+++=+++=+=+题2-3已知逻辑函数Y 1和Y 2的真值表如表JT2-4(a )、(b )所示,试写出Y 1和Y 2的逻辑函数式。