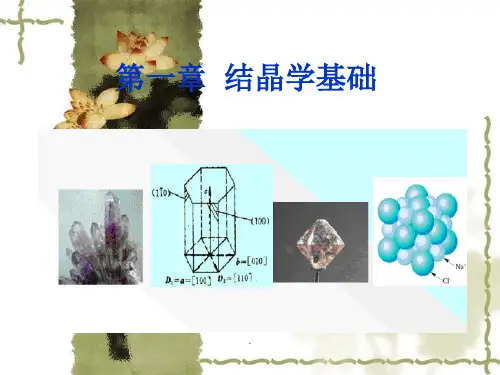
第一章晶体学基础

第一篇 X射线衍射分析（15万字）1 晶体学基础1.1 晶体结构的周期性与点阵晶体是由原子、离子、分子或集团等物质点在三维空间内周期性规则排列构成的固体物质，这种周期性是三维空间的。

晶体中按周期重复的原子、分子或离子团称为结构基元，也就是重复单元。

为了描述晶体内部原子排列的周期性，总是把一个结构基元抽象地看成为一个几何点，而不考虑它的实际内容（指原子、离子或分子）。

这些几何点按结构周期排列，这种几何点的集合就称为点阵，将点阵中的每个点叫阵点。

要构成点阵，必须具备三个条件：（1）点阵点数无限多；（2）各点阵点所处的几何环境完全相同；（3）点阵在平移方向的周期必须相同。

凡是能够抽取出点阵的结构可称为点阵结构或晶体点阵。

点阵中每一阵点对应于点阵结构中的一个结构基元，在晶体中则是一些组成晶体的实物粒子，即原子、分子或离子等，或是这些微粒的集团。

这样，晶体结构与晶体点阵是两个不同的概念，其关系如图1-1所示，晶体结构可以表示为：晶体结构= 晶体点阵+ 结构基元图1-1晶体结构与点阵的关系根据点阵的性质，把分布在同一直线上的点阵称为直线点阵或一维点阵，分布在同一平面内的点阵称为平面点阵或二维点阵，分布在三维空间中的点阵称为空间点阵或三维点阵。

1.1.1 一维周期性结构与直线点阵图1-2（a）是聚乙烯分子链的结构示意图，具有一维周期结构，其结构基元（CH2CH2）周期性地排列在一个方向上。

每一个结构基元的等同位置抽象成一个几何点，可形成一条直线点阵，是等距离分布在一条直线上的无限点列，如图1-2（b）所示。

取任一阵点作为原点O ，A 为相邻的阵点，则矢量a=OA 表示重复的大小和方向，称为初基（单位）矢量或基矢，若以单位矢量a 进行平移，必指向另一阵点，而矢量的长度a a =ρ称为点阵参数。

图1-2晶体结构与点阵的关系（a ）聚乙烯分子链的结构示意图；（b ）等效的一维直线点阵直线点阵中任何两阵点的平移矢量称为矢径，可表示为T p = p a (0, ±1, ±2……)矢径T p 完整而概括地描述了一维结构基元排列的周期性。

晶体学基础绪论刘彤固体中的晶体气态：内部微粒（原子、分子、离子）无规运动液态：内部微粒（原子、分子、离子）无规运动固态：内部微粒（原子、分子、离子）振动自然界中绝大多数固体物质都是晶体。

如：食盐、冰糖、金属、岩石等。

¾单质金属和合金在一般条件下都是晶体。

¾一些陶瓷材料是晶体。

¾高聚物在某些条件下也是晶体。

“德里紫蓝宝石”如何在千姿百态的晶体中发现其规律？熔体凝固液相结晶晶体并非局限于天然生成的固体人工单晶飞机发动机叶片飞机发动机晶体的共同规律和基本特征?水晶石英晶体具有规则的凸多面体外形。

α石英的内部结构大球代表小球代表晶体的概念NaCl的晶体结构晶体（crystal）：其内部质点（原子、分子或离子）在3维空间周期性重复排列的固体。

也称具有格子构造的固体。

晶体材料：单晶，多晶¾在一个单晶体的范围内，晶格中的质点均呈有序分布。

多晶体内形成许多局限于每个小区域内的有序结构畴，但在畴与畴之质点的分布是无序的或只是部分有序的。

晶界（晶体缺陷）Be 2O 3非晶体Be 2O 3 晶体分子晶体（范德华力）晶体学的发展历史¾有文字记载以前，人们对矿物晶体瑰丽的色彩和特别的多面体外形引起了的注意，开始观察研究晶体的外形特征。

¾17世纪中叶，丹麦学者斯丹诺（steno）1669年提出面角守恒定律，这可以说是晶体学作为一门正式科学的标志，它找出了晶体复杂外形中的规律性，从而奠定了几何晶体学的基础。

¾1801年，法国结晶学家阿羽依（Haüy）基于对方解石晶体沿解理面破裂现象的观察，发现晶体学基本定律之一的整数定律。

¾1805-1809年，德国学者魏斯(Weiss)发现晶带定律以及晶体外形对称理论。

几何晶体学发展到了相当高的程度。

¾1830年，德国学者赫塞尔（Hessel)推导出描述晶体外形对称性的32种点群。

¾1837年，英国学者米勒（Miller）提出晶面在三维空间位置的表示方法---米勒指数。

晶体学基础与材料结构第⼀章晶体学基础及材料结构⽆论是⾦属材料还是⾮⾦属材料，通常都是晶体。

因此，作为材料科学⼯作者，⾸先要熟悉晶体的特征及其描述⽅法。

本章将扼要的介绍晶体学的基础知识，并了解材料结构。

1-1 晶体⼀、晶体与⾮晶体固态物质按其原⼦（或分⼦）的聚集状态⽽分为两⼤类：晶体与⾮晶体。

虽然我们看到⾃然界的许多晶体具有规则的外形（例如：天然⾦刚⽯、结晶盐、⽔晶等等），但是，晶体的外形不⼀定都是规则的，这与晶体的形成条件有关，如果条件不具备，其外形也就变得不规则。

所以，区分晶体还是⾮晶体，不能根据它们的外观，⽽应从其内部的原⼦排列情况来确定。

在晶体中，原⼦（或分⼦）在三维空间作有规则的周期性重复排列，⽽⾮晶体就不具有这⼀特点，这是两者的根本区别。

应⽤X射线衍射、电⼦衍射等实验⽅法不仅可以证实这个区别，还能确定各种晶体中原⼦排列的具体⽅式（即晶体结构的类型）、原⼦间距以及关于晶体的其他许多重要情况。

显然，⽓体和液体都是⾮晶体。

在液体中，原⼦亦处于紧密聚集的状态，但不存长程的周期性排列。

固态的⾮晶体实际上是⼀种过冷状态的液体，只是其物理性质不同于通常的液体⽽已。

玻璃就是⼀个典型的例⼦，故往往将⾮晶态的固体称为玻璃体。

从液态到⾮晶态固体的转变是逐渐过渡的，没有明显的凝固点（反之亦然，⽆明显的熔点）。

⽽液体转变为晶体则是突变的，有⼀定的凝固点和熔点。

⾮晶体的另⼀特点是沿任何⽅向测定其性能，所得结果都是⼀致的，不因⽅向⽽异，称为各向同性或等向性；晶体就不是这样，沿着⼀个晶体的不同⽅向所测得的性能并不相同（如导电性、导热性、热膨胀性、弹性、强度、光学数据以及外表⾯的化学性质等等），表现出或⼤或⼩的差异，称为各向异性或异向性。

晶体的异向性是因其原⼦的规则排列⽽造成的。

⾮晶体在⼀定条件下可转化为晶体。

例如：玻璃经⾼温长时间加热后能形成晶态玻璃；⽽通常呈晶体的物质，如果将它从液态快速冷却下来也可能得到⾮晶体。

⾦属因其晶体结构⽐较简单，很难阻⽌其结晶过程，故通常得不到⾮晶态固体，但近些年来采⽤了特殊的制备⽅法，已能获得⾮晶态的⾦属和合⾦。

材料科学与基础第一章晶体结构第一节晶体学基础一、空间点阵晶体中原子或分子的空间规则排列，阵点周围环境相同，在空间的位置一定。

（一）晶胞点阵中取出的一个反映点阵对称性的代表性基本单元。

通过晶胞角上的某一阵点，沿其三个棱边作坐标轴X、Y、Z（称为晶轴），则此晶胞就可由其三个棱边的边长a、b、c（称为点阵常数）及晶轴之间的夹角α、β、γ六个参数表达出来。

事实上，采用三个点阵矢量a、b、c来描述晶胞更方便。

（二）晶系（三）布拉菲点阵只能有14种空间点阵，归属于7个晶系。

（四）晶体结构与空间点阵最简单的空间格子，又叫原始格子，以P表示。

对称性高的为高级晶族。

二、晶向指数和晶面指数（一）晶向指数1.以晶胞的晶轴为坐标轴X、Y、Z，以晶胞边长作为坐标轴的长度单位。

2.从晶轴系的原点O沿所指方向的直线取最近一个阵点的坐标u、v、w。

3.将此数化为最小整数并加上方括号，即为晶向指数。

[100],[110],[111̅]晶向指数表示所有相互平行、方向一致的晶向。

晶体中因对称关系而等同的各组晶向可并为一个晶向族，用<uvw>表示。

（二）晶面指数1.对晶胞作晶轴X、Y、Z以晶胞的边长作为晶轴上的单位长度。

2.求出待定晶面在三个晶轴上的截距（如该晶面与某轴平行，则截距为∞）。

3.取这些截距数的倒数。

4.将上述倒数化为最小的简单整数，并加上圆括号，即表示该晶面的指数，记为（hkl ）晶面指数所代表的不仅是某一晶面，而是代表着一组相互平行的晶面。

（化简相等）在晶体中，具有等同条件而只是空间位向不同的各组晶面，可归并为一个晶面族，用｛hkl ｝表示。

在立方晶系中，具有相同指数的晶向和晶面必定是相垂直的。

即[hkl ]⊥{hkl} （三）六方晶系指数晶面指数以（hkil ）四个指数来表示，有h +k +i =0； 晶向指数以[uvtw]表示，有u +v +t =0。

六方晶系按两种晶轴系所得的晶面指数和晶向指数可相互转换如下：对晶面指数来说，从（hkil ）转换成（hkl ）只需去掉i ；对晶向指数，[UVW]与[uvtw]的关系为：U =u −t; V =v −t; W =w 。