固体结构晶体学基础

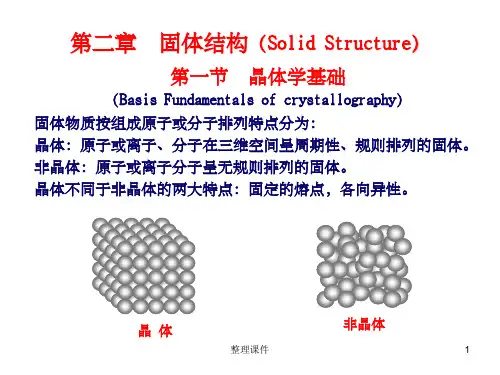
固体物理学的基础知识固体物理学是物理学的一个重要分支，研究物质固态状态的性质和行为。

在这篇文章中，我们将介绍一些固体物理学的基础知识，包括晶体结构、晶格常数、晶体缺陷和固体力学性质等内容。

一、晶体结构晶体是指由周期性排列的原子、离子或分子组成的物质。

晶体结构描述了这些粒子在空间中的排列方式。

最基本的晶体结构是简单立方、面心立方和体心立方。

简单立方是最简单的结构，每个原子与其六个相邻原子相接触；面心立方在每个立方的面心上添加了一个原子；体心立方在每个简单立方的中心添加了一个原子。

除了这些基本结构，还存在许多复杂的晶体结构，如钻石和蓝宝石。

二、晶格常数晶格常数是描述晶体结构的一个重要参数。

它表示晶体中相邻原子之间的距离。

晶格常数可以通过实验或计算得到。

对于简单立方结构来说，晶格常数就是原子间距离；对于面心立方和体心立方结构，晶格常数与原子间距离有特定的关系。

三、晶体缺陷晶体缺陷是指晶体结构中的一些缺陷或杂质。

晶体缺陷可以分为点缺陷、线缺陷和面缺陷。

点缺陷包括空位、间隙原子和替位原子；线缺陷包括位错和螺旋位错；面缺陷包括晶界和界面。

晶体缺陷对晶体的性质有重要影响，如电导率、热导率和光学性质等。

四、固体力学性质固体力学性质描述了固体对外界力的响应和变形行为。

其中最基本的性质是弹性模量。

弹性模量分为压缩模量、剪切模量和杨氏模量，它们分别描述了固体对压力、剪切力和应力的响应。

除了弹性模量，还有塑性、断裂和疲劳等力学性质值得研究。

结论固体物理学的基础知识包括晶体结构、晶格常数、晶体缺陷和固体力学性质等内容。

通过对这些知识的研究，我们可以更深入地理解固体的性质和行为，为材料科学和工程技术的发展做出贡献。

希望本文对你对固体物理学的学习有所帮助。

参考文献：[1] Ashcroft N W, Mermin N D. Solid State Physics. Cengage Learning, 1976.[2] Kittel C. Introduction to Solid State Physics. John Wiley & Sons, 2005.[3] Rao C N R, Rao C N R, Omar Syed Ismail. Angular Momentum in Quantum Physics: Theory and Application. World Scientific, 2014.。

第一篇 X射线衍射分析（15万字）1 晶体学基础1.1 晶体结构的周期性与点阵晶体是由原子、离子、分子或集团等物质点在三维空间内周期性规则排列构成的固体物质，这种周期性是三维空间的。

晶体中按周期重复的原子、分子或离子团称为结构基元，也就是重复单元。

为了描述晶体内部原子排列的周期性，总是把一个结构基元抽象地看成为一个几何点，而不考虑它的实际内容（指原子、离子或分子）。

这些几何点按结构周期排列，这种几何点的集合就称为点阵，将点阵中的每个点叫阵点。

要构成点阵，必须具备三个条件：（1）点阵点数无限多；（2）各点阵点所处的几何环境完全相同；（3）点阵在平移方向的周期必须相同。

凡是能够抽取出点阵的结构可称为点阵结构或晶体点阵。

点阵中每一阵点对应于点阵结构中的一个结构基元，在晶体中则是一些组成晶体的实物粒子，即原子、分子或离子等，或是这些微粒的集团。

这样，晶体结构与晶体点阵是两个不同的概念，其关系如图1-1所示，晶体结构可以表示为：晶体结构= 晶体点阵+ 结构基元图1-1晶体结构与点阵的关系根据点阵的性质，把分布在同一直线上的点阵称为直线点阵或一维点阵，分布在同一平面内的点阵称为平面点阵或二维点阵，分布在三维空间中的点阵称为空间点阵或三维点阵。

1.1.1 一维周期性结构与直线点阵图1-2（a）是聚乙烯分子链的结构示意图，具有一维周期结构，其结构基元（CH2CH2）周期性地排列在一个方向上。

每一个结构基元的等同位置抽象成一个几何点，可形成一条直线点阵，是等距离分布在一条直线上的无限点列，如图1-2（b）所示。

取任一阵点作为原点O ，A 为相邻的阵点，则矢量a=OA 表示重复的大小和方向，称为初基（单位）矢量或基矢，若以单位矢量a 进行平移，必指向另一阵点，而矢量的长度a a =ρ称为点阵参数。

图1-2晶体结构与点阵的关系（a ）聚乙烯分子链的结构示意图；（b ）等效的一维直线点阵直线点阵中任何两阵点的平移矢量称为矢径，可表示为T p = p a (0, ±1, ±2……)矢径T p 完整而概括地描述了一维结构基元排列的周期性。

固体物理学基础晶体的晶体学方位与晶体晶体学指数晶体学是固体物理学的重要分支，研究晶体结构和性质的科学。

在晶体学中，晶体的方位和晶体学指数是两个重要的概念。

本文将介绍晶体的晶体学方位和晶体学指数的基本概念和应用。

一、晶体学方位晶体学方位指的是表征晶体不同晶面朝向的方式。

常用的表示方式有：1. 晶体学坐标系晶体学坐标系是一种用坐标来表示晶体晶面方位的方式。

常见的晶体学坐标系有直角坐标系、直角三角坐标系和斜坐标系等。

在晶体学坐标系中，通过指定晶体晶面与坐标轴之间的夹角和晶面与坐标轴的截距，可以精确地描述晶体晶面方位。

2. 米勒指数米勒指数是用整数来表示晶体晶面方位的一种方式。

其表示方法为(hkl)，其中h、k、l为晶面与坐标轴之间的截距比。

米勒指数可以表示出各个晶面的夹角关系，并可以直观地反映晶体晶面的间隔和排列方式。

二、晶体学指数晶体学指数是晶体学中用来描述晶体晶面方位的一组整数。

指数的选取和表示方法有多种，常见的有：1. 维格纳-斯密特指数维格纳-斯密特指数是一种将晶面投影到晶胞边上的指数表示方法。

该表示方法通过规定某一晶面投影到晶胞边上的整数长度来表示晶面方位。

这种指数表示方法的好处是可以直观地展示晶体晶面的方位，并且易于进行晶体结构分析。

2. 间隔指数间隔指数是用来描述晶体晶面排列紧密程度的一组整数。

在间隔指数中，通过指定晶面的夹角和晶面之间的距离，可以判断出晶体的晶体结构和晶面的排列方式。

三、应用晶体学方位和晶体学指数在研究晶体结构和性质方面具有重要的应用价值。

它们可以帮助科学家确定晶体的晶体结构和晶面的排列方式，为材料的设计和制备提供理论依据。

在材料工程、化学和物理学等领域中，对晶体学方位和晶体学指数的研究和应用也日益重要。

总结：本文介绍了晶体学中晶体的方位和指数的基本概念和应用。

通过晶体学方位和晶体学指数的表示，科学家可以准确描述晶体的晶面方位和排列方式，为材料研究和应用提供了有力的工具。

晶体学基础与材料结构第⼀章晶体学基础及材料结构⽆论是⾦属材料还是⾮⾦属材料，通常都是晶体。

因此，作为材料科学⼯作者，⾸先要熟悉晶体的特征及其描述⽅法。

本章将扼要的介绍晶体学的基础知识，并了解材料结构。

1-1 晶体⼀、晶体与⾮晶体固态物质按其原⼦（或分⼦）的聚集状态⽽分为两⼤类：晶体与⾮晶体。

虽然我们看到⾃然界的许多晶体具有规则的外形（例如：天然⾦刚⽯、结晶盐、⽔晶等等），但是，晶体的外形不⼀定都是规则的，这与晶体的形成条件有关，如果条件不具备，其外形也就变得不规则。

所以，区分晶体还是⾮晶体，不能根据它们的外观，⽽应从其内部的原⼦排列情况来确定。

在晶体中，原⼦（或分⼦）在三维空间作有规则的周期性重复排列，⽽⾮晶体就不具有这⼀特点，这是两者的根本区别。

应⽤X射线衍射、电⼦衍射等实验⽅法不仅可以证实这个区别，还能确定各种晶体中原⼦排列的具体⽅式（即晶体结构的类型）、原⼦间距以及关于晶体的其他许多重要情况。

显然，⽓体和液体都是⾮晶体。

在液体中，原⼦亦处于紧密聚集的状态，但不存长程的周期性排列。

固态的⾮晶体实际上是⼀种过冷状态的液体，只是其物理性质不同于通常的液体⽽已。

玻璃就是⼀个典型的例⼦，故往往将⾮晶态的固体称为玻璃体。

从液态到⾮晶态固体的转变是逐渐过渡的，没有明显的凝固点（反之亦然，⽆明显的熔点）。

⽽液体转变为晶体则是突变的，有⼀定的凝固点和熔点。

⾮晶体的另⼀特点是沿任何⽅向测定其性能，所得结果都是⼀致的，不因⽅向⽽异，称为各向同性或等向性；晶体就不是这样，沿着⼀个晶体的不同⽅向所测得的性能并不相同（如导电性、导热性、热膨胀性、弹性、强度、光学数据以及外表⾯的化学性质等等），表现出或⼤或⼩的差异，称为各向异性或异向性。

晶体的异向性是因其原⼦的规则排列⽽造成的。

⾮晶体在⼀定条件下可转化为晶体。

例如：玻璃经⾼温长时间加热后能形成晶态玻璃；⽽通常呈晶体的物质，如果将它从液态快速冷却下来也可能得到⾮晶体。

⾦属因其晶体结构⽐较简单，很难阻⽌其结晶过程，故通常得不到⾮晶态固体，但近些年来采⽤了特殊的制备⽅法，已能获得⾮晶态的⾦属和合⾦。

固体物理学的基础和应用固体物理学是物理学的一个重要分支，主要研究的是固体的性质、结构、运动和相互作用等方面的问题。

固体物理学的理论基础主要是量子力学、热力学和统计物理学等，而其应用领域则广泛涉及到电子学、光学、磁学、超导学、半导体学、材料科学等多个领域。

本文将先对固体物理学的基础理论进行介绍，然后探讨其在实际应用中的具体应用。

一、固体物理学的基础理论1.1. 固体结构与晶体学固体的物理性质与其结构密切相关，因此我们需要了解固体的基本结构和组成方式。

固体物理学研究的主要对象是晶体，所谓晶体就是有规律、有序的空间排列方式。

晶体的基本单位是晶胞，一个完整的晶体就是由无数个晶胞无限重复堆积而成的。

晶体学是对晶体结构和性质进行分析和研究的学科。

其中最基本的是布拉维格子理论，即任何晶体都可以通过某一个晶胞的平移堆积而形成。

另外，X射线晶体学也是非常重要的工具，可以用来分析晶体的结构，确定各种原子的位置和排列方法，推测晶胞的大小和形状，从而了解晶体的性质。

1.2. 量子力学与能带理论考虑到固体中原子、分子和电子的量级都是非常小的，因此我们需要量子力学这一独特的理论体系来描述这些微观粒子的行为。

通过对固体中电子的能级分析，我们可以了解到对于不同原子之间的物理位置和相互作用方式，电子的能带结构也会出现一定的区别。

能带理论是用来描述固体中电子的能级分布的重要方法。

在体系中，电子可以占据各自的能级，而这些能级被分成若干个带（能带）。

固体中各种原子的结构和组成以及原子之间的相互作用等因素都会对电子的能级分布产生一定的影响，因此能带结构也会随之发生变化。

1.3. 热力学与统计物理学热力学和统计物理学是研究宏观物理规律的重要理论，也在固体物理学中得到了广泛应用。

在固体中，温度和压力等因素都可以影响到其物理性质，而热力学和统计物理学提供了从宏观角度分析这些问题的理论支持。

统计物理学主要是根据微粒子（如分子和电子）的统计规律，推导出宏观物理规律的学科。