1.2.1--1.2.2 中心投影与平行投影 空间几何体的三视图

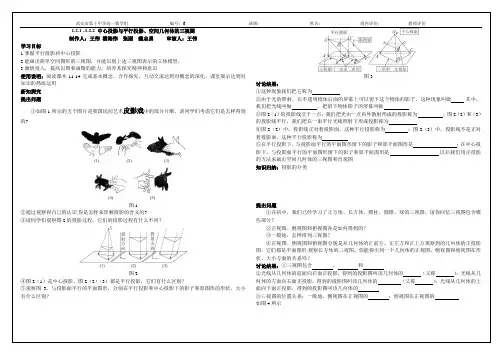
图1
你是怎样来理解投影的含义的?
的投影过程，它们的投影过程有什么不同？
图2
）是中心投影、图2（2）（3）都是平行投影，它们有什么区别？
，与投影面平行的平面图形，分别在平行投影和中心投影下的影子和原图形的形状、大小
图3
②由于光的照射，在不透明物体后面的屏幕上可以留下这个物体的影子，这种现象叫做
，把留下物体影子的屏幕叫做.
图4
的位置关系，即反映了物体的
(1) (2)
的位置关系，即反映了物体的
的位置关系，即反映了物体的
所示的矿泉水瓶的三视图.
引导学生认识这种容器的结构特征.矿泉水瓶是我们熟悉的一种容器，这种容器是简单的组合体，
其主要结构特征是从上往下分别是圆柱、圆台和圆柱
图6
7所示的几何体的三视图
图7
课堂小结。

§1.2空间几何体的三视图和直观图1.2.1中心投影与平行投影1.2.2空间几何体的三视图基础过关1．一个几何体的三视图如图所示，则该几何体可以是()A．棱柱B．棱台C．圆柱D．圆台解析先观察俯视图，再结合正视图和侧视图还原空间几何体．由俯视图是圆环可排除A，B，由正视图和侧视图都是等腰梯形可排除C，故选D.答案D2．某空间几何体的正视图是三角形，则该几何体不可能是()A．圆柱B．圆锥C．四面体D．三棱柱解析由三视图知识，知圆锥、四面体、三棱柱(放倒看)都能使其正视图为三角形，而圆柱的正视图不可能为三角形，故选A.答案A3．一个长方体去掉一个小长方体，所得几何体的正视图与侧视图分别如图所示，则该几何体的俯视图为()解析正视图中小长方形在左上方，对应俯视图应该在左侧，排除B，D，侧视图中小长方形在右上方，排除A，故选C.答案C4．下列物品：①探照灯；②车灯；③太阳；④月亮；⑤台灯中，所形成的投影是中心投影的是________(填序号)．解析探照灯、车灯、台灯的光线是由光源发出的光线，是中心投影；太阳、月亮距离地球很远，我们认为是平行光线，因此不是中心投影，故答案为①②⑤.答案①②⑤5．一几何体的直观图如图所示，下列给出的四个俯视图中正确的是________(填序号)．解析该几何体是组合体，上面的几何体是一个五面体，下面是一个长方体，且五面体的一个面即为长方体的一个面，五面体最上面的棱的两端点在底面的射影距左右两边距离相等，因此填②.答案②6．根据以下三视图想象物体原形，并画出物体的实物草图．解(1)此几何体上面为圆柱，下面为圆台，实物草图如图①.(2)此几何体上面为圆锥，下面为圆柱，实物草图如图②.能力提升7．某四棱锥的三视图如图所示，则该四棱锥的最长棱的长度为()A．32B．23C．22D．2解析由三视图知可把四棱锥放在一个正方体内部，四棱锥为D－BCC1B1，最长棱为DB1＝DC2＋BC2＋BB21＝4＋4＋4＝2 3.故选B.答案B8．如图，E，F分别为正方体的面ADD1A1、面BCC1B1的中心，则四边形BFD1E 在该正方体的面上的射影可能是()A．①②③B．②③C．①②④D．②④解析因为正方体是对称的几何体，所以四边形BFD1E在该正方体的面上的射影可分为：自上而下、自左至右、由前及后三个方向的射影，也就是在面ABCD、面BCC1B1、面DCC1D1上的射影．四边形BFD1E在面ABCD和面DCC1D1上的射影相同，如图②所示；四边形BFD1E在该正方体的对角面ABC1D1内，它在面BCC1B1上的射影显然是一条线段，如图③所示．故②③正确．答案B9．如图，在正方体ABCD－A1B1C1D1中，点P是上底面A1B1C1D1内一动点，则三棱锥P－ABC的正视图与侧视图的面积的比值为________．解析依题意得三棱锥P－ABC的正视图与侧视图分别是一个三角形，且这两个三角形的底边长都等于正方体的棱长，底边上的高也都等于正方体的棱长，因此三棱锥P－ABC的正视图与侧视图的面积的比值为1.答案110.某圆柱的高为2，底面周长为16，其三视图如图.圆柱表面上的点M在正视图上的对应点为A，圆柱表面上的点N在侧视图上的对应点为B，则在此圆柱侧面上，从M到N的路径中，最短路径的长度为________.解析由三视图可知，该几何体为如图①所示的圆柱，该圆柱的高为2，底面周长为16.画出该圆柱的侧面展开图，如图②所示，连接MN，则MS＝2，SN＝4，则从M到N的路径中，最短路径的长度为MS2＋SN2＝22＋42＝2 5.答案2511．画出下列几何体的三视图．解题图①为正六棱柱，可按棱柱的画法画出，其三视图如图a；题图②为一个圆锥与一个圆台的组合体，按圆锥、圆台的三视图画出它们的组合形状，其三视图如图b.创新突破12．一个物体由几块相同的小正方体组成，其三视图如图所示，试据图回答下列问题：(1)该物体有多少层？(2)该物体的最高部分位于哪里？(3)该物体一共由几个小正方体构成？解(1)该物体一共有两层，从正视图和侧视图都可以看出来．(2)该物体最高部分位于左侧第一排和第二排．(3)从侧视图及俯视图可以看出，该物体前后一共三排，第一排左侧2个，右侧1个；第二排左侧2个，右侧没有；第三排左侧1个，右侧1个．该物体一共由7个小正方体构成．。

高中数学必修2第1页 解密佛山吉红勇老师扣扣：一0七669八11高中数学必修二1.21-1.2.2《中心投影与平行投影与空间几何体的三视图》【知识要点】1、中心投影与平行投影（重点）（1）平行投影的概念： （2）平行投影的性质：性质1．直线或线段的平行投影仍是直线或线段； 性质2．平行直线的平行投影是平行或重合的直线； 性质3．平行于投射面的线段，它的投影与这条线段平行且等长；性质4．与投射面平行的平面图形，它的投影与这个图形全等； 性质5．在同一直线或平行直线上，两条线段平行投影的比等于这两条线段的比．2、空间几何体的三视图①正投影：在平行投影中，如果投射线与投射面垂直，这样的平行投影叫做正投影． ②三视图：主视图： 俯视图： 左视图： ③三视图：将空间图形向这三个平面做正投影，然后把三个投影按右图所示的布局放在一个水平面内，这样构成的图形叫空间图形的三视图．④三视图的基本原则：“主左一样高，主俯一样长，俯左一样宽”． 3、简单组合体的三视图【范例析考点】考点一．中心投影与平行投影例1：正方体ABCD-A 1B 1C 1D 1中，E,F 分别是A 1A ，C 1C 的中点，则下列判断正确的有（1）四边形BFD 1E 在底面ABCD 内的投影是正方形； （2）四边形BFD 1E 在面A 1D 1DA 内的投影是菱形；（3）四边形BFD 1E 在面A 1D 1DA 内的投影与在面ABB 1A 1内的投影是全等的平行四边形. 【针对练习】1、下列说法正确的是（ ）A 水平放置的正方形的直观图可能是梯形B 两条相交直线的直观图可能是平行直线C 平行四边形的直观图仍然是平行四边形D 互相垂直的两条直线的直观图仍然互相垂直 2、两条相交直线的平行投影是（ ）A 两条相交直线B 一条直线C 一条折线D 两条相交直线或一条直线3、有下列结论：①角的水平放置的直观图一定是角②相等的角在直观图中仍然相等③相等的线段在直观图中仍然相等④若两条线段平行，则在直观图中对应的两条线段仍然平行 其中正确的是————————————4、①如果一个几何体的三视图是完全相同的，则这个几何体一定是正方体。

1.2.1 中心投影与平行投影122 空间几何体的三视图1.2.1 中心投影与平行投影122 空间几何体的三视图②通过观察和自己的认识，你是怎样来理解投影的含义的④图2（2）（3）都是平行投影，它们有什么区别？⑤观察图3,与投影面平行的平面图形，分别在平行投影和中心投影下的影子和原图形的形状、大小有什么区别？活动：①教师介绍中国的民间艺术皮影戏，学生观察图片②从投影的形成过程来定义•③从投影方向上来区别这三种投影•④根据投影线与投影面是否垂直来区别•⑤观察图3并归纳总结它们各自的特点•讨论结果：①这种现象我们把它称为是投影•②由于光的照射，在不透明物体后面的屏幕上可以留下这个物体的影子，这种现象叫做投影•其中，我们把光线叫做投影线，把留下物体影子的屏幕叫做投影幕.③图2（1）的投影线交于一点，我们把光由一点向外散射形成的投影称为中心投影；图2（2）和（3）的投影线平行，我们把在一束平行光线照射下形成投影称为平行投影•④图2（ 2）中，投影线正对着投影面，这种平行投影称为正投影；图2（3）中，投影线不是正对着投影面，这种平行投影称为斜投影⑤在平行投影下，与投影面平行的平面图形留下的影子和原平面图形是全的三视图和直观图• 知识归纳：投影的分类如图提出问题①在初中，我们已经学习了正方体、长方体、圆柱、圆锥、球的三视图，请你回忆三视图包含哪些部分?②正视图、侧视图和俯视图各是如何得到的?③一般地，怎样排列三视图?④正视图、侧视图和俯视图分别是从几何体的正前方、正左方和正上你能得出同一个几何体的正视图、侧视图和俯视图在形状、大小方面的关系吗?讨论结果：①三视图包含正视图、侧视图和俯视图②光线从几何体的前面向后面正投影，得到的投影图叫该几何体的正视图（又称主视图）；光线从几何体的左面向右面正投影，得到的投影图叫该几何体的侧视图（又称左视图）；光线从几何体的上面向下面正投影，得到的投影图叫该几何体的俯视图③三视图的位置关系：一般地，侧视图在正视图的右边；俯视图在正视图的下边•如图5 所示.俯视图等的平面图形；在中心投影下, 与投影面平行的平面图形留下的影子和原平面图形是相似的平面图形.以后我们用正投影的方法来画出空间几何体方观察到的几何体的正投影图，它们都是平面图形.观察长方体的三视图,4所示.图4点评：本题主要考查简单几何体的三视图和空间想象能力 •有关三视图的题目往往依赖于丰富的空间想象能力 •要做到边想着几何体的实物图边画 着三视图，做到想图（几何体的实物图）和画图（三视图）相结合 变式训练说出下列图7中两个三视图分别表示的几何体例2试画出图8所示的矿泉水瓶的三视图活动：引导学生认识这种容器的结构特征 •矿泉水瓶是我们熟悉的一种容 器，这种容器是简单的组合体，其主要结构特征是从上往下分别是圆柱、 圆台和圆柱解：图6 （1）是圆柱的三视图，图 疋视圏 侧观图答案: 图7（ 1）是正六棱锥；图 7（ 2）是两个相同的圆台组成的组合体 正观图 测視图 正视图 测观图俯视图 俯观图正视圈侧视图俯视图图8解：三视图如图9所示.点评：本题主要考查简单组合体的三视图•对于简单空间几何体的组合体, 一定要认真观察，先认识它的基本结构，然后再画它的三视图变式训练图10 图11答案：三视图如图11 所示.课堂小结：本节课学习了：1.中心投影和平行投影•2.简单几何体和组合体的三视图的画法及其投影规律3.由三视图判断原几何体的结构特征.布置作业：习题1.2 A组第1、2题.。

1.2.1 中心投影与平行投影~1.2.2 空间几何体的三视图知识点一中心投影与平行投影提出问题《泰坦尼克号》是一部浪漫的爱情灾难电影，于1997年11月1日，在全球上映，票房收入超过18亿美元，并获得了多项奥斯卡奖项.15年之后，《泰坦尼克号》再次被搬上了荧屏，而这次的宣传噱头则是3D.《泰坦尼克号(3D)》让观众在明知下一步剧情发展的情况下，仍然会因为发生在“眼前”的真实爱情悲歌热泪盈眶．从上图中我们可以清楚地看到3D电影是怎么一回事：两个投影机会从不同的方向错开一定距离，把画面中有距离区别的部分投射到荧幕上．而观众所佩戴的3D眼镜也会选择不同的光线进入左右眼，这样你就能看到物体“前于画面”或“后于画面”的视觉假象了．电影的播放实质是利用了小孔成像原理，而太阳光下地面上人的影子是阳光照射到人后留下的影像．放电影和太阳光照射成影像都具备光线、不透明物体和投影面这些相同的条件．问题1：放电影成像与太阳光照射成像原理一样吗？问题2：放电影成像中的光线有何特点？问题3：太阳光照人成影像的光线又有何特点？导入新知1．投影的定义由于光的照射，在物体后面的屏幕上可以留下这个物体的，这种现象叫做投影．其中，把叫做投影线，把的屏幕叫做投影面．2．中心投影与平行投影平行投影和中心投影都是空间图形的一种画法，但二者又有区别 (1)中心投影的投影线交于一点，平行投影的投影线互相平行．(2)平行投影下，与投影面平行的平面图形留下的影子，与这个平面图形的形状和大小完全相同；而中心投影则不同． 知识点二 三视图 提出问题如梦似幻！——这是无数来自全世界的游客对国家游泳中心“水立方”的第一印象．同天安门、故宫、长城等北京标志性建筑一样，“水立方”成了游客在北京的必到之地．问题1：“水立方”的外观形状是什么？问题2：假如你站在“水立方”入口处的正前方或在“水立方”的左侧看“水立方”，你看到的是什么？问题3：若你在“水立方”的正上方观察“水立方”看到的是什么？问题4：根据上述三个方向观察到的平面，能否画出“水立方”的形状？ 导入新知1．每个视图都反映物体两个方向上的尺寸．正视图反映物体的上下和左右尺寸，俯视图反映物体的前后和左右尺寸，侧视图反映物体的前后和上下尺寸．2．画几何体的三视图时，能看见的轮廓线和棱用实线表示，看不见的轮廓线和棱用虚线表示．考点突破题型一中心投影与平行投影例1下列说法中：①平行投影的投影线互相平行，中心投影的投影线相交于一点；②空间图形经过中心投影后，直线变成直线，但平行线可能变成了相交的直线；③两条相交直线的平行投影是两条相交直线．其中正确的个数为()A．0B．1C．2 D．3类题通法1．判定几何体投影形状的方法．(1)判断一个几何体的投影是什么图形，先分清楚是平行投影还是中心投影，投影面的位置如何，再根据平行投影或中心投影的性质来判断．(2)对于平行投影，当图形中的直线或线段不平行于投影线时，平行投影具有以下性质：①直线或线段的投影仍是直线或线段；②平行直线的投影平行或重合；③平行于投影面的线段，它的投影与这条线段平行且等长；④与投影面平行的平面图形，它的投影与这个图形全等；⑤在同一直线或平行直线上，两条线段平行投影的比等于这两条线段的比．2．画出一个图形在一个平面上的投影的关键是确定该图形的关键点，如顶点、端点等，方法是先画出这些关键点的投影，再依次连接各投影点即可得此图形在该平面上的投影．活学活用1.如图，在正方体ABCD ­A′B′C′D′中，E，F分别是A′A，C′C的中点，则下列判断正确的序号是________．①四边形BFD′E在底面ABCD内的投影是正方形；②四边形BFD′E在平面A′D′DA内的投影是菱形；③四边形BFD′E在平面A′D′DA内的投影与在平面ABB′A内的投影是全等的平行四边形．题型二画空间几何体的三视图例2画出如图所示的四棱锥的三视图．类题通法画三视图的注意事项(1)务必做到长对正，宽相等，高平齐．(2)三视图的安排方法是正视图与侧视图在同一水平位置，且正视图在左，侧视图在右，俯视图在正视图的正下方．(3)若相邻两物体的表面相交，表面的交线是它们的分界线，在三视图中，要注意实、虚线的画法．活学活用2.沿一个正方体三个面的对角线截得的几何体如图所示，则该几何体的侧视图为()题型三由三视图还原空间几何体例3如图所示的三视图表示的几何体是什么？画出物体的形状．(1)(2)(3)类题通法由三视图还原几何体时，一般先由俯视图确定底面，由正视图与侧视图确定几何体的高及位置，同时想象视图中每一部分对应实物部分的形状．活学活用3.如图(1)(2)(3)(4)为四个几何体的三视图，根据三视图可以判断这四个几何体依次分别为()A．三棱台、三棱柱、圆锥、圆台B．三棱台、三棱锥、圆锥、圆台C．三棱柱、正四棱锥、圆锥、圆台D．三棱柱、三棱台、圆锥、圆台随堂即时演练1.将一个长方体沿相邻三个面的对角线截去一个棱锥，得到的几何体的正视图与俯视图如图所示，则该几何体的侧(左)视图为()2.如图，在正方体ABCD­A1B1C1D1中，M，N分别是BB1，BC的中点，则图中阴影部分在平面ADD1A1上的投影为()3．直线的平行投影可能是________．4.如图，在多面体ABC­A′B′C′中，底面ABC为正三角形，三条侧棱AA′，BB′，CC′分别平行，侧棱垂直于底面ABC，且3AA′＝32BB′＝CC′＝AB，则下面图形可视为多面体ABC­A′B′C′的正视图的是________．5．画出如图所示几何体的三视图．参考答案知识点一中心投影与平行投影问题1：【答案】不一样．问题2：【答案】光是由一点向外散射．问题3：【答案】一束平行光线．导入新知1．不透明影子光线留下物体影子2．一点交于一点平行光线互相平行正投影斜投影知识点二三视图问题1：【答案】长方体．问题2：【答案】“水立方”的一个侧面．问题3：【答案】“水立方”的一个表面．问题4：【答案】可以．导入新知前面后面左面右面上面下面高度长度宽度考点突破题型一中心投影与平行投影例1【答案】B活学活用1. 【答案】①③题型二画空间几何体的三视图例2解：几何体的三视图如下：活学活用2.【答案】B题型三由三视图还原空间几何体例3解：(1)该三视图表示的是一个四棱台，如图．(2)由俯视图可知该几何体是多面体，结合正视图、侧视图可知该几何体是正六棱锥．如下图．(3)由于俯视图有一个圆和一个四边形，则该几何体是由旋转体和多面体拼接成的组合体，结合侧视图和正视图，可知该几何体上面是一个圆柱，下面是一个四棱柱，所以该几何体的形状如图所示．活学活用3. 【答案】C随堂即时演练1. 【答案】B2. 【答案】A3．【答案】直线或点4. 【答案】④5．解：图①为正六棱柱，可按棱柱的画法画出；图②为一个圆锥与一个圆台的组合体，按圆锥、圆台的三视图画出它们的组合形状．三视图如图所示．。

1.2.1 中心投影与平行投影~1.2.2 空间几何体的三视图一、选择题1．给出下列命题，其中正确命题的个数是()①如果一个几何体的三视图是完全相同的，则这个几何体是正方体；②如果一个几何体的正视图和俯视图都是矩形，则这个几何体是长方体；③如果一个几何体的三视图都是矩形，则这个几何体是长方体；④如果一个几何体的正视图和侧视图都是等腰梯形，则这个几何体是圆台．A．0 B．1 C．2 D．32．某几何体及其俯视图如图所示，下列关于该几何体正视图和侧视图的画法正确的是()3．甲、乙两足球队决赛互罚点球时，罚球点离球门约10米，乙队守门员违例向前冲出了3米，扑住了球，结果被判犯规，扑球无效．事实上乙队守门员违例向前冲出了3米时，其要封堵的区域面积变小了．此时乙队守门员需封堵的区域面积是原来球门面积的()A．310B．710C．9100D．491004．如图所示，下列几何体各自的三视图中，有且仅有两个视图相同的是()A．①②B．①③C．①④D．②④5．如图，在底面边长为1，高为2的正四棱柱ABCD－A1B1C1D1中，点P是平面A1B1C1D1内一点，则三棱锥P－BCD的正视图与侧视图的面积之和为()A．2 B．3 C．4 D．56．下图是一个物体的三视图，则该物体对应的形状是()7．中央电视台有一个非常受欢迎的娱乐节目：墙来了！选手需按墙上的空洞造型摆出相同姿势，才能穿墙而过，否则会被墙推入水池．类似地，有一个几何体恰好无缝隙地以三个不同形状的“姿势”穿过“墙”上的三个空洞，则该几何体为()二、填空题8．如图，网格纸的各小格都是正方形，粗实线画出的是一个几何体的三视图，则这个几何体是________．9．若线段AB平行于投影面，O是AB上一点，且AO∶OB＝m∶n，则O的平行投影O′分AB的平行投影A′B′的长度之比为________．10．如图所示，正三棱柱ABC－A1B1C1的正视图是边长为4的正方形，则此正三棱柱的侧视图的面积为________．三、解答题11．画出图中几何体的三视图．12．如右图是由几个小立方块所搭几何体的俯视图，小正方形中的数字表示在该位置上的小立方块的个数，请画出这个几何体的正视图、侧视图．【参考答案】一、选择题1．【答案】B【解析】①中也可以是球，②横放的圆柱也可能是正视图和俯视图都是矩形，③正确，④中正四棱台也可以．2．【答案】A【解析】该几何体是由圆柱切割而得，如图1所示．由俯视图可知正视方向和侧视方向(如图1所示)，进一步可画出正视图和侧视图(如图2所示)，故选A ．3．【答案】D【解析】如图，从罚球点S 向球门ABCD 四个顶点引线，构成四棱锥S －ABCD ，守门员从平面ABCD 向前移动3米至平面A ′B ′C ′D ′，只需封堵区域A ′B ′C ′D ′即可，故S A′B′C′D′S ABCD ＝⎝⎛⎭⎫7102＝49100． 4．【答案】D【解析】在各自的三视图中，①正方体的三个视图都相同；②圆锥有两个视图相同；③三棱台的三个视图都不同；④圆台有两个视图相同．5．【答案】A【解析】该三棱锥的正视图的面积为S 1＝12×1×2＝1，侧视图的面积为S 2＝12×1×2＝1，所以其正视图与侧视图的面积之和为S＝S1＋S2＝2．故选A．6．【答案】C【解析】根据俯视图，A，C，D均符合；再根据正视图，只有C符合．7．【答案】A【解析】由题意知，图中正方形、圆形、三角形对应某几何体的三视图，结合选项中给出的图形分析可知，A中几何体满足要求．故选A．二、填空题8．【答案】三棱柱【解析】由三视图可得此几何体为底面是等腰直角三角形的棱柱．9．【答案】m∶n【解析】因为AB平行于投影面，所以A′B′与AB平行且相等，O′的相对位置不发生改变，把A′B′分成m∶n的两部分．10．【答案】83【解析】此三棱柱的侧视图的面积S＝4×32×4＝83．三、解答题11．解：该几何体的三视图如图所示．12．解：。

1.2.1 中心投影与平行投影~1.2.2 空间几何体的三视图1．投影的概念及分类思考：画三视图时一定要求光线与投射面垂直吗？初试身手1．哪个实例不是中心投影()A．工程图纸B．小孔成像C．相片D．人的视觉2．如图，小华拿一个矩形木框在阳光下玩，矩形木框在地面上形成的投影不可能是()A B C D3．有一个几何体的三视图如图所示，这个几何体应是一个________．4．水平放置的下列几何体，正视图是长方形的是________．(填序号)①②③④合作探究A．矩形的平行投影一定是矩形B．梯形的平行投影一定是梯形C．两条相交直线的投影可能平行D．一条线段的中点的平行投影仍是这条线段投影的中点(2)如图所示，在正方体ABCD­A1B1C1D1中，M、N分别是BB1、BC的中点，则图中阴影部分在平面ADD1A1上的正投影是()A B C D【规律方法】判断几何体投影形状的方法及画投影的方法：(1)判断一个几何体的投影是什么图形，先分清楚是平行投影还是中心投影，投影面的位置如何，再根据平行投影或中心投影的性质来判断．(2)画出一个图形在一个平面上的投影的关键是确定该图形的关键点，如顶点、端点等，方法是先画出这些关键点的投影，再依次连接各投影点即可得出此图形在该平面上的投影．跟踪训练1．已知△ABC，选定的投影面与△ABC所在平面平行，则经过中心投影后所得的△A′B′C′与△ABC()A．全等B．相似C．不相似D．以上都不对()(2)画出如图所示几何体的三视图：①②【规律方法】1．画组合体三视图的“四个步骤”(1)析：分析组合体的组成形式；(2)分：把组合体分解成简单几何体；(3)画：画分解后的简单几何体的三视图；(4)拼：将各个三视图拼合成组合体的三视图．2．画三视图时要注意的“两个问题”(1)务必做到“正侧一样高，正俯一样长，俯侧一样宽”．(2)把可见轮廓线画成实线，不可见轮廓线要画成虚线，重合的线只画一条．跟踪训练2．螺栓是棱柱和圆柱构成的组合体，如图，画出它的三视图．1．如何由三视图确定几何体的长、宽、高？2．如图所示的三视图，其几何体是什么？其正视图、侧视图中的三角形的腰是几何体的侧棱长吗？例3(1)若一个几何体的正视图和侧视图都是等腰三角形，俯视图是带圆心的圆，则这个几何体可能是()A．圆柱B．三棱柱C．圆锥D．球体(2)若某几何体的三视图如图所示，则这个几何体的直观图可以是()A B C D【规律方法】由三视图确定几何体一般分两步：第一步：通过正视图和侧视图确定是柱体、锥体还是台体．若正视图和侧视图为矩形，则原几何体为柱体；若正视图和侧视图为等腰三角形，则原几何体为锥体；若正视图和侧视图为等腰梯形，则原几何体为台体．第二步：通过俯视图确定是多面体还是旋转体．若俯视图为多边形，则原几何体为多面体；若俯视图为圆，则原几何体为旋转体．跟踪训练3．根据下列图中所给出的几何体的三视图，试画出它们的形状．①②课堂小结1．三视图的正视图、侧视图、俯视图是分别从几何体的正前方、正左方、正上方观察几何体画出的轮廓线，画几何体三视图的要求是正视图、俯视图长对正，正视图、侧视图高平齐，俯视图、侧视图宽相等，前后对应，画出的三视图要检验是否符合“长对正、高平齐、宽相等”的基本特征．2．画组合体的三视图的步骤特别提醒：画几何体的三视图时，能看见的轮廓线和棱用实线表示，看不见的轮廓线和棱用虚线表示．当堂达标1．中心投影的投影线()A．相互平行B．交于一点C．是异面直线D．在同一平面内2．如图网格纸的各小格都是正方形，粗实线画出的是一个几何体的三视图，则这个几何体是()A．三棱锥B．三棱柱C．四棱锥D．四棱柱3．一个正三棱柱(俯视图为正三角形)的三视图如图所示，则这个三棱柱的高和底面边长分别为________．4．画出如图所示的几何体的三视图．参考答案新知初探1．影子投影线投影面一点一点平行平行正对2.思考：[提示]正确．由画三视图的规则要求可知正确．初试身手1．【答案】A【解析】根据中心投影的概念可知A不是中心投影．2．【答案】A【解析】矩形的投影可以是线段，矩形，平行四边形，但不会是梯形．3．【答案】棱台【解析】从俯视图来看，上、下底面都是正方形，但大小不一样，可以判断是棱台．4．【答案】③④【解析】①③④的正视图均是长方形，②是等腰三角形．合作探究【解析】矩形的平行投影可能是线段、平行四边形或矩形，梯形的平行投影可能是线段或梯形，两条相交直线的投影还是相交直线．因此A、B、C均错，故D正确．(2)【答案】A【解析】由正投影的定义知，点M、N在平面ADD1A1上的正投影分别是AA1、DA的中点，D在平面ADD1A1上的投影还是D，因此A正确．跟踪训练1．【答案】B【解析】本题主要考查对中心投影的理解．根据题意画出图形，如图所示．由图易得OAOA′＝ABA′B′＝OBOB′＝BCB′C′＝OCOC′＝ACA′C′，则△ABC∽△A′B′C′.【解析】依题意，侧视图中棱的方向是从左上角到右下角．故选B.(2) [解]①此几何体的三视图如图③所示；②此几何体的三视图如图④所示．①④跟踪训练2．[解]它的三视图如图所示．类型3由三视图还原几何体1．[提示]由正视图可确定几何体的长、高；由俯视图可确定几何体的宽．2．[提示]由三视图可知，该几何体为正四棱锥，如图所示．正视图、侧视图中三角形的腰长不是四棱柱的侧棱长，应为四棱椎的侧面高线．【例3】【答案】(1) C【解析】正视图和侧视图都是等腰三角形，俯视图是带圆心的圆说明此几何体是圆锥．(2)【答案】D【解析】对于选项A，B，正视图均不符合要求；对于选项C，俯视图显然不符合要求．只有D符合要求．跟踪训练3．[解]由三视图的特征，结合柱、锥、台、球及简单组合体的三视图逆推．图①对应的几何体是一个正六棱锥，图②对应的几何体是一个三棱柱，则所对应的空间几何体的图形分别如下：当堂达标1．【答案】B【解析】由中心投影的定义知，中心投影的投影线交于一点，故选B.2．【答案】B【解析】由题意知，该几何体的三视图为一个三角形，两个四边形，经分析可知该几何体为三棱柱．3．【答案】2，4【解析】由正三棱柱三视图中的数据，知三棱柱的高为2，底面边长为23×23＝4.4．[解]该几何体的三视图如图所示．。

§1.2空间几何体的三视图和直观图1.2.1中心投影与平行投影1.2.2空间几何体的三视图一、选择题1.已知△ABC，选定的投影面与△ABC所在平面平行，则经过中心投影后所得的三角形与△ABC()A.全等B.相似C.不相似D.以上都不正确考点中心投影题点中心投影的判断与应用答案 B解析中心投影的投影线交于一点，几何体在这种投影下的形状相似.2.关于几何体的三视图，下列说法正确的是()A.正视图反映物体的长和宽B.俯视图反映物体的长和高C.侧视图反映物体的高和宽D.正视图反映物体的高和宽答案 C3.如图是一个物体的三视图，则此三视图所描述的物体的直观图是()答案 D4.将长方体截去一个四棱锥，得到的几何体如图所示，则该几何体的侧视图为()考点简单组合体的三视图题点切割形成几何体的三视图答案 D解析从左往右看，主体的轮廓是一个长方形，长方体的对角线可以看见，且该对角线是从左下角往右上角倾斜的.5.一几何体的直观图如图，下列给出的四个俯视图中正确的是()答案 B6.已知三棱柱的侧棱与底面垂直，且底面是边长为2的等边三角形.若三棱柱的正视图(如图所示)的面积为8，则侧视图的面积为()A.8B.4C.4 3D.2 3考点多`面体的三视图题点棱柱的三视图答案 C解析设该三棱柱的侧棱长为a，则2a＝8，所以a＝4，该三棱柱的侧视图是一个矩形，一边长为4，另一边长等于三棱柱底面等边三角形的高，即为3，所以侧视图的面积为43，故选C.7.一个长方体去掉一角，如图所示，关于它的三视图，下列画法正确的是( )考点 简单组合体的三视图 题点 切割形成几何体的三视图 答案 A解析 由于去掉一角后，出现了一个小三角形的面.正视图中，长方体上底面和右边侧面上的三角形的两边的正投影分别和矩形的两边重合，故A 对，B 错；侧视图中的线应是虚线，故C 错；俯视图中的线应是实线，故D 错.8.一个锥体的正视图和侧视图如图所示，下面选项中，不可能是该锥体的俯视图的是( )答案 C解析 注意到在三视图中，俯视图的宽度应与侧视图的宽度相等，而在选项C 中，其宽度为32，与题中所给的侧视图的宽度1不相等，故选C. 二、填空题9.如图，在多面体ABC －A ′B ′C ′中，底面ABC 为正三角形，三条侧棱AA ′，BB ′，CC ′分别平行，侧棱垂直于底面ABC ，且3AA ′＝32BB ′＝CC ′＝AB ，则下面图形可视为多面体ABC －A ′B ′C ′的正视图的是________.答案 ④10.如图，在正方体ABCD －A 1B 1C 1D 1中，点P 是上底面A 1B 1C 1D 1内一动点，则三棱锥P －ABC 的正视图与侧视图的面积的比值为________.考点 多面体的三视图 题点 棱锥的三视图 答案 1解析 依题意得三棱锥P －ABC 的正视图与侧视图分别是一个三角形，且这两个三角形的一条边长都等于正方体的棱长，这条边上的高也都等于正方体的棱长，因此三棱锥P －ABC 的正视图与侧视图的面积的比值为1.11.一个几何体的三视图如图所示，则其侧视图的面积为________.考点 简单组合体的三视图题点 其他柱、锥、台、球组合的三视图 答案 4＋ 3解析 依题意得几何体的侧视图面积为22＋12×2×3＝4＋ 3.12.已知某几何体的正视图和侧视图均如图所示，给出下列5个图形；其中可以作为该几何体的俯视图的图形个数是________.答案 4解析④不可以，因为等边三角形的边与高不等，所以正视图和侧视图不相同.其余4个图都可以作为俯视图，故其中可以作为该几何体的俯视图的图形个数是4.三、解答题13.画出所给几何体的三视图.考点多面体的三视图题点多面体的三视图解题图①为正六棱柱，可按棱柱的画法画出，其三视图如图a；题图②为一个圆锥与一个圆台的组合体，按圆锥、圆台的三视图画出它们的组合形状，其三视图如图b.14.将正方体(如图(1)所示)截去两个三棱锥，得到如图(2)所示的几何体，则该几何体的侧视图为下列选项中的()考点多面体的三视图题点多面体的三视图答案 B解析显然从左边看到的是一个正方形，因为割线AD1可见，所以用实线表示；而割线B1C 不可见，所以用虚线表示.故选B.15.一个物体由几块相同的正方体组成，其三视图如图所示，试据图回答下列问题：(1)该物体有多少层？(2)该物体的最高部分位于哪里？(3)该物体一共由几个小正方体构成？考点由三视图还原实物图题点由正(长)方体组合的三视图还原实物图解(1)该物体一共有两层，从正视图和侧视图都可以看出来.(2)该物体最高部分位于左侧第一排和第二排.(3)从侧视图及俯视图可以看出，该物体前后一共三排，第一排左侧2个，右侧1个；第二排左侧2个，右侧没有；第三排左侧1个，右侧1个.该物体一共由7个小正方体构成.。