第四章 核磁共振波谱
- 格式:ppt
- 大小:837.01 KB
- 文档页数:47





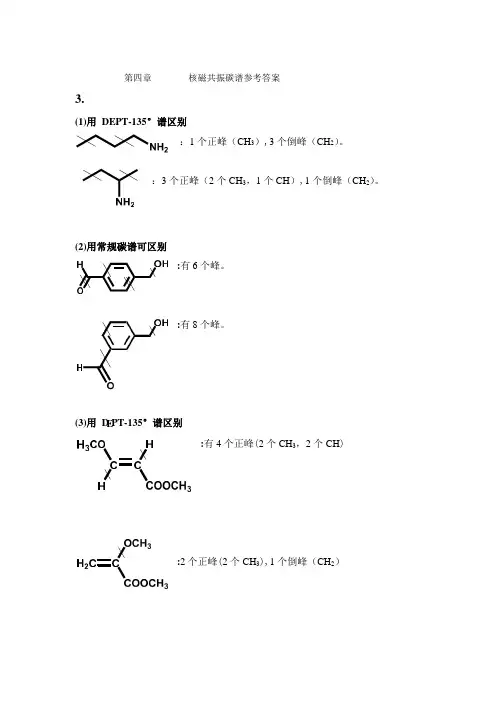
E : (3)用 D PT-135°谱区别 第四章 核磁共振碳谱参考答案3.(1)用 DEPT-135°谱区别:1 个正峰(CH 3),3 个倒峰(CH 2)。
:3 个正峰(2 个 CH 3,1 个CH ),1 个倒峰(CH 2)。
(2)用常规碳谱可区别:有 6 个峰。
有 8 个峰。
:有 4 个正峰(2 个 CH 3,2 个 CH ):2 个正峰(2 个 CH 3),1 个倒峰(CH 2)6.1)由分子式C5H9O2Br 计算不饱和度Ω=1,结构中可能含一个双键或一个环。
2)1H NMR 解析:1.25(t):CH x-CH2- ;2.85(t): 弱吸电子基团-CH y-CH2- ;3.55(t): 弱吸电子基团-CH z-CH2- ;4.20(q): -CO2-CH m-CH3(该基团CH m必定与吸电子基团相连。
根据化学位移和分子式可初步判断是与酯基氧原子相连) 3)13C NMR 解析:共有五条峰,与结构式中碳数一致,说明分子中不含对称元素。
178.2(s): 羧酸或其衍生物的C=O;60.8(t): -CH2-,与氧原子相连37.8(s): -CH2-,可能与弱吸电子原子相连26.5(t): -CH2-,可能与弱吸电子原子相连14.2(q): -CH34)推断过程:碳谱表明分子中有1 个羰基,3 个亚甲基和1 个甲基,因此氢谱中4.20ppm 处必定为亚甲基,所以分子中含CO2CH2CH3片段,再结合氢谱,该片段中CH3出峰应该在1.25ppm 处。
这样一来,可以进一步推断2.85 和3.55ppm 处的信号必然是剩余两个亚甲基,由于都为t 峰,这两个亚甲基必定相连,所以推测出分子含有片段CH2CH2,且两端都连有弱吸电子基团。
至此,分子中含有如下片段:一个B(r(端基),因此该化合物的结构为:端基),一个CH2CH2,一个CO2CH2CH38.1)由分子式C8H5NO2可算出不饱和度Ω=7,结构中可能含有苯环。



核磁共振波谱法第四章核磁共振波谱法核磁共振(Nuclear Magnetic Resonance NMR)波谱学是近几十年发展的一门新学科。
1945年以F.Block和E.M.Purcell为首的两个研究小组分别观测到水、石蜡中质子的核磁共振信号,为此他们荣获1952年Nobe1物理奖。
今天,核磁共振已成为化学、物理、生物、医药等研究领域中必不可少的实验工具,是研究分子结构、构型构象、分子动态等的重要方法。
第一节核磁共振基本原理一、核的自旋运动和NMR现象(一)原子核的自旋与原子核的磁矩核磁共振研究的对象是具有磁矩的原子核。
原子核是由质子和中子组成的带正电荷的粒子,其自旋运动将产生磁矩。
但并非所有同位素的原子核都具有自旋运动,只有存在自旋运动的原子核才具有磁矩。
原子核的自旋运动与自旋量子数I相关。
量子力学和实验均已证明,I与原子核的质量数(A)、核电荷数(Z)有关。
I为零、半整数、整数。
A为偶数、Z为偶数时,I=0。
如12C6,16O8,32S16等。
A为奇数、Z为奇数或偶数时,I为半整数。
如1H1,13C6,15N7,19F9,31P15等I = 1/2;11B,33S16,35C117,37C117,81Br35等I =3/2;17O8,25Mg12,27Al13等I =5/2。
5A为偶数、Z为奇数时,I为整数。
如2H1,6Li3,14N7等I =1;58Co27等I = 2;10B5等I =3。
I ≠ 0的原子核,都具有自旋现象,其自旋角动量(P)为P = h/2π I( I + 1),h为普朗克常数 6.624 ? 10-34 J.S具有自旋角动量的原子核也具有磁矩μ,μ与P的关系如下:μ=γ.Pγ称磁旋比(magnetogyric ratio)。
同一种核,γ为常数。
如1H:γ=2.6752 ? 108rad T-1S-1);13C:γ=6.728(107rad T-1S-1);T =104高斯。

