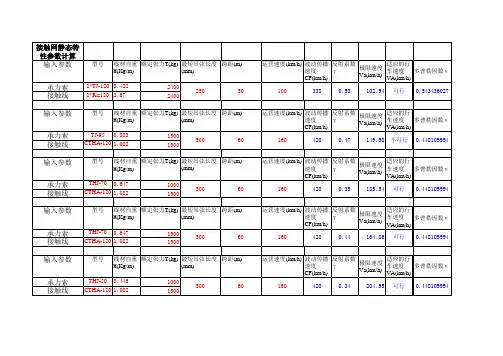
接触网计算公式

接触网常用计算公式附件一、接触网常用计算公式：1.平均温度t p和链形悬挂无弛度温度t o的计算t max+t min①t p=2t max+t min②t o弹= －52t max+t min③t o简= －102式中t p—平均温度℃（即吊弦、定位处于无偏移状态的温度）；t o弹、t o简—分别表示弹性链形悬挂和简单链形悬挂的无弛度温度℃；t max—设计最高温度℃；t min—设计最低温度℃；2.当量跨距计算公式n∑L I3LD= i=1n∑L I√ i=1式中L D—锚段当量跨距（m）；n∑L I3=（L13+ L23+……+ L n3）—锚段中各跨距立方之和；i=1n∑L I=（L1+ L2+……+ L n）—锚段中各跨距之和；i=13.定位肩架高度B的计算公式B≈H+e+I（h/d+1/10）h/2式中B—肩架高度（mm）；H—定位点处接触线高度（mm）；e—支持器有效高度（mm）；I—定位器有效长度（包括绝缘子）（mm）；d—定位点处轨距（mm）；h—定位点外轨超高（mm）；4.1 接触线拉出值a地的计算公式Ha地=a－ hd式中a地—拉出值标准时，导线垂直投影与线路中心线的距离（mm）。

a地为正时导线的垂直投影应在线路的超高侧，a地为负时导线的垂直投影应在线路的低轨侧。

H—定位点接触线的高度（mm）；a—导线设计拉出值（mm）；h—外轨超高（mm）；d—轨距（mm）；4.2 接触线拉出值a的计算公式a=m+c式中a—接触线拉出值（mm）；m—定位点处接触线与线路中心的水平距离（mm）；C—定位点处受电弓与线路中心的水平距离（mm），由C=h*H/L确定（h为外轨超高；H为接触线高度；L为轨距）。

5.接触线定位拉出值变化量Δa max的计算公式Δa max=I z－√I2z－E2max式中Δa max—定位点拉出值的最大变化量（mm）；I z—定位装置（受温度影响）偏转的有效长度（mm）；E max—极限温度时定位器的最大偏移值（mm）；由上式可知E=0时Δa=06.定位器无偏移时拉出值a15的确定：（取平均温度t p=15℃）a15=a±1/2Δa max式中 a—导线设计拉出值（mm）；Δa max—定位点拉出值的最大变化量（mm）；a15—定位器无偏移时（即平均温度时）的拉出值（mm）。

浅谈接触网腕臂计算中常被遗忘的要点众所周知，腕臂计算是接触网三大计算之一，应用很普遍也很重要，但其中总有一些细小的问题，值得大家注意和商榷，以提高计算精度和准确性，避免在计算环节出错、造成大量材料和人力浪费。

下面结合兰新线电气化改造工程北疆线段内乌北—乌东区间腕臂计算，谈谈自己的认识：1. 平腕臂计算时斜率不容忽视，即使是等径支柱也不例外，因为不可能保持所有支柱都中心直立，总有内倾和外倾，所以要引起我们的认识；钢柱肯定有斜率。

斜率是指同一侧柱顶边缘与柱底边缘的距离与柱身外露的比值，单位为mm/m，有内倾和外倾之分导致斜率有正负之分。

当将斜率反应到上底座安装高度时，即计算平腕臂时，要将斜率乘以上底座安装高度才能真实反应出此处偏移值。

2.腕臂上底座安装高度Hs不容有错误，一般取上底座中心线距轨面的距离。

因为根据三角形相似原理，高度不同，斜率一定，高度越高，偏移值越大。

3.平腕臂计算公式：PWBZC=Cx+Hs*&-M+200，其中M=a-c 正定位用M=c-a 反定位用公式c=H*h/L其中a---表示拉出值Cx---表示侧面限界Hs---表示上底座安装高度&---表示斜率4.套管双耳有厚度，不容忽略，不能直接将腕臂上下底座高度差值代入勾股定理，但一定要将腕臂管厚度减去后代入，只有这样斜腕臂长度才有保证。

5.扣料时一定分清楚单绝缘还是双绝缘，还有亲自复核棒式绝缘子长度和套筒长度。

因为绝缘子的长度是不同的，就乌北—乌东区间而言双重绝缘子平棒瓷为850，斜棒瓷只有760。

6.定位环位置要依据导高、超高，定位管开口确定。

公式为：定位环位置=（导高+开口高度-下底座中心线）*（斜腕臂长+斜棒瓷）/（承力索位置+平棒瓷）--斜棒瓷场+90（余量）7.为了保证计算的精确度，计算时一般多保留几位小数，不因超高值小或者斜率小而舍弃。

8.平腕臂扣料时从平腕臂销钉口中心起测，斜腕臂扣料时不忘与棒式绝缘子接触的部分，留够余量，一般电子表格误差也才此处产生。

接触网风偏移值计算接触网支柱结构设计风荷载取值1.接触网风偏设计风速小于30 m/s时，接触网风偏设计风速作为接触网支柱标准容量设计风速;当接触网风偏设计风速大于30 m/s时，以30 m/s作为接触网支柱标准容量设计风速。

2.路基地段接触网结构设计风速，按l0 m高度的风压高度系数考虑风速;高度小于等于30 m的桥梁，按照30 m高度的风压高度系数考虑风速;高度大于30 m的桥梁，建议采用其他悬挂安装方式，以提高悬挂的可靠性及稳定性。

3.接触网支柱标准容量按接触网风偏设计风速计算，同时应考虑列车气动力影响，初步选择支柱截面尺寸，再采用结构设计风速校核支柱的强度，并以此最终确定支柱截面尺寸。

4.接触网支柱基础、基础螺栓按照结构设计风速进行设计。

目前所设计的国内高速铁路，如:郑西、武广、京津城际等均未设置挡风墙，海南东环线也未设置挡风墙。

因此可以认为30 m/s就是列车运行的最大限制风速，超过该风速，列车停运。

接触网支柱标准容量风速设计1.当接触网风偏设计风速小于30 m/s时，接触网风偏设计风速作为接触网支柱标准容量设计风速;2.当接触网风偏设计风速大于30m/s时，以30 m/s作为接触网支柱标准容量设计风速。

接触线最大偏移值的公式为：式中——————接触线和承力索单位长度的风负载（KN/m）；——————接触线和承力索的张力（KN/m）。

曲线区段接触线拉出值的选择在直线区段受电弓中心与线路中心重和，接触线之字值沿线路中心对称，其标准为±300mm。

提速后为200～250mm之间；拉出值350～450mm之间。

在曲线区段，拉出值和曲线半径大小有关。

接触线拉出值是接触网自身结构参数，其取值直接影响弓网运行安全。

在运营中发现曲线区段拉出值超标严重，这是因为在设置拉出值时，未考虑受电弓中心线在气象条件、线路参数、机车及受电弓型号和参数、运营方式、运行速度等多种因素影响下的动态变化。

基于此种情况，有必要对运行速度、线路参数及施工误差等几个主要影响因素进行分析，找到曲线区段受电弓中心在动态下的侧偏规律，合理设置拉出值，提高施工质量，确保机车良好受流。

Ec （伏）
静电感应电压
K 单线取0．4复线取0．6Uj 接触网对地电压 b 接触网导线距地面的高度c 临近线距地面的高度
静电感应电压的计算公式
Ec=K×Uj×(bc/a×a ＋b×b ＋c×c)×L1/L2
Ec------为临近线上的静电感应电压；
K-------为常数(单线取0．4，复线取0．6)；
Uj------为接触网对地电压，取25 kV ；
L1-----为接触网平行长度；
L2-----为临近线平行接近长度；
a-------为接触网导线与临近线在大地上投影间的距离； b-------为接触网导线距地面的高度；
c-------为临近线距地面的高度。

a 接触网导线与临近线在大地上投影间的距离L1接触网平行长度 L2临近线平行接近长度
电压的计算公式
a×a ＋b×b ＋c×c)×L1/L2
．6)；
上投影间的距离；。

接触网的接触压力计算公式随着社会的发展和科技的进步，铁路交通成为人们出行的重要方式之一。

而接触网作为电气化铁路的重要组成部分，其质量和性能直接关系到铁路运输的安全和效率。

在接触网的设计和维护过程中，接触压力是一个重要的参数，它直接影响着接触网的稳定性和安全性。

因此，了解接触压力的计算公式对于铁路工作者来说是非常重要的。

接触网的接触压力是指接触线与受电弓之间的压力，它是由受电弓对接触线的压力和接触线对受电弓的弹性变形所产生的。

接触压力的大小直接影响着接触线的磨损和受电弓的损坏，因此在设计和维护接触网时需要对接触压力进行准确的计算和控制。

接触压力的计算公式可以通过以下步骤进行推导：首先，我们需要了解接触压力的定义。

接触压力可以用受电弓的垂直载荷和接触线的弹性变形来表示，即P=F/S，其中P为接触压力，F为受电弓的垂直载荷，S为接触线的弹性变形。

其次，我们需要了解受电弓的垂直载荷和接触线的弹性变形的计算方法。

受电弓的垂直载荷可以通过受电弓的自重和受电弓上的电流来计算，而接触线的弹性变形可以通过接触线的材料和几何形状来计算。

最后，我们可以将受电弓的垂直载荷和接触线的弹性变形代入接触压力的定义公式中，即P=F/S，从而得到接触压力的计算公式。

接触压力的计算公式可以用以下公式表示：P = (F1 + F2) / S。

其中，P为接触压力，F1为受电弓的垂直载荷，F2为接触线的弹性变形，S为接触线的弹性系数。

在实际的工程应用中，接触压力的计算需要考虑到多种因素，如受电弓和接触线的材料、几何形状、载荷大小等。

因此，需要对接触压力的计算公式进行适当的修正和调整，以满足实际工程的需要。

除了计算公式外，接触压力的控制也是非常重要的。

在铁路运输过程中，接触压力的大小会受到多种因素的影响，如列车的速度、受电弓的调整、接触线的材料状况等。

因此，需要对接触压力进行实时监测和控制，以确保接触网的稳定性和安全性。

总之，接触网的接触压力是一个重要的参数，它直接关系到铁路运输的安全和效率。