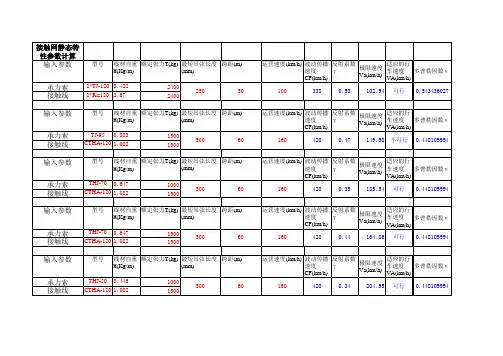
接触网常用计算公式
- 格式:doc
- 大小:162.50 KB
- 文档页数:7

高速铁路有关术语
1、反射系数:接触网的振动波在非均质点被反射,如吊弦点、线夹处等。
反射系数用下式表示:
γ=√ρm.F m /(√ρc.F c + √ρm.F m )
ρm.F m —分别代表承力索的线密度和承力索的张力;
ρc.F c ——分别代表接触线的线密度和接触线的张力。
2、多普勒因素:
α=(C – V)/(C + V)
V—行驶速度;
C—接触线波动传播速度,左右离线率和共振时的振幅。
3、增强因素:接触网的振动波在非均质处被反射,被反射回的波壁与该物体相向运动,并被继续向前运动的物体以输入能量的方式再次反射回去。
波的能量被增强,其增强系数用下式表示,为了使波能够衰减,必须满足γ<1的条件。
Φ = γ/α
γ—反射因素;
α—多普勒因素。
在上述三个动态标准中,最关键的动态标准为增强因素,应使增强因素尽可能的小。
因此,可通过减小反射系数,增大多普勒因素得以实现。
减少反射系数可以通过两个途径实现:减少承力索张力;增大接触线张力。
只有提高接触线的张力和波动传播速度才可能大幅度地减小增强因素,改善受流性能。
4、无量纲速度:β应小于0.7。
β= V/C。

接触网计算公式3 2接触网上部悬挂的载荷3 2 1负载分析接触网上部悬挂结构受到的主要外载荷包括:接触线和承力索在风作用下的风负载F风、以及接触线和承力索在覆冰作用下的冰负载Ft、接触线作用下的之字力P、地面对支柱的支持力F冰、受电弓作用下的抬升力N和其自身的重力Q。
由于接触网外部悬挂结构多种多样,但每一种结构的分析方法都大同小异。
本文选择一种典型的接触网上部悬挂结构作为研究对象,进行分析计算,即直线段中间支柱反定位悬挂形式。
其示意图如下其中F风=Pc+Pj,F冰.合成在Qo中以兰新线武威南至嘉峪关段直线段中间柱反安装为例,取侧面界限Cx=3.1m,安装角a=45°。
标准典型气象区选Ⅳ区,最大风度Vb=lOm/s,覆冰厚度b=5mm,吊弦单位长度自重取g。
=0.5×l03 KN/m,跨距取l =65m,拉出值a=200 mm。
承力索和接舷线的相关参数如表3.1。
表3.1 承力索和接触线的参数接触线长度65m,考虑弛度的影响,承力索实际长度为L=l+8F/3l计算得到承力索实际长度l=65. 02m。
(1)单位长度风负载P =0.615akv2d×106(kN/m)式中p——绳索所受的实际风负载:a——风速不均匀系数;k——风负载体型系数;d——绳索的直径。
代入数据计算得到:单位长度承力索风负载:P cb=1.494×10-3(KN/m)单位长发接触线风负载:P jb=1.494×10-3 (KN/m)(2)单位长度冰负载g b=πr b b(b+ d)g H l0-9 (KN/m)式中g b——绳索的覆冰重力负载b——覆冰厚度;d——绳索直径;r b——覆冰密度:g H——重力加速度。
代入数据计算得到:承力索单位长度冰负载9hr =2. 003×l0-3 (KN/m) 接触线单位长度冰负载g。
=1. 082×10-3(KN/m)。


接触网常用计算公式h —定位点外轨超高(mm ); 4. 接触线拉出值a 地的计算公式h dHa a -=地 式中 a 地—拉出值标准时,导线垂直投影与线路中心线的距离(mm )。
a 地为正时导线的垂直投影应在线路的超高侧,a 地为负时导线的垂直投影应在线路的低轨侧。
H —定位点接触线的高度(mm ); a —导线设计拉出值(mm ); h —外轨超高(mm ); d —轨距(mm );5. 接触线定位拉出值变化量m ax a ∆的计算公式2max 2max E I I a z z --=∆式中 Δa max —定位点拉出值的最大变化量(mm );Z L —定位装置(受温度影响)偏转的有效长度(mm );max E —极限温度时定位器的最大偏移值(mm );由上式可知 E=0时 Δa=06. 定位器无偏移时拉出值a 15的确定:(取平均温度t p =15℃)max 2115a a a ∆±=式中 a —导线设计拉出值(mm ); Δa max —定位点拉出值的最大变化量(mm );15a —定位器无偏移时(即平均温度时)的拉出值(mm )。
a 15与a 的变化关系,主要取决于定位器在极限温度时Δa max 的变化量的大小,当Δa max 变化量较大时,则a 15相对a 值的变化较大,当Δa max 变化量较小 时,则a 15相对a 值变化量较小。
但Δa max 的变化量又取决于定位器在极限温度时E max 值的大小,当定位器在极限温度时偏移值较大时,则Δa max 变化也较大,则a 15≠a ,反之偏移值较小时,则Δa max 变化也较小,则a 15≈a 。
所以确定平均温度时定位点拉出值a 15的目的是为了满足在极限温度时,拉出值不超过允许误差。
除直线反定位以外,当温度高于或低于平均温度时,拉出值都将是增大。
因此,调整a 15时应满足下列关系为好:即:270≤15a <300。
曲线区段由于Δa max 较小,15a ≈a 。
7 施工技术要求7.1技术标准与规范本项目遵循的主要技术标准及规范(包括但不限于)以下所示,所采用的标准均应为项目执行时的最新有效版本。
若投标人采用除上述之外的其它被承认的相关国内、国际标准,应明确提出并提供相应标准复印件,经招标人批准后方可采用。
当相关标准发生冲突时,以较高版本的技术要求为准。
《地铁设计规范》(GB50157-2003)《铁路电力牵引供电设计规范》(TB10009-2005)《城市轨道交通直流牵引供电系统》(GB10411-2005)《铁路电力牵引供电施工规范》(TB10208-98)《铁路电力牵引供电工程施工质量验收标准》(TB10421-2003)《地下铁道工程施工及验收规范》GB50299-1999由招标人组织设计,监理工程师就某些特殊项目制定的标准。
有关设备及材料的制造、试验及验收等标准详见技术规格书。
7.2施工技术条件7.2.1悬挂类型及组成绝缘等级按重污区标准,绝缘子标称泄漏距离不小于250mm。
7.2.5绝缘间隙绝缘间隙应符合GB50157-2003标准即带电体距结构体、车体之间的绝缘距离:静态为150mm,动态为100mm,绝对最小动态60mm。
7.2.6接触线悬挂高度刚性接触网正线的最大拉出值一般为±200mm,辅助线道岔处工作支一般不超过350mm。
7.2.8跨距刚性接触网悬挂点的间距一般为6~10m,最大不超过12m。
7.2.9锚段长度刚性悬挂锚段长度一般不大于250m,最大不超过300m。
7.2.10中心锚结刚性悬挂在锚段的中部设置中心锚结。
在车站和矩形隧道内采用悬挂点两旁设防爬金具(可用汇流排电连接线夹替代)形式的中心锚结;盾构隧道内采用2个棒形的合成绝缘子“V”形布置在悬挂点两侧构成的中心锚结。
7.2.11电连接设置刚性悬挂电连接设置(1)非绝缘锚段关节处设置电连接。
(2)道岔处设电连接。
(3)隧道口刚柔过渡处设纵向电连接。
(4)防淹门短锚段处设纵向电连接。
腕臂计算模型1、平腕臂低头52mm时与水平线夹角为1度,对平腕臂长度影响为0.3mm,忽略不计;2、斜腕臂计算以下三角直角三角形计算,其中A、B值按下面方法求得;3、测量数据为:支柱侧面限界CX、线路超高h、支柱斜率&。
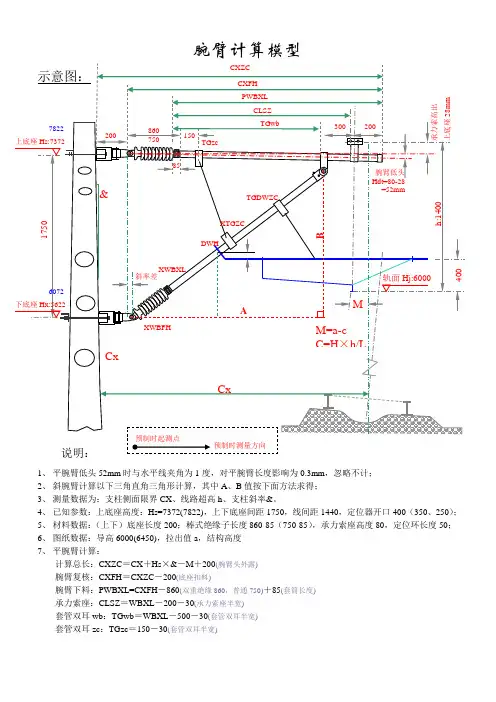
4、已知参数:上底座高度:Hs=7372(7822),上下底座间距1750,线间距1440,定位器开口400(350、250);5、材料数据:(上下)底座长度200;棒式绝缘子长度860-85(750-85),承力索座高度80,定位环长度50;6、图纸数据:导高6000(6450),拉出值a,结构高度7、平腕臂计算:计算总长:CXZC=CX+Hs×&-M+200(腕臂头外露)腕臂复核:CXFH=CXZC-200(底座扣料)腕臂下料:PWBXL=CXFH-860(双重绝缘860,普通750)+85(套筒长度)承力索座:CLSZ=WBXL-200-30(承力索座半宽)套管双耳wb:TGwb=WBXL-500-30(套管双耳半宽)套管双耳zc:TGzc=150-30(套管双耳半宽)8、斜腕臂计算:直角边A:A=TGwb+30(套管双耳半宽)+860(双重绝缘860,普通750)-85(套筒长度)-1.75&(斜率差)直角边B:B=1750(底座间距)-50(此处腕臂低头折算值)-80(套管双耳扣料长度)斜腕臂复核长度:XWBFH=SQRT(A^2+B^2)斜腕臂下料长度:XWBXL=XWBFH-860+85定位环位置:DWH=(6000+400-5622)×XWBFH÷A-860+85腕臂支持套管双耳位置:XTGZC= XWBXL -TGwb+150+85定位管支持套管双耳位置:TGDWZC= XTGZC+410(定位管支撑长度)+80(套管双耳扣料长度)9、定位管上计算:正定位定位管长度:ZDWGC=CX+5.622&-M-(6000+400-5622)×A÷B-200(底座扣料)-50(定位环扣料)+600(防风拉线长度)+200(定位管外露长度)反定位定位管长度:FDWGC=CX+5.622&-M-(6000+400-5622)×A÷B-200(底座扣料)-50(定位环扣料)+1200(1050定位器长度)+200(定位管外露长度)正定位管上定位环位置:ZGSDWH=ZDWGC-1200(1050定位器长度)-600-200反定位管上定位环位置:FGSDWH=FDWGC-200正定位防风拉线定位环位置:ZFFDWH= ZGSDWH-200正定位防风拉线定位环位置:FFFDWH= FGSDWH-1200(1050定位器长度)-600-200。


接触网六道计算题1.已知等高悬挂接触线实际长度计算式为L =l+8f 2/31,其中L 为接触线实际长度,l 跨距长度,f 为接触线弛度。
试导出不等高悬挂接触线实际长度计算式。
解:因为:L=l+8f 2/3l(1分)所以:L 1=2l 1+8f 21/3×2l 1,L 2=2l 2+8f 22/3×2l 2(2分)则:L=(1/2)(L 1+L 2)(1分)=1/2(2l 1+8f 21/3×2l 1+2l 2+8f 22/3×2l 2)(2分)=l 1+l 2+2f 21/3l 1+2f 22/3l 2(2分)=l+2/3[(f 21/l 1)+(f 22/l 2)](2分)2.某电化区段,覆冰时风速是10m/s ,最大风速为30m/s ,采用GJ-70+GLCA100/215链形悬挂,该地区在-5℃时出现覆冰,其最大覆冰厚度为16mm 。
试计算最大风速条件下线索的风负载及支柱的受风力。
已知:(1)av =0.85,K =1.25,GJ-70线索直径为11mm ,GLCA100/215接触线高度为16.5mm 。
(2)计算支柱风向荷载按15m 高钢柱计算上顶宽400mm ,下底宽800mm 。
解:已知:a v =0.85,K=1.25,d c =11mm ,h j =16.5mm(2分)根据公式:P cv =a v Kd c (v 2max /16)×10-2=0.85×1.25×11×302/16×10-2=6.57(N/m)(3分)P jv =a v Kh j v 2max /16×10-2=0.85×1.25×16.5×302/16×10-2=9.86(N/m)(3分)答:最大风速条件下承力索的风负载为6.57N/m ;接触线的风负载为9.86N/m 。

Ec (伏)
静电感应电压
K 单线取0.4复线取0.6Uj 接触网对地电压 b 接触网导线距地面的高度c 临近线距地面的高度
静电感应电压的计算公式
Ec=K×Uj×(bc/a×a +b×b +c×c)×L1/L2
Ec------为临近线上的静电感应电压;
K-------为常数(单线取0.4,复线取0.6);
Uj------为接触网对地电压,取25 kV ;
L1-----为接触网平行长度;
L2-----为临近线平行接近长度;
a-------为接触网导线与临近线在大地上投影间的距离; b-------为接触网导线距地面的高度;
c-------为临近线距地面的高度。
a 接触网导线与临近线在大地上投影间的距离L1接触网平行长度 L2临近线平行接近长度
电压的计算公式
a×a +b×b +c×c)×L1/L2
.6);
上投影间的距离;。

接触网常用参数标准及测量计算一、拉出值(跨中偏移值)1、技术标准160km/h及以下区段:标准值:直线区段200-300mm;曲线区段根据曲线半径不同在0-350mm之间选用。
安全值:之字值≤400mm;拉出值≤450mm。
限界值:之字值450mm;拉出值450mm。
160km/h以上区段:标准值:设计值。
安全值:设计值±30mm。
限界值:同安全值。
2、测量方法利用DJJ多功能激光接触网检测仪进行拉出值测量:受电弓滑板平面与两钢轨平面平行,检测仪与两钢轨平面平行,测量时无需考虑外轨超高,直接校准定位点在检测仪上的投影位置,此位置与检测仪中心点的距离就是拉出值。
二、导线高度1、技术标准标准值:区段的设计采用值。
安全值:标准值±100mm。
限界值:小于6500mm;任何情况下不低于该区段允许的最低值。
当隧道间距不大于1000m时,隧道内、外的接触线可取同一高度。
2、测量方法利用DJJ多功能激光接触网检测仪进行导高测量:将测量仪置于两钢轨之上与两轨面平行,利用测量仪上的观察窗校准定位点位置,测出定位点至两轨面的垂直距离即为导高。
三、导线坡度及坡变率1、技术标准标准值: 120km/h及以下区段≤3‰;120-160km/h区段≤2‰;200km/h区段≤2‰,坡度变化率不大于1‰;200-250km/h区段≤1‰,坡度变化率不大于1‰。
安全值:120km/h及以下区段≤5‰;120-160km/h区段≤4‰。
其他同标准值。
限界值:120km/h及以下区段≤8‰;120-200km/h区段≤5‰;200km/h及以上区段同安全值。
160km/h及以上区段,定位点两侧第一根吊弦处接触线高度应相等,相对该定位点的接触线高度允许误差±10mm,但不得出现V字型。
2、测量与计算方法定位点A与定位点B之间的坡度测量:1、测出A点的导高h a;2、测出B点的导高h b;3、测出或计算出A、B之间的距离H;4、计算出A、B两点之间的导线坡度P ab=(h b -h a)/H×1000‰;5、将P ab记入定位点B的导线坡度P b,即P ab=P b。
接触网的接触压力计算公式随着社会的发展和科技的进步,铁路交通成为人们出行的重要方式之一。
而接触网作为电气化铁路的重要组成部分,其质量和性能直接关系到铁路运输的安全和效率。
在接触网的设计和维护过程中,接触压力是一个重要的参数,它直接影响着接触网的稳定性和安全性。
因此,了解接触压力的计算公式对于铁路工作者来说是非常重要的。
接触网的接触压力是指接触线与受电弓之间的压力,它是由受电弓对接触线的压力和接触线对受电弓的弹性变形所产生的。
接触压力的大小直接影响着接触线的磨损和受电弓的损坏,因此在设计和维护接触网时需要对接触压力进行准确的计算和控制。
接触压力的计算公式可以通过以下步骤进行推导:首先,我们需要了解接触压力的定义。
接触压力可以用受电弓的垂直载荷和接触线的弹性变形来表示,即P=F/S,其中P为接触压力,F为受电弓的垂直载荷,S为接触线的弹性变形。
其次,我们需要了解受电弓的垂直载荷和接触线的弹性变形的计算方法。
受电弓的垂直载荷可以通过受电弓的自重和受电弓上的电流来计算,而接触线的弹性变形可以通过接触线的材料和几何形状来计算。
最后,我们可以将受电弓的垂直载荷和接触线的弹性变形代入接触压力的定义公式中,即P=F/S,从而得到接触压力的计算公式。
接触压力的计算公式可以用以下公式表示:P = (F1 + F2) / S。
其中,P为接触压力,F1为受电弓的垂直载荷,F2为接触线的弹性变形,S为接触线的弹性系数。
在实际的工程应用中,接触压力的计算需要考虑到多种因素,如受电弓和接触线的材料、几何形状、载荷大小等。
因此,需要对接触压力的计算公式进行适当的修正和调整,以满足实际工程的需要。
除了计算公式外,接触压力的控制也是非常重要的。
在铁路运输过程中,接触压力的大小会受到多种因素的影响,如列车的速度、受电弓的调整、接触线的材料状况等。
因此,需要对接触压力进行实时监测和控制,以确保接触网的稳定性和安全性。
总之,接触网的接触压力是一个重要的参数,它直接关系到铁路运输的安全和效率。
接触网常用计算公式接触网常用计算公式1. 平均温度t p 和链形悬挂无弛度温度t o 的计算① 2t t tp min max += ② 5-2t t t min max o +=弹 ③ 10-2t t t min max o +=简 式中 t p —平均温度℃(即吊弦、定位处于无偏移状态的温度);t o 弹、t o 简—分别表示弹性链形悬挂和简单链形悬挂的无弛度温度℃;t max —设计最高温度℃;t min —设计最低度℃;2. 当量跨距计算公式∑∑===n i In i I LLLD 113 式中L D —锚段当量跨距(m );).........(3323113n n i I L L L L+++=∑=—锚段中各跨距立方之和; ).........(211n n i I L L L L+++=∑=—锚段中各跨距之和;3. 定位肩架高度B 的计算公式2)101 +(hd h Ie H B ++≈ 式中 B —肩架高度(mm );H —定位点处接触线高度(mm );e —支持器有效高度(mm );I —定位器有效长度(包括绝缘子)(mm );d —定位点处轨距(mm );h —定位点外轨超高(mm );4. 接触线拉出值a 地的计算公式h dH a a -=地 式中 a 地—拉出值标准时,导线垂直投影与线路中心线的距离(mm )。
a 地为正时导线的垂直投影应在线路的超高侧,a 地为负时导线的垂直投影应在线路的低轨侧。
H —定位点接触线的高度(mm );a —导线设计拉出值(mm );h —外轨超高(mm );d —轨距(mm );5. 接触线定位拉出值变化量m ax a ∆的计算公式2max 2max E I I a z z --=∆式中 Δa max —定位点拉出值的最大变化量(mm );Z L —定位装置(受温度影响)偏转的有效长度(mm );max E —极限温度时定位器的最大偏移值(mm );由上式可知 E=0时 Δa=06. 定位器无偏移时拉出值a 15的确定:(取平均温度t p =15℃)max 2115a a a ∆±= 式中 a —导线设计拉出值(mm );Δa max —定位点拉出值的最大变化量(mm );15a —定位器无偏移时(即平均温度时)的拉出值(mm )。
三、腕臂长度计算1-12-15 直线与曲线外侧中间柱腕臂长度计算示意图由于目前接触网结构普遍采用平腕臂结构,所以在平腕臂安装和预配过程中,需要准确确定平腕臂和斜腕臂长度,根据平腕臂长度计算,在地面预配好整体结构,对今后一次性安装成功,减少调整工作量具有重要意义。
腕臂长度计算与支柱所在位置和用途密切相关,直线和曲线计算方法不同,同样是曲线,则支柱在曲线外侧和曲线内侧时的计算方法也不同。
转换柱与中心柱的计算方法也有区别。
现就上述几种情况分别作简单介绍(仅供参考)。
(一)直线和曲线支柱腕臂长度计算图1-12-15中符号说明如下:L 1、L 2-分别表示平腕臂承力索固定点至支柱固定点长度和承力索至腕臂头长度。
(m) L 3-斜腕臂水平投影长度。
(m)L 4-非工作支承力索与工作支承力索之间的水平距离。
(m )L 平、L 斜-分别表示平腕臂底座和斜腕臂底座突出支柱部分长度。
(m)h 1-平腕臂底座与斜腕臂底座之间的垂直安装距离。
(m)h 2-斜腕臂套管双耳零件连接长度。
(m)h 3-斜腕臂垂直投影长度。
(m)h 4-支柱侧面限界测量点至平腕臂支柱固定点之间的垂直距离。
(m)H c -承力索至钢轨面的垂直高度。
(m)C x -支柱侧面限界。
(m)m c -承力索在曲线上轨平面处垂直投影与线路中心的偏移距离(a- Lh H C )。
(m) h-曲线外轨超高。
(m)1.直线区段腕臂长度计算可根据下式确定:L 1= C x +βh 4±a (m )h 3= h 1- h 2 (m )L 3= L 1 -(承力索至承力索座中心的距离)-(承力索座中心至套管双耳的距离)- βh 1 式中:a-承力索拉出值。
(m)β-支柱斜率(要考虑支柱整正后产生的斜率)。
“±”- 正定位时取“-”号,反定位时取“+”号。
平腕臂钢管长度= L 1 + L 2- L 平-L 棒 (m)斜腕臂钢管长度=2323-h L L +)(斜 -L 棒 (m)其中L 2应考虑承力索至平腕臂钢管头的距离,L 棒棒式绝缘子安装长度。
接触网常用计算公式
1. 平均温度t p 和链形悬挂无弛度温度t o 的计算
① 2
t t tp min max += ② 5-2
t t t min max o +=弹 ③ 10-2t t t min max o +=
简 式中 t p —平均温度℃(即吊弦、定位处于无偏移状态的温度);
t o 弹、t o 简—分别表示弹性链形悬挂和简单链形悬挂的无弛度温度℃;
t max —设计最高温度℃;
t min —设计最低度℃;
2. 当量跨距计算公式
∑∑===n i I
n i I L
L
LD 113 式中L D —锚段当量跨距(m );
).........(332311
3n n i I L L L L
+++=∑=—锚段中各跨距立方之和; ).........(211n n i I L L L L
+++=∑=—锚段中各跨距之和;
3. 定位肩架高度B 的计算公式
2
)101 +(h
d h I
e H B ++≈ 式中 B —肩架高度(mm );
H —定位点处接触线高度(mm );
e —支持器有效高度(mm );
I —定位器有效长度(包括绝缘子)(mm );
d —定位点处轨距(mm );
h —定位点外轨超高(mm );
4. 接触线拉出值a 地的计算公式
h d
H a a -=地 式中 a 地—拉出值标准时,导线垂直投影与线路中心线的距离(mm )。
a 地为正时导线的垂直投影应在线路的超高侧,a 地为负时导线的垂直投影应在线路的低轨侧。
H —定位点接触线的高度(mm );
a —导线设计拉出值(mm );
h —外轨超高(mm );
d —轨距(mm );
5. 接触线定位拉出值变化量m ax a ∆的计算公式
2max 2max E I I a z z --=∆
式中 Δa max —定位点拉出值的最大变化量(mm );
Z L —定位装置(受温度影响)偏转的有效长度(mm );
max E —极限温度时定位器的最大偏移值(mm );
由上式可知 E=0时 Δa=0
6. 定位器无偏移时拉出值a 15的确定:(取平均温度t p =15℃)
max 2
115a a a ∆±= 式中 a —导线设计拉出值(mm );
Δa max —定位点拉出值的最大变化量(mm );
15a —定位器无偏移时(即平均温度时)的拉出值(mm )。
a 15与a 的变化关系,主要取决于定位器在极限温度时Δa max 的变化量的大小,当Δa max 变化量较大时,则a 15相对a 值的变化较大,当Δa max 变化量较小 时,则a 15相对a 值变化量较小。
但Δa max 的变化量又取决于定位器在极限温度时E max 值的大小,当定位器在极限温度时偏移值较大时,则Δa max 变化也较大,则a 15≠a ,反之偏移值较小时,则Δa max 变化也较小,则a 15≈a 。
所以确定平均温度时定位点拉出值a 15的目的是为了满足在极限温度时,拉出值不超过允许误差。
除直线反定位以外,当温度高于或低于平均温度时,拉出值都将是增大。
因此,调整a 15时应满足下列关系为好:
即:270≤15a <300。
曲线区段由于Δa max 较小,15a ≈a 。
即在调整时按a 值进行。
±—由定位的型式决定,直线反定位器取“+”号,其余定位型式取“-”号。
7. 定位器坡度X
1的确定: 5
11101≤∆+≤Ld hc X 任意温度时的坡度;
Ld —定位器的长度;
Δhc —定位点在极限温度和调整温度时高度变化Δh 之差,即调极h h hc ∆∆=∆-;
8. 吊弦间距的计算公式
①1420-⨯-=
K L X 简单 ②1
5820-⋅⨯-=K L X 弹性 式中 X 0简单—简单链形悬挂吊弦间距(m );
X 0弹性—弹性链形悬挂吊弦间距(m );
L —跨距长度(m );
K —跨中吊弦布置的根数;
9. 吊弦、定位、限制管偏移值计算公式
)(p x a t t L E -=
式中 E —偏移值(m );
L —所计算的吊弦、定位器、限制管距中心锚结或硬锚的距离(m );
a —线胀系数1/℃(全补偿吊弦偏移值E 计算时:c j a a a -=,a j 表示接触线线胀系数,C a 表示承力索线胀系数);
X t —检调时温度(℃);
P t —平均温度(℃);
10. 半补偿链形悬挂中心锚结线夹处导线高度Hzx 的确定
300+±∆+=f h H H ZX
式中ZX H —在任意温度时,中心锚结线夹处导线高度(mm );
0H —导线设计高度
Δh —第一吊弦点(即定位点)高度变化量
F —中心锚结辅助绳固定处接触线弛度
“±”—取决于调整时的温度,当调整温度大于无弛度温度时取“-”号,反之取“+” ;
11. 补偿器a 、b 值的计算公式
① )(min min t t nLa a a x -+=
② )(max min x t t nLa b b -+=
式中 a —补偿绳回头末端至定滑轮或制动部件的距离(m );
b — 补偿器坠砣底面距基础(或地)面最高点的距离(m );
n —传动比,传动比为1:2时,n=2;传动比为1:3时,n=3;
min a —a 的最小允许值,应为0.2m ;
m in b —b 的最小允许值,应为0.2m ;
L —补偿器距中心锚结(或硬锚)的距离(m ):
m ax t —设计最高温度(℃);
min t —设计最低温度(℃);
x t —检调时温度(℃);
a —线胀系数1/℃;
12. 下锚拉线长度计算公式
C T N U H --⨯+=5002L β钢绞线
式中 钢绞线L —拉线(钢绞线)下料长度(mm );
ß—计算系数,它的值由拉线与地面的夹角a 确定:当∠a=450
时,ß=1.414;
当∠a=600时,ß=1.155;
H —支柱出土点至承锚、线锚角钢的距离(mm );
T U —表示U T 楔形线夹(或调整螺栓)的长度(mm )
; G N —拉线拉杆长度(mm )
; 13. 曲线水平力RC P 和RJ P 的计算公式
① 承力索:R L T P C
RC = ② 接触线:R L T P C RC = 式中 RC P —承力索在曲线上产生的水平力(N );
RJ P —接触线在曲线上产生的水平力(N );
C T —承力索张力(N );
J T —接触线张力(N );
R —曲线半径(m );
L —跨距长度(m ),若支柱两侧的跨距L 不等时,则2
)(21L L L +=即取支柱两侧跨距的平均值;
14.直线定位之字力之p 的计算公式
L a T p j 4=之 式中 P 之—直线定位之字力(N );
T j —接触线张力(N );
a —定位点拉出值(m );
L —跨距长度(m ),若支柱两侧的跨距L 不等时,则2
)(21L L L +=即取支柱两侧跨距的平均值;
15. 承力索弛度的测量计算公式
B C A F -+=2)( 式中 F —承力索弛度(mm );
A 和C —两悬挂点承力索至轨面的高度(mm );
B —跨中承力索最低点至轨面的高度(mm );
16. 空气绝缘间隙的计算公式
150
1.0e U d += 式中 d —空气绝缘间隙(m );
e U —接触网额定电压(kv );
17. 吊弦长度计算公式
C T x L gx h C 2)
(--= 或 20)
(4L
x L XF h C --=
式中 C —所求吊弦长度(m );
L —跨距长度(m );
h —悬挂点结构高度(m );
x —所求吊弦距支柱定位点的距离(m );
g —每米接触悬挂的重量(kg );
C T —承力索的张力(kg );
0F —接触线无弛度时承力索的弛度(m );
18. 横向承力索分段长度的计算
2
2
n h n a c b +=
式中 n b 承力索分段长度(m );
h c —相邻两直吊弦的高度差(m );
n a —横向承力索上相邻两悬挂间的水平距离(m );如1a 、
2a 、3a …n a 。
19. 横向承力索修正长度的计算
C L F
B ∆-=∆316
式中 ΔB —横向承力索长度变化值(mm );
L —横向承力索在两支柱悬挂点间的水平距离(mm ); F —横向承力索的弛度(mm );
ΔC —最短吊弦长度变化值(mm );
20. 外轨超高h 的计算公式。