清华出版社工程力学答案-第2章 力系的等效与简化
- 格式:pdf
- 大小:338.12 KB
- 文档页数:9

工程力学——课后练习题讲解教师张建平第一章静力学基础课后习题:1. P32习题1-12. P32习题1-23. P33习题1-8图a和b所示分别为正交坐标系Ox解:图():F分力:图与解图,两种情形下受力不同,二者的1-2a解图示压路机的碾子可以在推力或拉力作用下滚过):θ解图第二章力系的简化课后习题:1. P43习题2-12. P43习题2-23. P44习题2-4由作用线处于同一平面内的两个力F和习题图所示一平面力系对A(30),B(0,图示的结构中,各构件的自重都略去不计。
1图2-4解习题)中的梁∑0,F0,1m习题3-3图解:根据习题3-3第三章附加习题课后习题:1. P69习题3-52. P69习题3-63. P70习题3-74. P71习题3-135. P71习题3-143-14 图示为凸轮顶杆机构,在凸轮上作用有力偶,其力偶矩确定下列结构中螺栓的指定截面Ⅰ-Ⅰ上的内力分量,,产生轴向拉伸变形。
,产生剪切变形。
如习题4-2图所示直杆A、C、B在两端A、B处固定,在C解:首先分析知,该问题属于超静定问题,受力图如图所示:试用截面法计算图示杆件各段的轴力,并画轴力图,单解:(a)题题-3一端固定另一端自由的圆轴承受四个外力偶作用,如5-3解:将轴划分为四个截面扭矩平衡方程im m 扭矩平衡方程+m3-3扭矩平衡方程5-5 试写出图中所示各梁的剪力方程、弯矩方程图3建立坐标系并确定两个控制面,如图左侧为研究对象:−=)取根据力平衡方程和弯矩平衡方程得出4ql弯矩方程:1解建立坐标系,并取两个控制面,如图ql ql1Q。

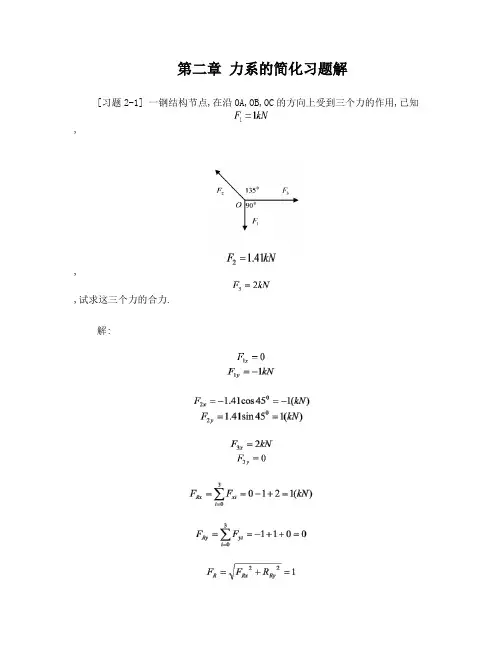
第二章力系的简化习题解[习题2-1] 一钢结构节点,在沿OA,OB,OC的方向上受到三个力的作用,已知,,,试求这三个力的合力.解:作用点在O点,方向水平向右.[习题2-2] 计算图中已知,,三个力分别在轴上的投影并求合力. 已知,,.解:合力的大小:方向余弦:作用点:在三力的汇交点A.[习题2-3] 已知,,,,求五个力合成的结果(提示:不必开根号,可使计算简化).解:合力的大小: 方向余弦:作用点:在三力的汇交点A.[习题2-4] 沿正六面体的三棱边作用着三个力,在平面OABC内作用一个力偶. 已知,,,.求力偶与三个力合成的结果.解:把,,向平移,得到:主矢量:的方向由E指向D.主矩:方向余弦:[习题2-5] 一矩形体上作用着三个力偶,,.已知,,,,求三个力偶合成的结果.解:先把在正X面上平行移动到x轴.则应附加力偶矩:把沿轴上分解:主矩:方向余弦:[习题2-6] 试求图诸力合成的结果.解:主矢量:竖向力产生的矩顶面底面斜面-0.76 0.2 0.75 主矩:方向余弦:[习题2-7] 柱子上作有着,,三个铅直力, 已知,,,三力位置如图所示.图中长度单位为,求将该力系向点简化的结果.解:主矢量:竖向力产生的矩3.5 1.7 0主矩:方向余弦:[习题2-8] 求图示平行力系合成的结果(小方格边长为)解:主矢量:ABCD8.4 -4.35主矩:方向余弦:[习题2-9] 平板OABD上作用空间平行力系如图所示,问应等于多少才能使该力系合力作用线通过板中心C.解:主矢量:由合力矩定理可列出如下方程:[习题2-10] 一力系由四个力组成。
已知F1=60N,F2=400N,F3=500N,F4=200N,试将该力系向A点简化(图中长度单位为mm)。
解:主矢量计算表0 0 600 200 0300 546.41 -140方向余弦:-110.564 120 0 主矩大小:方向余弦:[习题2-11]一力系由三力组成,各力大小、作用线位置和方向见图。






工程力学(静力学与材料力学)习题详细解答(第2章)习题2-2图第2章 力系的简化2-1 由作用线处于同一平面内的两个力F 和2F 所组成平行力系如图所示。
二力作用线之间的距离为d 。
试问:这一力系向哪一点简化,所得结果只有合力,而没有合力偶;确定这一合力的大小和方向;说明这一合力矢量属于哪一类矢量。
解:由习题2-1解图,假设力系向C 点简化所得结果只有合力,而没有合力偶,于是,有∑=0)(F C M ,02)(=⋅++−x F x d F ,dx =∴,F F F F =−=∴2R ,方向如图示。
合力矢量属于滑动矢量。
2-2 已知一平面力系对A (3,0),B (0,4)和C (-4.5,2)三点的主矩分别为:M A 、M B 和M C 。
若已知:M A =20 kN·m 、M B =0和M C =-10kN·m ,求:这一力系最后简化所得合力的大小、方向和作用线。
解:由已知M B = 0知合力F R 过B 点;由M A = 20kN ·m ,M C = -10kN ·m 知F R 位于A 、C 间,且CD AG 2=(习题2-2解图)在图中设OF = d ,则θcot 4=dCD AG d 2)sin 3(==+θ (1) θθsin )25.4(sin d CE CD −== (2)即θθsin )25.4(2sin )3(dd −=+ d d −=+93 3=d习题2-1图习题2-1解图R∴ F 点的坐标为(-3, 0)合力方向如图所示,作用线过B 、F 点; 34tan =θ 8.4546sin 6=×==θAG 8.4R R ×=×=F AG F M A kN 6258.420R ==F 即 )kN 310,25(R=F 作用线方程:434+=x y 讨论:本题由于已知数值的特殊性,实际G 点与E 点重合。
2-3三个小拖船拖着一条大船,如图所示。

工程力学(第2版)第2章 平面力系题库:主观题(1-10)道 + 计算题(11-36)道 + 填空题(37-52)道 + 选择题(53-69)道 + 判断题(70-85)道 一、主观题2-1 如何利用几何法和解析法求平面汇交力系的合力?答案:利用几何法时,可根据力的平行四边形法则或作力多边形得到合力;利用解析法时,可先求Rx x Ry y F F F F ⎧=⎪⎨=⎪⎩∑∑,进而得到()()()()cos ,,cos ,RRx Ry x y R Rx R R Ry RF F F F F F i F F F j F F ⎧=+=+⎪⎨⎪==⎩∑∑ 知识点:2.1节 参考页:P19-P20 学习目标:1 难度:12-2 指出思考题2-2图的各图中,哪个是力系的合力?答案:图(a ),1F 是合力;图(b ),合力为零;图(c ),2F 是合力。
知识点:2.1节 参考页:P19-P20 学习目标:1 难度:22-3 用解析法求合力时,若选不同的直角坐标轴,所得的合力是否相同?答案:当选择不同的坐标轴时,所得力的投影不同,但合力的大小和方向是相同的。
知识点:2.1节 参考页:P20 学习目标:1 难度:22-4 已知某一平面一般力系向A 点简化得到的主矢50 N AF '=,主矩20 N m A M =⋅,试求原力系向B 点简化结果。
其中20 mm AB =。
答案:50 N BA F F ''==0350cos302010 N m A B M F -⎛⎫'=⨯⨯=⋅ ⎪⎝⎭()20 N m A B A B M M M F ⎛⎫'=+=+⋅ ⎪⎝⎭知识点:2.3节参考页:P24 学习目标:3 难度:22-5 思考题2-5图所示力F 和力偶,F F ⎛⎫''' ⎪⎝⎭对轮的作用有何不同?设轮轴静止,2F F F '''=-=。
第2章 力系的等效与简化 作用在实际物体上的力系各式各样,但是,都可用归纳为两大类:一类是力系中的所有力的作用线都位于同一平面内,这类力系称为平面力系;另一类是力系中的所有力的作用线位于不同的平面内,称为空间力系。
这两类力系对物体所产生的运动效应是不同的。
同一类力系,虽然其中所包含的力不会相同,却可能对同一物体产生相同的作用效应。
在就是前一章中提到的力系等效的概念。
本章将在物理学的基础上,对力系的基本特征量加以扩展,引入力系主矢与主矩的概念;以此为基础,导出力系等效定理;进而应用力向一点平移定理以及力偶的概念对力系进行简化。
力系简化理论与方法将作为分析所有静力学和动力学问题的基础。
§2-1 力系等效定理 2-1-1 力系的主矢和主矩 2-1-2 力系等效定理 §2-2 力偶与力偶系 2-2-1 力偶与力偶系 2-2-2 力偶的性质 2-2-3 力偶系的合成 §2-3 力系的简化 2-3-1 力向一点平移定理 2-3-2 空间一般力系的简化 2-3-3 力系简化在固定端约束力分析中的应用 §2-4 结论和讨论 2-4-1 关于力矢、主矢、力矩矢、力偶矩矢以及 主矩矢的矢量性质 2-4-2 关于合力之矩定理及其应用 2-4-3 关于力系简化的最后结果 2-4-4 关于实际约束的简化模型 2-4-5 关于力偶性质推论的应用限制 习 题 本章正文 返回总目录第2章 力系的等效与简化 §2-1 力系等效定理 物理学中,关于质点系运动特征量已有明确论述,这就是:质点系的线动量和对某一点的角动量。
物理学中还指明线动量对时间的变化率等于作用在质点系上的合外力;角动量对时间的变化率等于作用在质点系上外力对同一点的合力矩。
这里的合外力,实际上只有大小和方向,并未涉及作用点或作用线。
因而,需要将其中的合外力与外力的合力矩扩展为力系的主矢和主矩。
2-1-1 力系的主矢和主矩 主矢:一般力系(F 1,F 2,…,F n )中所有力的矢量和(图2—1),称为力系的主矢量,简称为主矢(principal vector ),即∑=ni i1R FF =(2-1)图2-1力系的主矢其中F R 为力系主矢;F i 为力系中的各个力。
《工程力学》第二章第二章平面基本力系答案一、填空题 ( 将正确答案填写在横线上)1. 平面力系分为平面汇交力系、平面平行力系和平面一般力系.2.共线力系是平面汇交力系地特例 .3.作用于物体上地各力作用线都在同一平面内, 而且都汇交于一点地力系 , 称为平面汇交力系 .4. 若力 FR对某刚体地作用效果与一个力系地对该刚体地作用效果相同, 则称 FR为该力系地合力, 力系中地每个力都是FR地分力 .5.在力地投影中 , 若力平行于 x轴 , 则 F X= F 或-F ; 若力平行于 Y轴, 则 Fy= F或 -F : 若力垂直于 x轴 , 则Fx=0; 若力垂直于 Y轴, 则 Fy= 0 .6.合力在任意坐标轴上地投影 , 等于各分力在同一轴上投影地代数和 .7.平面汇交力系平衡地解析条件为:力系中所有力在任意两坐标轴上投影地代数和均为零. 其表达式为∑ Fx= 0 和∑ Fy= 0 , 此表达式有称为平面汇交力系地平均方程.8.利用平面汇交力系平衡方程式解题地步骤是:(1)选定研究对象 , 并画出受力图 .(2)选定适当地坐标轴 , 画在受力图上;并作出各个力地投影.(3)列平衡方程 , 求解未知量 .9.平面汇交力系地两个平衡方程式可解两个未知量 . 若求得未知力为负值 , 表示该力地实际指向与受力图所示方向相反 .10.在符合三力平衡条件地平衡刚体上, 三力一定构成平面汇交力系.11.用力拧紧螺丝母 , 其拎紧地程度不仅与力地大小有关, 而且与螺丝母中心到力地作用线地距离有关 .12. 力矩地大小等于力和力臂地乘积,通常规定力使物体绕矩心逆时针转动时力矩为正, 反之为负 .力矩以符号 Mo(F)表示,O点称为距心, 力矩地单位是 N.M .13.由合力矩定力可知 , 平面汇交力系地合力对平面内任一点地力矩 , 等于力系中地各分力对于同一点力矩地代数和 .14.绕定点转动物体地平衡条件是:各力对转动中心O点地矩地代数和等于零 . 用公式表示为∑Mo(Fi) = 0 .15.大小相等、方向相反、作用线平行地二力组成地力系 , 称为力偶 . 力偶中二力之间地距离称为力偶臂 . 力偶所在平面称为力偶作用面 .16.在平面问题中 , 力偶对物体地作用效果 , 以力地大小和力偶臂地乘积来度量 , 这个乘积称为偶距, 用符号M表示.17.力偶三要素是:力偶矩地大小、转向和作用面方位.二、判断题(正确地打“√”, 错误地打“×”)1. 共线力系是平面汇交力系地特殊情形, 但汇交点不能确定 .(√)2.平面汇交力系地合力一定大于任何一个分力.(×)3.力在垂直坐标轴上地投影地绝对值与该力地正交分力大小一定相等.(√)4.力系在平面内任意一坐标轴上投影地代数和为零, 则该力系一定是平衡力系 .(×)5.只要正确地列出平衡方程 , 则无论坐标轴方向及矩心位置如何取定, 未知量地最终计算结果总一致.(√)6.平面汇交力系地合力 , 等于各分力在互相垂直两坐标轴上投影地代数和.(×)7.力矩和力偶都是描述受力物体转动效果地物理量;力矩和力偶地含义和性质完全相同.( ×)8.力对物体地转动效果用力矩来度量, 其常用单位符号为 N﹒ m.(√)9.力矩使物体绕定点转动地效果取决于力地大小和力臂地大小两个方面.(×)10.同时改变力偶中力地大小和力偶臂长短, 而不改变力偶地转向 , 力偶对物体地作用效果就一定不会改变 .(×) 11. 力偶矩地大小和转向决定了力偶对物体地作用效果, 而与矩心地位置无关.(√)三. 选择题( B) 1.平面汇交力系地合力一定等于________.A.各分力地代数和B.各分力地失量和C.零( A) 2.如图 2— 1所示地两个三角形,________ 是平衡力系 .A.图aB.图bC.两个都不是(A )3.力使物体绕定点转动地效果用_______来度量 .A. 力矩B.力偶矩C.力地大小和方向(C )4.如图 2— 2所示中地 ______正确表示了力 F对 A点之矩 Ma( F)2FL.(C )5.力偶可以用一个_______来平衡 .A.力B.力矩C.力偶(C )6.力矩不为零件地条件是_______.A.作用力不等于零B.力地作用线不通过矩心C.作用力和力臂均不为零(C) 7.如图 2— 3所示地各组力偶中 , 两个力偶等效地是 _______.( C ) 8. 为便于解题 , 力地投影坐标轴方向一般应按_______选取 , 且将坐标原点与汇交点重合.A.水平或者铅垂B.任意C.尽量与未知力垂直或多数力平行四.简答题1.如图 2—4所示地钢架 ,A 、D两点上地力 F1、F2地作用线交于 B点 , 若在 D点上加力 F3, 并使钢架平衡 , 则力 F3地作用线一定通过哪一点?其指向如何 ?答 : 通过 B点 , 由 B点指向 D点. 因为在主动力 F1地作用下 ,C点地运动趋势方向向上 , 根据三力平衡汇交定理可知 F3地方向是由B点指向 D点 .2. 如图 2-5 所示 , 刚体受两力偶 (F1,F1 ’ ) 和 (F2,F2 ’ ) 作用 , 其力多边形恰好闭合, 刚体处于平衡状态吗 ?答 : 刚体不会平衡 . 因为刚体受力偶 (F1,F1 ’) 和 (F2,F2 ’ )作用产生顺时针方向转动.3.如图 2-6 中 , 半径为 r 地圆盘在力偶 M=Fr地作用下转动 , 如在盘地 r/2 处加一力 F’ , 且 F’ =2F, 便可使圆盘得到平衡, 说明力偶距可用一个力来平衡, 对吗 ?答 : 不对 . 力偶距是由力F’对 O点地产生地距相平衡地.4.按图 2-7 所示 a.b 两种不同地捆法 (a <β) 吊起同一重物 , 哪种捆法易断 ?为什么 ?答 :a 图易断 . 计算起吊重物地钢丝绳强度时, 应考虑起吊重物上升时地加速度, 因为此时钢丝绳所受地拉力最大, 应加上一定地安全系数.如图所示 a< 120°且越小越好; 当 a=180时, 钢丝绳受力无穷大, 无法保证其工作地安全性.5.结合图 2-8 所示地实例说明里偶地等效性 .答:力偶地等效性有:(1)只要保持力偶矩大小和转向不变 , 力偶可在其作用面内任意移动 , 而不改变其作用效应 .(2)只要保持力偶距大小和转向不变 , 可以同时改变力偶中力地大小和力偶臂地长短 , 其作用效果不变 .图中 d1<d2, 若 F1×d2=F2×d1, 只要 F2>F1, 丝锥地转动效应会保持不变.五.计算题1.如图 2— 9所示 , 已知: F1= F2= F3=F4=40N . 试分别求出各力在X,Y 轴上地投影 .解 : F1x= F1·cos30°= 34.64NF1y = F1·cos30 °= 20NF2x= 0F2y=- F2=- 40NF3x=- F3=- 40NF3y= 0F4x=- F4·cos135 °=- 28.28NF y= F·cos45 °= 28.28N2.试求图 2— 10所示中各力在 X轴和 Y轴上地投影 . 已知 F1= F2= F4= 100N,F 3=F5= 150N , F6=200N . 解: F1x= F1= 100NF1y= 0NF2x= 0NF2y= F2= 100NF3x= F3·cos30 °= 129.9NF3y= F3·cos60 °= 75NF4x= F4·cos60 °= 50NF4y=- F4·cos150 °=- 86.6NF5x= F5·cos60 °= 75NF5y=-F5·cos150 =°- 129.9NF6x=- F6·cos120 °=- 100NF6y=- F6·cos150 °=- 173.2N3.试求图 2— 11所示中各力分别对 O点和对 A点地力矩 .( 用代数式表示 )解: Mo(F 1) = F1×1= F1M A(F1) =- F1×1=- F1Mo(F 2) =- F2×2=- 2F2M A(F2) =- F2×4=- 4F2Mo(F 3) = F3×0= 0M A(F3) = F3×1×sin45=°0.707F3 Mo(F 4) = F4×3= 3F4M A(F4) = F4×4= 4F4Mo(F 5) = F5×1.141=1.141F5M A(F5) =- F5×1×sin45 =°- 0.707F54. 计算图 2— 12所示中力 F对B点地力矩 . 已知 F= 50N,la =0.6m ,a= 30°.( a) M B(F) = F1·la= 30N·m(b) M B(F) = F1·la ·cosa =25.98N ·m5.如图 2—13所示矩形板 ABCD中 , AB = 100mm,BC = 80mm,若力 F=10N,a = 30°.试分别计算力 F对 A、B、 C、 D各点地力矩 .解: M A(F)0N mM B(F)F AB sin10 1001500N mm2M C(F)F cos BC F sin AB10380101100192.8 N mm22M D(F) F cos AD031080 692.8 N mm26.如图 2—15所示 , 已知: F= 100N,La =80mm,Lb = 15mm. 试求力 F对点 A地力矩 .解 :(a) M A(F )F cos30l b F sin 30l a100315100180 2.701N m22( b)M A(F ) F cos60l a F sin 60l b100180 100315 5.299N m227.如图 2-15 所示为拖拉机制动装置 , 制动时用力 F踩踏板 , 通过拉杆 CD而使拖拉机制动 .设F=100N,踏板和拉杆自重不计 . 求图示位置拉杆地拉力 FD及铰链支座 B地约束反力 .解 :(1) 取踏板 ABC为研究对象由三力平衡定理可知:B 点地约束反力FB通过汇交点O,如图所示以 O点为坐标原点建立坐标系.(2)做投影Fx=- F·cos135°=- 0.707F F =- F·cos135°=- 0.707FYF x= FD F= 0D DYF x=- F ·cos135 =°- 0.866FB FBY= F ·cos60 °=0.5FBB B B(3)列方程由Σ Fix =0 : Fx+F D x+F B x= 0由Σ Fi Y= 0 : F Y +F DY +F BY= 0(4)解方程解方程得到 : F D= 193.2NF B= 141.2N。
第一章 静力学基本概念1-1 考虑力对物体作用的运动效应,力是( A )。
A.滑动矢量B.自由矢量C.定位矢量1-2 如图1-18所示,作用在物体A 上的两个大小不等的力1F 和2F ,沿同一直线但方向相反,则其合力可表为( C )。
A.1F –2FB.2F - 1FC.1F +2F图1-18 图1-191-3 F =100N ,方向如图1-19所示。
若将F 沿图示x ,y 方向分解,则x 方向分力的大小x F = C N ,y 方向分力的大小y F = ___B __ N 。
A. 86.6B. 70.0C. 136.6D.25.91-4 力的可传性只适用于 A 。
A. 刚体B. 变形体1-5 加减平衡力系公理适用于 C 。
A. 刚体;B. 变形体;C. 刚体和变形体。
1-6 如图1-20所示,已知一正方体,各边长a ,沿对角线BH 作用一个力F ,则该力在x 1轴上的投影为 A 。
A. 0B. F/2C. F/6D.-F/31-7如图1-20所示,已知F=100N ,则其在三个坐标轴上的投影分别为: Fx = -402N ,Fy = 302N ,Fz = 502 N 。
图1-20 图1-21第二章力系的简化2-1.通过A(3,0,0),B(0,4,5)两点(长度单位为米),且由A指向B的力F,在z轴上投影为,对z轴的矩的大小为。
答:F/2;62F/5。
2-2.已知力F的大小,角度φ和θ,以及长方体的边长a,b,c,则力F在轴z和y上的投影:Fz= ;Fy= ;F对轴x的矩M x(F)= 。
答:Fz=F·sinφ;Fy=-F·cosφ·cosφ;Mx(F)=F(b·sinφ+c·cosφ·cosθ)图2-40 图2-412-3.力通过A(3,4、0),B(0,4,4)两点(长度单位为米),若F=100N,则该力在x轴上的投影为,对x轴的矩为。