含源电路欧姆定律基尔霍夫定律
- 格式:ppt
- 大小:1.02 MB
- 文档页数:30

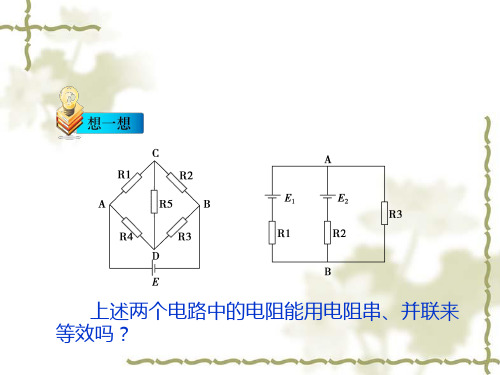

含源电路的等效化简
含源电路的等效化简是一种将复杂电路简化为更简单形式的方法,以便于电路分析和设计。
在等效化简过程中,通过替代电路元件、合并电路元件或建立等效电路模型,将原始电路转化为具有相同电性能但更简单的电路。
以下是含源电路等效化简的一般步骤:
1. 确定等效化简的目标:明确需要简化的电路部分以及所需的电路性能。
2. 根据电路的特性和元器件的性质应用电路定律:运用电路定律(如欧姆定律、基尔霍夫定律)分析电路中的电流、电压、电阻、功率等参数。
3. 利用等效原理简化电路元件:通过使用等效电阻、等效电容、等效电感、等效电流源、等效电压源等类型的等效元件,将一组或多组连续的电路元件简化为一个等效元件。
4. 合并电路元件:对于电路中的并联电阻、串联电阻、并联电容、串联电容等,可以根据电路性质和等效原理将它
们合并为一个等效元件。
5. 建立等效电路模型:根据等效化简的目标和电路特性,建立一个与原始电路相等效的简化电路模型。
最终,等效化简的结果是一个具有相同电路性能但更简单的电路,在电路分析和设计中更加方便和直观。
需要注意的是,等效化简是一种近似方法,可能会在某些情况下引入一定的误差,因此在实际应用中应根据具体需求和精度要求谨慎应用。

电学基本定律2.3.1、 焦耳定律电流在一段只有电阻元件的电路上所做的功等于电流通过这段电路时的所产生的热量Q 。
焦耳通过实验得到结论:如果通过一段只有电阻元件的电路的电流为I ,这段电路的电阻为R ,通电时间为t ,则Rt I Q 2=这就是焦耳定律,我们还可推出这段电路中电流的发热功率为R I P2=。
电流做功的过程,就是电能转化为其他形式的能的过程。
一般来讲,人们用电的目的往往不是为了发热。
如使用电动机是为了将电能转化为机械能,使用电解槽是为了将电能转化为化学能等等。
发热只是副效应,因此,一般说来电热只是电功的一部分,热功率是电功的一部分。
2.3.2、欧姆定律①部分电路欧姆定律:导体中的电流强度I 跟它两端所加的电压U 成正比,跟它的电阻R 成反比,即R UI =上式适用于金属导电和电解液导电的情况。
对非线线元件(如灯丝、二极管)和气体导电等情况不适用。
②一段含源电路欧姆定律:电路中任意两点间的电势差等于连接这两点的支路上各电路元件上电势降落的代数和,其中电势降落的正、负符号规定如下:a.当从电路中的一点到另一点的走向确定后,如果支路上的电流流向和走向一致,该支路电阻元件上的电势降取正号,反之取负号。
b.支路上电源电动势的方向和走向一致时,电源的电势降为电源电动势的负值(电源内阻视为支路电阻)。
反之,取正值。
如图2-3-1所示,对某电路的一部分,由一段含源电路欧姆定律可求得:3232222211111R I R I r I r I R I U U B A ----++-=-εεε③闭合电路欧姆定律和电源输出功率 〈1〉闭合电路欧姆定律 闭合电路欧姆定律公式:I =路端电压I r U ⋅-=εε⋅+=r R RU对于确定电源ε、r 一定,则I U-图线和R U - 图线如图2-3-2和2-3-3所示。
其中r I m ε=,为电源短路电流。
〈2〉电源输出功率电源的功率()r R I P +==2εε源图2-3-1mUε图2-3-2 图2-3-3电源输出功率()()rRr R R r R IU P 4222++=⋅+==εε出当r R =时电源输出功率为最大r P 42ε=最大此时电源效率 50=η%电源输出功率P 随外电阻R 变化如图2-3-4所示,若电源外电阻分别为1R 、2R 时,输出功率相等,则必有212R R r ⋅=例2、如图2-3-5所示电路,设电源电压不变,问:(1)2R 在什么范围内变化时,2R 上消耗的电功率随2R 的增大而增大?(2)2R 在什么范围内变化时,2R 上消耗的电功率随2R 增大而减小?(3)2R 为何值时,2R 上消耗的电功率为最大?解: 先求出2P 随2R 变化的表达式。


第一章 电路的三大定律一、欧姆定律欧姆定律是电路分析中的重要定律之一,主要用于进行简单电路的分析,它说明了流过线性电阻的电流与该电阻两端电压之间的关系,反映了电阻元件的特性。
遵循欧姆定律的电路叫线性电路,不遵循欧姆定律的电路叫非线性电路。
1、部分电路的欧姆定律定律: 在一段不含电源的电路中,流过导体的电流与这段导体两端的电压成正比,与这段导体的电阻成反比。
其数学表示为:RUI =(1-1) 式中 I ——导体中的电流,单位)(A ;U ——导体两端的电压,单位)(V ; R ——导体的电阻,单位)(Ω。
电阻是构成电路最基本的元件之一。
由欧姆定律可知,当电压U 一定时,电阻的阻值R 愈大,则电流愈小,因此,电阻R 具有阻碍电流通过的物理性质。
例1:已知某灯泡的额定电压为V 220,灯丝的电阻为Ω2000,求通过灯丝的电流为多少?解: 本题中已知电压和电阻,直接应用欧姆定律求得:A R U I 11.02000220===例2:已知某电炉接在电压为V 220的电源上,正常工作时通过电炉丝的电流为A 5.0,求该电炉丝的电阻值为多少?解: 本题中已知电压和电流,将欧姆定律稍加变换求得:Ω===4405.0220I U R欧姆定律的几种表现形式:电压和电流是具有方向的物理量,同时,对某一个特定的电路,它又是相互关联的物理量。
因此,选取不同的电压、电流参考方向,欧姆定律的表现形式便可能不同。
1) 在图1.1 a.d 中,电压参考方向与电流参考方向一致,其公式表示为: RI U = (1-2)2) 在图1.1 b.c 中,电压参考方向与电流参考方向不一致,其公式表示为:RI U -= (1-3)3) 无论电压、电流为关联参考方向还是非关联参考方向,电阻元件的功率为:RU R I P RR22== (1-4)上式表明,电阻元件吸收的功率恒为正值,而与电压、电流的参考方向无关。
因此,电阻元件又称为耗能元件。
例3:应用欧姆定律求图1.1所示电路中的电阻R图1.1 电路中的电阻解:在图1.1.a 中,电压和电流参考方向一致,根据公式RI U =得: Ω===326I U R 在图1.1.b 中,电压和电流参考方向不一致,根据公式RI U -=得: Ω=--=-=326I U R(a ) (b) (c) (d)在图1.1.c 中,电压和电流参考方向不一致,根据公式RI U -=得: Ω=--=-=326I U R 在图1.1.d 中,电压和电流参考方向一致,根据公式RI U =得: Ω=--==326I U R 结论:在运用公式解题时,首先要列出正确的计算公式,然后再把电压或电流自身的正、负取值代入计算公式进行求解。