【优质课件】高教版中职数学拓展模块3.1排列与组合2优秀课件.ppt
- 格式:ppt
- 大小:814.00 KB
- 文档页数:15


【课题】3.1排列与组合(三)
【教学目标】
知识目标:
利用排列数组合数计算公式解决简单的应用问题.
能力目标:
学生的数学计算技能、计算工具使用技能和数学思维能力得到提高.
【教学重点】
排列与组合的综合应用.
【教学难点】
排列与组合的综合应用.
【教学设计】
实际应用过程中,要注意区分以下3点:(1)元素是否允许重复.元素不允许重复的是排列与组合问题;元素允许重复的是直接应用计数原理的问题.(2)元素是否有序.有序是排列问题,无序是组合问题.(3)是否需要分类或分步骤来进行研究.例7是简单的排列与组合训练题.要注意分清是排列问题还是组合问题.例8是产品检验的抽样计算问题,是组合应用的典型问题.在题目的说明中,介绍了对立事件.例9是照相排队问题,是排列应用的典型问题.要注意“先考虑特殊元素或特殊位置,再考虑一般元素或位置”这种分步骤研究方法的使用.例10是排列组合综合应用问题.“先取出元素,然后再安排”是这类问题的典型方法.例11元素可以重复,不是排列与组合问题,直接应用分步计数原理计算.【教学备品】
教学课件.
【课时安排】
2课时.(90分钟)
【教学过程】
【教师教学后记】。




排列组合教案第一部分基本内容一.课标要求:1.分类加法计数原理、分步乘法计数原理通过实例,总结出分类加法计数原理、分步乘法计数原理;能根据具体问题的特征,选择分类加法计数原理或分步乘法计数原理解决一些简单的实际问题;2.排列与组合通过实例,理解排列、组合的概念;能利用计数原理推导排列数公式、组合数公式,并能解决简单的实际问题;3.二项式定理能用计数原理证明二项式定理;会用二项式定理解决与二项展开式有关的简单问题。
二.命题走向本部分内容主要包括分类计数原理、分步计数原理、排列与组合、二项式定理三部分;考查内容:(1)两个原理;(2)排列、组合的概念,排列数和组合数公式,排列和组合的应用;(3)二项式定理,二项展开式的通项公式,二项式系数及二项式系数和。
排列、组合不仅是高中数学的重点内容,而且在实际中有广泛的应用,因此新高考会有题目涉及;二项式定理是高中数学的重点内容,也是高考每年必考内容,新高考会继续考察。
考察形式:单独的考题会以选择题、填空题的形式出现,属于中低难度的题目,排列组合有时与概率结合出现在解答题中难度较小,属于高考题中的中低档题目;预测20XX年高考本部分内容一定会有题目涉及,出现选择填空的可能性较大,与概率相结合的解答题出现的可能性较大。
三.要点精讲1.排列、组合、二项式知识相互关系表2.两个基本原理(1)分类计数原理中的分类;(2)分步计数原理中的分步;正确地分类与分步是学好这一章的关键。
3.排列(1)排列定义,排列数(2)排列数公式:系mn A =)!(!m n n -=n·(n-1)…(n-m+1);(3)全排列列:nn A =n!;(4)记住下列几个阶乘数:1!=1,2!=2,3!=6,4!=24,5!=120,6!=720; 4.组合(1)组合的定义,排列与组合的区别; (2)组合数公式:C n m=)!(!!m n m n -=12)1(1)m -(n 1)-n (⨯⨯⨯-⨯+ m m n ;(3)组合数的性质 ①C n m=C nn-m;②rn r n r n C C C 11+-=+;③rC n r=n·C n-1r-1;④C n 0+C n 1+…+C n n =2n;⑤C n 0-C n 1+…+(-1)nC n n=0,即 C n 0+C n 2+C n 4+…=C n 1+C n 3+…=2n-1;5.二项式定理(1)二项式展开公式:(a+b)n=C n 0a n+C n 1a n-1b+…+C n k a n-k b k+…+C n n b n; (2)通项公式:二项式展开式中第k+1项的通项公式是:T k+1=C n k a n-k b k; 6.二项式的应用(1)求某些多项式系数的和; (2)证明一些简单的组合恒等式;(3)证明整除性。

【课题】3.1排列与组合(三)
【教学目标】
知识目标:
利用排列数组合数计算公式解决简单的应用问题.
能力目标:
学生的数学计算技能、计算工具使用技能和数学思维能力得到提高.
【教学重点】
排列与组合的综合应用.
【教学难点】
排列与组合的综合应用.
【教学设计】
实际应用过程中,要注意区分以下3点:(1)元素是否允许重复.元素不允许重复的是排列与组合问题;元素允许重复的是直接应用计数原理的问题.(2)元素是否有序.有序是排列问题,无序是组合问题.(3)是否需要分类或分步骤来进行研究.例7是简单的排列与组合训练题.要注意分清是排列问题还是组合问题.例8是产品检验的抽样计算问题,是组合应用的典型问题.在题目的说明中,介绍了对立事件.例9是照相排队问题,是排列应用的典型问题.要注意“先考虑特殊元素或特殊位置,再考虑一般元素或位置”这种分步骤研究方法的使用.例10是排列组合综合应用问题.“先取出元素,然后再安排”是这类问题的典型方法.例11元素可以重复,不是排列与组合问题,直接应用分步计数原理计算.【教学备品】
教学课件.
【课时安排】
2课时.(90分钟)
【教学过程】
【教师教学后记】。
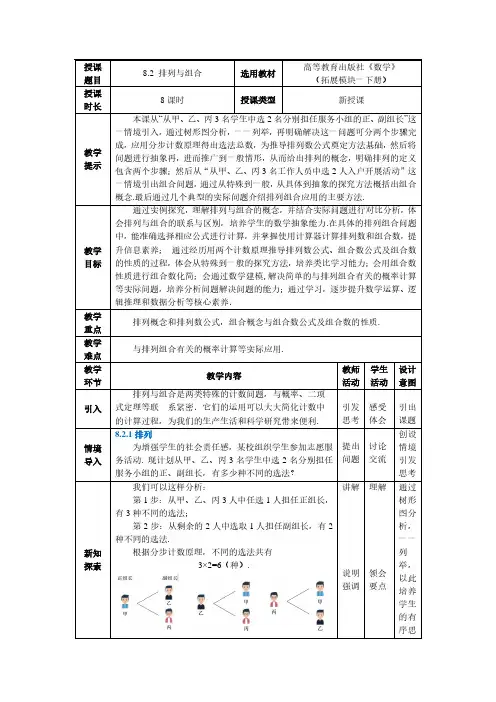
我们可以这样分析:第1步:从甲、乙、丙3人中任选1人担任正组长,有3种不同的选法;第2步:从剩余的2人中选取 1人担任副组长,有2种不同的选法.根据分步计数原理,不同的选法共有3×2=6(种). 讲解说明强调例1 写出从红、蓝、黄、绿4种不同的颜色中任取3种颜色的所有排列.分析要写出从4种不同的颜色中任取 3种颜色的排列,共需 3 个步骤.第1步,从红、蓝、黄、绿4种颜色中任取 1 种颜色放在第1位,有4种方法;第2步,从剩下的 3 种颜色中任取 1种颜色放在第2位,有3种方法;第3步,从剩下的2种颜色中任取1 种颜色放在第3位,有2种方法. 根据分步计数原理,从红、蓝、黄绿4种不同的颜色中任取3种颜色的所有排列方法有4×3×2=24种. 如图所示为第1 步选红色的排列情况,你能如图中这样列出其他的排列情况吗?解从红、蓝、黄、绿4种不同的颜色中任取 3种颜色的所有排列为:红蓝黄,红蓝绿,红黄蓝,红黄绿,红绿蓝,红绿黄;蓝红黄,蓝红绿,蓝黄红,蓝黄绿,蓝绿红,蓝绿黄;黄红蓝,黄红绿,黄蓝红,黄蓝绿,黄绿红,黄绿蓝;绿红蓝,绿红黄,绿蓝红,绿蓝黄,绿黄红,绿黄蓝. 提问引导讲解强调指导学习很多情况下,人们并不需要把所有的排列都写出来,讲解先研究排列数35P的计算方法,假定有顺序排列的3个空位,从5个不同元素a1,a2,a3,a4,a5中任取3个元素去填空位,1个空位填1个元素,1种填法就得到1个排列;反之,任一个排列都确定1种填法. 因此,所有不同的填法总数就是排列数.那么,有多少种不同的排法呢?具体可以分三个步骤完成.第1步:安排第1个位置的元素,可以从5 个元素中任选 1个元素填上,有5种方法.第2步:安排第2个位置的元素,可以从剩下的 4个元素中任选 1个元素填上,有4种方法.第3步:安排第3个位置的元素,可以从剩下的3个元素中任选1个元素填上,有3种方法.根据分步计数原理,得到不同的填法总数35P=5×4×3=60.同理,求排列数45P,可以按依次填4个空位来考虑,得到45P=5×4×3×2=120.下面研究从n个不同元素中取出m(m≤n)个元素的排列数P mn的计算方法,假定有顺序排列的m个空位,从n个不同元素a1,a2,a3,…,a n中任取m个元素去填空位,1个空位填1个元素,1种填法就得到 1个排列;反之,每1个排列确定1种填法.因此,所有不同的填法总数就是排列数P mn.第1步:从n个元素中任取1个元素填在第1位,共有n种方法;第2步:从剩余的(n-1)个元素中任取1个元素填在第2位,有(n-1)种方法;第3步:从剩余的(n-2)个元素中任取1个元素填在第3位,有(n-3)种方法;……第m步:从剩余的[n-(m-1)]个元素中任取1个元素填在第m位,有[n-(m-1)]种方法;根据分步计数原理,不同的填法总数为n (n-1)(n-2)…[n-(m-1)] .由此可得,从n个不同元素中任取m个元素的排列数讲解说明强调引领分析引导思考例2 计算.(1)运用公式(8-3)计算25P ,58P ,44P ; (2)运用计算器计算515P ,15101510P P . 解 (1) 25P =5×4=20;58P =8×7×6×5×4=6720; 44P =4×3×2×1=24.(2)利用计算器计算:由(2)看出,即.一般地,因此,排列数公式还可以写成为使公式在m =n 时也,规定0!=1.提问引导讲解强调指导学习引领分析补充说明1.填空.(1)若2Pn=30,则n=.(2)若2Pn =724Pn,则n=.2.利用排列数公式计算并用计算器验算结果.3.(1)小明打算从5本不同的笔记本中选2本分别作为日记本和纠错本,共有多少种选法?(2)小明打算从5种不同的笔记本中选2本分别作为日记本和纠错本,共有多少种选法?4.用 0,1,2,3可以组成多少个没有重复数字的四位数?提问巡视指导8.2.2 组合排列,如图所示.可以看出,对于每一个组合,相应的都有33P 种不同的排列.因此,从4个不同的元素中取3个元素的排列数34P ,可以分以下两个 步骤完成.第1步,先从4个不同的元素中选出3个元素组成一组,有34C 种选法;第2步,再将取出来的这3个元素进行全排列,有33P 种排法.根据分步计数原理,得34P =34C ·33P ,因此334433P 24C ===4P 6.一般地,从n 个不同元素中任取m 个元素的组合数为()()()121P C .P !==m mnnmmn n n n m m ---+ (8-7)公式(8-7)称为组合数公式,其中m ,n ∈N * ,且m ≤n . 由于()!P !mn n n m =-,因此,组合数的公式也可以写作()!C !!mn n m n m =-. (8-8)另外,规定0C n =1. 温馨提示公式(8-7)与公式(8-8)都是计算组合数的公式.计算组合数,通常使用公式(8-7),而进行有关组合数的证明,则通常使用公式(8-8). 讲解引领分析提示说明说明强调例6 计算.提问解 (1) 38C =876=56321⨯⨯⨯⨯;38C =87654=5654321⨯⨯⨯⨯⨯⨯⨯⨯;(3) 316C =161514=560321⨯⨯⨯⨯;利用计算器也可以方便地计算组合数.以计算 为例,依次输入“16nCr3”,即得560. 讲解强调指导探究与发现一般地,组合数具有如下性质: 性质1 C C =mn mn n -(m ≤n ).证明 因为()!C !!m n n m n m =-,所以C C =m n mn n-.性质1说明,从n 个不同的元素中取出 m 个元素的组合数就等于从n 个不同的元素中取出 n -m 个元素的组合数.一般地,当2n m >时,可以利用性质1,通过计算C n mn-的值得到C mn 的值,从而简化运算.性质2 11C C C =+mmm n n n -+(m ≤n ). 证明讲解引领分析提示说明即11C C C =+m m m n n n -+.说明强调例7 计算16171919C C +.解 由性质2,得161717191920C C C +=.由性质1,得1732020201918C =C ==1140.321⨯⨯⨯⨯例8 中国传统餐饮文化源远流长,菜肴在点任中形成了“八大菜系”,即鲁菜、川菜、粤菜、苏菜、闽菜、浙菜、湘菜、徽菜.某学校中餐烹饪专业为传承传统美食、弘扬工匠精神,计划举办“八大菜系” 厨艺大赛.(1)从 8个菜系中选出3个菜系作为比赛项目,有多少种选法?(2)从 8个菜系中选出3个菜系作为比赛项目,且川菜系必选,有多少种选法?分析 从8个菜系中选了个菜系的选法个数,等于从8 个不同的元素中取3个元素的组合数.如果川菜系必选,等于从除了川菜系以外的7个菜系中再取2个菜系的组合数. 解 (1)从 8个菜系中选出3个菜系作为比赛项目,不同的选法有(2)从 8个菜系中选出3个菜系作为比赛项目,且川菜系必选,不同的选法有例9 有2,3,5,7,11,13,17,19,23,29 十个质数.(1)从中任取两个数求它们的积,可以得到多少个不同的数?(2)从中任取两个数求它们的商,可以得到多少个不同的数?分析 在(1)中,求得的积与选出来的两个数的顺序无关,相当于求从10个不同元素中选出2个元素的组合数;在(2)中,商的结果与选出来的两个数谁是被除数、谁是除数有关,即与顺序有关,相当于求从10个不同的元素中选出2引领分析提问引导讲解强调指导引领分析个元素的排列数.解(1)从中任取两个数求它们的积,可以得到不同的数的个数为(2)从中任取两个数求它们的商,可以得到不同的数的个数为练习8.2.2先求从100 个三极管中任意抽取3个,有3100C种取法,再求从96个合格品中抽取3个合格品,有396C种取法,两者作差.解(1)抽取的3个三极管“全部是合格品”的不同方法有(2)根据分步计数原理,抽取的 3个三极管中“恰有2个次品”的不同方法有(3)抽取的3个三极管中“至少有 1个次品”的不同方法有讲解强调指导某技能大赛领奖典礼后,3 名老师与4名获奖学生站成(3)3名老师必须互不相邻,有多少种不同排法?分析在以上3个问题中,要“3名老师和4名学生站成一排”,就是这7个人进行全排列,有77P种排法:要实现“3 名老师必须站在一起”,可以分两步完成,第一步将3名老师视为一个整体,将其与4名学生进行排列,有55P种排法,第二步对3名老师进行排列,有33P种排法;要实现“3名老师必领互不相邻”,也需要分两步完成,第一步将4名学生排列好,有44P种排法,4 名学生之间和两端有5个空位,第二步将3名老师安排到这些空位中去,有35P种排法.解(1) 3 名老师与4名学生站成一排的不同排法有(2)根据分步计数原理,3名老师必须站在一起的不用排法有(3)根据分步计数原理,3名老师必须互不相邻的不用排法有提问引导讲解强调指导从数字 1,2,3,4,5 中任取了个,组成无重复数字提出如图所示,已知D、E、F三点分别为等边三角形ABC三边的中点,现从A、B、C、D、E、F这6个点中任取3点.(1)求这3个点构成三角形的概率;(2)求这3个点构成等边三角形的概率.提出问题分析从以上6个点中任取3个点,有36C种取法. 若这3个点构成三角形,则需从36C种方法中去除三点共线的3种取法,有(36C-3)种方法;这3个点可构成5个等边三角形,即ΔABC,ΔADF,ΔDBE,ΔDEF,ΔFEC.解(1)这3个点构成三角形的概率为(2)这3个点构成等边三角形的概率为提问引导讲解强调指导引导提问说明。

3.1排列与组合
重点分析:
本节课的重点是排列数与组合数的计算公式及其应用.难点是排列与组合的综合应用.突破难点的方法:
首先明确排列与组合的概念,可以把排列和组合的概念同时出示,让学生找出它们的联系与区别.排列的概念中有两个要素.一个是不同的元素,另一个是一定的顺序.在实际的运用过程中元素是否有序,元素有序的是排列问题,元素无序的是组合问题.对于排列与组合的综合运用问题,教学过程中讲清楚解决问题的思路、步骤,注重培养学生的分析问题、解决问题的能力.。


排列组合教案第一部分基本内容一.课标要求:1.分类加法计数原理、分步乘法计数原理通过实例,总结出分类加法计数原理、分步乘法计数原理;能根据具体问题的特征,选择分类加法计数原理或分步乘法计数原理解决一些简单的实际问题;2.排列与组合通过实例,理解排列、组合的概念;能利用计数原理推导排列数公式、组合数公式,并能解决简单的实际问题;3.二项式定理能用计数原理证明二项式定理;会用二项式定理解决与二项展开式有关的简单问题。
二.命题走向本部分内容主要包括分类计数原理、分步计数原理、排列与组合、二项式定理三部分;考查内容:(1)两个原理;(2)排列、组合的概念,排列数和组合数公式,排列和组合的应用;(3)二项式定理,二项展开式的通项公式,二项式系数及二项式系数和。
排列、组合不仅是高中数学的重点内容,而且在实际中有广泛的应用,因此新高考会有题目涉及;二项式定理是高中数学的重点内容,也是高考每年必考内容,新高考会继续考察。
考察形式:单独的考题会以选择题、填空题的形式出现,属于中低难度的题目,排列组合有时与概率结合出现在解答题中难度较小,属于高考题中的中低档题目;预测2007年高考本部分内容一定会有题目涉及,出现选择填空的可能性较大,与概率相结合的解答题出现的可能性较大。
三.要点精讲1.排列、组合、二项式知识相互关系表2.两个基本原理(1)分类计数原理中的分类;(2)分步计数原理中的分步;正确地分类与分步是学好这一章的关键。
3.排列(1)排列定义,排列数 (2)排列数公式:系mn A =)!(!m n n -=n·(n-1)…(n-m+1);(3)全排列列:nn A =n!;(4)记住下列几个阶乘数:1!=1,2!=2,3!=6,4!=24,5!=120,6!=720; 4.组合(1)组合的定义,排列与组合的区别; (2)组合数公式:C n m=)!(!!m n m n -=12)1(1)m -(n 1)-n (⨯⨯⨯-⨯+ m m n ;(3)组合数的性质 ①C n m=C nn-m;②rn r n r n C C C 11+-=+;③rC n r=n·C n-1r-1;④C n 0+C n 1+…+C n n =2n;⑤C n 0-C n 1+…+(-1)nC n n=0,即 C n 0+C n 2+C n 4+…=C n 1+C n 3+…=2n-1;5.二项式定理(1)二项式展开公式:(a+b)n=C n 0a n+C n 1a n-1b+…+C n k a n-k b k+…+C n n b n; (2)通项公式:二项式展开式中第k+1项的通项公式是:T k+1=C n k a n-k b k; 6.二项式的应用(1)求某些多项式系数的和; (2)证明一些简单的组合恒等式;(3)证明整除性。