当前位置：文档之家 › 3.1中职数学《排列与组合》ppt课件1(详细)

3.1中职数学《排列与组合》ppt课件1(详细)

  • 格式：ppt
  • 大小：688.00 KB
  • 文档页数：27

下载文档原格式

  / 27

合集下载

最新语文版中职数学拓展模块3.1排列、组合1课件PPT.ppt

最新语文版中职数学拓展模块3.1排列、组合1课件PPT.ppt

动 脑 思 考
= n(n 1)(n 2) (n m 1) 21 (n m) 21
（n
n! m)!
探
索 新
即
Pnm
（n
n! m)!
知
例2 计算 P52 和 P44．
解 P52 =5×4=20， P44 4！ 4 3 2 1 24．
巩
例3 小华准备从7本世界名著中任选3本，分别送给甲、乙、丙
第三章 概率与统计
3.1 排列与组合
基础模块中，曾经学习了两个计数原理．
一般地，完成一件事，有n类方式．第1类方式有 k1种方法， 第2类方式有 k2 种方法，……，第n类方式有 kn 种方法，那么完 成这件事的方法共有
创
N k1 k2 kn（种）．
设
上面的计数原理叫做分类计数原理．
导
北京→重庆，北京→上海， 重庆→北京，
入
重庆→上海，上海→北京， 上海→重庆．
我们将被取的对象（如上面问题中的民航站）叫做元素，那么上面的
动
问题就是：从3个不同元素中，任取2个，按照一定的顺序排成一列，可以
脑
得到多少种不同的排列．
思
考
一般地，从n个不同元素中任取m (m≤n)个不同元素，按照一定的顺
北京、重庆、上海3个民航站之间的直达航线，要准备多少种不同的机票？
创
这个问题就是从北京、重庆、上海3个民航站中，每次取出2个站，按照起
设 点在前，终点在后的顺序排列，求不同的排列方法的总数．
情
境
首先确定机票的起点，从3个民航站中任意选取1个，有3种不同的方法；然
兴 后确定机票的终点，从剩余的2个民航站中任意选取1个，有2种不同的方法． 趣 根据分步计数原理，有3×2=6种不同的方法，即需要准备6种不同的飞机票：

组合数学课件-第一章：排列与组合

组合数学课件-第一章：排列与组合

积分性质
若G(x)是母函数，则它的不定积分∫G(x)dx （其中C为常数）也是母函数。
线性性质
若G1(x)和G2(x)是两个母函数，则它们的 线性组合k1*G1(x)+k2*G2(x)（k1和k2是 常数）也是母函数。
微分性质
若G(x)是母函数，则它的导数G'(x)也是母 函数。
乘积性质
若G1(x)和G2(x)是两个母函数，则它们的 乘积G1(x)*G2(x)也是母函数。
对称性
C(n,m) = C(n,n-m)，即从n个元素中取出m个元 素的组合数与从n个元素中取出n-m个元素的组 合数相等。
递推关系
C(n,m) = C(n-1,m-1) + C(n-1,m)，即当前组合 数等于前一个元素在组合中和不在组合中的两种 情况之和。
边界条件
C(n,0) = C(n,n) = 1，即从n个元素中取出0个或 n个元素的组合数均为1。
典型例题解析
例1
从10个数中任取4个数，求其中最大数为6的组合数。
解析
此问题等价于从6个数（1至6）中取4个数的组合数，即 C(6,4)。
例2
在所有的三位数中，各位数字之和等于10的三位数有 多少个？
解析
此问题可转化为从9个数字（1至9）中取3个数字的组合 数，即C(9,3)，然后考虑三个数字的全排列，即3!，因此 总共有C(9,3) × 3!个符合条件的三位数。
组合与排列的关系
组合数可以看作是从n个元素中取出m个元素进行排 列的种数除以m的阶乘，即C(n，m)=A(n，m)/m!。 因此，在计算组合数时也可以利用排列数和容斥原 理来进行计算。
THANKS
隔板法
将n个相同的元素分成r组的方法数可以用母函数表示为 C(n+r-1,r)，其中C表示组合数。

人教版中职数学(拓展模块)3.1《排列、组合与二项式定理》ppt课件1

人教版中职数学(拓展模块)3.1《排列、组合与二项式定理》ppt课件1
所有组合的个数叫做组合数,用符号 Cnm表示.
组合与组合数
(3)组合数计数公式.
Cnm =⑥
Anm Amm
=⑦ n(n 1)(n 2) (n m 1) .
m!
n!
=⑧ m!(n m)! .
规定 Cn0 =1. (4)组合数的两个性质.
(ⅰ)
Cnm
=
C nm n
;
(ⅱ)
Cm n 1
=
Cnm
+ Cnm1
一、两个原理
3.分类和分步的区别 分类：完成一件事同时存在n类方法，每一类 都能独立完成这件事，各类互不相关.分步：完成一 件事须按先后顺序分n步进行，每一步缺一不可， 只有当所有步骤完成，这件事才完成.
一、两个原理
练习1： 书架上放有3本不同的数学书，5本 不同的语文书，6本不同的英语书．
（1）若从这些书中任取一本，有多少种不同的
二、 排列与排列数
(3)排列数计算公式.
Anm
=n(n-1)(n-2)…(n-m+1)=⑤
n!
(n m()其! 中m≤n).
(ⅰ)若m=n，排列称为全排列，记
=1·2·3·…·(n-1)·n=n!(称为n的阶乘)；
Ann (ⅱ)规定0!＝1.
组合与组合数
从n个不同元素中，取出m(m≤n)个不同元素组 成一组，叫做从n个不同元素中取出m个元素的一 个组合.
位整数（各位上的数字允许重复）？
解：要组成一个三位数，需要分成三个步骤：
第一步确定百位上的数字，从1～4这4个数字中任选一个数 字，有4种选法； 第二步确定十位上的数字，由于数字允许重复，共有5种选 法；
第三步确定个位上的数字，仍有5种选法．根据乘法原理， 得到可以组成的三位整数的个数是 N=4×5×5=100．

排列、组合 和二项式定理幻灯片PPT

排列、组合 和二项式定理幻灯片PPT

组合
组合数的概念和推导 组合数公式 组合数性质
CnmCnnm C n m 1C n mC n m 1
kCnk nCnk1
C k k C k k 1 C k k 2 C n k C n k 1 1
计数综合问题
先选后排
7.从3名男生和3名女生中，选出3名分别担 任语文、数学、英语的课代表，要求至少 有1名女生，则选派方案共有（ ）
其中能被5整除的四位数共有
个
二维：有5有0，有5无0，无5有0
主元：个位为0，个位为5（再根据需要细 分，选0与不选0）
在6名内科医生和4名外科医生中，内科主 任和外科主任各一名，现在要组成人医疗 小组送医下乡，依下列条件各有多少种方 法：
既有内科医生又有外科医生（间接考察）
既有主任又有外科医生
排列数应用
组合 组合数
组合数应用
二项式定理
教学内容
不仅有着许多直接应用，还是学习概率理 论的准备知识，而且由于其思维方法的新 颖性与独特性，因此它也是培养学生思维 能力的不可多得的好素材；作为初中多项 式乘法公式的推广——二项式定理，不仅 使前面组合等知识的学习得到强化，而且 与后面概率中的二项分布有着密切联系。
排列、组合 和二项式定理 幻灯片PPT
本课件PPT仅供大家学习使用 学习完请自行删除，谢谢！ 本课件PPT仅供大家学习使用 学习完请自行删除，谢谢！ 本课件PPT仅供大家学习使用 学习完请自行删除，谢谢！ 本课件PPT仅供大家学习使用 学习完请自行删除，谢谢！
知识结构
分类计数原理、分步计数原理
排列 排列数
3．展开式的每一项由若干个a和若干个b的乘积 构成，a和b的个数之和等于n，它可以表示为ankbk．

最新排列与组合ppt课件

最新排列与组合ppt课件

权变领导方式
菲德勒
组织环境 类型
上下级关 系
工作结构 职位权力 有效领导
方式
非常有利
好好好 高高低 强弱强
任务导向型
中间状态
好差 低高 弱强 人际关系型
பைடு நூலகம்
非常不利
差差差 高低低 弱强弱
任务导向型
目标途径领导理论(休斯)
理论观点：有效的领导者应该努力协助下属找到最好的途径，确定挑战 性的目标，并消除在实现过程中出现的重大障碍。 理论依据：期望理论和双因素领导理论。 四种领导方式： 指令型－领导者发布指示，下属不参加决策。 支持型－领导对下属很友善，并考虑职工要求。 成 就 指 向型 － 领导 为 下属 确 定 挑战 性 目标 ，并且 表 示相 信职 工 能 够达 到 这些目标。 参与型－职工参与决策和管理工作。
领导者的素质理论
▪ 领导素质是指领导者的品质、性格、学识、 能力、体质等方面特性的总和。
▪ 吉赛利： ▪ 领导八种个性特性：才智、主动性、督察
能力、自信、为员工所亲近、决断能力、 性别、成熟程度；
▪ 五种激励特征：对工作稳定的需求、对金 钱奖励的需求、对指挥别人和权力的需求、 对自我实现的需求、对职业成就的需求。
动组织和严格的劳动纪律，强调指标和效率，欣赏紧张有序、快节 奏的工作气氛，将全部精力用于工作任务本身，一定程度上忽视职 工利益、职工要求和工作情绪。 4. 关系型。 5. 兼备型。
领导方式连续统一体理论
以管理者为中心的领导――――――――――――――――― 以下属为中心的领导
一切由领 领导向其 领导提出 领导提出 领导提出 领导提出 领导允许
低 1.1 低
9.9
5.5
9.1

语文版中职数学拓展模块3.1《排列、组合》ppt课件3

语文版中职数学拓展模块3.1《排列、组合》ppt课件3
解1： 桔子：0 – 6；苹果：0 - 9 包括空篮：7*10=70 篮子不空：70-1=69
解2： s1=没有桔子的装法：9 s2=至少有1个桔子的装法：6*10 由加法原理 S=s1+s2 篮子不空： 9+60=69
例5 解：
在1000和9999之间有多少个具有不同数字 的奇数？
1-9 0-9 0-9 奇数
解 (1)每2个点唯一确定一条直线
n

C
2 25

25! 2!23!

25 24 2

300
(2)每3个点唯一确定一个三角形
n

C
3 25

25! 3!22!

25 24 23 23
例2 15选修数学课，其中12人来上课，他们随 便坐在教室的25个座位上。
共有多少中不同坐法？
解 (1)选择12个人来上课：
设8个车中有1个红车，3个蓝车，4个黄车。
S {1 R,3 B,4 Y}, 所以
8! 8!2
n 8!

1!3!4! 1!3!4!
定理3.4.3
设n个 车 共 有k种 颜 色 ， 第i种 颜 色 的 车ni个,
n n1 n2 nk。 则 在n n的 棋 盘 上 ， 非 攻

定理3.3.1
特别：

n r


P(n, r) r!

n! r!(n r)!
C
0 n

1,
C
1 n

n,
C
2 n

n(n 1) 2
C
r n

C
n n
r
定理3.3.2

排列组合ppt课件

排列组合ppt课件
排列组合基本公式 • 排列组合的应用 • 排列组合的扩展知识 • 练习题与答案解析
01
排列组合基本概念
排列的定义
排列的定义
从n个不同元素中取出m个元素（ m≤n），按照一定的顺序排成一列， 称为从n个不同元素中取出m个元素的 排列。
组合公式推导
根据乘法原理，组合数等 于从n个不同元素中取出m 个元素的排列数除以这m 个元素的全排列数。
组合公式证明
通过数学归纳法证明组合 公式。
排列组合公式的推导与证明
排列组合公式的推导
通过数学归纳法和乘法原理，逐步推导出排列和组合的公式。
排列组合公式的证明
通过数学归纳法和反证法，证明排列和组合公式的正确性。
机器学习
03
在机器学习中，排列组合用于描述样本空间和事件发生的可能
性，例如在朴素贝叶斯分类器中。
在统计学中的应用
概率分布
在统计学中，排列组合用于描述概率分布和随机事件的组合数量 ，例如在二项分布、多项分布等概率分布中。
统计推断
在统计推断中，排列组合用于计算样本数据的可能性和置信区间 ，例如在贝叶斯推断和参数估计中。
从n个不同元素中取出m个元素的所有组合方式。
排列组合在概率论中的应用
总结词
排列组合在概率论中有广泛的应用，它们是概率论中的基本概念之一。
详细描述
在概率论中，排列组合被广泛应用于各种概率模型和随机事件的计算中。例如，在计算随机事件的概率时，可以 使用排列组合来计算样本空间的大小和基本事件的数量。在计算条件概率时，可以使用排列组合来计算条件事件 的基本事件的数量。此外，在概率分布的计算中，排列组合也起着重要的作用。
3
组合的特性
组合无方向性，即顺序不影响组合的唯一性。

排列与组合综合应用课件

排列与组合综合应用课件

01
在数学领域的应用
排列与组合是数学的基础知识之一，其在数论、代数、几何等领域都有
广泛的应用。
02
在其他领域的应用
如物理学、化学、生物学等自然科学和社会科学领域都涉及到排列与组
合的应用。
03
数学建模和计算技术的应用
随着计算机技术的发展，排列与组合的应用更加广泛，如机器学习、数
据挖掘等领域都需要运用排列与组合的知识进行建模和计算。
区别
有序排列注重元素的顺序，无序排列注重元素的组合。
联系
在某些特定情况下，有序排列和无序排列可能相互转换。
组合中的“包含与排除”原则
包含
在组合中，如果一个集合 包括多个子集，那么这些 子集的并集就是该集合的 组合。
排除
在组合中，如果需要排除 某些特定的元素或子集， 那么这些元素或子集需要 从总集合中移除。
学、社会科学等领域都有广泛的应用。
排列与组合在解决实际问题中的具体应用
02
如组合优化问题、背包问题、图论中的最短路径问题等都可以
运用排列与组合的知识进行解决。
实际问题的抽象和建模
03
在实际问题中，需要将问题抽象为数学模型，如线性规划、整
数规划等，然后运用排列与组合的方法进行求解。
排列与组合在数学和其他领域的应用
排列与组合的公式及其推导方法也是解决复杂问题的基础，如加法 原理、乘法原理、容斥原理等。
排列与组合的公式应用
在解决实际问题时，需要根据问题的具体情况，灵活运用排列与组 合的公式，如组合数的应用、排列数的应用等。
排列与组合在解决实际问题中的应用
组合数学在实际问题中的应用
01
组合数学是排列与组合的理论基础，其在计算机科学、管理科

【人教版】中职数学(拓展模块)：3.1《排列、组合与二项式定理》课件

【人教版】中职数学(拓展模块)：3.1《排列、组合与二项式定理》课件
答：可以组成100个三位整数．
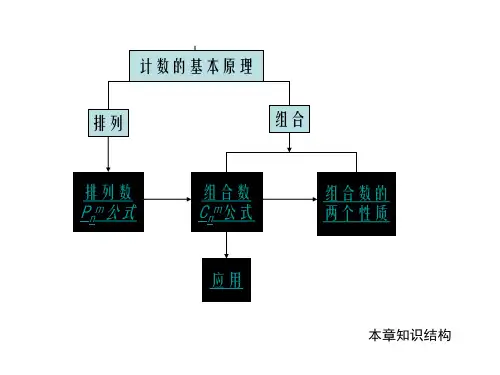
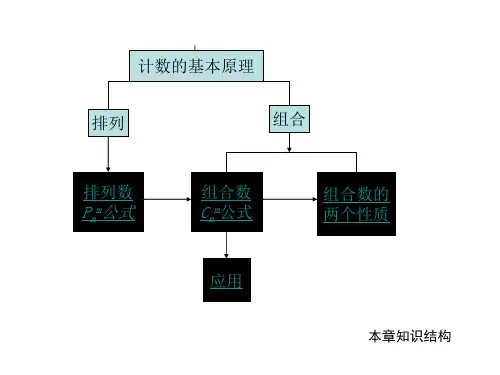
一、两个原理
题型一 利用两个计数原理求方法数
例1（1）现要排一份５天的值班表，每天
有一人值班，共有５人，每人可以多天值班 或不值班，但相邻两天不准由同一人值班， 问此值班表共有 1280 种不同排法.
一、两个原理
(1)值班表须依题设一天一天的分步 完成.第一天有5人可选，有5种排法，第二 天不能用第一天的人，有4种排法，同理， 第三天、第四天、第五天也有4种，故由分 步计数原理排值班表共有5×4×4×4×4=1280 种，应填1280.
一、两个原理
(2)三角形的三边长均为整数,且最长的边 长为11,则这样的三角形的个数有( C )
A.25个 B.26个 C.36个 D.37个
(2)设另两边长为x、y,且1≤x≤y≤11 (x、 y∈Z)， 构 成 三 角 形 ， 则 x+y≥12， 当 y取 11时 ， x=1,2,3,…,11,有 11个 ;当 y取 10时 ， x=2,3,…,10,有 ９ 个 ;当 y 取9时，x=3,4,…,9,共7个;……;当y取6时，x也只能为6，有 1个，故满足题设的三角形共有：11+9+7+5+3+1=36个，故
2.如果任何一类办法中的任何一种方 法都能完成这件事，即类与类之间是相互 独立的，即分类完成，则选用分类计数原 理；如果完成一件事要经历几个步骤（即 几步），且只有当这些步骤都做完，这件 事才能完成，即步与步之间是相互依存、 相互连续的，即分步完成，则选用分步计 数原理.
3.排列与组合的本质区别在于排列不 仅取而且排，即与顺序有关，而组合只取 出一组即可，与顺序无关.
为了参加学校的元旦文艺会演，某 班决定从爱好唱歌的４名男同学和５名女 同学中选派４名参加小合唱节目，如果要 求男女同学至少各选派１名，那么不同的 选派方法有多少种？

排列与组合ppt课件

排列与组合ppt课件

C34C11A22
C24C22
A
2 2
A22
）=84种.
探究提高 排列、组合综合题目，一般是将符合 要求的元素取出（组合）或进行分组，再对取出的 元素或分好的组进行排列.其中分组时，要注意 “平均分组”与“不平均分组”的差异及分类的标 准. 知能迁移3 已知10件不同产品中有4件是次品，现 对它们进行一一测试,直至找出所有4件次品为止. （1）若恰在第5次测试，才测试到第一件次品，第 十次才找到最后一件次品，则这样的不同测试方法 数是多少？ （2）若恰在第5次测试后，就找出了所有4件次品， 则这样的不同测试方法数是多少？
女生或没有女生，故可用间接法进行，
∴有 C152 C15 C74 C57=596种选法. （5）分三步进行：
第一步：选1男1女分别担任两个职务为 C17·C15 ；
第二步：选2男1女补足5人有
C
2 6
·
C14
种；
第三步：为这3人安排工作有
A
3 3
.
由分步乘法计数原理共有
C17 C15 C62 C14 A33 =12 600种选法.
列数公式即可.但要看清是全排列还是选排列；有
限制条件的排列问题，常见类型是“在与不在”、
“邻与不邻”问题，可分别用相应方法.
解 （1）从7个人中选5个人来排列，
有
A
5 7
=7×6×5×4×3=2
520种.
（2）分两步完成，先选3人排在前排，有 A种37方法，
余下4人排在后排，有 种A方44法，故共有
所以共有2
C
4 8
+
C83
=196种选法.
9分
方法二 间接法：
从10人中任选5人有C150种选法.

高教版中职数学(拓展模块)3.1《排列与组合》ppt课件3

高教版中职数学(拓展模块)3.1《排列与组合》ppt课件3
用符号Amn表示。
当两个排列的元素完全相同,且元素的排列 顺序相同称两个排列相同
判断下列问题是否是排列问题： 1、从2,3,4,5中任取两个数进行如下运算，分别有多少 种结果 A、相加 B、相减 C、相乘 D、相除
2、某班50名同学，假期约定每2人通一次信，共需写 多少信？
3、若把上题中写信改为通电话，共需通电话多少次？
排列数为： A53
排列问题，是取出m个元素后，还要按一定的 顺序排成一列，取出同样的m个元素，只要排 列顺序不同，就视为完成这件事的两种不同的 方法（两个不同的排列）．
由排列的定义可知，排列与元素的顺序有关， 也就是说与位置有关的问题才能归纳为排列问 题。当元素较少时，可以根据排列的意义写出 所有的排列．（树形图）
求从4个不同的元素中取出 3个元素的排列数
思考：从n个不同的元素中取出2个元素的排 列数 An2 是
多少？ An3 呢？
求从A、B、C、D四个元素中任取两个元 素的所有排列以及排列数．
解：所有排列有： AB、AC、AD、BA、BC、BD、CA、CB、
CD、DA、DB、DC．
排列数为： A42
排列数与排列是两个不同的概念：
注意： 定义中包含两个基本内容：
取出元素 按照一定的顺序排列
判断一个问题是否 是排列的标志
排列
从n个不同的元素中取出m(m≤n)个元素,按 照一定的顺序排成一列,叫做从n个不同元素中 取出m个元素的一个排列(arrangement).
从n个不同元素中取出m(m≤n)个元素的所有排 列的个数，叫做从n个不同元素中取出m个元素的 排列数，
用排列原理解决问题
求从3个不同的元素中取 出2个元素的排列数。
问题1 从甲、乙、丙3名同学中选出2名参加某天的一

3.1中职数学《排列与组合》ppt课件1(详细)

3.1中职数学《排列与组合》ppt课件1(详细)

探
序排成一列，叫做从n个不同元素中取出m个不同元素的一个排列．
索
新
当m＜n时叫做选排列，当m=n时叫做全排列．
知
例1 写出从4个元素a, b, c, d中任取2个元素的所有排列．
解 所有排列为
巩
ab, ac, ad,ba,bc,bd, ca, cb, cd, da.db, dc
固
知
分析 首先任取1个元
2023最新整理收集 do something
第三章 概率与统计
3.1 排列与组合
基础模块中，曾经学习了两个计数原理．
一般地，完成一件事，有n类方式．第1类方式有k1种方法， 第2类方式有 k2 种方法，……，第n类方式有kn 种方法，那么完
成这件事的方法共有
创
N k1 k2 kn（种）．
下面看一个问题：
北京、重庆、上海3个民航站之间的直达航线，要准备多少种不同的机票？
创
这个问题就是从北京、重庆、上海3个民航站中，每次取出2个站，按照起
设 点在前，终点在后的顺序排列，求不同的排列方法的总数．
情
境
首先确定机票的起点，从3个民航站中任意选取1个，有3种不同的方法；然
兴 后确定机票的终点，从剩余的2个民航站中任意选取1个，有2种不同的方法． 趣 根据分步计数原理，有3×2=6种不同的方法，即需要准备6种不同的飞机票：
本节完
从n个不同元素中任取m（m≤n）个不同元素的
所有排列的个数叫做从n个不同元素中任取m个不同
动 脑 思
A 元素的排列数．记做 m
n
考
探 索 新 知
如何计算 Amn 呢？
…
1号位
2号位
3号位
m号位

【优质课件】高教版中职数学拓展模块3.1排列与组合2优秀课件.ppt

【优质课件】高教版中职数学拓展模块3.1排列与组合2优秀课件.ppt

读书部分：阅读教材相关章节
继
续
书面作业：教材习题3.1（必做）
探
学习指导3.1（选做）
索
活
实践调查：用本课所学知识解决
动
探
生活中的实际问题
究
2005年11月7日7时33分
感谢各位老师！
祝： 身体健康
万事如意
例10 从6名男生和5名女生中选出3名男生和2名女生排成一 行，有多少种不同排法?
解 不同排法总数是
巩
C36
C52
P55

654 3 21

54 21
5 4 3
21

2400（0 种）．
固
知
分析
识
可以首先将男
典
生选出，再将女
型
生选出，然后对
例 题
选出的5名学生 排序．
例
题
例8 100件产品中有两件次品，从中任意抽取3件产品进行检
查．问
（1）一共有多少种不同的抽取方法？
巩
（2）抽取的3件产品中，恰有一件是次品的不同抽取方法有多 少种？
固
（3）抽取的3件产品中，至少有一件是次品的不同抽取方法有
知
多少种？
识
典
（2）分成两步来完成．第一本从2件次品中抽出1件，第二步从98 件正品中抽出的2件中.由分步计数原理知，恰有1件次品的不同抽取
例11 某城市的电话号码是从0、1、2、3、4、5、6、7、8、 9中取8个数字组成（允许数字重复），但0和1不能作为电话号码 的首位数．问该城市最多可以装多少部电话？
解 城市最多可以装电话的数量为
巩 固
C18 C研110究 C实110际 C问110 C110 C110 C110 C110 8107 8000000（ 0 部）．

排列与组合PPT教学课件

排列与组合PPT教学课件

小结
• 不用柔曼的音调来诉说个人的哀乐，也很少用热 烈的呼声来抒发对于旧世界的愤懑，而是用经过 锤炼的诗句，抒写旧中国农民的苦难与不幸，勤 劳与坚忍，让读者从咀嚼和回味中体会诗人深沉 的感情
臧克家正是以此独特的风格，为三十年代的诗坛吹来一阵 清新的风，引起读者的注意和重视
①能得到几个不同的分数？ ②其中有几个是真分数？几个假分数？
老马
总得叫大车装个够， 它横竖不说一句话， 背上的压力往肉里扣， 它把头沉重地垂下！
这刻不知道下刻的命， 它有泪只往心里咽， 眼里飘来一道鞭影， 它抬起头望望前面。
臧克家其人
• 臧克家(1905～ ) 现代诗人。山东诸 城人。有诗集《烙印》(1933)、《罪恶的 黑手》(1934) 。代表作《有的人》 。
加法原理：做一件事，完成它可以有 n 类办法，在第一类办法中
有m1种不同的方法，在第一类办法中有m2种不同的方法，… …， 在第n类办法中有mn种不同的方法。那麽完成这件事共有 N= m1+ m2+… …+ mn 种不同的方法。
乘法原理：做一件事，完成它需要分成n个步骤，做第一步有m1
种不同的方法，做第二步有m2种不同的方法，… …，做第n步有mn 种不同的方法。那麽完成这件事共有 N= m1× m2×… …×mn 种不 同的方法。
法； 含 1 本数学书和 1 本物理书的共有 7 × 5 = 35 种取法； 含 1 本语文书和 1 本物理书的共有 9 × 5 = 45 种取法。
由加法原理得 63 + 35 + 45 = 143 答：共有 143 种取法。
练习1：
1． 一件工作可以用两种方法完成。有5人会用第一种方 法完成，另有4人会用第二种方法完成。选出一个人来 完成这件工作，共有多少种选法？
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

探
序排成一列，叫做从n个不同元素中取出m个不同元素的一个排列．
索 当m＜n时叫做选排列，当m=n时叫做全排列．
新
知
.
4
例1 写出从4个元素a, b, c, d中任取2个元素的所有排列．
巩
解 所有排列为
固
a b ,a c ,a d ,b a ,b c ,b d ,c a ,c b ,c d ,d a .d b ,d c
第三章 概率与统计
3.1 排列与组合
.
1
基础模块中，曾经学习了两个计数原理．
一般地，完成一件事，有n类方式．第1类方式有 k 1 种方法，
第2类方式有 k 2 种方法，……，第n类方式有k n 种方法，那么完
创
成这件事的方法共有
设
Nk1k2Lkn （种）．
上面的计数原理叫做分类计数原理．
情
境
一般地，如果完成一件事，需要分成n个步骤，完成第1个步骤有
A3 100
970200
A
6 6
720
A15A52A35
85
A82结果的2倍
A84 2A82
1568
A
5 7
A
4 7
3
.
21
2计算：
n2345678 n!
.
22
3计算 ： 8名同学排成一排照相，有多少种排法？
.
23
3计算 ： 9名表演者站成一排表演，规定领唱者必须
站中间，朗诵者必须站在最右侧，问共有多 少种排法？
知
识
典 型
元元是素素本或或章象特 位 中例殊 置 经4这位 ， 常样置 分 使，， 步 用“然 骤 的首后 来 方先再 研 法考．考 究虑分 数 所 虑虑 问特字 以 问析一 题因殊不 分 题般”为能 成 ．百为两第位步一0上，考步的 先排百位上的数
例
字；第二步从剩
题
余的数字中任取 2个数排列．
.
14
分析 选出3本不同
A3 7765210．
的书，分别送给
典
即共有210种不同送法．
甲、乙、丙3位 同学，书的不同
型
排序，结果是不
例
同的.因此选法的 种数是从5个不
题
同元素中取3个
元素的排列数．
.
13
例4 用0，1，2，3，4，5可以组成多少个没有 重复数字的3位数？
解 所求三位数的个数为
巩 固
A 1 9A 9 29(98)648 ．
种 公
(n m )L2 1
式
考
（
n
n
! m
)
!
可 以
探
索
即
A
m n
（ n
n! m)!
新
知
.
12
例2
计算A
2 5
和
A
4．
4
解 ： A525420
巩
A 4 44 ！ 432 124 ．
固
例3 小华准备从7本世界名著中任选3本，分别送给甲、乙、丙
知
3位同学，每人1本，共有多少种选法？
识
解 不同的送法的种数是
自 解 ： A 5 2•A 2 15 4 24 0
我
反
思
百十个
目
2A、214
标 检
A
2 5
测
.
17
想一想：用0~9这10个数字，组成没有重复数字 的三位数?
自 解 ： A 5 2•A 2 15 4 24 0
我
反
思
百十个
目
标 检
A不为1 0 9
A
2 9
测
.
18
训练1： 由数字1，2，3，4能够组成多 少？
解 ：即：A 7 7 共= 7 有！ 5= 07 4 06 种 排5 法4 。 3 2 1 5 0 4 0
领唱者
朗诵者
.
24
4计算 ： 用1~5这5个数字，可以组成多少个没有重复
数字的4位数？其中有多少个4位数是5的倍 数？
解 没有重要数字的位数个数有： ： A54=5432120
其中是5的倍数有 ： A43=43224
知
分析
识
首先任取1个元 如果两个排列相同，那素么放不在仅左要边，然后
求这两个排列的元素完全在相剩同余，的而元素中任
典
且排列的顺序也要完全相取同1个．元素放在右边
型
．
例
题
.
5
例2 从10名集训的乒乓球运动员中，任选3名运动员，并排好 出场的先后次序参加比赛，有多少种不同的参赛方法？
解 由题意得参赛方法种数为：
考
探
A n m n n 1 n 2 L n m 1
索
新
特别地，当m=n时，由上式得全排列的种数为
这种记为n! 读作n的阶乘
知
An nnn1L321
.
11
变形，
动
A n m n (n 1 )(n 2 )L ( n - m + 1 )
计有 算两
脑 思
= n (n 1 )(n 2 )L(n m 1 )(n m )L2 1
巩
10x9x8=720(种）
固
知
分析
识
一
二
三
首先任取1个元 素放在左边，然后
在剩余的元素中任
典
取1个元素放在右边
．
型
例
10
9
8
题
.
6
习题 训练
1、写出红、黄、蓝3种颜色构成的全排列，并指出共有多少 种？
2、写出从a,b,c,d四个无素中任取2个元素的所有排列，并指 出共有多少种？
.
7
习题 训练
3、选排列和全排列有什么区别？
思考：
在A，B，C，D四个候选人中，选出正副班
运 长各一个，选法的种数是多少？
用
知
解：A42 4312
识
强 化 练 习
.
15
排列数计算公式的内容是什么？
理
论
A n m n • n 1 • n 2 L n m 1
升 华
A
m n
（ n
n! m)!
整
体
建
构
.
16
想一想：用1，2，3，4，5这五个数字，组成没 有重复数字的三位数， 其中偶数有多少个？
趣
北京→重庆，北京→上海， 重庆→北京，
导
入
重庆→上海，上海→北京， 上海→重庆．
.
3
我们将被取的对象（如上面问题中的民航站）叫做元素，那么上面的
动
脑
问题就是：从3个不同元素中，任取2个，按照一定的顺序排成一列，可以
思
得到多少种不同的排列．
考
一般地，从n个不同元素中任取m (m≤n)个不同元素，按照一定的顺
还有4名:
1 4
其余无要求:
A5 5-A4 45!4!96
A 1 4•A 4 44 4 3 2 1 9 6 此两学生也
有顺序
A
2 2
特点:此两名学生作为一个整体与其它三 人共四个元素进行排列(捆绑法)
A 2 2• A 4 4 2 1 4 3 . 2 1 4 8
20
P61 练习题
1、计算：
k 1 种方法，完成第2个步骤有 k 2 种方法，……，完成第n个步骤有 k n
兴
种方法，并且只有这n个步骤都完成后，这件事才能完成，那么完成
趣
这kn （种）．
入
上面的计数原理叫做分步计数原理．
.
2
下面看一个问题：
创
北京、重庆、上海3个民航站之间的直达航线，要准备多少种不同的机票？
5
.
25
本节完
： 课后任务
1、整理本课知识有解题思路 2、复习迎接期末考试。
.
26
此课件下载可自行编辑修改，此课件供参考！ 部分内容来源于网络，如有侵权请与我联系删除！
自
（1）三位数？
我 反
（2）没有重复数字三位数？
解 ： （ 1 ） 4 4 46 4
444
思
（ 2） A1 443224
目
标
检
测
.
19
训练2： 现有5名学生排成一排照相，问： （1）某名学生不能排在最左侧的不同排队方法有多少种？ （2）某两名学生必须相邻的不同排队方法有多少种？
某学 生
A 某学生除外
设
这个问题就是从北京、重庆、上海3个民航站中，每次取出2个站，按照起
点在前，终点在后的顺序排列，求不同的排列方法的总数．
情
境
首先确定机票的起点，从3个民航站中任意选取1个，有3种不同的方法；然
兴 后确定机票的终点，从剩余的2个民航站中任意选取1个，有2种不同的方法．
根据分步计数原理，有3×2=6种不同的方法，即需要准备6种不同的飞机票：
4、由2、3、5这3个数可组成多少个没有重复数字的3 位数？
.
8
本节完
.
9
从n个不同元素中任取m（m≤n）个不同元素的
动 所有排列的个数叫做从n个不同元素中任取m个不同
A 脑 元素的排列数．记做 m
思
n
考
探 索 新 知
.
10
如何计算
A
m n
呢？
…
1号位
2号位
3号位
m号位
动
脑
思
n 种 (n －1 )种 (n －2 )种 … [n －(m+1)]种