- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
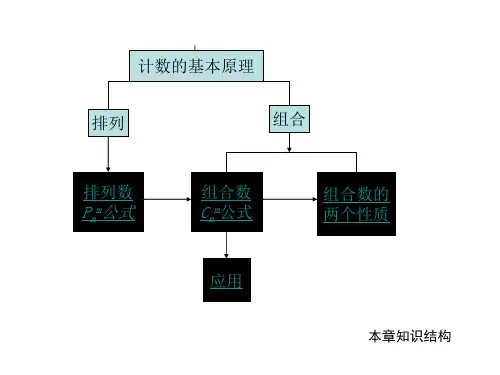
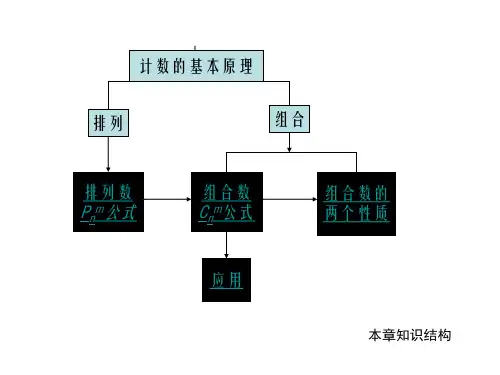
计数的基本原理
排列
组合
排列数
Pnm公式
组合数
Cnm公式
应用
组合数的 两个性质
本章知识结构
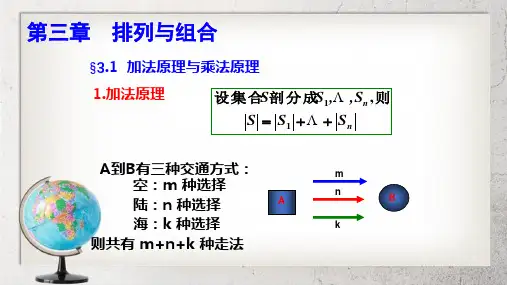
一、两个原理
1.分类加法计数原理 的n①类方m办法完1+法成,m在中2一+第有m件23m类 +事n办…种,有法+不mn中同类n种有的办不方m法同2法种,的在不方,第那同法1么类的.完办方成法法这中,件有…事m…共1种,有不在N同第=
少种不同的取法?
N=3×5+3×6+
5×6=63.
一、两个原理
练习2: 由数字0,1,2,3,4可以组成多少个三
位整数(各位上的数字允许重复)?
解:要组成一个三位数,需要分成三个步骤: 第一步确定百位上的数字,从1~4这4个数字中任选一个数 字,有4种选法; 第二步确定十位上的数字,由于数字允许重复,共有 5种选 法; 第三步确定个位上的数字,仍有5种选法.根据乘法原理, 得到可以组成的三位整数的个数是 N=4×5×5=100.
题型二 排列、组合数方程问题
例2 解下列方程:
(1)
P4 2x?1
=140
Px3;
(2)
C
x?1 x? 3
=
+ C x?1 x?1
+ C C x
x? 2
x?1
x? 2
.
(1)根据排列的意义及公式得 4≤2x+1 3≤x (2x+1)2x(2x-1)(2x-2)=140x(x-1)(x-2),
x≥3 则有
2.分步乘法计数原理 的种方 不法 同完的成,做方一第法件2步事,那有,么需m完要2种成分不这成同件n的个事方步共法骤有,,做…第…1步,做有第mn1步种有不m同n
N=② m1·m2·…·mn 种不同的方法 .
一、两个原理
3.分类和分步的区别 分类:完成一件事同时存在 n 类方法,每一类 都能独立完成这件事,各类互不相关 .分步:完成一 件事须按先后顺序分 n 步进行,每一步缺一不可, 只有当所有步骤完成,这件事才完成 .
二、 排列与排列数
(3)排列数计算公式 .
Anm =n(n-1)(n-2)…(n-m+1)=⑤
n!
(n ? m()其! 中m≤n).
(ⅰ)若m=n,排列称为 全排列,记
=1·2·3·…·(n -1)·n =n !(称为n 的阶乘 );
Ann (ⅱ)规定0!=1.
组合与组合数
从n个不同元素中,取出 m(m≤n)个不同元素组 成一组,叫做从 n 个不同元素中取出 m 个元素的一 个组合.
答:可以组成100个三位整数.
一、两个原理
题型一 利用两个计数原理求方法 数 例1(1)现要排一份5天的值班表,每天
有一人值班,共有5人,每人可以多天值班 或不值班,但相邻两天不准由同一人值班, 问此值班表共有 1280 种不同排法.
一、两个原理
(1)值班表须依题设一天一天的分步 完成.第一天有5人可选,有 5种排法,第二 天不能用第一天的人,有4种排法,同理, 第三天、第四天、第五天也有4种,故由分 步计数原理排值班表共有 5×4×4×4×4=1280种,应填1280.
一、两个原理
练习1: 书架上放有3本不同的数学书,5本 不同的语文书,6本不同的英语书.
(1)若从这些书中任取一本,有多少种不同的
取法?
答案:N=m1+m2+m3=3+5+6=14.
(2)若从这些书中,取数学书、语文书、英语 书各一本,有多少种不同的取法?
N=m 1×m 2×m 3=90.
(3)若从这些书中取不同的科目的书两本,有多
选C. 点评(1)是分步问题,用分步计数原
理;(2)是分类问题,用分类计数原理.
二、排列与排列数
从n个不同的元素中,任取M个元素, 按照一定的顺序排成一列,叫做从n个
不同的元素中取出M个元素的一个 排
列。
所有排列的个数叫做 排列数 ,用 Pnm
表示。
Pnm ? n(n?1)(n? 2)
(n? m?1)? n! (n? m)!
2
,
即
C1 x? 2
+
C2 x? 2
=
C2 x? 2
+
Cx4?
,
2
所以
C
1 x?
2
=C4 x?2源自,所以5=x+2,x=3,经检验知x=3.
点评 凡遇到解排列、组合的方程 ,
不等式问题时,应首先应用性质和 排列、组合的计算公式进行变形与 化简,并注意有关解排列、组合的 方程、不等式问题,最后结果都需 要检验.
所有组合的个数叫做 组合数,用符号 Cnm表示.
组合与组合数
(3)组合数计数公式.
Cnm =⑥
Anm Amm
=⑦ n(n ? 1)(n ? 2) ???(n ? m ? 1) .
m!
n!
=⑧ m!(n ? m)! .
规定 Cn0 =1. (4)组合数的两个性质.
(ⅰ)
Cnm
= Cn?m n
;
(ⅱ)
(4x-23)(x-3)=0, 解之并检验得x =3.
(2)由组合数的性质可得
+ + = + + C C C C C C x?1
x
x? 2
2
1
4
x?1
x?1
x? 2
x?1
x?1
x? 2
=
+ C C 2
4
x? 2
x? 2
.
又C x?1 x? 3
=
C
2 x?
3
,
所以Cx2? 3
=
C2 x? 2
+
C
4 x?
Cm n?1
=
Cnm
+ Cm?1 n
.
排列与组合的区别
排列与组合的共同点是“从 n个不同元
素中,任取 m 个不同元素”;而不同点是
排列要“按照一定的顺序排成一列”,而
组合却是“只需组成一组(与顺序无
关)” .因此,“有序”与“无序”是排列
与组合的重有要序标志.⑨“
”为无排序列问题,
⑩“ ”为组合问题.
题型三 结合两个计数原理 求排列、组合问题的方法数
例3用0,1,2,3,4 这五个数字,可以组
成多少个满足下列条件的没有重复数 字的五位数: (1)比21034大的偶数; (2)左起第二位、第四位是奇数的偶数.
(1)(方法一)可分五类:
当末位数字是0,而首位数字是2, A21 A22+ A22=6(个); 当末位数字是0,而首位数字是3或4,有A21 A33=12(个); 当末位数字是2,而首位数字是3或4,有A21 A33=12(个); 当末位数字是4,而首位数字是2,有 A22 +A11 =3(个); 当末位数字是4,而首位数字是3,有 A33 =6(个).
一、两个原理
(2)三角形的三边长均为整数 ,且最长的边 长为11,则这样的三角形的个数有( C )
A.25个 B.26个 C.36个 D.37个
(2)设另两边长为x、y,且1≤x≤y≤11 (x 、 y∈Z) , 构 成 三 角 形 , 则 x+y≥12 , 当 y 取 11 时 , x=1,2,3,…,11,有11个;当y取10时,x=2,3,…,10,有9个;当y取 9时,x=3,4,…,9,共7个;……;当y取6时,x也只能为 6,有1 个,故满足题设的三角形共有: 11+9+7+5+3+1=36个,故