下载文档原格式
基础部分——运动学第7 章刚体平面运动连杆作什么运动呢？行星齿轮机构行星轮作什么运动？第7章刚体平面运动运动过程中，刚体上任一点到某一固定平面的距离保持不变刚体上任一点都在与某一固定平面平行的平面内运动沿直线轨道滚动的车轮机械臂小臂的运动平面运动的刚体在自身平面内运动的平面图形SxyOxyOASIIxyOA SII平面图形上任一线段的位置位置x Ay AϕB )(1t f x A =)(2t f y A =)(3t f =ϕ平面运动平移+ 转动xyOASIIxAyAϕB基点⇒O ′O O ′O O ′O′三种运动?平面运动基点平移基点转动注意：平移动系不一定固结与某一实际刚不一定固结与某一实际刚体。
O ′xyO平移动系O'x'y'x ′y ′O ′基点推广结论：刚体的平面运动可以分解为随基点的平移和绕基点的转动问题一：x yOA SIIx Ay AϕB问题二：随基点的平移与基点的选择有无关系绕基点的转动与基点的选择有无关系结论：同一瞬时平面图形绕任一基点转动的ω、α都相同。
动点re a 点的速度合成定理SAv ωABB v A v ?=B v x ′y ′基点BA v 三种运动？大小? 方向?BAA B v v v +=AωA Av BAv Bv平面图形上任一点的速度等于基点的速度与该点随图形绕基点转动速度的矢量和。
SAv ωABAv BAv Bv BAA B v v v +=试一试：基点法作平面运动。
[例7-1] 曲柄—滑块机构解：转动。
r 3ABOωϕAv Bv BAv 基点大小方向?AvBA3ABOωϕAv B v BAv Av ABω转向？= v 滑块Bϕ大小方向A 32SAv ωAB Av BAv Bv 平面图形上任意两点的速度在该两点连线上的投影（大小和正负号）相等。
速度投影定理[][]ABA AB B v v =[]ABBA vr 3再分析例7-1ABOωϕAv Bv Bv解：请比较两种方法A 32如何解释这种现象？观察到了什么现象？[先看一照片]若选取速度为零的点作为基点，则求解速度问题•基点法•速度投影法优点：缺点:优点：缺点:SAv ωAv BAv Bv AA 为基点B有没有更好的方法呢？Aω0≠ω唯一存在AL ′证明:MAA M v v v +=SA v v MAv LMPωAv PA =∴0=⋅−=ωPA v v A P ∵该瞬时瞬时速度中心速度瞬心唯一性：瞬时性：不共线，故速度均不为零。
力学（第二版）漆安慎习题解答第七章刚体力学第七章 刚体力学 一、基本知识小结⒈刚体的质心定义：∑⎰⎰==dm dm r r mr m r c i i c //求质心方法：对称分析法，分割法，积分法。
⒉刚体对轴的转动惯量定义：∑⎰==dm r I r m I ii 22平行轴定理 I o = I c +md 2 正交轴定理 I z = I x +I y.常见刚体的转动惯量：（略） ⒊刚体的动量和质心运动定理∑==c c a m F v m p⒋刚体对轴的角动量和转动定理∑==βτωI I L⒌刚体的转动动能和重力势能c p k mgy E I E ==221ω⒍刚体的平面运动=随质心坐标系的平动+绕质心坐标系的转动动力学方程：∑∑==c c c c I a m F βτ（不必考虑惯性力矩）动能：221221cc c k I mv E ω+= ⒎刚体的平衡方程∑=0F， 对任意轴∑=0τ二、思考题解答7.1 火车在拐弯时所作的运动是不是平动？答：刚体作平动时固联其上的任一一条直线，在各时刻的位置（方位）始终彼此平行。
若将火车的车厢看作一个刚体，当火车作直线运行时，车厢上各部分具有平行运动的轨迹、相同的运动速度和加速度，选取车厢上的任一点都可代替车厢整体的运动，这就是火车的平动。
但当火车拐弯时，车厢上各部分的速度和加速度都不相同，即固联在刚体上任一条直线，在各时刻的位置不能保持彼此平行，所以火车拐弯时的运动不是平动。
7.2 对静止的刚体施以外力作用，如果合外力为零，刚体会不会运动？答：对静止的刚体施以外力作用，当合外力为了零，即0i c F ma ==∑时，刚体的质心将保持静止，但合外力为零并不表明所有的外力都作用于刚体的同一点。
所以，对某一确定点刚体所受合外力的力矩i i iM M r F ==⨯∑∑不一定为零。
由刚体的转动定律M J α=可知，刚体将发生转动。
比如，置于光滑水平面上的匀质杆，对其两端施以大小相同、方向相反，沿水平面且垂直于杆的两个作用力时，杆所受的外力的合力为零，其质心虽然保持静止，但由于所受合外力矩不为零，将作绕质心轴的转动。
教学时数:16 教学目的与要求:（1）本章以刚体绕固定轴的转动为重点，要使学生熟练掌握有关规律。
（2）着重讲述角速度、角加速度及转动惯量的概念。
（3）要指出质心与重心的联系和区别。
（4）讲授动量矩定理与动理矩守恒定律时均应包括质点的与质点组的两个方面。
通过实例说明动量矩守恒定律的重要性。
（5）对刚体的平面运动不作一般研究，仅讨论圆柱体滚动问题，可结合车轮的滚动进行讲授。
（6）对回转仪的运动可通过演示进行观察，并应用矢量方法定性地说明其初级原理，不作深入分析。
教学重点:刚体的平动、转动和定轴转动；刚体在定轴转动中的力矩，转动定律，转动惯量，力矩的功和转动动能，角动量和角动量守恒定律。
质心，质心运动定律；刚体的平面运动；进动。
教学难点:定轴转动；刚体在定轴转动中的力矩，转动定律; 转动动能，角动量和角动量守恒定律; 刚体的平面运动 本章主要阅读文献资料:顾建中编 《力学教程》 人民教育出版社 赵景员、王淑贤编 《力学》 人民教育出版社 漆安慎 杜婵英 《〈力学基础〉学习指导》 高等教育出版社刚体力学刚体 定义：物体内任意二点距离不变的物体称为刚体。
说明：⑴刚体是理想模型⑵刚体模型是为简化问题引进的。
刚体运动（1）平动：刚体内任一直线方位不变。
特点：各点运动状态一样，如：a 、v 等都相同，故可用一个点来代表刚体运动。
（2）转动：(a ）绕点转动(b ）绕轴转动：刚体中所有点都绕一直线作圆周运动说明：刚体的任何运动都可看作平动与转动的合成。
（乒乓球飞行等）定轴转动定义：转轴固定时称为定轴转动。
转动特点：⑴刚体上各点的角位移θ∆相同（如：皮带轮），各点的ω、α相同。
⑵刚体上各点的)(ωr v =、)(2ωr a n =、()αr a t=一般情况下不同。
说明：⑴ω 是矢量，方向可由右手螺旋法则确定。
见图4-1。
(2)r v ⨯=ω图 4-1刚体的动量和质心运动定理一、刚体的质心刚体的质心的计算，同质点系的质心的计算方法完全一样。
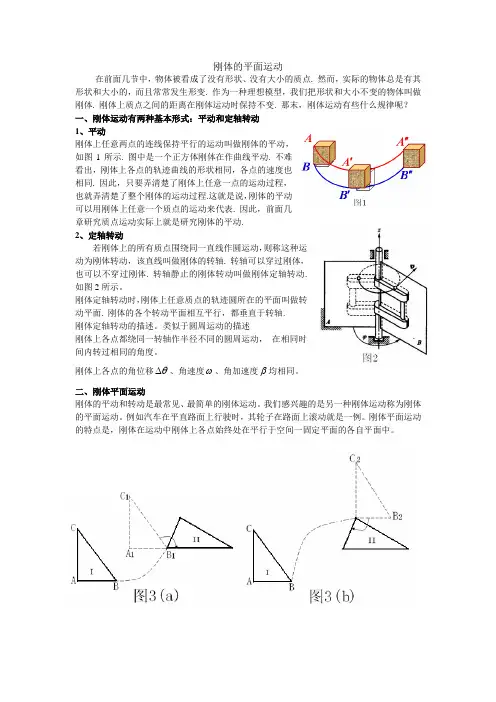
刚体的平面运动在前面几节中，物体被看成了没有形状、没有大小的质点. 然而，实际的物体总是有其形状和大小的，而且常常发生形变. 作为一种理想模型，我们把形状和大小不变的物体叫做刚体. 刚体上质点之间的距离在刚体运动时保持不变. 那末，刚体运动有些什么规律呢？一、刚体运动有两种基本形式：平动和定轴转动1、平动刚体上任意两点的连线保持平行的运动叫做刚体的平动，如图1所示. 图中是一个正方体刚体在作曲线平动. 不难看出，刚体上各点的轨迹曲线的形状相同，各点的速度也相同. 因此，只要弄清楚了刚体上任意一点的运动过程，也就弄清楚了整个刚体的运动过程.这就是说，刚体的平动可以用刚体上任意一个质点的运动来代表. 因此，前面几章研究质点运动实际上就是研究刚体的平动.2、定轴转动若刚体上的所有质点围绕同一直线作圆运动，则称这种运动为刚体转动，该直线叫做刚体的转轴. 转轴可以穿过刚体，也可以不穿过刚体. 转轴静止的刚体转动叫做刚体定轴转动.如图2所示。
刚体定轴转动时，刚体上任意质点的轨迹圆所在的平面叫做转动平面. 刚体的各个转动平面相互平行，都垂直于转轴.刚体定轴转动的描述。
类似于圆周运动的描述刚体上各点都绕同一转轴作半径不同的圆周运动，在相同时间内转过相同的角度。
刚体上各点的角位移θ∆、角速度ω、角加速度β均相同。
二、刚体平面运动刚体的平动和转动是最常见、最简单的刚体运动。
我们感兴趣的是另一种刚体运动称为刚体的平面运动。
例如汽车在平直路面上行驶时，其轮子在路面上滚动就是一例。
刚体平面运动的特点是，刚体在运动中刚体上各点始终处在平行于空间一固定平面的各自平面中。
1、刚体平面运动概述和运动分解（1）如图3所示，刚体运动中由位形Ⅰ到位形Ⅱ，总可以认为以刚体上任意选定的参考点（称为基点）为代表的刚体的平动，加上刚体绕此参考点的一个转动的叠加完成。
（2）由图3（a ）、（b ）看出，基点选取不同，刚体平动运动将不同，但绕基点的转动却是相同的。
力学（第二版）漆安慎习题解答第七章刚体力学第七章刚体力学一、基本知识小结1.刚体的质心定义：r c m i r i/ m r c rdm/ dm求质心方法：对称分析法，分割法，积分法。
2.刚体对轴的转动惯量定义：I m i r i2I r2dm平行轴定理I o = l c+md2正交轴定理I z = X+I y.常见刚体的转动惯量：（略）3.刚体的动量和质心运动定理p mv c F ma c4.刚体对轴的角动量和转动定理L I I5.刚体的转动动能和重力势能E k ?I 2E p mgy c6•刚体的平面运动=随质心坐标系的平动+绕质心坐标系的转动动力学方程： F ma c c I c c（不必考虑惯性力矩）动能：E k 2mv；今I c c27.刚体的平衡方程、思考题解答火车在拐弯时所作的运动是不是平动答：刚体作平动时固联其上的任一一条直线，在各时刻的位置（方位）始终彼此平行。
若将火车的车厢看作一个刚体，当火车作直线运行时，车厢上各部分具有平行运动的轨迹、相同的运动速度和加速度，选取车厢上的任一点都可代替车厢整体的运动，这就是火车的平动。
但当火车拐弯时，车厢上各部分的速度和加速度都不相同，即固联在刚体上任一条直线，在各时刻的位置不能保持彼此平行，所以火车拐弯时的运动不是平动。
对静止的刚体施以外力作用，如果合外力为零，刚体会不会运动r r答：对静止的刚体施以外力作用，当合外力为了零，即Fi ma c 0时，刚体的质心将保持静止，但合外力为零并不表明所有的外力都作用于刚体的同一点。
所以，对某一确定点刚体所受合外力的力矩M Mi r i Fi不一定为零。
由刚体的转动定律M J可知，刚体将发生转动。
比如，置于光滑水平面上的匀质杆，对其两端施以大小相同、方向相反，沿水平面且垂直于杆的两个作用力时，杆所受的外力的合力为零，其质心虽然保持静止，但由于所受合外力矩不为零，将作绕质心轴的转动。
如果刚体转动的角速度很大，那么（1）作用在它上面的力是否一定很大（2）作用在它上面的力矩是否一定很大M r i F sin j J J「答：由刚体的定轴转动定律dt可知，刚体受对轴的合外力矩正比于绕定轴转动角速度的时间变化率。
第7.5节 刚体平面运动的动力学
7.5.1 10m 搞得烟筒因底部损坏而倒下来，求其上端到达地面时的线速度。
设倾倒时底部未移动。
可近似认为烟筒为均质杆。
解：烟筒的长度l =10m 。
设烟筒上端到达地面的瞬间，烟筒绕其底部的转动角速度为ω。
在倾倒过程中，只受重力作用，做的功为：mg ⋅½l 。
由刚体定轴转动的动能定理：
l
g
ml
I I l mg 32
31221
21=
∴==⋅ωω
烟筒上端到达地面时的线速度为：
s m gl l v /2.17108.933≈⨯⨯===ω
7.5.2 用四根质量各为m 长度各为l 的均质细杆制成正方形框架，可围绕其中一边的中点在竖直平面内转动，支点O 是光滑的．最初，框架处于静止且AB 边沿竖直方向，释放后向下摆动，求当AB 边达到水平时，框架质心的线速度C v。
以及框架作用于支点
的压力N ．
解：先求正方形框架对通过其质心且与其垂直的转轴（质心轴）的转动惯量：
框架的质心位于框架的中心，即两条对角线的交点上。
每根细杆对其本身的质心轴的转动惯量：212
10ml I =
，细杆的质心与框架的质心的距离为l 21
，由平行轴定理：
234
2210])([4ml l m I I c =⋅+⋅=
再由平行轴定理，得框架对通过0点的转轴的转动惯量：
237221)(4ml l m I I c =⋅+=
(1)求框架质心的线速度v c
框架在下摆过程中，只有重力做功，机械能守恒。
选取杆AB 达到水平时框架质心位置位势能零点，得：
gl
l v l h m M I Mgh c l
g
c c 7
321712212
214=
==
∴===ωωω
（2）求框架对支点的压力N
以框架为研究对象，它受到重力M g 和支点的支撑力N 的作用，由质心运动定理：
c a M g M N =+
取自然坐标系，τ沿水平方向，n 铅直向上，得投影方程：
β
τττc n c c n n Mh Ma N mg
mg mg N mg l gl m h v M Ma Mg N n
===+=⇒=⋅===-73
7247
242173
2744:
ˆ:ˆ
在铅直位置时，外力矩为0，故角加速度β=0，==〉N τ = 0
7.5.3 由长为l ，质量各为m 的均质细杆组成正方形框架，其中一角连于光滑水平转轴O ，转轴与框架所在平面垂直．最初，对角线OP 处于水平，然后从静止开始向下自由摆动．求OP 对角线与水平成450时P 点的速度，并求此时框架对支点的作用力．
解：先求正方形框架对通过其质心且与其垂直的转轴（质心轴）的转动惯量：
框架的质心位于框架的中心，即两条对角线的交点上。
每根细杆对其本身的质心轴的转动惯量：212
10ml I =
，细杆的质心与框架的质心的距离为l 21
，由平行轴定理：
23
4
2210])([4ml l m I I c =⋅+⋅= 框架的质心距o 点的距离为：
l 2
2
，由平行轴定理得框架通过o 点的转轴的转动惯量为
()
23
102
2
24ml l m
I I c =+= （1）求p 点的速度vp
框架在下摆过程中，只有重力做功，机械能守恒。
选取对角线op 与水平成450角时框架质心位置为势能零点，得：
gl
l v l h m M I Mgh p l
g
c c 5
356212
212
24===
∴===ωωω
（2）求框架对支点的压力N
以框架为研究对象，它受到重力M g 和支点的支撑力N 的作用，由质心运动定理：
c a M g M N =+
取自然坐标系，n 沿op 方向，τ沿垂直于op 方向，得投影方程：
τ
τMa Mg N Ma Mg N n n =-=-0
045sin 45cos
β
ωτc l g c n l a g
l l a =⋅===5622
56222
mg mg mg N n 245
132
25212=⋅
+=∴ 由定轴转动定理:
=⇒=ββI l Mg 21
f 2
7.5.4 质量为m 长为l 的均质杆，其B 端放在桌上，A 端用手支住，
使杆成水平．突然释放A 端，在此瞬时，求： (1)杆质心的加速度, (2)杆B 端所受的力．
解：(1)βτI = →β⋅=⋅2
3
12ml l mg l g 23=∴β g l a 4
3
2=⋅=β
(2)由质心运动定理：
mg ma N mg 43=
=- →mg N 4
1
=
7.5.5 下面是均质圆柱体在水平地面上作无滑滚动的几种情况，求地面对圆柱体的静摩擦力
f .
(1)沿圆柱体上缘作用以水平拉力F ，柱体作加速滚动．
(2)水平拉力F 通过圆柱体中心轴线，柱体作加速滚动． (3)不受任何主动力的拉动或推动，柱体作匀速滚动．
(4)在主动力偶矩τ的驱动下加速滚动．设柱体牛径为R 解：规定前进方向和顺时针方向为正方向。
假设静摩擦力方向
向后，其余受力情况如图所示。
对每种情况，都可以根据质心
定理、绕质心轴的转动定理和无滑滚动条件，建立三个
方程求解。
⑴R a mR R f F ma f F c c ββ==+=-,)(,2
21
可求得f = - F/3,负号说明静摩擦力方向与假设方向相反，应向前。
⑵R a mR fR ma f F c c ββ===-,,2
21
可求得f = F/3,正号说明静摩擦力方向与假设方向相同，向后。
⑶ a c = 0 , f = 0
⑷R a mR fR ma f c c ββτ==+=-,,221,求得R f 32τ-=
负号说明静摩擦力方向与假设方向相反，应向前。
7.5.6 板的质量为M ，受水平力F 的作用，沿水平面运动．板与平面间的摩擦系数为μ．在板上放一半径为R 质量为M 2的实心圆柱，此圆柱只滚动不滑动．求板的加速度． 解：g M M f )(21+=μ 对圆柱：
F(1)F(2)
转动定理：ββ222
12R M I R f ==
质心运动定理：C a M f 22=
对板：质心运动定理：
Ma f f F =--12
由于圆柱在板上只滚不滑
C a R a +=β
联立解得：
23
12)(M M g
M M F a ++-=
μ
7.5.7 在水平桌面上放置一质量为m 的线轴，内径为b ，外径为R ，其绕中心轴转动惯量为
23
1mR ．线轴和地面之间的静摩擦系数为μ. 线轴受一水平拉力F ，如图所示．
(1)使线轴在桌面上保持无滑滚动之F 最大值是多少?
(2)若F 和水平方向成θ角，试证，cos θ>b/R 时，线轴向前滚动；cos θ<b/R 时，线轴向后滚动。
解：（1）当线轴在桌面上只滚不滑时
ββ2
3
1mR I fR Fb ==- ma F f =- mg f μ≤
βR a =
联立解得：b
R mgR
F 34+=
μ
（2）若线轴向前滚动，则有：
F f ττ> 且 f F ≥θcos
即：
Fb fR > →
R
b F f > f F ≥θcos →F
f
≥θcos
R b /cos >∴θ
若线轴向后滚动，则有：
F f ττ< 且 f F ≤θcos
即：
Fb fR < →
R
b F f < f F ≤θcos →F
f
≤θcos
R b /cos <∴θ
7.5.8氧分子总质量为5.30x10-26kg ，对于通过其质心且与二原子连线垂直的轴线的转动惯量为10x10-46kg ⋅m 2．设在气体中某氧分子运动的速率为500m/s ，且其转动动能为其平动动能的2/3，求这一氧分子的角速率．
7.5.9，一质量为m ，半径为r 的均质实心小球沿圆弧形导轨自静止开始无滑滚下，圆弧形导轨在铅直面内，半径为R ．最初，小球质心与圆环中心同高度．求小球运动到最低点时的速率以及它作用于导轨的正压力．
解：设小球运动到最低点时，其质心速度为v ，绕质心转动的角速度为ω，由机械能守恒，有
2252
21221)()(ωmr mv r R mg +=-
无滑滚动条件：ω=v/r , 代入上式，可求得 g r R v )(107
-=
在最低点应用质心运动定理： )/(2
r R mv mg N -=-
mg g g m r R v g m N 73
10722)()]/([=+=++=∴，
作用于导轨的正压力与此等大，方向向下。
7.5.10你用力蹬自行车，近似认为车匀速行驶于水平路面上．你能否估计研究一下所受的空气阻力是多少?(提示：参考(4.2.1)算输出给自行车轮盘的功率．设法通过简单的实验估计经链条传至后面驱动轮损失的功率．计算作用于驱动轮的功率．然后再设法估算空气阻力．因为是估算，你可以采用近似的手法)．。
