江西省丰城中学2016届高三上学期数学周练试卷(文科)(12.8)

丰城中学2015-2016学年上学期高三周练试卷数 学 （文科重点班，尖子班）命题人：张燃 审题人：张业彬 2016.3.15一.选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1. 已知}2,1,0,1,2{--=A ，)}12lg(|{+==x y x B ，则=B A ( )A.∅B. }1,0,1{-C.}2,1,0{D.}2,1,0,1{-2. 已知)1,2(-A ，)2,0(C ，)5,3(=AB ，则||BC =( )A.6B. 29C.8D.123. 已知i i z 31)3(-=-，则=z （ ）A.i --3B. i +-3C.i --6D.i +64. 2016年春节，小红、小芳、小英、小丽四个同学相互发短信，小红不给小英发短信的概率是（ ）A.41B. 43C.161D.8180 5. 已知椭圆)0(12222>>=+b a b y a x 的离心率31=e ，半焦距为c ，抛物线cy x 22=的准线方程为2-=y ， 则椭圆的标准方程为（ ）A.181222=+y xB.221144128x y += C.114412822=+y x D.112822=+y x 6. 扇形的半径为3，中心角为 120，把这个扇形折成一个圆锥，则这个圆锥的体积为（ ）A.πB.32C. 322D.π322 7. 设数列}{n a 是的等差数列，n S 为其前n 项和.若368S S =，853=-a a ，则20a =（ ）A. 4B. 36C. 74-D.808. 执行如图所示的程序框图，输出的S 值为-4时，则条件框内应填写（ ）A ．3?i >B ．5?i <C ．4?i >D ．4?i <。

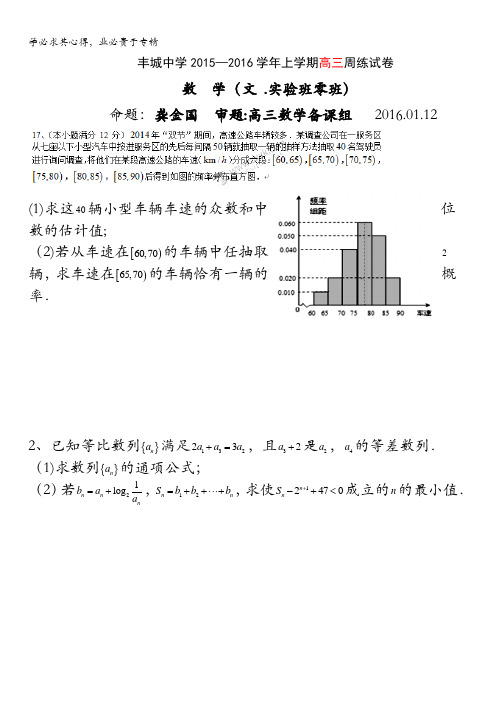
丰城中学2015—2016学年上学期高三周练试卷数 学（文 .实验班零班）命题：龚金国 审题:高三数学备课组 2016.01.12(1)求这40辆小型车辆车速的众数和中位数的估计值;（2)若从车速在[)60,70的车辆中任抽取2辆，求车速在[)65,70的车辆恰有一辆的概率．2、已知等比数列{}na 满足13223a a a +=，且32a +是2a ，4a 的等差数列． （1)求数列{}na 的通项公式； （2）若21log n n nb a a =+，12n n S b b b =++⋅⋅⋅+，求使12470n nS +-+<成立的n 的最小值．3．已知a，b，c分别是△ABC内角A，B，C的对边，sin2B=2sinAsinC．(Ⅰ）若a=b，求cosB；(Ⅱ)设B=90°，且a=,求△ABC的面积．4、已知直线:l43100++=，半径为2的圆C与l相切，圆心C在x轴上且x y在直线l的右上方．（1)求圆C的方程；（2）过点()1,0M的直线与圆C交于A，B两点(A在x轴上方)，问在x轴正半轴上是否存在定点N，使得x轴平分∠ANB？若存在，请求出点N的坐标；若不存在，请说明理由．5．如图，在多面体ABCDEF中,底面ABCD是边长为2的正方形，四边形BDEF是矩形,平面BDEF⊥平面ABCD，BF=3，G和H分别是CE和CF的中点．（Ⅰ）求证：AC⊥平面BDEF；（Ⅱ)求证：平面BDGH∥平面AEF；(Ⅲ)求多面体ABCDEF的体积．6．已知F1,F2是椭圆+=1（a＞b＞0）的两个焦点，O为坐标原点,点P（﹣1，)在椭圆上，且•=0,⊙O是以F1F2为直径的圆，直线l：y=kx+m与⊙O相切，并且与椭圆交于不同的两点A，B （1）求椭圆的标准方程；（2）当•=λ,且满足≤λ≤时,求弦长｜AB｜的取值范围．7．已知函数f（x）的导函数f′(x)=x2+2ax+b（ab≠0)，且f（0）=0．设曲线y=f(x)在原点处的切线l1的斜率为k1，过原点的另一条切线l2的斜率为k2．（1）若k1：k2=4：5，求函数f（x）的单调区间；（2）若k2=tk1时，函数f（x）无极值,且存在实数t使f（b）＜f（1﹣2t）成立，求实数a的取值范围．(I ）若函数()f x 在定义域内单调递减，求实数a 的取值范围； （II)若对任意()0,x e ∈,都有唯一的40,x e e -⎡⎤∈⎣⎦，使得()()2002g x f x x =+成立，求实数a 的取值范围．参考答案2016.01。

丰城中学2015-2016学年上学期高三周考试卷数 学（文 .实验班零班）一、选择题（本大题共小题，每小题分，共5分在每个题给出的四个选项中，有且只有一项是符合题目要求的，请将答案填写在答卷纸上）1、过点（4,0）且斜率为错误!未找到引用源。

的直线交圆错误!未找到引用源。

于A ，B 两点，C 为圆心，则错误!未找到引用源。

的值为（ ）A 、6B 、8C 、错误!未找到引用源。

D 、42、已知数列{错误!未找到引用源。

}为等差数列，错误!未找到引用源。

是它的前n 项和，若错误!未找到引用源。

，错误!未找到引用源。

，则错误!未找到引用源。

=（ ） A 、32 B 、36 C 、40 D 、423、已知双曲线错误!未找到引用源。

的一条渐近线方程是错误!未找到引用源。

，则该双曲线的离心率等于（ ）A 、错误!未找到引用源。

B 、错误!未找到引用源。

C 、错误!未找到引用源。

D 、错误!未找到引用源。

4、满足约束条件错误!未找到引用源。

的目标函数错误!未找到引用源。

的最大值是（ ）A 、-6B 、e+1C 、0D 、e-15、设定义域为R 的函数错误!未找到引用源。

，则关于x 的方程错误!未找到引用源。

有5个不同的实数解错误!未找到引用源。

，则错误!未找到引用源。

=（ ）A 、错误!未找到引用源。

B 、错误!未找到引用源。

C 、2D 、16、点A 是抛物线21:2(0)C y px p =>与双曲线22222:1(0,0)x y C a b a b-=>>的一条渐近线的交点（异于原点），若点A 到抛物线1C 的准线的距离为p ，则双曲线2C 的离心率等于（ ） A ．2 B ．2 C ．5 D ．47、已知符号函数1,0sgn()0,01,0x x x x >⎧⎪==⎨⎪-<⎩，则函数2()sgn(ln )ln f x x x =-的零点个数为（ ）A ．1B ．2C ．3D ．4 8、有下列命题： ①在函数cos()cos()44y x x ππ=-+的图象中，相邻两个对称中心的距离为π； ②“5a ≠且5b ≠-”是“0a b +≠”的必要不充分条件；③已知命题:p 对任意的x R ∈，都有sin 1x ≤，则“p ⌝是：存在x R ∈，使得sin 1x >”； ④在ABC ∆中，若3sin 4sin 6,4sin 3cos 1A B B A +=+=，则角C 等于30o或150o。

．向量()()AB MB BO BC OM ++++化简后等于（．AB B ．AC C ．AM D ．BC(,)απ∈π,1tan()47απ+=,那么αsin 15757- ．已知向量(1,1),(2,),a b x ==若a b +与a b -平行，则实数轴的交点，则tan APB ∠=．关于平面向量,,a b c ．下列判断中正确的是（ ）．若a b a c ⋅=⋅，则b c = ．若(1,)a k =，(2,6)b =-，//a b ，则1k =a b a b +=-，则0a b ⋅= ．若a 与b 是单位向量，则1a b ⋅=现有四个函数：①sin y x x =⋅；②c o s x ；③c o s y x x =⋅④2x y x =⋅的图象分）如下：xsin y x =．向左平移3π个单位长度，再把所得各点的横坐标缩短到原来的．向左平移3π个单位长度，再把所得各点的横坐标伸长到原来的π61OA =，3OB =(,)mOA n OB m n +∈，则nA ．3B ．3且21AP AB AC =+， AQ ＝5AP 1-AC ，4．如上图，在四边形ABCD 中，向量,,AB a AC b ==则AD = （ 22(1)2a b -+ B ．22(1)2a b ++22(1)2a b +-D ．22(1)2a b +-中，点D 是BC 的中点，过点()0>λλAE ，()0AC AF μμ=>，则41+的最小值是（C ．5 D 中，若2BE EA =，2AD DC =，()DE CA BC λ=-，则实数____________________5,0OB OC ⋅=，则六边形边长的一半．当小正六边形沿着大正六边形的边滚动4周后返回出发时的位置，记在这个过程中向量OA 围绕着点于 ．(0θ∈，当且仅当θ ∵AD DP = ∴2BAP θ=∠。

丰城中学2015-2016学年上学期高三周考试卷数 学（文 .实验班零班）一、选择题：本大题共12小题，每小题5分，共60分．在每个小题给出的四个选项中，只有一项是符合题目要求的． 1．已知集合{}2A y y x ==，(){}lg 2B x y x ==-，则AB =A ．[]0,2 B ．[)0,2 C ．(],2-∞D ．(),2-∞2．欧拉公式cos sin ix e x i x =+(i 为虚数单位)是由瑞士著名数学家欧拉发明的，它将指数函数的定义域扩大到复数，建立了三角函数和指数函数的关系，它在复变函数论里占有非常重要的地位，被誉为“数学中的天桥”．2ie 在复平面中表示的复数位于A ．第一象限B ．第二象限C ．第三象限D ．第四象限 3．已知()sin f x x x =-+，命题0)(),2,0(:<∈∀x f x p π，则A ．p 是假命题，0)(),2,0(:≥∈∀⌝x f x p πB ．p 是假命题，0)(),2,0(:0≥∈∃⌝x f x p πC ．p 是真命题，0)(),2,0(:≥∈∀⌝x f x p πD ．p 是真命题，0)(),2,0(:0≥∈∃⌝x f x p π4．设{}n a 是等差数列，n S 是其前n 项和，且56678,S S S S S <=>，则下列结论错误的是 A ．0d < B ．70a = C ．95S S >D ．67n S S S 与均为的最大值5．若偶函数()f x 在(,0]-∞上单调递减，3224(log 3),(log 5),(2)a f b f c f ===，则,,a b c 满足 A ．a b c <<B ．b a c <<C ．c a b <<D ．c b a << 6．已知正数,x y 满足20,350x y x y -≤⎧⎨-+≥⎩则2z x y =--的最小值为A ．2B ．0C ．2-D ．4- 7．在等腰ABC ∆中，4BC =，AB AC =，BA BC ⋅=A ．4-B ．4C ．8-错误！未找到引用源。

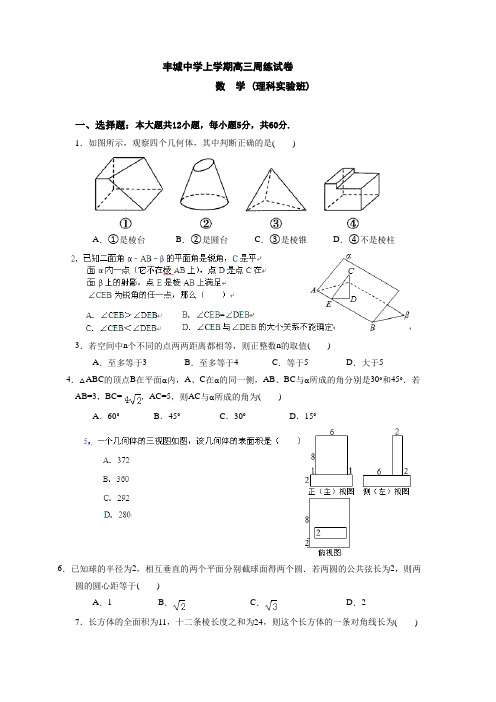
丰城中学上学期高三周练试卷数学 (理科实验班)一、选择题：本大题共12小题，每小题5分，共60分.1．如图所示，观察四个几何体，其中判断正确的是()A．①是棱台B．②是圆台C．③是棱锥D．④不是棱柱3．若空间中n个不同的点两两距离都相等，则正整数n的取值()A．至多等于3 B．至多等于4 C．等于5 D．大于54．△ABC的顶点B在平面α内，A、C在α的同一侧，AB、BC与α所成的角分别是30°和45°．若AB=3，BC=，AC=5，则AC与α所成的角为()A．60°B．45°C．30°D．15°6．已知球的半径为2，相互垂直的两个平面分别截球面得两个圆．若两圆的公共弦长为2，则两圆的圆心距等于()A．1 B．C．D．2 7．长方体的全面积为11，十二条棱长度之和为24，则这个长方体的一条对角线长为()A．B．C．5 D．69．已知二面角α﹣l﹣β的大小为50°，P为空间中任意一点，则过点P且与平面α和平面β所成的角都是35°的直线的条数为()A．1 B．2 C．3 D．4 10．已知将给定的两个全等的正三棱锥的底面粘在一起，恰得到一个所有二面角都相等的六面体，并且该六面体的最短棱长为2．则最远的两顶点的距离是()A．2 B．C．3 D．二、填空题：本大题共4小题，每小题5分，共20分.13．设有四个条件：①平面γ与平面α，β所成的锐二面角相等；②直线a∥b，a⊥平面α，b⊥平面β；③a，b是异面直线，a⊂平面α，b⊂平面β，a∥β，b∥α；④平面α内距离为d的两条平行直线在平面β内的射影仍为两条距离为d的平行直线，则其中能推出α∥β的条件有．(写出你认为正确的所有条件的序号)丰城中学上学期高三周练答题卡一、选择题(本大题共12个小题，每小题5分，共60分) 姓名：13． 14． 15． 16.三、解答题(本大题共有2小题，共20分，把答案填在所给区域内)丰城中学上学期高三周练参考答案数学(理科实验班)2015.12.8一、选择题(本大题共12个小题，每小题5分，共60分)4个点两两距离相等，由三角形的两边之和大于第三边，则不成立；n大于4，也不成立；在空间中，4个点两两距离相等，构成一个正四面体，成立；若n＞4，由于任三点不共线，当n=5时，考虑四个点构成的正四面体，，则小球的半径为：，=＞在两个Rt△PAM与Rt△PBM中，AM是公共边及PB=2PA∴PA2﹣t2=4PA2﹣(6﹣t)2解得PA2=12﹣4t∴PM=∴S=×AB×PM=×6×=3=3≤12即三角形面积的最大值为12故选A二、填空题(本大题共有4小题，每小题5分，共20分．把答案填在题中横线上)13．②③ 14。

2015-2016学年江西省宜春市丰城中学高三（上）第四次月考数学试卷（文科）一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，选出符合题目要求的一项.）1．已知集合A={x|y=}，B={y|y=}，则A∩B=（）A．[3，+∞）B．（﹣∞，﹣1]∪[3，+∞）C．（﹣∞，1]D．R2．已知i是虚数单位，若复数（a+i）（2﹣i）是纯虚数，则实数a等于（）A．2 B．C．﹣D．﹣23．已知a=，b=log2，c=，则（）A．a＞b＞c B．a＞c＞b C．c＞a＞b D．c＞b＞a4．已知命题“∃x∈R，使2x2+（a﹣2）x+2＜0”是假命题，则实数a的取值范围是（）A．（﹣∞，﹣2）B．[﹣2，6] C．（6，+∞）D．（﹣2，6）5．如图，某几何体的正视图与侧视图都是边长为1的正方形，且体积为．则该几何体的俯视图可以是（）A．B．C．D．6．下列命题中，m，n表示两条不同的直线，α、β、γ表示三个不同的平面．①若m⊥α，n∥α，则m⊥n；②若α⊥γ，β⊥γ，则α∥β；③若m∥α，n∥α，则m∥n；④若α∥β，β∥γ，m⊥α，则m⊥γ．正确的命题是（）A．①③B．②③C．①④D．②④7．函数f（x）=Asin（ωx+φ）（其中A＞0，|φ|＜）的图象如图所示，为了得到f（x）的图象，则只需将g（x）=sin2x的图象（）A．向右平移个长度单位B．向左平移个长度单位C．向右平移个长度单位D．向左平移个长度单位8．||=1，||=，且与的夹角为45°，当|﹣x|取得最小值时，实数x的值为（）A．1 B．2 C．D．9．从正方体六个面的对角线中任取两条作为一对．其中所成的角为60°的共有（）A．24对B．30对C．48对D．60对10．已知函数f（x）=，则下列结论正确的是（）A．f（x）是偶函数B．f（x）是增函数C．f（x）是周期函数D．f（x）的值域为[﹣1，+∞）11．正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为（）A．B．16πC．9πD．12．已知函数，且函数y=f（x）﹣x恰有3个不同的零点，则实数a的取值范围是（）A．（0，+∞）B．[﹣1，0）C．[﹣1，+∞）D．[﹣2，+∞）二、填空题（本大题共4小题，每小题5分，共20分）13．已知数列1，a1，a2，8是等差数列，数列1，b1，b2，b3，16是等比数列，则的值为．14．在△ABC中，内角A，B，C的对边分别是a，b，c，若a2﹣b2=bc，sinC=2sinB，则A=．15．若关于x，y的不等式组（k是常数）所表示的平面区域的边界是一个直角三角形，则k=．16．给出定义：若m﹣＜x≤m+（其中m为整数），则m叫做离实数x最近的整数，记作{x}，即{x}=m．在此基础上给出下列关于函数f（x）=x﹣{x}的四个命题：①点（k，0）是y=f（x）的图象的对称中心，其中k∈Z；②y=f（x）的定义域是R，值域是（﹣，]；③函数y=f（x）的最小正周期为1；④函数y=f（x）在（﹣，]上是增函数．则上述命题中真命题的序号是．三、解答题（本大题共6小题，共70分）17．设函数f（x）=|x﹣1|+|x﹣a|，（1）若a=﹣1，解不等式f（x）≥3；（2）如果x∈R，f（x）≥2，求a的取值范围．18．在△ABC中，角A，B，C所对的边分别为a，b，c，且满足csinA=acosC1）求角C大小；（2）求sinA﹣cos（B+）的最大值，并求取得最大值时角A，B的大小．19．已知等差数列{a n}满足a2=0，a6+a8=10．（1）求数列{a n}的通项公式；（2）求数列{}的前n项和．20．如图，在△ABC中，∠B=，AB=BC=2，P为AB边上一动点，PD∥BC，P为AB边上一动点，PD∥BC交AC于点D，现将△PDA沿PD翻折至△PDA′，使平面PDA′⊥平面PBCD．（1）当棱锥A′﹣PBCD的体积最大时，求PA的长；（2）若点P为AB的中点，E为A′C的中点，求证：A′B⊥DE．21．如图1，在矩形ABCD中，E，F分别是AB，CD的中点，沿EF将矩形BEFC折起，使∠CFD=90°，如图2所示；（Ⅰ）若G，H分别是AE，CF的中点，求证：GH∥平面ABCD；（Ⅱ）若AE=1，∠DCE=60°，求三棱锥C﹣DEF的体积．22．已知函数f（x）=e x（sinx+cosx）+a（a为常数）．（Ⅰ）已知a=﹣3，求曲线y=f（x）在（0，f（0））处的切线方程；（Ⅱ）当0≤x≤π时，求f（x）的值域；（Ⅲ）设g（x）=（a2﹣a+10）e x，若存在x1，x2∈[0，π]，使得|f（x1）﹣g（x2）|＜13﹣e成立，求实数a的取值范围．2015-2016学年江西省宜春市丰城中学高三（上）第四次月考数学试卷（文科）参考答案与试题解析一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，选出符合题目要求的一项.）1．已知集合A={x|y=}，B={y|y=}，则A∩B=（）A．[3，+∞）B．（﹣∞，﹣1]∪[3，+∞）C．（﹣∞，1]D．R【考点】交集及其运算．【分析】求出A中x的范围确定出A，求出B中y得到范围确定出B，找出两集合的交集即可．【解答】解：由A中y=，得到x2﹣2x﹣3≥0，即（x﹣3）（x+1）≥0，解得：x≤﹣1或x≥3，即A=（﹣∞，﹣1]∪[3，+∞），由B中y=≥0，得到B=[0，+∞），则A∩B=[3，+∞），故选：A．2．已知i是虚数单位，若复数（a+i）（2﹣i）是纯虚数，则实数a等于（）A．2 B．C．﹣D．﹣2【考点】复数代数形式的乘除运算．【分析】化简（a+i）（2﹣i）=（1+2a）+（2﹣a）i，再由复数（a+i）（2﹣i）是纯虚数，得到实部为零，虚部不为零，求解即可得答案．【解答】解：（a+i）（2﹣i）=2a﹣ai+2i+1=（1+2a）+（2﹣a）i，∵复数（a+i）（2﹣i）是纯虚数，∴实部为零，虚部不为零，即1+2a=0，2﹣a≠0．∴a=．故选：C．3．已知a=，b=log2，c=，则（）A．a＞b＞c B．a＞c＞b C．c＞a＞b D．c＞b＞a【考点】对数值大小的比较．【分析】判断a、b、c与1，0的大小，即可得到结果．【解答】解：a=∈（0，1），b=log2＜0，c=log＞1．∴c＞a＞b．4．已知命题“∃x∈R，使2x2+（a﹣2）x+2＜0”是假命题，则实数a的取值范围是（）A．（﹣∞，﹣2）B．[﹣2，6] C．（6，+∞）D．（﹣2，6）【考点】命题的真假判断与应用．【分析】根据特称命题的否定是全称命题，转化为不等式恒成立进行求解即可．【解答】解：命题“∃x∈R，使2x2+（a﹣2）x+2＜0”是假命题，则“∀x∈R，使2x2+（a﹣2）x+2≥0”是真命题，∵二次函数开口向上，要使它大于0恒成立，只需要判别式△≤0，即（a﹣2）2﹣4×2×2=a2﹣4a﹣12=（a﹣6）（a+2）≤0，得﹣2≤a≤6，故实数a的取值范围是[﹣2，6]．故选：B5．如图，某几何体的正视图与侧视图都是边长为1的正方形，且体积为．则该几何体的俯视图可以是（）A．B．C．D．【考点】简单空间图形的三视图．【分析】解法1：结合选项，正方体的体积否定A，推出正确选项C即可．解法2：对四个选项A求出体积判断正误；B求出体积判断正误；C求出几何体的体积判断正误；同理判断D的正误即可．【解答】解：解法1：由题意可知当俯视图是A时，即每个视图是变边长为1的正方形，那么此几何体是立方体，显然体积是1，注意到题目体积是，知其是立方体的一半，可知选C．解法2：当俯视图是A时，正方体的体积是1；当俯视图是B时，该几何体是圆柱，底面积是，高为1，则体积是；当俯视是C时，该几何是直三棱柱，故体积是，当俯视图是D时，该几何是圆柱切割而成，其体积是．6．下列命题中，m，n表示两条不同的直线，α、β、γ表示三个不同的平面．①若m⊥α，n∥α，则m⊥n；②若α⊥γ，β⊥γ，则α∥β；③若m∥α，n∥α，则m∥n；④若α∥β，β∥γ，m⊥α，则m⊥γ．正确的命题是（）A．①③B．②③C．①④D．②④【考点】平面的基本性质及推论．【分析】由题意，m，n是两条不同的直线，α，β，γ是三个不同的平面，由空间中的线与面、面与面的位置关系对四个选项进行判断得出正确选项，①选项由线面垂直的条件进行判断，②选项用面面平等的判定定理判断，③选项由线线平等的条件进行验证，④选项由平行于同一平面的两个平面互相平行和一条直线垂直于两个平行平面中的一个，则这条直线必平行于另一个平面进行判断．【解答】解：由题意，m，n是两条不同的直线，α，β，γ是三个不同的平面考察①选项，此命题正确，若m⊥α，则m垂直于α中所有直线，由n∥α，知m⊥n；考察②选项，此命题不正确，因为垂直于同一平面的两个平面的位置关系是平行或相交；考察③选项，此命题不正确，因为平行于同一平面的两条直线的位置关系是平行、相交或异面；考察④选项，此命题正确，因为α∥β，β∥γ，所以α∥γ，再由m⊥α，得到m⊥γ．故选C．7．函数f（x）=Asin（ωx+φ）（其中A＞0，|φ|＜）的图象如图所示，为了得到f（x）的图象，则只需将g（x）=sin2x的图象（）A．向右平移个长度单位B．向左平移个长度单位C．向右平移个长度单位D．向左平移个长度单位【考点】函数y=Asin（ωx+φ）的图象变换．【分析】由函数的最值求出A，由周期求出ω，由五点法作图求出φ的值，从而得到函数f （x）的解析式．再根据y=Asin（ωx+φ）的图象变换规律得出结论．【解答】解：由函数f（x）=Asin（ωx+φ）的图象可得A=1，=，解得ω=2．再由五点法作图可得2×+φ=π，解得φ=，故函数f（x）=2sin（2x+）=2sin2（x+），故把g（x）=sin2x的图象向左平移个长度单位可得f（x）的图象，故选B．8．||=1，||=，且与的夹角为45°，当|﹣x|取得最小值时，实数x的值为（）A．1 B．2 C．D．【考点】平面向量数量积的运算．【分析】|﹣x|取得最小值，即其平方取得最小值，其平方后变成关于x的二次函数，利用二次函数的性质即可求解即可．【解答】解：由题意可知：|﹣x|2=||2+x2||2﹣2x||•||cos45°=2x2﹣2x+1=2（x﹣）2+，所以x=时，原式最小．故选：C9．从正方体六个面的对角线中任取两条作为一对．其中所成的角为60°的共有（）A．24对B．30对C．48对D．60对【考点】排列、组合及简单计数问题；异面直线及其所成的角．【分析】利用正方体的面对角线形成的对数，减去不满足题意的对数即可得到结果．【解答】解：正方体的面对角线共有12条，两条为一对，共有=66条，同一面上的对角线不满足题意，对面的面对角线也不满足题意，一组平行平面共有6对不满足题意的直线对数，不满足题意的共有：3×6=18．从正方体六个面的对角线中任取两条作为一对．其中所成的角为60°的共有：66﹣18=48．故选：C．10．已知函数f（x）=，则下列结论正确的是（）A．f（x）是偶函数B．f（x）是增函数C．f（x）是周期函数D．f（x）的值域为[﹣1，+∞）【考点】余弦函数的单调性．【分析】由三角函数和二次函数的性质，分别对各个选项判断即可．【解答】解：由解析式可知当x≤0时，f（x）=cosx为周期函数，当x＞0时，f（x）=x2+1，为二次函数的一部分，故f（x）不是单调函数，不是周期函数，也不具备奇偶性，故可排除A、B、C，对于D，当x≤0时，函数的值域为[﹣1，1]，当x＞0时，函数的值域为（1，+∞），故函数f（x）的值域为[﹣1，+∞），故正确．故选：D11．正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为（）A．B．16πC．9πD．【考点】球内接多面体；球的体积和表面积．【分析】正四棱锥P﹣ABCD的外接球的球心在它的高PO1上，记为O，求出PO1，OO1，解出球的半径，求出球的表面积．【解答】解：设球的半径为R，则∵棱锥的高为4，底面边长为2，∴R2=（4﹣R）2+（）2，∴R=，∴球的表面积为4π•（）2=．故选：A．12．已知函数，且函数y=f（x）﹣x恰有3个不同的零点，则实数a的取值范围是（）A．（0，+∞）B．[﹣1，0）C．[﹣1，+∞）D．[﹣2，+∞）【考点】根的存在性及根的个数判断．【分析】由题意可得当x≥0时，函数的周期为1，而当x∈[﹣1，0）时，y=﹣x2﹣2x+a=﹣（x+1）2+1+a，图象为开口向下的抛物线，结合二次函数的图象，分类讨论可得．【解答】解：∵当x≥0时，f（x）=f（x﹣1），∴此时的周期为1，对于所有大于等于0的x代入得到的f（x）相当于在[﹣1，0）重复的周期函数，当x∈[﹣1，0）时，y=﹣x2﹣2x+a=﹣（x+1）2+1+a，图象为开口向下的抛物线，对称轴x=﹣1，顶点（﹣1，1+a），结合二次函数的图象可知：（1）如果a＜﹣1，函数y=f（x）﹣x至多有2个不同的零点；（2）如果a=﹣1，则y有一个零点在区间（﹣1，0），有一个零点在（﹣∞，﹣1），一个零点是原点；（3）如果a＞﹣1，则有一个零点在（﹣∞，﹣1），y右边有两个零点，综上可得：实数a的取值范围是[﹣1，+∞）故选：C．二、填空题（本大题共4小题，每小题5分，共20分）13．已知数列1，a1，a2，8是等差数列，数列1，b1，b2，b3，16是等比数列，则的值为．【考点】等差数列与等比数列的综合．【分析】利用等差数列、等比数列的性质，求出a1+a2=9，b2=4，即可求出的值．【解答】解：∵数列1，a1，a2，8是等差数列，∴a1+a2=1+8=9，∵数列1，b1，b2，b3，16是等比数列∴b22=1×16=16，在等比数列里，隔项的符号相同，∴b2=4，∴=，故答案为．14．在△ABC中，内角A，B，C的对边分别是a，b，c，若a2﹣b2=bc，sinC=2sinB，则A=30°．【考点】正弦定理．【分析】已知sinC=2sinB利用正弦定理化简，代入第一个等式用b表示出a，再利用余弦定理列出关系式，将表示出的c与a代入求出cosA的值，即可确定出A的度数．【解答】解：将sinC=2sinB利用正弦定理化简得：c=2b，代入得a2﹣b2=bc=6b2，即a2=7b2，∴由余弦定理得：cosA===，∵A为三角形的内角，∴A=30°．故答案为：30°15．若关于x，y的不等式组（k是常数）所表示的平面区域的边界是一个直角三角形，则k=﹣1或0．【考点】二元一次不等式（组）与平面区域．【分析】先画出满足约束条件的可行域，结合kx﹣y+1≥0表示地（0，1）点的直线kx﹣y+1=0下方的所有点（包括直线上的点）和已知可得：直线kx﹣y+1=0与y轴垂直或与y=x垂直，进而求出满足条件的k值．【解答】解：满足约束条件的可行域如下图阴影部分所示：kx﹣y+1≥0表示地（0，1）点的直线kx﹣y+1=0下方的所有点（包括直线上的点）由关于x，y的不等式组（k是常数）所表示的平面区域的边界是一个直角三角形，可得直线kx﹣y+1=0与y轴垂直，此时k=0或直线kx﹣y+1=0与y=x垂直，此时k=﹣1综上k=﹣1或0故答案为：﹣1或016．给出定义：若m﹣＜x≤m+（其中m为整数），则m叫做离实数x最近的整数，记作{x}，即{x}=m．在此基础上给出下列关于函数f（x）=x﹣{x}的四个命题：①点（k，0）是y=f（x）的图象的对称中心，其中k∈Z；②y=f（x）的定义域是R，值域是（﹣，]；③函数y=f（x）的最小正周期为1；④函数y=f（x）在（﹣，]上是增函数．则上述命题中真命题的序号是②③．【考点】命题的真假判断与应用．【分析】①根据f（2k﹣x）与f（x）的关系，可以判断函数y=f（x）的图象是否关于点（k，0）（k∈Z）对称；②根据让函数解析式有意义的原则确定函数的定义域，然后根据解析式易用分析法求出函数的值域；③再判断f （x +1）=f （x ）是否成立，可以判断③的正误；而由②的结论，易判断函数y=f （x ）在 （，]上的单调性，但要说明④不成立，我们可以举出一个反例．【解答】解：①∵f （2k ﹣x ）=（2k ﹣x ）﹣{2k ﹣x }=（﹣x ）﹣{﹣x }=， ∴点（k ，0）（k ∈Z ）不是y=f （x ）的图象的对称中心；故①错；②令x=m +a ，a ∈（﹣，]∴f （x ）=x ﹣{x }=a ∈（﹣，]，故②正确，③，∵f （x +1）=（x +1）﹣{x +1}=x ﹣{x }=f （x ）所以周期为1，故③正确；④x=﹣时，m=﹣1，f （﹣）=，x=时，m=0，则f （）=所以f （﹣）=f （），则函数y=f （x ）在（﹣，]上是增函数错误，故答案为：②③三、解答题（本大题共6小题，共70分）17．设函数f （x ）=|x ﹣1|+|x ﹣a |，（1）若a=﹣1，解不等式f （x ）≥3；（2）如果x ∈R ，f （x ）≥2，求a 的取值范围．【考点】绝对值不等式．【分析】（1）当a=﹣1，原不等式变为：|x ﹣1|+|x +1|≥3，下面利用对值几何意义求解，利用数轴上表示实数﹣左侧的点与表示实数右侧的点与表示实数﹣1与1的点距离之和不小3，从而得到不等式解集．（2）欲求当x ∈R ，f （x ）≥2，a 的取值范围，先对a 进行分类讨论：a=1；a ＜1；a ＞1．对后两种情形，只须求出f （x ）的最小值，最后“x ∈R ，f （x ）≥2”的充要条件是|a ﹣1|≥2即可求得结果．【解答】解：（1）当a=﹣1时，f （x ）=|x ﹣1|+|x +1|，由f （x ）≥3有|x ﹣1|+|x +1|≥3 据绝对值几何意义求解，|x ﹣1|+|x +1|≥3几何意义，是数轴上表示实数x 的点距离实数1，﹣1表示的点距离之和不小3，由于数轴上数﹣左侧的点与数右侧的点与数﹣1与1的距离之和不小3，所以所求不等式解集为（﹣∞，﹣]∪[，+∞）（2）由绝对值的几何意义知，数轴上到1的距离与到a 的距离之和大于等于2恒成立，则1与a 之间的距离必大于等于2，从而有a ∈（﹣∞，﹣1]∪[3，+∞）18．在△ABC中，角A，B，C所对的边分别为a，b，c，且满足csinA=acosC1）求角C大小；（2）求sinA﹣cos（B+）的最大值，并求取得最大值时角A，B的大小．【考点】正弦定理的应用；三角函数的最值．【分析】（1）利用正弦定理化简csinA=acosC．求出tanC=1，得到C=．（2）B=﹣A，化简sinA﹣cos（B+），通过0＜A＜，推出＜A+＜，求出2sin（A+）取得最大值2．得到A，B．【解答】解：（1）由正弦定理得sinCsinA=sinAcosC，因为0＜A＜π，所以sinA＞0．从而sinC=cosC，又cosC≠0，所以tanC=1，C=．（2）有（1）知，B=﹣A，于是sinA﹣cos（B+）=sinA+cosA=2sin（A+）．因为0＜A＜，所以＜A+＜，从而当A+=，即A=时2sin（A+）取得最大值2．综上所述sinA﹣cos（B+）的最大值为2，此时A=，B=．19．已知等差数列{a n}满足a2=0，a6+a8=10．（1）求数列{a n}的通项公式；（2）求数列{}的前n项和．【考点】数列的求和；等差数列的通项公式．【分析】（1）设等差数列{a n}的公差为d，由于a2=0，a6+a8=10．利用等差数列的通项公式即可得出．（2）=．利用“错位相减法”与等比数列的前n项和公式即可得出．【解答】解：（1）设等差数列{a n}的公差为d，∵a2=0，a6+a8=10．∴，解得，∴a n﹣1+（n﹣1）=n﹣2．（2）=．∴数列{}的前n项和S n=﹣1+0+++…+，=+0++…++，∴=﹣1++…+﹣=﹣2+﹣=，∴S n=．20．如图，在△ABC中，∠B=，AB=BC=2，P为AB边上一动点，PD∥BC，P为AB边上一动点，PD∥BC交AC于点D，现将△PDA沿PD翻折至△PDA′，使平面PDA′⊥平面PBCD．（1）当棱锥A′﹣PBCD的体积最大时，求PA的长；（2）若点P为AB的中点，E为A′C的中点，求证：A′B⊥DE．【考点】空间中直线与直线之间的位置关系；棱柱、棱锥、棱台的体积；平面与平面垂直的性质．【分析】（1）令PA=x（0＜x＜2）求出体积表达式，利用导数确定函数的单调性，求出函数的最大值．（2）设F为A′B的中点，连接PF，FE，通过PDEF是平行四边形，证明A′B⊥DE．【解答】解：（1）令PA=x（0＜x＜2），则A′P=PD=x．BP=2﹣x，因为A′P⊥PD且平面A′PD⊥平面PBCD，故A′P⊥平面PBCD，所以令f（x）=，由f′（x）=得x=，当x∈（0，）时，f′（x）＞0，f（x）单调递增，当x∈（，2）时，f′（x）＜0，f（x）单调递减，所以，当x=时，f（x）取得最大值，即：体积最大时，PA=．（2）设F为A′B的中点，连接PF，FE，则有EF∥BC，EF=BC，PD∥BC，PD=BC，所以DE∥PF，又A′P=PB，所以PF⊥A′B．故DE⊥A′B21．如图1，在矩形ABCD中，E，F分别是AB，CD的中点，沿EF将矩形BEFC折起，使∠CFD=90°，如图2所示；（Ⅰ）若G，H分别是AE，CF的中点，求证：GH∥平面ABCD；（Ⅱ）若AE=1，∠DCE=60°，求三棱锥C﹣DEF的体积．【考点】棱柱、棱锥、棱台的体积；直线与平面平行的判定．【分析】（Ⅰ）由三角形中位线的性质证得PG∥CH，PG=CH，从而得到四边形CPGH为平行四边形，得到GH∥PC．然后利用线面平行的判定得答案；（Ⅱ）由已知解三角形得到CF⊥DF，进一步求得EF=1，然后直接代入棱锥的体积公式得答案．【解答】（Ⅰ）证明：取AB中点P，连结PG、PC，∵G，H分别是AE，CF的中点，∴CH∥BE，且CH=BE，PG∥BE，且PG=BE，∴PG∥CH，PG=CH，∴四边形CPGH为平行四边形，∴GH∥PC．又GH⊄平面ABCD，PC⊂平面ABCD，∴GH∥平面ABCD；（Ⅱ）解：∵∠CFD=60°，∴CF⊥DF，∵CF⊥EF，EF∩DF=F，∴CF⊥平面ADEF，又AE=EB，∴CE=DE=，且CF=DE=1，∵∠DCE=60°，∴△DCE为等边三角形，而Rt△CDF中，CD=，∴，∴EF=1，∴．故三棱锥C﹣DEF的体积为．22．已知函数f（x）=e x（sinx+cosx）+a（a为常数）．（Ⅰ）已知a=﹣3，求曲线y=f（x）在（0，f（0））处的切线方程；（Ⅱ）当0≤x≤π时，求f（x）的值域；（Ⅲ）设g（x）=（a2﹣a+10）e x，若存在x1，x2∈[0，π]，使得|f（x1）﹣g（x2）|＜13﹣e成立，求实数a的取值范围．【考点】利用导数研究曲线上某点切线方程；导数在最大值、最小值问题中的应用．【分析】（Ⅰ）求出原函数的导函数，得到函数在x=0时的导数，再求出f（0），然后利用直线方程的点斜式得答案；（Ⅱ）由原函数的导函数的符号确定原函数的单调区间，从而求得原函数的极大值点，得到函数的最大值，再求出端点值得答案；（Ⅲ）由a2﹣a+10＞0，得g（x）在[0，π]上是增函数，从而求得g（x）的值域．由题意得到，求解关于a的不等式得答案．【解答】解：（Ⅰ）f′（x）=e x（sinx+cosx）+e x（cosx﹣sinx）=2e x cosx，∴f′（0）=2，f（0）=﹣2，∴切线方程为：y+2=2（x﹣0），即2x﹣y﹣2=0为所求的切线方程；（Ⅱ）由f′（x）=2e x cosx≥0，得0，f′（x）=2e x cosx≤0，得．∴y=f（x）在上单调递增，在上单调递减．∴．f（0）=1+a，f（π）=﹣eπ+a＜f（0），，∴f（x）的值域为；（Ⅲ）∵a2﹣a+10＞0，∴g（x）在[0，π]上是增函数，g（0）=a2﹣a+10，g（π）=（a2﹣a+10）eπ，∴g（x）的值域为[a2﹣a+10，（a2﹣a+10）eπ]．∵，依题意，，即a2﹣2a﹣3＜0，解得：﹣1＜a＜3．2016年11月10日。

丰城中学2015-2016学年上学期高四周练试卷命题人：熊文宏审题人：高四文科数学备课组 2015.12.15一选择题1、平行六面体ABCD﹣A1B1C1D1中，既与AB共面也与CC1共面的棱的条数为（）A 3B 4 C．5 D 62、下列说法中正确的是（） A．三点确定一个平面 B．两条直线确定一个平面 C．两两相交的三条直线一定在同一平面内 D．过同一点的三条直线不一定在同一平面内3、若直线，，则直线与的位置关系是（）A．异面 B．相交 C．平行 D．异面或相交4、给出下列四个命题：①分别与两条异面直线都相交的两条直线一定是异面直线；②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直；③垂直于同一直线的两条直线相互平行；④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直．其中为真命题的是（）A．①和② B．②和③ C．③和④ D．②和④5、如图，在正四棱柱中，、分别是、的中点，则下列结论不成立的是 ( )A．与垂直 B．与垂直C．与异面 D．与异面6、．直三棱柱ABC﹣A1B1C1中，若∠BAC=90°，AB=AC=AA1，则异面直线BA1与AC1所成的角等于（）A． 30° B． 45° C． 60° D． 90°7、如图,若是长方体被平面截去几何体后得到的几何体,其中E为线段上异于的点，F为线段上异于的点，且∥，则下列结论中不正确的是（）A. ∥B.四边形是矩形C. 是棱柱D. 是棱台8、已知在空间四边形ABCD中，AD⊥BC，AD⊥BD，且△BCD是锐角三角形，则必有( )A．平面ABD⊥平面ADC B．平面ABD⊥平面ABCC．平面ADC⊥平面BDC D．平面ABC⊥平面BDC9、如图，正方体ABCD﹣A1B1C1D1的棱长为1，线段B1D1上有两个动点E、F，且EF=则下列结论中错误的是（）A． AC⊥BE B． EF∥平面ABCDC．三棱锥A﹣BEF的体积为定值 D．△AEF的面积与△BEF的面积相等10、在正方体AC1中，E、F分别为AB和CD的中点，则异面直线A1E与BF所成角的余弦值为（） A．－ B． C．－或D．11、设α、β、γ为平面，为直线，则的一个充分条件是（）A． B．C． D．12、若P是两条异面直线l、m外的任意一点，则A.过点P有且仅有一条直线与l、m都平行B.过点P有且仅有一条直线与l、m都垂直C.过点P有且仅有一条直线与l、m都相交D.过点P有且仅有一条直线与l、m都异面二、填空题13、在棱长为1的正方体ABCD﹣A1B1C1D1中，若点P是棱上一点，则满足|PA|+|PC1|=2的点P的个数为14、三棱锥中，⊥底面，＝3，底面是边长为2的正三角形，则三棱锥的体积等于________．15、已知在长方体ABCDA1B1C1D1中，底面是边长为2的正方形，高为4，则点A1到截面AB1D1的距离是________．16、，，是空间中的三条直线，下面给出三个命题：①若，，则；②若与相交，与相交，则与相交；③若，与成等角，则．上述命题中正确的命题是（只填序号）．丰城中学2015-2016学年上学期高四周练答题卡班级: _____ 姓名：__________学号：_______ 得分：_______13． 14． 15． 16．三、解答题：17、如图所示，是正方形，，是的中点（1）求证：；（2）若，求三棱锥的体积．18、如图，正方形ADEF与梯形ABCD所在的平面互相垂直，AD⊥CD，AB∥CD，AB ＝AD＝2，CD＝4，M为CE的中点．(1)求证：BM∥平面ADEF； (2)求证：平面BDE⊥平面BEC.19（附加题）、在四边形ABCD中，BC∥AD，BC⊥CD，AD＝4，BC＝CD＝2，E，P分别为AD，CD的中点(如图K4510(1)所示)，将△ABE沿BE折起，使二面角A - BE C为直二面角，如图(2)，在线段AE上，是否存在一点M，使得PM∥平面ABC？若存在，请指出点M的位置，并证明你的结论；若不存在，请说明理由．参考答案(12.15)题中横线上）13．6． 14．15．16．①三、简答题17、（1）略（2）∵，∴是三棱锥的高，∵是正方形，是的中点，∴是等腰直角三角形，故,故18. 1)证明：延长DA与CB相交于P，∵AB＝AD＝2，CD＝4，AB∥CD，∴B为PC的中点，又M为CE的中点，∴BM∥EP，∵BM⊄平面ADEF，EP⊂平面ADEF，∴BM∥平面ADEF.∴BD2＋BC2＝CD2，∴BD⊥BC.又平面ADEF⊥平面ABCD，ED⊥AD，∴ED⊥平面ABCD，∴ED⊥BC，∵ED∩BD＝D，∴BC⊥平面BDE，又BC⊂平面BEC，∴平面BDE⊥平面BEC.19.存在点M，当M为线段AE的中点时，PM∥平面ABC，理由略。

丰城中学2015-2016学年上学期高二周练试卷文科数学(24—30班) 命题人：官世清 2015.12.8总分：100分 考试时间：20:30—21:50一、选择题：本大题共10小题。

每小题5分，共50分。

1．直线()011:1=-+-y x a l 和023:2=++ay x l 垂直，则实数a 的值为（ ）A 2．已知圆()()22:341C x y -+-=和两点(),0A m -，()(),00B m m >，若圆C 上存在点P ，使得90APB ∠=，则m 的最大值为A ．7B ．6C ．5D ．43．已知两点)0,1(1-F 、)0,1(F ，且的等差中项，则动点P 的轨迹方程是（ ）。

AC4有共同的焦点F ，O 为坐标原点，P在轴上方且在双曲线上，则FP OP ⋅的最小值为A5．平面上到定点(1,2)A 距离为1且到定点(5,5)B 距离为d 的直线共有4条，则d 的取值范是（ ）A ．(0,4)B ．(2,4)C ．(2,6)D ．(4,6)6．当双曲线C 不是等轴双曲线时，我们把以双曲线C 的实轴、虚轴的端点作为顶点的椭圆称为双曲线C 的“伴生椭圆” ）A 7．设椭圆的两个焦点分别为F 1、、F 2，过F 2作椭圆长轴的垂线交椭圆于点P ，若△F 1PF 2为等腰直角三角形，则椭圆的离心率是（ ）．A8．过双曲线C 1的左焦点1F 作圆C 2：222x y a +=的切线，设切点为M ，延长1F M 交抛物线C 3：22(0)y px p =>于点N ，其中13C C ，有一个共同的焦点，若1||||MF MN =，则双曲线1C 的离心率为（ ）（A （B （C （D 9．抛物线22(0)y px p =>的焦点为F ，准线为l ，A ，B 是抛物线上的两个动点，且满足，设线段AB 的中点M 在l 上的投影为N ，则 ）A 10．过抛物线：()220y px p =>的焦点F 作倾斜角为60︒的直线l ，若直线l 与抛物线在第一象限的交点为A ，并且点A 线的离心率为（ ）A 二、填空题：本大题共4小题，每小题5分，共20分。

丰城中学2015-2016学年上学期高三周练试卷数 学 （理科尖子，重点班）一．选择题（本大题共12小题，每小题5分，共60分）1．三条直线l 1：x －y ＝0；l 2：x ＋y －2＝0；l 3：5x －ky －15＝0围成一个三角形，则k 的取值范围（ ）A ．k≠±5且k≠1B ．k≠±5且k≠－10C ．k≠±1且k≠0D ．k≠±5 2．直线y ＝kx ＋3与圆（x －3）2＋（y －2）2＝4相交于M ，N 两点，若|MN|≥23，则k的取值范围是（ ） A ．[－34，0] B ．（－∞，－34]∪[0，＋∞） C ．[33．[－23，0] 3. 若直线cos sin 10x y θθ+-=与圆221(1)(sin )16x y θ-+-=相切，且θ为锐角，则这条直线的斜率是( ) A ．3 B ．3-334. 已知圆()()22:341C x y -+-=和两点(),0A m -，()(),00B m m >，若圆C 上存在点P ，使得90APB ∠=o ，则m 的最大值为（ ） A.7 B.6 C.5 D.45．已知圆O ：224x y +=上到直线:l x y a +=的距离等于1的点至少有2个，则a 的取值范围为（ ）A ．(32,32)-B ．(,32)(32,)-∞-+∞UC ．(22,22)-D ．[32,32]- 6．设点P 是函数22y x x =--Q 是直线260x y --=上的任意一点，则||PQ 的最小值为（ ）A 51B 51C 5．以上答案都不对 7．已知函数()ln 2sin f x x α=+（)2,0(πα∈）的导函数为()f x '，若存在01x <使得00()()f x f x '=成立，则实数α的取值范围为（ ）A ．,32ππ⎛⎫⎪⎝⎭B ．⎪⎭⎫ ⎝⎛3,0πC ．,62ππ⎛⎫⎪⎝⎭ D ．0,6π⎛⎫ ⎪⎝⎭8．由()y f x =的图象向左平移3π个单位，再把所得图象上所有点的横坐标伸长到原来的2倍得到12sin(3)6y x π=-的图象，则()f x 为（ ）A ．312sin()26x π+B ．12sin(6)6x π-C ．312sin()23x π+D ．12sin(6)3x π+ 9．已知实数变量,x y 满足1,0,220,x y x y mx y +≥⎧⎪-≥⎨⎪--≤⎩且目标函数3z x y =+的最大值为8，则实数m 的值为( ) A.32B.12C.2D.110.一个几何体的三视图如图所示，则该几何体的体积为（ ） A ．4B ．43C ．2D ．8311.已知圆221:(2)16O x y -+=和圆2222:(02)O x y r r +=<<，动圆M 与圆1O ,圆2O 都相切，动圆的圆心M 的轨迹为两个椭圆，这两个椭圆的离心率分别为1e ，2e （12e e >），则122e e +的最小值是（ ） A.3224+ B.32C.2D.38 12. 已知R λ∈，函数1,0,()lg ,0,x x f x x x ⎧+<=⎨>⎩2()414g x x x λ=-++，若关于x 的方程(())f g x λ=有6个解，则λ的取值范围为 （ ）A ．2(0,)3B ．12(,)23C ．21(,)52D ．2(0,)5 二．填空题（本大题共4小题，每小题5分，共20分）13．若点(1,2)P 在以坐标原点为圆心的圆上，则该圆在点P 处的切线方程_____. 14. ∆ABC 中，|CB →|cos ∠ACB =|BA →|cos ∠CAB =3，且AB →·BC →=0，则AB 长为 ． 15. 正实数,x y 满足2+30x y -=，则46y x xy-+的最小值为 ． 16. 四棱锥P ABCD -底面是一个棱长为2的菱形，且∠DAB=60º，各侧面和底面所成角均为60º，则此棱锥内切球体积为 ．丰城中学2015-2016学年上学期高三周练试卷数学答题卡（理科尖子、重点班）班级 姓名 学号 得分 一、选择题（本大题共10个小题，每小题5分，共60分） 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案二、填空题（本大题共有4小题，每小题5分共20分．把答案填在题中横线上） 13． 14． 15． 16． 三、解答题：（10分*2=20分）17. 已知过点A (0,1)，且方向向量为a ＝(1，k )的直线l 与圆C ：(x －2)2＋(y －3)2＝1相交于M 、N 两点．(1)求实数k 的取值范围；(2)若O 为坐标原点，且OM →·ON →＝12，求k 的值．18. 如图, 已知四边形ABCD 和BCEG 均为直角梯形，AD ∥BC ，CE ∥BG ，且2BCD BCE π∠=∠=，平面ABCD ⊥平面BCEG ,222=====BG AD CE CD BC（Ⅰ）证明：AG //平面BDE ;（Ⅱ）求平面BDE 和平面BAG 所成锐二面角的余弦值.参考答案1-6：BAAB AB 7-12：CBDDAD 13．250x y +-= 14．6．15．9 16． 6π 15.16.17. (1)∵直线l 过点A (0,1)且方向向量a ＝(1，k )，∴直线l 的方程为y ＝kx ＋1.由|2k －3＋1|k 2＋1＜1，得4－73＜k ＜4＋73.(2)设M (x 1，y 1)、N (x 2，y 2)，将y ＝kx ＋1代入方程(x －2)2＋(y －3)2＝1， 得(1＋k 2)x 2－4(1＋k )x ＋7＝0， ∴x 1＋x 2＝41＋k 1＋k 2，x 1x 2＝71＋k2，∴OM →·ON →＝x 1x 2＋y 1y 2＝(1＋k 2)x 1x 2＋k (x 1＋x 2)＋1.∴4k 1＋k1＋k2＋8＝12，∴4k 1＋k1＋k2＝4，解得k ＝1. 18. 【解析】由平面ABCD BCEG ⊥平面，平面ABCD BCEG BC =I 平面, ,CE BC CE ⊥⊂平面BCEG , ∴EC ABCD ⊥平面 .………2分根据题意建立如图所示的空间直角坐标系，可得(0,2,0(20,0(002(2,1,0)(0,2,1)B D E A G ），，），，，），………….3分（Ⅰ）设平面BDE 的法向量为(,,)m x y z =u r，则(0,2,2),(2,0,2)EB ED =-=-u u u r u u u rQ 0EB m ED m ∴⋅=⋅=u u u r u ru u u r u r即00y z x z -=⎧⎨-=⎩， x y z ∴==，∴平面BDE 的一个法向量为(1,1,1)m =u r，………………………………………………..5分(2,1,1)AG =-u u u rQ 2110AG m ∴⋅=-++=u u u r u r ，AG m ∴⊥u u u r u r，AG BDE ⊄Q 平面，∴AG ∥平面BDE . ……………………………………………….7分 （Ⅱ）设平面BAG 的法向量为()z y x n ,,=，平面BDE 和平面BAG 所成锐二面角为θ……….8分因为()0,1,2-=BA ,()1,0,0=BG ,由0,0=⋅=⋅BG n BA n 得⎩⎨⎧==-002z y x ， (10)分∴平面BAG 的一个法向量为()0,2,1=n ，∴5155321cos =⋅+=⋅=nm θ. 故平面BDE 和平面BAG 所成锐二面角的余弦值为515……….12分。