(完成)二阶电路响应的三种(欠阻尼、过阻尼及临界阻尼)状态轨迹及其特点

实验二二阶电路响应的三种（欠阻尼、过阻尼及临界阻尼）状态轨迹及其特点一、实验目的1、熟练掌握二阶电路微分方程的列写及求解过程；2、掌握RLC 二阶电路零输入响应及电路的过阻尼、临界阻尼和欠阻尼状态；3、学会利用MULTISIM 仿真软件熟练分析电路，尤其是电路中各电压电流的变化波形。

二、实验原理用二阶线性常微分方程描述的电路称为二阶电路，二阶电路中至少含有两个储能元件。

二阶电路微分方程式一个含有二次微分的方程，由二阶微分方程描述的电路称为二阶电路。

分析二阶电路的方法仍然是建立二阶微分方程，并利用初始条件求解得到电路的响应。

二阶方程一般都为齐次方程。

齐次方程的通解一般分为三种情况：（RLC 串联时）1、 21S S ≠ 为两个不等的实根（称过阻尼状态）t S t S h e A e A f 211121+= 此时，CL R 2>，二阶电路为过阻尼状态。

2、 σ==21S S 为相等实根（称临界状态）t h e A A f σ)21+=（ 此时，CL R 2=，二阶电路为临界状态。

3、 ωσj S ±-=21、为共轭复根（称欠阻尼状态）t h e t f σβω-+=)sin( 此时CL R 2<，二阶电路为欠阻尼状态。

这三个状态在二阶电路中式一个重要的数据，它决定了电路中电流电压关系以及电流电压波形。

三、实验内容电路中开关S 闭合已久。

t=0时将S 打开，并测量。

1、欠阻尼状态（R=10Ω,C=10mF,L=50mH ）如图所示，为欠阻尼状态时的二阶电路图。

波形图展示了欠阻尼状态下的C U 和L U 波形(橙色线条为电容电压衰减波形，红色线条为电感电压衰减波形)。

2、临界阻尼（R=10Ω,C=10mF,L=0.25mH ）如图所示，为临界状态的二阶电路图。

图展示了临界状态下的C U 的波形。

波形图展示了临界状态下的C U 和L U 波形。

3、过阻尼状态（R=10Ω,C=1mF,L=1mH ）如图所示，为过阻尼状态下的二阶电路图。

真验二之阳早格格创做二阶电路赞同的三种（短阻僧、过阻僧及临界阻僧）状态轨迹及其特性一、真验手段1、流利掌握二阶电路微分圆程的列写及供解历程；2、掌握RLC二阶电路整输进赞同及电路的过阻僧、临界阻僧战短阻僧状态；3、教会利用MULTISIM仿真硬件流利分解电路，更加是电路中各电压电流的变更波形.二、真验本理用二阶线性常微分圆程形貌的电路称为二阶电路，二阶电路中起码含有二个储能元件.二阶电路微分圆程式一个含有二次微分的圆程，由二阶微分圆程形貌的电路称为二阶电路.分解二阶电路的要领仍旧是修坐二阶微分圆程，并利用初初条件供解得到电路的赞同.二阶圆程普遍皆为齐次圆程.齐次圆程的通解普遍分为三种情况：（RLC串联时）1、为二个没有等的真根（称过阻僧状态）此时，，二阶电路为过阻僧状态.2、为相等真根（称临界状态）此时，，二阶电路为临界状态.3、为同轭复根（称短阻僧状态）此时，二阶电路为短阻僧状态.那三个状态正在二阶电路中式一个要害的数据，它决断了电路中电流电压关系以及电流电压波形.三、真验真质电路中启关S关合已暂.t=0时将S挨启，并丈量.1、短阻僧状态（R=10Ω,C=10mF,L=50mH）如图所示，为短阻僧状态时的二阶电路图.波形图展示了短阻僧状态下的战波形(橙色线条为电容电压衰减波形，白色线条为电感电压衰减波形).2、临界阻僧（R=10Ω,C=10mF,L=0.25mH）如图所示，为临界状态的二阶电路图.图展示了临界状态下的的波形.波形图展示了临界状态下的战波形.3、过阻僧状态（R=10Ω,C=1mF,L=1mH）如图所示，为过阻僧状态下的二阶电路图.波形图展示了临界状态下的战波形图.四、真验分解由本理公式以及仿真截止，咱们不妨考证得出1）当二阶电路为短阻僧状态时，其特性圆程特性根为一对于复根，且为同轭复根.2）当二阶电路为过阻僧状态时，其特性圆程特性根为二个没有等的真根.3）当二阶电路为临界阻僧状态时，其特性圆程特性根为相等真根五、真验报告1、归纳、分解真验要领取截止正在真验历程中，真验需要举止多次电路的变换.真验时需要留神审慎，以预防堕落.正在真验截止中，大部分取表面相切合，但是仍存留些微缺面（简略定量分解）.2、心得体验及其余通过本次真验的教习，尔认识了二阶电路微分圆程的列写及供解历程，认识了RLC二阶电路整输进赞同及电路的过阻僧、临界阻僧战短阻僧状态，更流利天力用仿真仪器分解电路，那将对于以来的仿真正在验有要害的前提效率.。

1实验八 二阶电路的响应与状态轨迹一、实验目的1.学习用实验方法研究二阶动态电路的响应，了解电路元件参数对响应的影响。

2.观察、分析二阶电路响应的三种状态轨迹及其特点，以加深对二阶电路响应的认识与理解。

二、实验原理一个二阶电路在方波正、负阶跃信号的激磁下，可获得零状态与零输入响应，其响应的变化轨迹决定于电路的固有频率，当调节电路的元件参数值，使电路的固有频率分别为负实数、共轭复数及虚数时，可获得单调地衰减、衰减振荡和等幅振荡的响应。

在实验中可获得过阻尼，欠阻尼和临界阻尼这三种响应图形。

简单而典型的二阶电路是一个RLC 串联电路和GCL 并联电路，这二者之间存在着对偶关系。

本实验仅对GCL 并联电路进行研究。

三、实验仪器及设备四、实验内容与步骤利用动态线路板中的元件与开关的配合作用，组成如图8-1所示的GCL 并联电路。

令R 1＝10KΩ，L ＝10mH ，C ＝1000PF ，R 2为10KΩ可调电阻器，令函数信号发生器的输出为Um ＝3V ，f ＝1KHz 的方波脉冲信号，通过同轴电缆线接至上图的激励端，同时用同轴电缆线将激励端和响应输出端接至双踪示波器的Y A 和YB 两个输入口。

图 8-1 GCL 并联电路1.调节可变电阻器R 2之值，观察二阶电路的零输入响应和零状态响应由过阻尼过渡到临界阻尼，最后过渡到欠阻尼的变化过渡过程，分别定性地描绘、记录响应的典型变化波形。

2.调节R 2使示波器荧光屏上呈现稳定的欠阻尼响应波形，定量测定此时电路的衰减常数α和振荡频率ωd 。

3.改变一组电路参数，如增、减L 或C 之值，重复步骤2的测量，并作记录。

随后仔细观察，改变电路参数时，ω与α的变化趋势，并作记录。

五、实验注意事项1.调节R2时，要细心、缓慢，临界阻尼要找准。

2.观察双踪时，显示要稳定，如不同步，则可采用外同步法（看示波器说明）触发。

六、预习思考题1.根据二阶电路实验线路元件的参数，计算出处于临界阻尼状态的R2之值。

二阶电路的三种状态计算
二阶电路的三种状态分别是过阻尼状态、临界阻尼状态和欠阻尼状态。

这些状态是根据二阶电路的阻尼比大小来区分的。

1. 过阻尼状态：当二阶电路的阻尼比大于临界阻尼比时，电路处于过阻尼状态。

在这种状态下，电路的响应会快速衰减，没有振荡现象。

2. 临界阻尼状态：当二阶电路的阻尼比等于临界阻尼比时，电路处于临界阻尼状态。

在这种状态下，电路的响应会快速衰减，没有振荡现象。

3. 欠阻尼状态：当二阶电路的阻尼比小于临界阻尼比时，电路处于欠阻尼状态。

在这种状态下，电路的响应会出现振荡现象，振荡的幅度随时间逐渐减小。

要计算二阶电路的三种状态，需要根据电路的参数（如电阻、电感、电容等）和输入信号的频率来确定阻尼比，并根据阻尼比的大小来判断电路的状态。

可以通过使用相关的电路模型和数学方法来进行计算和分析。

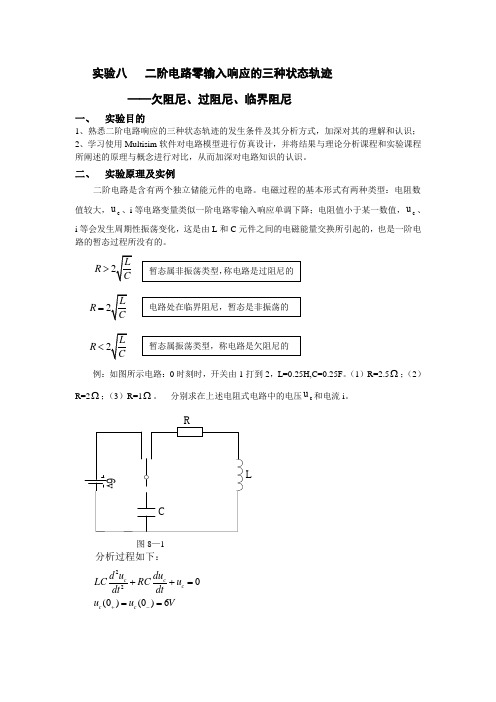
实验八 二阶电路零输入响应的三种状态轨迹——欠阻尼、过阻尼、临界阻尼一、 实验目的1、熟悉二阶电路响应的三种状态轨迹的发生条件及其分析方式，加深对其的理解和认识；2、学习使用Multisim 软件对电路模型进行仿真设计，并将结果与理论分析课程和实验课程所阐述的原理与概念进行对比，从而加深对电路知识的认识。

二、 实验原理及实例二阶电路是含有两个独立储能元件的电路。

电磁过程的基本形式有两种类型：电阻数值较大，c u 、i 等电路变量类似一阶电路零输入响应单调下降；电阻值小于某一数值，c u 、i 等会发生周期性振荡变化，这是由L 和C 元件之间的电磁能量交换所引起的，也是一阶电路的暂态过程所没有的。

R >R=R < 例：如图所示电路：0时刻时，开关由1打到2，L=0.25H,C=0.25F 。

（1）R=2.5Ω；（2）R=2Ω；（3）R=1Ω。

分别求在上述电阻式电路中的电压c u 和电流i 。

L图8—1分析过程如下：220(0)(0)6c c c c c d u du LC RC u dt dtu u V +-++===0(0)(0)0c du i i C dt ++-==-=210LCp RCp ++= 210LCp RCp ++=(1) R=2.5Ω时，过阻尼状态122.5,2,8R R p p =Ω>=-=-2812126t tc u A e A e A A --=++=01212(0)(28)082cdu i C C A A dtA A ++=-=---===-2828()(82),()4()t t t t c c du u t e e v i t Ce e A dt ----=-=-=- （2）R=2Ω，临界阻尼状态。

2,R R =Ω= 124p p ==-412()t c u A A t e -=+ 1(0)6c A u -== 021(0)(4)0c du i C C A A dt++=-=--= 12624A A == 444()6(14)(),()66(14)()t t t c c du u t t e v i t Ce t e A dt ---=+=-=-++（3）R=1Ω,欠阻尼状态，振荡放电过程1201,2 3.46sin(3.46)(0)sin 6(0)(2sin 3.46cos )0t c c cR R p j u Ae t u A du i C C A A dt ββββ+-++=Ω<=-±=+===-=--+=660, 6.93sin A ββ===22() 6.93sin(3.4660)(),() 6.93sin 3.46()t t c c du u t e t v i t C e t A dt --=+=-=三、 仿真设计步骤：1、根据电路设计题目要求设计电路；2、用visio 做出电路原理图并对其进行理论计算分析；3、根据电路模拟图在电路仿真软件上做出仿真模型，通过示波器分析电容电压和电流变化过程，进行电路仿真；4、将测量的结果与理论计算值进行比较，对仿真结果进行分析；5、做出实验小结四、 仿真实验结果如图所示，设计仿真电路图8—2R=2.5Ω时，过阻尼状态波形如下所示：图8—3当将R值换成2Ω时，；临界阻尼波形图如下图8—4当将R值换成1Ω时，欠阻尼振荡放电波形图如下：图8—5图中蓝色为电感电流波形轨迹，红色为电容电压波形轨迹。

实验二二阶电路响应的三种（欠阻尼、过阻尼及临界阻尼）状态轨迹及其特点一、实验目的1、熟练掌握二阶电路微分方程的列写及求解过程；2、掌握 RLC 二阶电路零输入响应及电路的过阻尼、临界阻尼和欠阻尼状态；3、学会利用 MULTISIM 仿真软件熟练分析电路， 尤其是电路中各电压电流的变化波形。

二、实验原理用二阶线性常微分方程描述的电路称为二阶电路， 二阶电路中至少含有两个储能元件。

二阶电路微分方程式一个含有二次微分的方程， 由二阶微分方程描述的电路称为二阶电路。

分析二阶电路的方法仍然是建立二阶微分方程， 并利用初始条件求解得到电路的响应。

二阶方程一般都为齐次方程。

齐次方程的通解一般分为三种情况： （ RLC 串联时）1、S 1 S 2 为两个不等的实根（称过阻尼状态）f hS t S tA 1e 11 A 2 e 12 此时， R 2 L，二阶电路为过阻尼状态。

C2、 S 1 S 2为相等实根（称临界状态） f h （ A 1 A 2 )e t此时， R 2L ，二阶电路为临界状态。

C 3、 S 1、2j 为共轭复根（称欠阻尼状态） f h sin( t)e t此时 R2 L ，二阶电路为欠阻尼状态。

C 这三个状态在二阶电路中式一个重要的数据， 它决定了电路中电流电压关系以及电流电压波形。

三、实验内容电路中开关 S 闭合已久。

t=0 时将 S 打开，并测量。

1、欠阻尼状态（ R=10Ω,C=10mF,L=50mH）如图所示，为欠阻尼状态时的二阶电路图。

波形图展示了欠阻尼状态下的U C和 U L波形(橙色线条为电容电压衰减波形，红色线条为电感电压衰减波形) 。

2、临界阻尼（ R=10Ω ,C=10mF,L=0.25mH）如图所示，为临界状态的二阶电路图。

图展示了临界状态下的U C的波形。

波形图展示了临界状态下的U C和 U L波形。

3、过阻尼状态（ R=10Ω,C=1mF,L=1mH）如图所示，为过阻尼状态下的二阶电路图。

欠阻尼、过阻尼和临界阻尼是描述电路动态过程的三种状态。

欠阻尼电路：在激励信号作用下，电路中的电流和电压关系呈线性关系，即没有能量耗散。

这种状态下，电路响应迅速，但响应不够强烈。

过阻尼电路：在激励信号作用下，电路中的电流和电压关系呈非线性关系，即存在能量耗散。

这种状态下，电路响应缓慢，但响应强烈。

临界阻尼电路：介于欠阻尼和过阻尼之间的状态。

在这种状态下，电路的响应既不是非常迅速也不是非常缓慢，响应强度也适中。

这些状态的变化是由电路中的阻尼系数和激励频率决定的。

对于给定的电路，可以通过调整这些参数来改变其动态特性。

实验报告二 二阶电路响应的三种状态轨迹及其特点
1、电路课程设计目的
观察二阶电路响应的三中状态电压电流波形。

2、设计电路原理与说明
二阶电路是含有两个独立储能元件的电路，描述电路行为的方程是二阶线性常微分方程。

设计电路图如下： U 0
L
图一 C
L R 2>时，过阻尼非振荡放电 C
L R 2<时，欠阻尼非振荡放电 C L R 2
=时，临界阻尼放电 若取200L mH =、5C F μ=，则当400R =Ω时为临界阻尼状态。

故此次仿真分别选用100Ω 400Ω 700Ω的电阻进行测试。

3、电路课程设计仿真内容与步骤及结果
（1）接好电路，设置电感、电容值；
图二
（2）选择700Ω电阻，观察电感的电压及电流波形；
图三
（3）选择100Ω电阻，观察电感的电压及电流波形；
图四
（4）选择400 电阻，观察电感的电压及电流波形；
图五
综上，波形符合理论结果。

4、仿真结果与理论分析对比及仿真中的注意事项
仿真结果与理论计算相一致。

仿真中用到了单刀双掷开关，在实际测试时要留意开关的切换，同时由于此次仿真中利用到了示波器，而且所测波形在很小的一段范围内，所以在操作是要注意开关和示波器的相互配合，这样才容易得到理想波形图。

5、电路课程设计总结
通过这次仿真，我们深一层次的认识了二阶电路的三种状态特性，并观察了各个状态的电路波形图。

二阶电路由于设计到二阶常微分方程，计算方面相当麻烦，我们在研究时可以借助示波器等器材做辅助，帮助我们理解掌握新知识。

二阶电路响应的三种欠阻尼、过阻尼及临界阻尼状态轨迹及其特点一、 实验目的1.了解二阶电路响应的三种欠阻尼、过阻尼及临界阻尼状态轨迹及其特点;2掌握二阶电路响应的三种欠阻尼、过阻尼及临界阻尼状态轨迹及其特点的测试方法;二、 实验原理二阶电路是含有立个独立储能元件的电路,描述电路行为的方程是二阶线性常系数微分方程; 应用经典定量分析开关闭合后U C 、i 等零输入响应的变化规律0=++-L R C u u u将如下R 、L 、C 元件的电压电流表达式dtdu C i C C -= dtdu RC Ri u C R == dtu d LC dt di L u C L 2-== 代入KVL 方程,可得022=++C C C u dtdu RC dt u d LC 由数学分析可知,要确定二阶微分方程的解,除应知道函数的初始值外,还应知道函数的一阶导数初始值,它可根据下列关系求得 由于c i dt du C-= 所以"+'=u u u C C C 所示二阶微分方程的解可设为st C C Ae u u ="=012=++RCs LCs特征根为LC L R L R S 1222-⎪⎭⎫ ⎝⎛±-= 因此 t t C e A e A u 21s 2s 1+=由初始条件Uc0+=Uo,可得 A1+A2=Uo 又t t C e A e A dtdu 21s 2s 1+= 可求得⎪⎪⎩⎪⎪⎨⎧--=-=1201212021s s U s A s s U s A （1） CL R 2>,S1和S2为不相等的负实数,暂态属非振荡类型,称电路是过阻尼的; （2） CL R 2=, S1和S2为两相等的负实数,电路处于临界阻尼,暂态是非振荡的; （3） C L R 2< ,S1和S2为一对共轭复数,暂态属振荡类型,称电路是欠阻尼的; 三、 仿真实验设计与测试解：800LC 1_)2L R (2L R s2200LC 1_)2L R (2L R s1240010*5.125.022226———特征根程。