7.2 二阶电路的零状态响应和全响应

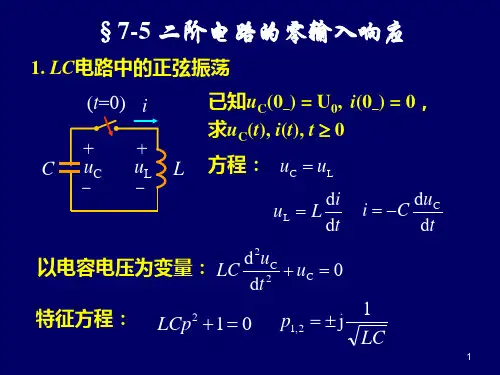
二阶电路的零状态响应
电路的响应指的是电路在不同输入下的输出情况，分为零状态响
应和零输入响应。

所谓零状态响应，指的是电路从某一时刻开始，经过一段时间后
的输出情况，而这段时间内电路的电容和电感等元件是没有存储能量的。

这种响应与电路的初始状态有关，在输入信号改变前电路中的电
势和电流已经存在了一些初值，这些初值会对电路的响应产生影响。

对于二阶电路而言，其响应可以用二阶微分方程来表示。

二阶微
分方程的通解形式为：
y(t) = C1 e^(αt) + C2 e^(βt)
其中，C1和C2为待定常数，α和β分别为根号下b^2-4ac得到
的两个实数或者共轭复数。

根据初值条件和输入信号，可以解得C1和
C2的值，然后带入通解中即可得到响应的具体表达式。

二阶电路的响应除了受到初值的影响外，还受到电路的频率特性
的影响。

根据电路的传输函数，可以得到电路的幅频特性和相频特性。

在实际应用中，需要调节电路的参数以满足特定的频率响应要求。

总之，二阶电路的零状态响应是电路在一定的初值状态下对输入
信号的响应，需要通过求解微分方程和考虑频率特性，来得到电路的
具体响应情况。

二阶电路算法摘要：一、引言二、二阶电路基本概念1.二阶系统的定义2.二阶系统的组成部分三、二阶电路算法1.欧拉公式2.零状态响应的计算方法3.完全响应的计算方法四、二阶电路算法的应用1.交流信号的放大与衰减2.滤波器的设计五、总结正文：二阶电路算法是电子工程和通信工程领域中常用的计算方法，主要应用于二阶系统的分析和设计。

二阶系统是一个具有两个存储元件的电路系统，通常包括电容器和电感器。

这种系统广泛应用于放大器、滤波器和振荡器等电路设备。

首先，我们来了解一下二阶电路的基本概念。

二阶系统是指由两个线性时不变元件组成的电路系统，其中包括一个电感器（L）和一个电容器（C）。

根据电感器和电容器的电压- 电流关系，可以得到二阶系统的微分方程。

这个微分方程是一个二阶微分方程，因此称为二阶系统。

二阶电路算法主要包括欧拉公式、零状态响应的计算方法和完全响应的计算方法。

欧拉公式是将二阶系统的微分方程转换为一个关于时间t 的三角函数的公式。

通过欧拉公式，我们可以求解系统的零状态响应和完全响应。

零状态响应是指在初始时刻，电感和电容的电压为零时，系统的响应。

计算零状态响应的方法主要是根据欧拉公式，求解系统的传递函数，然后通过逆Z 变换得到零状态响应。

完全响应则包括零状态响应和初始状态响应。

初始状态响应是指在初始时刻，电感和电容的电压不为零时，系统的响应。

计算完全响应的方法是将零状态响应和初始状态响应相加。

二阶电路算法在电子工程和通信工程领域具有广泛的应用。

例如，在交流信号的放大与衰减过程中，可以通过调整二阶电路的参数来实现信号的放大或衰减。

此外，在滤波器的设计中，二阶电路算法也发挥着重要作用。

通过改变二阶电路的元件参数，可以实现不同截止频率和不同通带衰减特性的滤波器。

总之，二阶电路算法是一种在电子工程和通信工程领域中常用的计算方法，主要应用于二阶系统的分析和设计。

第七章 二阶电路 §7-1 二阶电路的零输入响应用二阶方程描述的动态电路称为二阶电路，当电路有电感，又有电容时就是一个二阶电路，二阶电路中给定的初始条件有2个 一、方程及特征根（RLC 串联）022=++C CC u dt du RC dtu d LC特征根为：LC L R L R p 12221-⎪⎭⎫⎝⎛+-=LC L R L R p 12221-⎪⎭⎫⎝⎛--=零输入响应为：t t P P C e A e A u 2121+= 1．电路的初始条件有三种情况，分别为：①0)0(0)0(≠≠++L C i u ②0)0(0)0(=≠++L C i u ③0)0(0)0(≠=++L C i u我们讨论第二种情况，设0)0()0()0()0(====-+-+L L C C i i u u u2．特征根p 1、p 2有不等负实数根、相等负实数根、一对共轭复数根三种情况，这三种情况决定零输入响应不同。

二、CLR 2>（1P 、2P 有不等负实根）时电路的响应 —是一个非振荡放电过程 1．电容上的电压和电流及电感上的电压响应表达式为：)(2112120t t P P C e P e P P P U u --=LCp p 121=)()()(2121120112210t t t t P P P P C e e P P L U e P e P P P P CU dt du Ci ---=---=-=)(2121120t t P P L e P e P P P U dt di Lu ---==2．响应曲线2112)/ln(P P P P T m -=此时电感电压过0，电流取得最大值m t t 2= 此时电感电压有极值三、CLR 2<（1P 、2P 有共轭复根）时电路的响应—是一个振荡放电过程1．电容上的电压和电流及电感上的电压为： )(2112120t t P P C e P e P P P U u --=[])2)(0)(00t j i t j j e e e e j U ωδβωδβωωω---+-+--=⎥⎦⎤⎢⎣⎡-=+-+-j e e eU t j t t j t2)()(00βωβωδωω)sin(00βωωωδ+=-t e U t)sin(0t e LU i tωωδ-=)sin(00βωωωδ--=-t e U u t其中：2RLδ=0ω=ω= arctg ωβδ= 2．波形图如下：ttπδ3．理想情况下，,2,1,0,00πβωωδ=====LCR 则：)2sin(00πω+=t U u Ct CLUt L U i 00000sin sin ωωω==C L u t U t U u =+=--=)2sin()2sin(0000πωπω 即等幅振荡放电过程。

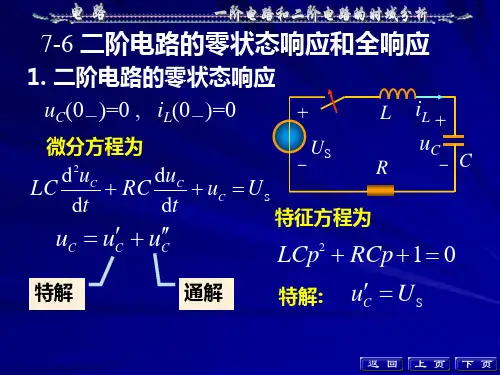
§7-2 RLC 串联电路中的零输入响应—过阻尼情况7.2.1 RLC 串联电路方程对含有一个电容和一个电感的二阶电路仍运用分解法进行分析。

1. 电路的分解和等效将含有一个电容和一个电感的二阶电路分解为两个互连的单口网络，其中一个单口为电容和电感的串联构成，一个单口为含源线性单口，并将该单口用戴维南等效电路等效. 2. 电路方程的建立由V AR ：22dtu d LC dt di L u dtdu RCRi u dt du Ci c LL cL R cL =====由KVL ：oc c L R u u u u =++则occ c cu u dt du RC dt u d LC =++223.初始条件及的确定)0(c u )0(c u )0()0()0(-+==c c c u u uCi C t i dtdu u L t L t c c )0()()0(00===== 只要已知二阶电路的初始状态和i 及)0(c u )0(L 0≥t 时电路的输入，就可以完全确定0≥t 时的响应。

)(t u c 7.2.2 RLC 串联电路的零输入响应令，则有0)(=t u oc 022=++c c cu dt du RC dt u d LC特征方程： 012=++LC s L R s特征根：LCL R L R s 1-)2(2-22,1±=特征根取值的三种情况：1. 当LC LR 1)2(2>时，，为两个不相等的负实根； 1s 2s 2. 当LC LR 1)2(2=时，，为两个相等的负实根； 1s 2s 3. 当LC LR 1)2(2<时，，为两个共轭的复根，且实部为负； 1s 2s 当特征根为第一种取值时，响应是非振荡性的，称为过阻尼情况； 当特征根为第二种取值时，响应处于临界振荡状态，称为临界阻尼情况； 当特征根为第三种取值是，响应是振荡性的，称为欠阻尼情况7.2.3 LC LR 1)2(2>时的响应及其意义 由于此时特征根为两个不相等的实根，故，齐次方程的解为)1(e e )(2121ts t s c k k t u +=1. 由初始条件和确定待定常数k 和。