2月12日(对数正态分布)-2
- 格式:docx
- 大小:104.67 KB
- 文档页数:2



正态分布概念及图表正态分布(Normal distribution),也称“常态分布”,又名高斯分布(Gaussian distribution),最早由A·棣莫弗在求二项分布的渐近公式中得到。
C.F.高斯在研究测量误差时从另一个角度导出了它。
P·S·拉普拉斯和高斯研究了它的性质。
是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。
正态曲线呈钟型,两头低,中间高,左右对称因其曲线呈钟形,因此人们又经常称之为钟形曲线。
若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布,记为N(μ,σ^2)。
其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。
当μ = 0,σ = 1时的正态分布是标准正态分布。
目录1历史发展2定理3定义▪一维正态分布▪标准正态分布4性质5分布曲线▪图形特征▪参数含义6研究过程7曲线应用▪综述▪频数分布▪综合素质研究▪医学参考值历史发展正态分布概念是由德国的数学家和天文学家Moivre于1733年首次提出的,但由于德国数学家Gauss率先将其应用于天文学家研究,故正态分布又叫高斯分布,高斯这项工作对后世的影响极大,他使正态分布同时有了“高斯分布”的名称,后世之所以多将最小二乘法的发明权归之于他,也是出于这一工作。
但现今德国10马克的印有高斯头像的钞票,其上还印有正态分布的密度曲线。
这传达了一种想法:在高斯的一切科学贡献中,其对人类文明影响最大者,就是这一项。
在高斯刚作出这个发现之初,也许人们还只能从其理论的简化上来评价其优越性,其全部影响还不能充分看出来。
这要到20世纪正态小样本理论充分发展起来以后。
拉普拉斯很快得知高斯的工作,并马上将其与他发现的中心极限定理联系起来,为此,他在即将发表的一篇文章(发表于1810年)上加上了一点补充,指出如若误差可看成许多量的叠加,根据他的中心极限定理,误差理应有高斯分布。
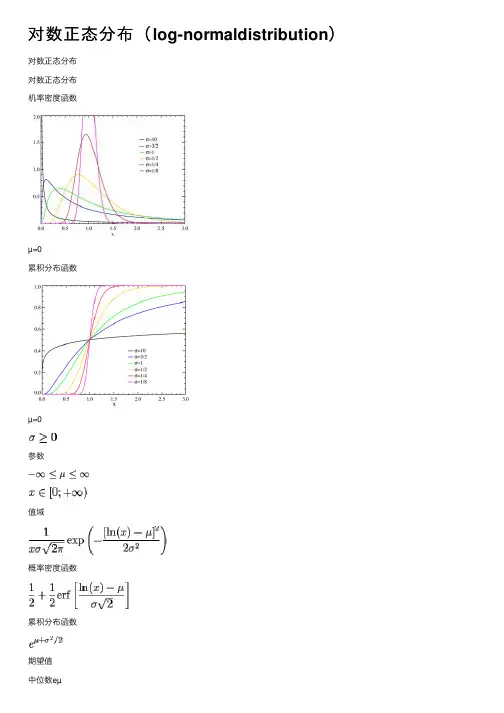
对数正态分布(log-normaldistribution)对数正态分布对数正态分布机率密度函数µ=0累积分布函数µ=0参数值域概率密度函数累积分布函数期望值众数⽅差偏态峰态熵值动差⽣成函数(参见原始动差⽂本)特征函数isasymptotically divergent but sufficientfor numerical purposes在概率论与统计学中,对数正态分布是对数为正态分布的任意随机变量的概率分布。
如果X 是正态分布的随机变量,则exp(X)为对数分布;同样,如果Y是对数正态分布,则 ln(Y) 为正态分布。
如果⼀个变量可以看作是许多很⼩独⽴因⼦的乘积,则这个变量可以看作是对数正态分布。
⼀个典型的例⼦是股票投资的长期收益率,它可以看作是每天收益率的乘积。
对于x > 0,对数正态分布的概率分布函数为其中µ与σ分别是变量对数的平均值与标准差。
它的期望值是⽅差为给定期望值与标准差,也可以⽤这个关系求µ与σ⽬录[隐藏]1 与⼏何平均值和⼏何标准差的关系2 矩3 局部期望4 参数的最⼤似然估计6 进⼀步的阅读资料7 参考⽂献8 参见[编辑]与⼏何平均值和⼏何标准差的关系对数正态分布、⼏何平均数与⼏何标准差是相互关联的。
在这种情况下,⼏何平均值等于exp(µ),⼏何平均差等于 exp(σ)。
如果采样数据来⾃于对数正态分布,则⼏何平均值与⼏何标准差可以⽤于估计置信区间,就像⽤算术平均数与标准差估计正态分布的置信区间⼀样。
其中⼏何平均数µgeo = exp(µ),⼏何标准差σgeo = exp(σ)[编辑]矩原始矩为:或者更为⼀般的矩[编辑]局部期望随机变量X在阈值k上的局部期望定义为其中f(x) 是概率密度。
对于对数正态概率密度,这个定义可以表⽰为其中Φ是标准正态部分的累积分布函数。
对数正态分布的局部期望在保险业及经济领域都有应⽤。

对数正态分布参数
对数正态分布是一种常见的概率分布,其参数包括均值和方差。
均值和方差分别影响着分布的形状和分布范围。
对于对数正态分布,其均值和方差的计算公式如下:
均值:μ = exp(μ+σ^2/2)
方差:σ^2 = (exp(σ^2)-1)*exp(2μ+σ^2)
其中,μ表示对数正态分布的自然对数的均值,σ表示对数正态分布的自然对数的标准差。
对数正态分布的参数估计是一种重要的统计方法,可以利用极大似然估计或贝叶斯方法进行。
极大似然估计是常用的参数估计方法之一,通过最大化样本的似然函数来估计参数值。
贝叶斯方法则是一种更加灵活的方法,通过引入先验知识和后验概率来估计参数值。
在实际应用中,对数正态分布常用于描述随机变量的对数值分布,例如金融、生物学和环境科学等领域。
对数正态分布的参数估计对于这些领域的研究具有重要的意义。
- 1 -。


对数正态分布公式
正态分布函数公式如下:
其中μ为均数,σ为标准差。
μ决定了正态分布的位置,与μ越近,被取到的概率就越大,反之越小。
σ描述的是正态分布的离散程度。
σ越大,数据分布越分散曲线越扁平;σ越小,数据分布越集中曲线越陡峭。
在一个标准正态分布中,约有 68.2% 的点落在±1 个标准差的范围内。
约有 95.5% 的点落在±2 个标准差的范围内。
约有 99.7% 的点落在±3 个标准差的范围内。
正态分布概念是由法国数学家棣莫弗于1733年首次提出的,后由德国数学家高斯率先将其应用于天文学研究,故正态分布又叫高斯分布,高斯这项工作对后世的影响极大,所以有了“高斯分布”的美称。
在我们的自然界,大多数物种的高度和重量都满足正态分布,它们围绕着均值对称分布,而且不会包含特别大或特别小的事件.
例如:我们从来没有遇到过1米长的蚂蚁,也没有看到过1千克重的大象。
世界似乎被代表正态分布的“钟形”包围着,很多事物都是服从正态分布的:人的高度、胖瘦、寿命、雪花的尺寸、测量误差、灯泡的寿命、IQ分数、面包的分量、学生的考试分数,员工上班所需时间等等。



标准正态分布、对数正态分布和威布尔正态分布的性质和应用场景
在统计学中,分布是描述数据如何分散的重要工具。
有多种分布,其中最常用的三种是标准正态分布、对数正态分布和威布尔正态分布。
这些分布各有其特性和应用场景。
1.标准正态分布
标准正态分布是一种连续概率分布,其形状由均值(μ=0)和标准差(σ=1)决定。
它的曲线呈钟形,对称轴为y=0。
在许多科学和工程领域中,许多随机变量都服从或近似服从标准正态分布,因为它的数学性质非常简单,这使得分析和建模变得相对容易。
2.对数正态分布
对数正态分布是一种连续概率分布,其取值范围在0和无穷大之间。
它的概率密度函数是均值为μ、标准差为σ的自然对数函数。
对数正态分布常用于描述那些自然增长或衰减过程,如人口增长、金融资产价值等。
由于这些过程通常遵循对数增长或对数衰减规律,因此对数正态分布在这些领域中非常有用。
3.威布尔正态分布
威布尔正态分布是一种连续概率分布,常用于描述生物和机械系统的寿命。
它的形状由三个参数决定:形状参数、尺度参数和位置参数。
威布尔分布的曲线形状介于指数分布和正态分布之间,取决于形状参数的大小。
当形状参数接近1时,威布尔分布接近指数分布;当形状参数接近无穷大时,威布尔分布接近正态分布。
由于其独特的特性,威布尔分布在可靠性工程、生存分析和生命科学等领域中广泛应用。
总结:标准正态分布、对数正态分布和威布尔正态分布是统计学中三种重要的概率分布。
它们各有不同的特性和应用场景,但都是描述数据分散性的有力工具。
正确选择和应用这些分布,对于准确理解和预测各种现象至关重要。
对数正态分布是一种概率分布,它的概率密度函数如下:
f(x)=12πσlnxe−(lnx−μ)22σ2f(x)=\frac{1}{\sqrt{2\pi}\sigmax}\exp\left(-\frac{(\lnx-\mu)^2}{2\sigma^2}\right)f(x)=2πσxe−(lnx−μ)22σ2其中μ为位置参数,σ为尺度参数。
在对数坐标下,对数正态分布的概率密度函数与正态分布的概率密度函数类似,但是变量的对数被作为新的变量。
在对数坐标下,对数正态分布的累积分布函数为:
F(x)=12(1+erf(lnx−μσ))F(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\lnx-\mu}e^{-t^2/2}dtF(x)=π2∫−∞lnx−μe−t2dt其中erf为误差函数。
在实践中,对数正态分布常用于建模和分析那些其值在几何尺度上呈现出一定概率分布的随机变量,例如股票价格、公司收入等。
对数正态分布lognormaldistribution为了⽅便后⾯的描述,我们先定义正态分布的两个参数为:均值mean表⽰为µN, 标准差standard deviation 表⽰为σN(对应⽅差Variance 表⽰为σ2N)。
为了区分,我们⽤m和v分别表⽰对数正态分布的均值和⽅差, 他们与其对应的正太分布的关系如下:lognormal均值: m LogN=eµN+σ2N/2;lognormal⽅差: v LogN=(eσ2N−1)e2µN+σ2N.另外:lognormal 众数(mode) = eµN−σ2N;lognormal 中位数(median) = eµN.⽣成符合lognromal distribution 的随机数(n个数),⽆论是Python还是Matlab, 都利⽤µN和σN来⽣成对数正态分布随机数:1. Python (numpy)import numpy as npy0 = np.random.lognormal(mu_N, sigma_N, n)⽰例:我们取µN=0.5,σN=0.5, n=10000, 执⾏并画出Python⽣成的随机数histogram (bin数量取50)如下:2. Matlab%% method 1: build-in matlab makedist functionpd = makedist('Lognormal', 'mu' ,mu_N,'sigma',sigma_N);rng('default'); % For reproducibilityy1 = random(pd,n,1);% logx = log(y1); %logx distributed as normal distribution with mu and sigma% mean(logx); % 可以验证为 mu_N%% method 2: build-in matlab lognrnd functionrng('default'); % For reproducibilityy2 = lognrnd(mu_N, sigma_N, [n,1]);%% method 3: from normal distriutionrng('default'); % For reproducibilityz = randn([n,1]); %standard normalx = mu_N + sigma_N.*z;% x follows normal distribution N(mu_N, sigma_N)y3 = exp(x); % y follows lognormal distribution⽰例:我们取µN=0.5,σN=0.5, n=10000, 执⾏并画出Matlab⽣成的随机数histogram (bin数量取50)如下:Processing math: 100%。
伽马分布、威布尔分布和对数正态分布是统计学中常见的概率分布,它们在不同领域有着广泛的应用。
虽然它们都属于连续型概率分布,但在数学特性和实际应用中却各有不同。
接下来,我们将从深度和广度两个方面来探讨这三种分布的区别。
一、数学特性1. 伽马分布伽马分布是概率论和统计学中的一种连续概率分布。
它通常用来描述连续随机变量的等待时间或寿命,并且适合于描述达到指定事件所需要的时间。
伽马分布有两个参数,即形状参数和尺度参数,形状参数决定了分布的形状,尺度参数则影响了分布的幅度。
2. 威布尔分布威布尔分布是另一种连续概率分布,它常用来描述可靠性工程中的产品寿命。
威布尔分布的密度函数是一个类似指数函数的形式,其参数包括形状参数和尺度参数,形状参数影响了分布的形状,尺度参数则影响了分布的幅度。
3. 对数正态分布对数正态分布是正态分布的一种变体,它是由正态分布取对数得到的分布。
对数正态分布常用来描述一些生物学和经济学中的现象,如生物体的体重和收入的分布。
对数正态分布的形状和幅度同样受到参数的影响,但与伽马分布和威布尔分布有所不同。
二、实际应用1. 伽马分布伽马分布在实际应用中常用于描述生物体的寿命、机器的寿命、信号的持续时间等现象。
研究人员常通过伽马分布来分析某种设备的寿命分布情况,以确定其可靠性和维护周期。
2. 威布尔分布威布尔分布则更多地应用于可靠性工程领域,用来描述产品的寿命分布情况。
工程师们可以根据威布尔分布来进行产品寿命的可靠性评估,从而制定相应的维护和更换计划。
3. 对数正态分布对数正态分布在生物学和经济学中有着广泛的应用。
例如在研究生物体的体重分布时,常常会采用对数正态分布来描述,因为生物体的体重通常呈现出这种分布特征。
个人观点和理解在我看来,这三种分布各有其独特的数学特性和实际应用。
虽然它们都属于连续型概率分布,但在形状和幅度的描述上有所不同。
了解和掌握这些分布的特性,对于我们在实际问题中的建模和分析是非常有帮助的。
今日(2月12号)内容:
第二章:概率论基础知识
2.3 常用的连续分布
2.3.4对数正态分布
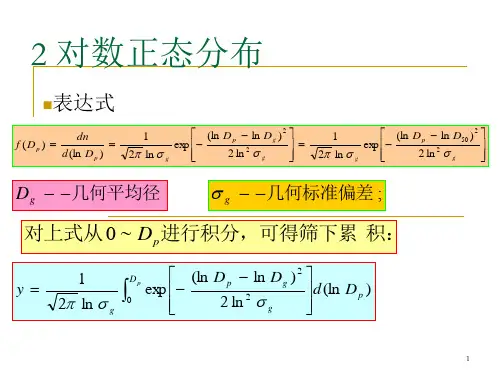
如果随机变量X只取正数值,而取自然对数后,lnX服从正态分布,则称X服从对数正态分布。
对数正态分布出现在很多领域,如某些电器的寿命、化学反应时间、混凝土的强度、针刺麻醉的镇痛效果、流行病的蔓延时间、绝缘材料的被击穿电压等。
在机床维修中,大量机床在短时间内都可修理好,但有少量机床需要长时间维修,个别机床可能需要更长的维修时间,因此机床维修时间常常是对数正态分布。
其分布密度的表达式为:
(2-34)这时,lnX~N(μ,σ2)。
我们称μ为位置参数,称σ为尺度参数。
其分布密度的图形显示为图2-38,从中可以看出,服从对数正
态分布的随机变量X的大量取值(“大头”)在左侧,长尾在右侧,虽然尾巴很细但拖得很长,随机变量X所取数值非常分散,这样的分布属于典型的“正偏分布”(见图2-38)。
图2-38对数正态分布密度图
对数正态分布的均值和方差为:
(2-35)
对数正态分布也可以有第3信阈值参数T,做为分布的起始点。
第二章未完待续······
200
150100
5000.0350.030
0.0250.0200.015
0.010
0.005
0.000
X 密度分布图对数正态, 位置=3, 尺度=1.2, 阈值=0。