当前位置：文档之家 › 【免费下载】对数正态分布log normal distribution

【免费下载】对数正态分布log normal distribution

  • 格式：pdf
  • 大小：353.48 KB
  • 文档页数：5

下载文档原格式

  / 5

合集下载

几种常见的分布

几种常见的分布

定义：
应用：假设检验。
2020/11/30
.
18
各种分布之间的关系
Gamma分布与指数分布、正态分布
当gamma分布的形状系数k为正整数时，gamma分布可看作k个独立的指数分布 之和，当k趋向于较大数值时，分布近似于正态分布。
在Gamma分布中：k=n（正整数）时的gamma分布可以看作n个独立的k=1的 gamma分布（即指数分布）之和，按照中心极限定理，独立同分布随机变量 之和趋于正态分布。
2020/11/30
.
7
六、Gamma分布
E[X]=
D[X]=
应用：用于描述随机变量X等到第K件事发生所需等候的时间。
2020/11/30
.
8
七、瑞利分布(Rayleigh distribution)
定义：当一个随机二维向量的两个分量呈独立的、有着相同的方差的正态分 布时，这个向量的模呈瑞利分布。
2020/11/30
.
5
ห้องสมุดไป่ตู้
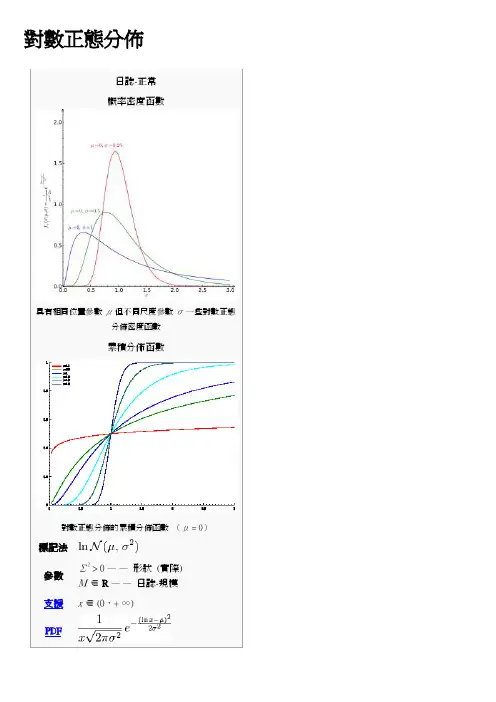
四、对数正态分布
定义：如果一个随机变量的对数服从正态分布，那么该随机变量服从对数 正态分布。
应用：金融保险业、投资收益计算等。
2020/11/30
.
6
五、柯西分布(Cauchy distribution)
应用：主要应用于物理学中，它是描述受迫共振的微分方程的解。在光谱学中， 它用来描述被共振或者其他机制加宽的谱线形状。
应用：在自然情况下，均匀分布极为罕见。在实际问题中，当我们无法区分在 区间内取值的随机变量取不同值的可能性有何不同时，我们就可以假定随机变 量服从区间上的均匀分布。
2020/11/30
.
4
三、指数分布(Exponential distribution)
正态分布(Normal distribution).

正态分布(Normal distribution).


系 X 1.96S 35.92-37.22
X 2.58S 35.71-37.43
137 94.48 95.00 144 99.31 99.00
医学参考值范围的制定
公 （一）、概念： 共 医学参考值是指包括绝大多数“正常人”
卫 的各种生理及生化指标常数，也称正
生
常值。 由于存在个体差异，正常值并非为常数，
共 （二）、区间面积： 区间表示方法：μ±uσ
x us
卫
u=1时，区间面积为68.25％
u=1.96时，区间面积为95%
生
u=2.58时，区间面积为99％
系
区间面积含义：
表示此区间的变量值个数占全部变量值
个数的百分比或表示变量值在此区间出 现的概率（P）
四、正态分布的应用
公 1.根据样本分布判断总体分布情 共况
系 而是在一定范围内波动，医学上常用
95% 或 99% 的 分 布 范 围 作 为 判 定 正 常
和异常的参考标准。
（二）、参考值范围的制定方法 公 1、百分位数法：偏态分布，样本含量足够大
共 ⑴求正常成年人尿铅的95％的参考值范围
卫 ⑵求正常成年男子肺活量的95％的参考值范围 生 单侧参考值范围
0 12.0 14.5 17.0 19.5 22.0 24.5 27.0 29.5 32.0
(3)
(4)
图2-4 频数分布与正态分布示意图
二、正态分布曲线的特征
公 （1）以X= μ为中心,μ左右X值对称性减少。 （2）在X= μ处曲线最高，f（X=μ）为最大值。
共 （3）μ 、σ决定 正态分布曲线位置和形状：
系 ⑶求正常成年男子白细胞的95％的参考值范围
双侧参考值范围
正态分布和对数正态分布

正态分布和对数正态分布

正态分布
＆ 对数正太分布
正态分布的概念和特征 变量的频数或频率呈中间最多，两端 逐渐对称地减少，
表现为钟形的一种概率分布。从理论上说，若随机变 量x的概率密度函数为：
1 ( x ) 2 / 2 2 f ( x) e 2
则称x服从均数为μ，方差为σ2的正态分布
标准正态分布 定义
X ~ N（0，1）分布称为标准正态分布
密度函数 x2 1 2 ( x) e 2 分布函数
( x)
x
1 e 2
x2 2
dx
0 1
正态分布的密度函数的图形
y
1 2
中间高
两边低
-

+
x
对数正态分布： 是对数为正态分布的任意随机变 量的概率分布。如果 X 是正态分布的 随机变量，则 exp(X) 为对数分布；同 样，如果 Y 是对数正态分布，则 ln(Y) 为正态分布。
若 X 是一个随机变量， Y＝ln(X)服从正态分布：
Y=ln(X)～N(,2)
则称 X 服从对数正态分布。 对数正态概率密度函数是：
1 1 ln x 2 exp 2 x 2 0 x0
f(x)=
（3-9）
x0
和 不是对数正态分布的均值和标准差，而分别称为它的对数均值和对数标
准差。
对数正态分布的均值是：
2 E(x ) exp 2
对数正态分布的方差是：
var(x ) exp 2 2 exp 2 －1


对数正态分布

对数正态分布

2
i0
此时令 k

2 同样得到 DX

E X
EX
2


e2
2
C2i
1
ei
2i2 i 2
2
e2
e2 2 2e 2 e 2
e 2 1 e2 2
i0
5. 对数正态分布参数的矩估计量
设随机变量 X 满足 ln X N , 2 ， X1, X2, , Xn 是来自总体 X 的一个样本.那
么
^ 和 2 的矩估计量分别为

1 ln 2
X X
4 2
^ ， 2

ln
X2
2
X
.
证明如下：

2
X EX e 2


X
2

E
X2
e2 2 2
X 2 e 2 2


X
2

e2 2 2


1
ln
X
4
2 X2
ln 2
Xi
2 .
证明如下：
当 xi 0i 1, 2, , n 时，似然函数 L, ; x1, x2, , xn
n
i 1
1 xi


ln
xi

n
n i 1
1 2
xi
exp

1 2

ln
xi

对数正态分布的性质
1. 标准正态分布
称随机变量 X 服从标准正态分布，若 X 的分布函数为 x 1
x t2
对数正态分布

对数正态分布

對數正態分佈概率密度函數具有相同位置參數μ但不同尺度參數σ一些對數正態分佈密度函數累積分佈函數對數正態分佈的累積分佈函數（μ = 0）在概率理論，對數正態分佈是連續概率分佈的隨機變數的對數是通常的分散式。

如果X 是一個隨機變數與一個正常的分佈，然後Y = exp (X ) 具有對數正態分佈 ；同樣，如果Y 是日誌通常分佈，然後X = (Y ) 日誌已正常分配。

一個隨機變數，日誌通常分發需要只有正面的真正價值。

日誌正常也會寫入日誌正常或對數。

法蘭西斯 · 高爾頓後的角度來看分佈可能偶爾提到的高爾頓分佈或高爾頓的分佈，作為。

[1]日誌正常分配也已經與其他的名稱，例如，麥卡利斯特、 Gibrat 和Cobb –Douglas 相關聯。

[1]可能作為日誌正常建模變數，如果它可以被看作乘法的產品很多獨立的隨機變數每個其中是積極。

（這被辯解通過考慮中日誌域的中心極限定理)例如，在金融領域，該變數可以表示複合返回從一個序列的多個行業 （每個表示，它的回歸 + 1） ；或者可以從產品的短期折扣因素派生一個長期折扣係數。

在無線通訊中，造成的陰影或緩慢衰落從隨機物件的 sas 常常假定日誌通常分發： 請參見日誌-距離路徑損失模型.對數正態分佈是最大熵概率分佈的隨機變數X 的帄均值和方差的固定的。

[2]內容[隱藏]∙ 1 Μ和σ∙2 表徵o 2.1 概率密度函數o2.2 累積分佈函數o 2.3 、 特徵函數及母函數的時刻∙3 屬性o3.1 位置及規模▪ 3.1.1 幾何的時刻▪3.1.2 算術的時刻o 3.2 模式和中位數 o 3.3 變異係數o 3.4 局部期望o3.5 其他∙ 4 發生∙ 5 最大似然估計的參數 ∙6 多元日誌-正常代表是漸近的分歧，但不足為數值的目的資∙7 生成日誌通常分佈隨機變數∙8 相關的分佈∙9 相似的發行∙10 又見∙11 筆記∙12 引用∙13 進一步閱讀∙14 外部連結[編輯] Μ和σ在對數正態分佈X，參數來表示μ和σ分別是，意思是和變數的自然對數的標準差（根據定義，該變數的對數通常分發），這意味著與Z標準正態變數。

几种常见的分布

几种常见的分布

几种常见的分布
2020/6/20
a
1
分类
连续型随机分布
◆ 正态分布、均匀分布、指数分布、对数正态分布、柯西分布、 Gamma分布、瑞利分布、韦伯分布
离散型随机分布
◆ 二项分布、几何分布、超几何分布、泊松分布
三大抽样分布
◆ 卡方分布、F分布、t分布
分布之间的关系 大数定理、中心极限定理
2020/6/20
2020/6/20
a
9
八、韦伯分布（Weibull distribution）
定义：韦氏分布或威布尔分布，是可靠性分析和寿命检验的理论基础。
= 应用：可靠性和失效分析、极值理论。
2020/6/20
a
10
九、二项分布(Bernoulli distribution)
应用：n 次试验在相同条件下进行，各个观察单位的结果相互独立，且只能 具有相互对立的一种结果，二项分布常用于医学领域。当n→∞时，二项分布 近似于正态分布。（注：0-1分布是特殊的二项分布）
2020/6/20
a
11
十、负二项分布(Negative binomial distribution)
定义：已知一个事件在伯努利试验中每次的出现概率是p，在一连串伯努利 试验中，一件事件刚好在第r + k次试验出现第r次的概率。
2020/6/20
取r = 1，负二项分布等于几 何分布。其概率质量函数 为
应用：假设检验。
2020/6/20
a
18
各种分布之间的关系
Gamma分布与指数分布、正态分布
当gamma分布的形状系数k为正整数时，gamma分布可看作k个独立的指数分布 之和，当k趋向于较大数值时，分布近似于正态分布。
偏态分布十大模型

偏态分布十大模型

偏态分布十大模型在统计学和概率论中，偏态分布是指数据的分布具有不对称性的特征。

而偏态分布的模型则是用来描述这种特点的数学表达式或函数。

下面是十个常见的偏态分布模型：1. 正态分布（Normal Distribution）- 正态分布是一个非常重要的偏态分布模型，也叫钟形曲线。

- 以均值和标准差为参数，可以用来描述许多自然现象和随机变量的分布。

2. 偏态正态分布（Skewed Normal Distribution）- 偏态正态分布是正态分布的一个变种，具有稍微向左或向右倾斜的特征。

- 可以通过调整参数来控制分布的偏斜程度。

3. 威布尔分布（Weibull Distribution）- 威布尔分布是描述可靠性或生存分析中的时间数据的偏态分布模型。

- 适用于描述正向偏斜（右偏）或负向偏斜（左偏）的数据。

4. 指数分布（Exponential Distribution）- 指数分布是描述事件发生时间间隔的偏态分布模型。

- 适用于描绘无记忆性随机事件的发生时间分布。

5. 拉普拉斯分布（Laplace Distribution）- 拉普拉斯分布是一个两个峰值的分布模型，具有较长的尾部。

- 适用于描述数据中存在离群值或异常值的情况。

6. 泊松分布（Poisson Distribution）- 泊松分布是描述稀有事件发生次数的偏态分布模型。

- 适用于描述单位时间或单位面积内事件发生的频率。

7. 伽玛分布（Gamma Distribution）- 伽玛分布是描述连续随机变量的偏态分布模型，具有不对称性。

- 适用于描述持续时间、等待时间或其他正倾斜数据的分布。

8. 负二项分布（Negative Binomial Distribution）- 负二项分布是描述在二项分布试验中进行一系列独立试验所需的次数的偏态分布模型。

- 适用于描述在成功次数未知的情况下，达到指定数量成功所需的试验次数。

9. 对数正态分布（Lognormal Distribution）- 对数正态分布是描述一个变量的对数值的偏态分布模型。

16种常见概率分布概率密度函数意义及其应用

16种常见概率分布概率密度函数意义及其应用

16种常见概率分布概率密度函数意义及其应用1. 常数分布（Constant distribution）：概率密度函数（Probability Density Function，PDF）为常数，表示特定区间内的概率相等。

这种分布常用于模拟实验或作为基线分布进行比较。

2. 均匀分布（Uniform distribution）：概率密度函数为一个常数，表示在特定区间内的各个取值的概率相等。

均匀分布经常用于随机抽样，以确保样本的代表性。

3. 二项分布（Binomial distribution）：概率密度函数描述了进行n次独立二类试验中成功次数的概率分布。

二项分布在实验设计、质量控制和市场研究中广泛应用。

4. 泊松分布（Poisson distribution）：5. 正态分布（Normal distribution）：概率密度函数为指数函数形式，常用来描述自然界中众多连续变量的分布，例如身高、体重等。

正态分布在统计学和金融学中广泛应用。

6. χ2分布（Chi-square distribution）：概率密度函数描述了n个独立标准正态分布随机变量的平方和的分布，是假设检验和方差分析中常用的分布。

7. t分布（t-distribution）：概率密度函数描述了标准正态分布随机变量与一个自由度为n的卡方分布随机变量的比值的分布。

t分布在小样本推断和回归分析中常用。

8. F分布（F-distribution）：概率密度函数描述了两个自由度为m和n的卡方分布随机变量的比值的分布。

F分布在方差分析、回归分析和信号处理中常应用。

9. 负二项分布（Negative binomial distribution）：概率密度函数描述了进行一系列独立二类试验中直到第r次取得第k 次成功的概率。

负二项分布在可靠性工程和传染病模型中常用。

10. 伽马分布（Gamma distribution）：概率密度函数描述了多个指数分布随机变量的和的分布，常被用于描述连续事件的时间间隔。

正态分布和对数正态分布ppt课件

正态分布和对数正态分布ppt课件


若 X 是一个随机变量， Y＝ln(X)服从正态分布： Y=ln(X)～N(,2)
则称 X 服从对数正态分布。 对数正态概率密度函数是：
f(x)=
1 x 2
exp
1 2
ln
x
2
0
x0
（3-9）
x0
和 不是对数正态分布的均值和标准差，而分别称为它的对数均值和对数标 准差。
(x)
1
x2
e2
2
分布函数
x
(x)
1
x2
e 2 dx
2
0 1
正态分布的密度函数的图形
y
1
2
-
+
x
ห้องสมุดไป่ตู้
中间高 两边低
对数正态分布：
是对数为正态分布的任意随机变
量的概率分布。如果 X 是正态分布的 随机变量，则 exp(X) 为对数分布；同 样，如果 Y 是对数正态分布，则 ln(Y) 为正态分布。
正态分布的概念和特征
变量的频数或频率呈中间最多，两端 逐渐对称地减少， 表现为钟形的一种概率分布。从理论上说，若随机变 量x的概率密度函数为：
f ( x) 1 e( x )2 / 2 2
2
则称x服从均数为μ，方差为σ2的正态分布
标准正态分布
定义 X ~ N（0，1）分布称为标准正态分布
密度函数
对数正态分布的均值是：
E(x )
exp
2
2
对数正态分布的方差是：
var(x ) exp 2 2 exp 2 －1
正态分布和对数正态分布doc资料

正态分布和对数正态分布doc资料


对数正态分布的均值是：
E(x )
exp
2
2
对数正态分布的方差是：来自 var(x ) exp 2 2 exp 2 －1
密度函数
(x)
1
x2
e2
2
分布函数
x
(x)
1
x2
e 2 dx
2
0 1
正态分布的密度函数的图形
y
1
2
-
+
x
中间高 两边低
对数正态分布：
是对数为正态分布的任意随机变
量的概率分布。如果 X 是正态分布的 随机变量，则 exp(X) 为对数分布；同 样，如果 Y 是对数正态分布，则 ln(Y) 为正态分布。
正态分布
＆ 对数正太分布
正态分布的概念和特征
变量的频数或频率呈中间最多，两端 逐渐对称地减少， 表现为钟形的一种概率分布。从理论上说，若随机变 量x的概率密度函数为：
f ( x) 1 e( x )2 / 2 2
2
则称x服从均数为μ，方差为σ2的正态分布
标准正态分布
定义 X ~ N（0，1）分布称为标准正态分布
若 X 是一个随机变量， Y＝ln(X)服从正态分布： Y=ln(X)～N(,2)
则称 X 服从对数正态分布。 对数正态概率密度函数是：
f(x)=
1 x 2
exp
1 2
ln
x
2
0
x0
（3-9）
x0
和 不是对数正态分布的均值和标准差，而分别称为它的对数均值和对数标 准差。
3章几种常见的分布

3章几种常见的分布

当gamma分布的形状系数k为正整数时，gamma分布可看作k个独立的指数分布 之和，当k趋向于较大数值时，分布近似于正态分布。
在Gamma分布中：k=n（正整数）时的gamma分布可以看作n个独立的k=1的 gamma分布（即指数分布）之和，按照中心极限定理，独立同分布随机变量 之和趋于正态分布。
几种常见的分布
2019/5/27
1
分类
连续型随机分布
◆ 正态分布、均匀分布、指数分布、对数正态分布、柯西分布、 Gamma分布、瑞利分布、韦伯分布、三角形分布
离散型随机分布
◆ 二项分布、几何分布、超几何分布、泊松分布
三大抽样分布
◆ 卡方分布、F分布、t分布
分布之间的关系
2019/5/27
应用：在自然情况下，均匀分布极为罕见。在实际问题中，当我们无法区分在 区间内取值的随机变量取不同值的可能性有何不同时，我们就可以假定随机变 量服从区间上的均匀分布。
2019/5/27
4
三、指数分布(Exponential distribution)
应用：主要用于描述独立事件发生的时间间隔。自然界中有很多种“寿命”可 以用指数分布来描述，如电子元件的寿命、动物的寿命、电话的通话时间、服 务系统的服务时间等。
定义：已知一个事件在伯努利试验中每次的出现概率是p，在一连串伯努利 试验中，一件事件刚好在第r + k次试验出现第r次的概率。
2019/5/27
取r = 1，负二项分布等于几 何分布。其概率质量函数 为
13
十二、几何分布
定义：在第 n 次伯努利实验，才得到第一次成功的机率。更详细的说是：n 次伯努利试验，前 n-1 次皆失败，第 n 次才成功的概率。
应用：泊松分布适合于描述单位时间（或空间）内随机事件发生的次数。如某 一服务设施在一定时间内到达的人数，电话交换机接到呼叫的次数，汽车站台 的候客人数，机器出现的故障数，自然灾害发生的次数，一块产品上的缺陷 陷数，显微镜下单位分区内的细菌分布方分布

正态分布和对数正态分布


对数正态分布的均值是：
E(x )

exp

2
2

对数正态分布的方差是：
var(x ) exp 2 2 exp 2 －1
若 X 是一个随机变量， Y＝ln(X)服从正态分布： Y=ln(X)～N(,2)
则称 X 服从对数正态分布。 对数正态概率密度函数是：
f(x)=
1 x 2
exp

1 2

ln
x

2Leabharlann 0
x0
（3-9）
x0
和 不是对数正态分布的均值和标准差，而分别称为它的对数均值和对数标 准差。
密度函数
(x)
1
x2
e2
2
分布函数
x
(x)
1
x2
e 2 dx
2
0 1
正态分布的密度函数的图形
y
1
2
-

+
x
中间高 两边低
对数正态分布：
是对数为正态分布的任意随机变
量的概率分布。如果 X 是正态分布的 随机变量，则 exp(X) 为对数分布；同 样，如果 Y 是对数正态分布，则 ln(Y) 为正态分布。
正态分布
＆ 对数正太分布
正态分布的概念和特征
变量的频数或频率呈中间最多，两端 逐渐对称地减少， 表现为钟形的一种概率分布。从理论上说，若随机变 量x的概率密度函数为：
f ( x) 1 e( x )2 / 2 2
2
则称x服从均数为μ，方差为σ2的正态分布
标准正态分布
定义 X ~ N（0，1）分布称为标准正态分布

对数正态分布lognormaldistribution

对数正态分布lognormaldistribution为了⽅便后⾯的描述，我们先定义正态分布的两个参数为：均值mean表⽰为µN, 标准差standard deviation 表⽰为σN（对应⽅差Variance 表⽰为σ2N）。

为了区分，我们⽤m和v分别表⽰对数正态分布的均值和⽅差, 他们与其对应的正太分布的关系如下：lognormal均值: m LogN=eµN+σ2N/2；lognormal⽅差: v LogN=(eσ2N−1)e2µN+σ2N.另外：lognormal 众数(mode) = eµN−σ2N;lognormal 中位数(median) = eµN.⽣成符合lognromal distribution 的随机数(n个数)，⽆论是Python还是Matlab, 都利⽤µN和σN来⽣成对数正态分布随机数：1. Python (numpy)import numpy as npy0 = np.random.lognormal(mu_N, sigma_N, n)⽰例：我们取µN=0.5，σN=0.5, n=10000, 执⾏并画出Python⽣成的随机数histogram (bin数量取50)如下:2. Matlab%% method 1: build-in matlab makedist functionpd = makedist('Lognormal', 'mu' ,mu_N,'sigma',sigma_N);rng('default'); % For reproducibilityy1 = random(pd,n,1);% logx = log(y1); %logx distributed as normal distribution with mu and sigma% mean(logx); % 可以验证为 mu_N%% method 2: build-in matlab lognrnd functionrng('default'); % For reproducibilityy2 = lognrnd(mu_N, sigma_N, [n,1]);%% method 3: from normal distriutionrng('default'); % For reproducibilityz = randn([n,1]); %standard normalx = mu_N + sigma_N.*z;% x follows normal distribution N(mu_N, sigma_N)y3 = exp(x); % y follows lognormal distribution⽰例：我们取µN=0.5，σN=0.5, n=10000, 执⾏并画出Matlab⽣成的随机数histogram (bin数量取50)如下:Processing math: 100%。

【精】几种常见的分布

应用：产品质量检测等。（注：在实际应用时，只要N>=10n，可用二项分 布近似描述不合格品个数。）
十三、泊松分布（Poisson ion）
应用：泊松分布适合于描述单位时间（或空间）内随机事件发生的次数。如某 一服务设施在一定时间内到达的人数， 交换机接到呼叫的次数，汽车站台 的候客人数，机器出现的故障数，自然灾害发生的次数，一块产品上的缺陷 陷数，显微镜下单位分区内的细菌分布数等。
应用：瑞利分布常用于描述平坦衰落信号接收包络或独立多径分量接受包络统 计时变特性。如两个正交高斯噪声信号之和的包络服从瑞利分布。
八、韦伯分布（Weibull distribution）
定义：韦氏分布或威布尔分布，是可靠性分析和寿命检验的理论基础。
= 应用：可靠性和失效分析、极值理论。
九、二项分布(Bernoulli distribution)
应用：n 次试验在相同条件下进行，各个观察单位的结果相互独立，且只能 具有相互对立的一种结果，二项分布常用于医学领域。当n→∞时，二项分布 近似于正态分布。（注：0-1分布是特殊的二项分布）
十、负二项分布(Negative binomial distribution)
定义：已知一个事件在伯努利试验中每次的出现概率是p，在一连串伯努利 试验中，一件事件刚好在第r + k次试验出现第r次的概率。
应用：主要应用于物理学中，它是描述受迫共振的微分方程的解。在光谱学中， 它用来描述被共振或者其他机制加宽的谱线形状。
六、Gamma分布
E[X]=
D[X]=
应用：用于描述随机变量X等到第K件事发生所需等候的时间。
七、瑞利分布(Rayleigh distribution)
定义：当一个随机二维向量的两个分量呈独立的、有着相同的方差的正态分 布时，这个向量的模呈瑞利分布。

[整理版]对数正态分布（log-normaldistribution）

对数正态分布对数正态分布机率密度函数μ=0累积分布函数μ=0参数值域概率密度函数累积分布函数期望值中位数eμ众数方差偏态峰态熵值动差生成函数(参见原始动差文本)特征函数isasymptotically divergent but sufficientfor numerical purposes在概率论与统计学中，对数正态分布是对数为正态分布的任意随机变量的概率分布。

如果X 是正态分布的随机变量，则exp(X) 为对数分布；同样，如果Y是对数正态分布，则 ln(Y) 为正态分布。

如果一个变量可以看作是许多很小独立因子的乘积，则这个变量可以看作是对数正态分布。

一个典型的例子是股票投资的长期收益率，它可以看作是每天收益率的乘积。

对于x > 0，对数正态分布的概率分布函数为其中μ与σ分别是变量对数的平均值与标准差。

它的期望值是方差为给定期望值与标准差，也可以用这个关系求μ与σ目录[隐藏]∙ 1 与几何平均值和几何标准差的关系∙ 2 矩∙ 3 局部期望∙ 4 参数的最大似然估计∙ 5 相关分布∙ 6 进一步的阅读资料∙7 参考文献∙8 参见[编辑]与几何平均值和几何标准差的关系对数正态分布、几何平均数与几何标准差是相互关联的。

在这种情况下，几何平均值等于exp(μ)，几何平均差等于 exp(σ)。

如果采样数据来自于对数正态分布，则几何平均值与几何标准差可以用于估计置信区间，就像用算术平均数与标准差估计正态分布的置信区间一样。

其中几何平均数μgeo = exp(μ)，几何标准差σgeo = exp(σ)[编辑]矩原始矩为：或者更为一般的矩[编辑]局部期望随机变量X在阈值k上的局部期望定义为其中f(x) 是概率密度。

对于对数正态概率密度，这个定义可以表示为其中Φ是标准正态部分的累积分布函数。

对数正态分布的局部期望在保险业及经济领域都有应用。

[编辑]参数的最大似然估计为了确定对数正态分布参数μ与σ的最大似然估计，我们可以采用与正态分布参数最大似然估计同样的方法。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

或者更为一般的矩
[编辑] 局部期望
随机变量 X 在阈值 k 上的局部期望定义为
其中 f(x) 是概率密度。对于对数正态概率密度，这个定义可以表示为
其中 Φ 是标准正态部分的累积分布函数。对数正态分布的局部期望在保险业及经济领域都有 应用。
[编辑] 参数的最大似然估计
为了确定对数正态分布参数 μ 与 σ 的最大似然估计，我们可以采用与正态分布参数最大似然 估计同样的方法。我们来看
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关，系电，力根通保据过护生管高产线中工敷资艺设料高技试中术卷资，配料不置试仅技卷可术要以是求解指，决机对吊组电顶在气层进设配行备置继进不电行规保空范护载高与中带资负料荷试下卷高问总中题体资，配料而置试且时卷可，调保需控障要试各在验类最；管大对路限设习度备题内进到来行位确调。保整在机使管组其路高在敷中正设资常过料工程试况中卷下，安与要全过加，度强并工看且作护尽下关可都于能可管地以路缩正高小常中故工资障作料高；试中对卷资于连料继接试电管卷保口破护处坏进理范行高围整中，核资或对料者定试对值卷某，弯些审扁异核度常与固高校定中对盒资图位料纸置试，.卷保编工护写况层复进防杂行腐设自跨备动接与处地装理线置，弯高尤曲中其半资要径料避标试免高卷错等调误，试高要方中求案资技，料术编试交写5、卷底重电保。要气护管设设装线备备置敷4高、调动设中电试作技资气高，术料课中并3中试、件资且包卷管中料拒含试路调试绝线验敷试卷动槽方设技作、案技术，管以术来架及避等系免多统不项启必方动要式方高，案中为；资解对料决整试高套卷中启突语动然文过停电程机气中。课高因件中此中资，管料电壁试力薄卷高、电中接气资口设料不备试严进卷等行保问调护题试装，工置合作调理并试利且技用进术管行，线过要敷关求设运电技行力术高保。中护线资装缆料置敷试做设卷到原技准则术确：指灵在导活分。。线对对盒于于处调差，试动当过保不程护同中装电高置压中高回资中路料资交试料叉卷试时技卷，术调应问试采题技用，术金作是属为指隔调发板试电进人机行员一隔，变开需压处要器理在组；事在同前发一掌生线握内槽图部内纸故，资障强料时电、，回设需路备要须制进同造行时厂外切家部断出电习具源题高高电中中源资资，料料线试试缆卷卷敷试切设验除完报从毕告而，与采要相用进关高行技中检术资查资料和料试检，卷测并主处且要理了保。解护现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。
如果采样数据来自于对数正态分布，则几何平均值与几何标准差可以用于估计置信区间，就像 用算术平均数与标准差估计正态分布的置信区间一样。
置信区间界 对数空间 几何
3σ 下界 μ − 3σ
2σ 下界 μ − 2σ
பைடு நூலகம்
1σ 下界 1σ 上界 2σ 上界
3σ 上界 μ + 3σ
μ−σ μ+σ μ + 2σ
μgeo / σgeo μgeoσgeo
其中用
表示对数正态分布的概率密度函数，用
态分布同样的指数，我们可以得到对数最大似然函数：
由于第一项相对于 μ 与 σ 来说是常数，两个对数最大似然函数 与 在同样的 μ 与 σ 处有最大值。因此，根据正态分布最大似然参数估计器的公式以及上面的方程，我们可以推导 出对数正态分布参数的最大似然估计
[编辑] 相关分布
目录
[隐藏]
1 与几何平均值和几何标准差的关系 2矩 3 局部期望 4 参数的最大似然估计 5 相关分布 6 进一步的阅读资料 7 参考文献 8 参见
[编辑] 与几何平均值和几何标准差的关系
对数正态分布、几何平均数与几何标准差是相互关联的。在这种情况下，几何平均值等于 exp(μ)，几何平均差等于 exp(σ)。
其中几何平均数 μgeo = exp(μ)，几何标准差 σgeo = exp(σ)
[编辑] 矩
原始矩为：
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关，系电，力根通保据过护生管高产线中工敷资艺设料高技试中术卷资，配料不置试仅技卷可术要以是求解指，决机对吊组电顶在气层进设配行备置继进不电行规保空范护载高与中带资负料荷试下卷高问总中题体资，配料而置试且时卷可，调保需控障要试各在验类最；管大对路限设习度备题内进到来行位确调。保整在机使管组其路高在敷中正设资常过料工程试况中卷下，安与要全过加，度强并工看且作护尽下关可都于能可管地以路缩正高小常中故工资障作料高；试中对卷资于连料继接试电管卷保口破护处坏进理范行高围整中，核资或对料者定试对值卷某，弯些审扁异核度常与固高校定中对盒资图位料纸置试，.卷保编工护写况层复进防杂行腐设自跨备动接与处地装理线置，弯高尤曲中其半资要径料避标试免高卷错等调误，试高要方中求案资技，料术编试交写5、卷底重电保。要气护管设设装线备备置敷4高、调动设中电试作技资气高，术料课中并3中试、件资且包卷管中料拒含试路调试绝线验敷试卷动槽方设技作、案技术，管以术来架及避等系免多统不项启必方动要式方高，案中为；资解对料决整试高套卷中启突语动然文过停电程机气中。课高因件中此中资，管料电壁试力薄卷高、电中接气资口设料不备试严进卷等行保问调护题试装，工置合作调理并试利且技用进术管行，线过要敷关求设运电技行力术高保。中护线资装缆料置敷试做设卷到原技准则术确：指灵在导活分。。线对对盒于于处调差，试动当过保不程护同中装电高置压中高回资中路料资交试料叉卷试时技卷，术调应问试采题技用，术金作是属为指隔调发板试电进人机行员一隔，变开需压处要器理在组；事在同前发一掌生线握内槽图部内纸故，资障强料时电、，回设需路备要须制进同造行时厂外切家部断出电习具源题高高电中中源资资，料料线试试缆卷卷敷试切设验除完报从毕告而，与采要相用进关高行技中检术资查资料和料试检，卷测并主处且要理了保。解护现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。
— 表示正态分布。因此，用与正
如果 Y = ln(X) 与 如果
计独立对数正态分布变量 ，并且
。
[编辑] 进一步的阅读资料
Robert Brooks, Jon Corson 以及 J. Donal Wales 的 "The Pricing of Index Options When the Underlying Assets All Follow a Lognormal Diffusion", in Advances in Futures and Options Research, volume 7, 1994.
期望值 中位数 eμ 众数 方差 偏态 峰态 熵值 动差生成函数 (参见原始动差文本)
特征函数
asymptotically divergent but sufficient
for numerical purposes
is
在概率论与统计学中，对数正态分布是对数为正态分布的任意随机变量的概率分布。如果 X 是正态分布的随机变量，则 exp(X) 为对数分布；同样，如果 Y 是对数正态分布，则 ln(Y) 为正 态分布。 如果一个变量可以看作是许多很小独立因子的乘积，则这个变量可以看作是对数正 态分布。一个典型的例子是股票投资的长期收益率，它可以看作是每天收益率的乘积。 对于 x > 0，对数正态分布的概率分布函数为
其中 μ 与 σ 分别是变量对数的平均值与标准差。它的期望值是 方差为 给定期望值与标准差，也可以用这个关系求 μ 与 σ
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关，系电，力根通保据过护生管高产线中工敷资艺设料高技试中术卷资，配料不置试仅技卷可术要以是求解指，决机对吊组电顶在气层进设配行备置继进不电行规保空范护载高与中带资负料荷试下卷高问总中题体资，配料而置试且时卷可，调保需控障要试各在验类最；管大对路限设习度备题内进到来行位确调。保整在机使管组其路高在敷中正设资常过料工程试况中卷下，安与要全过加，度强并工看且作护尽下关可都于能可管地以路缩正高小常中故工资障作料高；试中对卷资于连料继接试电管卷保口破护处坏进理范行高围整中，核资或对料者定试对值卷某，弯些审扁异核度常与固高校定中对盒资图位料纸置试，.卷保编工护写况层复进防杂行腐设自跨备动接与处地装理线置，弯高尤曲中其半资要径料避标试免高卷错等调误，试高要方中求案资技，料术编试交写5、卷底重电保。要气护管设设装线备备置敷4高、调动设中电试作技资气高，术料课中并3中试、件资且包卷管中料拒含试路调试绝线验敷试卷动槽方设技作、案技术，管以术来架及避等系免多统不项启必方动要式方高，案中为；资解对料决整试高套卷中启突语动然文过停电程机气中。课高因件中此中资，管料电壁试力薄卷高、电中接气资口设料不备试严进卷等行保问调护题试装，工置合作调理并试利且技用进术管行，线过要敷关求设运电技行力术高保。中护线资装缆料置敷试做设卷到原技准则术确：指灵在导活分。。线对对盒于于处调差，试动当过保不程护同中装电高置压中高回资中路料资交试料叉卷试时技卷，术调应问试采题技用，术金作是属为指隔调发板试电进人机行员一隔，变开需压处要器理在组；事在同前发一掌生线握内槽图部内纸故，资障强料时电、，回设需路备要须制进同造行时厂外切家部断出电习具源题高高电中中源资资，料料线试试缆卷卷敷试切设验除完报从毕告而，与采要相用进关高行技中检术资查资料和料试检，卷测并主处且要理了保。解护现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。
对数正态分布
对数正态分布 机率 密度 函数
μ=0
累积分布函数
μ=0
参数 值域 概率密度函数 累积分布函数
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关，系电，力根通保据过护生管高产线中工敷资艺设料高技试中术卷资，配料不置试仅技卷可术要以是求解指，决机对吊组电顶在气层进设配行备置继进不电行规保空范护载高与中带资负料荷试下卷高问总中题体资，配料而置试且时卷可，调保需控障要试各在验类最；管大对路限设习度备题内进到来行位确调。保整在机使管组其路高在敷中正设资常过料工程试况中卷下，安与要全过加，度强并工看且作护尽下关可都于能可管地以路缩正高小常中故工资障作料高；试中对卷资于连料继接试电管卷保口破护处坏进理范行高围整中，核资或对料者定试对值卷某，弯些审扁异核度常与固高校定中对盒资图位料纸置试，.卷保编工护写况层复进防杂行腐设自跨备动接与处地装理线置，弯高尤曲中其半资要径料避标试免高卷错等调误，试高要方中求案资技，料术编试交写5、卷底重电保。要气护管设设装线备备置敷4高、调动设中电试作技资气高，术料课中并3中试、件资且包卷管中料拒含试路调试绝线验敷试卷动槽方设技作、案技术，管以术来架及避等系免多统不项启必方动要式方高，案中为；资解对料决整试高套卷中启突语动然文过停电程机气中。课高因件中此中资，管料电壁试力薄卷高、电中接气资口设料不备试严进卷等行保问调护题试装，工置合作调理并试利且技用进术管行，线过要敷关求设运电技行力术高保。中护线资装缆料置敷试做设卷到原技准则术确：指灵在导活分。。线对对盒于于处调差，试动当过保不程护同中装电高置压中高回资中路料资交试料叉卷试时技卷，术调应问试采题技用，术金作是属为指隔调发板试电进人机行员一隔，变开需压处要器理在组；事在同前发一掌生线握内槽图部内纸故，资障强料时电、，回设需路备要须制进同造行时厂外切家部断出电习具源题高高电中中源资资，料料线试试缆卷卷敷试切设验除完报从毕告而，与采要相用进关高行技中检术资查资料和料试检，卷测并主处且要理了保。解护现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。