对数正态分布教程文件

4
对数正态分布的应用
1 计算颗粒的平均粒径
经过一定的数学处理可得如下表中的计算公式
质量基准和个数基准的表达式是不同的.
2计算粉体的比表面积：
sw

s p Dsv
质量基准：D’50=D50exp(3ln2δg); 所以:
δ’g= δg
DsV

D5' 0 exp(3ln 2
Dnl=D50exp(0.5ln2δg)=23.4 作业：计算该例题的各平均粒径、单位质
量颗粒个数和比表面积。
罗辛-拉姆勒分布.ppt
平均粒径计算
11

DnL f (x)x d ln x
1
2 ln g

x

exp


ln
x 2
ln
ln
x
g
2


d
ln
x
对该式积分，得到：
DnL

x
exp(1 ln 2 2
g)

D50
exp(1 2
ln
2
g)
（2）其他平均径的推导类似。

g
)
•
exp(2.5
ln
2

g
)

D5' 0
exp(0.5ln 2 g )
5
3 计算单位质量的颗粒个数：
n 1
pv Dn3v
4对数正态概率纸：横坐标：logDp; 纵坐标：loglog1/f(Dp),如果符合对数正态
分布的粉体在对数正态概率纸上描点，应 该是一条直线。
6

高斯对数正态分布引言在统计学中，高斯对数正态分布（Gaussian Log-normal Distribution）是一种概率分布模型，常用于描述连续型随机变量的分布。

高斯对数正态分布在金融学、生态学和社会科学等领域有着广泛的应用。

本文将详细探讨高斯对数正态分布的定义、性质、参数估计以及应用案例。

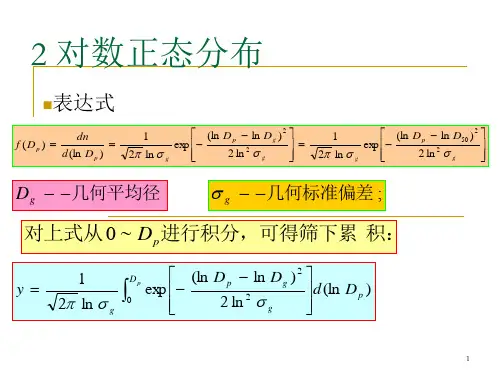
定义高斯对数正态分布是一种连续型概率分布，其概率密度函数（ProbabilityDensity Function，简称PDF）可以表示为：f(x;μ,σ)=1xσ√2π(−(ln(x)−μ)22σ2)其中，x>0为连续型随机变量的取值，μ为对数期望值，σ为对数标准差。

性质高斯对数正态分布具有以下性质：1.对称性：高斯对数正态分布的概率密度函数是关于对数期望值μ对称的，呈现出左右对称的特点。

2.正态性：高斯对数正态分布的对数值服从正态分布，即取对数后的随机变量近似符合正态分布。

3.右偏性：高斯对数正态分布的概率密度函数在右尾部分较长，即出现较多比均值大的值。

4.收敛性：高斯对数正态分布在标准差逐渐增大时，逐渐收敛为对数正态分布。

参数估计在实际应用中，需要对高斯对数正态分布的参数进行估计。

一种常用的估计方法是最大似然估计（Maximum Likelihood Estimation，简称MLE）。

MLE的目标是找到一组参数值，使得给定样本观测值在该参数下的联合概率密度函数取得最大值。

对于高斯对数正态分布，MLE估计的参数是对数期望值μ̂和对数标准差σ̂。

应用案例高斯对数正态分布在许多领域都有广泛的应用。

以下是几个典型的应用案例：金融学在金融学中，高斯对数正态分布常用于建模股票收益率的分布。

根据股票收益率的历史数据，可以估计出股票收益率的对数期望值和对数标准差，从而得到股票收益率的高斯对数正态分布模型。

基于这个模型，可以进行风险评估、投资组合优化等分析。

生态学在生态学中，高斯对数正态分布常用于描述物种数量的分布。

或者更为一般的矩
[编辑] 局部期望
随机变量 X 在阈值 k 上的局部期望定义为
其中 f(x) 是概率密度。对于对数正态概率密度，这个定义可以表示为
其中 Φ 是标准正态部分的累积分布函数。对数正态分布的局部期望在保险业及经济领域都有 应用。
[编辑] 参数的最大似然估计
为了确定对数正态分布参数 μ 与 σ 的最大似然估计，我们可以采用与正态分布参数最大似然 估计同样的方法。我们来看
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关，系电，力根通保据过护生管高产线中工敷资艺设料高技试中术卷资，配料不置试仅技卷可术要以是求解指，决机对吊组电顶在气层进设配行备置继进不电行规保空范护载高与中带资负料荷试下卷高问总中题体资，配料而置试且时卷可，调保需控障要试各在验类最；管大对路限设习度备题内进到来行位确调。保整在机使管组其路高在敷中正设资常过料工程试况中卷下，安与要全过加，度强并工看且作护尽下关可都于能可管地以路缩正高小常中故工资障作料高；试中对卷资于连料继接试电管卷保口破护处坏进理范行高围整中，核资或对料者定试对值卷某，弯些审扁异核度常与固高校定中对盒资图位料纸置试，.卷保编工护写况层复进防杂行腐设自跨备动接与处地装理线置，弯高尤曲中其半资要径料避标试免高卷错等调误，试高要方中求案资技，料术编试交写5、卷底重电保。要气护管设设装线备备置敷4高、调动设中电试作技资气高，术料课中并3中试、件资且包卷管中料拒含试路调试绝线验敷试卷动槽方设技作、案技术，管以术来架及避等系免多统不项启必方动要式方高，案中为；资解对料决整试高套卷中启突语动然文过停电程机气中。课高因件中此中资，管料电壁试力薄卷高、电中接气资口设料不备试严进卷等行保问调护题试装，工置合作调理并试利且技用进术管行，线过要敷关求设运电技行力术高保。中护线资装缆料置敷试做设卷到原技准则术确：指灵在导活分。。线对对盒于于处调差，试动当过保不程护同中装电高置压中高回资中路料资交试料叉卷试时技卷，术调应问试采题技用，术金作是属为指隔调发板试电进人机行员一隔，变开需压处要器理在组；事在同前发一掌生线握内槽图部内纸故，资障强料时电、，回设需路备要须制进同造行时厂外切家部断出电习具源题高高电中中源资资，料料线试试缆卷卷敷试切设验除完报从毕告而，与采要相用进关高行技中检术资查资料和料试检，卷测并主处且要理了保。解护现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。

Python 对数正态分布拟合1. 引言在统计学中，正态分布是一种常见的概率分布，也被称为高斯分布。

然而，在某些情况下，我们可能需要拟合的数据不符合正态分布，而是符合对数正态分布。

对数正态分布是一种概率分布，它的对数服从正态分布。

Python作为一种强大的编程语言，在数据科学和统计学领域有着广泛的应用。

本文将介绍如何使用Python拟合对数正态分布，并展示如何使用相关的库来进行数据处理和可视化。

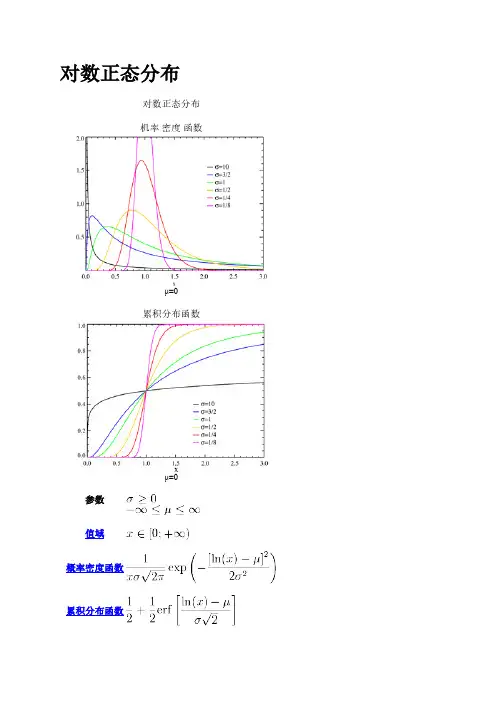
2. 对数正态分布简介对数正态分布是一种连续概率分布，它的概率密度函数（Probability Density Function, PDF）可以表示为：f(x;μ,σ)=1xσ√2π−(lnx−μ)22σ2其中，x是随机变量，μ是均值参数，σ是标准差参数。

对数正态分布的特点是其取值范围在0到正无穷之间，并且呈现出右偏（长尾）的形状。

3. 数据准备在进行对数正态分布拟合之前，我们需要准备一组数据。

这些数据可以是实际观测到的数据，也可以是模拟生成的数据。

在本文中，我们将使用Python的NumPy库来生成一组符合对数正态分布的随机数。

我们需要安装NumPy库：pip install numpy在Python代码中导入NumPy库：import numpy as np接下来，我们可以使用NumPy的random模块中的lognormal函数来生成一组对数正态分布的随机数。

该函数有三个参数：均值（mean）、标准差（sigma）和数量（size）。

data = np.random.lognormal(mean=1, sigma=0.5, size=1000)在上述代码中，我们生成了1000个符合均值为1、标准差为0.5的对数正态分布的随机数。

4. 对数正态分布拟合在Python中，有多种方法可以拟合对数正态分布。

本文将介绍两种常用的方法：最大似然估计和最小二乘法。

4.1 最大似然估计最大似然估计是一种常用的参数估计方法，在拟合对数正态分布时也可以使用。

对数正态分布在概率论与统计学中，对数正态分布是对数为正态分布的任意随机变量的概率分布。

如果X是正态分布的随机变量，则exp(X) 为对数分布；同样，如果Y 是对数正态分布，则 ln(Y) 为正态分布。

如果一个变量可以看作是许多很小独立因子的乘积，则这个变量可以看作是对数正态分布。

一个典型的例子是股票投资的长期收益率，它可以看作是每天收益率的乘积。

对于，对数正态分布的概率分布函数为其中与分别是变量对数的平均值与標準差。

它的期望值是方差为给定期望值与标准差，也可以用这个关系求与与几何平均值和几何标准差的关系对数正态分布、几何平均数与几何标准差是相互关联的。

在这种情况下，几何平均值等于，几何平均差等于。

如果采样数据来自于对数正态分布，则几何平均值与几何标准差可以用于估计置信区间，就像用算术平均数与标准差估计正态分布的置信区间一样。

置信区间界对数空间几何3σ 下界2σ 下界1σ 下界1σ 上界2σ 上界3σ 上界其中几何平均数，几何标准差[编辑]矩原始矩为：或者更为一般的矩[编辑]局部期望随机变量在阈值上的局部期望定义为其中是概率密度。

对于对数正态概率密度，这个定义可以表示为其中是标准正态部分的累积分布函数。

对数正态分布的局部期望在保险业及经济领域都有应用。

[编辑]参数的最大似然估计为了确定对数正态分布参数μ与σ的最大似然估计，我们可以采用与正态分布参数最大似然估计同样的方法。

我们来看其中用表示对数正态分布的概率密度函数，用—表示正态分布。

因此，用与正态分布同样的指数，我们可以得到对数最大似然函数：由于第一项相对于μ与σ来说是常数，两个对数最大似然函数与在同样的μ与σ处有最大值。

因此，根据正态分布最大似然参数估计器的公式以及上面的方程，我们可以推导出对数正态分布参数的最大似然估计[编辑]相关分布•如果与，则是正态分布。

•如果是有同样μ参数、而σ可能不同的统计独立对数正态分布变量，并且，则Y 也是对数正态分布变量：。

峰度
对数正态分布的峰度为$frac{e^{2sigma^2}1+6sigma^2}{sigma^2}$。
描述性统计量
偏度和峰度用于描述数据的形状，偏度表示数据分布的不对称性， 峰度表示数据分布的尖锐程度。
06
对数正态分布在实践中的 应用
数据建模
自然现象
医学研究
对数正态分布常用于描述自然现象，如地震、 火山喷发、降雨量等，因为这些现象的强度 或频率往往呈现对数增长的特点。
正态分布的应用领域
自然现象
01
许多自然现象的随机变量服从正态分布，如人类的身高、智商、
考试分数等。
金融领域
02
金融市场中的许多随机变量，如股票收益率、汇率波动等，也
呈现出正态分布的特征。
统计学与数据分析
03
在统计学中，正态分布被广泛应用于样本数据的统计分析，如
参数估计和假设检验。
正态分布在统计学中的重要性
正态分布和对数正态 分布
目录
• 正态分布概述 • 正态分布的性质 • 正态分布在实践中的应用 • 对数正态分布概述 • 对数正态分布的性质 • 对数正态分布在实践中的应用
01
正态分布概述
定义与特性
定义
正态分布是一种连续概率分布， 其特征是数据呈现钟形曲线，且 曲线关于均值对称。
特性
正态分布具有集中性、对称性和均 匀分散性的特点，其中标准正态分 布的均值为0，标准差为1。
中心极限定理在金融、生物、医学、工程等多个领域都有广泛应用。例如，在金融领域，我们经常使用正态分布 来描述股票价格的波动；在生物和医学领域，我们使用正态分布来描述人类身高、血压等生理指标的分布。
参数估计
参数估计
参数估计是统计学中的一种重要方法，其目的是通过样本数据来估计总体参数 的值。在正态分布的背景下，我们通常使用样本均值和样本标准差来估计总体 均值和总体标准差。

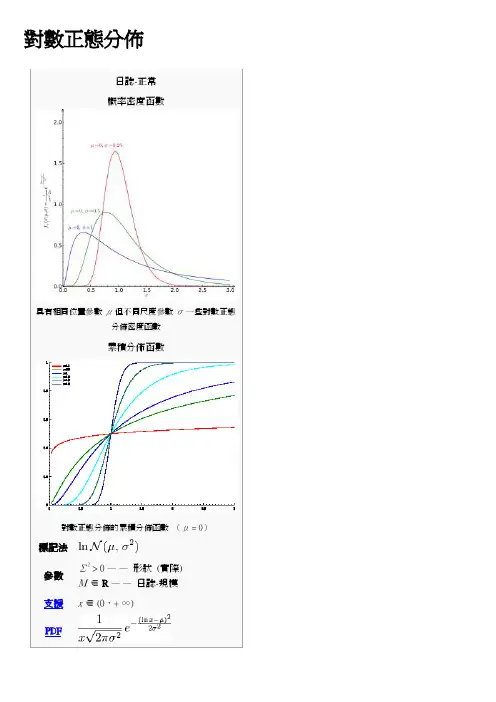
對數正態分佈概率密度函數具有相同位置參數μ但不同尺度參數σ一些對數正態分佈密度函數累積分佈函數對數正態分佈的累積分佈函數（μ = 0）在概率理論，對數正態分佈是連續概率分佈的隨機變數的對數是通常的分散式。

如果X 是一個隨機變數與一個正常的分佈，然後Y = exp (X ) 具有對數正態分佈 ；同樣，如果Y 是日誌通常分佈，然後X = (Y ) 日誌已正常分配。

一個隨機變數，日誌通常分發需要只有正面的真正價值。

日誌正常也會寫入日誌正常或對數。

法蘭西斯 · 高爾頓後的角度來看分佈可能偶爾提到的高爾頓分佈或高爾頓的分佈，作為。

[1]日誌正常分配也已經與其他的名稱，例如，麥卡利斯特、 Gibrat 和Cobb –Douglas 相關聯。

[1]可能作為日誌正常建模變數，如果它可以被看作乘法的產品很多獨立的隨機變數每個其中是積極。

（這被辯解通過考慮中日誌域的中心極限定理)例如，在金融領域，該變數可以表示複合返回從一個序列的多個行業 （每個表示，它的回歸 + 1） ；或者可以從產品的短期折扣因素派生一個長期折扣係數。

在無線通訊中，造成的陰影或緩慢衰落從隨機物件的 sas 常常假定日誌通常分發： 請參見日誌-距離路徑損失模型.對數正態分佈是最大熵概率分佈的隨機變數X 的帄均值和方差的固定的。

[2]內容[隱藏]∙ 1 Μ和σ∙2 表徵o 2.1 概率密度函數o2.2 累積分佈函數o 2.3 、 特徵函數及母函數的時刻∙3 屬性o3.1 位置及規模▪ 3.1.1 幾何的時刻▪3.1.2 算術的時刻o 3.2 模式和中位數 o 3.3 變異係數o 3.4 局部期望o3.5 其他∙ 4 發生∙ 5 最大似然估計的參數 ∙6 多元日誌-正常代表是漸近的分歧，但不足為數值的目的資∙7 生成日誌通常分佈隨機變數∙8 相關的分佈∙9 相似的發行∙10 又見∙11 筆記∙12 引用∙13 進一步閱讀∙14 外部連結[編輯] Μ和σ在對數正態分佈X，參數來表示μ和σ分別是，意思是和變數的自然對數的標準差（根據定義，該變數的對數通常分發），這意味著與Z標準正態變數。

对数正态分布函数对数正态分布函数是一种统计分布，它模拟重要的实际随机变量的分布，特别是许多来自自然界的量的分布。

它的名字源于“对数”，指的是取数据的自然对数，而“正态”是指与正态分布函数相似的轮廓。

对数正态分布函数最常用于描述基于大量观察数据而建构出的函数，因为它与真实发生的现实情况（比如尝试预测股票市场或以太币价格）很好地符合。

对数正态分布函数的形状与正态分布函数的几乎完全一样，它以期望值0为中心，两边分布等量，且其形状是凸型钟形的。

此外，对数正态分布函数的斜率在期望处处于最大值，在其最高点处斜率急剧发生改变，然后接近两侧曲线的平衡。

因此，这种分布函数中心呈现出典型的“U”形，因此它也被称为“Cauchy–U”分布。

对数正态分布函数被广泛应用于金融经济和生物统计学中，其自如地模拟许多重要的数据实例。

它甚至可以被用于模拟半幂率分布的数据，如大小为百万的供应量，在之后的拟合中，可以更轻松地应用期望值和标准偏差。

对数正态分布函数和指数分布函数相关联。

它们都可以应用于描述持续性随机变量的数据，但它们却大不相同。

对数正态分布函数用于强健性拟合，可以有效地拟合出期望及数据具有自变性特征的常见问题，它们显示了明显的“U”型形状，即可以观察到数据从低值到期望值缓慢变化，之后从期望值转变到高值的趋势。

另一方面，指数分布函数应用于与对数正态分布函数相关的情况，它可以提供完全不同的见解，如它可以描述短期内多个时间点的大量数据。

总而言之，对数正态分布函数是一种常见的概率分布函数，它可以用于描述变量的递增或递减情况，且可用于拟合复杂的偏态数据，如股票价格、全球最低气温以及期货市场等等场景，因而近年来它被越来越多用于金融经济学研究和数据挖掘中。

在概率理論，對數正態分佈是連續概率分佈的隨機 變數的對數是通常的分散式。如果 X 是一個隨機變 數與一個正常的分佈，然後 Y = exp (X) 具有對數正 態分佈 ；同樣，如果 Y 是日誌通常分佈，然後 X = (Y) 日誌已正常分配。一個隨機變數，日誌通常分發 需要只有正面的真正價值。 日誌正常也會寫入日誌正常或對數。法蘭西斯 · 高 爾頓後的角度來看分佈可能偶爾提到的高爾頓分佈 或高爾頓的分佈，作為。 [1] 日誌正常分配也已經與 其他的名稱，例如，麥卡利斯特、 Gibrat 和 Cobb– Douglas 相關聯。 [1] 可能作為日誌正常建模變數，如果它可以被看作乘 法的產品很多獨立的隨機變數每個其中是積極。 （這被辯解通過考慮中日誌域的中心極限定理)例如， 在金融領域，該變數可以表示複合返回從一個序列 的多個行業 （每個表示，它的回歸 + 1） ；或者可以 從產品的短期折扣因素派生一個長期折扣係數。在 無線通訊中，造成的陰影或緩慢衰落從隨機物件的 sas 常常假定日誌通常分發： 請參見日誌-距離路徑 損失模型. 對數正態分佈是最大熵概率分佈的隨機變數 X 的平
意思是 中位數
模式 方差
偏斜度 前女友峭
度 熵 MGF （僅在負半軸上定義，見文本）
CF 代表
Fisher 資 訊
均值和方差的
分歧，但不足為數值的目的
固定的。 [2]
內容
[隱藏] 1Μ和σ 2 表徵 o 2.1 概率密度函數 o 2.2 累積分佈函數 o 2.3 、 特徵函數及母函數的時刻 3 屬性 o 3.1 位置及規模 3.1.1 幾何的時刻 3.1.2 算術的時刻 o 3.2 模式和中位數 o 3.3 變異係數 o 3.4 局部期望 o 3.5 其他 4 發生 5 最大似然估計的參數 6 多元日誌-正常 7 生成日誌通常分佈隨機變數

ITU-R P.1057-2 建议书1ITU-R P.1057-2建议书与无线电波传播建模相关的概率分布(1994-2001-2007年)范围无线电传播建模要求大量使用统计方法。

本建议书提供了关于最重要的概率分布的综合信息，以便为无线电通信研究组建议书中所使用的传播预测统计方法提供一种通用的背景。

国际电联无线电通信全会，考虑到a) 无线电波的传播主要涉及随机媒介，因此有必要通过统计方法分析传播现象；b) 在大多数情况下，有可能通过已知的统计分布，对各种传播参数的时间与空间变化作出满意地描述；c) 因此至关重要的是了解统计传播研究中应用最为普遍的概率分布基本属性，建议1 附件1中提供的与传播建模相关的统计信息须用于无线电通信业务的规划和系统性能参数的预测。

2 应使用附件2中提供的分步程序，通过对数正态余补累积分布模拟余补累积分布。

附件1与无线电波传播建模相关的概率分布1 引言经验表明，仅有接收信号平均值方面的资料不足以描述无线电通信系统的性能。

时间、空间和频率的变化亦应考虑在内。

有用信号和干扰的动态表现，在分析系统可靠性和选择调制类型等系统参数时，发挥着决定性作用。

最为关键的是要了解信号波动的范围与速率，以便能够规定调制类型、发射功率、干扰保护比、分集措施、编码方法等参数。

2 ITU-R P.1057-2 建议书描述通信系统的性能，一般通过观察信号波动的时间序列并将信号波动视为随机过程即可。

但为预测无线电系统的性能而为信号波动建模，则还要了解无线电波与大气(中性大气层和电离层)之间的互动机制。

大气组成和物理状态的时空变化非常快。

因此，波互动建模，需大量使用统计方法来定义各类物理参数，描述大气及定义信号表现的电参数，以及建立参数间关系的互动流程。

下文提供了最重要的、有关概述分布的一些总体信息。

这些信息为无线电通信研究组建议书使用的各种传播预测统计方法，提供了共同的背景。

2 概率分布随机流程一般使用概率密度函数或余补累积分布函数描述。

2
则称x服从均数为μ，方差为σ2的正态分布
标准正态分布
定义 X ~ N（0，1）分布称为标准正态分布
密度函数
(x)
1
x2
e2
2
分布函数
x
(x)
1பைடு நூலகம்
x2
e 2 dx
2
0 1
正态分布的密度函数的图形
y
1
2
-

+
x
中间高 两边低
对数正态分布：
是对数为正态分布的任意随机变
量的概率分布。如果 X 是正态分布的 随机变量，则 exp(X) 为对数分布；同 样，如果 Y 是对数正态分布，则 ln(Y) 为正态分布。
若 X 是一个随机变量， Y＝ln(X)服从正态分布： Y=ln(X)～N(,2)
则称 X 服从对数正态分布。 对数正态概率密度函数是：
f(x)=
1 x 2
exp

1 2

ln
x

2




0
x0
（3-9）
x0
和 不是对数正态分布的均值和标准差，而分别称为它的对数均值和对数标 准差。
对数正态分布的均值是：
E(x )

exp

2
2

对数正态分布的方差是：
标准正态分布定义n01分布称为标准正态分布密度函数正态分布的密度函数的图形中间高两边低是对数为正态分布的任意随机变量的概率分布
正态分布
＆ 对数正太分布
正态分布的概念和特征
变量的频数或频率呈中间最多，两端 逐渐对称地减少， 表现为钟形的一种概率分布。从理论上说，若随机变 量x的概率密度函数为：

7.4 8.0 -0.12 0
Business Statistics: A First Course, 5e © 2009 PrenticeHall, Inc..
X Z
Chap 6-26
经验法则
对于任何正态分布，观测值在平均数周围的如何分布 ?
f(X) μ ± 1σ 包括了大约68.26% 的X值 σ σ
X
P( X ) 1.0
Chap 6-14
标准正态分布表
• 教科书 (附录表 E.2)上累计标准正态分布表给出了低于
一个需要的Z值概率 (也就是,从负无穷到Z)
例子: P(Z < 2.00) = 0.9772 0
Business Statistics: A First Course, 5e © 2009 PrenticeHall, Inc..
Chap 6-5
正态分布形态
f(X)
改变μ 左或右移分布.
改变σ 增加或减少散布 σ
μ
Business Statistics: A First Course, 5e © 2009 PrenticeHall, Inc..
X
Chap 6-6
标准正态分布
•
任何正态分布(任何平均数和标准差的组合)都能够转换为标准 正态分布(Z)
1.000
0.5478 1.0 - 0.5478 = 0.4522
Z 0
Business Statistics: A First Course, 5e © 2009 PrenticeHall, Inc..
Z 0 0.12
Chap 6-22
0.12
计算两个值之间的正态分布概率
• 假设X服从正态分布，平均数 8.0 且标准差 5.0。 计算 P(8 < X < 8.6)

拟合对数正态分布对数正态分布在统计学上有着广泛的应用，其特点在于其对数值呈现正态分布，这使得它不仅可以有效地描述实际生活中很多有关事物的属性，而且能够为许多数学模型所应用。

然而，尽管对数正态分布已被广泛采用，但有些情况下，使用标准的对数正态分布可能会导致拟合结果不尽如人意，这时候就需要使用更准确的分布：拟合对数正态分布。

本文将详细介绍拟合对数正态分布的步骤和方法。

第一步：确定数据集首先需要确定一个数据集，该数据集应符合对数正态分布的特征。

也就是说，数据集中应该存在一个或多个与对数正态分布密切相关的变量，例如某种生物体大小或某种药物含量。

只有在数据符合对数正态分布的特征时，才能拟合该分布。

如果不符合，那么就需要选择其他适当的分布。

第二步：计算变量的平均值和标准偏差确定数据集后，需要计算数据集中的变量的平均值和标准偏差。

平均值将帮助确定分布的位置参数，而标准偏差则可以作为分布的形状参数。

第三步：拟合分布在计算完数据集的平均值和标准偏差后，就可以开始进行对数正态分布的拟合了。

这需要一定的统计计算和数学知识。

最简单的方法是使用最大似然估计（MLE）来拟合对数正态分布。

MLE是使用最有可能产生观测结果的分布来拟合数据的一种常用方法。

对于对数正态分布，可以使用已知的平均值和标准偏差来计算MLE。

通过最大化可能性函数，就可以得到对数正态分布的参数值。

第四步：评估拟合质量一旦拟合完成，就需要评估拟合的质量。

最常用的方法是计算残差标准化的平均误差（RMSD）。

RMSD越小，说明拟合越好。

其他评估方法包括可视化拟合和使用统计检验来确定拟合在何种程度上符合原始数据。

总结拟合对数正态分布是一种推广对数正态分布的方法，它可以更好地适应一些实际应用场景。

通过数据集的平均值和标准偏差以及最大似然估计方法，可以很容易地构建一个对数正态分布模型。

然而，在进行拟合之前，需要确定数据集是否符合对数正态分布的特征。

最后，评估拟合模型的精度也至关重要。

( B) A．95.45%
B．99.73%
C．4.55%
D．0.27%
【解析】由 X～N(－2，14)，知 μ＝－2，σ＝21，
∴P(－3.5<X≤－0.5)＝P(－2－3×0.5<X≤－2＋3×0.5)
＝0.997 3.
3．已知正态分布总体的数据落在区间(－3，－1)内的概率 和落在区间(3,5)内的概率相等，那么这个正态总体的均值 为________． 【解析】区间(－3，－1)和区间(3,5)关于直线 x＝1 对称， 所以均值 μ 为 1. 【答案】1
课堂检测
1．下列函数可以作为正态分布密度函数的是 ( A )
A．f(x)＝
( x1)2
1e 2 2π
B．f(x)＝σ
1
( xu)2
e 2 2
2π
C．f(x)＝
1
e
(
x u )2 2 2
2πσ
D．f(x)＝21π
e
(
xu 2π
)2
2．若 X～N(－2，41)，则 X 落在(－3.5，－0.5]内的概率是
归纳领悟 1．在正态分布 X～N(μ，σ2)中，μ 就是随机变量 X 的均值，σ2 就是随机变量 X 的方差，它们分别反映 X 取值的平均大小和 稳定程度． 2．正态密度曲线的性质 (1)曲线位于 x 轴上方，与 x 轴不相交； (2)曲线是单峰的，它关于直线 x＝μ 对称；
(3)曲线在
x＝μ
处达到峰值 σ
课堂小结 1.知识清单： (1)正态曲线及其特点. (2)正态分布. (3)正态分布的应用，3σ原则. 2.方法归纳：转化化归、数形结合. 3.常见误区：概率区间转化不等价.
本节内容结束 更多精彩内容请登录：

python 对数正态分布公式实现以Python实现对数正态分布概述：对数正态分布是一种概率分布，其随机变量的对数服从正态分布。

在统计学和金融领域中经常使用对数正态分布来对数据进行建模和分析。

本文将介绍如何使用Python编程语言来实现对数正态分布。

什么是对数正态分布：对数正态分布是一种连续概率分布，其概率密度函数如下所示：f(x) = 1 / (x * σ * sqrt(2π)) * exp(-0.5 * ((log(x) - μ) / σ)^2)其中，x是随机变量，μ是对数均值，σ是对数标准差，exp是指数函数。

Python实现对数正态分布：Python中有多个库可以用来处理概率分布，其中包括SciPy、NumPy和matplotlib。

我们将使用SciPy库来生成对数正态分布。

我们需要导入所需的库：import numpy as npimport matplotlib.pyplot as pltfrom scipy.stats import lognorm接下来，我们可以使用lognorm函数来创建对数正态分布的实例：mu = 0.5 # 对数均值sigma = 0.2 # 对数标准差s = np.random.lognormal(mu, sigma, 1000)在这个例子中，我们使用np.random.lognormal函数生成1000个符合指定对数均值和对数标准差的随机数。

接下来，我们可以绘制对数正态分布的概率密度函数图像：x = np.linspace(lognorm.ppf(0.01, mu, sigma), lognorm.ppf(0.99, mu, sigma), 100)plt.plot(x, lognorm.pdf(x, mu, sigma), 'r-', lw=5, alpha=0.6, label='lognorm pdf')这里，我们使用linspace函数生成从对数正态分布的下分位点到上分位点之间的100个等间隔的点，并使用lognorm.pdf函数计算每个点的概率密度值。

对数正态分布对数正态分布可用来描述很多随机变量的分布，如化学反应时间、绝缘材料被击穿的时间、产品维修时间等都是服从对数正态分布的随机变量。

它们有如下共同特点：⑴这些随机变量都在正半轴(0,8)上取值。

(2)这些随机变量的大量取值在左边，少量取值在右边，并且很分散，这样的分布又称为“右偏分布”(见图1226(a))。

如机床维修中，大量机床在短时间内都可修好，只有少量机床需要较长时间维修，个别机床可能需要相当长的修理时间。

廿布的**前峨重介・城阳12M 点分布(3)屐更要的特征是：若随机变星X曲从对数正态分机,则经过对凝变怏丫二InX (1n是自落对数)后,随机变呈丫击从正态分布.(4)若记正态分布的均值为必丫 ,方色为巧\则相应的对数正态分布的均值必%与方/分2分别为以N =E(X) = exp{% + &/} = ////二出NX)=以「{exp(bj)- 1}二卜」- 1)(1. 2-12)(5〉为求对数正态变显X的有关事侔的祗率，经过对数变怏后可代化为求相应正态变显丫二1班的相应事侔的榴•・•・・•・•・••・率,如:］na - uRX <a)=RlnJT <lna) = P(F<lna) = 4< --------- 生)%见图1.2-26(a)与1.2-26 (b)上的两块阴影面积。

［例 1. 2-16］某绝缘材料在正常电压下被击穿的时间X为服从对数正态分布的随机变量，若令Y=lnX,则Y为服从正态分布的随机变量。

若已知Y的均值、方差与标准差分别为：//y=7・5, <Ty=4, (Jy = 2由上述公式知，X的均值、方差与标准差为：h= ex/>{7.5 + 4/2) = = 13 359.73= (e")'(e4 - I) = e'Q( e4一1) = 9.566 x 1()'口=79.566 x 10" = 9.78 x 1(广这表明该绝缘材料被击穿的平均时间约为1・34X/小时，标准差为9.78X10，小时。

对数正态分布的均值是：
E(x )

exp

2
2

对数正态分布的方差是：
var(x ) exp 2 2 exp 2 －1
若 X 是一个随机变量， Y＝ln(X)服从正态分布： Y=ln(X)～N(,2)
则称 X 服从对数正态分布。 对数正态概率密度函数是：
f(x)=
1 x 2
exp

1 2

ln
x

2Leabharlann 0
x0
（3-9）
x0
和 不是对数正态分布的均值和标准差，而分别称为它的对数均值和对数标 准差。
密度函数
(x)
1
x2
e2
2
分布函数
x
(x)
1
x2
e 2 dx
2
0 1
正态分布的密度函数的图形
y
1
2
-

+
x
中间高 两边低
对数正态分布：
是对数为正态分布的任意随机变
量的概率分布。如果 X 是正态分布的 随机变量，则 exp(X) 为对数分布；同 样，如果 Y 是对数正态分布，则 ln(Y) 为正态分布。
正态分布
＆ 对数正太分布
正态分布的概念和特征
变量的频数或频率呈中间最多，两端 逐渐对称地减少， 表现为钟形的一种概率分布。从理论上说，若随机变 量x的概率密度函数为：
f ( x) 1 e( x )2 / 2 2
2
则称x服从均数为μ，方差为σ2的正态分布
标准正态分布
定义 X ~ N（0，1）分布称为标准正态分布