轴承支承刚度及齿轮啮合刚度计算

斜齿轮副时变啮合刚度计算方法
斜齿轮副时变啮合刚度是指在实际运行过程中，由于副体尺寸误差、
加工精度等原因导致轮齿的啮合关系发生变化，进而使得副体的刚度发生
变化。

斜齿轮副时变啮合刚度的计算方法主要包括以下几个方面：轮齿啮
合误差计算、副体刚度计算和时变啮合刚度计算。

首先，轮齿啮合误差计算是斜齿轮副时变啮合刚度计算的基础。

根据
啮合误差的定义，可以通过测量轮齿的实际尺寸和理论尺寸之间的差异来
计算。

具体的计算方法包括齿根啮合误差、齿顶啮合误差和齿侧啮合误差等。

其次，副体刚度的计算是斜齿轮副时变啮合刚度计算的关键。

副体刚
度包括副体的刚度系数、副体的刚度矩阵和副体的刚度特性等。

副体刚度
的计算可以通过有限元分析或实验测试等方法获得。

最后，根据轮齿啮合误差和副体刚度，可以计算斜齿轮副的时变啮合
刚度。

时变啮合刚度可以用于评估斜齿轮副在实际运行中的运动特性和工
作性能。

计算时变啮合刚度的方法主要包括静态方法和动态方法。

静态方
法是通过将斜齿轮副视为刚体系统，计算系统在给定位移和外载荷下的刚度；动态方法是通过考虑斜齿轮副的动力学特性，计算系统在给定速度和
加速度下的刚度。

综上所述，斜齿轮副时变啮合刚度的计算方法包括轮齿啮合误差计算、副体刚度计算和时变啮合刚度计算。

这些方法可以用于评估斜齿轮副在实
际工作中的性能，并指导优化设计和制造过程。

面齿轮传动啮合刚度数值计算-机械工程论文-工程论文——文章均为WORD文档，下载后可直接编辑使用亦可打印——0、引言作为机械装置中的一个重要零部件,齿轮传动被广泛应用于航空、风电、汽车等领域。

随着工作转速的逐步提高,齿轮传动的动力学性能越来越受到设计、制造及使用者的重视。

相比较其他类型的传动系统,齿轮传动系统的主要不同之处在于: 它不但会因为外部激励而产生动态响应,同时会因为传动过程中啮合齿对数的改变、轮齿的弹性变形及轮齿误差而导致啮合刚度发生变化,从而产生轮齿动态啮合力,且此种由于啮合综合刚度的时变性引起的动态激励是齿轮传动中最主要的动态激励形式之一。

因此,确定齿轮传动的时变啮合刚度一直是齿轮动力学研究中的重要问题。

对于圆柱齿轮的啮合刚度计算问题,已有较多的学者进行过深入研究,得到了一些比较成熟的计算方法。

对于面齿轮及螺旋锥齿轮等结构相对复杂的齿轮传动形式的啮合刚度计算问题,由于其齿面为复杂曲面,要准确计算时变啮合刚度存在较大难度,因此相关研究文献较少。

Gosselin 等基于有限条法给出了计算螺旋锥齿轮刚度的方法,但也只得到了沿齿高和齿长方向的位移曲线,并没有得到刚度曲线。

Mennem等使用有限单元法计算了不同载荷下轮齿接触柔度,获得了时变刚度。

面齿轮传动是近二十年才真正发展起来的一种主要用于航空领域的齿轮传动形式,针对其啮合刚度的计算方法,目前尚未见文献报道。

在面齿轮的动力学研究中,齿轮啮合刚度都采用经过傅里叶变换后的一次正余弦函数来近似,与实际啮合刚度存在比较大的差异。

有学者研究发现,采用近似时变啮合刚度得到的系统动态因子比采用实际啮合刚度时大,而且不能有效地得到系统在低频阶段的动态响应。

因此,采用近似时变啮合刚度来拟合实际啮合刚度研究齿轮传动系统动力学行为,并不能正确反映齿轮系统的动态特性。

本文提出了一种新的齿轮传动时变啮合刚度数值计算方法。

首先以直齿圆柱齿轮为例,建立合理的有限元模型,得到直齿圆柱齿轮时变啮合刚度曲线,并与ISO6336方法计算结果进行对比,说明该啮合刚度计算方法的正确性及有限元模型的精确性; 然后应用该啮合刚度计算方法,研究面齿轮传动时变啮合刚度变化规律,得到精确的面齿轮传动时变啮合刚度曲线。

齿轮啮合振动力计算公式
齿轮啮合振动力的计算公式可以通过振动模态分析来确定，通常使用的是有限元分析方法（FEA）。

在齿轮啮合振动分析中，需要考虑齿轮齿面的接触、齿面的摩擦和齿轮齿面的形状等因素。

具体的计算公式会根据所采用的分析方法和模型而有所不同，但通常可以使用以下公式来计算齿轮啮合振动力：
F = k * ω2 * X
其中，F 表示齿轮啮合振动力；k 是一个系数，取决于齿轮的几何参数、材料特性和载荷情况等因素；ω 是齿轮啮合角速度；X 是齿轮啮合点处的位移或加速度。

需要注意的是，上述公式仅适用于理想情况下的齿轮啮合振动分析，实际应用中还需要考虑各种因素的综合影响，如齿轮的制造精度、安装偏差、润滑条件、负载类型和大小等。

因此，在进行齿轮啮合振动分析时，需要综合考虑多种因素，并采用适当的分析方法和模型。

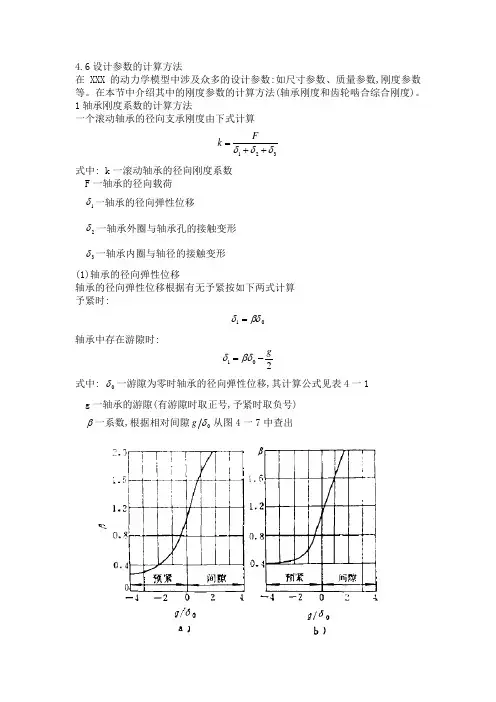
4.6设计参数的计算方法在XXX 的动力学模型中涉及众多的设计参数:如尺寸参数、质量参数,刚度参数等。

在本节中介绍其中的刚度参数的计算方法(轴承刚度和齿轮啮合综合刚度)。

1轴承刚度系数的计算方法一个滚动轴承的径向支承刚度由下式计算321δδδ++=Fk式中: k 一滚动轴承的径向刚度系数F 一轴承的径向载荷1δ一轴承的径向弹性位移2δ一轴承外圈与轴承孔的接触变形3δ一轴承内圈与轴径的接触变形(1)轴承的径向弹性位移轴承的径向弹性位移根据有无予紧按如下两式计算予紧时:01βδδ=轴承中存在游隙时:201g -=βδδ 式中: 0δ一游隙为零时轴承的径向弹性位移,其计算公式见表4一1g 一轴承的游隙(有游隙时取正号,予紧时取负号)β一系数,根据相对间隙0δg 从图4一7中查出系数表4一10δ的计算公式表中:i 为滚动体的列数;z 为每列中滚动体书;θd 为滚动体的直径;d 为轴承孔直径;α为轴承的接触角;a l 为滚动体的有效长度"(2)轴承配合表面的接触变形轴承外圈与轴承孔的接触变形2δ和轴承内圈与轴径的接触变形3δ按以下两种情况分别计算:间隙配合时:∆=1H δ过盈配合时:bd F H πδ2204.0=式中: ∆一直径上的配合间隙(m μ)b 一轴承套圈的宽度(cm )d 一配合表面的直径(cm )1H 一系数,根据n 由图4一8查出2H 一系数,根据d∆由图4一9查出1H - n 的曲线 2H - d∆的曲线 n 由下式计算bdF n 2096.0∆= 2齿轮啮合综合刚度的计算方法轮齿的啮合综合刚度是指在整个啮合区中参与啮合的各对轮齿的综合效应，主要与单齿的弹性变形，单对轮齿的综合弹性变形以及齿轮的重合度有关。

单齿的弹性变形是指单个轮齿的啮合面在载荷作用下的弹性变形，其中包括弯曲变形,剪切变形和接触变形等。

单对轮齿的综合弹性变形是指一对轮齿在啮合过程中弹性变形的总和。

可以表示为g p s δδδ+=式中：s δ一单对轮齿的综合弹性变形p δ一单个主动齿轮的弹性变形 g δ一单个被动齿轮的弹性变形单对轮齿的综合刚度按下式计算 g p gp s s k k k k k +==δ1式中：s k 一单对轮齿的综合刚度p k 一主动齿轮的单齿刚度g k 一被动齿轮的单齿刚度直齿轮轮齿刚度计算模型对重合度21≤≤ε的齿轮,其平均综合啮合刚度按下式计算()()min max 21k k k m ---=εε式中：ε一齿轮的重合度m ax k 一两对齿啮合时的轮齿刚度m in k 一一对齿啮合时的轮齿刚度下面介绍各项弹性变形的计算方法计算直齿轮的弹性变形有材料力学方法、数学弹性力学方法和有限元法。

斜齿轮副时变啮合刚度计算方法斜齿轮组副时变啮合刚度计算方法主要是基于斜齿轮模型参数和齿轮梯度(Gear Gradient)的仿真数值解析求解法，即通过改变参数模型，可以模拟出不同大小、不同型号斜齿轮副间的啮合过程，从而可以获得啮合副组的刚度参数，即峰值刚度和谐振特性。

具体的计算方法是：首先，指定斜齿轮组的轮齿数、模数、压力角和齿形角度，然后求解啮合副组的微扰刚度方程；再通过数学函数求解斜齿轮副间啮合刚度峰值和谐振特性；最后，根据计算结果，可以得出啮合副组的有关刚度参数。

人字齿行星传动多体动力学建模与分析刘振州;汪建;张俊【摘要】根据人字齿行星传动的结构特点,借助ADAMS建立该类传动的多体动力学模型,对其进行自由振动特性分析.结果表明,当人字齿轮左右两部分结构完全对称时,人字齿行星传动存在中心构件扭转振动、中心构件平移振动和行星轮振动3种典型模式,且3种振动模式的特点与直齿行星传动基本一致.在不考虑传动件结构柔性的情况下,基于多体动力学模型的自由振动分析结果与采用集中参数模型的仿真结果完全一致,表明本文所建模型的正确性,可为后续的参数敏感度分析及动响应分析提供模型依据.【期刊名称】《安徽工业大学学报（自然科学版）》【年(卷),期】2015(032)002【总页数】5页(P152-156)【关键词】人字齿行星传动;多体动力学;固有特性;自由振动【作者】刘振州;汪建;张俊【作者单位】安徽工业大学机械工程学院,安徽马鞍山243032;安徽工业大学机械工程学院,安徽马鞍山243032;安徽工业大学机械工程学院,安徽马鞍山243032【正文语种】中文【中图分类】TH132.425行星轮系的动力学建模是进行后续模态分析、振动分析、参数灵敏度分析和抑振分析的基础[1-4]。

按照建模方法和模型的精细化程度，行星轮系的动力学模型大致可分为集中质量模型、分布质量模型和刚柔耦合模型。

其中，集中质量模型因建模简单求解方便而被广泛采用。

Kahraman[5]在绝对坐标系下建立了直齿行星传动模型，分析了啮合相位与制造误差、装配误差对系统动力学性能的影响。

此后，Lin等[6]在随动坐标系下建立了计入构件平面复合运动的平移-扭转耦合动力学模型，并进一步分析了该类传动的自由振动特性。

随后张俊等[7]修正了前人建模中的若干错误，推导了固有频率的解析表达式，更为准确地揭示了直齿行星传动模态特性的一般规律。

延续这一思路，学者们进一步研究了行星传动的参数灵敏度[8]、稳态动响应[9]等。

与集中质量模型将轮系处理为弹簧-阻尼-振子系统不同，分布质量模型因能计入系统各构件的柔性而具有较高的计算精度。

标题：SolidWorks轴承刚度计算一、概述SolidWorks是一款广泛应用于工程设计领域的三维计算机辅助设计软件，通过它可以进行轴承的刚度计算。

轴承的刚度是轴承元件在受力作用下产生弹性变形的能力，是衡量轴承性能的重要指标。

本文将介绍如何利用SolidWorks进行轴承刚度计算，包括计算步骤、相关原理和注意事项。

二、轴承刚度计算步骤1. 创建轴承模型在SolidWorks中创建轴承模型，包括内外圈和滚动体等组成部分。

可以通过绘制线条、旋转实体等功能来完成轴承模型的设计。

在设计轴承模型时需要考虑到轴承内外圈的几何形状和尺寸、滚动体的数量和分布等因素。

2. 设置边界条件在完成轴承模型的设计后，需要设置轴承模型的边界条件，包括外部加载条件和约束条件。

外部加载条件包括轴向载荷、径向载荷和扭矩等加载方式，约束条件包括轴承座的固定约束和转动约束等。

3. 运行分析设置好边界条件后，可以使用SolidWorks中的仿真模块对轴承模型进行分析。

首先需要选择适当的分析类型（如静力学分析、模态分析等），然后设置分析参数（包括材料性质、网格划分、收敛准则等），最后运行分析并获取结果数据。

4. 计算刚度根据分析结果数据，可以计算轴承的刚度。

根据受力分析得到的轴承受力与变形关系，可以求解得到轴承的刚度系数，包括径向刚度、轴向刚度和扭矩刚度等。

三、轴承刚度计算原理轴承的刚度是指轴承在受力作用下产生弹性变形的能力，通常通过轴承的受力分析和变形关系求解得到。

在进行轴承刚度计算时，需要考虑到轴承的几何形状、材料性质和加载条件等因素，通过有限元分析等手段进行求解。

四、轴承刚度计算注意事项1. 模型准确性在进行轴承刚度计算时，需要确保轴承模型的准确性，包括轴承的几何形状和尺寸、材料性质和加载条件等。

模型的准确性对计算结果的准确性具有重要影响。

2. 加载和约束条件设置轴承模型的外部加载条件和约束条件时，需要考虑到轴承在实际工作中的受力情况，选择合适的加载方式和约束方式，以获得真实可靠的刚度计算结果。

齿轮啮合刚度单位
齿轮啮合刚度是指齿轮在受到外力作用时，其变形程度与所受力的关系。

它是齿轮传动系统中一个重要的参数，直接影响着传动系统的精度和可靠性。

齿轮啮合刚度的单位通常是牛顿/米。

这个单位表示了单位长度的齿轮在受到单位力作用下的变形量。

齿轮啮合刚度越大，说明齿轮在受力时变形越小，传动系统的刚度越高，对外力的响应能力就越强。

齿轮啮合刚度的大小取决于齿轮的几何形状、材料的弹性模量以及齿轮啮合面的接触刚度等因素。

一般来说，齿轮的几何形状越精确，材料的弹性模量越高，齿轮啮合面的接触刚度越大，齿轮啮合刚度就越大。

齿轮啮合刚度的大小对传动系统的性能有着重要的影响。

如果齿轮啮合刚度过小，当传动系统受到外力作用时，齿轮的变形量会变大，导致传动误差增大，影响传动精度。

此外，齿轮啮合刚度过小还会导致齿轮传动系统的振动增大，影响传动的平稳性和可靠性。

因此，在设计齿轮传动系统时，需要根据实际应用要求选择合适的齿轮啮合刚度。

对于要求传动精度高、传动平稳可靠的场合，应选择具有较大齿轮啮合刚度的齿轮；而对于传动要求不高的场合，可以选择具有较小齿轮啮合刚度的齿轮。

齿轮啮合刚度是齿轮传动系统中一个重要的参数，它直接影响着传
动系统的精度和可靠性。

在设计和选择齿轮传动系统时，需要合理地考虑齿轮啮合刚度，以满足实际应用要求。

只有在刚度合适的情况下，齿轮传动系统才能稳定可靠地工作，发挥其应有的功能。