弯曲变形的强度条件和强度计算
- 格式:docx
- 大小:175.31 KB
- 文档页数:4




第8章 弯曲变形本章要点【概念】平面弯曲,剪力、弯矩符号规定,纯弯曲,中性轴,曲率,挠度,转角。
剪力、弯矩与荷载集度的关系;弯曲正应力的适用条件;提高梁的弯曲强度的措施;运用叠加法求弯曲变形的前提条件;截面上正应力分布规律、切应力分布规律。
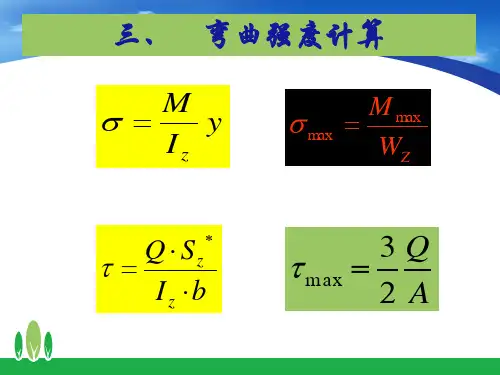
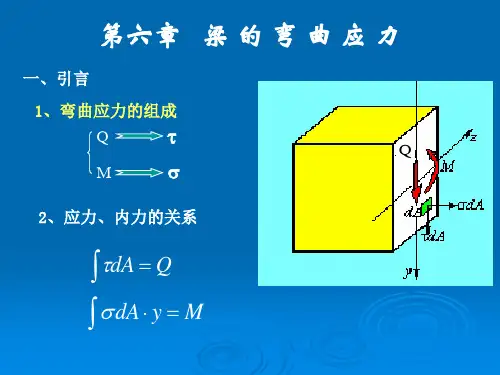
【公式】 1. 弯曲正应力 变形几何关系:yερ=物理关系:Ey σρ=静力关系:0N AF dA σ==⎰,0y AM z dA σ==⎰,2zz AAEI EM y dA y dA σρρ===⎰⎰中性层曲率:1MEIρ=弯曲正应力应力:,My Iσ=,max max z M W σ=弯曲变形的正应力强度条件:[]maxmax zM W σσ=≤ 2. 弯曲切应力矩形截面梁弯曲切应力:bI S F y z z S ⋅⋅=*)(τ,A F bh F S S 2323max ==τ工字形梁弯曲切应力:dI S F y z z S ⋅⋅=*)(τ,A F dh F S S ==max τ圆形截面梁弯曲切应力:bI S F y z z S ⋅⋅=*)(τ,A F S 34max =τ弯曲切应力强度条件:[]ττ≤max3. 梁的弯曲变形梁的挠曲线近似微分方程:()''EIw M x =-梁的转角方程:1()dwM x dx C dx EIθ==-+⎰ 梁的挠度方程:12()Z M x w dx dx C x C EI ⎛⎫=-++ ⎪⎝⎭⎰⎰ 练习题一. 单选题1、 建立平面弯曲正应力公式zI My /=σ,需要考虑的关系有()。
查看答案A 、平衡关系,物理关系,变形几何关系B 、变形几何关系,物理关系,静力关系;C 、变形几何关系,平衡关系,静力关系D 、平衡关系, 物理关系,静力关系;2、 利用积分法求梁的变形,不需要用到下面那类条件()来确定积分常数。
查看答案A 、平衡条件B 、边界条件C 、连续性条件D 、光滑性条件3、 在图1悬臂梁的AC 段上,各个截面上的()。

梁的弯曲变形简单计算方法
梁是传动重要机构之一,其弯曲变形是广泛应用于结构力学设计中的一项重要技术。
它可
以用来分析梁承载的荷载情况,为梁的安全性能设计提供参考。
计算梁的弯曲变形是构造设计中的重要部分,因此有必要掌握有效的简便方法。
梁的弯曲变形一般是有三种计算方法:等强度线法、活荷载平移法、真实三维变形法。
这
三种计算方法的计算时间和计算精度不同,可根据实际情况选择合适的计算方法。
等强度线法是最简单且计算时间最短的方法,利用梁受力后形成的抗压线和抗张线构成图形,并将图形转化为梁形成的弯曲变形。
活荷载平移法则分析了活荷载作用于梁的变形状,将活荷载平移线与梁截面结合起来,表征出梁的弯曲变形。
而真实三维变形则完整量化了
梁的受力状态,找出真实的变形轮廓,从而获得准确的弯曲变形。
总之,梁的弯曲变形计算方法可根据实际应用场合选择合适的方法,以便为梁的设计提供参考。
在工程应用中,其梁的弯曲变形计算通常使用简便方法,如等强度线法和活荷载平
移法,而对于有特殊要求的情况,可以采用真实三维变形法,以保证梁的安全性能。

混凝土弯曲变形试验标准一、前言弯曲试验是混凝土力学试验中的一种常见试验方法,用于研究混凝土在受弯曲荷载作用下的变形性能,是评价混凝土抗弯强度和变形能力的重要依据。
因此,制定一套完整的混凝土弯曲变形试验标准对于混凝土工程的设计和施工具有重要的指导意义。
二、试验目的本试验的目的是研究混凝土在受弯曲荷载作用下的变形特性和抗弯强度,并为混凝土的设计和施工提供科学依据。
三、试验设备1. 试验机:承载力不小于200kN,采用比例秤或应变计来测量荷载。
2. 弯曲试验模具:模具应符合GB/T50081-2002《混凝土试件制作规范》中的规定,模具尺寸为100mm×100mm×500mm,模具内表面应平整、无明显损伤。
3. 试验钢模:钢模尺寸为50mm×50mm×500mm,钢模表面应平整、无明显损伤。
4. 底座:底座应具有足够的强度和稳定性。
5. 量具:包括卡尺、游标卡尺等。
四、试验原理混凝土在受弯曲荷载作用下,内部产生剪应力和弯曲应力,导致混凝土产生弯曲变形。
根据梁的基本理论,可得出混凝土抗弯强度和变形能力的相关参数。
五、试验步骤1. 混凝土试件制作:按照GB/T50081-2002《混凝土试件制作规范》的要求制作100mm×100mm×500mm的混凝土试件。
2. 试件表面处理:试件表面要平整,去除松散物质和突出物。
3. 钢模和混凝土试件的安装:将钢模放置于底座上,将试件放置在钢模上,调整试件与钢模的位置,使试件的中心线与钢模的中心线重合。
4. 荷载施加:将试验机的压头移动到试件的上方,调整高度,使荷载与试件中心线重合。
调整试验机的速度,每10秒钟增加一次荷载,直至试件破坏。
5. 记录数据:记录荷载和试件的挠度数据,并绘制荷载-挠度曲线。
六、试验结果的计算1. 抗弯强度:按照GB/T50081-2002《混凝土试件制作规范》的公式计算。
2. 弯曲变形模量:根据荷载-挠度曲线的斜率计算。
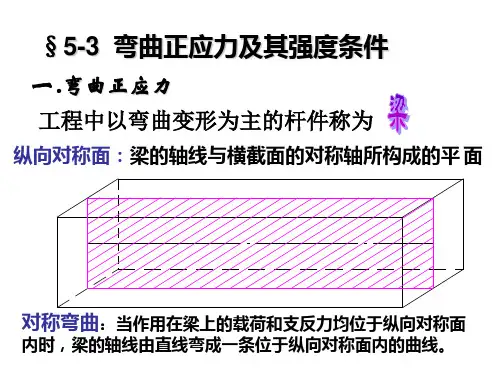


弯曲正应力强度条件的内容弯曲正应力强度条件的内容一、弯曲正应力强度条件的定义弯曲正应力强度条件是指在材料受到弯曲时,其最大正应力不能超过该材料的屈服极限。
这个条件是一种基本的材料设计原则,它可以用来保证材料在使用过程中不会发生破坏。
二、弯曲正应力强度条件的计算公式在进行弯曲试验时,我们通常会测量出受试样件上的最大正应力。
这个最大正应力可以通过下面的公式来计算:σ = M*y/I其中,σ表示最大正应力;M表示试样受到的最大弯矩;y表示试样截面上离中性轴距离最远的点到中性轴距离;I表示试样截面对中性轴的惯性矩。
三、弯曲正应力强度条件与屈服极限之间的关系根据材料学理论,屈服极限是指材料在受到外部载荷作用下开始发生塑性变形并且无法恢复原来形态时所承受的最大载荷。
因此,在进行材料设计时,我们需要确保所选用的材料的屈服极限大于或等于试样受到的最大正应力。
四、弯曲正应力强度条件的应用弯曲正应力强度条件是一种非常重要的材料设计原则,它可以用来保证材料在使用过程中不会发生破坏。
这个原则在许多不同领域都有广泛的应用,例如:1. 桥梁设计:在桥梁设计中,我们需要确保桥梁所使用的材料能够承受车辆和行人的重量。
因此,在进行桥梁设计时,我们需要计算出桥梁受到最大荷载时所承受的最大正应力,并且确保该正应力小于所选用材料的屈服极限。
2. 航空航天工业:在航空航天工业中,我们需要确保飞机和火箭等载具所使用的材料能够承受高速飞行时产生的巨大载荷。
因此,在进行航空航天工业设计时,我们需要计算出载具受到最大荷载时所承受的最大正应力,并且确保该正应力小于所选用材料的屈服极限。
3. 机械制造业:在机械制造业中,我们需要确保机械零件所使用的材料能够承受工作时所产生的载荷。
因此,在进行机械设计时,我们需要计算出机械零件受到最大荷载时所承受的最大正应力,并且确保该正应力小于所选用材料的屈服极限。
五、弯曲正应力强度条件的局限性尽管弯曲正应力强度条件是一种非常重要的材料设计原则,但是它仍然存在一些局限性。
第7章 梁弯曲变形的计算§7-1 挠度与转角及梁的刚度条件梁变形前后形状的变化称为变形,一般用各段梁曲率的变化表示。
梁变形前后位置的变化称为位移,位移包括线位移和角位移,如图7-1所示。
在小变形和忽略剪力影响的条件下,线位移是截面形心沿垂直于梁轴线方向的位移,称为挠度,用v 表示;角位移是横截面变形前后的夹角,称为转角,用θ表示。
而dxx dv x )()(=θ,可见确定梁的位移,关键是确定挠曲线方程Y=f(x)。
梁的设计中,除了需要满足强度条件外,在很多情况下,还要将其弹性变形限制在一定范围内,即满足刚度条件][][max max θθ≤≤v v式中的和][v ][θ分别为梁的许用挠度和许用转角,可从有关设计手册中查得。
§7-2 挠度曲线的近似微分方程忽略剪力对变形的影响,梁平面弯曲的曲率公式为: 式(a)表明梁轴线上任一点的曲率)(1x ρ与该点处横截面上的弯矩成正比,而与该截面的抗弯刚度)(x M EI 成反比。
如图7-2所示。
而梁轴线上任一点的曲率与挠曲线方程v 之间存在下列关系:)(xEIx M x )()(1=ρ (a) 232221)(1⎥⎥⎦⎤⎢⎢⎣⎡⎟⎠⎞⎜⎝⎛+±dx dv dx vd x ρ (b)将上式代入式(a),得到EIx M dx dv dx v d )(12322=⎥⎥⎦⎤⎢⎢⎣⎡⎟⎠⎞⎜⎝⎛+±(c) 小挠度条件下,1<<=θdxdv,式(c)可简化为: EI x M dxv d )(22=±(d)在图7-3所示的坐标系中,正弯矩对应着22dx vd 的正值(图7-3a),负弯矩对应着22dxvd 的负值(图7-3b),故式(d)左边的符号取正值EI x M dx v d )(22= (8-1)式(7-1)称为小挠度曲线微分方程,简称小挠度微分方程。
显然,小挠度微分方程仅适用于线弹性范围内的平面弯曲问题。
弯曲变形的强度条件和强度计算
当梁受到一组垂直于其轴线的力即横向力或位于轴线平面内的外力偶作用时,梁的轴线由一条直线变为曲线,称为弯曲变形。
如果梁的几何形状材料性能和外力都对称于梁的纵向对称面则称为对称弯曲。
如果梁变形后的轴为形心主惯性平面内的平面曲线则称为平面弯曲。
本课程中主要研究以对称弯曲为主的平面弯曲,如图1所示。
图1 平面弯曲
一、梁弯曲时的内力——剪力和弯矩
梁的横截面上有两个分量——剪力和弯矩,它们都随着截面位置的变化而变化,可表示为F S=F S(x)和M=M (x),称为剪力方程和弯矩方程。
为了研究方便,通常对剪力和弯矩都有正负规定:使微段梁发生顺时针转动的剪力为正,反之为负,如图2所示;使微段梁上侧受拉下侧受压的弯矩为正,反之为负,如图3所示。
图2 剪力的正负
图3 弯矩的正负
例1:试写出下图所示梁的内力方程,并画出剪力图和弯矩图。
解:(
1
)求支反力
=
∑C M:0
3
10
12
6=
⨯
-
-
⋅
Ay
F,kN
7
=
Ay
F
=
∑Y:0
10=
-
+By
Ay
F
F,kN
3
=
By
F
(2)列内力方程
剪力:
⎩
⎨
⎧
<
<
-
<
<
=
6
3
kN
3
3
kN
7
)
(
S x
x
x
F
弯矩:
⎩
⎨
⎧
≤
≤
≤
≤
⋅
-
⋅
-
=
6
3
3
m
kN
)
6(3
m
kN
12
7
)
(
x
x
x
x
x
M
(3)作剪力图和弯矩图
二、梁弯曲时的正应力
在一般情况下,梁的横截面上既有弯矩又有剪力。
若梁上只有弯矩没有剪力,称为纯弯曲。
本讲主要讨论纯弯曲时横截面上的应力——正应力。
梁横截面上的正应力大小与该点至中性轴的距离成正比,即正应力沿截面宽度均匀分布,沿高度呈线性分布,如图4所示。
图4 梁弯曲时的正应力分布图
即有y
I
x
M
z
)
(
=
σ(1)
中性轴把截面分成受拉区和受压区两部分,且最大拉应力和最大压应力发生在上下边缘处,其值为max max y I M
z
=
σ。
令max y I W z z
=,即有:
z
W M =
max σ (2)
式中,W z 称为抗弯截面系数,它与横截面的几何尺寸和形状有关,量纲为[长度]3,常用单位为mm 3或m 3。
(1)对于矩形截面(高为h ,宽为b ,z 轴通过截面形心且平行于矩形的宽度方向。
):
6
2
h b W Z =
(3)
(2)对于圆形截面(直径为D ):
32
3
d W Z π=
(4)
(3)对于圆环形截面(外径为D ,内径为d ):
()
D
d D W Z
324
4-=π (5)
三、梁的强度计算
梁的强度要求可概括为两个方面,即梁内的最大正应力不超过材料的许用应力和最大切应力不超过材料的许用切应力。
一般说来,梁的正应力强度占主要地位,切应力强度是次要的,所以只考虑正应力强度问题。
对于等直梁,强度条件为:
][max
max σσ≤=
z
W M (6)
根据梁的正应力强度条件,可以解决梁的强度校核、选择截面尺寸和确定许用荷载三类工程强度设计问题。
例2:图示悬臂梁,横截面为矩形,承受载荷F 1与F 2作用,且F 1=2×F 2=5kN ,试计算梁内的最大弯曲正应力,及该应力所在截面上K 点处的弯曲正应力。
解:(1)求最大弯矩(位于固定端)
max 7.5 kN M =
(2)计算最大应力
(3)计算K 点的应力
6
max max max
227.510176 MPa
408066
Z
M M bh W σ⨯====⨯6max max 337.51030
132 MPa
40801212
K Z
M y M y bh I σ⋅⋅⨯⨯====⨯
1 z。