当前位置：文档之家 › 第八章 组合变形强度计算

第八章 组合变形强度计算

  • 格式：ppt
  • 大小：2.49 MB
  • 文档页数：50

下载文档原格式

  / 50

合集下载

第八章 组合变形 构件的强度计算1

第八章 组合变形 构件的强度计算1
s max = M y max Wy M z max 6.58创 103 2.39 103 + = + - 6 Wz 141创 10 21.2 10- 6
P
D1

=159.4MPa<[ ]
图示矩形截面梁，截面宽度b＝90mm，高度h＝180mm。 梁在两个互相垂直的平面内分别受有水平力F1和铅垂 力F2 。若已知F1＝800N， F2＝1650N， L ＝1m，试 求梁内的最大弯曲正应力并指出其作用点的位置。 M y = F1 L F2 M z = F2 L
或单向压缩)，故：
FN M z ,max s max = + A Wz
强度条件
max≤ [ ]
例1
• 最大吊重P=8kN的起重机， AB杆的工字钢，材料为A3 钢，[]=100MPa，选择工 字钢型号。
“M”
“N”
Mmax=12kN· m

N=40kN
先按弯曲正应力选择工字钢型号； 再按组合变形的最大正应力校核强度，必要 时选择大一号或大二号的工字钢； 若剪力较大时，还需校核剪切强度。

-3
2
求内力(作用于截面形心) 取研究对象如图
N=P kN, -2 My =42.5´ 10 P kNm
危险截面 各截面相同 应力分布

危险截面 各截面相同 应力分布


N引起的应力

My引起的应力
N P = MPa σ¢ = A 15
σⅱ t max =
M y zo Iy M y z1 Iy
z
x
F1
L L
σ max =
My Wy
+
Mz Wz

JY第八章 组合变形T

JY第八章 组合变形T

（1）受力分析，作计算简图
F2 R M e
F2
M e 300 1500 N R 0.2
（2）作内力图,确定危险面
128.6N.m
危险截面E 左处
120N.m
危险面上内力
T 300 N.m
2 M My M z2 176N.m
（3）由强度条件设计d
r3
M T W
y1
z0
yc
z1
50
截面面积
A 15000 mm2
形心位置 zc
z0 75mm
z1 125mm
150 50 150
计算形心主惯性矩
I yc 5.31 107 mm4
（3）求内力
F
350
M F 350 75 103
M
FN F
425F 10
3
N.m
FN
t 30 106 F
667 667
45000 N
c.max 934F c
c 160 106 F
934 934
171300 N
许可压力为 F 45000 N 45kN
例 传动轴左端的轮子由电机带动，传入的扭转力 偶矩Me=300Nm。两轴承中间的齿轮半径R=200mm，径 向啮合力F1=1400N，轴材料许用应力[σ ]=100MPa。 试按第三强度理论设计轴的直径d。a=150 b=200
T 5 103 25.5MPa Wt 0.13 16
（5） 强度分析
r3 2 4 2 137MPa
该杆件强度足够。
[ ]
塑性材料的圆截面轴弯扭组合变形 第三强度理论：

第八章组合变形时的强度计算

第八章组合变形时的强度计算

Iy
IY
由 mz 产生的正应力
s"' MZ .y Fyp y
IZ
IZ
假设C 点在第一象限内,根据杆件的变形可知, s ',s '',s ''' 均为拉应
力，由叠加原理，即得 C点处的正应力为：
σ σ' σ'' σ'''
任意横截面 n-n上的 C点的正应力为
c
σ F F zP z F yP y
与y轴的夹角θ为：
tgθ z0 Mz Iy Iy tgφ y0 My Iz Iz
公式中角度 是横截面上合成弯矩 M 的矢量与 y 轴的夹角 . 横截面上合成弯矩 M 为：
M
M
2 y
M
2 z
tgθ Iy tgφ Iz
讨论：
（1） 一般情况下，截面的 IzIy ,故中性轴与合成弯矩 M 所在平面不垂直，此为斜弯曲的受力特征。导致挠曲线与外 力（合成弯矩）所在面不共面,此为斜弯曲的变பைடு நூலகம்特征。
s s ' s '' My z - Mz y
Iy
Iz
式中，Iy和Iz分别为横截面对于两对称轴y和z的惯性矩； M y和Mz分别是截面上位于水平和铅垂对称平面内的弯矩，且 其力矩矢量分别与y轴和z轴的正向相一致。在具体计算中，
也可以先不考虑弯矩M y、Mz和坐标y、z的正负号，以它们的 绝对值代入，然后根据梁在P1和P2分别作用下的变形情况， 来判断上式右边两项的正负号。
FN A
Mz Wz
158 MPa
s
所以强度是安全
【例8-4】矩形截面柱如图所示。P1的作用线与杆轴线重合， P2作用在 y 轴上。已知， P1= P2=80kN，b=24cm , h=30cm。 如要使柱的m—m截面只出现压应力，求P2的偏心距e。

第八章 组合变形构件的强度

第八章 组合变形构件的强度

弯曲与拉伸（或压缩）组合变形构件的应力和强度计算 弯曲与拉伸（或压缩）
P = Pcosϕ x P = Psin ϕ y
（1）轴向 分力P 为轴向外力，在此力有单独作用下， 分力Px为轴向外力，在此力有单独作用下，杆将产生 轴向拉伸，杆横截面上各点将产生数值相等的拉应力， 轴向拉伸，杆横截面上各点将产生数值相等的拉应力， 其值为： 其值为：
例8-1 悬臂吊车如图示。横梁用25a号工字钢制成，梁长l=4m, 悬臂吊车如图示。横梁用25a号工字钢制成 梁长l=4m, 号工字钢制成， 斜杆与横梁的夹角α=30 电葫芦重Q =4kN， 斜杆与横梁的夹角α=30o，电葫芦重Q1=4kN，起重量 Q2=20kN，材料的许用应力[σ]=100MPa，试校核横梁的强度。 =20kN，材料的许用应力[ ]=100MPa，试校核横梁的强度。
解：（1）外力分析 ：（1 （2）作内力图
1 M = Q = 0.2Q l 4 1 T = Q = 0.18Q D 2
（3）求最大安全载荷 由于轴的危险点牌复杂应力状态， 由于轴的危险点牌复杂应力状态，故应按强度理论进行 强度计算。采用第三强度理论： 强度计算。采用第三强度理论：
M2 +T2 σeq3 = ≤[σ] W 即 :
解：（1）计算内力 ：（1 由于钢板在截面1 处有一半圆槽，因而外力P 由于钢板在截面1-1处有一半圆槽，因而外力P对此截面为偏 心拉伸，其偏心距之值为： 心拉伸，其偏心距之值为：
b b−r e= − = 0.5cm 2 2 截面1 处的轴力和弯矩分别为： 截面1-1处的轴力和弯矩分别为：
N = P =80kN =80000N M = Pe =80000×0.005= 400N.m
15000 6000 σt max = + 3 =32.5M <[σ] Pa 2 πd πd 4 32

第八章 组合变形的强度计算

第八章 组合变形的强度计算

FAx A FAy FN
l/2
F2
C
B F1
b
cmax
σcmax
l/2
FB F1
h
z
y
＋

z
=
z
M

M max F2 l 4
tmax
Mmax max Wz
σtmax
5.强度计算 （脆性材料）
F M max 1 max t t max A Wz F M c max max 1 max c A Wz
y My M y max Wy

z
My
讨论：无棱角的截面如何确定危险点
b

h
z

y
z

z
Mz
My
y
z
F
y
F
y
t max
Mz M y Wz Wy
Mz M y c max Wz Wy
此时，应先找出组合变形的 中性轴，距中性轴最远的点有最 大的正应力。
F
l
Mz Fy x Fx cos
M y Fz x Fx sin
3.应力计算 (计算A(y，z)点的正应力)
Mz A Mz y Iz
A A A
Mz y M y z A Iz Iy
M y A
M yz Iy
§8-3
概述 两相互垂直平面内的弯曲
拉伸（压缩）与弯曲
§8-4
扭转与弯曲
§8-1 概述
组合变形：由两种或两种以上基本变形组合形成的变形。 工程实例：

《材料力学》第八章组合变形

《材料力学》第八章组合变形
解 (1)外力分析，确定变形类型—拉弯组合；
（2）内力分析，确定危险截面—整个轴；
M=600(kN·cm) FN=15(kN)
(3)应力计算，确定危险点—ａ、b点；
P产生拉伸正应力： t
FN AFNd 2源自4FNd 24
M拉产弯生组弯合曲：的正应力：wmax
M Wy
M
d3
32
32M
d3
P M= a Pe
补例8.1 已知： P=2kN,L求=：1mσm,Iazx=628×104mm4,Iy=64×1040mm2740 2844
解:1.分解P力。 Py Pcos φ Pz Psin φ 2．画弯矩图，确定危险截面--固定端截面。 3．画应力分布图，确定危险点—A、 B点
σ” σ’
A
x
y
Pyl
M
z
践中，在计算中，往往忽略轴力的影响。
4.大家考虑扭转、斜弯曲与拉（压）的组合怎么处理？
例8.5 图8.14a是某滚齿机传动轴AB的示意图。轴的直径为35 mm，材料为45钢， [σ]=85 MPa。轴是由P=2.2kW的电动机通过
带轮C带动的，转速为n=966r／min。带轮的直径为D=132 mm，
Mz Py l - x Pcosφ l - x Mcosφ My Pz l - x Psinφ l - x Msinφ
式中的总弯矩为：M Pl- x
3.计算两个平面弯曲的正应力。在x截面上任取一点A(z 、y)，
与弯矩Mz、My对应的正应力分别为σ’和σ”，故
- Mz y , - M yz
第八章 组合变形
基本要求: 掌握弯曲与拉伸（或压缩）的组合、扭转与弯曲的组合 的强度计算。
重点： 弯曲与拉伸（或压缩）的组合，扭转与弯曲的组合。

材料力学第八章组合变形及连接部分的计算

材料力学第八章组合变形及连接部分的计算
t . max
Mz 0 FN Iy A
F
350
M
FN
425 10 3 F 0.075 F 5.3110 5 15 10 3 667 F Pa F Mz c. max 1 N Iy A
t .max
c.max
425 10 3 F 0.125 F 5 5.31 10 15 10 3 934 F Pa
50 150
425F 103 N.m
A 15000 mm2 z0 75mm z1 125mm I y 5.31107 mm4
y1
z0
y
z1
150 50 150
（2）立柱横截面的内力 FN F 50 M 425103 F N.m （3）立柱横截面的最大应力
az
中性轴
z0 0 y0 0
i z2 a y yo ey 2 iy a z zo ez
截面核心
y
中性轴
F (e y , e z )
z
求直径为D的圆截面的截面核心.
d a y1 2
i z2 ay ey
a z1
az
2 iy
2 4 d d 64 2 iy i z2 2 A d 4 16
F
1， 首先将斜弯曲分解 为两个平面弯曲的叠加
Fy F cos

L2
L2
Z y
My Wy
Fz F sin
2， 确定两个平面弯曲的最大弯矩
Z y
Wz 70.758cm 3
Mz
Fy L 4
Fz L My 4
查表： W y 692.2cm 3

材料力学第8章组合变形强度计算

材料力学第8章组合变形强度计算
M
e
偏心受拉——拉弯组合 偏心受压——压弯组合

正应力计算
任意一点单向应力状态 正应力代数相加

M
N
内力单独作用
N N A My M Iz
e N
(-) (+) (+) (+)
组合应力 N My N M
A
N
M

Iz

最大最小正应力

e
截面边缘应力最大或最小 边缘到弯矩中性轴的距离分别为y1和y2
F e a 1 , A 5
F e b 1 A 5
A 180 30 10 3600 F a b 2 2
N
2.5 A 2.5 180 a b 30 10 2.5 mm e F 3600
b E b 200103 50106 10
MPa MPa
梯形分布
（2）计算 F 和 e 的数值
Wz h 5 mm , A 30 6 180 mm2 A 6
max
min
N e F e 1 1 A Wz / A A 5
103 kPa
103k和抗压能力相同，最大应力满足条件
2. 脆性材料
e N M N 1 max f 或 [ ] A Wz A Wz / A
常用作受压，当压力作用于截面核心内时
c max
e N M N 1 f c 或 [ c ] A Wz A Wz / A N e 1 f t 或 [ t ] A Wz / A
压力梯 M 216 h 3 e 0.206 m 0.5 m 形分布 N 1050 6 6

第八章组合变形构件的强度-

第八章组合变形构件的强度-
1.外力分析
Fx F cos; Fy F sin 2.内力分析
FN Fx F cos FS Fy F sin M z Fy (l x) 上侧受拉
F sin(l x)
m
xm l
z
Fx
x
Fy
F
y
z
FS
FN x
y Mz
§8-2 弯曲与拉伸(或压缩)得组合
一、拉(压)与弯曲组合变形
第八章组合变形构件的强度
第八章 组合变形构件得强度
轴向拉(压)
F
内
FN
力
FN F
扭转
m
x
T
T m
F
应
T
力
FN (x)
A
max
(ρ) T ρ Ip
对称弯曲
FS
M
σ
τ FS
M
My
;
FS
S
z
Iz
bI z
§8-1 概述 一、组合变形
F2
F1
Me
F1 — 轴向拉伸 F2 — 弯曲变形 Me — 扭转变形
F2
2
F1
1
z
FN F1
A bh
x 3
My Wy
F1 b h b2
2 6
3F1 bh
4
l
l
y
Mz Wz
F1 h b h2
2 6
3F1 bh
1
F1 bh
3F1 bh
3F1 bh
F1 bh
3
2
F1 bh
3F1 bh
3F1 bh
7 F1 bh
4
F1 bh
3F1 bh
3F1 bh

第八章-组合变形强度计算

第八章-组合变形强度计算
W
T 15kN·m + x
M x
20kN.m
W D 3 (1 a 4 ) 32
34
例8-6、确定图示手摇绞车所能起吊的重量P。
材料为Q235钢
[]80MPa
400
400
[t]48MPa
d=30mm
M 0.18 P
解：1、外力分析（略）
2、内力分析
T m ax 0.18 P
塑
性材
M max

料
M m ax Wz
脆
性 材

M
m
ax

料
M max
y m ax
IZ
M max

M max
y m ax
IZ
12
4、强度计算 单向应力状态 强度条件 max [ ]
计算最大应力
塑性材料
m ax

M m ax

N
脆性材料
拉弯组合变形(若拉伸应力大于弯曲压应力，则只需校 核拉应力强度)
M2 0.75T2 W
32
例8-5、空心圆杆AB和CD杆焊接成整体结构，受力如图。AB杆
的外径 D=140mm，内、外径之比α= d/D=0.8，材料的许用应力
[]=160MPa。试用第三强度理论校核AB杆的强度。
10kN
解： (1) 外力分析 将力向AB杆的B截面形心简化得
F 25 kN

m ax

M m ax

N
m ax

M m ax

N
压弯组合变形(若压缩应力大于弯曲拉应力，则只需
校核压应力强度)

08第八章 组合变形构件的强度

08第八章 组合变形构件的强度

M z1 17106 125 40(MP a) c Iy 5310 104
t
c
t max t N 242.67 26.7(MPa) [ t ] c max c N 402.67
37.3(MPa) [ c ]
N
∴该立柱安全！
1020 3 [ 102025 2 ] 12
PPLeabharlann 7.27105 mm 4M P zC 500 m N
N 应力分析如图
max
t
M
N M z max A I yc
100 103 500 103 55 800 7.27105
N M
12537.8162.8MPa
My
Mz
－
2 2 2 M M y M z2 2.1 4.2
+
4.7(kNm)
z
y
d
P
m l
P
l
M 2 T 2 r3 W
4.7 2 1.52 10 6 3.14100 3 32
T My Mz
－
50.3MPa
－
安全!
+
[例7] 图示空心圆轴，内径d=24mm，外径D=30mm，轮子
( z P , yP )
，z0）
M y z0 P M z y0 yz x A Iz Iy
P M z y0 M y z0 令： x 0 A Iz Iy
y
中性轴
即
y P y0 z P z 0 P P y P y0 P z P z0 P ( 1 2 2 ) 0 2 2 A iz iy A Aiz Ai y
§8 –3 弯曲与扭转的组合

材料力学第八章组合变形

材料力学第八章组合变形

0.456qa2 0.383qa2
弯矩图 (z轴为中性轴)
A DC 0.444qa2 0.321qa2
B My图 z轴往下
在xoz主轴平面内的 弯矩图(y轴为中性轴)
0.266qa2
0.642qa2
材料力学
中南大学土木工程学院
26
横截面在xoz、 xoy平面的弯曲截面系数，可查表得
W z 2 3 7 1 0 6 m 3 W y 3 1 .5 1 0 6 m 3
解：图中所有外荷载虽在同一平 面但并不位于梁的形心主惯性平 面内，所以是斜弯曲。将均布荷 载q向形心主惯性轴分解为
qy=qcos ，qz=qsin
在檩条跨中处弯矩最大，其值为
M z m a x 1 8 q y l2 1 8 q l2 c o s M y m a x 1 8 q z l2 1 8 q l2 s in
40.810.88 16066m348.280.35106m317.80MPa[]160MPa
材料力学
中南大学土木工程学院
30
可见选25a工字钢不能满足强度条件，于是再改选大一号的25b工字钢。 由附录查得查得25b工字钢的Wz=422.72cm3，Wy=52.423 cm3，自重 q1=0.41KN/m。所以，强度条件为
12
键 连 接
M
材料力学
中南大学土木工程学院
13
木榫接头
F
材料力学
m
m
c
n
n
l
l
中南大学土木工程学院
F
14
榫齿 连接
材料力学
中南大学土木工程学院
15
§8.2 相互垂直平面内的弯曲－斜弯曲

第八章组合变形构件的强度

第八章组合变形构件的强度

偏心距e。
P
εa
P
e e h
【解】1）将P向轴线平移。
M e Pe
P
2）由虎克定律得：
Me
z
εb
b
εa
P
εb
Me
a b
a
E
b
E
1 E
1 E
P A
P A
Me Wz
Me Wz
1 E
1 E
P bh P bh
12Pe b h3
12Pe b h3
P
Ebh( a
2
e
h(
a
b)
6( a b)
A
F
+
σ'
2)当梁上只有P作用时，其弯
P ab
矩图和应力图为：
A
B
C
σ''
正应力：σ M (x) y
Iz
3)F、P同时作用时正应力：
Pab/(a+b)
+
AC
B
σmin σ σmax
F M (x) y
A
Iz
4)整个梁正应力在C截面上 下边缘取得极值：
Hale Waihona Puke 5)梁处于单向应力状 态，强度条件为：
σ
态，处于二向应力状态。
τ
5)强度计算：
eq3 2 4 2
2 m
ax
4
2max
M ma Wz
x
2
4
Tm W
ax t
2
M max Wz
2
4
T max 2W z
2
1 W
z
M
2 m
ax
T

8-第八章组合变形时的强度资料

8-第八章组合变形时的强度资料

第八章组合变形8.1 组合变形和叠加原理一、组合变形的概念1. 简单基本变形：拉、压、剪、弯、扭。

2. 组合变形：由两种或两种基本变形的组合而成的变形。

例如：烟囱、传动轴、吊车梁的立柱等。

烟囱：自重引起轴向压缩+ 水平方向的风力而引起弯曲；传动轴：在齿轮啮合力的作用下，发生弯曲+ 扭转立柱：荷载不过轴线，为压缩= 轴向压缩+ 纯弯曲Ph g水坝qPh g二、组合变形的计算方法1. 由于应力及变形均是荷载的一次函数，所以采用叠加法计算组合变形的应力和变形。

2. 求解步骤①外力分解和简化②内力分析——确定危险面。

③应力分析：确定危险面上的应力分布，建立危险点的强度条件。

§8.2 斜弯曲一、 斜弯曲的概念1. 平面弯曲：横向力通过弯曲中心，与一个形心主惯性轴方向平行,挠曲线在纵向对称面内。

2. 斜弯曲：横向力通过弯曲中心，但不与形心主惯性轴平行挠曲线不位于外力所在的纵向平面内。

二、斜弯曲的应力计算 1. 外力的分解对于任意分布横向力作用下的梁，先将任意分布的横向力向梁的两相互垂直的形心主惯性矩平面分解，得到位于两形心主惯性矩平面内的两组力。

位于形心主惯性平面内的每组外力都使梁发生平面弯曲。

如上所示简支梁。

2. 内力计算形心主惯性平面xOy 内所有平行于y 轴的外力将引起横截面上的弯矩z M ，按弯曲内力的计算方法可以列出弯矩方程z M 或画出z M 的弯矩图。

同样，形心主惯性平面xOz 内所有平行于z M 矩方程y M 或画出其弯矩图。

合成弯矩：2Z 2y M M M +=合成弯矩矢量M 与y 轴的夹角为：y z M Mtan =ϕ以上弯矩z M 和y M 均取绝对值计算，由力偶的矢量表示法可知，合成弯矩M 3. 计算xyz I zI y yz M M +=''+'=σσσ4. 轴的位置两平面弯曲组合成斜弯曲，只在横截面上正应力为零的点的连线才是斜弯曲的中性轴。

设中性轴上任一点的坐标）（00,y z ，将0y ，0z 代入应力计算公式，并令σ等于方程：零，得中性轴： 0M M 0y 0z =+yz I z I y中性轴与y 轴的夹角α,ϕαtan tan z z 00I I M M I I y z y y z y =⋅==5. 最大正压力中性轴把横截面分为两个区域，一个受拉区，另一个受压区，离中性轴最远的点，正应力最大。

组合变形时的强度计算.

组合变形时的强度计算.

式中角度φ是横截面上合成弯矩M矢量与y轴间的夹角。一 般情况下，由于截面的Iy不等于Iz ，因而中性轴与合成弯矩M所 在的平面并不相互垂直。并由于截面的挠度垂直于中性轴，所 以挠曲线将不在合成弯矩所在的平面内。故这种弯曲称为斜弯 曲。
§83 拉伸(压缩)与弯曲组合变形
q P y P
一、计算方法：
§84弯曲与扭转组合变形
一、单向弯曲与扭转组合变形 1.引例：以钢制摇臂轴为例。 ①外力向形心简化(建立计算模型)： ②作弯矩、扭矩图(找危险截面)：
由弯矩图知：A截面|M|→max；全梁Mn处处相同，
∴A截面为危险截面：
|M A | PL T Pa n
③危险截面的危险点：A截面K1、K2点，t、s数值均为最大， ∴K1、K2点均为危险点： |M A | Mn t K1点： s s tmax Wz Wn |M A | Mn t K2点：s s cmax Wz Wn
2
s
s
2
⑤进行强度计算： s r 3 s 2 4t 2 [s ] 1) 2 M 2 Tn (圆轴：Wn=2Wz) sr3 [s ] 2) Wz 2 2 3) s r 4 s 3t [s ] 2 M 2 0.75Tn s r 4 [s ] 4) Wz 2.讨论： 公式1)、3)可用于一般构件中只有一对s的平面应力状态； 公式2)、4)只能用于圆轴单向弯扭变形。 二、双向弯曲和扭转强度计算(基本步骤与前相同)
例 图 示 皮 带 轮 传 动 轴 ， 传 递 功 率 N=7kW ， 转 速 n=200r/min 。皮带轮重量 Q=1.8kN 。左端齿轮上啮合力 Pn 与齿 轮 节 圆 切 线 的 夹 角 ( 压 力 角 ) 为 20o 。 轴 材 料 的 许 用 应 力 [s]=80MPa，试按第三强度理论设计轴的直径。 解：①外力简化(建立计算模型)：外力向AB轴轴 线简化，并计算各力大小。

材料力学-第八章组合变形

材料力学-第八章组合变形

M z y M y sin
Iz
Iz
x
M y z M z cos
Iy
Iy
x
y
z
y
z

M
y sin
z

cos
对于圆形截面
因为过形心的任意轴均为截面的对称轴，所以当横 截面上同时作用两个弯矩时，可以将弯矩用矢量表示， 然后求二者的矢量和。于是，斜弯曲圆截面上的应力计 算公式为：
A
C
B
D
2 kN 5 kN
300 500
2 kN (a)
500
解：
1.5 kN Am
7 kN
C
1.5 kN m
B
D
（1）分析载荷 如图b所示
5 kN
12 kN (b)
T 1.5 kN m
（2）作内力图 x
如图c、d、e、f 所示
(c)
MC MD
1.5 kN Am
7 kN
C
1.5 kN m
B
FN A


F (2a)2
1 4
F a2
（2）开槽后的正应力
My
FN F
My

Fa 2
FN
2
max


FN A

My Wy




F 2a2

Fa / 2 2a2 a2 /
6


2
F a2
2a
2a
z
a
所以：
2
1
8
y
§8.3 斜弯曲
F1

组合变形强度计算

组合变形强度计算

第6章 组合变形强度计算6.1 组合变形与弹性叠加原理6.1.1 组合变形的概念在工程实际中，有许多杆件在外力作用下会产生两种或两种以上的基本变形，这种情况称为组合变形。

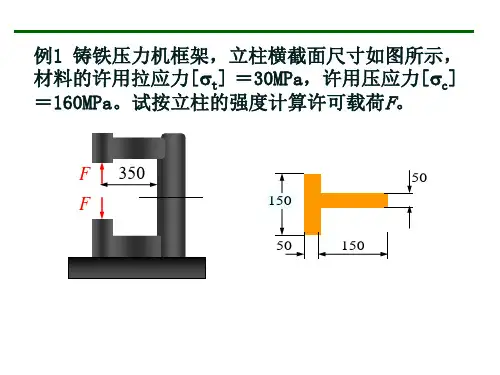
如图6-1（a ）所示小型压力机的框架。

为分析框架立柱的变形，将外力向立柱的轴线简化（图6-1b ），便可看出，立柱承受了由F 引起的拉伸和由Fa M =引起的弯曲。

图6-16.1.2 弹性叠加原理弹性叠加原理也称为线性叠加原理。

该原理对于求解弹性力学问题极为有用，它使我们可以把一个复杂问题化为两个或多个简单问题来处理。

在分析组合变形时，可先将外力进行简化或分解，把构件上的外力转化成几组静力等效的载荷，其中每一组载荷对应着一种基本变形。

例如，在行面对例子中，把外力转化为对应着轴向拉伸的F 和对应着弯曲的M 。

这样，可分别计算每一基本变形各自引起的应力、内力、和位移，然后将所得结果叠加，便是构件在组合变形下的应力、内力、应变和位移，这就是叠加原理。

现在再作一些更广泛的阐述。

设构件某点的位移与载荷的关系是线性的，例如，在简支梁的跨度中点作用集中力F 时，右端支座截面的转角为EIFl 162=θ这里转角θ与载荷F 的关系是线性的。

EI l 162是一个系数，只要明确F 垂直于轴线且作用于跨度中点，则这一系数与F 的大小无关。

类似的线性关系还可举出很多，可综合为，构件A 点因载荷1F引起的位移1δ与1F 的关系是线性的，即111F C =δ (a)这里1C 是一个系数，在1F 的作用点和方向给定后，1C 与1F 的大小无关，亦即1C 不是1F 的函数。

同理，A 点因另一载荷引起的位移为222F C =δ （b ）系数2C 也不是2F 的函数。

若在构件上先作用1F ，然后再作用2F 。

因为在未受力时开始作用1F ，这与（a ）式所表示的情况相同，所以A 点的位移为11F C 。

在作用时2F ，因构件上已存在1F ，它与（b ）式所代表的情况不同，所以暂时用一个带撇的系数'2C 代替2C ，得A 点的位移为22'F C 。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第八章
组合变形强度计算
§8-1 组合变形概述 §8-2 拉（压）弯组合变形强度计算 §8-3 弯扭组合变形强度计算
2
§8-1 组合变形概述
组合变形工程实例
压弯组合变形
3
组合变形工程实例
拉弯组合变形
4
组合变形工程实例
弯扭组合变形
5
一、基本概念
1、基本变形： 拉（压） 剪切 扭转 弯曲
2、组合变形：构件上同时存在两种或两种以上的基本变 形的组合。 3、叠加原理 构件在小变形和服从胡克定理的条件下，力的独立性原理成立。 即所有载荷共同作用下的内力、应力、应变等于各个载荷单独 F F 作用下相应值的叠加。 拉 + P P mC mC 弯 F F + mC mC 扭
11
拉（压）弯组合变形强度计算
1、外力分析 外力分解及平移，分组 分成对应于拉（压）及弯曲的两组 2、内力分析 画轴力图及弯矩图，从而找出危险截面 3、应力计算 分别算出拉（压）正应力及弯曲最大正应力（均取绝对值） 拉(压)正应力：
N
FN A
M max ymax
弯曲变形最大正应力： 脆 塑 M y M max max max 性 性 M max 材 材 M max IZ Wz 料 料
M max
IZ
12
4、强度计算 计算最大应力
单向应力状态 强度条件
N max M max
max [ ]
塑性材料
脆性材料
拉弯组合变形(若拉伸应力大于弯曲压应力，则只需校 核拉应力强度)

max M max N
8
§8-2 拉（压）弯组合变形强度计算
F Fl l F
Fl
=
F
+
1、外力分析
压弯组合变形
9
x
x
2、内力分析: 确定危险截面位置 3、应力分析: 确定危险点
M
F (-)
+
Fl
FN
t,max
,max c
N
F F A A
t ,max
c ,max
=
+
Fl W Fl Fl M max WW Fl F max [ ] W A Fl F [ ] max W A
FBx
a
Py
A FN 19.3kN
B x
P
x
+
Mz
A M (kN.m)
5.3
B
0.926
x
15
3） 应力分析及强度计算 FN x A
A截面
19.3kN
B
0.926
M (kN.m)
5.3
48
x
FN 2.1 MPa N A M y A max 9.7 MPa M max Iz M y A max 28.7 MPa M max Iz
+] <[ max M =7.6 MPa max N -] <[ max M =30.8 MPa max N
142
O Y
Z
16
3） 应力分析及强度计算 FN x A
B截面
19.3kN
B
0.926
M (kN.m)
5.3
48
x
FN 2.1 MPa N A M y A max 5 MPa M max Iz M y A max 1.7 MPa M max Iz
+ max M max N =2.9MPa <[ ] max M max N =3.8MPa <[ ]
142
O Y
Z
17
讨论：如下分组是否正确？
Py
Mz
A
P
A
P
B
Mz
B
Mz
x
x
A
Py
P
B
A
Py
x
B
A
B
A
B
18
例8-2:悬臂吊车水平梁为工字型钢，试确定它的型号。 d=20mm C W=15kN
2m
a
B
5m
A F A
D W
悬臂吊车
由手册查得钢材的许用应力为：[]=150MPa 解：1、外力分析（略） FBx 2、内力分析 B A截面为危险截面 FBy
a
D W
M A W (5 2 3) 23.04 KN .m
19
[]=150MPa
M A 23.04 KN .m
3、应力分析及强度计算
max
MA [ ] Wz
Wz 153.6cm3
由型钢表（408页）查得： 应采用18号工字钢
20
初步确定悬臂吊车水平梁为18号工字型钢
C
2m
[]=150MPa d=20mm W=15kN
a
B
5m
A F A
D W
悬臂吊车 重新选型钢 1、外力分析 F 43kN 2、内力分析 A截面为危险截面
Mz Px
48
15º
A
1.2m
B
x
142
P
O
Y
Z
解： 1）外力分析 Py = Psin =5.18(kN) Px= Pcos =19.3(kN) 压弯组合变形。 Mz= 48 Px =926(N.m)
14
Py = 5.18(kN) Px= 19.3(kN) Mz= 926(N.m) 2）内力分析:(FN，M图） 可能的危险截面在A或B处
压弯组合变形(若压缩应力大于弯曲拉应力，则只需 校核压应力强度)

max

M max
N

max
M max N
13
例8-1、 已知P=20kN, =15°，l=1.2m，A=9.2103mm2， Iz=26.1106mm4， [ +]=20MPa ， [ -]=80MPa 。 试校核其正应力强度？ Py P
M max
10
选择：当杆件处于拉—弯组合变形时，对横截面上中性轴有这 样的结论。（ 2 ） （1）一定存在横截面区域内。 （2）不一定存在横截面区域内。 （3）一定不存在横截面区域内。 注意： 1. 在拉弯、压弯组合变形中，危险点处属 单向应力状态。 2. 中性轴与弯曲时的中性轴不重合。
若为拉弯组合，对塑性材料和脆性材料梁如何建立强 度条件？
6
二、组合变形强度计算的一般分析方法
外力分析 外力（分解，向轴线平移） 内力分析 分别进行内力分析 应力分析 危险点 危险截面
分组
根据各种变形横 截面上的应力分布
选择相应的 应力叠加并找出主应力 强度理论 强度计算 强度计算
计算相当应力
分组原则：对应同一种基本变形的载荷分在同一组
7
注：在组合变形强度计算中,剪力引起的切应力(对 细长杆件)忽略不计。