当前位置：文档之家 › 组合变形的强度计算.

组合变形的强度计算.

  • 格式：doc
  • 大小：1.27 MB
  • 文档页数：17

下载文档原格式

  / 17

合集下载

12组合变形的强度计算.

12组合变形的强度计算.

例 一桥墩如图示。承受的荷载为：上部结构传递给桥墩的压力F0＝ 1920kN，桥墩墩帽及墩身的自重F1＝330kN，基础自重F2＝1450kN， 车辆经梁部传下的水平制动力FT＝300kN。试绘出基础底部AB面上的 正应力分布图。已知基础底面积为b×h＝8m×3.6m的矩形。
3700kN 1740kNm
例
FB
FAx
FBy
FAy
FBx
F
49.7kN
30kNm
B左截面压应力最大
max
FN M z A Wz
3
Mz Wz
Wz 187.5cm3
查表并考虑轴力的影响：
20a Wz 237cm
A 35.5cm
2

max
49.7 103 30 106 140.6MPa 2 3 35.5 10 237 10
bh 2 a b 1.786mm 12 F


12.1 弯扭组合变形的强度计算
一、弯扭组合变形的应力分析F
MBy B Iz M max max Wz
a
L
F Fa
T IP T max WP
2


B
x x 2 13 x 2 2
B
FL
1 3
2 4 2
1 1 2 2 2 3 2 3 1 2 2


Fa
2 3 2
二、弯扭组合变形的强度计算
图示圆轴.已知,F=8kN,M=3kNm,［σ］=100MPa,试用第 三强度理论求轴的最小直径. T 3kNm M max FL 4kNm F

12-2 工程力学-组合变形的强度计算

12-2 工程力学-组合变形的强度计算



故，安全。
3 2 4 2
6.37 2 435.7 2 71.7 MPa
[例7] 方形截面杆的横截面面积在 mn 处减少一半，试求由 轴向载荷 P 引起的 mn 截面上的最大拉应力。
解：
N M m ax A W
a2 a a a2 P P/ P / 8 2 2 4 4 6 a
§12–3
拉(压)弯组合 偏心拉（压）
一、拉(压)弯组合变形：杆件同时受横向力和轴向力的作用而产
生的变形。
P P R
x z
P
x y z Mz
P
My
y My
二、应力分析： x z Mz P
P
MZ
My
y My
P xP A
Mzy xM z Iz
xM
y
Myz Iy
P Mz y Myz x A Iz Iy
max
F1 M max A Wz F1 F e A Wz
m
m
4）强度计算 因危险点的应力是单向应力 状态，所以其强度条件为：
F1 F e max 135MPa [ ] A Wz
例11-11 如图所示为一起重支架。已知a =3.0m， b=1.0m，F=36.0kN，AB梁材料的许用应力[ ]=140 MPa。试确定AB梁槽钢的型号。
拉压与弯曲组合变形的分析步骤
(1)、外力分析：
y
x
y P1
y
y P
x
=
P1
x
+
x P2
P2
P
P1 P cos
P2 P sin
(2)、内力分析：

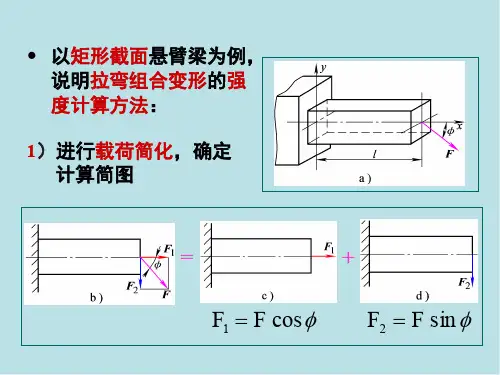
材料力学组合变形的强度计算第2节 拉压与弯曲的组合变形

材料力学组合变形的强度计算第2节 拉压与弯曲的组合变形

=
+
=
1

F1 A
+
2

M max Wz
4）强度计算
因危险点的应力是单向应力状态，所以其强度
条件为：
max

F1 A

M max Wz
[ ]
若为F1 压力，则危险截面上、下边缘处的正应
力分别为：
max

F1 A

M max Wz
，
m
in


F1 A

M max Wz
此时，危险截面的下边缘上的各点是危险点，
查附表，选两 根 18a 槽钢
注意 检验： max 144 MPa [ ] 140 MPa
虽然最大应力大于许用应力，但其值不超过许 用应力的5%，在工程上是允许的。
补充例 如图所示的钩头螺栓中，若已知螺纹内径 d =10mm，偏心距e =12mm，载荷F =1kN，许用应力
[ ]=140MPa 。试校核螺栓杆的强度。
为压应力。它的强度条件为：

max min

F1 A
Mmax Wz
[ ]
例9-1 夹具如图示，已知 F 2.0 kN ，l 60 mm ， b 10 mm，h 22 mm。材料许用正应力[ ] 160 MPa 。
试校核夹具竖杆的强度。
解：（1）外力分析
竖
夹具竖杆所受载荷是偏心载荷， 杆

F e Wz
135MPa
[ ]
b=1.0m，F=36.0kN，AB梁材料的许用应力[ ]=140
MPa。试确定AB梁槽钢的型号。
解： 1）外力分析
n

组合变形的强度计算

组合变形的强度计算

组合变形的强度计算 组合变形的概念拉伸与弯曲的组合一.组合变形的概念1.组合变形:在外力的作用下，构件若同时产生两种或两种以上基本变形的情况在小变形和线弹性的前提下，可以采用叠加原理研究组合变形问题所谓叠加原理是指若干个力作用下总的变形等于各个力单独作用下变形的总和（叠加）在复杂外载作用下，构件的变形会包含几种简单变形PRzxyPP2、组合变形的研究方法——叠加原理叠加原理应用的基本步骤：①外力分析：将载荷进行分解，得到与原载荷等效的几组载荷，使构件在每一组载荷的作用下，只产生一种基本变形.②内力分析：分析每种载荷的内力，确定危险截面.③应力分析：分别计算构件在每种基本变形情况下的危险将各基本变形情况下的应力叠加，确定最④强度计算:二.弯曲与拉伸(的组合杆件在外力作用下同时产生弯曲和拉伸（压缩）变形称为弯曲与拉伸（压缩）的组合偏心拉伸:弯曲与拉伸的组合变形链环受力立柱受力拉伸与弯曲组合的应力分析ϕϕsin p p cos p p y x ==A P x ='σy I M x l P M zy =''-=σ)(作用下：z T W M A N max max +=σzC W M A N max max -=σ危险截面处的弯矩抗弯截面模量y I M A N z +=''+'=σσσ根据叠加原理，可得x 横截面上的总应力为[]T z max max T W M A N σσ≤+=[]c zmax max C W M A N σσ≤-=强度条件为例:悬臂吊车,横梁由25 a 号工字钢制成，l =4m ，电葫芦重Q 1=4kN ，起重量Q2=20kN , α=30º, [σ]=100MPa，试校核强度。

取横梁AB为研究对象，受力如图b所示。

梁上载荷为P =Q1+Q2= 24kN，斜杆的拉力S 可分解为X B和Y B（1）外力计算横梁在横向力P和Y A、Y B作用下产生弯曲；同时在X A和X B作用下产生轴向压缩。

第八章组合变形时的强度计算

第八章组合变形时的强度计算

Iy
IY
由 mz 产生的正应力
s"' MZ .y Fyp y
IZ
IZ
假设C 点在第一象限内,根据杆件的变形可知, s ',s '',s ''' 均为拉应
力，由叠加原理，即得 C点处的正应力为：
σ σ' σ'' σ'''
任意横截面 n-n上的 C点的正应力为
c
σ F F zP z F yP y
与y轴的夹角θ为：
tgθ z0 Mz Iy Iy tgφ y0 My Iz Iz
公式中角度 是横截面上合成弯矩 M 的矢量与 y 轴的夹角 . 横截面上合成弯矩 M 为：
M
M
2 y
M
2 z
tgθ Iy tgφ Iz
讨论：
（1） 一般情况下，截面的 IzIy ,故中性轴与合成弯矩 M 所在平面不垂直，此为斜弯曲的受力特征。导致挠曲线与外 力（合成弯矩）所在面不共面,此为斜弯曲的变பைடு நூலகம்特征。
s s ' s '' My z - Mz y
Iy
Iz
式中，Iy和Iz分别为横截面对于两对称轴y和z的惯性矩； M y和Mz分别是截面上位于水平和铅垂对称平面内的弯矩，且 其力矩矢量分别与y轴和z轴的正向相一致。在具体计算中，
也可以先不考虑弯矩M y、Mz和坐标y、z的正负号，以它们的 绝对值代入，然后根据梁在P1和P2分别作用下的变形情况， 来判断上式右边两项的正负号。
FN A
Mz Wz
158 MPa
s
所以强度是安全
【例8-4】矩形截面柱如图所示。P1的作用线与杆轴线重合， P2作用在 y 轴上。已知， P1= P2=80kN，b=24cm , h=30cm。 如要使柱的m—m截面只出现压应力，求P2的偏心距e。

组合变形时的强度计算

组合变形时的强度计算

§84弯曲与扭转组合变形
一、单向弯曲与扭转组合变形
1.引例：以钢制摇臂轴为例。
①外力向形心简化(建立计算模型)：
②作弯矩、扭矩图(找危险截面)：
由弯矩图知：A截面|M|→max；全梁Mn处处相同，
∴A截面为危险截面：
|TMn AP|aPL
③危险截面的危险点：A截面K1、K2点，t、s数值均为最大，
⑤用强度准则进行强度计算
§8-2 两相互垂直平面内的弯曲
平面弯曲：对于横截面具有对称轴的梁，当横向外力或
外力偶作用在梁的纵向对称面内时，梁发生对称弯曲。这时， 梁变形后的轴线是一条位于外力所在平面内的平面曲线。
斜弯曲：双对称截面梁在水平和垂直两纵向对称平面内
同时承受横向外力作用的情况，这时梁分别在水平纵对称面
∴K1、K2点均为危险点：
K1点：
sstmax|M W A z|
tMn W n
K2点：sscmax|M W A z|
tMn W n
y
A d
z
L
Tn
_
PL
M
_
P C
B a x
P Pa
K1
st Pa
K1 A
t s
s K2 t
K2
ss t
s
Байду номын сангаас
④对危险点进行应力分析：(从K1、K2点取单元体，因它们的 s、t数值分别相同，危险程度也相同，不妨取K1点研究)：
一、单向弯曲与扭转组合变形
④对危险点进行应力分析(s1≥s2≥s3)
在梁的任意横截面m—m上，由P1和P2引起的弯矩值依次为：
在梁的任意横截面m—m上，由P 和P 引起的弯矩值依次为： 试校核此夹具竖杆的强度。

拉伸(压缩)与弯曲的组合变形

拉伸(压缩)与弯曲的组合变形

max
26103 N 26.1104 m2
22.5103 N m 141106 m3
9.96159.57 106 P a
169.53MPa 170MPa
选用16号工字钢能满足强度要求。
目录
组合变形\拉伸（压缩）与弯曲的组合变形 【例9.4】 如图所示桥墩，其上承
受的荷载为：上部结构传递给桥墩的压 力F 1=1920 kN，桥墩墩帽及墩身自重 F2 =334 kN，基础自重F3=1450 kN，车 辆的水平制动力F4=300kN，试绘出基础 底部截面上的正应力分布图。
目录
组合变形\拉伸（压缩）与弯曲的组合变形
1. 内力分析 拉伸（压缩）与弯曲 的组合变形杆件，其内力 一般有轴力FN、弯矩M和 剪力FS。通常情况下，剪 力对强度的影响较小，可 不予考虑。只需绘出杆件 的FN图和M图（如图）。
目录
组合变形\拉伸（压缩）与弯曲的组合变形
2. 应力分析 轴力FN引起的正应力在横截面上均匀分布（如图），其值为
曲截面系数Wz=185×10-6 m3，代入上式得
max
26103 N 30.6 104 m2
22.5103 N m 185106 m3
8.50121.62 106 P a
130.12MPa 170MPa
所以该横梁强度足够。
从此例看出，由弯曲引起的正应力远比由压缩引起的正应力大， 故在设计截面时，可先按弯曲正应力强度条件选择工字钢型号，然 后再同时考虑由弯曲和轴向压缩（或拉伸）引起的正应力，校核最 大正应力是否满足强度条件，若不能满足强度条件，再另行选择。
应力状态，所以拉伸（压缩）与弯曲组合变形杆件的强度条件可表
示为
max
FN A

第4章 材料力学基础

第4章 材料力学基础
I p d 3 Wt r 16
4 π π D I p (D4 d 4 ) (1 4 ) 32 32
（4-32）
3 Ip π π D Wt ( D4 d 4 ) (1 4 ) （4-33） r 16D 16
4.4 梁的弯曲
4.4.1 梁的弯曲内力
图4-12 剪切
4.2.2 挤压与挤压应力
图4-13 剪切与挤压
图4-14 挤压应力的分布
4.2.3 剪切与挤压的强度
1．剪切强度计算
由于受剪构件的变形及受力比较复 杂，剪切面上的应力分布规律很难用理 论方法确定，因而工程上一般采用实用 计算方法来计算受剪构件的应力。
在这种计算方法中，假设应力在剪 切面内是均匀分布的。 若以A表示销钉横截面面积，则应 力为 FQ （4-19）
图4-11 应力集中现象
4.2 剪切和挤压
4.2.1 剪切与剪应力
在工程实际中，经常遇到剪切和挤压 的问题。 剪切变形的主要受力特点是构件受到 与其轴线相垂直的大小相等、方向相反、 作用线相距很近的一对外力的作用，如图 4-12（a）所示。
构件的变形主要表现为沿着与外力 作用线平行的剪切面（ m-n面）发生相 对错动，如图4-12（b）所示。
第4章 材料力学基础
4.1
轴向拉伸与压缩
4.2
剪切和挤压
4.3
圆轴扭转
4.4
梁的弯曲
4.5
组合变形的强度计算
【学习目标】 1．掌握受拉压杆件的强度及变形量的计 算方法 2．理解剪切与挤压的特点和实用计算 3．理解受扭转杆件的应力特点
4．理解受纯弯曲梁的内力及应力特点， 掌握弯矩图的作法 5．理解组合变形的类型及特点，了解强 度理论的涵义及应用特点

工程力学组合受力与变形时的强度计算

工程力学组合受力与变形时的强度计算


FN A
M W


3103
d 2

8 103
d 3
81.1

MPa
81.9
4
32
位置？
例题：图示钢板受集中力P=128KN作用，当板在
一侧切去深4cm的缺口时，求缺口截面的最大正应 力？若在板两侧各切去深4cm的缺口时，缺口截面 的最大正应力为多少?(不考虑应力集中) 10
P
360
求： 1．链环直段部分横截面上 的最大拉应力和最大压应力； 2. 中性轴与截面形心之间 的距离。
解：根据平衡，截面上将
作用有内力分量FNx 和Mz
Fx 0 M C 0
得到 FNx＝800 N
Mz＝ 12 N·m
x FNx
FNx A

4FNx πd 2


π
4 800 122 106
简支梁在中点受力的情
形下，最大弯矩
Mmax=FPl / 4。得到两个 平面弯曲情形下的最大
d
弯矩：
c
M max
FPz
FPx l FPsin l
4
4
M max
(FPy )

FPy l 4

FP
cos l 4
在Mmax(FPy)作用的截面上，截面上边缘的角点 a、b 承受最大压应力；下边缘的角点c、d 承受最 大拉应力。
Pz P cos
以y为中性轴弯曲 M y Pz (l x)
P cos(l x) M cos
M z Py (l x)
P sin(l x) M sin
M z y M y sin M y z M z cos

材料力学组合变形的强度计算第3节 弯曲与扭转的组合变形

材料力学组合变形的强度计算第3节 弯曲与扭转的组合变形
• 以曲拐 AB 杆为例，说明杆的弯曲与扭转这种组 合变形时的强度计算方法和步骤
1）外力分析
=
+
2）内力分析，确定危险截面的位置 —— A+ 截面
M max Fl M T M B Fa
k、k 两点为危险点
M max
Wz
MT
WP
3）强度计算
危险点的应力是二向应力状态，轴类零件一般都采 用塑性材料——钢材，因此应选用第三或第四强度理 论建立强度条件，即：
r3

32
F
l2 πd 3
R2
[ ]
按第四强度理论得到强度条件为
r4 32 F
l 2 0.75 R2 πd 3
[ ]
例9-3 卷扬机结构尺寸如图所示，l = 0.8m，R =0.18m，AB轴径 d = 0.06m。已知电动机的功率 P = 22kW，轴AB的转速 n =150r/min，轴材料的许用
应力[ ] = 100MPa，试校核AB轴的强度。
解： 1）外力分析 — 计算电动机输入的力偶矩 M0
M0

9550
P n

9550 22 150
Nm
1.4
k
N m
卷扬机的最大起重量 G M0 1.4 kN 7.78 kN R 0.18
2）内力分析，确定危险截面的位置 —— C_截面
1 3


2



2
2


2
2 0
r3 2 4 2 [ ]
r4 2 3 2 [ ]

WZ

d3
32
，WP

第八章组合变形构件的强度

第八章组合变形构件的强度

偏心距e。
P
εa
P
e e h
【解】1）将P向轴线平移。
M e Pe
P
2）由虎克定律得：
Me
z
εb
b
εa
P
εb
Me
a b
a
E
b
E
1 E
1 E
P A
P A
Me Wz
Me Wz
1 E
1 E
P bh P bh
12Pe b h3
12Pe b h3
P
Ebh( a
2
e
h(
a
b)
6( a b)
A
F
+
σ'
2)当梁上只有P作用时，其弯
P ab
矩图和应力图为：
A
B
C
σ''
正应力：σ M (x) y
Iz
3)F、P同时作用时正应力：
Pab/(a+b)
+
AC
B
σmin σ σmax
F M (x) y
A
Iz
4)整个梁正应力在C截面上 下边缘取得极值：
Hale Waihona Puke 5)梁处于单向应力状 态，强度条件为：
σ
态，处于二向应力状态。
τ
5)强度计算：
eq3 2 4 2
2 m
ax
4
2max
M ma Wz
x
2
4
Tm W
ax t
2
M max Wz
2
4
T max 2W z
2
1 W
z
M
2 m
ax
T

工程力学-弯扭组合

工程力学-弯扭组合
M
∴
d 3
32 M T π[σ ]
2
图
664669 N· mm
3
32 1940.9 664.7 π 100 10
6
2
= 0.0593 m = 59.3 mm T图 圆整，取： d = 60 mm
上海应用技术学院
18 例5 图示空心圆轴，内径d=24mm，外径D=30mm，F1=600N， B轮直径为0.4m，D轮直径为0.6m，[s]=100MPa。 F2 试用第三强度理论校核此杆的强度。 y 80º F1 解： 1. 外力分析
㊉
|M|max=F1l T = Me
上海应用技术学院
FN=F2
O T O
㊉
Me
x x
3. 应力分析 a点为危险点： 取单元体：
F1
s
a
s
tT tT
σ σM σ N
τT T Wp T 2W
a b A M O
6 Me B
F2
l
M W

FN A
㊀
x F2
㊉
FN –Fl 为单拉(压)与纯剪切组合应力状态。 O 注意：此时b点应力s为 T M FN σ σM σN O W A
M
Fy
A
y M2
B
F'y
C D
13 x
Fz T
z
1kN· m
㊉
F'z
My
z
Mz
O Mz O
㊀
0.568kN· m
x x
㊉
0.364kN· m 1.0kN· m ㊉ 1.064kN· m
对圆形截面，可将Mz、My My 合成为： M O

第五章 拉弯组合变形.ppt

第五章 拉弯组合变形.ppt

课间游戏吹泡泡作文
课间活动时间，我和小明、小刚约好来一场吹泡泡比赛。

我们来到操场上。

随着我的一声令下，大家就迫不及待地开始比赛了。

只见小明先打开瓶盖，，将吹泡泡用的小棒沾了一点水，接着用嘴对准棒前面的圈圈用力一吹，一个乒乓球大小的泡泡就诞生了，看到他吹了个这么大的泡泡，我心里可不服气啦。

于是我也用小棒沾了沾水，然后对准圈圈小心翼翼地吹起泡泡来，果然，在我的努力下，一个网球一样大的泡泡飘向空中，看着我的大泡泡，我得意地向小明挑了挑眉毛。

我们三个好朋友不停地吹着泡泡，，不一会儿，我们就置身在泡泡的海洋中。

一个个泡泡就像一个个淘气的胖娃娃，它们在阳光的照耀下仿佛穿上了漂亮的五彩衣，一个个你争我抢的向天空中飘去。

多么迷人的景象，我们欢呼起来。

很快，上课铃声响了，我们依依不舍的回到教室。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第8章组合变形的强度计算8.1 组合变形的概念在前面几章中，研究了构件在发生轴向拉伸(压缩)、剪切、扭转、弯曲等基本变形时的强度和刚度问题。

在工程实际中，有很多构件在荷载作用下往往发生两种或两种以上的基本变形。

若有其中一种变形是主要的，其余变形所引起的应力(或变形)很小，则构件可按主要的基本变形进行计算。

若几种变形所对应的应力(或变形)属于同一数量级，则构件的变形为组合变形。

例如，如图8.1(a)所示吊钩的AB段，在力P作用下，将同时产生拉伸与弯曲两种基本变形；机械中的齿轮传动轴(如图8.1(b)所示)在外力作用下，将同时发生扭转变形及在水平平面和垂直平面内的弯曲变形；斜屋架上的工字钢檀条(如图8.2(a)所示)，可以作为简支梁来计算(如图8.2(b)所示)，因为q的作用线并不通过工字截面的任一根形心主惯性轴(如图8.2(c)所示)，则引起沿两个方向的平面弯曲，这种情况称为斜弯曲。

图8.1 吊钩及传动轴屋架屋面檀条qzyqyqxO(a)(b)(c)(a) (b) (c)图8.2 斜屋架上的工字钢檀条求解组合变形问题的基本方法是叠加法，即首先将组合变形分解为几个基本变形，然材料力学180后分别考虑构件在每一种基本变形情况下的应力和变形。

最后利用叠加原理，综合考虑各基本变形的组合情况，以确定构件的危险截面、危险点的位置及危险点的应力状态，并据此进行强度计算。

实验证明，只要构件的刚度足够大，材料又服从胡克定律，则由上述叠加法所得的计算结果是足够精确的。

反之，对于小刚度、大变形的构件，必须要考虑各基本变形之间的相互影响，例如大挠度的压弯杆，叠加原理就不能适用。

下面分别讨论在工程中经常遇到的几种组合变形。

8.2 斜 弯 曲前面已经讨论了梁在平面弯曲时的应力和变形计算。

在平面弯曲问题中，外力作用在截面的形心主轴与梁的轴线组成的纵向对称面内，梁的轴线变形后将变为一条平面曲线，且仍在外力作用面内。

在工程实际中，有时会遇到外力不作用在形心主轴所在的纵向对称面内，如上节提到的屋面檀条的受力情况(如图8.2所示)。

在这种情况下，杆件可考虑为在两相互垂直的纵向对称面内同时发生平面弯曲。

实验及理论研究指出，此时梁的挠曲线不再在外力作用平面内，这种弯曲称为斜弯曲。

现在以矩形截面悬臂梁为例(如图8.3(a)所示)，分析斜弯曲时应力和变形的计算。

这时梁在F 1和F 2作用下，分别在水平纵向对称面(Oxz 平面)和铅垂纵向对称面(Oxy 平面)内发生对称弯曲。

在梁的任意横截面m —m 上，由F 1和F 2引起的弯矩值依次为1y M F x =，2()z M F x a =-在横截面m —m 上的某点(C y ,)z 处由弯矩M y 和M z 引起的正应力分别为y y M z I σ'=，z zMy I σ''=- 根据叠加原理，σ'和σ''的代数和即为C 点的正应力，即y z y zM Mz y I I σσ'''+=- (8-1)式中，I y 和I z 分别为横截面对y 轴和z 轴的惯性矩；M y 和M z 分别是截面上位于水平和铅垂对称平面内的弯矩，且其力矩矢量分别与y 轴和z 轴的正向一致(如图8.3(b)所示)。

在具体计算中，也可以先不考虑弯矩M y 、M z 和坐标y 、z 的正负号，以其绝对值代入，然后根据梁在F 1和F 2分别作用下的变形情况，来判断式(8-1)右边两项的正负号。

(a) (b)图8.3 斜弯曲第8章 组合变形的强度计算181为了进行强度计算，必须先确定梁内的最大正应力。

最大正应力发生在弯矩最大的截面(危险截面)上，但要确定截面上哪一点的正应力最大(就是要找出危险点的位置)，应先确定截面上中性轴的位置。

由于中性轴上各点处的正应力均为零，令00()y z ,代表中性轴上的任一点，将它的坐标值代入式(8-1)，即可得中性方程00y z y zM Mz I I -= (8-2) 从上式可知，中性轴是一条通过横截面形心的直线，令中性轴与y 轴的夹角为α，则00tan tan y yZ y z zI I z M y M I I αϕ==⋅=式中，角度ϕ是横截面上合成弯矩22y z M M M =+的矢量与y 轴的夹角(如图8.3(b)所示)。

一般情况下，由于截面的y z I I ≠，因而中性轴与合成弯矩M 所在的平面并不垂直。

而截面的挠度垂直于中性轴(如图8.4(a)所示)，所以挠曲线将不在合成弯矩所在的平面内，这与平面弯曲不同。

对于正方形、圆形等截面以及某些特殊组合截面，其中y z I I =，就是所有形心轴都是主惯性轴，故αϕ=，因而，正应力可用合成弯矩M 进行计算。

但是，梁各横截面上的合成弯矩M 所在平面的方位一般并不相同，所以，虽然每一截面的挠度都发生在该截面的合成弯矩所在平面内，梁的挠曲线一般仍是一条空间曲线。

可是，梁的挠曲线方程仍应分别按两垂直平面内的弯曲来计算，不能直接用合成弯矩进行计算。

图8.4 斜弯曲时横截面上的应力情况确定中性轴的位置后，就可看出截面上离中性轴最远的点是正应力σ值最大的点。

一般只要作与中性轴平行且与横截面周边相切的线，切点就是最大正应力的点。

如图8.4(b)所示的矩形截面梁，显然右上角1D 与左下角2D 有最大正应力值，将这些点的坐标(y 1, z 1)或(y 2, z 2)代入式(8-1)，可得最大拉应力t,max σ和最大压应力c,max σ。

在确定了梁的危险截面和危险点的位置，并算出危险点处的最大正应力后，由于危险点处于单轴应力状态，于是，可将最大正应力与材料的许用正应力相比较来建立强度条材料力学182件，进行强度计算。

【例题8.1】 一长2m 的矩形截面木制悬臂梁，弹性模量41.010MPa E =⨯，梁上作用有两个集中荷载1 1.3kN F =和2 2.5kN F =，如图8.5(a)所示，设截面0.6b h =，[]10MPa σ=。

试选择梁的截面尺寸，并计算自由端的挠度。

图8.5 例题8.1图解：(1) 选择梁的截面尺寸。

将自由端的作用荷载1F 分解11sin150.336kN y F F ==11cos15 1.256kN z F F ==此梁的斜弯曲可分解为在xy 平面内及xz 平面内的两个平面弯曲，如图8.5(c)所示。

由图8.5可知M z 和M y 在固定端的截面上达到最大值，故危险截面上的弯矩2232232.510.33623.172(kN m)1.25622.215(kN m)110.60.16611(0.6)0.0666z y z y M M w bh h h h w hb h h h =⨯+⨯=⋅=⨯=⋅==⨯⋅===⨯⋅=上式中M z 与M y 只取绝对值，且截面上的最大拉压应力相等，故 66max 333.17210 2.512100.10.06y z z y M M W W h h σ⨯⨯=+=+第8章 组合变形的强度计算1836373.58710[]h σ⨯=≤即194.5(mm)h = 可取h =200mm ，b =120mm 。

(2) 计算自由端的挠度。

分别计算y w 与z w ，如图8.5(c)所示，则232123362y y z z l F F l l w l EI EI ⎛⎫ ⎪⎛⎫⎝⎭=--- ⎪⎝⎭333346310.336102 2.5101(321)2(m)13 1.010100.120.212⨯⨯+⨯⨯⨯⨯⨯-=-⨯⨯⨯⨯⨯⨯33.7210m 3.72(mm)-=-⨯=-33314631.256102(m)133 1.010100.20.1212z z y F l w EI ⨯⨯==⨯⨯⨯⨯⨯⨯0.0116m 11.6(mm)==12.18(mm)w =11.6arctan 72.453.7β⎛⎫== ⎪⎝⎭8.3 拉伸(压缩)与弯曲的组合拉伸或压缩与弯曲的组合变形是工程中常见的情况。

如图8.6(a)所示的起重机横梁AB ，其受力简图如图8.6(b)所示。

轴向力x F 和Ax F 引起压缩，横向力Ay F ，W ，y F 引起弯曲，所以杆件产生压缩与弯曲的组合变形。

对于弯曲刚度EI 较大的杆，由于横向力引起的挠度与横截面的尺寸相比很小，因此，由轴向力引起的弯矩可以略去不计。

于是，可分别计算由横向力和轴向力引起的杆横截面上的正应力，按叠加原理求其代数和，即得横截面上的正应力。

下面我们举一简单例子来说明。

悬臂梁AB (如图8.7(a)所示)，在它的自由端A 作用一与铅直方向成ϕ角的力F (在纵向对称面xy 平面内)。

将F 力分别沿x 轴y 轴分解，可得sin cos x y F F F F ϕϕ==x F 为轴向力，对梁引起拉伸变形(如图8.7(b)所示)；y F 为横向力，引起梁的平面弯曲(如图8.7(c)所示)。

距A 端x 的截面上的内力为轴力 N sin x F F F ϕ==材料力学184弯矩 cos z y M F x F x ϕ=-=-⋅图8.6 起重机在轴向力x F 作用下，杆各个横截面上有相同的轴力N x F F =。

而在横向力作用下，固定端横截面上的弯矩最大，max cos M F l ϕ=-⋅，故危险截面是在固定端。

图8.7 拉弯组合变形第8章 组合变形的强度计算185与轴力N F 对应的拉伸正应力t σ在该截面上各点处均相等，其值为N t sin x F F F A A Aϕσ===而与max M 对应的最大弯曲正应力b σ，出现在该截面的上、下边缘处，其绝对值为 max b cos z zM Fl W W ϕσ== 在危险截面上与N F ，max M 对应的正应力沿截面高度变化的情况分别如图8.8(a)和 图8.8(b)所示。

将弯曲正应力与拉伸正应力叠加后，正应力沿截面高度的变化情况如图8.8(c)所示。

若t σ＞b σ，则min σ为拉应力；若t σ＜b σ，则min σ为压应力。

所以min σ之值须视轴向力和横向力分别引起的应力而定。

如图8.7(c)所示的应力分布图是在t σ＜b σ的情况下作出的。

显然，杆件的最大正应力是危险截面上边缘各点处的拉应力，其值为max sin cos zF Fl A W ϕϕσ=+(8-3) 由于危险点处的应力状态为单轴应力状态，故可将最大拉应力与材料的许用应力相比较，以进行强度计算。

应该注意，当材料的许用拉应力和许用压应力不相等时，杆内的最大拉应力和最大压应力必须分别满足杆件的拉、压强度条件。

若杆件的抗弯刚度很小，则由横向力所引起的挠度与横截面尺寸相比不能略去，此时就应考虑轴向力引起的弯矩。

图8.8 拉弯组合变形的应力叠加【例题8.2】 最大吊重8kN W =的起重机如图8.9(a)所示。