2017江西育华第一次月考 数学

2016-2017学年九年级（上）第一次月考数学试卷江西省南昌市()解析版8324分）每小题只有一个答案是正确的，个小题，每小题一、选择题：（本大题共分，共请将正确答案的代号填入下列对应题号内．2x1xm1y=mx ）．已知二次函数的图象与的取值范围是（+轴有两个交点，则﹣mDm Bm Cmm0 Am≠．．≠≥﹣且≥﹣．．＞﹣＞﹣且20B6bxcxA20y=ax2），则该二次函数的对称+（+，与，．已知抛物线轴交点为），（﹣）轴为（yx=1 x=1BCx=2 DA轴﹣．．．．2 3y=ax0bxca）的图象如图所示，给出以下结论：．已知二次函数（≠++ ya0①有最大值；＞，所以函数因为x=1②对称；该函数的图象关于直线﹣x=2y0③；当时，函数﹣的值等于3x=1y0x=④．或的值都等于当时，函数﹣）其中正确结论的个数是（12 DA4 B3 C．．．．23CBy3y4yyy=xc6xA1+（），，+的图象过（，），则，（﹣．若二次函数，﹣），2131 yy），的大小关系是（32 yyyyCyy yyAyBy y Dy＞．＞＞＞．＞＞．＞．＞212112331233l15时，拱顶（拱桥洞的最高点）离．图（）是一个横断面为抛物线形状的拱桥，当水面在4m2m2））建立平面直角坐标系，则抛物线的关系式是（．如图（，水面宽水面．2222Dy= By=2xx Cy=x2xAy=．﹣．．．﹣2 y=x136）﹣（的图象的顶点坐标是（﹣．二次函数）+ 3 D133A13 B1 C1）．（﹣），，﹣）．（﹣．（．（，﹣，）2y=2x7的图象是抛物线，现在同一坐标系中，将该抛物线分别向上、向左平移．已知函数2）个单位，那么所得到的新抛物线的解析式22222xx222 D2Ay=2xy=22By=2x2C2y=2+﹣﹣．）（﹣+）．+．﹣．（（+））（2 x8Cy=xC1C）．抛物线轴对称，则抛物线：的解析式为（+ 与抛物线关于21222221y=x1 xy=D y=xBy=x1 CA﹣﹣﹣﹣．．+．﹣．2173分）个小题，每小题二、填空题（本大题共分，共22 k=mxy=mmkk39y=x2x．（﹣）++．若把函数的形式，其中﹣﹣化为，为常数，则22m=0x10y=m4xxx4x+．已知二次函数的一元二次方程﹣﹣+++的部分图象如图，则关于．的解是2 ycx11y=axbx的对应值如表：上部分点的横坐标．抛物线++，纵坐标1 2 ......2 0 x 1 ﹣﹣ (4)64y6．（填写序号）从表可知，下列说法中正确的是x30 ①）；轴的一个交点为（抛物线与，2bxc6 y=ax②；的最大值为++函数．x=③；抛物线的对称轴是直线yx④增大而增大．在对称轴左侧，随2 yx3x112y=2x．，．函数，与﹣轴的交点的坐标为+ 与轴的交点坐标为0x1331②①时，，当）；．请写出符合以下三个条件的一个函数的解析式，＞过点（2x2y③．当自变量的值为的增大而减小；时，函数值小于随2 cbx14y=x． +．抛物线﹣的图象如图所示，则此抛物线的解析式为+2c=0bca0a15 y=axbx①；≠++．如图，是二次函数）的图象的一部分，给出下列命题：（++20a2bcb2aax1bxc=03④②③只 +．+＞的两根分别为﹣（和；．其中正确的命题是﹣＞； +要求填写正确命题的序号）三、解答题1216分）解方程．（22=0 x3x①+﹣211 8x4x7=②﹣﹣﹣2=0 5x2x③﹣2 1=0x6x④．﹣+2 hxky=a178的形式，并写出顶点坐标和对称轴）+．（分）用配方法将二次函数化成（﹣212 y=2x6x ①﹣+2 0.5xy=3x3②．+﹣﹣．24x6 188y=2x．﹣．（分）已知二次函数﹣22kh 6y=a1y=2xx4x的形式；化成）（（）用配方法将+﹣﹣﹣2 ）在平面直角坐标系中，画出这个二次函数的图象；（3xyx 的增大而减少？（取何值时，）当随4xy=0y0y0 ，，，＞（＜）当取何值是，50x4y 的取值范围；）当＜时，求＜（6 ）求函数图象与两坐标轴交点所围成的三角形的面积．（2 ACybxcx819y=axB点．+两点，与的图象与+、轴交于．（分）二次函数轴交于bc1a的符号，并说明理由；、（、）根据图象确定ACB=603ABC=45 2A0°°，求这个二次函数的解析式．，﹣）如果点，∠的坐标为（），∠（22 ym2x310A820Cy=x2m．）+的顶点（轴的距离为+．（﹣分）已知抛物线：到﹣1 mA1的值；的坐标及）求顶点（BS=6Cx2CDB的坐上，且两点．点（，求点）若抛物线与轴交于在抛物线、BCD1△标．921”“来临前夕，购进一种品牌粽子，．（分）为满足市场需求，某超市在五月初五端午节4540当售价定为元．元．根据以往销售经验发现；每盒进价是超市规定每盒售价不得少于70045120盒．每盒元时，每天可以卖出盒，每盒售价每提高元，每天要少卖出yx1（元）之间的函数关系式；（盒）与每盒售价）试求出每天的销售量（．2P （元）最大？最大利润是多少？）当每盒售价定为多少元时，每天销售的利润（358元．如果超市想要）（为稳定物价，有关管理部门限定：这种粽子的每盒售价不得高于6000 元的利润，那么超市每天至少销售粽子多少盒？每天获得不低于260xx20y=axyx 228增大而减小，求：时，+＞分）已知函数，在随．（1a 的取值范围；（）2ymxs）之间的函数关系，已知函（（（）若该函数为飞机着陆后滑行距离）与滑行时间x=20，请写出自变量滑行时间的取值范围，并求出飞机着陆后需滑行多数的对称轴为直线少米才能停下来？2bx4aA10y=axC04x23141轴交+）、﹣，经过（（﹣，．（分）如图）两点，与，抛物线B ．于另一点1 ）求抛物线的解析式；（22PCBP 坐标；（为第一象限抛物线上一点，满足到线段）如图，点距离最大，求点33EFEBCFM为线段（为抛物线顶点）与线段（，）如图，若抛物线的对称轴相交于点BCMMNEFNEFMN为顶点的四边形，，，上的任意一点，过点作∥交抛物线于点，以N 的坐标；若不能，请说明理由．能否为平行四边形？若能，求点2016-2017学年江西省南昌市九年级（上）第一次月考数学试卷参考答案与试题解析8324分）每小题只有一个答案是正确的，一、选择题：（本大题共分，共个小题，每小题请将正确答案的代号填入下列对应题号内．2x1xy=mxm 1） +轴有两个交点，则﹣的图象与．已知二次函数的取值范围是（0 mm Cm0 DmAm Bm≠≥﹣．＞﹣且．．≥﹣≠．且＞﹣x轴的交点．【考点】抛物线与221x1x=1y=mx4m）＞﹣﹣【分析】根据二次函数的图象与×（﹣+轴有两个交点，可得△0m0．且≠解：∵原函数是二次函数，【解答】m0．∴≠2 x1xy=mx轴有两个交点，则+的图象与∵二次函数﹣2 04ac=b，﹣＞△2 04m=11，△×（﹣）＞﹣m．∴＞﹣mmm0，＞﹣综上所述，且的取值范围是：≠C．故选2x=b04acx轴有两时图象与轴的交点，关键是熟记当△﹣【点评】本题考查了抛物线与＞22x0=b4ac=0x=b4ac轴没有交时图象与时图象与轴有一个交点；当△个交点；当△﹣﹣＜点．2002B6Ay=ax2cbxx），则该二次函数的对称），，（++与轴交点为，（﹣．已知抛物线）轴为（yx=2 Cx=1 1x=ABD轴．．﹣．．x轴的交点．抛物线与【考点】．ABAB的对和点和点是抛物线上的对称点，所以点【分析】根据抛物线的对称性得到点称轴即为抛物线的对称轴．2bxcxA20By=ax60 ），（﹣（【解答】解：∵抛物线轴交点为+，+，与），x=2 ．∴该二次函数的对称轴为直线C ．故选xy=axxxxa，﹣﹣（）（【点评】本题考查了抛物线与轴的交点：从二次函数的交点式）（21bca0xx0x0）．解决本）中可直接得到抛物线与），（，轴的交点坐标（是常数，，≠，21题的关键是掌握抛物线的对称性．2bxca03y=ax ）的图象如图所示，给出以下结论：++．已知二次函数≠（a0y ①有最大值；因为，所以函数＞x=1 ②对称；该函数的图象关于直线﹣x=2y0 ③；时，函数﹣当的值等于x=3x=1y0 ④．当时，函数﹣的值都等于或）其中正确结论的个数是（1D3 C2 A4 B．．．．二次函数的性质．【考点】x②①轴的交点坐标【分析】观察图象即可判断．根据抛物线与开口向上，应有最小值；x2x=③轴下方，所以函数值小﹣来确定抛物线的对称轴方程；时，对应的图象上的点在03x=1yx=x031④．或的值都等于于，所以当；图象与﹣轴交于﹣和时，函数解：由图象知：【解答】①函数有最小值；错误．x=1②对称；正确．﹣该函数的图象关于直线0x=2y③；错误．﹣时，函数当的值小于0yx=13x=④．正确．的值都等于时，函数或﹣当．C ．故正确的有两个，选此题考查了根据函数图象解答问题，体现了数形结合的数学思想方法．【点评】2y3yB3yC4y=x6xcA1y，（．若二次函数+﹣，+，的图象过），（﹣），则，（），1312 yy），的大小关系是（32 yyyyyAyyy Byy Cyy D＞．＞＞＞．．＞．＞＞＞223111213323二次函数图象上点的坐标特征．【考点】yyy，此题得解．【分析】根据二次函数的性质结合二次函数的解析式即可得出＞＞2132 x=36xy=xc，+﹣【解答】解：二次函数的对称轴为0a=1，∵＞yx=3y最小．时，∴当值最小，即243=13=43，﹣|+|∵﹣＞﹣，||，yy．＞∴点31 yyy．＞∴＞213 B．故选CAB三点纵坐标的大、【点评】本题考查了二次函数的性质，根据二次函数的性质确定、小是解题的关键．l51时，拱顶（拱桥洞的最高点）离．图（）是一个横断面为抛物线形状的拱桥，当水面在2m4m2））建立平面直角坐标系，则抛物线的关系式是（水面，水面宽．如图（2222 x2xAy=B y=2x Cy=D y=x．．．﹣﹣．根据实际问题列二次函数关系式．【考点】y可设此函数解析式为：对称轴为【分析】由图中可以看出，所求抛物线的顶点在原点，轴，2 y=ax，利用待定系数法求解．2 ay=ax0；≠，解：设此函数解析式为：【解答】．22 ）应在此函数解析式上．那么（，﹣2=4a 则﹣a=，即得﹣2 y=x．﹣那么C．故选：关键在于找到在此函数解根据题意得到函数解析式的表示方法是解决本题的关键，【点评】析式上的点．2 x136y=）﹣的图象的顶点坐标是（） +．二次函数﹣（D131 B13 C3A13）．（．（，﹣，，，﹣））．（﹣）．（﹣二次函数的性质．【考点】根据二次函数的顶点式一般形式的特点，可直接写出顶点坐标．【分析】2 31y=x13）．【解答】解：二次函数为顶点式，其顶点坐标为（﹣（+﹣，）B．故选主要考查了求抛物线的顶点坐标的方法．【点评】2y=2x7的图象是抛物线，现在同一坐标系中，将该抛物线分别向上、向左平移．已知函数2）个单位，那么所得到的新抛物线的解析式是（22222y=2xx2Cy=2222 2y=2Ax22By=2xD+（．（）﹣+）．．﹣（+））+﹣﹣．（二次函数图象与几何变换．【考点】直接利用平移规律（左加右减，上加下减）求新抛物线的解析式．【分析】22 2y=2xy=22x2．+向上、向左平移+个单位后的解析式为：【解答】解：抛物线（）A．故选：”“直接代入函数解【点评】左加右减，上加下减主要考查的是函数图象的平移，用平移规律析式求得平移后的函数解析式．2 CxC8Cy=x1）关于轴对称，则抛物线．抛物线：的解析式为（+ 与抛物线21222221xy=Dy=xCxy=Bxy=A 1 1 ﹣﹣﹣﹣．﹣．+．．二次函数图象与几何变换．【考点】．【分析】画出图形后可根据开口方向决定二次项系数的符号，开口度是二次项系数的绝对值；y 轴的交点为抛物线的常数项进行解答．与x轴对称的两个函数解析式的开口方向改变，开口度不变，二次项的系数解：关于【解答】yD ．互为相反数；对与轴的交点互为相反数，那么常数项互为相反数，故选x轴对称的特点：二次项系数，一次项系数，常数项均【点评】根据画图可得到抛物线关于互为相反数．2137分）二、填空题（本大题共分，共个小题，每小题222x3y=xmkmmy=x9k k=3﹣+．）．+为常数，其中若把函数的形式，﹣﹣，化为（则﹣二次函数的三种形式．【考点】mk ，再相加即可．【分析】利用配方法操作整理，然后根据对应系数相等求出、22x3 y=x，﹣【解答】解：﹣22x113 =x，﹣）﹣+﹣（24 =x1，﹣（﹣）m=1k=4 ，所以，﹣，mk=14=3 ．）所以，（﹣+﹣+3 ．故答案为：﹣本题考查了二次函数的三种形式，熟练掌握配方法的操作是解题的关键．【点评】224xxm=0y=xm4xx10+﹣的一元二次方程﹣++．已知二次函数+的部分图象如图，则关于x=1x=5 ．，﹣的解是21x 轴的交点．抛物线与【考点】．24xmxy=x轴的【分析】由二次函数+﹣的部分图象可以得到抛物线的对称轴和抛物线与+x轴交点的横坐标与相应的然后可以求出另一个交点坐标，再利用抛物线与一个交点坐标，24xm=0 xx 的解．一元二次方程的根的关系即可得到关于+的一元二次方程﹣+24xmx=2x5y=x，与+（【解答】解：根据图示知，二次函数的对称轴为﹣轴的一个交点为，+0 ），x50）关于对称轴对称，轴的另一个交点横坐标与点（，根据抛物线的对称性知，抛物线与x=1 ，﹣即10 ），则另一交点坐标为（﹣x=1x=5y=0 ，﹣则当时，函数值或24xm=0x ，+即﹣+24xm=0x=1x=5xx ．+，的解为+故关于﹣的一元二次方程﹣21x=1x=5 ．故答案是：﹣，21x轴的交点．解答此题需要具有一定的读图的能力．【点评】本题考查了抛物线与2 ybxc11y=axx的对应值如表：++．抛物线上部分点的横坐标，纵坐标2 1 ......2 0 x 1 ﹣﹣ (4)6y64．（填写序号）从表可知，下列说法中正确的是x30 ①）；抛物线与轴的一个交点为（，2bxc6y=ax ②；+函数的最大值为+x= ③抛物线的对称轴是直线；yx ④增大而增大．随在对称轴左侧，x 轴的交点；二次函数的性质；二次函数的最值．抛物线与【考点】．y=0x=3，即时，【分析】根据表中数据和抛物线的对称性，可得到抛物线的开口向下，当=x=32030x，，﹣）和（；，抛物线与因此可得抛物线的对称轴是直线轴的交点为（﹣）再根据抛物线的性质即可进行判断．y=0x=2y=0x=3，即抛物线【解答】﹣，根据抛物线的对称性，当，解：根据图表，当时，2030x）；，，与）和（轴的交点为（﹣x=3=，∴抛物线的对称轴是直线﹣根据表中数据得到抛物线的开口向下，x=x=016，，或时，函数有最大值，而不是对应的函数值∴当yxx=增大而增大．随的左侧，并且在直线②①③④错．所以正确，①③④．故答案为：2xcy=axbx轴的两个交【点评】本题考查了抛物线+的性质：抛物线是轴对称图形，它与+0a时，函数有最大值，在对称轴点是对称点，对称轴与抛物线的交点为抛物线的顶点；＜xy增大而增大．随左侧，2x112y=2x03x1y，），与（．函数（，﹣+轴的交点的坐标为与轴的交点坐标为010 ．（），），x 轴的交点．抛物线与【考点】23x1yx=0yx=0y=1y=2xy．故与与的值．当+轴的交点坐标，即为【分析】函数，﹣时，01 ）；轴的交点坐标为（，23x1=0x=xxy=02x=1x轴的交点的坐轴的交点的坐标为，与时方程+的两个根为﹣，21标为010 ）．（，），（，x=0y=1y01 ），解：把【解答】轴的交点坐标为（代入函数可得，，故y=0x=1x010 ）．轴的交点的坐标为（，把，代入函数可得或），（，故与23x1yx=0yxy=2x轴的交+与的值；轴的交点坐标即为解答此题要明白函数【点评】时﹣23x1=02xy=0的两个根．+﹣时方程点的坐标为x23113y=②①当，．请写出符合以下三个条件的一个函数的解析式，）；﹣过点（+x0yx22 ③．的增大而减小；随＞时，函数值小于时，当自变量的值为二次函数的性质；一次函数的性质．【考点】①②③的条件确定函数的解析式．【分析】由题意设出函数的一般解析式，再根据y=kxb ，+【解答】解：设函数的解析式为：31 ），∵函数过点（，3kb=1 …①+∴x0yx 的增大而减小，时，＞∵当随k0 …②，∴＜22 ，又∵当自变量的值为时，函数值小于x=2y=2kb2 …③＜时，函数+当b=2k=2kb=22 ①②③，+＜由知可以令﹣，可得+﹣，此时y=x2 ．﹣∴函数的解析式为：+y=x2 ．﹣+答案为【点评】此题是一道开放性题，主要考查一次函数的基本性质，函数的增减性及用待定系数法来确定函数的解析式．222x3 cbxy=xx14y=．+++的图象如图所示，则此抛物线的解析式为﹣ +．抛物线﹣待定系数法求二次函数解析式．【考点】x=130bc的值此图象告诉：函数的对称轴为【分析】，且过点（，）；用待定系数法求，即可．解：据题意得【解答】解得2x32xy=．+∴此抛物线的解析式为+﹣考查同时还考查了方程组的解法，【点评】本题考查了用待定系数法求函数解析式的方法，了数形结合思想．2c=00a y=axbbxca15①；++）的图象的一部分，给出下列命题：+．如图，是二次函数+（≠202bcbxc=031axb2aa④③②的两根分别为﹣+和﹣+＞；；．其中正确的命题是＞+①③．（只要求填写正确命题的序号）x 轴的交点．【考点】二次函数图象与系数的关系；二次函数图象上点的坐标特征；抛物线与b=2a1c=0=10ab；根据图；根据﹣+﹣【分析】由图象可知过（+，），代入得到，推出a2baX30102bc=a ﹣轴的交点是（﹣，﹣），（+象关于对称轴对称，得出与，﹣）；由﹣0b=3b，根据结论判断即可．﹣＜10abc=0①正确；），代入得：+，∴【解答】解：由图象可知：过（，+=1，﹣﹣b=2a②错误；∴，∴1x=对称，﹣根据图象关于对称轴X3001③正确；，），（），∴，与轴的交点是（﹣b=2a0，＞∵0b，＜∴﹣c=0ab，∵++ c=ba，﹣﹣∴．a2bc=a2bab=3b0 ，﹣﹣∴﹣﹣+＜﹣④错误．∴①③．故答案为：X轴的交点，二次函数图象上点的坐标特征，二次函本题主要考查对二次函数与【点评】数图象与系数的关系等知识点的理解和掌握，能根据图象确定系数的正负是解此题的关键．三、解答题16122016 ?南昌校级月考）解方程．（秋分）（23x2=0 x①+﹣28x7=11 4x②﹣﹣﹣2=0 5x2x③﹣26x1=0 x④．+﹣--直接开平方法．【考点】解一元二次方程因式分解法；解一元二次方程①因式分解法求解可得；【分析】②整理成一般式后，因式分解法求解可得；③因式分解法求解可得；④公式法求解可得．x1x2=0 ①，）（﹣解：【解答】）（﹣x1=0x2=0 ，或﹣﹣∴x=1x=2 ；解得：或22x1=0x ②，原方程整理可得：﹣+2=0 x1，﹣∴（）x=1 ；解得：x52x=0 ③，﹣（）x=052x=0 ，或∴﹣x=x=0；解得或a=1b=6c=1 ④，，∵﹣，=364=400 ，+＞∴△3x==．∴﹣配解一元二次方程常用的方法有直接开平方法，【点评】本题考查了一元二次方程的解法．方法，公式法，因式分解法，要根据方程的特点灵活选用合适的方法．2 hk17y=ax的形式，并写出顶点坐标和对称轴）（+．用配方法将二次函数化成﹣212 y=2x6x①﹣+2 3x3y=0.5x②．﹣﹣+二次函数的三种形式．【考点】①②利用配方法先提出二次项系数，再加上一次项系数的一半的平方来凑成完全【分析】平方式，可把一般式转化为顶点式，从而得出顶点坐标和对称轴．22xy=2x12=26x①，）+）﹣﹣【解答】解：，（﹣+则该抛物线的顶点坐标是﹣，（x=；对称轴是﹣22333=x0.5xy=3x②），对称轴是﹣（，+）﹣，则该抛物线的顶点坐标是（﹣+﹣+ x=3．﹣并要求熟练掌握顶点公式和【点评】此题考查了二次函数表达式的一般式与顶点式的转换，对称轴公式．2 6y=2x184x．．已知二次函数﹣﹣22 xy=ay=2x164xhk的形式；（）用配方法将）﹣﹣化成（+﹣2）在平面直角坐标系中，画出这个二次函数的图象；（x3yx的增大而减少？（）当取何值时，随0yy=0x40y，＜，（）当取何值是，＞，4xy05的取值范围；时，求＜）当（＜6）求函数图象与两坐标轴交点所围成的三角形的面积．（．二次函数的三种形式；二次函数的图象；二次函数的性质．【考点】1）直接利用配方法得出函数顶点式即可；【分析】（2）利用顶点式得出顶点坐标，进而得出函数与坐标轴交点进而画出函数图象；（3）利用函数顶点式得出对称轴进而得出答案；（4）利用函数图象得出答案即可；（x=1x=45是求出函数值进而得出答案；）利用（以及6）利用函数图象得出三角形面积即可．（26 1y=2x4x﹣）【解答】解：（﹣26 x2x=2）﹣﹣（2 18=2x；）﹣（﹣2 80=2x1y=02，（﹣，则﹣）（）当=31x=x，解得：，﹣21 03x10），故图象与轴交点坐标为：（﹣，，），（y=x=06，﹣当，0y6），，﹣故图象与轴交点坐标为：（如图所示：；x1y3x的增大而减少；时，＜（）当随3x=1y=04，或﹣）当（时，y0x1x3，＜﹣＞或当时，＞y01x3；＜时；当﹣＜＜450x时，）当＜（＜y=10y=8x=4x=1，﹣时，时，，108yy；≤的取值范围是：﹣＜故6）如图所示：（6=124．××函数图象与两坐标轴交点所围成的三角形的面积为：此题主要考查了配方法求函数顶点坐标以及利用图象判断函数值以及三角形面积求【点评】法，正确画出函数图象是解题关键．2 Ayy=axcbxxBC19点．+轴交于+的图象与．二次函数两点，与轴交于、a1bc的符号，并说明理由；）根据图象确定、（、ACB=6002 A3ABC=45°°，求这个二次函数的解析式．，∠），∠，﹣的坐标为（）如果点（．二次函数综合题；解三元一次方程组；待定系数法求二次函数解析式．【考点】aa1的符号，结合起来可确【分析】（的符号，由对称轴的符号，）根据开口方向可确定ycb的符号；轴的交点可确定的符号，看抛物线与定COACB2OA=3OAB的坐标，设抛物线解析式的交点式，（可得）已知、，解直角△、△BCA代入即可求解析式．、把、1）∵抛物线开口向上【解答】解：（0a＞∴y轴的左侧又∵对称轴在0，＜∴0b＞∴y轴的负半轴又∵抛物线交0 c＜∴AC2AB，）连接（ABO=45RtAOB°中，∠∵在△OAB=45°，∴∠OB=OA ∴30B）（﹣∴，RtACOACO=60°中，∠又∵在△OC=OAcot=60=°∴C0），∴（2 cbxy=ax0a）≠（++设二次函数的解析式为由题意：21xy=x3．）﹣+∴所求二次函数的解析式为（﹣需要本题考查了点的坐标求法，正确设抛物线解析式，求二次函数解析式的方法，【点评】学生熟练掌握．22 xm310Ay20Cy=xm22．+的顶点轴的距离为﹣（﹣．已知抛物线+：到）1 m1A的值；）求顶点的坐标及（B=6BCSC2xD的坐在抛物线两点．点）若抛物线与，求点轴交于、（上，且BCD1△标．x轴的交点．抛物线与【考点】31Ay3A3，根据公式轴的距离为的横坐标为【分析】（，说明顶点）根据顶点到或﹣Am；也可以直接配﹣代入列式，求出的值，分别代入解析式中，求出对应的顶点坐标方求得；m=12xm=5时，轴的交点坐标，发现当时不符合题意，因此根据﹣（）先计算抛物线与CDB的坐标．对应的抛物线计算的长，求出点=313 ，）由题意得：﹣或﹣【解答】解：（2=3mm2=3，++或∴﹣5m=1，∴或﹣22 3y=xCm=19=6xx18，（﹣﹣当时，抛物线：）﹣﹣1 318A）；的坐标为（∴顶点，﹣22 x15=y=x6xC5m=36，）++（+：﹣当时，抛物线+1 A63）；，的坐标为（﹣∴顶点．2Bab ），）设（，（2218 xy=x36x9=C时，﹣﹣﹣：﹣）（当抛物线1218=03x y=0，﹣）当﹣时，（3=33x=3x，+﹣，213=63CD=33 ﹣∴，++=6S ∵，BCD△=6bCD ?||，∴=6b6 ?|，∴×| b=2，∴±2 b=26x9=2x，﹣当时，﹣2x=3，±解得：2 6x9=b=2x2，﹣﹣当﹣﹣时，x=71，解得：或﹣21222B32327），）或（﹣﹣∴，（+，﹣，）或（）或（，﹣22 C6x15=xy=x36时，当抛物线）：++++（12 6=0y=0x3，当）时，（++ x轴无交点，不符合题意，此方程无实数解，所以此时抛物线与2712232B322）．）或（﹣）或（，）或（，﹣﹣，∴（+，﹣x对于利用三【点评】本题是二次函数性质的应用，考查了抛物线与轴的交点及顶点坐标，设出该点的坐标，根据面积列方程，求出未知数的角形面积求点的坐标问题，解题思路为：值，再代入解析式中求另一坐标即可；同时要注意数形结合的思想的应用．21”“来临前夕，购进一种品牌粽子，每盒进价端午节．为满足市场需求，某超市在五月初五454045元．根据以往销售经验发现；当售价定为每盒是元．超市规定每盒售价不得少于170020盒．元时，每天可以卖出盒，每盒售价每提高元，每天要少卖出1yx（元）之间的函数关系式；（盒）与每盒售价（）试求出每天的销售量2P（元）最大？最大利润是多少？（）当每盒售价定为多少元时，每天销售的利润583如果超市想要（）为稳定物价，有关管理部门限定：这种粽子的每盒售价不得高于元．6000元的利润，那么超市每天至少销售粽子多少盒？每天获得不低于二次函数的应用．【考点】1457001“元，）根据元时，每天可以卖出当售价定为每盒【分析】（盒，每盒售价每提高20yx”（元）之间的函数关系式；每天要少卖出盒（盒）与每盒售价即可得出每天的销售量2=1盒粽子所获得的利润×销售量列式整理，根据利润（再根据二次函数的最值问题解答；）32Px58元，中所求得的的函数关系式，（与）先由（根据这种粽子的每盒售价不得高于）6000x1）（元，求出中所求得的销售量的取值范围，再根据且每天销售粽子的利润不低于yx （元）之间的函数关系式即可求解．（盒）与每盒售价1y=70020x45=20x1600 ；（﹣﹣+【解答】解：（）由题意得，）﹣228000 20x1600=20x602400x64000=2P=x4020x，）（﹣）++（﹣）﹣（+﹣）（﹣﹣x45a=200 ，，≥＜∵﹣x=60P=8000 元，∴当时，最大值60P8000 元；即当每盒售价定为（元）最大，最大利润是元时，每天销售的利润28000=600060 320x，）（）由题意，得﹣﹣（+x=50x=70 ．解得，212800060 P=20x的开口向下，﹣）∵抛物线（+﹣50x706000 元的利润．∴当≤≤时，每天销售粽子的利润不低于x58 ，又∵≤50x58 ．∴≤≤y=20x1600k=200 ，﹣∵在中，﹣+＜yx 的增大而减小，∴随x=58y=20581600=440 ，+﹣时，×∴当最小值440 盒．即超市每天至少销售粽子=1盒粽【点评】本题考查的是二次函数与一次函数在实际生活中的应用，主要利用了利润子所获得的利润×销售量，求函数的最值时，注意自变量的取值范围．260xx20yy=ax22x 增大而减小，求：时，．已知函数随+，在＞1a 的取值范围；）（．2ymxs）之间的函数关系，已知函（（（）若该函数为飞机着陆后滑行距离）与滑行时间x=20，请写出自变量滑行时间的取值范围，并求出飞机着陆后需滑行多数的对称轴为直线少米才能停下来？二次函数的应用．【考点】a201x=的不等（【分析】，得出关于）根据二次函数性质可知该抛物线的对称轴≤﹣式，解之即可；a2，即可得二次函数解析式，将其配方成顶点式，根据函数取得最大（）根据对称轴求出值时即飞机滑行停止滑行，据此解答即可．2 xx201y=axy60x增大而减小，＞解：（）∵函数，在随+时，【解答】020a，且﹣＜≤∴a；≤﹣解得：a= =202，﹣）根据题意得：﹣（，解得22 20xxy=60060x=，∴﹣）﹣++﹣（20600x0x米才能停下来．则自变量，且飞机着陆后需滑行的范围为≤≤熟练掌握二次函数的性质及顶点在具体问题中的实【点评】本题主要考查二次函数的应用，际意义是解题的关键．20A1123142016y=axbx4a?）、（﹣，抛物线经过，．（+分）（秋﹣南昌校级月考）如图xC04B．（）两点，与，轴交于另一点1）求抛物线的解析式；（PCB22P坐标；（为第一象限抛物线上一点，满足到线段）如图，点距离最大，求点MFE33EFBC为线段，（相交于点）如图，若抛物线的对称轴（为抛物线顶点）与线段NFENEFMNMBCM为顶点的四边形，，，以∥上的任意一点，过点作交抛物线于点，N的坐标；若不能，请说明理由．能否为平行四边形？若能，求点．二次函数综合题．【考点】2ba04A101y=axCbx4a和（﹣，，【分析】（经过）根据抛物线（）、+﹣）两点，列出BCbB a的解析式；的值，进而求出点和的二元一次方程组，求出的坐标，即可求出直线24xx3x4QPPQyBCQPxx2）；∥+轴，交直线+于，﹣）过点作，设），则（+，﹣（（xS=PQOBPQS?的二次函数，利用函数的性质求出面积的长，利用列出关于求出PCB△P的坐标；的最大值，进而求出点24MxNxxx3x43EF），利用平行四边形对（（，﹣+）首先求出），则的长，设+，﹣+（xx的值即可．边平行且相等列出的一元二次方程，解方程求出1，【解答】解：（）由题意得．解得2 3xy=x4．﹣∴抛物线的解析式：++4y=xBC2B40C04；﹣（：）由，（，）可知，直线）、+（24xxx43xQxPPQ 1PyBCQ）；，﹣，﹣（+轴，交直线于+，设（如图，过点+作∥），则22 4x4=xPQ=x3x4x；﹣）+）﹣（﹣+∴（﹣++22 224=x8x=SPQOB=4x?；﹣（+﹣×（﹣）+）×PCB△PCB6P2的面积最大；）时，△，∴当（3）存在．（2 xy=E3x4），，（的顶点坐标++﹣抛物线4x=FBCy=x），；当（+直线时，：，﹣EF=．∴24xx3x4MxMN 2MEFBCMNx）；（++，设如图（，过点+作∥，﹣，交直线），则于，﹣22 4x4=xMN=x3x4x；）|+）﹣（﹣∴||（﹣++﹣+| EFNMEFMN是平行四边形，当平行且相等时，四边形与2 4xx=；|+∴|﹣2 ==xxx4x=（不合题意，舍去）．由﹣，+时，解得2124=y=3 x=+），当+时，×﹣（N）．∴（，12 4x=x=x，﹣+时，解得当﹣y=x= 时，当，N，），∴（2y= x=时，当，N，（∴），3N）或）点综上所述，或），，（坐标为（，（．二次函数此题涉及到待定系数法求函数解析式，【点评】本题主要考查了二次函数综合题，PQ2x 表示出的性质、三角形面积的计算、平行四边形的判定等知识，解答（）问关键是用EF3的长，利用平行四边形对边平行且相等进行解答，此题的长，解答（）问关键是求出有一定的难度．。

江西省南昌市 2016-2017 学年九年级 （上）第一次月考数学试卷(分析版 )一、选择题： （本大题共 8 个小题，每题 3 分，共 24 分）每题只有一个答案是正确的，请将正确答案的代号填入以下对应题号内．1．已知二次函数y=mx 2+x ﹣ 1 的图象与x 轴有两个交点，则m 的取值范围是（）A ． m ＞﹣B ．m ≥﹣C ． m ＞﹣且 m ≠ 0D ．m ≥﹣且 m ≠ 02．已知抛物线 y=ax 2+bx+c 与 x 轴交点为 A （﹣ 2， 0）， B （ 6，0），则该二次函数的对称轴为（）A ． x=﹣ 1B ．x=1C ． x=2D ．y轴3．已知二次函数 y=ax 2+bx +c （ a ≠ 0）的图象如下图，给出以下结论：① 由于a ＞ 0，所以函数y 有最大值；② 该函数的图象对于直线x= ﹣1 对称；③ 当 x= ﹣ 2 时，函数 y 的值等于 0；④ 当 x= ﹣ 3 或 x=1 时，函数 y 的值都等于 0．此中正确结论的个数是（ ）A ． 4B ． 3C ． 2D ． 14．若二次函数y=x2﹣ 6x +c的图象过A （﹣ 1， y 1），B （3， y 2），C （ 3+， y 3），则 y 1，y 2， y 3 的大小关系是（）A ． y 1＞y 2＞ y 3B ． y 1＞ y 3＞ y 2C ． y 2＞ y 1＞ y 3D ． y 3＞y 1＞ y 25．图（ 1）是一个横断面为抛物线形状的拱桥，当水面在l 时，拱顶（拱桥洞的最高点）离水面2m ，水面宽4m ．如图（2）成立平面直角坐标系，则抛物线的关系式是（）A ． y= 2x 2B ．y=2x2C ． y=x 2D ．y= x 26．二次函数 y= （ x 1） 2+3 的 象的 点坐 是（） A ．（ 1，3） B ．（ 1，3） C ．（ 1， 3） D．（ 1， 3）7．已知函数 y=2x 2的 象是抛物 ， 在同一坐 系中，将 抛物 分 向上、向左平移2 个 位，那么所获取的新抛物 的分析式是（）2 2 B ． y=2 x 2 2 2C ． y=2 （ x 222 D ． y=2 x22 2A． y=2（ x 2） +（ + ） ）（） + +8．抛物 C 1： y=x 2+1 与抛物 C 2 对于 x 称， 抛物 C 2 的分析式 （）A ． y= x2B ．y= x2+1 C ． y=x 2 1 D ．y= x 21二、填空 （本大 共7 个小 ，每小3 分，共 21 分）9．若把函数y=x 2 2x 3 化y=（ xm ） 2+k的形式，此中m ， k常数，m+k=．10．已知二次函数y=x 2+4x+m 的部分 象如 ， 对于x 的一元二次方程x 2 +4x+m=0的解是．2bx cx， 坐y的 如表：11．抛物 y=ax + + 上部分点的横坐x⋯211 2 ⋯ y ⋯ 0 4 6 64⋯从表可知，以下 法中正确的选项是 ．（填写序号）① 抛物 与 x 的一个交点 （3， 0）；②函数 y=ax 2+bx+c 的最大 6；③ 抛物线的对称轴是直线 x= ；④ 在对称轴左边， y 随 x 增大而增大．12．函数 y=2x 2﹣ 3x+1 与 y 轴的交点坐标为，与 x 轴的交点的坐标为 ，．13．请写出切合以下三个条件的一个函数的分析式，① 过点（ 3， 1）； ② 当 x ＞0 时，y 随 x 的增大而减小； ③ 当自变量的值为 2 时，函数值小于 2．2bx c的图象如下图，则此抛物线的分析式为．14．抛物线 y= ﹣ x + +15．如图，是二次函数y=ax 2+bx+c （ a ≠ 0）的图象的一部分，给出以下命题：① a+b+c=0；2bx c=0 的两根分别为﹣ 3 1 ④ a 2b c 0．（只② b ＞ 2a ；③ ax + + 和 ； ﹣ + ＞ ．此中正确的命题是 要求填写正确命题的序号）三、解答题16．（ 12 分）解方程2① x ﹣ 3x+2=0②4x 2﹣ 8x ﹣ 7=﹣ 11③ 5x ﹣ 2x 2=0④ x 2+6x ﹣ 1=0．17．（ 8 分）用配方法将二次函数化成y=a （ x ﹣ h ） 2+k 的形式，并写出极点坐标和对称轴① y=2x 2+6x ﹣ 12② y=﹣ 0.5x 2﹣3x+3．18．（ 8 分）已知二次函数y=2x 2﹣ 4x﹣ 6．1）用配方法将y=2x24x﹣6化成y=a x h2k的形式；（﹣（﹣）+（2）在平面直角坐标系中，画出这个二次函数的图象；（3）当 x 取何值时， y 随 x 的增大而减少？（4）当 x 取何值是， y=0 ， y＞ 0， y＜0，（5）当 0＜ x＜ 4 时，求 y 的取值范围；（6）求函数图象与两坐标轴交点所围成的三角形的面积．19．（ 8 分）二次函数y=ax 2+bx+c 的图象与 x 轴交于 B 、C 两点，与y 轴交于 A 点．（1）依据图象确立 a、 b、 c 的符号，并说明原因；（2）假如点 A 的坐标为（ 0，﹣ 3），∠ ABC=45 °，∠ ACB=60 °，求这个二次函数的分析式．20．（ 8 分）已知抛物线 C1：y=x22m 2x m210的极点A到y3﹣（+ ） +﹣轴的距离为．（1）求极点 A 的坐标及 m 的值；（2）若抛物线与 x 轴交于 C、D 两点．点 B 在抛物线 C1上，且 S△BCD =6，求点 B 的坐标．21．（ 9 分）为知足市场需求，某商场在五月初五“端午节”到临前夜，购进一种品牌粽子，每盒进价是 40 元．商场规定每盒售价不得少于45 元．依据过去销售经验发现；当售价定为每盒 45 元时，每日能够卖出 700 盒，每盒售价每提升 1 元，每日要少卖出20 盒．（1）试求出每日的销售量y（盒）与每盒售价x（元）之间的函数关系式；（2）当每盒售价定为多少元时，每日销售的收益P（元）最大？最大收益是多少？（3）为稳固物价，相关管理部门限制：这类粽子的每盒售价不得高于58 元．假如商场想要每日获取不低于 6000 元的收益，那么商场每日起码销售粽子多少盒？260x，在x＞20时，y随x增大而减小，求：22．（ 8 分）已知函数 y=ax+（1） a 的取值范围；（2）若该函数为飞机着陆后滑行距离 y（ m）与滑行时间 x（ s）之间的函数关系，已知函数的对称轴为直线 x=20，请写出自变量滑行时间的取值范围，并求出飞机着陆后需滑行多少米才能停下来？23．（ 14 分）如图1，抛物线 y=ax 2+bx﹣ 4a 经过 A （﹣ 1，0）、 C（ 0，4）两点，与 x 轴交于另一点 B ．（1）求抛物线的分析式；（2）如图2，点P 为第一象限抛物线上一点，知足到线段CB距离最大，求点P 坐标；（3）如图3，若抛物线的对称轴EF（ E 为抛物线极点）与线段BC订交于点F， M为线段BC上的随意一点，过点M 作MN ∥ EF 交抛物线于点N，以E， F，M，N为极点的四边形可否为平行四边形？若能，求点N 的坐标；若不可以，请说明原因．2016-2017 学年江西省南昌市九年级（上）第一次月考数学试卷参照答案与试题分析一、选择题： （本大题共 8 个小题，每题3 分，共 24 分）每题只有一个答案是正确的，请将正确答案的代号填入以下对应题号内．1．已知二次函数 y=mx 2+x ﹣ 1 的图象与 x 轴有两个交点，则m 的取值范围是（）A ． m ＞﹣B ．m ≥﹣C ． m ＞﹣ 且 m ≠ 0D ．m ≥﹣ 且 m ≠ 0【考点】 抛物线与 x 轴的交点．【剖析】 依据二次函数 y=mx 2 x ﹣ 1 的图象与 x轴有两个交点，可得△ =124m 1+ ﹣ ×（﹣ ）＞0 且 m ≠ 0．【解答】 解：∵原函数是二次函数，∴m ≠ 0．∵二次函数 y=mx 2+x ﹣ 1 的图象与 x 轴有两个交点，则△ =b 2﹣ 4ac ＞ 0，△ =1 2﹣ 4m ×（﹣ 1）＞ 0，∴m ＞﹣．综上所述， m 的取值范围是： m ＞﹣ 且 m ≠ 0，应选 C ．【评论】 本题考察了抛物线与 x 轴的交点，重点是熟记当△=b 2﹣ 4ac ＞ 0 时图象与 x 轴有两个交点；当△ =b 2﹣ 4ac=0 时图象与 x 轴有一个交点；当△=b 2﹣ 4ac ＜0 时图象与 x 轴没有交点．2 bx c 与 x 轴交点为 A 2 0 B 6 0），则该二次函数的对称 2．已知抛物线 y=ax + +（﹣，）， （ ， 轴为（ ）A ． x=﹣ 1B ．x=1C ． x=2D ．y 轴【考点】 抛物线与 x 轴的交点．【剖析】依据抛物线的对称性获取点 A 和点 B 是抛物线上的对称点，所以点A和点 B的对称轴即为抛物线的对称轴．【解答】解：∵抛物线y=ax2bx c与x轴交点为A 2 0B 6 0+ +（﹣，），（，），∴该二次函数的对称轴为直线x=2．应选 C．【评论】本题考察了抛物线与 x 轴的交点：从二次函数的交点式 y=a（ x﹣ x1）（ x﹣ x2）（ a，b，c 是常数， a≠ 0）中可直接获取抛物线与 x 轴的交点坐标（ x1，0），（ x2，0）．解决本题的重点是掌握抛物线的对称性．3．已知二次函数y=ax2+bx +c（ a≠ 0）的图象如下图，给出以下结论：① 由于a＞ 0，所以函数y 有最大值；② 该函数的图象对于直线x= ﹣1 对称；③当 x= ﹣ 2 时，函数y 的值等于0；④当 x= ﹣ 3 或x=1时，函数y 的值都等于0．此中正确结论的个数是（）A．4B．3C．2D．1【考点】二次函数的性质．【剖析】察看图象即可判断．① 张口向上，应有最小值；② 依据抛物线与x 轴的交点坐标来确立抛物线的对称轴方程；③ x= ﹣ 2 时，对应的图象上的点在x 轴下方，所以函数值小于 0；④图象与 x 轴交于﹣ 3 和 1，所以当 x= ﹣ 3 或 x=1 时，函数 y 的值都等于 0．【解答】解：由图象知：② 该函数的图象对于直线x= ﹣1 对称；正确．③当 x= ﹣ 2 时，函数y 的值小于0；错误．④当 x= ﹣ 3 或x=1时，函数y 的值都等于0．正确．故正确的有两个，选C ．【评论】 本题考察了依据函数图象解答问题，表现了数形联合的数学思想方法．4．若二次函数26x c A 1 y 1）， B 3 y C 3 + y 3），则 y1，y=x ﹣ + 的图象过 （﹣ ， （ ， 2）， （ ， y 2， y 3 的大小关系是（ ）A ． y 1＞y 2＞ y 3B ． y 1＞ y 3＞ y 2C ． y 2＞ y 1＞ y 3D ． y 3＞y 1＞ y 2【考点】 二次函数图象上点的坐标特色．【剖析】 依据二次函数的性质联合二次函数的分析式即可得出 y 1＞ y 3＞ y 2，本题得解．【解答】 解：二次函数 y=x 2﹣6x +c 的对称轴为 x=3， ∵a=1＞ 0，∴当 x=3 时， y 值最小，即 y 2 最小．∵| ﹣1﹣3| =4，| 3+ ﹣3| = ，4＞，∴点 y 1＞ y 3．∴y 1＞ y 3＞ y 2． 应选 B ．【评论】 本题考察了二次函数的性质，依据二次函数的性质确立 A 、 B 、 C 三点纵坐标的大小是解题的重点．5．图（ 1）是一个横断面为抛物线形状的拱桥，当水面在l 时，拱顶（拱桥洞的最高点）离水面2m ，水面宽4m ．如图（2）成立平面直角坐标系，则抛物线的关系式是（）A ． y=﹣ 2x 2B ．y=2x 2C ． y= ﹣ x 2D ．y=x2【考点】 依据实质问题列二次函数关系式．【剖析】 由图中能够看出， 所求抛物线的极点在原点，对称轴为 y 轴，可设此函数分析式为：y=ax 2，利用待定系数法求解．【解答】 解：设此函数分析式为：y=ax 2，a ≠ 0；那么（ 2，﹣ 2）应在此函数分析式上．则﹣ 2=4a即得 a=﹣，那么 y= ﹣ x 2．应选： C ．【评论】 依据题意获取函数分析式的表示方法是解决本题的重点，重点在于找到在此函数解析式上的点．6．二次函数y= ﹣（ x ﹣ 1） 2+3的图象的极点坐标是（）A ．（﹣1， 3）B ．（ 1，3）C ．（﹣1，﹣ 3） D ．（ 1，﹣ 3）【考点】 二次函数的性质．【剖析】 依据二次函数的极点式一般形式的特色，可直接写出极点坐标．【解答】 解：二次函数 y= ﹣（ x ﹣ 1） 2+3 为极点式，其极点坐标为（1， 3）．应选 B ．【评论】 主要考察了求抛物线的极点坐标的方法．7．已知函数 y=2x 2的图象是抛物线，此刻同一坐标系中，将该抛物线分别向上、向左平移2 个单位，那么所获取的新抛物线的分析式是（）2 2 B ． y=2 x 2 2 ﹣ 2 C ． y=2 x2 22 D ． y=2x2 ） 2 2A． y=2x 2） +（ + ） （﹣ ） ﹣（﹣+ （ +【考点】 二次函数图象与几何变换．【剖析】 直接利用平移规律（左加右减，上加下减）求新抛物线的分析式．【解答】 解：抛物线 y=2x 2向上、向左平移2 个单位后的分析式为：y=2（ x+2） 2+2．应选： A ．【评论】 主要考察的是函数图象的平移，用平移规律“左加右减，上加下减 ”直接代入函数解析式求得平移后的函数分析式．8．抛物线 C 1： y=x 2+1 与抛物线 C 2 对于 x 轴对称，则抛物线 C 2 的分析式为（）A ． y=﹣ x 2B ．y= ﹣ x2+1 C ． y=x 2﹣1 D ．y= ﹣ x 2﹣ 1 【考点】 二次函数图象与几何变换．【剖析】画出图形后可依据张口方向决定二次项系数的符号，张口度是二次项系数的绝对值；与 y 轴的交点为抛物线的常数项进行解答．【解答】 解：对于 x 轴对称的两个函数分析式的张口方向改变，张口度不变，二次项的系数互为相反数；对与y 轴的交点互为相反数，那么常数项互为相反数，应选 D ．【评论】 依据绘图可获取抛物线对于x 轴对称的特色：二次项系数，一次项系数，常数项均互为相反数．二、填空题（本大题共7 个小题，每题 3 分，共 21 分）9．若把函数y=x 2﹣ 2x ﹣ 3 化为 y=（ x ﹣ m ）2+k 的形式， 此中 m ，k 为常数，则 m+k=﹣3 ．【考点】 二次函数的三种形式．【剖析】 利用配方法操作整理，而后依据对应系数相等求出m 、 k ，再相加即可．【解答】 解： y=x 2﹣ 2x ﹣ 3，=（x 2﹣ 2x+1）﹣ 1﹣ 3，=（x ﹣ 1） 2﹣ 4，所以， m=1， k=﹣ 4，所以， m+k=1 +（﹣ 4） =﹣3．故答案为：﹣ 3．【评论】 本题考察了二次函数的三种形式，娴熟掌握配方法的操作是解题的重点．10．已知二次函数 y=﹣ x 2+4x+m 的部分图象如图，则对于x 的一元二次方程﹣ x 2+4x+m=0的解是x 1=﹣ 1， x 2=5 ．【考点】 抛物线与 x 轴的交点．【剖析】 由二次函数 y= x 2+4x+m 的部分 象能够获取抛物 的 称 和抛物 与x 的一个交点坐 ， 而后能够求出另一个交点坐 ，再利用抛物 与 x 交点的横坐 与相 的一元二次方程的根的关系即可获取对于x的一元二次方程 x 24x m=0 的解．+ + 【解答】解：依据 告知， 二次函数 y=x 24x + m的 称 x=2 ，与 x 5+ 的一个交点 （ ，0），依据抛物 的 称性知，抛物 与x 的另一个交点横坐 与点（ 5，0）对于 称 称，即 x= 1，另一交点坐 （ 1， 0）当 x= 1 或 x=5 ，函数 y=0，即 x 2+4x+m=0，故对于 x 的一元二次方程x 2+4x+m=0 的解 x 1=1，x 2=5．故答案是： x 1= 1， x 2=5．【点 】 本 考 了抛物 与x 的交点．解答此 需要拥有必定的 的能力．11．抛物 y=ax 2+bx+c 上部分点的横坐 x ， 坐 y 的 如表： x ⋯ 2 1 0 1 2 ⋯ y⋯4664⋯从表可知，以下 法中正确的选项是 ．（填写序号）① 抛物 与 x 的一个交点 （ 3， 0）； ② 函数 y=ax 2+bx+c 的最大 6；③ 抛物 的 称 是直x= ；④ 在 称 左 ，y 随 x 增大而增大．【考点】 抛物 与 x 的交点；二次函数的性 ；二次函数的最 ．【剖析】依据表中数据和抛物线的对称性，可获取抛物线的张口向下，当x=3 时， y=0，即抛物线与x 轴的交点为（﹣ 2，0）和（ 3，0）；所以可得抛物线的对称轴是直线x=3 ﹣=，再依据抛物线的性质即可进行判断．【解答】解：依据图表，当x= ﹣ 2，y=0 ，依据抛物线的对称性，当x=3 时， y=0 ，即抛物线与 x 轴的交点为（﹣2， 0）和（ 3， 0）；∴抛物线的对称轴是直线x=3﹣=，依据表中数据获取抛物线的张口向下，∴当 x=时，函数有最大值，而不是x=0 ，或 1 对应的函数值6，而且在直线x=的左边，y随x增大而增大．所以①③④正确，② 错．故答案为：①③④．【评论】本题考察了抛物线 y=ax 2+bx+c 的性质：抛物线是轴对称图形，它与 x 轴的两个交点是对称点，对称轴与抛物线的交点为抛物线的极点； a＜ 0 时，函数有最大值，在对称轴左边， y 随 x增大而增大．12．函数 y=2x 2﹣ 3x+1 与 y 轴的交点坐标为（0，1），与x轴的交点的坐标为（，0），（ 1，0）．【考点】抛物线与x 轴的交点．【剖析】函数y=2x 2﹣3x+1与y 轴的交点坐标，即为x=0时， y 的值．当x=0，y=1．故与y 轴的交点坐标为（0， 1）；x 轴的交点的坐标为y=0 时方程 2x 2﹣ 3x+1=0 的两个根为x1=，x2=1，与x轴的交点的坐标为（， 0），（ 1，0）．【解答】解：把x=0代入函数可得y=1，故y 轴的交点坐标为（0，1），把y=0代入函数可得x=或 1，故与x 轴的交点的坐标为（， 0），（ 1， 0）．【评论】解答本题要理解函数y=2x2﹣3x+1与 y轴的交点坐标即为x=0时 y的值； x轴的交点的坐标为y=0时方程2x2﹣3x+1=0的两个根．13． 写出切合以下三个条件的一个函数的分析式y=x+2，① 点（ 3，1）；② 当x ＞ 0 ， y 随x 的增大而减小； ③ 当自 量的2 ，函数 小于2．【考点】 二次函数的性 ；一次函数的性 ． 【剖析】 由 意 出函数的一般分析式，再依据 ①②③的条件确立函数的分析式．【解答】 解： 函数的分析式 ：y=kx +b ，∵函数 点（ 3， 1），∴ 3k +b=1 ⋯①∵当 x ＞ 0 ， y 随 x 的增大而减小，∴k ＜ 0⋯② ，又∵当自 量的2 ，函数 小于 2，当 x=2 ，函数 y=2k +b ＜ 2⋯③由①②③知能够令 b=2 ，可得 k=，此 2k+b= +2＜2，∴函数的分析式 ：y=x+2．答案 y=x+2．【点 】 此 是一道开放性 ， 主要考 一次函数的基天性 ， 函数的增减性及用待定系数法来确立函数的分析式．14．抛物y=x 2+bx+c 的 象如 所示， 此抛物 的分析式 y= x 2+2x+3 ．【考点】 待定系数法求二次函数分析式．【剖析】 此 象告 ：函数的 称 x=1，且 点（ 3，0）；用待定系数法求b ，c 的即可．【解答】 解：据题意得解得∴此抛物线的分析式为 y= ﹣ x 2 2x 3+ + ．【评论】 本题考察了用待定系数法求函数分析式的方法， 同时还考察了方程组的解法，考察了数形联合思想．15．如图，是二次函数y=ax 2+bx+c （ a ≠ 0）的图象的一部分，给出以下命题：① a+b+c=0；② b ＞ 2a ； ③ ax 2+bx +c=0 的两根分别为﹣ 3 和 1；④ a ﹣ 2b+c ＞0．此中正确的命题是①③．（只需求填写正确命题的序号）【考点】二次函数图象与系数的关系； 二次函数图象上点的坐标特色； 抛物线与 x 轴的交点．【剖析】 由图象可知过（ 1 0a b c=0；依据﹣= 1 ，推出 b=2a；依据图， ），代入获取+ +﹣ 象对于对称轴对称，得出与X 轴的交点是（﹣ 3， 0），（ 1， 0）；由 a ﹣ 2b+c=a ﹣ 2b ﹣a ﹣b=﹣ 3b ＜ 0，依据结论判断即可．【解答】 解：由图象可知：过（ 1， 0），代入得： a+b+c=0，∴ ① 正确；﹣=﹣1，∴ b =2a ，∴ ② 错误；依据图象对于对称轴 x= ﹣ 1 对称，与 X 轴的交点是（﹣ 3， 0），（ 1，0），∴ ③ 正确；∵b=2a ＞ 0，∴﹣ b ＜ 0，∵ a +b+c=0，∴c= ﹣ a ﹣ b ，∴ a ﹣ 2b+c=a ﹣2b ﹣ a ﹣ b=﹣ 3b ＜ 0， ∴④ 错误．故答案为： ①③ ．【评论】 本题主要考察对二次函数与 X 轴的交点，二次函数图象上点的坐标特色，二次函数图象与系数的关系等知识点的理解和掌握，能依据图象确立系数的正负是解本题的重点．三、解答题16．（ 12 分）（ 2016 秋 ?南昌校级月考）解方程① x 2﹣ 3x+2=0② 4x 2﹣ 8x ﹣ 7=﹣ 112③ 5x ﹣ 2x =0④ x 2+6x ﹣ 1=0．【考点】 解一元二次方程 -因式分解法；解一元二次方程-直接开平方法．【剖析】 ① 因式分解法求解可得；② 整理成一般式后，因式分解法求解可得；③ 因式分解法求解可得；④ 公式法求解可得．【解答】 解： ① （ x ﹣ 1）（ x ﹣ 2） =0，∴ x ﹣ 1=0 或 x ﹣ 2=0 ，解得： x=1 或 x=2 ；② 原方程整理可得： x 2﹣ 2x+1=0 ，∴（ x ﹣ 1）2=0 ，解得： x=1 ；③ x （ 5﹣ 2x ） =0， ∴x=0 或 5﹣2x=0 ，解得 x=0 或 x= ；④ ∵a=1， b=6 ，c=﹣ 1，∴△ =36+4=40＞ 0，∴x==﹣ 3．【评论】本题考察了一元二次方程的解法．解一元二次方程常用的方法有直接开平方法，方法，公式法，因式分解法，要依据方程的特色灵巧采用适合的方法．配17．用配方法将二次函数化成y=a（ x﹣ h）2+k 的形式，并写出极点坐标和对称轴①y=2x 2+6x﹣ 12②y=﹣ 0.5x 2﹣3x+3．【考点】二次函数的三种形式．【剖析】①② 利用配方法先提出二次项系数，再加前一次项系数的一半的平方来凑成完整平方式，可把一般式转变为极点式，从而得出极点坐标和对称轴．【解答】解：①y=2x26x﹣12=2 x+2，则该抛物线的极点坐标是（﹣，﹣），+（）﹣对称轴是x=﹣；② y=﹣ 0.5x 2﹣3x+3=﹣（x+3）2+，则该抛物线的极点坐标是（﹣3，），对称轴是x=﹣ 3．【评论】本题考察了二次函数表达式的一般式与极点式的变换，并要求娴熟掌握极点公式和对称轴公式．18．已知二次函数y=2x 2﹣ 4x﹣6．（1）用配方法将 y=2x 2﹣ 4x﹣6 化成 y=a（ x﹣ h）2+k 的形式；（2）在平面直角坐标系中，画出这个二次函数的图象；（3）当 x 取何值时， y 随 x 的增大而减少？（4）当 x 取何值是， y=0 ， y＞ 0， y＜0，（5）当 0＜ x＜ 4 时，求 y 的取值范围；（6）求函数图象与两坐标轴交点所围成的三角形的面积．【考点】 二次函数的三种形式；二次函数的图象；二次函数的性质．【剖析】 （1）直接利用配方法得出函数极点式即可；（ 2）利用极点式得出极点坐标，从而得出函数与坐标轴交点从而画出函数图象；（ 3）利用函数极点式得出对称轴从而得出答案；（ 4）利用函数图象得出答案即可；（ 5）利用 x=1 以及 x=4 是求出函数值从而得出答案；（ 6）利用函数图象得出三角形面积即可．【解答】 解：（ 1） y=2x 2﹣ 4x ﹣6=2（ x 2﹣ 2x ）﹣ 6=2（ x ﹣ 1）2﹣ 8；（ 2）当 y=0，则 0=2（ x ﹣ 1） 2﹣8，解得： x 1=﹣ 1， x 2=3 ，故图象与 x 轴交点坐标为：（﹣ 1， 0），（ 3， 0），当 x=0 ， y=﹣ 6，故图象与 y 轴交点坐标为：（ 0，﹣ 6），如下图：；（3）当 x＜ 1 时， y 随 x 的增大而减少；（4）当 x=1 或﹣ 3 时， y=0 ，当 x＜﹣ 1 或 x＞ 3 时， y＞ 0，当﹣ 1＜ x＜3 时； y＜ 0；（5）当 0＜ x＜ 4 时，x=1 时， y=﹣ 8， x=4 时， y=10，故 y 的取值范围是：﹣8≤ y＜ 10；（6）如下图：函数图象与两坐标轴交点所围成的三角形的面积为：×4× 6=12．【评论】本题主要考察了配方法求函数极点坐标以及利用图象判断函数值以及三角形面积求法，正确画出函数图象是解题重点．19．二次函数y=ax 2+bx+c 的图象与x 轴交于 B 、C 两点，与y 轴交于 A 点．（1）依据图象确立 a、 b、 c 的符号，并说明原因；（2）假如点 A 的坐标为（ 0，﹣ 3），∠ ABC=45 °，∠ ACB=60 °，求这个二次函数的分析式．【考点】二次函数综合题；解三元一次方程组；待定系数法求二次函数分析式．【剖析】（1）依据张口方向可确立 a 的符号，由对称轴的符号， a 的符号，联合起来可确定 b 的符号，看抛物线与y 轴的交点可确立 c 的符号；（2）已知 OA=3 ，解直角△ OAB 、△ OAC 可得 B 、C 的坐标，设抛物线分析式的交点式，把A 、B、 C 代入即可求分析式．【解答】解：（ 1）∵抛物线张口向上∴a＞ 0又∵对称轴在y 轴的左边∴＜ 0，∴b＞ 0又∵抛物线交y 轴的负半轴∴c＜ 0（2）连结 AB ， AC∵在 Rt△ AOB 中，∠ ABO=45 °∴∠ OAB=45 °，∴OB=OA∴B （﹣ 3， 0）又∵在 Rt△ACO 中，∠ ACO=60 °∴O C=OAcot=60 °=∴C（，0）设二次函数的分析式为y=ax 2+bx+c（ a≠ 0）由题意：∴所求二次函数的分析式为y=x 2+（﹣ 1）x ﹣ 3．【评论】 本题考察了点的坐标求法，正确设抛物线分析式，求二次函数分析式的方法，需要学生娴熟掌握．20．已知抛物线 C 1： y=x 2﹣ 2（ m+2） x+m 2﹣ 10 的极点 A 到 y 轴的距离为 3． （1）求极点 A 的坐标及 m 的值；（2）若抛物线与 x 轴交于 C 、D 两点．点 B 在抛物线 C 1 上，且 S △ BCD =6 ，求点 B 的坐标．【考点】 抛物线与 x 轴的交点．【剖析】 （1）依据极点A 到y 轴的距离为3，说明极点A 的横坐标为 3 或﹣ 3，依据公式﹣代入列式，求出m 的值，分别代入分析式中，求出对应的极点坐标A ；也能够直接配方求得；（2）先计算抛物线与x 轴的交点坐标，发现当m= ﹣5 时不切合题意，所以依据m=1时，对应的抛物线计算CD的长，求出点B 的坐标．【解答】 解：（ 1）由题意得：﹣=3 或﹣ 3，∴m+2=3 或 m+2=﹣ 3，∴ m =1 或﹣ 5，当 m=1 时，抛物线 C 1： y=x 2﹣ 6x ﹣ 9=（ x ﹣3） 2﹣ 18，∴极点 A 的坐标为（ 3，﹣ 18）；当 m=﹣ 5 时，抛物线 C 1： y=x 2 +6x+15= （ x+3） 2+6，∴极点 A 的坐标为（﹣ 3， 6）；（2）设 B （ a ， b ），当抛物线 C 1： y=x 2﹣ 6x ﹣ 9=（ x ﹣ 3）2﹣ 18 时，当 y=0 时，（ x ﹣ 3）2﹣ 18=0 ，x 1=3 +3， x∴ C D=3 +3∵S △ BCD =62=3﹣3，+3﹣3=6，，∴ CD? b =6，| | ∴× 6?| b| =6 ，∴ b = ± 2，当 b=2 时， x 2﹣ 6x ﹣ 9=2，解得： x=3 ±2，当 b=﹣ 2 时， x 2﹣ 6x ﹣ 9=﹣ 2，解得： x=7 或﹣ 1，∴ B3 2 2 3 2 2 ）或（ 7 2 1 2（ +， ）或（ ﹣ ， ，﹣ ）或（﹣ ，﹣ ），当抛物线 C 1： y=x 2+6x+15= （ x+3） 2+6 时，当 y=0 时，（ x+3） 2+6=0 ，此方程无实数解，所以此时抛物线与x 轴无交点，不切合题意，∴B （ 3+2，2）或（ 3﹣ 2 ， 2）或（ 7，﹣ 2）或（﹣ 1，﹣ 2）．【评论】 本题是二次函数性质的应用，考察了抛物线与 x 轴的交点及极点坐标， 对于利用三角形面积求点的坐标问题，解题思路为：设出该点的坐标，依据面积列方程，求出未知数的值，再代入分析式中求另一坐标即可；同时要注意数形联合的思想的应用．21．为知足市场需求，某商场在五月初五 “端午节 ”到临前夜，购进一种品牌粽子，每盒进价 是 40 元．商场规定每盒售价不得少于45 元．依据过去销售经验发现；当售价定为每盒45元时，每日能够卖出700 盒，每盒售价每提升1 元，每日要少卖出20 盒．（ 1）试求出每日的销售量 y （盒）与每盒售价 x （元）之间的函数关系式；（ 2）当每盒售价定为多少元时，每日销售的收益P （元）最大？最大收益是多少？（3）为稳固物价，相关管理部门限制：这类粽子的每盒售价不得高于58 元．假如商场想要每日获取不低于 6000 元的收益，那么商场每日起码销售粽子多少盒？【考点】 二次函数的应用．【剖析】 （ 1）依据 “当售价定为每盒45 元时，每日能够卖出700 盒，每盒售价每提升1 元，每日要少卖出20 盒”即可得出每日的销售量y （盒）与每盒售价x （元）之间的函数关系式；（2）依据收益=1盒粽子所获取的收益×销售量列式整理，再依据二次函数的最值问题解答；（3）先由（2）中所求得的P 与 x 的函数关系式， 依据这类粽子的每盒售价不得高于58 元，且每日销售粽子的收益不低于6000 元，求出 x 的取值范围，再依据 （ 1）中所求得的销售量y （盒）与每盒售价 x （元）之间的函数关系式即可求解．【解答】 解：（ 1）由题意得， y=700 ﹣20（ x ﹣ 45） =﹣ 20x +1600 ；（ 2） P=（ x ﹣ 40）（﹣ 20x+1600） =﹣ 20x 2+2400x ﹣ 64000= ﹣20（ x ﹣60） 2+8000，∵x ≥ 45， a=﹣ 20＜ 0，∴当 x=60 时， P 最大值 =8000 元，即当每盒售价定为60 元时，每日销售的收益 P （元）最大，最大收益是 8000 元；（ 3）由题意，得﹣ 20（ x ﹣ 60）2+8000=6000 ，解得 x 1=50 ，x 2=70 ．∵抛物线 P=﹣ 20（x ﹣ 60） 2+8000 的张口向下，∴当 50≤ x ≤ 70 时，每日销售粽子的收益不低于6000 元的收益．又∵ x ≤ 58，∴ 50≤ x ≤ 58．∵在 y= ﹣ 20x+1600 中， k= ﹣ 20＜ 0，∴y随x 的增大而减小，∴当x=58时， y 最小值 =﹣20× 58+1600=440 ，即商场每日起码销售粽子440 盒．【评论】 本题考察的是二次函数与一次函数在实质生活中的应用，主要利用了收益=1 盒粽子所获取的收益×销售量，求函数的最值时，注意自变量的取值范围．222．已知函数 y=ax +60x ，在 x ＞20 时， y 随 x 增大而减小，求：（ 2）若该函数为飞机着陆后滑行距离 y （ m ）与滑行时间 x （ s ）之间的函数关系，已知函数的对称轴为直线 x=20，请写出自变量滑行时间的取值范围，并求出飞机着陆后需滑行多少米才能停下来？【考点】 二次函数的应用．【剖析】 （1）依据二次函数性质可知该抛物线的对称轴x=﹣≤ 20，得出对于 a 的不等式，解之即可；（2）依据对称轴求出a ，即可得二次函数分析式，将其配方成极点式，依据函数获得最大值时即飞机滑行停止滑行，据此解答即可．【解答】 解：（ 1）∵函数 y=ax 2+60x ，在 x ＞ 20 时， y 随 x 增大而减小，∴a ＜ 0 且﹣≤20，解得：a ≤﹣；（2）依据题意得：﹣ =20 ，解得 a=﹣ ，∴y= ﹣x 2+60x= ﹣ （x ﹣ 20） 2+600，则自变量 x 的范围为 0≤ x ≤ 20，且飞机着陆后需滑行600 米才能停下来．【评论】 本题主要考察二次函数的应用， 娴熟掌握二次函数的性质及极点在详细问题中的实质意义是解题的重点．2bx﹣ 4a 经过 A1 0 ）、 2314分）（ 2016秋 ?南昌校级月考）如图 1y=ax+（﹣ ，．（，抛物线C （ 0， 4）两点，与 x 轴交于另一点 B ．（1）求抛物线的分析式； （2）如图 2，点P 为第一象限抛物线上一点，知足到线段CB 距离最大，求点P 坐标；（3）如图3，若抛物线的对称轴EF （ E 为抛物线极点）与线段BC订交于点 F ， M 为线段BC上的随意一点，过点M 作MN ∥ EF 交抛物线于点N ，以E ，F ，M ，N 为极点的四边形可否为平行四边形？若能，求点N 的坐标；若不可以，请说明原因．【考点】 二次函数综合题．1 ）依据抛物线 y=ax2bx ﹣4a 经过 A （﹣1 0 C 0 4a 和b 【剖析】 （ + ， ）、 （ ， ）两点，列出的二元一次方程组，求出a 和b 的值，从而求出点 B 的坐标，即可求出直线 BC 的分析式； 2 ）过点 P 作 PQ ∥ y 轴，交直线BC 于 Q ，设 P x，﹣x23x 4 Q x ，﹣ x 4 ）；（ （+ +），则 （ + 求出 PQ 的长，利用 S △ PCB = PQ?OB 列出 S 对于 x 的二次函数，利用函数的性质求出头积的最大值，从而求出点P 的坐标；3 ）第一求出 EF 的长，设 N x ，﹣ x 23x 4 M x，﹣ x 4 ），利用平行四边形对 （ （ + + ），则 （ +边平行且相等列出 x 的一元二次方程，解方程求出 x 的值即可．【解答】 解：（ 1）由题意得，解得．∴抛物线的分析式： y=﹣ x 2+3x+4．（2）由 B （ 4， 0）、 C （0， 4）可知，直线 BC ： y= ﹣ x+4；如图 1，过点 P 作 PQ ∥ y 轴，交直线 BC 于 Q ，设 P （ x ，﹣ x 2+3x+4），则 Q （x ，﹣ x+4）； ∴PQ= （﹣ x 2+3x+4）﹣（﹣ x+4） =﹣ x 2+4x ；S △ PCB = PQ?OB=×（﹣ x 2+4x ）× 4=﹣2（ x ﹣ 2）2+8；∴当 P （ 2， 6）时，△ PCB 的面积最大；（3）存在．抛物线 y=﹣ x 2+3x+4 的极点坐标 E （ ，），直线 BC ： y=﹣ x+4；当 x=时， F （ ， ），∴EF=．如图 2，过点 M 作 MN ∥ EF ，交直线 BC 于 M ，设 N （ x ，﹣ x 2+3x+4），则 M （ x ，﹣x+4）； ∴MN= | （﹣ x 2+3x +4）﹣（﹣ x+4） | =| ﹣ x 2+4x| ；当 EF 与 NM 平行且相等时，四边形 EFMN 是平行四边形，∴| ﹣ x 2+4x| =；由﹣ x 24x= 时，解得 x1= ， x 2= （不合题意，舍去）．+当 x= 时，y=23×4= ，﹣（ ）++∴N 1（，）．当﹣ x 2+4x=﹣时，解得 x=，当 x=时， y=，∴N 2（，），当 x=时， y=，∴N 3（，），综上所述， 点 N 坐标为（ ， ）或（ ，）或（ ，）．【评论】本题主要考察了二次函数综合题，本题波及到待定系数法求函数分析式，二次函数的性质、三角形面积的计算、平行四边形的判断等知识，解答（2）问重点是用x 表示出 PQ 的长，解答（ 3）问重点是求出EF 的长，利用平行四边形对边平行且相等进行解答，本题有必定的难度．。

江西省南昌市2016-2017学年九年级（上）第一次月考数学试卷(解析版)一、选择题：（本大题共8个小题，每小题3分，共24分）每小题只有一个答案是正确的，请将正确答案的代号填入下列对应题号内．1．已知二次函数y=mx2+x﹣1的图象与x轴有两个交点，则m的取值范围是（）A．m＞﹣B．m≥﹣C．m＞﹣且m≠0 D．m≥﹣且m≠02．已知抛物线y=ax2+bx+c与x轴交点为A（﹣2，0），B（6，0），则该二次函数的对称轴为（）A．x=﹣1 B．x=1 C．x=2 D．y轴3．已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下结论：①因为a＞0，所以函数y有最大值；②该函数的图象关于直线x=﹣1对称；③当x=﹣2时，函数y的值等于0；④当x=﹣3或x=1时，函数y的值都等于0．其中正确结论的个数是（）A．4 B．3 C．2 D．14．若二次函数y=x2﹣6x+c的图象过A（﹣1，y1），B（3，y2），C（3+，y3），则y1，y2，y3的大小关系是（）A．y1＞y2＞y3B．y1＞y3＞y2C．y2＞y1＞y3D．y3＞y1＞y25．图（1）是一个横断面为抛物线形状的拱桥，当水面在l时，拱顶（拱桥洞的最高点）离水面2m，水面宽4m．如图（2）建立平面直角坐标系，则抛物线的关系式是（）A．y=﹣2x2B．y=2x2C．y=﹣x2D．y=x26．二次函数y=﹣（x﹣1）2+3的图象的顶点坐标是（）A．（﹣1，3）B．（1，3） C．（﹣1，﹣3） D．（1，﹣3）7．已知函数y=2x2的图象是抛物线，现在同一坐标系中，将该抛物线分别向上、向左平移2个单位，那么所得到的新抛物线的解析式是（）A．y=2（x+2）2+2 B．y=2（x+2）2﹣2 C．y=2（x﹣2）2﹣2 D．y=2（x﹣2）2+2 8．抛物线C1：y=x2+1与抛物线C2关于x轴对称，则抛物线C2的解析式为（）A．y=﹣x2B．y=﹣x2+1 C．y=x2﹣1 D．y=﹣x2﹣1二、填空题（本大题共7个小题，每小题3分，共21分）9．若把函数y=x2﹣2x﹣3化为y=（x﹣m）2+k的形式，其中m，k为常数，则m+k=．10．已知二次函数y=﹣x2+4x+m的部分图象如图，则关于x的一元二次方程﹣x2+4x+m=0的解是．11．抛物线y=ax2+bx+c上部分点的横坐标x，纵坐标y的对应值如表：从表可知，下列说法中正确的是．（填写序号）①抛物线与x轴的一个交点为（3，0）；②函数y=ax2+bx+c的最大值为6；③抛物线的对称轴是直线x=；④在对称轴左侧，y随x增大而增大．12．函数y=2x2﹣3x+1与y轴的交点坐标为，与x轴的交点的坐标为，．13．请写出符合以下三个条件的一个函数的解析式，①过点（3，1）；②当x＞0时，y随x的增大而减小；③当自变量的值为2时，函数值小于2．14．抛物线y=﹣x2+bx+c的图象如图所示，则此抛物线的解析式为．15．如图，是二次函数y=ax2+bx+c（a≠0）的图象的一部分，给出下列命题：①a+b+c=0；②b＞2a；③ax2+bx+c=0的两根分别为﹣3和1；④a﹣2b+c＞0．其中正确的命题是．（只要求填写正确命题的序号）三、解答题16．（12分）解方程①x2﹣3x+2=0②4x2﹣8x﹣7=﹣11③5x﹣2x2=0④x2+6x﹣1=0．17．（8分）用配方法将二次函数化成y=a（x﹣h）2+k的形式，并写出顶点坐标和对称轴①y=2x2+6x﹣12②y=﹣0.5x2﹣3x+3．18．（8分）已知二次函数y=2x2﹣4x﹣6．（1）用配方法将y=2x2﹣4x﹣6化成y=a（x﹣h）2+k的形式；（2）在平面直角坐标系中，画出这个二次函数的图象；（3）当x取何值时，y随x的增大而减少？（4）当x取何值是，y=0，y＞0，y＜0，（5）当0＜x＜4时，求y的取值范围；（6）求函数图象与两坐标轴交点所围成的三角形的面积．19．（8分）二次函数y=ax2+bx+c的图象与x轴交于B、C两点，与y轴交于A点．（1）根据图象确定a、b、c的符号，并说明理由；（2）如果点A的坐标为（0，﹣3），∠ABC=45°，∠ACB=60°，求这个二次函数的解析式．20．（8分）已知抛物线C1：y=x2﹣2（m+2）x+m2﹣10的顶点A到y轴的距离为3．（1）求顶点A的坐标及m的值；=6，求点B的坐（2）若抛物线与x轴交于C、D两点．点B在抛物线C1上，且S△BCD标．21．（9分）为满足市场需求，某超市在五月初五“端午节”来临前夕，购进一种品牌粽子，每盒进价是40元．超市规定每盒售价不得少于45元．根据以往销售经验发现；当售价定为每盒45元时，每天可以卖出700盒，每盒售价每提高1元，每天要少卖出20盒．（1）试求出每天的销售量y（盒）与每盒售价x（元）之间的函数关系式；（2）当每盒售价定为多少元时，每天销售的利润P（元）最大？最大利润是多少？（3）为稳定物价，有关管理部门限定：这种粽子的每盒售价不得高于58元．如果超市想要每天获得不低于6000元的利润，那么超市每天至少销售粽子多少盒？22．（8分）已知函数y=ax2+60x，在x＞20时，y随x增大而减小，求：（1）a的取值范围；（2）若该函数为飞机着陆后滑行距离y（m）与滑行时间x（s）之间的函数关系，已知函数的对称轴为直线x=20，请写出自变量滑行时间的取值范围，并求出飞机着陆后需滑行多少米才能停下来？23．（14分）如图1，抛物线y=ax2+bx﹣4a经过A（﹣1，0）、C（0，4）两点，与x轴交于另一点B．（1）求抛物线的解析式；（2）如图2，点P为第一象限抛物线上一点，满足到线段CB距离最大，求点P坐标；（3）如图3，若抛物线的对称轴EF（E为抛物线顶点）与线段BC相交于点F，M为线段BC上的任意一点，过点M作MN∥EF交抛物线于点N，以E，F，M，N为顶点的四边形能否为平行四边形？若能，求点N的坐标；若不能，请说明理由．2016-2017学年江西省南昌市九年级（上）第一次月考数学试卷参考答案与试题解析一、选择题：（本大题共8个小题，每小题3分，共24分）每小题只有一个答案是正确的，请将正确答案的代号填入下列对应题号内．1．已知二次函数y=mx2+x﹣1的图象与x轴有两个交点，则m的取值范围是（）A．m＞﹣B．m≥﹣C．m＞﹣且m≠0 D．m≥﹣且m≠0【考点】抛物线与x轴的交点．【分析】根据二次函数y=mx2+x﹣1的图象与x轴有两个交点，可得△=12﹣4m×（﹣1）＞0且m≠0．【解答】解：∵原函数是二次函数，∴m≠0．∵二次函数y=mx2+x﹣1的图象与x轴有两个交点，则△=b2﹣4ac＞0，△=12﹣4m×（﹣1）＞0，∴m＞﹣．综上所述，m的取值范围是：m＞﹣且m≠0，故选C．【点评】本题考查了抛物线与x轴的交点，关键是熟记当△=b2﹣4ac＞0时图象与x轴有两个交点；当△=b2﹣4ac=0时图象与x轴有一个交点；当△=b2﹣4ac＜0时图象与x轴没有交点．2．已知抛物线y=ax2+bx+c与x轴交点为A（﹣2，0），B（6，0），则该二次函数的对称轴为（）A．x=﹣1 B．x=1 C．x=2 D．y轴【考点】抛物线与x轴的交点．【分析】根据抛物线的对称性得到点A和点B是抛物线上的对称点，所以点A和点B的对称轴即为抛物线的对称轴．【解答】解：∵抛物线y=ax2+bx+c与x轴交点为A（﹣2，0），B（6，0），∴该二次函数的对称轴为直线x=2．故选C．【点评】本题考查了抛物线与x轴的交点：从二次函数的交点式y=a（x﹣x1）（x﹣x2）（a，b，c是常数，a≠0）中可直接得到抛物线与x轴的交点坐标（x1，0），（x2，0）．解决本题的关键是掌握抛物线的对称性．3．已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下结论：①因为a＞0，所以函数y有最大值；②该函数的图象关于直线x=﹣1对称；③当x=﹣2时，函数y的值等于0；④当x=﹣3或x=1时，函数y的值都等于0．其中正确结论的个数是（）A．4 B．3 C．2 D．1【考点】二次函数的性质．【分析】观察图象即可判断．①开口向上，应有最小值；②根据抛物线与x轴的交点坐标来确定抛物线的对称轴方程；③x=﹣2时，对应的图象上的点在x轴下方，所以函数值小于0；④图象与x轴交于﹣3和1，所以当x=﹣3或x=1时，函数y的值都等于0．【解答】解：由图象知：①函数有最小值；错误．②该函数的图象关于直线x=﹣1对称；正确．③当x=﹣2时，函数y的值小于0；错误．④当x=﹣3或x=1时，函数y的值都等于0．正确．故正确的有两个，选C．【点评】此题考查了根据函数图象解答问题，体现了数形结合的数学思想方法．4．若二次函数y=x2﹣6x+c的图象过A（﹣1，y1），B（3，y2），C（3+，y3），则y1，y2，y3的大小关系是（）A．y1＞y2＞y3B．y1＞y3＞y2C．y2＞y1＞y3D．y3＞y1＞y2【考点】二次函数图象上点的坐标特征．【分析】根据二次函数的性质结合二次函数的解析式即可得出y1＞y3＞y2，此题得解．【解答】解：二次函数y=x2﹣6x+c的对称轴为x=3，∵a=1＞0，∴当x=3时，y值最小，即y2最小．∵|﹣1﹣3|=4，|3+﹣3|=，4＞，∴点y1＞y3．∴y1＞y3＞y2．故选B．【点评】本题考查了二次函数的性质，根据二次函数的性质确定A、B、C三点纵坐标的大小是解题的关键．5．图（1）是一个横断面为抛物线形状的拱桥，当水面在l时，拱顶（拱桥洞的最高点）离水面2m，水面宽4m．如图（2）建立平面直角坐标系，则抛物线的关系式是（）A．y=﹣2x2B．y=2x2C．y=﹣x2D．y=x2【考点】根据实际问题列二次函数关系式．【分析】由图中可以看出，所求抛物线的顶点在原点，对称轴为y轴，可设此函数解析式为：y=ax2，利用待定系数法求解．【解答】解：设此函数解析式为：y=ax2，a≠0；那么（2，﹣2）应在此函数解析式上．则﹣2=4a即得a=﹣，那么y=﹣x2．故选：C．【点评】根据题意得到函数解析式的表示方法是解决本题的关键，关键在于找到在此函数解析式上的点．6．二次函数y=﹣（x﹣1）2+3的图象的顶点坐标是（）A．（﹣1，3）B．（1，3） C．（﹣1，﹣3） D．（1，﹣3）【考点】二次函数的性质．【分析】根据二次函数的顶点式一般形式的特点，可直接写出顶点坐标．【解答】解：二次函数y=﹣（x﹣1）2+3为顶点式，其顶点坐标为（1，3）．故选B．【点评】主要考查了求抛物线的顶点坐标的方法．7．已知函数y=2x2的图象是抛物线，现在同一坐标系中，将该抛物线分别向上、向左平移2个单位，那么所得到的新抛物线的解析式是（）A．y=2（x+2）2+2 B．y=2（x+2）2﹣2 C．y=2（x﹣2）2﹣2 D．y=2（x﹣2）2+2 【考点】二次函数图象与几何变换．【分析】直接利用平移规律（左加右减，上加下减）求新抛物线的解析式．【解答】解：抛物线y=2x2向上、向左平移2个单位后的解析式为：y=2（x+2）2+2．故选：A．【点评】主要考查的是函数图象的平移，用平移规律“左加右减，上加下减”直接代入函数解析式求得平移后的函数解析式．8．抛物线C1：y=x2+1与抛物线C2关于x轴对称，则抛物线C2的解析式为（）A．y=﹣x2B．y=﹣x2+1 C．y=x2﹣1 D．y=﹣x2﹣1【考点】二次函数图象与几何变换．【分析】画出图形后可根据开口方向决定二次项系数的符号，开口度是二次项系数的绝对值；与y轴的交点为抛物线的常数项进行解答．【解答】解：关于x轴对称的两个函数解析式的开口方向改变，开口度不变，二次项的系数互为相反数；对与y轴的交点互为相反数，那么常数项互为相反数，故选D．【点评】根据画图可得到抛物线关于x轴对称的特点：二次项系数，一次项系数，常数项均互为相反数．二、填空题（本大题共7个小题，每小题3分，共21分）9．若把函数y=x2﹣2x﹣3化为y=（x﹣m）2+k的形式，其中m，k为常数，则m+k=﹣3．【考点】二次函数的三种形式．【分析】利用配方法操作整理，然后根据对应系数相等求出m、k，再相加即可．【解答】解：y=x2﹣2x﹣3，=（x2﹣2x+1）﹣1﹣3，=（x﹣1）2﹣4，所以，m=1，k=﹣4，所以，m+k=1+（﹣4）=﹣3．故答案为：﹣3．【点评】本题考查了二次函数的三种形式，熟练掌握配方法的操作是解题的关键．10．已知二次函数y=﹣x2+4x+m的部分图象如图，则关于x的一元二次方程﹣x2+4x+m=0的解是x1=﹣1，x2=5．【考点】抛物线与x轴的交点．【分析】由二次函数y=﹣x2+4x+m的部分图象可以得到抛物线的对称轴和抛物线与x轴的一个交点坐标，然后可以求出另一个交点坐标，再利用抛物线与x轴交点的横坐标与相应的一元二次方程的根的关系即可得到关于x的一元二次方程﹣x2+4x+m=0的解．【解答】解：根据图示知，二次函数y=﹣x2+4x+m的对称轴为x=2，与x轴的一个交点为（5，0），根据抛物线的对称性知，抛物线与x轴的另一个交点横坐标与点（5，0）关于对称轴对称，即x=﹣1，则另一交点坐标为（﹣1，0）则当x=﹣1或x=5时，函数值y=0，即﹣x2+4x+m=0，故关于x的一元二次方程﹣x2+4x+m=0的解为x1=﹣1，x2=5．故答案是：x1=﹣1，x2=5．【点评】本题考查了抛物线与x轴的交点．解答此题需要具有一定的读图的能力．11．抛物线y=ax2+bx+c上部分点的横坐标x，纵坐标y的对应值如表：从表可知，下列说法中正确的是．（填写序号）①抛物线与x轴的一个交点为（3，0）；②函数y=ax2+bx+c的最大值为6；③抛物线的对称轴是直线x=；④在对称轴左侧，y随x增大而增大．【考点】抛物线与x轴的交点；二次函数的性质；二次函数的最值．【分析】根据表中数据和抛物线的对称性，可得到抛物线的开口向下，当x=3时，y=0，即抛物线与x轴的交点为（﹣2，0）和（3，0）；因此可得抛物线的对称轴是直线x=3﹣=，再根据抛物线的性质即可进行判断．【解答】解：根据图表，当x=﹣2，y=0，根据抛物线的对称性，当x=3时，y=0，即抛物线与x轴的交点为（﹣2，0）和（3，0）；∴抛物线的对称轴是直线x=3﹣=，根据表中数据得到抛物线的开口向下，∴当x=时，函数有最大值，而不是x=0，或1对应的函数值6，并且在直线x=的左侧，y随x增大而增大．所以①③④正确，②错．故答案为：①③④．【点评】本题考查了抛物线y=ax2+bx+c的性质：抛物线是轴对称图形，它与x轴的两个交点是对称点，对称轴与抛物线的交点为抛物线的顶点；a＜0时，函数有最大值，在对称轴左侧，y随x增大而增大．12．函数y=2x2﹣3x+1与y轴的交点坐标为（0，1），与x轴的交点的坐标为（，0），（1，0）．【考点】抛物线与x轴的交点．【分析】函数y=2x2﹣3x+1与y轴的交点坐标，即为x=0时，y的值．当x=0，y=1．故与y 轴的交点坐标为（0，1）；x轴的交点的坐标为y=0时方程2x2﹣3x+1=0的两个根为x1=，x2=1，与x轴的交点的坐标为（，0），（1，0）．【解答】解：把x=0代入函数可得y=1，故y轴的交点坐标为（0，1），把y=0代入函数可得x=或1，故与x轴的交点的坐标为（，0），（1，0）．【点评】解答此题要明白函数y=2x2﹣3x+1与y轴的交点坐标即为x=0时y的值；x轴的交点的坐标为y=0时方程2x2﹣3x+1=0的两个根．13．请写出符合以下三个条件的一个函数的解析式y=﹣x+2，①过点（3，1）；②当x＞0时，y随x的增大而减小；③当自变量的值为2时，函数值小于2．【考点】二次函数的性质；一次函数的性质．【分析】由题意设出函数的一般解析式，再根据①②③的条件确定函数的解析式．【解答】解：设函数的解析式为：y=kx+b，∵函数过点（3，1），∴3k+b=1…①∵当x＞0时，y随x的增大而减小，∴k＜0…②，又∵当自变量的值为2时，函数值小于2，当x=2时，函数y=2k+b＜2…③由①②③知可以令b=2，可得k=﹣，此时2k+b=﹣+2＜2，∴函数的解析式为：y=﹣x+2．答案为y=﹣x+2．【点评】此题是一道开放性题，主要考查一次函数的基本性质，函数的增减性及用待定系数法来确定函数的解析式．14．抛物线y=﹣x2+bx+c的图象如图所示，则此抛物线的解析式为y=﹣x2+2x+3．【考点】待定系数法求二次函数解析式．【分析】此图象告诉：函数的对称轴为x=1，且过点（3，0）；用待定系数法求b，c的值即可．【解答】解：据题意得解得∴此抛物线的解析式为y=﹣x2+2x+3．【点评】本题考查了用待定系数法求函数解析式的方法，同时还考查了方程组的解法，考查了数形结合思想．15．如图，是二次函数y=ax2+bx+c（a≠0）的图象的一部分，给出下列命题：①a+b+c=0；②b＞2a；③ax2+bx+c=0的两根分别为﹣3和1；④a﹣2b+c＞0．其中正确的命题是①③．（只要求填写正确命题的序号）【考点】二次函数图象与系数的关系；二次函数图象上点的坐标特征；抛物线与x轴的交点．【分析】由图象可知过（1，0），代入得到a+b+c=0；根据﹣=﹣1，推出b=2a；根据图象关于对称轴对称，得出与X轴的交点是（﹣3，0），（1，0）；由a﹣2b+c=a﹣2b﹣a﹣b=﹣3b＜0，根据结论判断即可．【解答】解：由图象可知：过（1，0），代入得：a+b+c=0，∴①正确；﹣=﹣1，∴b=2a，∴②错误；根据图象关于对称轴x=﹣1对称，与X轴的交点是（﹣3，0），（1，0），∴③正确；∵b=2a＞0，∴﹣b＜0，∵a+b+c=0，∴c=﹣a﹣b，∴a﹣2b+c=a﹣2b﹣a﹣b=﹣3b＜0，∴④错误．故答案为：①③．【点评】本题主要考查对二次函数与X轴的交点，二次函数图象上点的坐标特征，二次函数图象与系数的关系等知识点的理解和掌握，能根据图象确定系数的正负是解此题的关键．三、解答题16．（12分）（2016秋•南昌校级月考）解方程①x2﹣3x+2=0②4x2﹣8x﹣7=﹣11③5x﹣2x2=0④x2+6x﹣1=0．【考点】解一元二次方程-因式分解法；解一元二次方程-直接开平方法．【分析】①因式分解法求解可得；②整理成一般式后，因式分解法求解可得；③因式分解法求解可得；④公式法求解可得．【解答】解：①（x﹣1）（x﹣2）=0，∴x﹣1=0或x﹣2=0，解得：x=1或x=2；②原方程整理可得：x2﹣2x+1=0，∴（x﹣1）2=0，解得：x=1；③x（5﹣2x）=0，∴x=0或5﹣2x=0，解得x=0或x=；④∵a=1，b=6，c=﹣1，∴△=36+4=40＞0，∴x==﹣3．【点评】本题考查了一元二次方程的解法．解一元二次方程常用的方法有直接开平方法，配方法，公式法，因式分解法，要根据方程的特点灵活选用合适的方法．17．用配方法将二次函数化成y=a（x﹣h）2+k的形式，并写出顶点坐标和对称轴①y=2x2+6x﹣12②y=﹣0.5x2﹣3x+3．【考点】二次函数的三种形式．【分析】①②利用配方法先提出二次项系数，再加上一次项系数的一半的平方来凑成完全平方式，可把一般式转化为顶点式，从而得出顶点坐标和对称轴．【解答】解：①y=2x2+6x﹣12=2（x+）2﹣，则该抛物线的顶点坐标是（﹣，﹣），对称轴是x=﹣；②y=﹣0.5x2﹣3x+3=﹣（x+3）2+，则该抛物线的顶点坐标是（﹣3，），对称轴是x=﹣3．【点评】此题考查了二次函数表达式的一般式与顶点式的转换，并要求熟练掌握顶点公式和对称轴公式．18．已知二次函数y=2x2﹣4x﹣6．（1）用配方法将y=2x2﹣4x﹣6化成y=a（x﹣h）2+k的形式；（2）在平面直角坐标系中，画出这个二次函数的图象；（3）当x取何值时，y随x的增大而减少？（4）当x取何值是，y=0，y＞0，y＜0，（5）当0＜x＜4时，求y的取值范围；（6）求函数图象与两坐标轴交点所围成的三角形的面积．【考点】二次函数的三种形式；二次函数的图象；二次函数的性质．【分析】（1）直接利用配方法得出函数顶点式即可；（2）利用顶点式得出顶点坐标，进而得出函数与坐标轴交点进而画出函数图象；（3）利用函数顶点式得出对称轴进而得出答案；（4）利用函数图象得出答案即可；（5）利用x=1以及x=4是求出函数值进而得出答案；（6）利用函数图象得出三角形面积即可．【解答】解：（1）y=2x2﹣4x﹣6=2（x2﹣2x）﹣6=2（x﹣1）2﹣8；（2）当y=0，则0=2（x﹣1）2﹣8，解得：x1=﹣1，x2=3，故图象与x轴交点坐标为：（﹣1，0），（3，0），当x=0，y=﹣6，故图象与y轴交点坐标为：（0，﹣6），如图所示：；（3）当x＜1时，y随x的增大而减少；（4）当x=1或﹣3时，y=0，当x＜﹣1或x＞3时，y＞0，当﹣1＜x＜3时；y＜0；（5）当0＜x＜4时，x=1时，y=﹣8，x=4时，y=10，故y的取值范围是：﹣8≤y＜10；（6）如图所示：函数图象与两坐标轴交点所围成的三角形的面积为：×4×6=12．【点评】此题主要考查了配方法求函数顶点坐标以及利用图象判断函数值以及三角形面积求法，正确画出函数图象是解题关键．19．二次函数y=ax2+bx+c的图象与x轴交于B、C两点，与y轴交于A点．（1）根据图象确定a、b、c的符号，并说明理由；（2）如果点A的坐标为（0，﹣3），∠ABC=45°，∠ACB=60°，求这个二次函数的解析式．【考点】二次函数综合题；解三元一次方程组；待定系数法求二次函数解析式．【分析】（1）根据开口方向可确定a的符号，由对称轴的符号，a的符号，结合起来可确定b的符号，看抛物线与y轴的交点可确定c的符号；（2）已知OA=3，解直角△OAB、△OAC可得B、C的坐标，设抛物线解析式的交点式，把A、B、C代入即可求解析式．【解答】解：（1）∵抛物线开口向上∴a＞0又∵对称轴在y轴的左侧∴＜0，∴b＞0又∵抛物线交y轴的负半轴∴c＜0（2）连接AB，AC∵在Rt△AOB中，∠ABO=45°∴∠OAB=45°，∴OB=OA∴B（﹣3，0）又∵在Rt△ACO中，∠ACO=60°∴OC=OAcot=60°=∴C（，0）设二次函数的解析式为y=ax2+bx+c（a≠0）由题意：∴所求二次函数的解析式为y=x2+（﹣1）x﹣3．【点评】本题考查了点的坐标求法，正确设抛物线解析式，求二次函数解析式的方法，需要学生熟练掌握．20．已知抛物线C1：y=x2﹣2（m+2）x+m2﹣10的顶点A到y轴的距离为3．（1）求顶点A的坐标及m的值；=6，求点B的坐（2）若抛物线与x轴交于C、D两点．点B在抛物线C1上，且S△BCD标．【考点】抛物线与x轴的交点．【分析】（1）根据顶点A到y轴的距离为3，说明顶点A的横坐标为3或﹣3，根据公式﹣代入列式，求出m的值，分别代入解析式中，求出对应的顶点坐标A；也可以直接配方求得；（2）先计算抛物线与x轴的交点坐标，发现当m=﹣5时不符合题意，因此根据m=1时，对应的抛物线计算CD的长，求出点B的坐标．【解答】解：（1）由题意得：﹣=3或﹣3，∴m+2=3或m+2=﹣3，∴m=1或﹣5，当m=1时，抛物线C1：y=x2﹣6x﹣9=（x﹣3）2﹣18，∴顶点A的坐标为（3，﹣18）；当m=﹣5时，抛物线C1：y=x2+6x+15=（x+3）2+6，∴顶点A的坐标为（﹣3，6）；（2）设B（a，b），当抛物线C1：y=x2﹣6x﹣9=（x﹣3）2﹣18时，当y=0时，（x﹣3）2﹣18=0，x1=3+3，x2=3﹣3，∴CD=3+3+3﹣3=6，=6，∵S△BCD∴CD•|b|=6，∴×6•|b|=6，∴b=±2，当b=2时，x2﹣6x﹣9=2，解得：x=3±2，当b=﹣2时，x2﹣6x﹣9=﹣2，解得：x=7或﹣1，∴B（3+2，2）或（3﹣2，2）或（7，﹣2）或（﹣1，﹣2），当抛物线C1：y=x2+6x+15=（x+3）2+6时，当y=0时，（x+3）2+6=0，此方程无实数解，所以此时抛物线与x轴无交点，不符合题意，∴B（3+2，2）或（3﹣2，2）或（7，﹣2）或（﹣1，﹣2）．【点评】本题是二次函数性质的应用，考查了抛物线与x轴的交点及顶点坐标，对于利用三角形面积求点的坐标问题，解题思路为：设出该点的坐标，根据面积列方程，求出未知数的值，再代入解析式中求另一坐标即可；同时要注意数形结合的思想的应用．21．为满足市场需求，某超市在五月初五“端午节”来临前夕，购进一种品牌粽子，每盒进价是40元．超市规定每盒售价不得少于45元．根据以往销售经验发现；当售价定为每盒45元时，每天可以卖出700盒，每盒售价每提高1元，每天要少卖出20盒．（1）试求出每天的销售量y（盒）与每盒售价x（元）之间的函数关系式；（2）当每盒售价定为多少元时，每天销售的利润P（元）最大？最大利润是多少？（3）为稳定物价，有关管理部门限定：这种粽子的每盒售价不得高于58元．如果超市想要每天获得不低于6000元的利润，那么超市每天至少销售粽子多少盒？【考点】二次函数的应用．【分析】（1）根据“当售价定为每盒45元时，每天可以卖出700盒，每盒售价每提高1元，每天要少卖出20盒”即可得出每天的销售量y（盒）与每盒售价x（元）之间的函数关系式；（2）根据利润=1盒粽子所获得的利润×销售量列式整理，再根据二次函数的最值问题解答；（3）先由（2）中所求得的P与x的函数关系式，根据这种粽子的每盒售价不得高于58元，且每天销售粽子的利润不低于6000元，求出x的取值范围，再根据（1）中所求得的销售量y（盒）与每盒售价x（元）之间的函数关系式即可求解．【解答】解：（1）由题意得，y=700﹣20（x﹣45）=﹣20x+1600；（2）P=（x﹣40）（﹣20x+1600）=﹣20x2+2400x﹣64000=﹣20（x﹣60）2+8000，∵x≥45，a=﹣20＜0，=8000元，∴当x=60时，P最大值即当每盒售价定为60元时，每天销售的利润P（元）最大，最大利润是8000元；（3）由题意，得﹣20（x﹣60）2+8000=6000，解得x1=50，x2=70．∵抛物线P=﹣20（x﹣60）2+8000的开口向下，∴当50≤x≤70时，每天销售粽子的利润不低于6000元的利润．又∵x≤58，∴50≤x≤58．∵在y=﹣20x+1600中，k=﹣20＜0，∴y随x的增大而减小，=﹣20×58+1600=440，∴当x=58时，y最小值即超市每天至少销售粽子440盒．【点评】本题考查的是二次函数与一次函数在实际生活中的应用，主要利用了利润=1盒粽子所获得的利润×销售量，求函数的最值时，注意自变量的取值范围．22．已知函数y=ax2+60x，在x＞20时，y随x增大而减小，求：（1）a的取值范围；（2）若该函数为飞机着陆后滑行距离y（m）与滑行时间x（s）之间的函数关系，已知函数的对称轴为直线x=20，请写出自变量滑行时间的取值范围，并求出飞机着陆后需滑行多少米才能停下来？【考点】二次函数的应用．【分析】（1）根据二次函数性质可知该抛物线的对称轴x=﹣≤20，得出关于a的不等式，解之即可；（2）根据对称轴求出a，即可得二次函数解析式，将其配方成顶点式，根据函数取得最大值时即飞机滑行停止滑行，据此解答即可．【解答】解：（1）∵函数y=ax2+60x，在x＞20时，y随x增大而减小，∴a＜0且﹣≤20，解得：a≤﹣；（2）根据题意得：﹣=20，解得a=﹣，∴y=﹣x2+60x=﹣（x﹣20）2+600，则自变量x的范围为0≤x≤20，且飞机着陆后需滑行600米才能停下来．【点评】本题主要考查二次函数的应用，熟练掌握二次函数的性质及顶点在具体问题中的实际意义是解题的关键．23．（14分）（2016秋•南昌校级月考）如图1，抛物线y=ax2+bx﹣4a经过A（﹣1，0）、C（0，4）两点，与x轴交于另一点B．（1）求抛物线的解析式；（2）如图2，点P为第一象限抛物线上一点，满足到线段CB距离最大，求点P坐标；（3）如图3，若抛物线的对称轴EF（E为抛物线顶点）与线段BC相交于点F，M为线段BC上的任意一点，过点M作MN∥EF交抛物线于点N，以E，F，M，N为顶点的四边形能否为平行四边形？若能，求点N的坐标；若不能，请说明理由．【考点】二次函数综合题．【分析】（1）根据抛物线y=ax2+bx﹣4a经过A（﹣1，0）、C（0，4）两点，列出a和b 的二元一次方程组，求出a和b的值，进而求出点B的坐标，即可求出直线BC的解析式；（2）过点P作PQ∥y轴，交直线BC于Q，设P（x，﹣x2+3x+4），则Q（x，﹣x+4）；=PQ•OB列出S关于x的二次函数，利用函数的性质求出面积求出PQ的长，利用S△PCB的最大值，进而求出点P的坐标；（3）首先求出EF的长，设N（x，﹣x2+3x+4），则M（x，﹣x+4），利用平行四边形对边平行且相等列出x的一元二次方程，解方程求出x的值即可．【解答】解：（1）由题意得，解得．∴抛物线的解析式：y=﹣x2+3x+4．（2）由B（4，0）、C（0，4）可知，直线BC：y=﹣x+4；如图1，过点P作PQ∥y轴，交直线BC于Q，设P（x，﹣x2+3x+4），则Q（x，﹣x+4）；∴PQ=（﹣x2+3x+4）﹣（﹣x+4）=﹣x2+4x；=PQ•OB=×（﹣x2+4x）×4=﹣2（x﹣2）2+8；S△PCB∴当P（2，6）时，△PCB的面积最大；（3）存在．抛物线y=﹣x2+3x+4的顶点坐标E（，），直线BC：y=﹣x+4；当x=时，F（，），∴EF=．如图2，过点M作MN∥EF，交直线BC于M，设N（x，﹣x2+3x+4），则M（x，﹣x+4）；∴MN=|（﹣x2+3x+4）﹣（﹣x+4）|=|﹣x2+4x|；当EF与NM平行且相等时，四边形EFMN是平行四边形，∴|﹣x2+4x|=；由﹣x2+4x=时，解得x1=，x2=（不合题意，舍去）．当x=时，y=﹣（）2+3×+4=，∴N1（，）．当﹣x2+4x=﹣时，解得x=，当x=时，y=，∴N2（，），当x=时，y=，∴N3（，），综上所述，点N坐标为（，）或（，）或（，）．【点评】本题主要考查了二次函数综合题，此题涉及到待定系数法求函数解析式，二次函数的性质、三角形面积的计算、平行四边形的判定等知识，解答（2）问关键是用x表示出PQ 的长，解答（3）问关键是求出EF的长，利用平行四边形对边平行且相等进行解答，此题有一定的难度．。

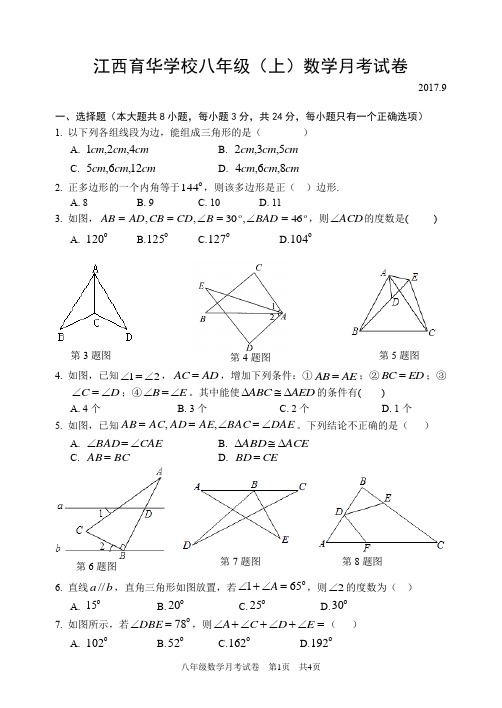
江西育华学校八年级（上）数学月考试卷2017.9一、选择题（本大题共8小题，每小题3分，共24分，每小题只有一个正确选项） 1. 以下列各组线段为边，能组成三角形的是（ ） A. cm cm cm 4,2,1 B. cm cm cm 5,3,2 C. cm cm cm 12,6,5D. cm cm cm 8,6,42. 正多边形的一个内角等于 144，则该多边形是正（ ）边形. A. 8 B. 9 C. 10 D. 113. 如图， 46,30,,=∠=∠==BAD B CD CB AD AB ，则ACD ∠的度数是( ) A.120 B.125 C.127D.1044. 如图，已知12∠=∠，AC AD =，增加下列条件：①AB AE =；②BC ED =；③C D ∠=∠；④B E ∠=∠。

其中能使ABC AED ∆≅∆的条件有( )A. 4个B. 3个C. 2个D. 1个5. 如图，已知DAE BAC AE AD AC AB ∠=∠==,,。

下列结论不正确的是（ ） A. CAE BAD ∠=∠ B. ACE ABD ∆≅∆ C. BC AB =D. CE BD =6. 直线b a //，直角三角形如图放置，若651=∠+∠A ，则2∠的度数为（ ）A.15B.20C.25D.307. 如图所示，若 78=∠DBE ，则=∠+∠+∠+∠E D C A （ ） A. 102 B. 52 C.162D.192第8题图第7题图第6题图第5题图第4题图第3题图8. 如图，在ABC ∆中，D 为AB 的中点，AF CF BE CE 2,3==，四边形CEDF 的面积为17，则ABC ∆的面积为（ ） A. 22 B. 23 C. 24D. 25二、填空题（本大题共6小题，每小题3分，共18分）9. 已知等腰三角形的两边分别为2和5，则它的周长为_________10. 若从一个多边形的一个顶点出发,最多可以引10条对角线,则它是________边形.11. 已知在ABC ∆中， 40,40=∠-∠=∠C B A ，则=∠B _____． 12. 如右图，DF BE CD AB CD AB ==,,//，则图中有________对全等三角形。

育华初三第一次月考数学试卷一、选择题（本题16小题，1—10题每题3分，11—16题每题2分，共42分） 1、 下列函数中，y 关于x 的二次函数是（ ）。

A. 12+=x yB. ()12+=x x yC. 22xy =D. ()222x x y --=2、 在平面直角坐标系中，若将抛物线442+-=x x y 先向右平移3个单位长度，再向上平移2个单位长度，则经过这两次平移后，所得到的抛物线的顶点坐标为（ ）。

A. （－2，3） B. （－1，2） C. （5，2） D. （4，3） 3、 若抛物线)1()(2++-=m m x y 的顶点在第一象限，则m 的取值范围为（ ）A. m ＞1B. m ＞0C. m ＞﹣1D. ﹣1＜m ＜04、 若二次函数1)(2--=m x y ，当1≤x 时，y 随x 的增大而减小，则m 的取值范围是（ ）A. 1=mB. 1>mC. 1≥mD. 1≤m5、 关于抛物线3)1(212++-=x y ，下列结论：①抛物线的开口向下；②对称轴为直线x =1；③顶点坐标为（﹣1，3）；④x >1是，y 随x 的增大而减小，其中正确结论的个数是（ ） A 、1 B 、2 C 、3 D 、46、 已知二次函数c bx ax y ++=2（a ＞0）的图象过点A （1，2），B （3，2），若点M （－2，1y ），N （－1，2y ），K （8，3y ）也在此二次函数的图象上，则下列结论正确的是（ ）。

A. 1y ＜2y ＜3yB. 2y ＜1y ＜3yC. 3y ＜1y ＜2yD. 1y ＜3y ＜2y7、 某广场有一喷水池，水从地面喷出，如图，以水平地面为x 轴，出水点为原点，建立平面直角坐标系，水在空中划出的曲线是抛物线x x y 42+-=（单位：米）的一部分，则水喷出的最大高度是（ ） A. 4米 B. 3米C. 2米D. 1米8、 二次函数2224c x x y +-=的图象的顶点在x 轴上，则c 的值是（ ）。

江西育华学校七年级下学期第一次数学月考卷 一、选择题1.513=±2；④(23=5112.其中正确的有（）A.1个B.2个C.3个D.4个2.如图，是一个镶边的模板，分析它的内部是由哪个“基本图案”通过一次平移得到的（）A. B. C. D.3.下列实数3π，78-，03.15-中，无理数有（）A.1个B.2个C.3个D.4个 4.下列式子一定有意义的是（）B.C.D.5.如图，含30︒角的直角三角尺DEF 放置在ABC △上，30︒角的顶点D 在边AB 上，DE AB ⊥，若B ∠为锐角，BC DF ∥，则B ∠的大小为（） A.60︒ B.45︒ C.30︒ D.75︒6.如图所示，内错角共有（）A.4对B.6对C.8对D.10对7.如图所示，将长方形纸片ABCD （图①）按如下步骤操作：（1）以过点A 的直线为折痕折叠纸片，使点B 落在AD 边上，折痕为BC 边交于点E （如图②）； （2）以过点E 的直线为折痕折叠纸片，使点A 落在BC 边上，折痕EF 交AD 边于点F （如图③）； （3）将纸片展平，那么AFE ∠的度数为（）A.67.5︒B.70︒C.64.5︒D.72︒FEDCB ADCBA图①DCBA 图②图③8.如图，AB EF ∥，90C ∠=︒，则α∠，β∠，γ∠之间的关系是（）A.βαγ∠=∠+∠B.180αβγ∠+∠+∠=︒C.90αβγ∠+∠-∠=︒D.90βγα∠+∠-∠=︒ 二、填空题9.把命题“等角的补角相等”改写成“如果 ，那么 ”的形式________.10.已知210a +，则ba=______.11.如图，有一个与地面成30︒角的斜坡，现要在斜坡上竖一电线杆，当电线杆与斜坡相交得到的1∠=_____时，电线杆与地面垂直.12.如图，已知AB CD ∥，BE 平分ABC ∠，150CDE ∠=︒，则ABC ∠=_______.13.如果a 的平方根是3±_______.14.有下列四个说法：①1的算术平方根是1，②18的立方根是12±，③27-没有立方根，④互为相反数的两数的立方根互为相反数，其中正确的是_______（填序号）. 三、作答题15.（1（2）解方程()2253216x += 16.完成下列推理说明： 如图，已知12∠=∠，B C ∠=∠，可推得AB CD ∥，理由如下：12∠=∠∵（已知）， 且1CGD ∠=∠（________）， 2CGD ∠=∠∴（等量代换）. CE BF ∴∥（________）.∠∴_______C =∠（_________）. 又B C ∠=∠∵（已知），∠∴_______B =∠（等量代换） AB CD ∴∥（_______）.17.已知一个正数x 的平方根是31a +和11a +，求这个正数x 的立方根. 18.某公路规定行驶汽车速度不得超过80km/h ，当发生交通事故时，交通警察通常根据刹车后车轮滑过130°EDCBA21H GFE D CBA的距离估计车辆行驶的速度，所用的经验公式是v =，其中v 表示车速（单位：km/h ），d 表示刹车后轮滑过的距离（单位：m ），f 表示摩擦系数，在一次交通事故中，经测量25m d =， 1.2f =，请你帮助判断以下，肇事汽车当时的速度是否超出了规定的速度？ 四、解答题19.如图，EF AD ∥，AD BC ∥，CE 平分BCF ∠，120DAC ∠=︒，20ACF ∠=︒，求FEC ∠的度数.20.已知如图，AGF ABC ∠=∠，12180∠+∠=︒， （1）试判断BF 与DE 的位置关系，并说明理由. （2）若BF AC ⊥，2150∠=︒，求AFG ∠的度数.21.已知：如图，AD BC ⊥于D ，EG BC ⊥于G ，AD 是BAC ∠的角平分线，试说明3E ∠=∠.五、综合题22.如图，AB CD ∥，P 为定点，E 、F 分别是AB ，CD 上的动点. （1）求证：P BEP PFD ∠=∠+∠；（2）若M 为CD 上一点，如图2，FMN BEP ∠=∠，且MN 交PF 于N .试说明EPF ∠与PNM ∠关系，并证明你的结论；（3）移动E 、F 使得90EPF ∠=︒，如图3，作PEG BEP ∠=∠，求AEG ∠与PFD ∠度数的比值.FE DCB A321F E DC BAEGDCBA 54321图1PF EDCBA图2MA BCDEF P 图3GPFEDCBA。

江西育华学校七年级上学期数学月考试卷一、细心选一选（本大题共8小题，每题3分，共24分）1. 比-3小-1的数是（ ）A.2B.-2C.4D.-42. 在-（-5），-（-5）2, --5，()2--5中负数有（ ）个A.0B.1C.2D.33.若关于x 的方程231m m x m ---=（）是一元一次方程，则这个方程的解是（ ）A.-1B.1C.3D.1或34.日历上竖列相邻的三个数，它们的和是39，则第一个数是（ ）A.6B.12C.13D.205.下列图形中，经过折叠一定不能围成一个立方体的是（ ）6.下列说法正确的是（ ）A.如果ac=ab ，那么c=bB.如果a 2=b 2，那么a=bC.如果193x π-=，那么x=-3D. 如果a b c c=，那么a=b 7.如图的几何体的俯视图是（ ）8.育华学校初一（8）班“元旦”活动中有这样一项游戏，每位选手朝特制的靶子上各投了三支飞镖，在同一圆环内得分相同，如图所示，熊浩宇、蔡昊言、廖思明的成绩分别为11分、15分，则廖思明的成绩是（ ）A.10分B.12分C.13分D.14分二、精心填一填（本大题共6小题，每题3分，共18分）9. 1-2018的倒数是 . 10.已知方程111+3420182x -（）=，则代数式31+642018x -（）的值为 . 11.一家商店将某种服装按照成本价提高20%后标价，又以9折优惠卖出，结果每件服装仍可获利8元，则这种服装每件的成本是 .12.一场篮球比赛中，天懿同学共投中22个球（含三分球、两分球和罚球），得到26分，其中两分球数量是三分球的2倍，则罚中 球（罚中1球得1分）.13.如图，由一些完全相同的小正方形搭成的几何体的俯视图和左视图，组成这个几何体的小正方体的个数是 .14.数列121123211234321,,,,,,,,,,,,,,222333334444444,…记第一个数a 1，第二个数为a 2,…,第n 个数为a n 若a n 是方程1-311284x x --=的解，则n= . 三、耐心算一算（本大题共4小题，每题5分，共20分）15.计算：()424-8+-6.2+-2-3995⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭16.计算()()3231-5-+32-2-154⎛⎫⎛⎫⨯÷⨯ ⎪ ⎪⎝⎭⎝⎭17解方程：()()321221x x --+=18.解方程：131124x x ---=四、用心求一求（本大题共3小题，每题6分，共18分）19. 用“☆”定义一种新运算：对于任意有理数a 和b ，规定a ☆b=ab 2+2ab+a ，如：1☆3=1×32+2×1×3+1=16.若12a +☆3=8，求a 的值.20.已知关于x 的方程23x m m x -=+的解是方程1322x x +=-的解的2倍，求m 的值.21.如图所示是九江大千世界部分旅游路线示意图，其中B 、C 、D 为游玩点，E 为两条路的交叉点，图中数据为相应两点间的路程（单位：km ）．文亭从A 处出发，以2km/h 的速度步行游玩，每个游玩点的逗留时间均为0.5h ．（1）当他沿着路线A-D-C-E-A游览回到A处时，共用了3.1h，求CE的长；（2）若他打算从A处出发后，步行速度与在景点的逗留时间保持不变，且在最短时间内看完三个景点返回到A处，请你为他设计一条步行路线，并说明这样设计的理由（不考虑其他因素）．五、全心做一做（本大题共2个小题，每题10分，共20分）22.2018年元旦中国移动推出“自由派”资费套餐，其计费方式有两种如下表：请根据表格解决下列问题：（1）如果甲平均每月的通话时长为120分钟，乙平均每月的通话时长为200分钟，请你通过计算说明：甲、乙分别选择哪种计费方式省钱；（2）设某人一个月内用移动电话主叫时长为t分钟（t是正整数）．请你为用户设计一个方案，使用户能合理地选择这种资费套餐的计费方式．23.将棱长为n（n>1且n为整数）的正方体的各面都染成红色后再切成棱长为1的小正体，表面积，个数等都会发生有规律的变化.（1）①当n=2时，所有小正方体的表面积的和是原正方体表面积的倍；②当n=3时，所有小正方体的表面积的和是原正方体表面积的倍；③当n=2018时，所有小正方体的表面积是原正方体表面积的倍.（2）①三面带红色的棱长为1的小正方体有个；②二面带红色的棱长为1的小正方体有个；③一面带红色的棱长为1的小正方体有个.（3）如果二面带红的小正方体的个数是三面带红色的小正方体的个数的30倍，求n得值.（4）当n=2018时，一面带红色的小正方体的个数能否为两面带红色的小正方体的个数的整数倍？说明你的理由.。

江西育华学校七年级数学月考试卷一、选择题1.计算24--的结果是（）A.2B.2-C.6-D.8-2.下列四个选项中，所画数轴正确的是（）A B C D3.将596800保留两个有效数字的近似数是（）A.590000B.600000C.55.910⨯D.56.010⨯4.已知245A a b =+，232B a b =--，则2A B -的结果是（）A.277a b -B.2109a b +C.2512a b -D.2109a b -5.把方程3457x x -=-变形为3574x x -=-+，这种变形的过程称为方程中的（）A.移项B.去分母C.去括号D.系数化为16.按某种标准把多项式分类，222a ab b -+与37x y +-属于同一类，则下列多项式中也属于此类的是（） A.5x y + B.29a xy +- C.44a b - D.22234x y xy x +-+7.某商场进了一批商品，每件商品的进价为a 元，提价10%后作为销售价，由于商品滞销，商场决定降价10%作为促销价，则商场对每件商品（）A.赚了0.01a 元B.亏了0.01a 元C.赚了0.99a 元D.不赔不赚8.某市按以下标准收取水费：用水不超过20吨，按每吨1.2元收费；超过20吨，超过的部分按每吨1.5元收费.如果某家庭五月份的水费是平均每吨1.25元，那么这个家庭五月份应交水费（）A.20元B.24元C.30元D.36元二、填空题9.化简()22x y x y +--的最后结果____________.10.单项式2534x y z -的系数是_________，次数是___________. 11.若关于x 的方程60ax +=的解是2x =，则a 的值是___________.12.若0ab >，则代数式a b ab a b ab++的值是__________. 13.小华的妈妈为爸爸买了一件衣服和一条裤子，共用了306元，其中衣服按标价打七折，裤子按标价打八折，若衣服的标价为300元，则裤子的标价是__________.14.小洋在纸上画了一条数轴后，折叠纸面，使数轴上表示1的点与表示5-的点重合，若数轴上A 、B 两点之间的距离为4（A 在B 的左侧），且A 、B 两点经上述折叠后重合，则A 点表示的数是_____，B 点表示的数是___________.三、解答题15.计算：()()320.2527325⎡⎤⨯-+-⨯-+⎣⎦.16.计算：12345699100-+-+-++- .17.化简：()2225432a a a a a ⎡⎤----⎣⎦.18.求值：()22123242x x x x ⎛⎫---+ ⎪⎝⎭，其中1x =-. 四、解答题19.解方程()23413x x --=.20.解方程12223x x x -+-=-. 五、解答题21.已知()130m m x -+=是关于x 的一元一次方程. （1）求m 的值，并写出这个过程；（2）判断0x =， 1.5x =是否为方程的解.10-12110-110-122.某工厂计划为灾区生产A、B两种型号的学生桌椅500套，以解决1200名学生的学习问题.一套A型桌椅为一桌两椅，一套B型桌椅为一桌三椅.（1）问需要生产A、B型桌椅各多少套？（2）已知每套A型桌椅的生产成本为100元，运费2元；每套B型桌椅的生产成本为120元，运费4元，现要把桌椅全部生产完并运往灾区，求所需总费用.23.东方制衣厂某车间计划用10天时间加工童装和成人装共360件，该车间的加工能力是：每天能单独加工童装45件或成人装30件.（1）该车间应安排几天加工童装，几天加工成人装，才能如期完成任务？（2）若加工两件童装和一件成人装共可获利280元，在这次加工中该车间共获利36000元，求加工一件童装和一件成人装各可获利多少元?六、解答题24.某市移动通讯公司开设了两种通讯业务：“全球通”使用者先缴20元月租费，然后每通话1分钟，再付0.20元；“神州行”不缴月租费，每通话1分钟，需付电话费0.30元（指本地市区通话）.（1）一个月内在本地通话100分钟和300分钟，按两种通讯方式各需交费多少元？（2）一个月内在本地通话多少分钟，会出现两种通讯方式的交费相同情况？请你通过计算说明；（3）根据（1）、（2）的结果分析，你认为在什么情况下选择哪种通讯方式更省钱？请你直接写出结论；（4）如果王老师预计一个月内在本地通话需交费120元，请你帮他选择，使用哪种通讯方式较合算？。

江西育华学校八年级数学月考试卷命题人：荣齐辉 审题人：冯祥永 时间：2019.3 3 分，共 8 题，共 24 分）1 x -2 ，则 x 的取值范围是（ ）A ． x x ＜2 C ． x ＞2 D ． x ≥22(A B ．-1C ．D ．3= 3 ）A B C4．已知△ABC 的三边分别为 a ，b ，c ．．能．．．判断△ABC 为直角三角形的是A ． a 2 + b 2 ≠ c 2B ． a = 1 ， b cC ．∠A :∠B :∠C =3:4:5D ．三边长分别为 n 2 - 1 ， 2n ， n 2 + 1(n ＞1) （ ）5．已知 ab < 0 ）A ．B ．-C ．D ．-6．下列条件，不能使四边形 ABCD 是平行四边形的是（ ）A ．AB ∥CD ，AB =CD B ．AB ∥CD ，BC ∥ADC ．AB ∥CD ，BC =AD D ．AB =CD ，BC =AD7．如图，在平面直角坐标系中，以 O （0，0），A （1，1），B （3，0）为顶点，构造平行 四边形，下列各点中不．能．作为平行四边形顶点坐标的是（ ） A ．（﹣3，1） B ．（4，1） C ．（﹣2，1） D ．（2，﹣1）8．如图,已知点 D 是等边三角形 ABC 中 BC 的中点，BC =2，点 E 是 AC 边上的动点，则 BE ）A B C ．3 D 1第 7 题图 第 8 题图二、填空题（每小题 3 分，共 6 题，共 18 分）9 x 的取值范围是 ．10．比较大小： ； >”，“<”或“=”）．11．如图是北京第 24 届国际数学家大会会徽，由 4 个全等的直角三角形拼合而成，若大 正方形、小正方形的面积分别为 52 和 4，则直角三角形的两直角边之和为 ．12．如图，在平行四边形 ABCD 中，E 、F 分别是 AD 、DC 的中点，若△CEF 的面积为 3， 则平行四边形 ABCD 的面积为 ．13．如图，平行四边形 ABCD 中，∠ADB =90°，AC =10，BD =6，则 AD 的长为 ．第 11 题图 第 12 题图 第 13 题图14．如图，在直角坐标系中，已知点 A （﹣3，0），B （0，4），对△OAB 连续作旋转变 换，依次得到△1．△2．△3．△4…，则△2019 的直角顶点的坐标为．第 14 题图三、解答题（每小题 6 分，共 4 题，共 24 分）15．(6 分)计算: （1）（2）3-12÷ 16．(6 分)计算:（1）2- （2）747a 17.（6 分）如图，正方形网格中的小方格边长为 1，△ABC的三个顶点都在格点上．（1）判断△ABC 的形状，并说明理由；（2）求△ABC 中 BC 边上的高．18.（6 分）已知 a , b 分别是 6（1）求 a , b 的值；（2）求 3a - b 2 的值四、解答题（每小题 8 分，共 3 题，共 24 分）19.（8 分）在长方形 ABCD 中，点 E ，点 F 为对角线 BD 上两点，且 DE =EF =FB(1)求证：四边形(2)若 AE ⊥BD ，AF = ，AB =4，求 BF 的长度.20.（8 分) 小明在解决问题：“已知 a,求 2a 2 - 8a + 1 的值”时， 他是这样分析与解的：∵a2∴ a - 2 = ,∴ (a - 2) 2 = 3, a 2 - 4a + 4 = 3∴ a 2 - 4a = -1,∴ 2a 2 - 8a + 1 = 2(a 2 - 4a ) + 1 = 2 ⨯ (-1) + 1 = -1. 请你根据小明的分析过程，解决如下问题：...的值； （2）若 a,①求 4a 2 - 8a + 1 的值； ②直接写出代数式的值：a 3 - 2a 2 + a - 2 = ；2a 2 - 5a +1a+ 2 = .21．（8 分）操作发现：将一副直角三角板如图1 摆放，能够发现等腰直角三角板ABC 的斜边与含30°角的直角三角板DEF 的较长直角边DE 重．合．．问题解决：将图①中的等腰直角三角板ABC 绕点B 顺时针旋转30°，点C 落在BF 上，AC 与BD 交于点O，连接CD，如图2．（1）求证：△CDO 是等腰三角形；（2）若DF=8，求AD 的长度．五、综合题（10分）22．如图，在梯形ABCD 中，AD∥BC，∠B＝90°，AD=16cm，AB＝12cm，BC＝21cm，动点P 从点B 出发，沿射线BC 的方向以每秒2cm 的速度运动，动点Q 从点A 出发，在线段AD 上以每秒1cm 的速度向点D 运动，点P，Q 分别从点B，A 同时出发，当点Q 运动到点D 时，点P 随之停止运动，设运动的时间为t（秒）。