线性分组码的matlab实现

matlab求解方程组代码
要在MATLAB中求解方程组，你可以使用`linsolve`函数或者反斯密特正交分解（QR分解）来求解线性方程组。

假设你有一个形如Ax = b的线性方程组，其中A是系数矩阵，x是未知向量，b是常数向量。

首先，使用`linsolve`函数可以直接求解线性方程组。

例如，如果你有一个3x3的系数矩阵A和一个3x1的常数向量b，你可以这样做：
matlab.
A = [1 2 3; 4 5 6; 7 8 10];
b = [3; 6; 10];
x = linsolve(A, b);
另一种方法是使用QR分解来求解方程组。

你可以使用MATLAB 中的`qr`函数来进行QR分解，然后使用得到的分解来求解方程组。

这是一个示例代码：
matlab.
A = [1 2 3; 4 5 6; 7 8 10];
b = [3; 6; 10];
[Q, R] = qr(A);
y = Q'b;
x = R\y;
以上是两种常见的方法，你可以根据具体情况选择合适的方法来求解你的线性方程组。

希望这些信息能帮助到你。

实验四 纠错编码基本实验一、实验目的1、通过实验理解线性分组码的基本原理；2、练习根据理论分析自行设计实验方法的能力。

二、实验内容1、已知一(10,4)线性分组码的生成矩阵为1001110111111000111001101101011101111001G ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦试用Matlab 求出该码的全部码字和最小汉明距离。

2、用Matlab 求x 15+1的所有因子，构造(15,4)循环码的所有可能的生成多项式；选择其中一个作为(15,4)循环码的生成多项式，求出所有的许用码字，并计算最小汉明距离。

三、实验原理1、线性生成码的原理线性分组码的构成方式是把信息序列分成每k 个码元一段，并由这k 个码元按一定规则产生r 个校验位，组成长度为n = k + r 的码字，用(n, k) 表示信息码元与校验位之间为线性关系。

一个[n ,k ]线性分组码，是把从信源输出的以k 个码元为一组的信息组m ，通过信道编码器后，变成长度为n ≥k 的码组（码字）c 作为[n ,k ]线性分组码的一个码字。

设GF(q )是一个含有q 个元素的有限数域，若每位码元的取值有q 种（取自GF(q )），则信息组m 共有kq 种不同的状态，因此，需要kq 个码字c 。

而长为n 的数组共有nq 个，二进制时(q =2)共有n2个。

显然，nq 个n 维向量组成有限域GF(q )上的一个n 维线性空间V ，编码就是要在这个n 维线性空间中选出k q 个向量作为合法码字，其余的n q -kq 个向量为禁用码字。

如果选出的kq 个作为合法码字的向量的集合构成了V 的一个k 维线性子空间，则称它是一个q 进制[n ,k ]线性分组码。

如果值取自GF(q )上的[n ,k ]分组码的kq 个码字的集合C ，便构成了有限域GF(q )上的n 维线性空间V 的一个k 维线性子空间，则称C 是一个q 进制[n ,k ]线性分组码。

摘要近年来，随着计算机、卫星通信及高速数据网的飞速发展，数据的交换、处理和存储技术得到了广泛的应用，人们对数据传输和存储系统的可靠性提出了越来越高的要求。

因此，如何控制差错、提高数据传输和存储的可靠性，成为现代数字通信系统设计工作者面临的重要课题。

目前，几乎所有得到实际应用的纠错码都是线性的。

线性分组码的应用上越来越广泛，首先介绍有关纠错码的基本概念，然后重点论述线性分组码的定义及其编译码理论。

再编制MATLAB程序对其纠错能力进行仿真。

关键词：纠错；线性分组码；MATLAB目录1 课题描述 (1)2设计原理 (1)2.1 线性分组码的基本原理 (1)2.2 线性分组码编码过程 (2)3设计过程 (5)3.1设计思路 (5)3.2设计内容 (6)总结 (8)参考文献 (9)1 课题描述数字通信最主要的优点之一是抗干扰能力强 ,采用各种差错控制编码进一步改善传输质量 ,因此差错控制编码是对数字信号进行抗干扰编码 ,目的是提高数字通信的可靠性.随着差错控制编码理论和数字技术的发展 ,差错控制编码在各种通信系统中得到了广泛的应用.差错控制编码的方法很多 ,线性分组码是其中的一种重要方法.线性分组码的检错和纠错能力由检错和纠错定理给出.现有的教科书在证明该定理时直接把一个码字看成一个点 ,这在逻辑上是不成立的.在分组码中 ,把两个码组对应位上数字不同的位数称为码组的距离 ,简称码距 ,又称汉明 (Ham2ming)码距.一种编码的最小码距 dmin 的大小直接关系着这种编码的检错和纠错能力 ,因而最小码距是信道编码的一个重要参数 ,在一般情况下 ,对于分组可以通过检错编码定理进行计算，同样可以编写matlab 程序进行仿真。

2设计原理2.1 线性分组码的基本原理1、在长为n 的二元序列集中选出与消息序列数2k 相同数目的码元序列，并使两者一一对应。

几个概念：码字：对应于消息的长n 的2k 个码元序列，用 c 表示。

二、创新实验设计创新实验一：（7,4）汉明码的编码与译码实现1、实验目的实现（7,4）汉明码的编码与译码，通过这次实验不但加深了对汉明码编码和译码原理了解，而且对线性分组码有所了解。

2、实验原理线性分组码的构造方法比较简单、理论较为成熟，应用比较广泛。

汉明码是一种能够纠正一个错码的效率比较高的线性分组码，下面以（7,4）码为例就汉明码的编码与译码分别进行介绍：（1）编码原理一般来说，若汉明码长为n ，信息位数为k ，则监督位数r=n-k 。

若希望用r 个监督位构造出r 个监督关系式来指示一位错码的n 种可能位置，则要求21r n -≥或211rk r -≥++ (1)设汉明码（n,k ）中k=4，为了纠正一位错码，由式（1）可知，要求监督位数r ≥3。

若取r=3,则n=k+r=7。

这样就构成了（7,4）码。

用6543210a a a a a a a 来表示这7个码元，用123s s s 的值表示3个监督关系式中的校正子，则123s s s 的值与错误码元位置的对应关系可以规定如表1所列。

表2.1 校正子和错码位置的关系则由表1可得监督关系式：16542s a a a a =⊕⊕⊕()226531s a a a a =⊕⊕⊕()3 36430s a a a a =⊕⊕⊕()4 在发送端编码时，信息位6543a a a a 的值决定于输入信号，因此它们是随机的。

监督位2a 、1a 、0a 应根据信息位的取值按监督关系来确定，为使所编的码中无错码，则123,,S S S 等于0，即65426531643000(5)0a a a a a a a a a a a a ⊕⊕⊕=⎧⎪⊕⊕⊕=⎨⎪⊕⊕⊕=⎩方程组（5）可等效成如下矩阵形式6543210111010001101010010110010a a a a a a a ⎡⎤⎢⎥⎢⎥⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎢⎥⎣⎦（6）式(6)可简化为0T T HA =，H 为监督矩阵，则由式(6)可得到监督矩阵11101001101010=[P I ] (7)1011001r H ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦因为生成矩阵'=[I Q]=[I ]k k G P ，所以由(7)得生成矩阵G 如下：[]k 10001110100110[']00101010001011k G I Q I P ⎡⎤⎢⎥⎢⎥===⎢⎥⎢⎥⎣⎦然后利用信息位和生成矩阵G 相乘产生整个码组，即有[][]65432106543=(8)A a a a a a a a a a a a G=其中A 为整个码组矩阵，6543a a a a 是信息位。

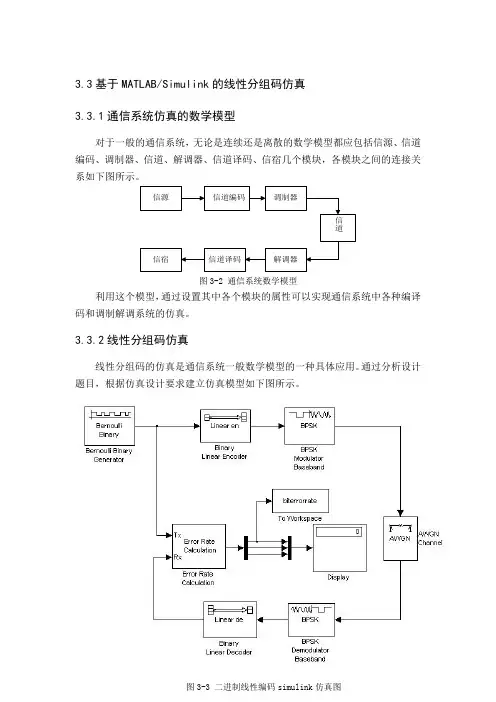
3.3基于MATLAB/Simulink的线性分组码仿真3.3.1通信系统仿真的数学模型对于一般的通信系统，无论是连续还是离散的数学模型都应包括信源、信道编码、调制器、信道、解调器、信道译码、信宿几个模块，各模块之间的连接关系如下图所示。

信源信道编码调制器信宿信道译码解调器信道图3-2 通信系统数学模型利用这个模型，通过设置其中各个模块的属性可以实现通信系统中各种编译码和调制解调系统的仿真。

3.3.2线性分组码仿真线性分组码的仿真是通信系统一般数学模型的一种具体应用。

通过分析设计题目，根据仿真设计要求建立仿真模型如下图所示。

图3-3 二进制线性编码simulink仿真图上图为二进制线性编码的simulink仿真图信源、信道编译码器和误码率计算器等模块的参数设置情况见表3-1至表3-6。

调制器选用调制性能较好的BPSK调制器；与调制和编码相对应的，解调器选用BPSK解调器，译码器选用二进制线性译码器。

本设计希望借助线性分组码的误码率曲线来研究其性能，所以需要加入误码率计算器（Error Rate Calculation）。

通过学习MATLAB/simulink相关知识，了解到误码率计算器输出三个结果：误码率、正确码元个数和错误码元个数。

设计所关心的是误码率，所以先用分路器将三路信号分离，然后将误码率的值输出到工作空间（workspace）便于提取每一秒的仿真数据，为了实现和显示模块（display）的连接，必须用合路器将分开的信号重新组合起来。

而选用Display作为显示模块，是因为它可以方便快捷的观察到三路输出信号的动态变化过程。

其中主要模块的参数设置如下表所示。

表3-1是信源模块的参数设置表，由于在实际通信过程中，具体环境不同信源信号的形式可能多种多样，为了模拟最一般的信号形式，图中信源选择能产生伯努利分布的二进制随机数的Bernoulli Random Binary Generator模块；编码器选用二进制线性编码器；表3-1 伯努利二进制随机数生成器（Bernoulli Random Binary Generator）参数表参数名称参数值Probability of zer（0出现的概率）0.5Initial seed（初始化种子）21375Sample time（抽样时间）0.0001Frame-based outputs（输出基于帧）√Samples per frame（每帧抽样数）(根据要仿真信号的信息位数设定数值如（7,4）码则此项值为4)研究二进制线性码的性能当然用二进制线性编码器。

竭诚为您提供优质文档/双击可除74线形分组码实验报告篇一：线性分组码实验报告综合性设计性实验报告专业：学号：姓名：实验所属课程：实验室(中心)：信息技术软件实验室指导教师：2一、题目线性分组码编译码实验二、仿真要求1.分别用不同的生成矩阵进行（7,4）线性分组码的编码，经调制解调后译码，并比较两种线性分组码的纠错能力。

2.掌握线性分组码的编码原理、编码步骤和译码方法。

3.熟悉matlab软件的基本操作，学会用matlab软件进行线性分组码的编码和译码。

三、仿真方案详细设计编码：本实验采用的是（7，4）线性分组码，线性分组码的编码由监督矩阵和生成矩阵实现，监督矩阵h为（3×4）的矩阵，由监督方程和（4×4）的单位矩阵构成，生成矩阵g为（4×7）的矩阵，由（4×4）的单位矩阵和监督矩阵的转置矩阵构成。

实现过程为：1、将要编码的序列先整形，整为4列2、如果序列不能被4整除在后边补0使其能被4整除3、将整形后的序列与生成矩阵g相乘即得到编码后的码字在本实验中，分别生成两种生成矩阵，在产生了生成矩阵后根据输入的四位信息位和生成矩阵相乘即可得到编码矩阵。

译码：在译码过程中，我们利用错误图样和伴随式来进行纠错。

1、设一个接收码字矩阵为R，R*h=s（模2乘），则s为码字对应的伴随式矩阵如果s=0则说明接受码字无差错；2、如果s不为0，查看矩阵s中不为0的那行所在行数，该行即收码字错误所在行i；3、将s转置，将不为0的一列与h每一列进行比较，找到h中相同列，该列的列数即为错误所在列；4、由步骤2和3得到错误具体位置，模2加对应的错误图样就可得到正确码字。

bpsK调制:bpsK调制利用载波的相位变化来传递数字信息，振幅和频率保持不变。

双极性的全占空矩形脉冲序列与正弦载波相乘就得到调制信号。

因此进行调制时首先进行码形变换变为双极性的，再经乘法器与载波相乘得到调制信号。

其具体实现方法如下：1、将0、1序列变为-1、1序列；2、将序列与载波相乘，为‘1’时与载波相位相同，为‘-1’时与载波相位相反。

LDPC（Low-Density Parity-Check）码是一种优秀的纠错编码技术，具有较低的解码复杂度和接近容量的性能。

LDPC码的译码算法可以使用数学推导来实现，也可以借助计算机进行编程实现。

在本文中，我们将介绍如何使用MATLAB编写LDPC码的译码算法，并给出具体的代码实现。

一、LDPC码的基本原理LDPC码是一种线性分组码，由Gallager于1962年首次提出。

它是一种分布式稀疏矩阵编码，其校验矩阵的权重分布较为均匀，是一种充分利用了校验密度低的码。

LDPC码的译码算法通常采用迭代译码的方式，通过不断更新变量节点和校验节点的信息来逐步逼近发送端发送的原始信息。

LDPC码的译码算法有多种实现方式，其中以BP算法（Belief Propagation）最为常见。

二、BP算法的基本思想BP算法是一种迭代译码算法，其基本思想是将LDPC码的译码过程转化为图论中的消息传递过程。

在BP算法中，变量节点和校验节点之间通过消息传递的方式来更新各自的信息，并不断迭代直到收敛为止。

BP算法的收敛性和解码性能与LDPC码的结构和参数设置密切相关，因此需要仔细选择合适的算法参数和调整策略。

三、MATLAB代码实现1. 参数设置在MATLAB中，我们首先需要设置LDPC码的参数，包括码长、码率、校验矩阵等。

通过调用MATLAB中的矩阵运算库，我们可以方便地实现LDPC码的相关参数设置。

2. 译码算法实现接下来，我们编写LDPC码的译码算法。

在MATLAB中，我们可以利用向量化操作和矩阵运算来高效地实现BP算法。

需要注意的是，由于BP算法是一种迭代算法，我们需要设置适当的迭代次数和终止准则。

3. 性能评估我们可以利用MATLAB中的仿真工具来评估LDPC码的译码性能。

通过绘制误比特率曲线和分析译码性能参数，可以直观地了解LDPC码的表现，并进一步优化译码算法。

四、总结在本文中，我们介绍了LDPC码的基本原理和BP算法的实现方式，并给出了在MATLAB中的代码实现方法。