当前位置：文档之家 › 力矩力偶与平面力偶系

力矩力偶与平面力偶系

  • 格式：ppt
  • 大小：1.37 MB
  • 文档页数：24

下载文档原格式

  / 24

合集下载

工程力学I-第3章 力矩与平面力偶系

工程力学I-第3章 力矩与平面力偶系

D
x
§3-2 关于力偶的概念

力偶：一对等值、反向而不共线的平行力，用 符号（F ,F′）表示。

力偶臂：两个力作用
线之间的垂直距离d。

F’
F
力偶的作用面：两个 力作用线所决定的平 面
§3-2 关于力偶的概念
F F
d
d
F
d
F
F
F
转动游戏方向盘
拧水龙头
扳手拧螺母
§3-2 关于力偶的概念

Q AABD AABC 显然， 并注意到力偶矩的转向也相同， 则有M ( F , F ) M ( P, P) P
M (P 1, P 1 ) M ( P, P ) 显然， 1, P 1) 从而有M ，( F , F ) M ( P
P1
力偶等效
M ( F , F ) M ( P 1, P 1)
（1）力对点之矩，不仅取决于力的大小，还与矩心的位置有关。
（2）力对任一点之矩，不因该力的作用点沿其作用线移动而改变。 *（3）力的大小等于零或其作用线通过矩心时，力矩等于零。 （4）互成平衡的两个力对同一点之矩的代数和为零。
Mo(F)＝±Fd
§3-1 关于力矩的概念及其计算

合力矩定理：
y Fy
(3)将力P和P’沿各自的作用 线移至任意点A’，B’，根 据力的可传性原理，有 (P,P’) =(P1,P1’) 。
§3-2 关于力偶的概念
(4) A′
P1′ b F′ A A F B Q′ D P′ B′ C
M (F , F ) AB BD 2 AABD ,
M（P, P'） AB BC 2 AABC

力对点的矩与平面力偶系—平面力偶系的合成与平衡(建筑力学)

力对点的矩与平面力偶系—平面力偶系的合成与平衡(建筑力学)

平面力偶系
例3-4 如图示的梁AB，受一力偶的作用，已知力偶， M=20kNm，梁长l=4m,梁自重不计，求A、B支座处反力。
解 取梁AB为研究对象。
梁在力偶和A、B两处支座反力作用下平衡。
M 0
FByl M 0
FBy
M l
20 kN 5kN 4FAyLeabharlann FBy 5kN平面力偶系
第三节 平面力偶系的合成与平衡
作用在物体上的两个或两个以上的力偶，称为力偶系。 作用在同一平面内的力偶系称为平面力偶系。 一、平面力偶系的合成
平面力偶系可以合成为一个合力偶，其合力偶矩等于各个 力偶矩的代数和。即
M R M1 M 2 M n M
式中MR表示合力偶矩, M 、M … … Mn表示原力偶系中各 力偶的力偶矩。
合力偶矩大小为
M M1 M 2 M 3 (64 60 24)N m 28N m （ ）
平面力偶系
二、平面力偶系的平衡条件 平面力偶系合成的结果为一个合力偶，力偶系的平衡就
要求合力偶矩等于零。 平面力偶系平衡的必要和充分条件是：力偶系中所有各
力偶矩的代数和等于零。
M 0
上式又称为平面力偶系的平衡方程。利用其可以求解一 个未知量。
平面力偶系
例3-3 如图示有三个力偶同时作用在物体某平面内。已知 F1=80N，d1=0.8m，F2=100N ，d2=0.6m，M3=24N.m ，求其合 成的结果。
解 三个共面力偶合成的结果是一个合力偶。各力偶矩为
M1 F1d1 80 0.8 64N m M 3 24N m
M 2 F2d2 100 0.6 60N m

第三章 力偶与平面力偶理论)

第三章 力偶与平面力偶理论)

M 0 F F h
力对点之矩（力矩）是一个代数量，它的绝 对值等于力的大小与力臂的乘积；
它的正负：力使物体绕矩心逆时针转向时为正，反之为负。 常用单位为 N· m 或 kN· m。 注意：力矩在下列几种情况下等于零 （1）力的大小等于零；
（2）力的作用线通过矩心，即力臂等于零；
（3） 互成平衡的二力对同一点之矩为零。
78.93N m
按合力矩定理 M O F M O Ft M O Fr



F cos θ r 78.93N m
例3-2 已知：q,l； 求： 合力及合力作用线位置. 解： 取微元如图
x q q l l x 1 P q dx ql 0 l 2
M Mi Mi
i 1 n
平面力偶系平衡的充要条件 M = 0，有如下平衡方程
Mi
0
平面力偶系平衡的必要和充分条件是：所有各力 偶矩的代数和等于零。
例3-1
已知: F=1400N, θ 20 , r 60mm
求: M O F .
解:直接按定义
MO

F F h F r cos θ
M1 F1 d M2 F2 d
M1 F1d
M 2 F2d
Mn Fn d
M n Fnd
=
=
FR F1 F2 Fn
F1 F2 Fn FR
=
=
=
M FRd F1d F2d Fnd M1 M 2 M n
定理：同平面内的两个力偶，如果力偶矩相等，则两力偶 彼此等效。 推论： 任一力偶可在它的作用面内任意转移，而不改变它对刚体 的作用。因此力偶对刚体的作用与力偶在其作用面内的位置无 关。 只要保持力偶矩不变，可以同时改变力偶中力的大小与 力偶臂的长短，对刚体的作用效果不变.

第三章-力矩和平面力偶系-第四章-平面任意力系

第三章-力矩和平面力偶系-第四章-平面任意力系

例3－1 试计算力对A点之矩。
解 本题有两种解法。 方法一： 按力矩的定义计算 由图中几何关系有：
d=ADsinα =(AB-DB)sinα =(AB- BCctgα)sinα =(a- bctgα)sinα =asinα-bcosα
所以
mA(F)=F•d =F(asinα-bcosα)
方法二：
解：
图（a）：
MA = - 8×2 = -16 kN ·m
MB = 8×2 = 16 kN ·m
图（b）： MA = - 4×2×1 = -8 kN · m
MB = 4×2×1 = 8 kN ·m
第二节 力偶
▪ 一、力偶 力偶矩
▪
在日常生活和工程实际中经常见到物体受动两个大小相等、方向相反，
但不在同一直线上的两个平行力作用的情况。例如
2．力偶矩：
▪ 作为力偶对物体转动效应的量度，称为力偶矩，
用m或m( F ,F′)表示。在平面问题中，将力偶中
的一个力的大小和力偶臂的乘积冠以正负号，如图：
即m(F)＝F•d=±2ΔABC
通常规定：力偶使物体逆时针方 向转动时，力偶矩为正，反之为 负。
在国际单位制中，力矩的单位 是牛顿•米（N•m）或千牛顿•米 （kN•m）。
▪
在同一平面内的两个力偶，只要两力偶的
力偶矩的代数值相等，则这两个力偶相等。这
就是平面力偶的等效条件。
▪ 根据力偶的等效性，可得出下面两个推论：
▪ 推论1 力偶可在其作用面内任意移动和转动， 而不会改变它对物体的效应。
▪ 推论2 只要保持力偶矩不变，可同时改变力 偶中力的大小和力偶臂的长度，而不会改变它 对物体的作用效应。
主矩： Mo=m1+m2+···+mn

工程力学第三章力矩与平面力偶系

工程力学第三章力矩与平面力偶系

位置无关，因此力偶对刚体的效
应用力偶 矩度量。
F
A B
d
F'
x
O
mO ( F ) mO ( F ') F ( x d ) F 'x F d
4.力偶的表示方法
用力和力偶臂表示，或用带箭头的弧线表示，箭头表示 力偶的转向，M表示力偶的大小。
第三章力矩与平面力偶系
湖南工业大学土木工程学院
y

Fx
x
则
r cos x, r sin y
mo ( F ) xFy yFx
湖南工业大学土木工程学院
( )
a
第三章力矩与平面力偶系
§3-1力矩的概念和计算
mo (F ) xFy yFx
若作用在
( )
a
y
Fy
F

F2 、 A 点上的是一个汇交力系（ F1 、 则可将每个力对 o 点之矩相加，有 Fn ）， o
r
d
，
x
A
y

Fx
m (F ) x F
o
y
y Fx
(b)
x
由式（ a ），该汇交力系的合力 R 它对矩心的矩
F
m0 (R) xRy yRx x Fy y Fx ( c )
比较（ b ）、（ c ）两式有
mo (R) M o (F )
第三章力矩与平面力偶系 湖南工业大学土木工程学院
l
A
o
第三章力矩与平面力偶系 湖南工业大学土木工程学院
d
F
力矩计算
简支刚架如图所示，荷载F=15kN，α=45 ,尺寸如图。试分别计 算F对A、B两点之矩。

力对点的矩和平面力偶系

力对点的矩和平面力偶系

第三章 力对点的矩和平面力偶系一、内容提要本章研究了力矩和力偶。

1．力矩及计算（1）力矩 力矩表示力使物体绕矩心的转动效应。

力矩等于力的大小与力臂的乘积。

在平面问题中它是一个代数量。

一般规定：力使物体绕矩心产生逆时针方向转动为正，反之为负。

用公式表达为()Fd F M O ±=（2）合力矩定理 平面汇交力系的合力对平面内任一点的力矩，等于力系中各力对同一点的力矩的代数和。

用公式表达为()()F M F M O O ∑=R2．力偶的基本理论（1）力偶 由两个大小相等、方向相反、不共线的平行力组成的力系，称为力偶。

力偶与力是组成力系的两个基本元素。

（2）力偶矩 力与力偶臂的乘积称为力偶矩。

为代数量，规定：逆时针方向转动为正，反之为负。

用公式表达为：Fd M ±=（3）力偶的性质力偶不能合成为一个合力，不能用一个力代替，力偶只能与力偶平衡。

力偶在任一轴上的投影恒为零。

力偶对其平面内任一点矩都等于力偶矩，与矩心位置无关。

在同一平面内的两个力偶，如果它们的力偶矩大小相等，转向相同，则这两个力偶等效。

力偶对物体的转动效应完全取决于力偶的三要素：力偶矩的大小、力偶的转向和力偶所在的作用面。

（4）平面力偶系的合成与平衡平面力偶系的合成结果为一个合力偶，合力偶矩等于平面力偶系中各个力偶矩的代数和。

用公式表达为：M R =ΣM平面力偶系的平衡条件是合力偶矩等于零。

用公式表达为：ΣM = 0二、思考题提示或解答3-1 试比较力矩与力偶矩的异同点。

答：平面汇交力系的合力对平面内任一点的力矩，等于力系中各分力对同一点的力矩的代数和。

这就是平面力系的合力矩定理。

应用合力矩定理在于简化力矩的计算。

当力臂不易确定时，可将力分解为易找到力臂的两个互相垂直的分力，在求出两分力的力矩后，再代数相加即可。

3-3 二力平衡中的两个力，作用与反作用公理中的两个力，构成力偶的两个力各有什么不同?答：二力平衡中的两个力等值、反向、共线，共同作用在一个物体上；作用与反作用公理中的两个力等值、反向、共线，分别作用在两个物体上； 构成力偶的两个力等值、反向、互相平行，也作用在一个物体上。

力矩和平面力偶系

力矩和平面力偶系

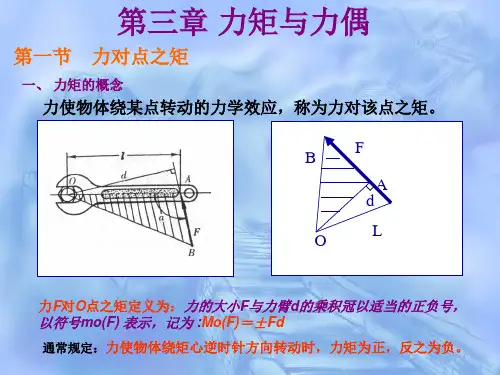
第五节力矩和平面力偶系一、力矩1．力矩概念力对刚体的移动效应取决于力的大小、方向和作用线；而力对刚体的转动效应则用力矩来度量。

实践告诉我们，用扳手拧（转动）螺母时，见图7-18a，其转动效应取决于力F的大小、方向（扳手的旋向〕以及力F到转动中心O的距离h。

a) b)图7-18 力矩概念一般情况下，刚体在图示平面内受力F作用，见图7-18b，并绕某一点O转动，则点O称为矩心，矩心O到力F作用线的距离h称为力臂，乘积F·h并加上适当的正负号称为力对O点之矩，简称力矩，用符号M O（F）或M O表示。

即M O＝M O（F）＝±Fh （7-9）力矩的正、负号规定如下：力使刚体绕矩心作逆时针方向转动时为正，反之为负。

因此，力矩是一个与矩心位置有关的代数量。

力矩的单位为N·m。

2．合力矩定理设刚体受到一合力为F的平面力系F1，F2，…，F n的作用，在平面内任取一点O为矩心，由于合力与整个力系等效，所以合力对O点的矩一定等于各个分力对O点之矩的代数和（证明从略），这一结论称为合力矩定理。

记为M O（F）＝M O（F1）＋M O（F2）＋…＋M O（F n）＝ΣM O（F i）（7-10）或M O＝M O l＋M O2＋…＋M O n＝ΣM Oi=ΣM O例7-4图7-19所示为一渐开线（在平面上，一条动直线（发生线）沿着一个固定的圆（基圆）作纯滚动时，此动直线上一点的轨迹）直齿圆柱齿轮，其齿廓在分度圆上的P点处受到一法向力F n的作用，且已知F n＝1000N，分度圆直径d＝200mm，分度圆压力角(P点处的压力角)α＝20°，试求力F n对轮心O点之矩。

图 7-19 力炬计算举例解：1．根据力矩的定义求解m N 94m N 20cos 22.01000cos 2)(⋅-=⋅⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛︒⨯-=⎪⎭⎫ ⎝⎛-=-=αd F h F F M n n n O 2．用合力矩定理求解。

力矩平面力偶

力矩平面力偶

30◦
B RB
∑ mi = 0
R A ⋅ L sin 30o = M 2M 方向如图所示 R A = RB = L
15
16
NB =
60 = 300N 0.2
N A = N B = 300 N
14
平衡时, 处和 处的反力 处和B处的反力? [例2] 已知M 和 L，图示梁AB平衡时,A处和 处的反力? 解: BC 杆为二力杆
C M A L M RA
RB 沿BC 杆方向
由力偶只能与力偶平衡的性质， 由力偶只能与力偶平衡的性质， 与力R 组成一力偶。 力RA与力 B组成一力偶。 根据平面力偶系平衡方程有: 根据平面力偶系平衡方程有:
1
第三章 平面汇交力系 §3–1 力对点之矩 §3–2 力偶与力偶矩 §3–3 力偶的等效 §3–4 平面力偶系的合成与平衡
2
§3-1 力对点之矩
一、平面上力对点之矩 力对物体可以 产生运动效应 移动效应——取决于力的大小、方向 取决于力的大小、 移动效应 取决于力的大小
转动效应——取决于力矩的大小、转向 取决于力矩的大小、 转动效应 取决于力矩的大小 r 点的矩， 力F 对O 点的矩，简称力矩 M O F = ± F ⋅ d + O 点称为力矩中心（简称矩心） 点称为力矩中心（简称矩心）
(
)
现沿力偶臂AB方向 现沿力偶臂 方向 r r 加一对平衡力 Q， Q′ r r r r r r 将Q， F合成R， 将Q′， F ′合成R′， r r 得到新力偶 R， R′ r r r r r r 将R和R′移到 A′, B′点， 则 R , R′ 取代了原力偶 F , F ′ ，
(
)
(
( )
( )

力矩与平面力偶系

力矩与平面力偶系

工程力学与建筑结构
1.4 力偶的合成 作用在同一物体上的若干个力偶组成一个力偶系，若
力偶系中各力偶均作用在同一平面，则称为平面力偶系。 平面力偶系合成的结果为一合力偶，其合力偶矩等于
各分力偶矩的代数和。即 M =M1＋M2＋…＋Mn=∑M
1.5力偶系的平衡条件 平面力偶系平衡的必要和充分条件是：力偶系中各力
偶矩的代数和为零。即 ∑M=0
工程力学与建筑结构
工程力学与建筑结构
工程力学与建筑结构
力矩与平面力偶系 1.1力矩的概念
用力的大小F与d的乘积度量力F使扳手绕O点的转动 效示应。，即称为力F对O点之矩，简称力矩，用符号MO（F）表
MO（F）=±Fd 式中，O点称为“矩心”，d称为“力臂”。 力矩的正负规定为：力使物体绕矩心逆时针方向转动时， 力矩为正；反之为负。
M=±Fd
力偶矩的正负规定与力矩正负规定一致，即：使物体 逆时针方向转动的力偶矩为正；反之为负。
F
F
B
h
铰杠
丝锥
F'
F d
F'

A
(a)
F' (b)
(c)
工程力学与建筑结构
在平面问题中，力偶矩也是代数量。力偶矩的单位与力矩 单位相同，即N•m。 根据力偶的概念可以证明，力偶具有以下性质： （1）力偶在其作用面上任一轴的投影为零。 （2）力偶对其作用面上任一点之矩，与矩心位置无关，恒 等于力偶矩。
系中所有分力对同一点之矩的代数和。
MO（FR）=MO（F1）＋ MO （F2）＋…＋ MO （Fn）=∑ MO （F）
F1 y
A
FR
F2
O x
工程力学与建筑结构
1.3 力偶的概念

力矩与平面力偶系

力矩与平面力偶系
4.力偶没有合力，力偶只能由力偶来平衡.
5.力偶对物体不产生移动效应，只产生转动效应。
力偶的三要素： 力偶对物体的转动效应，取决于下列三个因素： 1.力偶矩的大小 2.力偶的转向 3.力偶的作用面
1 8
§3-3平面力偶系的合成和平衡条件
平面力偶系：作用在物体上同一平面内的若干力偶。
已知：M1, M2 ,Mn;
FAl M1 M 2 M3 0
解得
FA
FB
M1
M2 l
M3
200N
2 2
综合例题
已知 M 2kN m,OA r 0.5m,θ 30 ; 1
求：平衡时的 M 2及铰链O，B处的约束力.
解：取轮,由力偶只能由力偶平衡的性质,画受力图.
M 0 M1 FA r sin 0
解得 FO FA 8kN
cos
AB
r2
r1
cos
d
AB
cos
r2
cos
r1
mA (F ) Fd F (r1 r2 cos )
1 0
§3-2 平面力偶理论
一.力偶和力偶矩
1.力偶
由两个等值、反向、作用线平行的力组成的力系称为力偶，
记作
F
,
F
1
1
2.力偶矩 力偶中两力所在平面称为力偶作用面
力偶两力之间的垂直距离称为力偶臂
:逆时针转动为正,反之为负.
力对点之矩是一个代数量，它的绝对值等于力的大小与力臂
的乘积，它的正负：力使物体绕矩心逆时针转向时为证，反之为
负.常用单位Nm或kNm
4
例:F=50N,d=0.3m. 求F力对O点之矩. 解:Mo(F)= Fd = … = 15Nm (1)当F=0,或d=0（力作用线通过矩心）时，力矩为零。 (2)当力沿其作用线 滑移时，力矩不变。 (3)力矩与矩心有关。 在平面问题中，力对点之矩实际上指力使物体绕通过矩心的 某一轴转动效果的度量，该轴垂直于由力的作用线和矩心所 决定的平面。

理论力学03力矩力偶与平面力偶系

理论力学03力矩力偶与平面力偶系

本章讨论平面力偶系的合成与平衡问题
一、平面力偶系的合成 平面力偶系可合成为一个合力偶； 合力偶矩等于各分力偶矩的代数和，即
M1
M2 M3
M4
M Mi
二、平面力偶系的平衡方程
Mi 0
M
说明：根据平面力偶系的平衡方程，可解 一个未知量。
ቤተ መጻሕፍቲ ባይዱ
[例2] 已知梁长 l = 5 m，M = 100 kN·m ；若不计梁的自重，试求 铰支座 A 、B 处的约束力。
2. 力偶中的两个力对任一点的矩的代数和 恒等于力偶矩，与矩心位置无关。
dF F
3. 作用于刚体同一平面内两个力偶等效的充要条件为其力偶矩 相等。
结论：力偶矩唯一决定了力偶对刚体的作用效应。
◆ 通常用力偶矩符号来代表力偶：
F
d
M Fd
F
M 或M
第三节 平面力偶系
平面力偶系：由位于同一平面内的一群力偶所组成的力系
构平衡。试求作用于摆杆 BO1上的力偶矩 M2 （各构件的自重不计）
解： 1）首先研究曲柄 AO与套筒A 的组合 画受力图 列平衡方程
Mi 0, M1 FA r sin 30 0
解得
FA
FO
2M1 r
M1
O
FO
FA
FA
FO
2M1 r
2）再选取摆杆 BO1 为研究对象
画受力图
列平衡方程
Mi 0, M 2 FA AO1 0
的平行力称为一个力偶，记作 F, F。
dF F
二、力偶矩 定义
M Fd
为平面内力偶 F, F 的矩，简称力偶矩。
说明： 1）平面内力偶矩为代数量，其正负号表转向，一般规定 逆时针转向为正，反之为负。

力矩与平面力偶系课件

力矩与平面力偶系课件
- F22d ＝M2
FR＝F11-F22
d2F1有作偶个一力设用两平同内成系偶合力平的一.
FR' ＝ F11 '-F22 '
MR = FR d= ( F11- F22 )d
=F1 1d- F22 d= M 1 - M2
F1
F
d1
2
d2
F1'
F'
2
F2
2
F11'
d
F11
F22
'
FR' d
F
R
? MR为合力F R ，F R '组成的力偶(F R ，F R ' ) (称 为合力偶)的力偶矩， 称为合力偶矩； 也是原来两个力 偶的力偶矩的和。
作偶对该力用面)内偶力的‘，F物体有作偶臂一力设用为(
力偶对作用面内任一点的矩之大小恒等于力偶中 一力的大小和力偶臂的乘积，而与矩心的位置无关。
力偶对物体的转动效应可用力与力偶臂的乘积Fd 及转向来度量，该物理量称为力偶矩。
?力偶矩用符号M (F ，F')或M表示；即 M (F ，F') = ±Fd 规定：逆时针转动时，力偶矩取正号；
?力的作用线如通过矩心，则力矩为零； 反之，如一个大小不为零的力对一点之 矩为零，则此力的作用线必通过该点。
?互成平衡的二力对同一点的力矩之和为 零
虽然力矩概念由力对物体上固定点的 作用引出。实际上，作用于物体上的力 可以对任意点取矩，即矩心可是空间中 的任意点。
二．力对轴的矩
力对轴的矩用来度量力对 所作用的刚体绕某一固定轴转 动的效应。
a
，力偶矩为 -
4
3
Fa F1y与F2y组成一个力偶，力偶臂为1

工程力学5 力偶及平面力偶系的合成

工程力学5 力偶及平面力偶系的合成

M 60° 30°
0.25m
数值为正，M使物体顺时针转动，计算时数值为负。
M1=P1d1=200 ×1=200(N·M) M2=P结2d果2=为60正0 数×，0.2代5/表si最n3后0°合=成300(N·M)
M3=-M的=合-1力00偶(N为·M逆) 时针，即：物
P2
P1
则合力体偶最M后合为将：逆时针转动。
即： M i 0
平面力偶系的平衡条件有何作用呢？
例题2：如图所示，梁AB受荷载作用。M=10kN·m，P=P’=5kN，
不计梁自重，求支座A、B的反力。
解：取AB为研究对象。作用在梁
P
M 上的力有：M、P和P’形成的力
A
B
偶，以及支座A和B的反力形成的
P'
力偶。由于梁处于平衡状态，因
此，整个体系力偶矩之和为零。
力偶三要素：力偶矩的大小、力偶的转向和力偶的作用面。
10KN 2m
5KN
20KN
1m
M=20KN ·m
10KN
5KN
20KN
3.平面力偶系的合成
10KN 5KN
2m
20KN
10KN
5KN
1m 20KN
在物体的某一平面内同时作用有两个或两个以上的力偶时， 这些力偶就称为平面力偶系。
（1）平面力偶系的合成
1m
M合=M1+M2+M3
=200+300-100=400(N·M)
3.平面力偶系的合成
（2）平面力偶系的平衡条件
平面力偶系可以合成为一个合力偶，当合力偶矩等于零时，则 力偶系中各力偶对物体的转动效应相互抵消，物体处于平衡状态； 反之，当合力偶不等于零时，物体必有转动效应而不平衡。平面力 偶系平衡的充要条件是：力偶系中所有各力偶矩的代数和等于零。

力矩与平面力偶系 PPT课件

力矩与平面力偶系 PPT课件
F1 d A F 1 B A F2 D ABD , M ( P , P ) 2 S ABC S ABD S ABC M ( F , F ) M ( P , P ) M ( P , P ) M ( P1 , P1) M ( F , F ) M ( P1 , P1)
F′ F
F2 F O F1
o 图 3-2 (b)
图 3-2 (c)
2. 合力矩定理 表达式： M O ( FR ) M O ( F ) 证明：由图得 y
M O ( F ) F d F r sin( ) F r (sin cos sin cos ) F r sin cos
图 3-4
图3-5
(2) 力偶的性质 (a) 力偶在任何坐标轴上的投影等于零； (b)力偶不能合成为一力，或者说力偶没有合力， 即它不能与一个力等效，因而也不能被一个力平 衡； (c) 力偶对物体不产生移动效应，只产生转动效 应，即它可以也只能改变物体的转动状态。
F d F′ 力偶作用面 力偶臂
图3-6
而
O x r Fy F
A

y Fx x

F r sin cos
F cos Fx , F sin Fy r cos x A , r sin y A
d
M

图 3-3
则
MO (F) xA Fy yA Fx
(a)
MO (F) xA Fy yA Fx
谁曾经想过用杠杆来移动地球？ 古希腊科学家阿基米德曾说过“如果给我一个支点，我就能
撬起地球”。这句名言从理论上讲是完全正确的，
因为杠杆能使力变大，只要杠杆足够长，就 能产生足够大的力来“搬动”地球。

力偶矩 平面力偶系的简化

力偶矩 平面力偶系的简化
偶臂的长短。
讨论平面力偶系的简化问题 设平面力偶系由n个力偶组成，其力偶矩分别为 M1 ，M2 ， ，Mn
图2-7 平面力偶系的简化
（1）保持各力偶矩不变，同时调整其力与力偶臂，使其有共同的臂长d。
由于 M i Fidi Fpid ，所以有
Fpi
Fi
di d
(i 1，2 ， ，n)
（2）将各力偶在平面内移动和转动，使各对力的作用线分别共线。
（3）求各共线力系的代数和，每个共线力系得一合力，而这两个合力
等值、反向，相距为d，构成一个合力偶，其力偶矩为
n
n
M FRd Fpid Mi
i 1
i 1
即平面力偶系可以用一个力偶等效代替， 其力偶矩为原来各力偶矩的代数和。
图 2-8
理论力学
力ห้องสมุดไป่ตู้不能与单个力等效，也不能与单个力相平衡
力和力偶是静力学中的两个基本要素。
根据力偶的特性，可以得到一个重要的结论，即同平面内力 偶的等效定理：
同一平面内的两个力偶等效的唯一条件是其力偶矩相等。
该定理等价于下列事实： （1）力偶矩是力偶作用的唯一量度。 （2）在力偶矩不变的前提下，可以在作用面内任意移动和转动力偶。 （3）在力偶矩不变的前提下，可以同时改变力偶中力的大小和力
理论力学
力偶矩 平面力偶系的简化
力偶是由一对等值、反向、不共线的平行力组成的特殊力系。 它对物体的作用效果是使物体转动。
力偶中的两个力对其作用面内某点之矩的代数和，称为该力
偶的力偶矩，记为
，M简(F记，为F )M。
如图2-6所示：
F 与F 组成一个力偶，两力之间的距离d，称为力偶臂。
在力偶作用面内任选一点O，设点O到力 F 的距离为a； 按定义，该力偶的力偶距 M (F ，F) 为

建筑力学课件 第四章 力矩与平面力偶系

建筑力学课件 第四章 力矩与平面力偶系
力矩的概念可以推广到普遍的情形。在具 体应用时，对于矩心的选择无任何限制， 作用于物体上的力可以对平面内任一点取 矩。
4.1力对点之矩、合力矩定理
3.力矩的性质 综上所述，得出如下力矩性质：
（1）力F对点O的矩，不仅决定于力的大 小，同时与矩心的位置有关。矩心的位 置不同，力矩随之而异。
（2）力F对任一点的矩，不因为F的作用 点沿其作用线移动而改变，因为力和力 臂的大小均未改变。
2.力矩的计算
在平面问题中,我们把乘积Fd加上适当的正负号,
作为力F使物体绕点O转动效应的度量,并称为
力F对点O的矩,简称力矩,用Mo(F) 或MO表示
即 MO (F)=± Fd
（4-1）
点O称为矩心，力作用线到矩心的垂直距离d称
为力臂。正负号通常用来区别力使物体矩心
转动的方向，并规定：若力使物体绕矩心作
4.1力对点之矩、合力矩定理
（3）力的大小等于零或力的作用线通过 矩心，即公式（4-1）中的F=0或者d = 0,则 力矩等于零。
（4）相互平衡的两个力对同一点的矩的 代数和等于零。（相互抵消）
4.关于力矩的量纲单位：
在国际单位制中，力矩的单位是牛·米（ N·m）或千牛·米（kN·m）。
4.1力对点之矩、合力矩定理
M1 = F1 d1 M2 = F2 d2 M3 = －F3d3
4.3 平面力偶系
在力偶作用面内取任意线段AB = d，在保持力偶 矩不改变的条件下将各力偶的臂都化为d，于是 各力偶的力的大小应改变为
4.3 平面力偶系
然后移转各力偶,使它们的臂都 与AB重合,则原平面力偶系变换 为作用在点A及B的两个共线力 系。
在同一平面内的两个力偶，只要两力 偶的力偶矩（包括大小和转向）相等 ，则此两力偶的效应相等。这就是平 面力偶的等效条件。

工程力学力偶和平面力偶系

工程力学力偶和平面力偶系
力偶臂
力偶和平面力偶系
1）力偶矩的大小
力偶对物体作用 效果的决定因素
2）力偶在作用平面
内的转向
影响力偶作用效果的因素与距心的位置无关
力偶和平面力偶系
2.力偶的等效条件
同平面内的力偶等效条件：力偶距大小相等，力偶转向相同
力偶和平面力偶系
由此可得出以下两个重要推论
（1）只要不改变力偶矩的大小和力偶的转向，力偶就可以 在它的作用平面内任意移动或转动，而不改变它对物体的作用效 果。
复习
力偶和平面力偶系
力偶和平面力偶系
力偶和平面力偶系
一、力偶的概念和性质
1.力偶与力偶矩
力偶：由大小相等、方向相反且不共线的 两个平行力组成 力偶的作用面：两力作用线所决定的平面 力偶臂：力作用线间的垂直距离
力偶和平面力偶系
力偶距：力与力偶臂的乘积 M=F· d 方向：逆时针为正，顺时针为负
2.力偶没有合力，因此力偶不能与一个力平衡，它必须 用力偶来平衡。 3.力偶对物体的作用效应取决于力偶的三要素，而与矩 心位置无关。
n
4.平面力偶系的平衡方程 Mi 0 i 1, 2,..., n i 1
力偶和平面力偶系
作业
在一钻床上水平放置工件，在工件上同时钻4个等直径的孔， 每个钻头的力偶矩M1= M2= M3= M4=15N·m，求工件的总切削力偶 矩和A、B端水平约束力。
力偶对于作用面内任一点之矩为一常量并等于其力偶矩。
力偶和平面力偶系
二、平面力偶系的合成与平衡
1.平面力偶系的合成
在物体上同时作用有两个或两个以上的力偶时，这些力偶组 成力偶系。在同一个平面内的力偶系叫作平面力偶系。
n
M Mi i 1, 2,..., n i 1
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

A O —— 矩心 d —— 力臂
d
M O (F ) 2AO A B
“＋ ”—— 使物体逆时针转时力矩为正； MO（F）——代数量 “－” —— 使物体顺时针转时力矩为负。
力矩的单位为 N （m 牛顿·米）。
3
2、力矩的性质 （1）力沿作用线移动时，对某点的矩不变; （2）力作用过线矩心时，此力对矩心之矩等于零; （３）互成平衡的力对同一点的矩之和等于零。
平面力偶系—— 作用在物体同一平面内的若干个 力偶所组成的力系。
一、平面力偶系的合成
F1 d1
F2
d2 F 2 F1
F3
F 4
Ad B
F4
F 3
F
A dB F
F3dF1d1M1 F4dF2d2M 2
F F4 F3 F F4 F3
M F d (F 4 F 3 )d M 2 M 1
16
平面力偶系可合成为一个合力偶，合力偶矩等于 各分力偶矩的代数和，即
力矩力偶与平面力 偶系
第三章 力矩、力偶与平面力偶系
本章内容: 1 力对点的矩 2 合力矩定理 3 力偶与力偶矩 的概念 4 力偶的性质 5 平面力偶系的合成 6 平面力偶系的平衡
2
第一节 力对点的矩
一、平面力对点的矩（力矩）
力矩是度量力对物体的转动效应的物理量。
BF
1、力矩的定义
MO(F)Fd
y
Fy
x
AyOF来自Fx xMO(F)MO(Fy)MO(Fx)
xFsinyFcosxFyyFx
M O (F R )(x iF y i y iF x i)
5
例 3-1 如图所示，F1 50kN，F2 100kN，AB6m。
试分别求F1 、F2 对 A 点的矩。
F1
B
30
A
解：力F1使杆 AB 绕 A 点逆时针转动
8
补充例题，水平梁AB 受三角形分布的载荷作用，如图所示。 已知：q，l；试求合力及合力作用线的位置。
A l
qx
A
l
解：在距A端为x的微段dx的
q
B x 梁上，作用力的大小为qx， 由相似三角形关系可知
qx
xq l
q 因此分布载荷的合力大小
Bx
F R
0lqxdx
1ql
2
9
设合力F 的作用线距A端的距离为h，
力偶作用面——力偶中两力所在平面。 力偶臂——力偶中两力作用线之间的垂直距离。
11
二、力偶矩 力偶矩—— 力偶对其作用面内任一点之矩，
以 M(F，F)表示，一般简记为M。 M Fd2 ABC
正负：逆时针转向为正，反之则为负。
力偶矩的两个要素 （1）大小：力与力偶臂的乘积 （2）方向：转动方向
力偶矩的单位为 N （m 牛顿·米）。
r ，在小圆轮最右侧 B 点处受一力F 的作用。试计算力F
对大圆轮与地面接触 A点的矩。
解：由于 F 对点 A的力臂不易确定，
Fy
F
故先将力F 分解为两个正交分力Fx 与Fy ，然后利用合力矩定理来求出 F 对点 A 的矩
O
B
Fx
A
M A(F )M A(F x)M A(F y)
F yrF xRF (rsinRcos)
MA(F1)F1AB
F2
506kNm300kNm
C
力F2 将使AB杆绕 A 点顺时针转动
MA(F2)F2AC 1003kNm300kNm
6
例 3-2 简支刚架如图所示，已知 F 、a 、b 和 。
试计算 F 对 A点的矩。
解：（1）根据定义求MA(F)
Fy
F
dAEsin(ADED)sin
(abcot)sin
根据合力矩定理，有
l
FRh 0qxxdx
FR
qx
A
x
dx
将qx 和 FR的值代入上式，得
h
l
h 2l 3
合力大小等于三角形分布荷载的面积; 合力作用线通过三角形的几何中心。
q Bx
10
第二节 力偶和力偶矩
一、力偶
力偶 —— 由两个等值、反向、不共线的平行力
组成的力系，记作 F,F
dd F
F
3、力矩的两个要素 （1）大小：力与力臂的乘积 （2）方向：转动方向
4
二、合力矩定理
定理：平面汇交力系合力对于平面内任一点之矩 等于其各分力对于该点之矩的代数和。
M O ( F R ) M O ( F 1 ) M O ( F 2 ) M O ( F n ) M O ( F i )
力矩与合力矩的解析表达式
A
E
C Fx b
BD
asinbcos
d
a
M A ( F ) F d F a s in F b c o s
（2）利用合力矩定理求 MA(F)
M A (F )M A (F x)M A (F y)
F xbF yaF asinF bcos
7
例 3-3 如图所示，已知大圆轮半径为 R ，小圆轮半径为
12
三、力偶的性质
1、力偶不能与一个力等效，也不能与一个力平衡。
力偶对刚体只产生转动效应，而不产生移动效应; 力偶的两个力在任一坐标轴上投影的代数和均为零； 力与力偶是静力学的二基本要素。
2、力偶的两个力对其作用面内任一点的矩的代 数和恒等于力偶矩，而与矩心位置无关。
MOFMOF
F
F(xd)FxFdM
M M 1 M 2 M n M i
二、平面力偶系的平衡
力偶系平衡的充要条件是：
合力偶矩等于零, 即力偶系各力偶矩的代数和等于零
M i0
平面力偶系的平衡方程
17
例 3-4 已知梁长 l 5 m，M100kN m ；若不计梁的自
重，试求支座 A 、B 的约束力。
M
A
B
M
A
B
l
FA
l
FB
解：（1）选梁 AB为研究对象
（2）画受力图 （3）列平衡方程
M i 0 , F A l M 0
解得：
M100
F BF Al
kN20kN 5
FA 、FB 为正值，说明图中的假设方向是正确的。
18
例 3-5 如图所示的工件上作用有三个力偶，已知三个力
由于矩心O是任取的，因此， O x
d
力偶矩与矩心的位置无关。
F
13
3、平面力偶等效定理:作用于刚体同一平面内两 个力偶等效的充分且必要条件为其力偶矩相等。
推论 (1) 力偶可以在其作用面内任意移转， 而不改变它对刚体的作用效应。 推论 (2) 只要保持力偶矩大小和转向不变， 可以任意同时变化力偶中力的大小和力偶臂 的长短，而不改变它对刚体的作用效应。
M
14
力偶与力矩的区别和联系 1、力偶是自由量,可以在作用面内任意移动和转 动的，与矩心的位置无关；力矩是定位量，定位于 矩心，与矩心的位置有关。
2、力偶矩不标矩心，而力矩一定要标明矩心。
3、力偶是一个基本的力学量，力矩只是力使 物体绕某点转动效应的度量。
4、力偶矩与力矩量纲相同。
15
第三节 平面力偶系的合成与平衡