当前位置：文档之家 › 力矩与平面力偶系

力矩与平面力偶系

  • 格式：pdf
  • 大小：238.64 KB
  • 文档页数：6

下载文档原格式

  / 6

合集下载

工程力学I-第3章 力矩与平面力偶系

工程力学I-第3章 力矩与平面力偶系

D
x
§3-2 关于力偶的概念

力偶：一对等值、反向而不共线的平行力，用 符号（F ,F′）表示。

力偶臂：两个力作用
线之间的垂直距离d。

F’
F
力偶的作用面：两个 力作用线所决定的平 面
§3-2 关于力偶的概念
F F
d
d
F
d
F
F
F
转动游戏方向盘
拧水龙头
扳手拧螺母
§3-2 关于力偶的概念

Q AABD AABC 显然， 并注意到力偶矩的转向也相同， 则有M ( F , F ) M ( P, P) P
M (P 1, P 1 ) M ( P, P ) 显然， 1, P 1) 从而有M ，( F , F ) M ( P
P1
力偶等效
M ( F , F ) M ( P 1, P 1)
（1）力对点之矩，不仅取决于力的大小，还与矩心的位置有关。
（2）力对任一点之矩，不因该力的作用点沿其作用线移动而改变。 *（3）力的大小等于零或其作用线通过矩心时，力矩等于零。 （4）互成平衡的两个力对同一点之矩的代数和为零。
Mo(F)＝±Fd
§3-1 关于力矩的概念及其计算

合力矩定理：
y Fy
(3)将力P和P’沿各自的作用 线移至任意点A’，B’，根 据力的可传性原理，有 (P,P’) =(P1,P1’) 。
§3-2 关于力偶的概念
(4) A′
P1′ b F′ A A F B Q′ D P′ B′ C
M (F , F ) AB BD 2 AABD ,
M（P, P'） AB BC 2 AABC

第三章 力偶与平面力偶理论)

第三章 力偶与平面力偶理论)

M 0 F F h
力对点之矩（力矩）是一个代数量，它的绝 对值等于力的大小与力臂的乘积；
它的正负：力使物体绕矩心逆时针转向时为正，反之为负。 常用单位为 N· m 或 kN· m。 注意：力矩在下列几种情况下等于零 （1）力的大小等于零；
（2）力的作用线通过矩心，即力臂等于零；
（3） 互成平衡的二力对同一点之矩为零。
78.93N m
按合力矩定理 M O F M O Ft M O Fr



F cos θ r 78.93N m
例3-2 已知：q,l； 求： 合力及合力作用线位置. 解： 取微元如图
x q q l l x 1 P q dx ql 0 l 2
M Mi Mi
i 1 n
平面力偶系平衡的充要条件 M = 0，有如下平衡方程
Mi
0
平面力偶系平衡的必要和充分条件是：所有各力 偶矩的代数和等于零。
例3-1
已知: F=1400N, θ 20 , r 60mm
求: M O F .
解:直接按定义
MO

F F h F r cos θ
M1 F1 d M2 F2 d
M1 F1d
M 2 F2d
Mn Fn d
M n Fnd
=
=
FR F1 F2 Fn
F1 F2 Fn FR
=
=
=
M FRd F1d F2d Fnd M1 M 2 M n
定理：同平面内的两个力偶，如果力偶矩相等，则两力偶 彼此等效。 推论： 任一力偶可在它的作用面内任意转移，而不改变它对刚体 的作用。因此力偶对刚体的作用与力偶在其作用面内的位置无 关。 只要保持力偶矩不变，可以同时改变力偶中力的大小与 力偶臂的长短，对刚体的作用效果不变.

第三章-力矩和平面力偶系-第四章-平面任意力系

第三章-力矩和平面力偶系-第四章-平面任意力系

例3－1 试计算力对A点之矩。
解 本题有两种解法。 方法一： 按力矩的定义计算 由图中几何关系有：
d=ADsinα =(AB-DB)sinα =(AB- BCctgα)sinα =(a- bctgα)sinα =asinα-bcosα
所以
mA(F)=F•d =F(asinα-bcosα)
方法二：
解：
图（a）：
MA = - 8×2 = -16 kN ·m
MB = 8×2 = 16 kN ·m
图（b）： MA = - 4×2×1 = -8 kN · m
MB = 4×2×1 = 8 kN ·m
第二节 力偶
▪ 一、力偶 力偶矩
▪
在日常生活和工程实际中经常见到物体受动两个大小相等、方向相反，
但不在同一直线上的两个平行力作用的情况。例如
2．力偶矩：
▪ 作为力偶对物体转动效应的量度，称为力偶矩，
用m或m( F ,F′)表示。在平面问题中，将力偶中
的一个力的大小和力偶臂的乘积冠以正负号，如图：
即m(F)＝F•d=±2ΔABC
通常规定：力偶使物体逆时针方 向转动时，力偶矩为正，反之为 负。
在国际单位制中，力矩的单位 是牛顿•米（N•m）或千牛顿•米 （kN•m）。
▪
在同一平面内的两个力偶，只要两力偶的
力偶矩的代数值相等，则这两个力偶相等。这
就是平面力偶的等效条件。
▪ 根据力偶的等效性，可得出下面两个推论：
▪ 推论1 力偶可在其作用面内任意移动和转动， 而不会改变它对物体的效应。
▪ 推论2 只要保持力偶矩不变，可同时改变力 偶中力的大小和力偶臂的长度，而不会改变它 对物体的作用效应。
主矩： Mo=m1+m2+···+mn

力矩与平面力偶系

力矩与平面力偶系
变化规律
在非平衡状态下，平面力偶中的两个力将不再保持大小相等、方向相反的关系。它们的大小和方向将发生变化， 以适应物体转动的需要。同时，随着物体转动的进行，作用于物体的力矩也将发生变化，以满足物体转动加速度 的要求。
04
实际应用案例分析
工程领域应用举例
桥梁设计
在桥梁设计中，力矩与平面力偶系的概念对于确定桥梁结构的稳定性和安全性至关重要。 通过计算和分析桥梁各部分的受力情况，工程师可以确保桥梁能够承受各种荷载和外部环 境因素的影响。
当平面力偶系处于平衡状态时，若受到微小扰动而偏离平衡位置，若系统能自动 恢复到原平衡状态，则称该系统是稳定的；若不能自动恢复，则称该系统是不稳 定的。稳定性与系统的结构、刚度、阻尼等因素有关。
03
力矩与平面力偶系关系探讨
相互作用原理阐述
力矩与平面力偶相互作用
力矩是力对物体产生的转动效应，而平面力偶是一对大小相等、方向相反且作用线平行的力，它们共 同作用在物体上，使物体产生转动。
力矩方向判断步骤
首先确定力的作用点和方向，然后确定转动轴的位置，最后根据右手螺旋定则 判断力矩的方向。
02
平面力偶系简介
定义及性质
定义
平面力偶系是由两个大小相等、方向相反且不共线的平行力 组成的力系。
性质
力偶系中的两个力不产生合力，只产生转动效应，即力偶矩 。力偶矩的大小与两力的大小和两力之间的距离有关，而与 力的作用点位置无关。
力矩与平面力偶系
汇报人：XX
contents
目录
• 力矩基本概念 • 平面力偶系简介 • 力矩与平面力偶系关系探讨 • 实际应用案例分析 • 实验设计与操作演示 • 知识拓展与前沿动态
01
力矩基本概念

第三章力矩和平面力偶系第四章平面任意力系

第三章力矩和平面力偶系第四章平面任意力系

解：
图（a）：
MA = - 8×2 = -16 kN ·m
MB = 8×2 = 16 kN ·m
图（b）： MA = - 4×2×1 = -8 kN · m
MB = 4×2×1 = 8 kN ·m
第二节 力偶
▪ 一、力偶 力偶矩
▪
在日常生活和工程实际中经常见到物体受动两个大小相等、方向相反，
但不在同一直线上的两个平行力作用的情况。例如
第三节 平面力偶系的合成与平衡
一、平面力偶系的合成
作用在物体同一平面内的各力偶组成平面力偶系。
m1＝F1•d1，m2＝F2•d2， m3＝－F3•d3，
P1•d=F 1•d1 ，P2•d＝F2•d2 ， －P3•d ＝－F3•d3
FR＝P1＋P2－p3
FR′＝P1′＋P2′－P3′
M＝FR d＝（P1＋P2－P3）d
二、力偶的性质
▪ 力和力偶是静力学中两个基本要素。力 偶与力具有不同的性质：
▪ （1）力偶不能简化为一个力，即力偶不 能用一个力等效替代。因此力偶不能与 一个力平衡，力偶只能与力偶平衡。
▪ （2）无合力，故不能与一个力等效；
▪ （3）力偶对其作在平面内任一点的矩恒 等于力偶矩，与矩心位置无关。
结论：
第三章 力矩与力偶
第一节 力对点之矩
一、 力矩的概念
力使物体绕某点转动的力学效应，称为力对该点之矩。
B
F
A d
O
L
力F对O点之矩定义为：力的大小F与力臂d的乘积冠以适当的正负号， 以符号mo(F) 表示，记为 :Mo(F)＝±Fd
通常规定：力使物体绕矩心逆时针方向转动时，力矩为正，反之为负。
▪ 力 F 对O 点之矩的大小，

力矩与平面力偶系

力矩与平面力偶系

工程力学与建筑结构
1.4 力偶的合成 作用在同一物体上的若干个力偶组成一个力偶系，若
力偶系中各力偶均作用在同一平面，则称为平面力偶系。 平面力偶系合成的结果为一合力偶，其合力偶矩等于
各分力偶矩的代数和。即 M =M1＋M2＋…＋Mn=∑M
1.5力偶系的平衡条件 平面力偶系平衡的必要和充分条件是：力偶系中各力
偶矩的代数和为零。即 ∑M=0
工程力学与建筑结构
工程力学与建筑结构
工程力学与建筑结构
力矩与平面力偶系 1.1力矩的概念
用力的大小F与d的乘积度量力F使扳手绕O点的转动 效示应。，即称为力F对O点之矩，简称力矩，用符号MO（F）表
MO（F）=±Fd 式中，O点称为“矩心”，d称为“力臂”。 力矩的正负规定为：力使物体绕矩心逆时针方向转动时， 力矩为正；反之为负。
M=±Fd
力偶矩的正负规定与力矩正负规定一致，即：使物体 逆时针方向转动的力偶矩为正；反之为负。
F
F
B
h
铰杠
丝锥
F'
F d
F'

A
(a)
F' (b)
(c)
工程力学与建筑结构
在平面问题中，力偶矩也是代数量。力偶矩的单位与力矩 单位相同，即N•m。 根据力偶的概念可以证明，力偶具有以下性质： （1）力偶在其作用面上任一轴的投影为零。 （2）力偶对其作用面上任一点之矩，与矩心位置无关，恒 等于力偶矩。
系中所有分力对同一点之矩的代数和。
MO（FR）=MO（F1）＋ MO （F2）＋…＋ MO （Fn）=∑ MO （F）
F1 y
A
FR
F2
O x
工程力学与建筑结构
1.3 力偶的概念

理论力学03力矩力偶与平面力偶系

理论力学03力矩力偶与平面力偶系

本章讨论平面力偶系的合成与平衡问题
一、平面力偶系的合成 平面力偶系可合成为一个合力偶； 合力偶矩等于各分力偶矩的代数和，即
M1
M2 M3
M4
M Mi
二、平面力偶系的平衡方程
Mi 0
M
说明：根据平面力偶系的平衡方程，可解 一个未知量。
ቤተ መጻሕፍቲ ባይዱ
[例2] 已知梁长 l = 5 m，M = 100 kN·m ；若不计梁的自重，试求 铰支座 A 、B 处的约束力。
2. 力偶中的两个力对任一点的矩的代数和 恒等于力偶矩，与矩心位置无关。
dF F
3. 作用于刚体同一平面内两个力偶等效的充要条件为其力偶矩 相等。
结论：力偶矩唯一决定了力偶对刚体的作用效应。
◆ 通常用力偶矩符号来代表力偶：
F
d
M Fd
F
M 或M
第三节 平面力偶系
平面力偶系：由位于同一平面内的一群力偶所组成的力系
构平衡。试求作用于摆杆 BO1上的力偶矩 M2 （各构件的自重不计）
解： 1）首先研究曲柄 AO与套筒A 的组合 画受力图 列平衡方程
Mi 0, M1 FA r sin 30 0
解得
FA
FO
2M1 r
M1
O
FO
FA
FA
FO
2M1 r
2）再选取摆杆 BO1 为研究对象
画受力图
列平衡方程
Mi 0, M 2 FA AO1 0
的平行力称为一个力偶，记作 F, F。
dF F
二、力偶矩 定义
M Fd
为平面内力偶 F, F 的矩，简称力偶矩。
说明： 1）平面内力偶矩为代数量，其正负号表转向，一般规定 逆时针转向为正，反之为负。

力矩和平面力偶系

力矩和平面力偶系
（力偶三要素：力偶矩旳大小；力偶旳转向和力 偶旳作用面。）
所以两个力偶等效，必须是该两个力偶旳力偶矩 大小相同，转向相同，作用面相同。（对刚体， 可作用面平行。）
例题：
F
1.习题3-2
a
b
Fx F cosa
a
Fy f sin a
M A (F ) -Fx b Fy 0 -Fb cosa
M B (F ) -Fx b Fy a F (a sin a - b cosa )
2．习题3-7
正三角形ABC
B F2
F1 F2 F3 F
X F1 cos 60 F2 cos 60 - F3 0
F1
Y F1 sin 60 - F2 sin 60 0
A
即合力FR=0
F1x
F
cos 60
第三章: 力矩与平面力偶系
本章研究力矩和力偶旳概念、力偶旳 性质、平面力偶系旳合成与平衡。本 章与第二章旳理论是研究平面一般力 系旳基础。
§3-1 力矩旳概念和计算
一般情况下，力对物体作用时能够产 生移动和转动两种外效应。力旳移动 效应取决于力旳大小和方向。为了度 量力旳转动效应，需要引入力矩旳概 念。
设物体上作用有一 力偶臂为d旳力偶 （Ｆ，Ｆ‘）
该力偶对作用面内任 一点Ｏ之矩为：
Ｏ x
F
F’ d
Ｍo(F)+Mo(F’)=F(x+d)-Fx=Fd
力偶对作用面内任一点旳矩之大小恒等于力偶中 一力旳大小和力偶臂旳乘积，而与矩心旳位置无关。
力偶对物体旳转动效应可用力与力偶臂旳乘积Fd 及转向来度量，该物理量称为力偶矩。
互成平衡旳二力对同一点旳力矩之和为 零
虽然力矩概念由力对物体上固定点旳 作用引出。实际上，作用于物体上旳力 能够对任意点取矩，即矩心可是空间中 旳任意点。

静力学 力矩 平面力偶系

静力学 力矩 平面力偶系

解得
FA
FB
M1 M2 l
M3
200N
感谢观看
静力学 力矩 平面力 偶系
§3-1 力对点之矩
一、平面力对点之矩
力矩作用面
两个要素： 1.大小：力F与力臂的乘积 2.方向：转动方向
M0 F F h
二、汇交力系的合力矩定理
FR Fi F1 F2 Fn
平面汇交力系
M0 FR M0 Fi
例3-1
已知: F =1400N, θ 20 , r 60mm
力偶的性质: ①.力偶在任意坐标轴上的投影恒等于零。
②.力偶没有合力，力偶只能由力偶来平衡。
力偶对任意点的矩恒等于力偶矩，与矩心无关。 力偶在任意坐标轴上的投影恒等于零。
M F A F MF 二力大由力力 力§由§力大二 大力二由§力力力力§力只二力、偶小两偶偶偶3两3偶小、小偶、两3偶偶偶偶3偶要、偶----3442汇 在 ： 个 对 对两 个 在 ： 汇： 两 汇 个 中 对 矩 矩 (保 汇 两co平平交任力等任任 力等任力交 力力交等两任((持交力力平ummp面面力意F值意意 之值意F力 F之力值力意力力之偶面looe与与与力力mm)系坐、点点 间、坐系 间系、所点偶系间的力?力力力ee偶偶的标反的的 的反标的 的的反在的矩的的等偶nn臂臂臂tt系系合轴向矩矩 垂向轴合 垂合向平矩不合垂效与oo的的的ff的的力上、恒恒 直、上力 直力、面恒变力直力aa乘乘乘合合cc矩的不等等 距不的矩 距矩不称等，矩距偶oo积 积 积成成uu定投共于于离共投定离定共为于力定离矩pp与与ll理影线力力 称线影理 称理线力力偶理称eeA ))平平恒的偶偶 为的恒为的偶偶可为衡衡等（矩矩 力（等力（作矩在力于平，， 偶平于偶平用，其偶零行与与 臂行零臂行面与作臂。）矩矩 。）。。）。矩用。心心 心面无无 无内关关 关任。。 。意移转，且可以同时改变力偶中力及力偶臂的大小，对刚体的作用效果不变。 M F §3-1 力对点之矩

03--第三章 力矩与平面力偶系(修订)

03--第三章 力矩与平面力偶系(修订)

例3-5 ：
已知 M 2kN m,OA r 0.5m,θ 30; 1
求：平衡时的 M 2及铰链O，B处的约束力.
解：取轮,由力偶只能由力偶平衡的性质,画受力图.
M 0 M1 FA r sin 0
解得 FO FA 8kN
取杆BC，画受力图.
M 0
FA'
r
sin
M2
0
解得 M2 8kNm
F 'd Fd
力矩的符号 M F 力偶矩的符号 M O
3.只要保持力偶矩不变，力偶可在其作用面内任 意移转，且可以同时改变力偶中力的大小与力 臂的长短，对刚体的作用效果不变.
=
=
=
ABC ABD
ABC？ABD
M FR，Fi R FRd1 2ABD
M
F,
Fi
Fd
2ABC
=
=
=
=
l
q dx x
0
l
0
x2 l
q dx
得 h 2l 3
例3-4
已知：M1 M 2 10N m, M3 20N m, l 200mm;
求： 光滑螺柱AB所受水平力.
解：由力偶只能由力偶平衡的性质， 其受力图为
M 0
FAl M1 M2 M3 0
解得
FA
FB
M1 M2 l
M3
200N
力偶矩 M F d 2 1 F d 2ABC
2
二. 力偶与力偶矩的性质 1.力偶在任意坐标轴上的投影等于零.
2.力偶对任意点取矩都等于力偶矩， 不因矩心的改变而改变.
M F d
MO1 F
F,
d
F
x1
MO1 F M

力矩与平面力偶系 PPT课件

力矩与平面力偶系 PPT课件
F1 d A F 1 B A F2 D ABD , M ( P , P ) 2 S ABC S ABD S ABC M ( F , F ) M ( P , P ) M ( P , P ) M ( P1 , P1) M ( F , F ) M ( P1 , P1)
F′ F
F2 F O F1
o 图 3-2 (b)
图 3-2 (c)
2. 合力矩定理 表达式： M O ( FR ) M O ( F ) 证明：由图得 y
M O ( F ) F d F r sin( ) F r (sin cos sin cos ) F r sin cos
图 3-4
图3-5
(2) 力偶的性质 (a) 力偶在任何坐标轴上的投影等于零； (b)力偶不能合成为一力，或者说力偶没有合力， 即它不能与一个力等效，因而也不能被一个力平 衡； (c) 力偶对物体不产生移动效应，只产生转动效 应，即它可以也只能改变物体的转动状态。
F d F′ 力偶作用面 力偶臂
图3-6
而
O x r Fy F
A

y Fx x

F r sin cos
F cos Fx , F sin Fy r cos x A , r sin y A
d
M

图 3-3
则
MO (F) xA Fy yA Fx
(a)
MO (F) xA Fy yA Fx
谁曾经想过用杠杆来移动地球？ 古希腊科学家阿基米德曾说过“如果给我一个支点，我就能
撬起地球”。这句名言从理论上讲是完全正确的，
因为杠杆能使力变大，只要杠杆足够长，就 能产生足够大的力来“搬动”地球。

力矩与平面力偶系

力矩与平面力偶系

力矩与平面力偶系2.2.1 力对点之矩(简称为力矩)1.力对点之矩的概念为了描述力对刚体运动的转动效应，引入力对点之矩的概念。

（F）来表示，即力对点之矩用MOMo(F) = ± Fd一般地，设平面上作用一力F，在平面内任取一点O——矩心，O点到力作用线的垂直距离d称为力臂。

Mo(F) = ± 2△OAB力对点之矩是一代数量，式中的正负号用来表明力矩的转动方向。

矩心不同，力矩不同。

规定：力使物体绕矩心作逆时针方向转动时，力矩取正号；反之，取负号。

力矩的单位是Nmm。

由力矩的定义可知：（1）若将力F沿其作用线移动，则因为力的大小、方向和力臂都没有改变，所以不会改变该力对某一矩心的力矩。

（2）若F=0，则Mo(F) = 0；若Mo(F) = 0，F≠0，则d=0，即力F通过O点。

力矩等于零的条件是：力等于零或力的作用线通过矩心。

2.合力矩定理设在物体上A点作用有平面汇交力系F1、F2、---Fn，该力的合力F可由汇交力系的合成求得。

计算力系中各力对平面内任一点O的矩，令OA=l，则---由上图可以看出，合力F对O点的矩为据合力投影定理，有F y=F1y+F2y+---+F ny两边同乘以l，得F y l=F1y l+F2y l+---+F ny l即M o(F)=M o(F1)+M o(F2)+---+M o(F n)合力矩定理：平面汇交力系的合力对平面内任意一点之矩，等于其所有分力对同一点的力矩的代数和。

3.力对点之矩的求法(力矩的求法)（1）用力矩的定义式，即用力和力臂的乘积求力矩。

注意：力臂d 是矩心到力作用线的距离，即力臂必须垂直于力的作用线。

例2-3 如图所示，构件OBC 的O 端为铰链支座约束，力F 作用于C 点，其方向角为α，又知OB=l，BC=h ，求力F 对O 点的力矩。

解 （1）利用力矩的定义进行求解如图，过点O作出力F作用线的垂线，与其交于a点,则力臂d即为线段o a。

05力矩与平面力偶系

05力矩与平面力偶系

NB 0.2 m1 m2 m3 m4 0
N
B

60 0.2
300N
N A NB 300 N
例2
一简支梁作用一矩为M 的力偶，不
计梁重，求二支座约束力。
M
l
A
B
M
FA
l
A
B
FB
解：以梁为研究对象。
梁上除作用有力偶 M 外，还 有反力FA，FB 。
因为力偶只能与力偶平衡，所 以 FA=FB。
（1）力偶矩的大小 （2）力偶在作用面的转向。
因此，平面力偶矩是一个代数量，以M表示，即
M=±Fd=±2A△ABC
转向用正负号表示，用力矩规定。力偶矩的单位为 N•m，与力矩相同。
18
2．同平面内力偶的等效定理 定理：在同平面内的两个力偶，如果力偶矩相 等，则两力偶彼此等效。
19
由此可得两个推论：
B
约束力必沿AD杆。根据力偶只能与力偶
l
D
45
平衡的性质，可以判断A与B 端的约束 力FA 和FB 构成一力偶，因此有： FA = FB 。梁AB受力如图。
列平衡方程：
FA
M
A
B
M 0, M FA l cos 45 0
FB
解得
FA

FB

M l cos 45

2M l 29
例4
如图所示的铰接四连杆机构OABD，在杆OA和BD 上分别作用着矩为M1和M2的力偶，而使机构在图示位 置处于平衡。已知OA=r，DB=2r， =30°，不计杆重， 试求M1和M2间的关系。
B
A
M1
O
M2
D

建筑力学课件 第四章 力矩与平面力偶系

建筑力学课件 第四章 力矩与平面力偶系
力矩的概念可以推广到普遍的情形。在具 体应用时，对于矩心的选择无任何限制， 作用于物体上的力可以对平面内任一点取 矩。
4.1力对点之矩、合力矩定理
3.力矩的性质 综上所述，得出如下力矩性质：
（1）力F对点O的矩，不仅决定于力的大 小，同时与矩心的位置有关。矩心的位 置不同，力矩随之而异。
（2）力F对任一点的矩，不因为F的作用 点沿其作用线移动而改变，因为力和力 臂的大小均未改变。
2.力矩的计算
在平面问题中,我们把乘积Fd加上适当的正负号,
作为力F使物体绕点O转动效应的度量,并称为
力F对点O的矩,简称力矩,用Mo(F) 或MO表示
即 MO (F)=± Fd
（4-1）
点O称为矩心，力作用线到矩心的垂直距离d称
为力臂。正负号通常用来区别力使物体矩心
转动的方向，并规定：若力使物体绕矩心作
4.1力对点之矩、合力矩定理
（3）力的大小等于零或力的作用线通过 矩心，即公式（4-1）中的F=0或者d = 0,则 力矩等于零。
（4）相互平衡的两个力对同一点的矩的 代数和等于零。（相互抵消）
4.关于力矩的量纲单位：
在国际单位制中，力矩的单位是牛·米（ N·m）或千牛·米（kN·m）。
4.1力对点之矩、合力矩定理
M1 = F1 d1 M2 = F2 d2 M3 = －F3d3
4.3 平面力偶系
在力偶作用面内取任意线段AB = d，在保持力偶 矩不改变的条件下将各力偶的臂都化为d，于是 各力偶的力的大小应改变为
4.3 平面力偶系
然后移转各力偶,使它们的臂都 与AB重合,则原平面力偶系变换 为作用在点A及B的两个共线力 系。
在同一平面内的两个力偶，只要两力 偶的力偶矩（包括大小和转向）相等 ，则此两力偶的效应相等。这就是平 面力偶的等效条件。

工程力学-力矩与平面力偶

工程力学-力矩与平面力偶

RA
RB
2 Pa RB R A l cos α
[练习2]
在一钻床上水平放置工件,在工件上同时钻四个等
直径的孔,每个钻头的力偶矩为 m1 m 2 m3 m 4 15 N m 求工件的总切削力偶矩和A 、B端水平反力? 解:
NA NB
各力偶的合力偶距为
M m1 m 2 m 3 m 4 4 ( 15 ) 60 N m
mo ( F ) F ( h x )
mo ( F ) F x
mo ( F , F ) F ( h x ) F x F h
性质3：力偶等效定理 作用在同一平面的两个力偶，只要它的力偶矩相等，则该两个力偶彼此等 效。
包含以下内容： ①力偶可以在其作用面内任意移动，而不影响它对刚体的
l d Q 0 l
2、研究曲柄ACD
l2 d2 m 0 N AB l d M 0 l2 d2 M Q N AB l d
思考题： 1、m可否又BC上移至AC上？
a
m
结构视为一体时，m 可移动，若分开考虑，则 m不能从一体移至另一体。
2.既然一个力不能与力偶平衡，为什么下图的圆轮能平衡？
M O ( F ) 2 S ABC
① 说明： M O (F ) 是代数量。
② F↑,h↑转动效应明显。
③ M O (F ) 是影响转动的独立因素。当F=0 或 h=0时，M O ( F ) 0 ④国际单位Nm。
2、解析式 y
Fy
F
Fx
M O ( F ) F h Fr sin
解： 1、研究对象二力杆：AD
RC

土木工程力学教案——力矩与平面力偶系

土木工程力学教案——力矩与平面力偶系

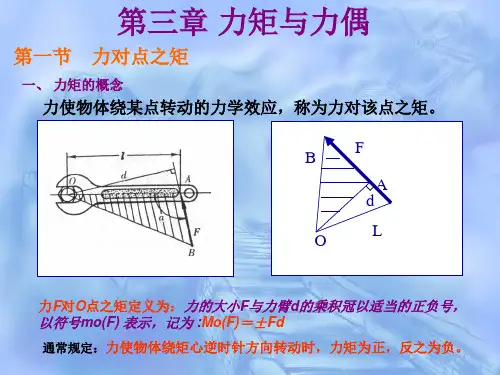
力矩与平面力偶系第一节 力对点之矩力对点的矩是很早以前人们在使用杠杆、滑车、绞盘等机械搬运或提升重物时所形成的一个概念。

现以板手拧螺母为例来说明。

如图3－1所示，在板手的A 点施加一力F ，将使板手和螺母一起绕螺钉中心O 转动，这就是说，力有使物体（扳手）产生转动的效应。

实践经验表明，扳手的转动效果不仅与力F 的大小有关，而且还与点O 到力作用线的垂直距离d 有关。

当d 保持不变时，力F 越大，转动越快。

当力F 不变时，d 值越大，转动也越快。

若改变力的作用方向，则扳手的转动方向就会发生改变，因此，我们用F 与d 的乘积再冠以适当的正负号来表示力F 使物体绕O 点转动的效应，并称为力F 对O 点之矩，简称力矩，以符号M O （F ）表示，即d F F M ⋅±=)(O （3－1）O 点称为转动中心，简称矩心。

矩心O 到力作用线的垂直距离d 称为力臂。

式中的正负号表示力矩的转向。

通常规定：力使物体绕矩心作逆时针方向转动时，力矩为正，反之为负。

在平面力系中，力矩或为正值，或为负值，因此，力矩可视为代数量。

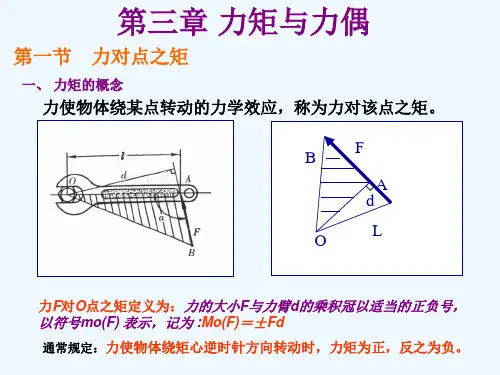
由图3－2可以看出，力对点之矩还可以用以矩心为顶点，以力矢量为底边所构成的三角形的面积的二倍来表示。

即面积OAB 2)(O ∆±=F M （3－2）显然，力矩在下列两种情况下等于零：（1）力等于零；（2）力的作用线通过矩心，即力臂等于零。

力矩的单位是牛顿•米（N •m ）或千牛顿•米（kN •m ）【例3－1】 分别计算图3－3所示的F 1、F 2对O 点的力矩。

【解】：由式（3－1），有 m kN 455.130)(mkN 530sin 110)(222O 111O ⋅-=⨯-=⋅-=⋅=︒⨯⨯=⋅=d F F M d F F M第二节合力矩定理图3-1我们知道平面汇交力系对物体的作用效应可以用它的合力R 来代替。

这里的作用效应包括物体绕某点转动的效应，而力使物体绕某点的转动效应由力对该点之矩来度量，因此，平面汇交力系的合力对平面内任一点之矩等于该力系的各分力对该点之矩的代数和。

理论力学--力矩-平面力偶系

理论力学--力矩-平面力偶系

F
d d
F
F
F
M F d
M O1 F , F M O1 F M O1 F




F d x1 F x1 Fd
§2-2 平面力对点之矩 · 平面力偶
平面力偶的等效定理： 在同平面内的两个力偶，若 力偶矩相等，则两力偶彼此等效。 两个推论：
M F
O i
平面汇交力系: M O FR M O Fi


平面汇交力系的合力矩定理：合力对平面内任一点 的矩，等于所有各分力对同一点的矩的代数和。
§2-2 平面力对点之矩 · 平面力偶 力矩与合力矩的解析表达式
(1)力矩的解析表达式 y
M O F M O Fx M O Fy
F
y
l M O (F ) F d F sin
O
MO (Q) Q l
② 应用合力矩定理
Fy
Fx A
d
x
l

Q
M O (F ) Fx l Fy l cot
F sin l F cos lcot l F sin
③ 应用合力矩公式
§2-2 平面力对点之矩 · 平面力偶 平面力偶系的合成证明:
已知：M 1 , M 2 ,
Mn;
求：它们的合成结果。
证明：
任选一段距离d：
M 1 F1d , F1 M 1 / d
M 2 F2 d , F2 M 2 / d
M2 Mn
M1
M n Fn d , Fn M n / d
第二章
平面力系
第二章 平面力系（之二）
§2-2 平面力对点之矩 · 平面力偶
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2. 平面力偶等效定理 定理：在同一平面内（或两平行平面）的两
个力偶，如它们的力偶矩的大小相等，而且转向
相同，则此两力偶等效。 F1
例如：方向盘
A
F
C D
F′
B 图3-8 F1′
工程力学电子教案
力矩与平面力偶系
14
证明：设有一力偶 (F, F ′),如图所示 . 运用加减 平衡力系的公理并注意到：
(F , F ) ~ (F , F ,Q,Q) ~ (P, P)
20
例 题 3- 1 两力偶作用在板上，尺寸如图，已
知 F1 = F2=1.5 kN , F3 =F4 = 1 kN, 求作用在板上
的合力偶矩。
解：由式
F 1 180mm
F2
则 M = M1 + M2
F 4 M =-F1 · 0.18 –
F3 · 0.08
F3
80mm
= -350 N· m
图3-14
Fn） 则可将每个力对O点之矩相加，有
MO(F) xA Fy yA Fx
(b)
该汇交力系的合力FR=∑F，由式(a)，它对O点的矩 为：
MO(FR) xA FR y yA FRx xA Fy yA Fx (c)
比较(b)、(c)两式有
MO (FR ) MO (F )
F1
D
d
A
BA
F2 B
F2 F1
(a)
(b)
图3-11
注意：上述结论只适用于刚体，而不适用于变形体。
工程力学电子教案
力矩与平面力偶系
17
§3-3 平面力偶系的合成与平衡
平面力偶系：作用在物体上同一平面内的若干力偶的
总称。 1. 合成 (1) 两个力偶的情况
F1
d1
F2 d2
F1′
=
M1 F1 dF12′, M 2 F2 d2
12
(3) 力偶矩 其转动效应——力对点之矩，即用力偶中
的两个力对其作用面内任一点之矩的代数和来
度量。
M(F , F) F d 或 M F d
例如：
MO (F ) MO (F ) F x F (d x) F d
Fd
O
x
F
图3-7
工程力学电子教案
力矩与平面力偶系
13
(4) 力偶的三要素 (a) 力偶矩的大小； (b) 力偶的转向； (c) 力偶作用面在空间的方位。
证毕。
工程力学电子教案
力矩与平面力偶系
10
§3-2 力偶的概念
1. 力偶和力偶矩
(1) 力偶的概念 把大小相等、方向相反、作用线平行的
两个力叫做力偶。并记作（F，F′）。可用 图3-4表示, 例如：方向盘等
Fd
力偶臂
F′
图 3-4
力偶作用面
F1
C
F′
A
D F
B F1′
图3-5
工程力学电子教案
力矩与平面力偶系
(F2 ，F2′)作用在Oyz平面内,它们的力偶矩大小相等 (如图)。试问此两力偶是否等效，为什么？
z F2
F2′ O
y
F1
F1′
x
图3-16
工程力学电子教案
力矩与平面力偶系
27
思考题 3-2
如图所示，在物体上作用有两力偶(F1,F1′) 和 (F2,F2′)其力多边形封闭。问该物体是否平 衡？为什么？
工程力学电子教案
力矩与平面力偶系
15
两个重要推论：
推论1 力偶可以在其作用面内任意移转而不改变 它对物体的转动效应
M
M
A
BA
C
B
(a)
(b)
图3-10
工程力学电子教案
力矩与平面力偶系
16
推论2 在保持力偶矩的大小和转向不变的条件下，
可以任意改变力偶中力和力偶臂的大小而不
改变力偶对物体的转动效应，其中F1d=F2D
F22 d
F11′
=
d
FR
FR′
F11
F22′
M1 F11 d ,
M 2 F22 d
FR F11 F22 , FR F11 F22
工程力学电子教案
力矩与平面力偶系
18
这样得到新的力偶(FR , FR′),则 M= FRd= (F11 - F22)d=F11d - F22 d=M1+M2
力矩与平面力偶系
29
思考题 3-5
两轮半径同为 r ，一轮在轮缘上受一大小为F
的力作用，另一轮在轮缘上受两个方向相反、大小
都是F/2 的力作用，各轮上的力对轮心的矩是否相
同？两轮上的力对轮的外效应是否相同？
r O1
F/2 r
O2
F
(a)
图3-19
F/2 (b)
工程力学电子教案
力矩与平面力偶系
30
思考题 3-6
F d
(2) 开门，关门。
O
图3-1
由上图知，力F 使物体绕O点转动的效应，不仅与
力的大小，而且与O点到力的作用线的垂直距离d
有关，故用乘积F·d 来度量力的转动效应。该乘积
工程力学电子教案
力矩与平面力偶系
5
根据转动效应的转向取适当的正负号称为力F对点O 之矩，简称力矩，以符号M O (F)表示。
即 MO(F) F d
工程力学电子教案
力矩与平面力偶系
1
第 3 章 力矩与平面力偶系
§3-1 力矩的概念和计算 §3-2 力偶的概念 §3-3 平面力偶系的合成与平衡
工程力学电子教案
力矩与平面力偶系
2
力对物体作用时可以产生移动和转动两种效应。力 的移动效应取决于力的大小和方向，为了度量力的转动 效应，需引入力矩的概念。
主要研究内容： (1) 力矩和力偶的概念； (2) 力偶的性质； (3) 平面力偶系的合成与平衡。
工程力学电子教案
力矩与平面力偶系
3
工程力学电子教案
力矩与平面力偶系
4
谁曾经想过用杠杆来移动地球？ 古希腊科学家阿基米德曾说过“如果给我一个支点，我就能撬
起地球”。这句名言从理论上讲是完全正确的， 因为杠杆能使力变大，只要杠杆足够长，就 能产生足够大的力来“搬动”地球。
动力臂越长，施力的一方经过的距离越
F2
F
O
o 图 3-2 (b)
F1
图 3-2 (c)
工程力学电子教案
力矩与平面力偶系
2. 合力矩定理
表达式： MO (FR ) MO (F )
证明：由图得
y
MO (F ) F d F r sin( )
Fy
F r (sin cos
sin cos ) F r sin cos
FA、FB为正值，说明图中所示FA、FB的指向正确。
工程力学电子教案
力矩与平面力偶系
23
例 题 3- 3
如图所示的铰接四连杆机构OABD，在杆OA
和BD上分别作用着矩为M1和M2的力偶，而使机 构在图示位置处于平衡。已知OA=r，DB=2r，θ
=30°，不计各杆自重，试求M1和M2间的关系。
B
A
M1 O
11
(2) 力偶的性质 (a) 力偶在任何坐标轴上的投影等于零；
(b)力偶不能合成为一力，或者说力偶没有合力，
即它不能与一个力等效，因而也不能被一个力平
衡； (c) 力偶对物体不产生移动效应，只产生转动效 应，即它可以也只能改变物体的转动状态。
Fd
力偶臂
F′
图3-6
力偶作用面 x
工程力学电子教案
力矩与平面力偶系
图中所示两轮在图示主动力作用下能否处于平
衡？为什么？若不能平衡，可否再在轮上加一个力 使之平衡？如何加？
r O1
(a)
F/2
r
O2
F
F/2
图3-20 (b)
工程力学电子教案
力矩与平面力偶系
31
力矩与平面力偶系
25
写出杆OA和DB的平衡方程： ∑M = 0
FBA
B
A
FAB
M1
FO
O
M2 D
FD
M1 FABrcos 0 M 2 2FBArcos 0 因为 FAB FBA
所以求得 M 2 2M1
工程力学电子教案
力矩与平面力偶系
26
思考题 3-1 一力偶(F1,F1′)作用在Oxy平面内,另一力偶
(F , F ) ~ (P1 , P1)
M (F , F ) 2S ABD ,
M ( P, P) 2S ABC
QA
A′ b
P1 D
F′ P′
B′P1′ C
S ABD S ABC
a PF
B Q′
M(F , F ) M(P, P)
ቤተ መጻሕፍቲ ባይዱ
图3-9
M (P, P) M (P1 , P1)
M (F , F ) M (P1 , P1)
d
工程制 公斤力米（kgf·m） 图 3-2 (a) 力矩的性质：
(1) 力对任一已知点之矩，不会因该力沿作用线移动 而改变；
工程力学电子教案
力矩与平面力偶系
7
(2) 力的作用线如通过矩心，则力矩为零；反之，如 果一 个力其大小不为零，而它对某点之矩为零， 则此力的作用线必通过该点；
(3) 互成平衡的二力对同一点之矩的代数和为零。
F2′
F1 F1′
F1
F2
F2′
F2
F1′
图3-17
工程力学电子教案
力矩与平面力偶系
28
思考题 3-3
图3-18所示圆盘由O点处的轴承支持，在力偶 M 和力F 的作用下处于平衡。能不能说力偶被力F 所平衡？为什么？