信号完整性分析笔记(全)
- 格式:pdf
- 大小:934.94 KB
- 文档页数:38




一所要面临的问题二一些有用的常识三电感电容及电阻的基础以及要注意的问题四传输线的问题以及反射等问题五有损线的损耗六差分信号和查分对的问题一所要面临的问题一单一网络的信号完整性二两个或多个网络间的串扰三电源和地分配中的轨道塌陷四来自整个系统中的电磁干扰和辐射一个重要的概念1:带宽的问题(注释2)对任意一个非理想的方波信号而言(电子系统这种波形非常常见,比如系统的时钟),该信号均可认为是由同频率的基波信号和高次谐波叠加而成。
假设一个1GHz 的时钟它是有1G 的基波加3次谐波再加5次谐波再加7次谐波组成的。
那个这个时钟信号的带宽就是7G.如果加到31次谐波了,那么这个信号的带宽就是31G。
随着叠加的谐波数越多叠加后的信号就越接近完美的方波。
换句话说那就是10%到90%上升时间越小。
可见信号的上升时间决定了信号的带宽。
这样确定系统时钟的上升时间就非常重要了。
为什么上升时间会这么重要呢?下面举例说明:大多数电路板而言会采用FR4板材,FR4板并非理想的无耗板材。
损耗的机理有两种第一导体损耗,第二介质损耗。
比损耗更为严重的是损耗对不同频率信号的损耗是不同,因为在物理上这涉及到介质充放电过程的快慢以及带来的损耗。
对一个4英寸(4000mil)的FR4传输线而言,这样的导线对8GHz的信号损耗达到能量的50%或幅值的70%.试想如果用这样的线去传导一个带宽为9G的1GHz的方波会怎样?结果就是组成这个方波的信号中九次谐波分量被严重损耗,而其他谐波分量也将不同成度的损耗。
这就导致方波的上升沿退化,比如原来上升边是50ps变成了1.5ns。
如果传输的信号频率是10MHz影响不大。
如果传输信号是500M,(2ns的周期)这下麻烦就大了去了。
下面引入带宽和上升时间的关系这是一个近似的经验上的估计:对于10%到90%上升时间来讲关系为:BW=0.35/RT(RT为10%到90%上升时间)也有一些资料给的上升时间是20%-80%上升时间。

参数如何影响产品性能。
1.时序 Timing3.电磁干扰 EMI原理:电压电流作为噪声传递到邻近网络,而两者相对独立。
情形:互连线均匀与不均匀(插件、封装)。
均匀平面返回路径,感性耦合与容性耦合相当,是实现最低串扰结构。
感性比容性增加噪声多。
感性耦合主导,归为开关噪声、ΔI噪声、dI-dt噪声、地弹、同时开关噪声(SSN)或者同时开关输出噪声(SSO)。
也是耦合电感,即互感造成。
解决:1.从本质出发,在设计上优化2.选介电常数较小的材料3.简短互连线,使用最小封装(CSP,Chip Scale Packege)与高密度互连线(HDI,High DensityInterconnector)3.电源与地分配的轨道塌陷原理:过电源与地的电流发生变化,在电源或地路径间阻抗上产生压降(即轨道塌陷)。
高性能CPU与ASIC趋势:低电压电源供电,高功率损耗。
大开关电流降低了可容忍噪声。
解决:设计低阻抗电源分配系统(PDS,Power Distribution System)低阻抗1.邻电源与地分配层平面介质尽可能薄,慢慢靠近2.低电感去耦电容3.封装安排多个多个很短的电源与地引脚4.片内加去耦电容4.来自系统的电磁干扰与辐射原理:电子产品谐波干扰通信,共模电流辐射的远场强度随频率线性增加、差分电流辐射的远场强度与频率的平方成正比。
常见的两种干扰源:(1)部分差分信号转共模信号,在外部双绞线输出(2)电路板上地弹在外部单端屏蔽线上产生共模电流产生辐射的大多数电压源来自电源与地的分配网络。
上一点的解决方法也适用。
解决:1.使用屏蔽方法隔离2.电缆线正确使用铁氧体3.使用低阻抗电缆信号完整性的两个重要推论一、随上升边减小,四种问题会更严重(即dI/dt或dV/dt越大)。
二、解决SI的有效办法基本就基于互联线阻抗联系。
电子产品趋势大约每两年时钟频率翻一倍。
上升边与时钟频率关系:RT:上升边,单位为nsF clock:时钟频率,单位为GHz测量的信号转换时间都为终值的10%~90%这段时间,称为10-90上升边。

信号完整性分析1.背景在一次奇怪的设计失败之后,信号完整性问题首先引起了人们的注意。
当时,美国硅谷一家著名的图像检测系统制造商早在7年前就已经成功上市设计、制造和产品,但在最近出现的问题中,从生产线的产品来看,新产品的正常运行,这是一款20兆赫的系统设计,似乎是不需要考虑的设计上的问题,更使产品设计工程师在设计新产品时不做任何修改,甚至使用元件模型都与原设计要求一致,唯一不同的是集成电路制造技术的进步,新采购的电子元器件实现了小型化、快速化。
新的器件技术使每个芯片都成为一个高速器件,而正是这些高速器件应用中的信号完整性问题导致了系统的失效。
随着IC开关速度的提高和信号上升和下降时间的迅速缩短,无论信号频率如何,系统都将成为一个高速系统,并会出现各种信号完整性问题。
在高速PCB系统设计方面,信号完整性问题主要体现在以下几个方面:工作频率的提高和信号上升/下降时间的缩短会降低系统的定时裕度,甚至出现时序问题;传输线效应导致噪声容限,信号传输中的单调性甚至逻辑错误。
信号间的串扰随着信号传播时间的减少而加剧。
当信号传播时间接近0.5ns或以下时,供电系统的稳定性降低,产生电磁干扰。
2.含义(1)信号完整性(Signal Integrity)简称SI,指信号从驱动端沿传输线到达接收端后波形的完整程度。
即信号在电路中以正确的时序和电压作出响应的能力。
如果电路中信号能够以要求的时序、持续时间和电压幅度到达IC,则该电路具有较好的信号完整性。
反之,当信号不能正常响应时,就出现了信号完整性问题。
从广义上讲,信号完整性问题指的是在高速产品中由互连线引起的所有问题,主要表现为五个方面:(2)延迟。
延迟是指信号在PCB 的导线上以有限的速度传输,从驱动端到接收端存在的传输延时。
信号的延时会对系统的时序产生影响,在高速PCB 设计中,传输延迟主要取决于导线的长度和导线周围介质的介电常数。
(2)反射。
当传输线的特性阻抗与负载阻抗不匹配时,信号到达接收端后有一部分能量将沿着传输线反射回去,使得信号波形发生畸变,甚至出现信号的过冲和下冲。

信号完整性基础信号完整性问题过冲(overshoot/undershoot)振铃(ringing/ring back)非单调性(non-monotonic)码间串扰(ISI)同步开关噪声(SSN)噪声余量(noise margin)串扰(crosstalk)信号完整性(Signal Integrity)主要包括以下几方面问题:1.过冲(Overshoot/Undershoot)一般IC对于过冲的高度和宽度的容忍度都有指标。
因为过冲会使IC内部的ESD防护二极管导通,通常电流有100mA左右。
信号长期的过冲会使IC器件降质,并是电源噪声和EMI的来源之一。
2. 振铃(Ringing/Ring Back)振铃会使信号的threshold域值模糊,而且容易引起EMI。
3.非单调性(Non-monotonic)电平上升过程中的平台会产生非单调性,这有可能对电路有危害,特别是针对异步信号如:Reset、Clock等会有影响。
4. 码间串扰(ISI)主要是针对高速串行信号。
其产生的本质是前一个波形还没有进入稳态,另外也有可能是传输线对不同频率衰减不同所造成的。
一般通过眼图来观察,方法是输入一伪随机码,观察输出眼图。
5. 同步开关噪声(SSN)同步开关噪声会使单根静止的信号线上出现毛刺?V,另外还会影响输入电平的判断。
SSN的另一种现象是SSO(同步开关输出),这会使得传输线的特性如阻抗、延时等特性发生改变。
6. 噪声裕量(Noise Margin)控制噪声余量的目的是防止外界干扰,用于克服仿真没有分析到的一些次要因素。
一般对于TTL信号应留有200~300mV的余量。
7. 串扰(Crosstalk)串扰主要有线间串扰、回路串扰、通过平面串扰(常见于数模混合电路)三种形式。
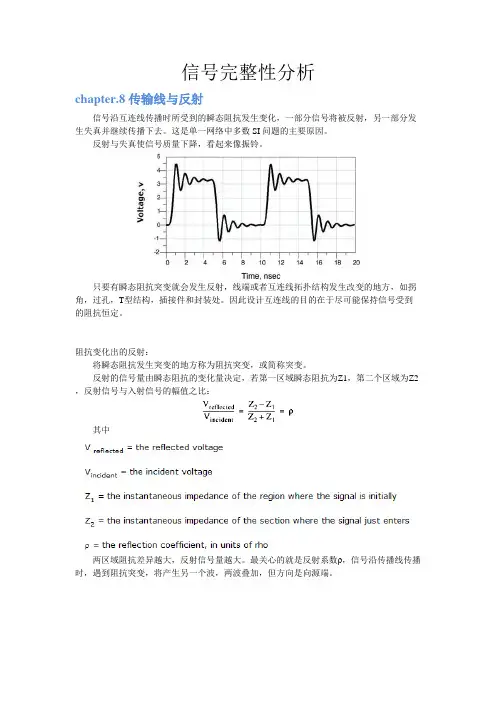
通常示波器所观察到的数字信号。
图中为各相关的信号完整性参数:•Overshoot、Undershoot指信号的过冲。
•Ringback 指信号的振铃。
信号完整性分析chapter.8 传输线与反射信号沿互连线传播时所受到的瞬态阻抗发生变化,一部分信号将被反射,另一部分发生失真并继续传播下去。
这是单一网络中多数 SI 问题的主要原因。
反射与失真使信号质量下降,看起来像振铃。
只要有瞬态阻抗突变就会发生反射,线端或者互连线拓扑结构发生改变的地方,如拐角,过孔,T型结构,插接件和封装处。
因此设计互连线的目的在于尽可能保持信号受到的阻抗恒定。
阻抗变化出的反射:将瞬态阻抗发生突变的地方称为阻抗突变,或简称突变。
反射的信号量由瞬态阻抗的变化量决定,若第一区域瞬态阻抗为Z1,第二个区域为Z2,反射信号与入射信号的幅值之比:其中两区域阻抗差异越大,反射信号量越大。
最关心的就是反射系数ρ,信号沿传播线传播时,遇到阻抗突变,将产生另一个波,两波叠加,但方向是向源端。
反射形成机理由上一特性,在设计高速板时,要运用以下设计要素:1.使用可控阻抗互连线2.传输线末端至少有一个终端匹配3.使用能使多分支产生影响最小的布线拓扑结构4.最小化几何结构的不连续性产生反射:区域1,2交界面两侧电压,电流应该相等,否则两侧不等会产生无限大电场与磁场。
V1=V2,I1=I2,而,I=V /R,当区域阻抗不同时,关系式绝不会同时成立。
为平衡系统,交界处区域1侧产生反射回源端的电压,唯一目的就是吸收入射信号和传输信号之间不匹配的电压与电流。
满足的条件:且两区域应满足:代换即最终,得到反射系数ρ同样,可以推导出传输系数t没有确切的原因知道怎么产生反射电压,但知道反射电压会遵循上述关系,电压电流要保持连续阻性负载的反射假定传输线特性阻抗为50Ω,传输线的终端匹配有三种情况:5.传输线的终端开路,末端未连接。
末端瞬态阻抗为无穷大。
反射系数ρ为1。
例:6.传输线末端与返回路径短路,即末端阻抗为0。
此时反射系数ρ为-1,短路突变处测的电压为(入射电压与反射电压之和)0V。
7.特殊情况,终端阻抗等于传输线的特性阻抗,即匹配。

信号完整性分析我们在滤除较为低频的噪声的时候,就应当选择电容值比较高的电容,想滤去频率较高的噪声,比如我们前面所说的EMI,则应该选择数值比较小的电容。
所以,在实际中,我们通常放置一个1uf到10uf左右的去耦电容在每个电源输出管脚处,来抑制低频成分,而选取0.01uf到0.1uf左右的去耦电容来滤除高频部分。
何为高速电路“高速电路”已经成为当今电子工程师们经常提及的一个名词,但究竟什么是高速电路?这的确是一个“熟悉”而又“模糊”的概念。
而事实上,业界对高速电路并没有一个统一的定义,通常对高速电路的界定有以下多种看法:有人认为,如果数字逻辑电路的频率达到或者超过45MHZ-50MHZ,而且工作在这个频率之上的电路已经占到了整个电子系统一定的份量(比如说1/3),就称为高速电路;也有人认为高速电路和频率并没有什么大的联系,是否高速电路只取决于它们的上升时间;还有人认为高速电路就是我们早些年没有接触过,或者说能产生并且考虑到趋肤效应的电路;更多的人则对高速进行了量化的定义,即当电路中的数字信号在传输线上的延迟大于1/2上升时间时,就叫做高速电路,本文也沿用这个定义作为考虑高速问题的标准。
此外,还有一个容易产生混淆的是“高频电路”的概念,“高频”和“高速”有什么区别呢?对于高频,很多人的理解就是较高的信号频率,虽然不能说这种看法有误,但对于高速电子设计工程师来说,理解应当更为深刻,我们除了关心信号的固有频率,还应当考虑信号发射时同时伴随产生的高阶谐波的影响,一般我们使用下面这个公式来做定义信号的发射带宽,有时也称为EMI发射带宽:F=1/(Tr*π),F是频率(GHz);Tr(纳秒)指信号的上升时间或下降时间。
通常当F>100MHz的时候,就可以称为高频电路。
所以,在数字电路中,是否是高频电路,并不在于信号频率的高低,而主要是取决于上升沿和下降沿。
根据这个公式可以推算,当上升时间小于3.185ns左右的时候,我们认为是高频电路。
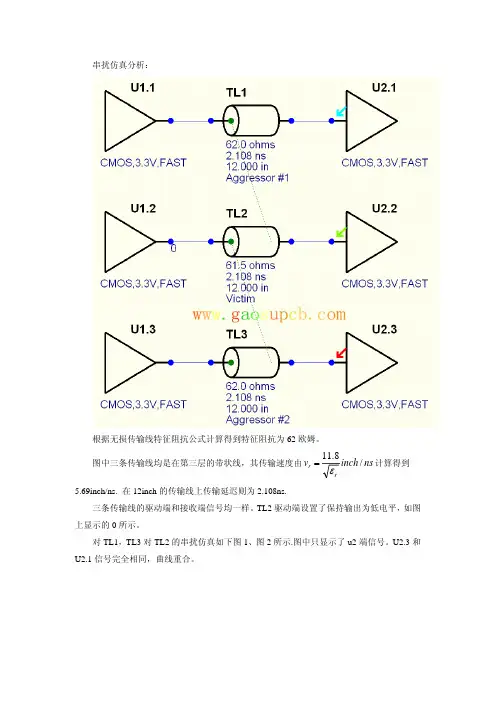
串扰仿真分析:
根据无损传输线特征阻抗公式计算得到特征阻抗为62欧姆。
图中三条传输线均是在第三层的带状线,其传输速度由ns inch v r r /8.11ε=
计算得到
5.69inch/ns.在12inch 的传输线上传输延迟则为2.108ns.
三条传输线的驱动端和接收端信号均一样。
TL2驱动端设置了保持输出为低电平,如图上显示的0所示。
对TL1,TL3对TL2的串扰仿真如下图1、图2所示.图中只显示了u2端信号。
U2.3和U2.1信号完全相同,曲线重合。
图1
如图1所示,TL1和TL3延迟约2.2ns(对应上述的计算结果)。
TL2驱动端设置了保持输出为低电平,故在TL1和TL3对其产生串扰前TL2保持低电平不变。
一旦其来到,TL2即刻(仿真图上显示TL2产生串扰的时间比TL1和TL3到来的时间延迟约100ps)产生串扰信号。
图2
图2显示串扰的较长时间波形。
显示的结果表明U2.2比U2.1和U2.3延迟。
此处的问题是串扰信号产生的延迟时间如何计算?通过波形图还可以得出U2.1和U2.3对串扰信号U2.2峰峰值产生叠加作用(此处是否是叠加,有待确认)。
图3
经过一定时间后信号衰减至0.
分别观察TL1、TL2、TL3驱动端和接收端的信号波形,如下图4、图5、图6所示(这些是截图显示的,上图是复制保存的):
图4思考:串扰之后为什么U2.1得到负电平信号?
图5思考:U2.1U2.3上的信号如何串扰到U2.2上的/?
图6
如果修改耦合方向couping direction则耦合结果会是什么样的呢?下一篇将一起探讨。

第1章 高速电路基础要点1、 高速电路的定义:数字逻辑电路的频率达到或超过50MHZ ,而且工作在这个频率之上的电路占整个系统的1/3以上,就可以称为高速电路。
2、 高速信号实质:信号传输时间大于数字信号驱动端上升时间的1/2,则可以认为是高速信号并产生传输线效应,实质是,:传输时间小于上身时间的一半时,那么在本次信号状态改变前,接收端的反射信号就已经到达驱动端,不会引起逻辑错误,反之,大于一半时,接收端的反射信号就可能会与下一次驱动端的输出信号进行叠加,若反射信号很强,就可能会影响下一次输出的正常逻辑。
3、 高信号的确定:Tr 表示信号上升时间,Tpd 表示传输延迟,若Tr>4Tpd,信号在安全区域,若2 Tpd<T r≤4 Tpd,信号在不确定区域,若Tr ≤2 Tpd ,信号落在问题区域,设计需保证信号落在安全区域。
4、 传输线:传输线上由两个具有一定长度的导体组成的回路的连接线,有时也称延迟线,传输线上每一点都有不同的电势。
(可以理解为机械波的振动,或电场吸纳促使电子移动导致电位变化模型,需要时间,故不同点电位不一致,不深按纠)5、 传输线的确定:信号传输路径长度大于信号波长的1%,或接收端元器件是边缘敏感,或系统没有过冲和下冲容限,此时虚认为传输路径是传输线。
(实质:边沿时间、波形变化时间、传输时间三者很接近时就必须考虑为传输线)零碎常识:(1)、PCB 上走线等效电阻阻值约为0.25~0.55Ω(2)、空气电信号传播速度85ps/in ,空气介电常数约为1,真空为1.(2)、FR4内层布线180ps/in ,介电常数为4.5;外层:140~180,2.8~4.56、反射系数:Z L 是当次传播负载端等效阻抗,Z O 当次传播输出端等效阻抗。
ρL =OL O L Z Z Z Z + 7、反射电压:反射系数乘ρL 以输入电压Vi 。
即Vf=ρL *Vi注:上表达式是乘以输入电压,即得反射电压,不在需要与1或原始量进行加减运算。
信号完整性的分析报告关于信号完整性的分析报告篇一:信号完整性分析--信号反射信号沿传输线向前传播时,每时每刻都会感受到一个瞬态阻抗,这个阻抗可能是传输线本身的,也可能是中途或末端其他元件的。
对于信号来说,它不会区分到底是什么,信号所感受到的只有阻抗。
如果信号感受到的阻抗是恒定的,那么他就会正常向前传播,只要感受到的阻抗发生变化,不论是什么引起的(可能是中途遇到的电阻,电容,电感,过孔,PCB转角,接插件),信号都会发生反射。
那么有多少被反射回传输线的起点?衡量信号反射量的重要指标是反射系数,表示反射电压和原传输信号电压的比值。
反射系数定义为:ρ= Z2Z1。
其中:Z1为变化前的阻 Z2Z1抗,Z2为变化后的阻抗。
假设PCB线条的特性阻抗为50欧姆,传输过程中遇到一个100欧姆的贴片电阻,暂时不考虑寄生电容电感的影响,把电阻看成理想的纯电阻,那么反射系数为:ρ=100501,信号有1/3被反射回源端。
如果传输信号的电压是3.3V电压,100503 反射电压就是1.1V。
纯电阻性负载的反射是研究反射现象的基础,阻性负载的变化无非是以下四种情况:阻抗增加有限值、减小有限值、开路(阻抗变为无穷大)、短路(阻抗突然变为0)。
阻抗增加有限值:反射电压上面的例子已经计算过了。
这时,信号反射点处就会有两个电压成分,一部分是从源端传来的3.3V电压,另一部分是在反射电压1.1V,那么反射点处的电压为二者之和,即4.4V。
阻抗减小有限值:仍按上面的例子,PCB线条的特性阻抗为50欧姆,如果遇到的电阻是30欧姆,则反射系数为ρ=3050=-0.25,反射电压为3.3*(-0.25)V= -0.825V。
此时反射点电压为3.3V+3050(-0.825V)=2.475V。
开路:开路相当于阻抗无穷大,反射系数按公式计算为1。
即反射电压3.3V。
反射点处电压为6.6V。
可见,在这种极端情况下,反射点处电压翻倍了。
短路:短路时阻抗为0,电压一定为0。
写在前言:作为一个还在layout门口徘徊的小虾米,贸然记录自己的学习想法是可笑的。
但每个人并不是出生就会成为大神。
只不过有的人天分好,机遇也把握得当,在相对短的时间内,成为万众瞩目的高手。
很可惜本人天生愚钝,机遇又很差,在毕业后的三年里浑浑噩噩的憧憬自己的人生,做着自己不喜欢的工程,每天跟着工程队奔波在广阔的祖国大地。
不经意在工作的最后阶段接触到PCB设计。
对于没有耐心和毅力的我,突然感觉这才是我的人生方向,因为突然发现在绘制板图的时候,我可以很有耐心的拉扯每一条线,呵呵难道这一条条显示屏上的线便是我的命运之线么?如饥似渴的读完买回来的书,又囫囵吞枣的大致看了两遍。
感觉到一个人的学习是空虚乏味的,于是想在咱们论坛与各位同我一样,还趴在门缝里仰慕者殿堂中的大神的新手们共同体会我的学习体会。
本人至今自学,没有老师带路,言语中的偏差错误,望各位高手给予我醍醐灌顶的指正。
在此感谢Eric Bogatin 感谢国内的翻译者李玉山、李丽平等,是他们让我趴在SI的门缝,让我有机会一窥我的成神目标。
让论坛记录成神的历程吧!哈哈有些夸口,目标定的太高,大家勿笑。
我的第一本SI教材:Signal integrity:simplified(信号完整性讲义)也是我目前唯一学习过的教材。
废话不多说,直接上酸菜!信号完整性问题十个基本准则:前三个为设计理念,后八个为设计思路。
影响研发进度并造成产品产品交货推迟,就是企业付出的最昂贵代价。
体会:在论坛中常常争论,是质量重要还是工期重要!我认为都重要,所有的工程都是一个平衡过程,而不是单单一种。
质量固然重要,但最重要的是适应性,因为整个工业流程中并不仅仅只是画线路板,最终交到消费者手里才是完整的工艺流程。
如果仅仅是为了吹毛求疵而耽误了工期,那么整个工业流程都会耽误。
导致产品上市时间推迟,损失不可计量。
但为了赶工期,而设计出不合格的产品,那么只能说设计者能力不够。
或者这家公司没有这个实力在行业内生存。
在AD出Gerber的时候,在layer选项下有2个栏,Layer to Plots和Mechanical layers to Add to All Plot. 一般情况下Mechanical layers to Add to All Plot.可以不予理会,此处的意思表示需要添加到任何层面的mechanical layers出Gerber的时候,如果没有删除room,有时会提示The film is too small for this PCB.因为room 会在角落离开PCB很远,但是gerber需要包含room的信息,如果gerber时候设置的film 的大小比较小,就会有这个问题。
如果有些object实在无法寻找,而需要的object比较好选择,可以ctrl+A,然后deselect需要的object,直接del即可将无法找寻的objectdel掉用PCB Inspector批量修改pad的soldermask expansion的时候,必须先勾选soldermask override,表示可以自定义soldermask expansion在Altium Designer里面设置内层pad和via的连接的时候,需要将pad设置为thermal,而via不需要,在设置all pad thermal connect以后,需要再add一个all direct connect的rule,优先级设置低于all pad thermal connect..否则所有的via将不会被连接到内层的plane低阻抗PDS的设计要点使GND与VCC尽量靠近 / 低电感值的去耦电容 / 封装assign多个寄生电感低的VCC与GND Via/常见的电磁干扰源差分信号转化为公模信号,在外部双绞线缆上输出PCB地弹在外部单端屏蔽线上产生公模电流。
附加的噪声可以由内部产生的辐射泄露溢出屏蔽罩引起做PCB NPTH的时候,可以在mechaincal 1层做一个NPTH,选中,Tool -> Convert -> Creat Board Cutout from Select Primitives可以在PCB上做一个针对所有层的Routing Keepout(not all electronical layer),首先在mechaincal 1 layer上做一个primitive,选中,Tool -> Convert -> Creat Cutout from Select Primitives在allegro中,框选一个封闭的line,可以compose 以line为外框的shape。
也可以选择一个unfill的shape,compose一个static shape返回路径是平面时是实现串扰最低的结构,一旦返回路径的平面发生变化,就会增加传输线之间的串扰上升沿时间与频率的关系:RT=1/10F其中:RT单位为ns,F的单位为GHz信号沿传输线传输,电压形成传输线之间的电场,电流形成传输线周围的磁场,传输线上信号的传播也是电磁波的传输。
信号的传输不仅传输电流和电压,同时还传播着电场和磁场单位长度导线的自感约为25nH/in圆形线圈的回路自感 L=32XRXIn(4R/D)nHR为线圈半径,D为导线直径,单位均为in在每个频率点,反射电压与入射电压之比称为S参数任何谐波的幅度都可以由V×2/(nπ)计算得出,V为最大电压值带宽用来描述频谱中有效的最高正弦波频率导体损耗和介质损耗,每种损耗过程对高频分量和低频分量的衰减是不一样的,所以以传输线传输的信号在到达load的时候信号的上升时间会有所改变在FR4介质上, 2G以下的频率的衰减不过-1dB,10G以上频率的衰减为-4dB带宽与上升时间的关系:BW=0.35/RT其中BW为带宽,单位为GHz; RT表示10%~90%的上升时间,单位为ns理想方波的谐波幅度下降的速度近似于1/f, 当实际波形的谐波幅度下降速度大于1/f的时候,此时谐波的频率即带宽电路中的振铃可能会使高频分量的幅度增加。
当波形出现振铃时,其带宽约等于振铃频率如果电流有理想方波的特性,尽管各次谐波的幅度已1/f的速度下降,但是由于共模电流的辐射是随着频率线性增加的,各次谐波的辐射能力也随着频率f上升,因此各次谐波对EMI 的影响都是相等的,为了减小EMI,应在设计中尽量减小信号的带宽。
带宽与时钟的经验公式BW=5 X F(以上升时间为7%周期为前提)测量的带宽指在带宽频率的范围内,测量得到的数据有比较好的精度。
注意与器件的带宽相区别。
模型的带宽指在带宽的范围内,利用模型可以得到比较精确的结果。
传输线带宽指用传输线传输信号,当信号传输损耗不影响系统工作时最高正弦波的频率传输线的3dB带宽:在实际应用中,传输线的带宽指传输的频率分量减小了3dB,也就是幅度减小为入射值的70%。
传输线的本征上升时间指传输线的带宽对应的最快上升时间。
比如传输线的带宽是1G,那么对应的传输线的最小的上升时间为RT=0.35/1G=0.35ns.,如果不考虑传输线带宽,一个信号的带宽是8G,对应的上升时间RT=0.35/8G=0.044ns,.当这个信号以1G带宽的传输线作为载体的时候,他的上升时间会受到传输线带宽的制约,具体的计算公式R tout=sqrt(RT in2+RT interconnect2)其中所有RT均为10%~90%的上升时间正弦电流与正弦电压之比不是正弦波,而是一些包含每个频率点上幅度的比值和相移的信息在频域中,阻抗所表示的相移指的是电压超前电流的相移随着频率的升高,流经电容器的电流(I=C×w×V×cos(wt))会增大流经电容的电流超前于电压π/4的相位,流经电感的电流滞后于电压π/4的相位。
实际零件模型的带宽很难计算,只能通过测量得到电阻值的计算公式R表示电阻值,单位 Ohmρ表示导线的体电阻率,单位为Ω.cmd表示互联线2端的距离,单位为cmA表示导线的横截面,单位为cm*cm直径为1mil, 长为80mil的键合线的电阻值大约为0.1 Ohm,键合线(铜)的单位长度的电阻大约是1 Ohm/in宽10mil,厚度为0.5 oz的铜导线的单位长度电阻是0.1 Ohm/in。
对于1oz的铜导线,电阻在20MHz处开始增加体电阻率与体电导率的积为1电阻率的单位是Ω.m,电导率的单位为Ω/m2个同心球面之间的电容为C=4πε*r*r1/(r1-r)ε:空间的介电常数,自由空间的介电常数为0.089pF/cm或者0.225pF/inr,r1: 球体的内外径,单位为cm或者in当内球面半径大于外球面半径10倍以上时候C=4πε*r(r为内球面半径)相对于某个表面,每个孤立的导体都有电容,这个电容不一定很小,而是有个与直径相关的最小值,导体距离附近的某个表面越近,他的电容量就越大。
通常1in的直径的球面电容量约为2pF平行板电容近似有一个前提条件,他假定了平行板周围的的边缘场效应是不存在的。
在实际中,考虑边缘场效应后,实际的电容量要大于近似值介电常数的本质是相对于空气的介电常数,所以是没有单位的,空气的介电常数为0.089pF/cm或者0.225pF/in。
介电常数越大,电容值越高。
水的介电常数约为80,同质固体材料介电常数会随频率的变化而变化,FR4从1KHz到10MHz,介电常数由4.8为4.4,而从1G到10G,介电常数就非常稳定了互联线中常用介质的相对介电常数多层板中存在的地与电源的平板电容,无法提供有效的去耦(相差3个数量级),他的作用只是为芯片和去耦电容提供低电感的路径如果线宽是介质厚度的2倍,介电常数为4,针对50 Ohm的传输线,则microstrip单位长度的电容C=2.7pF/in, Stripline的单位长度电容为3.5pF/in传输线厚度对传输线的寄生电容的影响是微小的传输线线宽的变化会影响微带线的有效介电常数,当线很宽时,大部分电力线都在介质中,这时有效介电常数约等于介质的介电常数。
当微带线的线宽比较小的时候,大部分的电力线都在空气中,此时有效介电常数会小于介质的介电常数若要求阻抗精度小于10%,则不能应用IPC关于阻抗的计算公式电介质不会对磁力线产生影响导线中电流愈大,导线越长,磁力线的匝数越多,磁场越强。
当导体中含有铁钴镍(铁磁金属,磁导率大于1)时,磁力线将显著增加,其他的任何金属都不会对磁力线产生任何影响电感是导体上流过单位安培电流时,导体周围磁力线的韦伯值L=N/IL表示电感,单位为HN表示电流导体周围的的磁力线匝数,单位为韦伯I是流过导体的电流,单位为安培此处应该深刻理解电感的定义,电感只与导体的几何结构有关。
影响电感的唯一因素就是导体的分布和在铁磁金属情况下导体的磁导率电感应与磁场强度区分开,电感源自导线上的电流,可以用比较具体的实物描述为以导线为轴心,有一定半径的圆柱体体积,导线越长,圆柱体越高,包含的体积越大,即电感越大。
影响电感的唯一因素是导体的分布和在铁磁金属情况时导体的磁导率导线周围的磁力线发生变化,则导线两端就会产生压降V=△N/△t△N标示磁力线的变化量,△t表示磁力线变化的时间当导线上电流发生变化时,电流的自感会发生变化,由于自感的变化而在导线上产生压降,这就是电流变化产生感应电压的原因V=△N/△t=L△I/△t=L(dI/dt)感应电压的极性可以根据原则判断:感应电压产生的感应电流将阻止导线上的电流的变化由电流变化产生的感应电压是所有有电感引起的信号完整性问题的根本原因串扰形成的原因是由于导线之间的互感,当其中一根导线的电流发生变化的时候,另一条导线的互感会发生变化,产生感应电压,从而对自身的信号产生影响,产生的噪声电压为Vnoise=M(dI/dt)Vnoise表示目标导线干扰电压M为两条导线之间的互感I为噪声源导线上的电流由于感应电压取决与电流变化速度,所以也用开关噪声此处所有电感均为局部电感直环形导线局部自感计算公式(精度优于几个百分点)L: 局部自感,单位为mHd:导线的长度,单位为inr: 导线的半径,单位为in从公式中可以看出,导体的局部自感与导体的长度成正比。
但是在实际中,还应考虑互感在新增长的导线上所起的增加的作用。
同时可以从上式看出,导体截面增大时,电感会减小,即电流越分散,局部电感就越小此处注意局部自感与局部互感的区别导线的局部自感大约为25nH/in或1nH/mm经验法则:从电容到via约50mil的线的局部自感约为1.2nH;板厚为64mil的过孔的局部自感约1.6nH。
局部互感当局部互感大于局部自感的20%时当导线的间距远大于导线长度时,两段导线的局部互感小于任意导线的局部自感的10%,这时互感通常可以忽略不计。