(一) 圆的相关概念及垂径定理
- 格式:doc
- 大小:266.50 KB
- 文档页数:5



CDABOE C ADOOABM 垂径定理的应用一、圆是轴对称(有无数条对称轴,过圆心的任一条直线都是对称轴);又是中心对称,对称中心是圆心. 二、垂径定理垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧.符号语言:∵CD 为⊙O 的直径,AB 为⊙O 的弦,且CD ⊥AB ,垂足为E ,∴ AE =BE,推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.∵CD 为⊙O 的直径,AB 为⊙O 的弦(不是直径),且AE =BE.弦心距:圆心到弦的距离(垂线段OE ) 考点分析:垂径定理及推论的应用,证明. 典型例题分析类型1. 垂径定理及推论概念1.下面四个命题中正确的一个是( )A .平分一条直径的弦必垂直于这条直径B .平分一条弧的直线垂直于这条弧所对的弦C .弦的垂线必过这条弦所在圆的圆心D .在一个圆内平分一条弧和它所对弦的直线必过这个圆的圆心 2. 如图1-2,如果AB 为⊙O 直径,弦AB CD ⊥,垂足为E ,那么下列结论中错误的是……( )A .DE CE =B .C .BAD BAC ∠=∠D .AD AC >3. 如图1-3在⊙O 中,弦CD 垂直平分半径OA ,且CD =6cm , 则半径OA 的长为………( )A. cm 34B. cm 54C. cm 32D. cm 8图1-2 图1-3 图1-4 图2-14. 如图1-4,⊙O 的直径CD 与弦AB 交于点M ,添加条件:_____________(写出一个即可),就可得到M 是AB 的中点.类型2. 垂径定理的运用在垂径定理的运用中,通常的是要利用定理构建直角三角形,利用勾股定理进行运算.5.过⊙O 内一点M 的最长的弦长为cm 10,最短的弦长为cm 8,那么⊙O 的半径等于___cm ,OM 的长为___cm类型2. 垂径定理分类讨论1. 如图2-1,⊙O 的直径为10,弦AB 的长为8,M 是弦AB 上的动点,则OM 的长的取值范围是( ) A. 5OM 3≤≤ B. 5OM 4≤≤ C. 5OM 3<< D. 5OM 4<<2.已知:AB 、CD 为⊙O 的两条弦,且AB ∥CD ,⊙O 的半径为5cm ,AB =8cm ,CD =6cm ,求AB 、CD 之间的距离.3. 已知:△ABC 内接于⊙O ,AB =AC ,半径OB =5cm ,圆心O 到BC 的距离为3cm ,求AB 的长.类型3. 利用垂径定理求线段长度,角度ACBDABD C E.O1.如图3-1,在圆O中,直径AB垂直于弦CD,并且交CD于E,直径MN交CD于F,且OEFDFO2==,求COD∠.2.如图3-2,AB为⊙O的直径,且AB⊥弦CD于E,CD=16,AE=4,求OE的长.图3-23.如图3-3,在ABCRt∆中,∠C=900,AC=5cm,BC=12cm,以C为圆心、AC为半径的圆交斜边于D,求AD的长.图3-34.如图3-4,已知:AB是⊙O的直径,弦CD交AB于E点,BE=1,AE=5,∠AEC=300,求CD的长.5. 如图3-5,O 是两个同心圆的圆心,大圆的弦AB 交小圆于C 、D 两点,OE ⊥CD 于E ,若AB =2CD =4OE 求:大圆半径R 与小圆半径r 之比.类型4. 垂径定理相关证明1.如图4-1,BF ,CE 是⊙O 的直径,.求证:OCM OBN ∠=∠.图4-12.如图4-2,F 是以O 为圆心,BC 为直径的半圆上任一点,A 是的中点,AD ⊥BC 于D.求证:.21BF AD =图4-23.已知:如图4-3,⊙O 的弦AB ,CD 相交于点P ,PO 是APC ∠的平分线,点M ,N 分别是,的中点,MN 分别交AB ,CD 于点E ,F .求证:PO MN ⊥.图4-3类型5. 垂径定理的综合应用 1. 一水平放置的圆柱型水管的横截面如图5-1所示,如果水管横截面的半径是13cm ,水面宽24=AB cm ,则水管中水深是_______cm. 图5-1 2. 如图5-2,某地有一座圆弧形拱桥,桥下水面宽度为2.7米,拱顶高出水面4.2米,现有一艘宽3米,船仓顶部为方形并高出水面2米的货船要经过这里.问货船能否顺利通过这座拱桥?图5-2 3. 如图5-3,在某养殖场A 处发现高致病性禽流感,为防止禽流感蔓延,政府规定离疫点3千米范围内为捕杀区;离疫点3至5千米范围内为免疫区.现有一条笔直的公路EB 通疫区,若在捕杀区内CD =4千米,问这条公路在改免疫区内多少千米?图5-3【拓展提升】1. 如图6-1,已知在⊙O 中,弦CD AB =,且CD AB ⊥,垂足为H ,AB OE ⊥于E ,CD OF ⊥ 于F .(1)求证:OEHF 是正方形.(2)若3=CH ,9=DH ,求圆心O 到弦图6-12.如图6-2,AB 是⊙O 的直径,P 是AB 上一动点,C 、D 是⊙O 的两点,有∠CPB =∠DPB.求证:PC =PD.COABE F D3. 已知:如图6-3,A,是半圆O 上的两点,CD 是⊙O 的直径,∠AOD =800,B 是中点.(1)在CD 上求作一点P ,使得AP+PB 最短;(2)若CD =4cm ,求AP+PB 的最小值.图6-34. 如图6-4,AB 是⊙O 的直径,CD 是弦,AE ⊥CD 于E ,BF ⊥CD 于F .求证: CE =DF ;OE =OF.图6-4 变式1. 如图6-5,⊙O 的直径AB 和弦CD 相交于点M ,CD AE ⊥,CD BF ⊥,垂足分别是E ,F .(1)求证:DF CE =.(2)若26=AB ,24=CD ,求BF AE -的值.图6-52:如果弦CD 是动弦,与直径AB 不相交,AE ⊥CD 于E ,BF ⊥CD 于F ,此时是否有: CE =DF ;OE =OF.如果有请证明,如果不成立,请说明.。
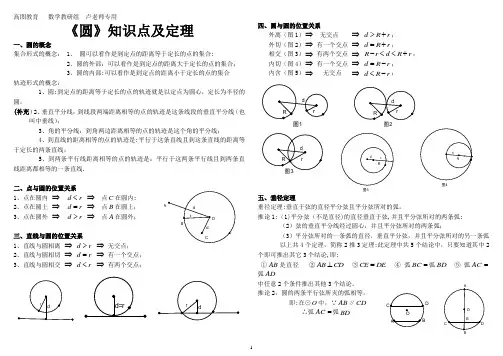
《圆》知识点及定理一、圆的概念集合形式的概念: 1、圆可以看作是到定点的距离等于定长的点的集合;2、圆的外部:可以看作是到定点的距离大于定长的点的集合;3、圆的内部:可以看作是到定点的距离小于定长的点的集合轨迹形式的概念:1、圆:到定点的距离等于定长的点的轨迹就是以定点为圆心,定长为半径的圆;(补充)2、垂直平分线:到线段两端距离相等的点的轨迹是这条线段的垂直平分线(也叫中垂线);3、角的平分线:到角两边距离相等的点的轨迹是这个角的平分线;4、到直线的距离相等的点的轨迹是:平行于这条直线且到这条直线的距离等于定长的两条直线;5、到两条平行线距离相等的点的轨迹是:平行于这两条平行线且到两条直线距离都相等的一条直线.二、点与圆的位置关系1、点在圆内⇒d r<⇒点C在圆内;2、点在圆上⇒d r=⇒点B在圆上;3、点在圆外⇒d r>⇒点A在圆外;三、直线与圆的位置关系1、直线与圆相离⇒d r>⇒无交点;2、直线与圆相切⇒d r=⇒有一个交点;3、直线与圆相交⇒d r<⇒有两个交点;四、圆与圆的位置关系外离(图1)⇒无交点⇒d R r>+;外切(图2)⇒有一个交点⇒d R r=+;相交(图3)⇒有两个交点⇒R r d R r-<<+;内切(图4)⇒有一个交点⇒d R r=-;内含(图5)⇒无交点⇒d R r<-;五、垂径定理垂径定理:垂直于弦的直径平分弦且平分弦所对的弧。
推论1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧以上共4个定理,简称2推3定理:此定理中共5个结论中,只要知道其中2个即可推出其它3个结论,即:①AB是直径②AB CD⊥③CE DE=④弧BC=弧BD⑤弧AC=弧AD中任意2个条件推出其他3个结论。
自学资料一、圆的相关定义【知识探索】1.定理:不在同一直线上的三点确定一个圆.【说明】(1)过平面上一点能作无数多个圆;(2)过平面上两点能做无数多个圆,这些圆的圆心在两点连线的垂直平分线上;(3)过平面上三点:①三点不在同一直线上,能作唯一一个圆;②三点在同一直线上,不能作圆.【错题精练】例1.下列命题正确的个数有()①过两点可以作无数个圆;②经过三点一定可以作圆;③任意一个三角形有一个外接圆,而且只有一个外接圆;④任意一个圆有且只有一个内接三角形.A. 1个B. 2个C. 3个D. 4个第1页共23页自学七招之日计划护体神功:每日计划安排好,自学规划效率高非学科培训【解答】解:①过两点可以作无数个圆,正确;②经过三点一定可以作圆,错误;③任意一个三角形有一个外接圆,而且只有一个外接圆,正确;④任意一个圆有且只有一个内接三角形,错误,正确的有2个,故选:B.【答案】B例2.有下列四个命题,其中正确的有()①圆的对称轴是直径;②经过三个点一定可以作圆;③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.A. 4个B. 3个C. 2个D. 1个【答案】C例3.如图,在平面直角坐标系中,点A坐标为(﹣4,0),⊙O与x轴的负半轴交于B(﹣2,0).点P是⊙O上的一个动点,PA的中点为Q.当点Q也落在⊙O上时,cos∠OQB的值等于()A.B.C.D.【解答】第2页共23页自学七招之错题本锁骨术:巧用智能错题本,错题定期反复练非学科培训【答案】C例4.如图,已知△ABC.(1)尺规作图作△ABC的外接圆(保留作图痕迹,不写作法);(2)设△ABC是等腰三角形,底边BC=10,腰AB=6,求圆的半径r.【答案】解:(1)如图所示;(2)连接OB,连接OA交BC于点E,∵△ABC是等腰三角形,底边BC=10,腰AB=6,∴BE=CE=5,AE=√AB2−BE2=√11,在Rt△BOE中,r2=52+(r-√11)2∴r=18√11=18√1111.第3页共23页自学七招之预习轻身术:预习习惯培养好,课堂轻松没烦恼非学科培训第4页 共页自学七招之错题本锁骨术:巧用智能错题本,错题定期反复练非学科培训【解答】【解答】解:如图:连接OA,作OM⊥AB与M,∵⊙O的直径为10,∴半径为5,∴OP的最大值为5,∵OM⊥AB与M,∴AM=BM,∵AB=6,∴AM=3,在Rt△AOM中,OM==4,OM的长即为OP的最小值,∴4≤OP≤5.【答案】4≤OP≤55.已知:△ABC(如图)(1)求作:△ABC的外接圆(要求:用尺规作图,保留作图痕迹,不要求写作法及证明).(2)若∠A=60°,BC=8√3,求△ABC的外接圆的半径.【答案】解:(1)如图所示:⊙O即为所求△ABC的外接圆;(2)过点O作OD⊥BC于点D,∵∠A=60°,BC=8√3,∴∠COD=60°,CD=4√3,第5页共23页自学七招之预习轻身术:预习习惯培养好,课堂轻松没烦恼非学科培训∴CO=4√3sin60°=8,答:△ABC的外接圆的半径为8.二、圆心角、弧、弦、弦心距、圆周角之间的关系【知识探索】年份题量分值考点题型2015114圆内接四边形的性质;点与圆的位置关系选择、简答201613圆周角定理;填空2017219弧长面积;切线的性质;圆周角定理选择、填空、简答201824圆周角定理;填空2019216扇形面积;切线长定理;圆心角、圆周角、垂径定理填空、解答【错题精练】例1.如图所示,小华从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走.按照这种方式,小华第五次走到场地边缘时处于弧AB上,此时∠AOE=52°,则α的度数是()A. 51.5°B. 60°C. 72°D. 76°【解答】解:连接OD.∵∠BAO=∠CBO=α,∴∠AOB=∠BOC=∠COD=∠DOE,∵∠AOE=52°,∴∠AOB=(360°-52°)÷4=77°,第6页共23页自学七招之错题本锁骨术:巧用智能错题本,错题定期反复练非学科培训第7页 共23页自学七招之预习轻身术:预习习惯培养好,课堂轻松没烦恼 非学科培训∴α=(180°-77°)÷2=51.5°. 故选:A .【答案】A例2.如图,在△ABC 中,∠C=90°,以点C 为圆心,BC 为半径的圆交AB 于点D ,交AC 于点E .(1)若∠A=25°,求BD̂的度数. (2)若BC=9,AC=12,求BD 的长.【答案】解:(1)连接CD ,如图, ∵∠ACB=90°,∴∠B=90°-∠A=90°-25°=65°,∵CB=CD ,∴∠CDB=∠B=65°, ∴∠BCD=180°-2∠B=50°, ∴BD ̂的度数为50°;(2)作CH ⊥BD ,如图,则BH=DH , 在Rt △ACB 中,AB=√92+122=15, ∵12CH•AB=12BC•AC , ∴CH=9×1215=365, 在Rt △BCH 中,BH=√92−(365)2=275,∴BD=2BH=545.̂的度数为()例3.已知如图,在⊙O中,OA⊥OB,∠A=35°,则CDA. 20°B. 25°C. 30°D. 35°【解答】解:连接OC,∵OA⊥OB,∴∠AOB=90°,∵∠A=35°,∴∠OBC=90°-35°=55°,∴OB=OC,∴∠OBC=∠OCB=55°,∴∠COB=70°,∴∠COD=90°-70°=20°,̂的度数为20°,∴CD故选:A.【答案】A例4.已知AB是⊙O的直径,点C,D是⊙O上的点,∠A=50°,∠B=70°,连接DO,CO,DC (1)如图①,求∠OCD的大小:(2)如图②,分别过点C,D作OC,OD的垂线,相交于点P,连接OP,交CD于点M已知⊙O的半径为2,求OM及OP的长.第8页共23页自学七招之错题本锁骨术:巧用智能错题本,错题定期反复练非学科培训【答案】解:(1)∵OA=OD,OB=OC,∴∠A=∠ODA=50°,∠B=∠OCB=70°,∴∠AOD=80°,∠BOC=40°,∴∠COD=180°-∠AOD-∠BOC=60°,∵OD=OC,∴△COD是等边三角形,∴∠OCD=60°;(2)∵PD⊥OD,PC⊥OC,∴∠PDO=∠PCO=90°,∴∠PDC=∠PCD=30°,∴PD=PC,∵OD=OC,∴OP垂直平分CD,∴∠DOP=30°,∵OD=2,∴OM=√32OD=√3,OP=4√33.例5.如图,AB为⊙O的直径,△ABC的边AC,BC分别与⊙O交于D,E,若E为BD̂的中点.(1)求证:DE=EC;(2)若DC=2,BC=6,求⊙O的半径【答案】解:(1)连结AE,BD,∵E为BD̂的中点,∴ED̂=BÊ,∴∠CAE=∠BAE,∵∠AEB是直径所对的圆周角,第9页共23页自学七招之预习轻身术:预习习惯培养好,课堂轻松没烦恼非学科培训第10页 共23页自学七招之错题本锁骨术:巧用智能错题本,错题定期反复练 非学科培训∴∠AEB=90°, 即AE ⊥BC ,∴∠AEB=∠AEC=90°,在△AEC 和△AEB 中{∠CAE =∠BAE AE =AE ∠AEC =∠AEB ,∴△AEC ≌△AEB (ASA ), ∴CE=BE , ∴DE=CE=BE=12BC ;(2)在Rt △CBD 中,BD 2=BC 2-CD 2=32, 设半径为r ,则AB=2r , 由(1)得AC=AB=2r , AD=AC-CD=2r-2,在Rt △ABD 中AD 2+BD 2=AB 2, ∴(2r-2)2+32=(2r )2, 解得:r=4.5,∴⊙O 的半径为4.5.例6.如图,点A ,B ,C 在⊙O 上,AB ∥OC .(1)求证:∠ACB+∠BOC=90°;(2)若⊙O 的半径为5,AC=8,求BC 的长度.【答案】(1)证明:∵AB̂对的圆周角是∠ACB ,对的圆心角是∠AOB , ∴∠AOB=2∠ACB , ∵OB=OA ,∴∠ABO=∠BAO , ∵AB ∥OC ,∴∠ABO=∠BOC ,∠BAO+∠AOC=180°, ∴∠BAO+∠AOB+∠BOC=180°, 即2∠ACB+2∠BOC=180°, ∴∠ACB+∠BOC=90°;(2)延长AO 交⊙O 于D ,连接CD ,则∠ACD=90°,由勾股定理得:CD=√AD2−AC2=√(5+5)2−82=6,∵OC∥AB,∴∠BOC=∠ABO,∠COD=∠BAO,∵∠BAO=∠ABO,∴∠BOC=∠COD,在△BOC和△DOC中{OB=OD∠BOC=∠DOC OC=OC∴△BOC≌△DOC(SAS),∴BC=CD,∵CD=6,∴BC=6.例7.如图,AB是半圆O的直径,AC是弦,∠CAB=60∘,若AB=6cm.(1)求弦AC的长;(2)点P从点A开始,以1cm/s的速度沿AB向点B运动,到点B停止,过点P作PQ∥AC,交半圆O于点Q,设运动时间为t(s).①当t=1时,求PQ的长;②若△OPQ为等腰三角形,直接写出t(t>0)的值.【解答】(1)解:如图1中,∵OA=OC,∠CAB=60∘,∴△AOC是等边三角形,∴AC=OA=3(cm);(2)解:①如图2中,作OH⊥PQ于H,连接OQ,由题意得:AP=1,OP=2,∵PQ∥AC,∴∠OPH=∠CAB=60∘,在Rt△OPH中,∵∠POH=90∘−∠OPH=30∘,OP=2,∴PH=1OP=1,OH=√3PH=√3,2在Rt△QOH中,HQ=√OQ2−OH2=√6,∴PQ=PH+HQ=1+√6;②如图3中,∵△OPQ是等腰三角形,观察图象可知,只有OP=PQ,作PH⊥OQ于H.∵PQ∥AC,∴∠QPB=∠CAB=60∘,∵PQ=PO,PH⊥OQ,,∠POQ=∠PQO=30∘,∴OH=HQ=32∴OP=OH÷cos30∘=√3,∴AP=3+√3,∴t=3+√3秒时,△OPQ是等腰三角形.【答案】(1)3cm;(2)①1+√6;②t=3+√3.例8.如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D、E,且.(1)试判断△ABC的形状,并说明理由.(2)已知半圆的半径为5,BC=12,求sin∠ABD的值.【解答】(1)解:△ABC为等腰三角形.理由如下:连结AE,如图,∵,∴∠DAE=∠BAE,即AE平分∠BAC,∵AB为直径,∴∠AEB=90∘,∴AE⊥BC,∴△ABC为等腰三角形;(2)解:∵△ABC为等腰三角形,AE⊥BC,∴BE=CE=12BC=12×12=6,在Rt△ABE中,∵AB=10,BE=6,∴AE=√102−62=8,∵AB为直径,∴∠ADB=90∘,∴12AE⋅BC=12BD⋅AC,∴BD=8×1210=485,在Rt△ABD中,∵AB=10,BD=485,∴AD=√AB2−BD2=145,∴sin∠ABD=ADAB =14510=725.【答案】(1)略;(2)725.【举一反三】1.如图,弦AC、BD相交于点E,且AB̂=BĈ=CD̂,若∠AED=80°,则∠ACD的度数为()A. 20°B. 25°C. 30°D. 15°【解答】解:如图,设AB̂的度数为m,AD̂的度数为n,∵AB̂=BĈ=CD̂,∴BĈ、CD̂的度数都为m,∴3m+n=360°①∵∠AED=80°,∴∠C+∠D=80°,∴12m+12n=80°②,由①②组成{3m+n=360°12m+12n=80°,解得m=100°,n=60°∴∠ACD=12n=30°.故选:C.【答案】C2.已知△ABC内接于⊙O,点D平分弧BmĈ.(1)如图①,若∠BAC=2∠ABC.求证:AC=CD;(2)如图②,若BC为⊙O的直径,且BC=10,AB=6,求AC,CD的长.【答案】(1)证明:∵点D平分弧BmĈ,∴弧DC=弧DB,∵∠BAC=2∠ABC,∴弧BDC=2弧AC,∴弧CA=弧CD,∴AC=CD;(2)解:连结BD,如图②,∵BC为⊙O的直径,∴∠BAC=∠BDC=90°,在Rt △BAC 中,∵BC=10,AB=6,∴AC=√BC 2−AB 2=8;∵弧DC=弧DB ,∴DB=DC ,∴△BCD 为等腰直角三角形,∴CD=√22BC=5√2.3.如图,在⊙O 中,点C 是优弧ACB 的中点,D 、E 分别是OA 、OB 上的点,且AD=BE ,弦CM 、CN 分别过点D 、E .(1)求证:CD=CE .(2)求证:AM̂=BN ̂.【答案】(1)证明:连接OC .∵AĈ=BC ̂, ∴∠COD=∠COE ,∵OA=OB ,AD=BE ,∴OD=OE ,∵OC=OC ,∴△COD ≌△COE (SAS ),∴CD=CE .(2)分别连结OM ,ON ,∵△COD ≌△COE ,∴∠CDO=∠CEO ,∠OCD=∠OCE ,∵OC=OM=ON ,∴∠OCM=∠OMC ,∠OCN=∠ONC ,∴∠OMD=∠ONE ,∵∠ODC=∠DMO+∠MOD ,∠CEO=∠CNO+∠EON ,∴∠MOD=∠NOE ,∴AM̂=BN ̂.4.如图,已知△ABC中,AB=AC,以AB为直径的⊙O与边BC相交于点D,过点D作⊙O的切线与AC交于点E.(1)求BDBC的值.(2)判断DE与AC的位置关系,并证明你的结论.(3)已知BC:AB=2:3,DE=4√2,求⊙O的直径.【解答】(1)解:如图,连接AD,∵AB是⊙O的直径,∴AD⊥BC,∵AB=AC,∴BD=DC,∴BDBC =12;(2)解:DE⊥AC;连接OD,∵DE是⊙O的切线,∴DE⊥OD,∵AB=AC,∴∠B=∠C,∵OB=OD,∴∠B=∠ODB,∴∠ODB=∠C,∴AC∥OD,∴DE⊥AC;(3)解:∵BDBC =12且BC:AB=2:3,∴AB:CD=3,∵∠ADB =∠DEC =90∘,∠B =∠C ,∴△ABD ∽△DCE ,∴DC AB =CE BD =13,设CE =a ,则BD =CD =3a ,AB =9a ,在Rt△DEC 中,由勾股定理得:DE =2a √2=4√2,∴a =2,∴AB =18.【答案】(1)12;(2)DE ⊥AC ;(3)18.5.已知直径CD ⊥弦BF 于 E ,AB 为ʘO 的直径.(1)求证:FD̂=AC ̂; (2)若∠DAB=∠B ,求∠B 的度数.【答案】(1)证明:∵直径CD ⊥弦BF ,∴FD̂=BD ̂, ∵∠AOC=∠BOD ,∴BD̂=AC ̂, ∴FD̂=AC ̂; (2)解:由圆周角定理得,∠BOD=2∠DAB ,∵∠DAB=∠B ,∴∠BOD=2∠B ,∵CD ⊥BF ,∴∠B=30°.6.如图,⊙O 的半径为2,弦BC =2√3,点A 是优弧BC 上一动点(不包括端点),△ABC 的高BD 、CE 相交于点F ,连结ED .下列四个结论:①∠A 始终为60°;②当∠ABC =45∘时,AE =EF ;③当△ABC 为锐角三角形时,ED =√3;④线段ED 的垂直平分线必平分弦BC .其中正确的结论是 .(把你认为正确结论的序号都填上)【答案】①②③④.7.圆O的直径为10cm,A是圆O内一点,且OA=3cm,则圆O中过点A的最短弦长=__________cm【答案】88.如图,在圆O中,AB为直径,CD为弦,已知∠ACD=40°,则∠BAD=__________°【答案】501.如图,AB圆O的直径,点C在圆O上,若∠OCA=50°,AB=4,则弧BC的长为()πA. 103B. 109π C. 59πD. 518π【答案】B2.如图,将钢珠放在一个边长AB=8mm 的正方形的方槽内,测得钢珠顶端离零件表面的距离为8mm ,则这个钢珠的直径为______mm .【答案】103.如图,AB 是半圆的直径,E 是弦AC 上一点,过点E 作EF ⊥EB ,交AB 于点F ,过点A 作AD ∥EF ,交半圆于点D .若C 是BD ̂的中点,AF AE =√54,则EFAD 的值为 .【解答】解:延长BE 交AD 于A',∵AD ∥EF ,EF ⊥BE ,∴AA'⊥BA',∴∠AA'B=90°,∵AB 为⊙O 的直径,∴∠ADB=90°,∴D 与A'重合,∵AFAE =√54,∴设AF=√5a,AE=4a,过F作FG⊥AE于G,∵C是BD̂的中点,∴CD̂=BĈ,∴∠DAC=∠BAC,∵AD∥EF,∴∠BFE=∠DAB=2∠BAC=∠BAC+∠AEF,∴∠BAC=∠AEF,∴AF=EF,∴AG=EG=2a,由勾股定理得:FG=a,∵∠DAE=∠GAF,∠ADE=∠AGF=90°,∴△ADE∽△AGF,∴ADAE =AGAF,∴AD4a =2a√5a,AD=8a√5,∴EFAD =√5a8a√5=58,故答案为:58.【答案】584.在⊙O的内接△ABC中,AD⊥BC于D,(1)①图1中,若作直径AP,求证:AB.AC=AD.AP;②已知AB+AC=12,AD=3,设⊙O的半径为y,AB的长为x.求y与x的函数关系式及自变量x的取值范围;(2)图2中,点E为⊙O上一点,且弧AE=弧AB,求证:CE+CD=BD.【答案】5.在⊙O的内接△ABC中,AB+AC=12,AD⊥BC,垂足为D,且AD=3,设⊙O的半径为y,AB的长为x。


圆的知识点概念公式大全一.圆的定义1.在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫圆.这个固定的端点O叫做圆心,线段OA叫做半径.以O点为圆心的圆记作⊙O,读作圆O.2.圆是在一个平面内,所有到一个定点的距离等于定长的点组成的图形.3.确定圆的条件:⑴圆心;⑵半径,其中圆心确定圆的位置,半径长确定圆的大小.二.同圆、同心圆、等圆1.圆心相同且半径相等的圆叫做同圆;2.圆心相同,半径不相等的两个圆叫做同心圆;3.半径相等的圆叫做等圆.三.弦和弧1.连结圆上任意两点的线段叫做弦.经过圆心的弦叫做直径,并且直径是同一圆中最长的弦,直径等于半径的2倍.2.圆上任意两点间的部分叫做圆弧,简称弧.以A B、为端点的弧记作»AB,读作弧AB.在同圆或等圆中,能够重合的弧叫做等弧.3.圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.在一个圆中大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧.4.从圆心到弦的距离叫做弦心距.5.由弦及其所对的弧组成的图形叫做弓形.四.与圆有关的角及相关定理1.顶点在圆心的角叫做圆心角.将整个圆分为360等份,每一份的弧对应1︒的圆心角,我们也称这样的弧为1︒的弧.圆心角的度数和它所对的弧的度数相等.2.顶点在圆上,并且两边都和圆相交的角叫做圆周角.圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论1:在同圆或等圆中,如果两个圆周角相等,它们所对的弧一定相等.推论2:半圆(或直径)所对的圆周角是直角,90 的圆周角所对的弦是直径.(在同圆中,半弧所对的圆心角等于全弧所对的圆周角)3.顶点在圆内,两边与圆相交的角叫圆内角.圆内角定理:圆内角的度数等于圆内角所对的两条弧的度数和的一半.4.顶点在圆外,两边与圆相交的角叫圆外角.圆外角定理:圆外角的度数等于圆外角所对的长弧的度数与短弧的度数的差的一半.5.圆内接四边形的对角互补,一个外角等于其内对角.6.如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.7.圆心角、弧、弦、弦心距之间的关系定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量分别相等.五.垂径定理1.垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;2.其它正确结论:⑴弦的垂直平分线经过圆心,并且平分弦所对的两条弧;⑵平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.⑶圆的两条平行弦所夹的弧相等.3.知二推三:⑴直径或半径;⑵垂直弦;⑶平分弦;⑷平分劣弧;⑸平分优弧.以上五个条件知二推三.注意:在由⑴⑶推⑵⑷⑸时,要注意平分的弦非直径. 4.常见辅助线做法:⑴过圆心,作垂线,连半径,造RT △,用勾股,求长度; ⑵有弧中点,连中点和圆心,得垂直平分.相关题目:1.平面内有一点到圆上的最大距离是6,最小距离是2,求该圆的半径2.(08郴州)已知在O ⊙中,半径5r =,AB CD ,是两条平行弦,且86AB CD ==,,则弦AC 的长为__________.. 六.点与圆的位置关系 1.点与圆的位置有三种:⑴点在圆外⇔d r >;⑵点在圆上⇔d r =;⑶点在圆内⇔d r <. 如下表所示:2.过已知点作圆⑴经过点A 的圆:以点A 以外的任意一点O 为圆心,以OA 的长为半径,即可作出过点A 的圆,这样的圆有无数个.⑵经过两点A B、的圆:以线段AB中垂线上任意一点O作为圆心,以OA的长为半径,即可作出过点A B、的圆,这样的圆也有无数个.⑶过三点的圆:若这三点A B C、、三点、、共线时,过三点的圆不存在;若A B C 不共线时,圆心是线段AB与BC的中垂线的交点,而这个交点O是唯一存在的,这样的圆有唯一一个.⑷过n()4n≥个点的圆:只可以作0个或1个,当只可作一个时,其圆心是其中不共线三点确定的圆的圆心.3.定理:不在同一直线上的三点确定一个圆.注意:⑴“不在同一直线上”这个条件不可忽视,换句话说,在同一直线上的三点不能作圆;⑵“确定”一词的含义是“有且只有”,即“唯一存在”.4.三角形的外接圆⑴经过三角形三个顶点的圆叫做三角形的外接圆,外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心,这个三角形叫做这个圆的内接三角形.⑵三角形外心的性质:①三角形的外心是指外接圆的圆心,它是三角形三边垂直平分线的交点,它到三角形各顶点的距离相等;②三角形的外接圆有且只有一个,即对于给定的三角形,其外心是唯一的,但一个圆的内接三角形却有无数个,这些三角形的外心重合.⑶锐角三角形外接圆的圆心在它的内部(如图1);直角三角形外接圆的圆心在斜边中点处(即直角三角形外接圆半径等于斜边的一半,如图2);钝角三角形外接圆的圆心在它的外部(如图3).图3图2图1CBCC五.直线和圆的位置关系的定义、性质及判定设O ⊙的半径为r ,圆心O 到直线l 的距离为d ,则直线和圆的位置关系如下表:从另一个角度,直线和圆的位置关系还可以如下表示:四.切线的性质及判定1. 切线的性质:定理:圆的切线垂直于过切点的半径.推论1:经过圆心且垂直于切线的直线必经过切点. 推论2:经过切点且垂直于切线的直线必经过圆心. 2. 切线的判定定义法:和圆只有一个公共点的直线是圆的切线; 距离法:和圆心距离等于半径的直线是圆的切线;定理:经过半径的外端并且垂直于这条半径的直线是圆的切线. 3. 切线长和切线长定理:⑴ 在经过圆外一点的圆的切线上,这点和切点之间的线段的长,叫做这点到圆的切线长.⑵ 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.五.三角形内切圆1. 定义:和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.2. 多边形内切圆:和多边形的各边都相切的圆叫做多边形的内切圆,该多边形叫做圆的外切多边形.六.圆和圆的位置关系的定义、性质及判定设12O O 、⊙⊙的半径分别为R r 、(其中R r >),两圆圆心距为d ,则两圆位置关系如下表:位置关系图形定义性质及判定外离两个圆没有公共点,并且每个圆上的点都在另一个圆的外部.d R r >+⇔两圆外离外切两个圆有唯一公共点,并且除了这个公共点之外,每个圆上的点都在另一个圆的外部.d R r=+⇔两圆外切相交两个圆有两个公共点.R r d R r-<<+⇔两圆相交内切两个圆有唯一公共点,并且除了这个公共点之外,一个圆上的点都在另一个圆的内部.d R r=-⇔两圆内切内含两个圆没有公共点,并且一个圆上的点都在另一个圆的内部,两圆同心是两圆内含的一种特例.0d R r≤<-⇔两圆内含说明:圆和圆的位置关系,又可分为三大类:相离、相切、相交,其中相离两圆没有公共点,它包括外离与内含两种情况;相切两圆只有一个公共点,它包括内切与外切两种情况.七.正多边形与圆1. 正多边形的定义:各条边相等,并且各个内角也都相等的多边形叫做正多边形.2. 正多边形的相关概念:⑴正多边形的中心:正多边形的外接圆的圆心叫做这个正多边形的中心.⑵正多边形的半径:正多边形外接圆的半径叫做正多边形的半径.⑶正多边形的中心角:正多边形每一边所对的圆心角叫做正多边形的中心角.⑷正多边形的边心距:中心到正多边形的一边的距离叫做正多边形的边心距.3. 正多边形的性质:⑴正n边形的半径和边心距把正n边形分成2n个全等的直角三角形;⑵正多边形都是轴对称图形,正n 边形共有n 条通过正n 边形中心的对称轴; ⑶偶数条边的正多边形既是轴对称图形,也是中心对称图形,其中心就是对称中心.八、圆中计算的相关公式设O ⊙的半径为R ,n ︒圆心角所对弧长为l , 1. 弧长公式:π180n Rl =2. 扇形面积公式:21π3602n S R lR ==扇形 3. 圆柱体表面积公式:22π2πS R Rh =+4. 圆锥体表面积公式:2ππS R Rl =+(l 为母线) 常见组合图形的周长、面积的几种常见方法: ① 公式法;② 割补法;③ 拼凑法;④ 等积变换法。

1、在同圆或等圆中,如果两个圆心角、两条弦、两条弧中有一组量相等,那么其余两组也相等2、垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧.3、圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于其相对圆心角的一半。
4、确定圆的条件:不在同一直线上的三点确定一个圆。
5、直线与圆位置关系:直线与圆相离 <=> d>r直线与圆相切 <=> d=r直线与圆相交 <=> d<r6、切线的性质:见切点,连半径,得垂直7、切线的判定:先判断直线与圆有无交点有交点,连半径,证垂直无交点,作垂直,证半径8、三角形的外心:三角形外接圆的圆心,它是三角形各边中垂线的交点,它到三角形各顶点的距离相等。
锐角三角形外心在三角形内;直角三角形外心在三角形斜边中点上;钝角三角形外心在三角形外。
9、三角形的内心:三角形内切圆的圆心,它是三角形各内角平分线的交点,它到三角形各边的距离相等;三角形内心均在三角形内。
10、普通三角形内切圆半径:cb a S r ++=2(S 为三角形面积,a 、b 、c 为三角形的边) 直角三角形内切圆半径: 2c b a r -+=(c 为斜边,a 、b 为直角边) 11、正多边形: 内角和180)2(⋅-=n ;外角和=360 每个内角n 1802-n ⋅=)( 每个外角=n360=中心角 正三角形的边长为a ,那么正三角形的中心角是120度,半径是a 33,边心距是a 63; 正四边形的边长为a ,那么正四边形的中心角是90度,半径是a 22,边心距是2a ; 正六边形的边长为a ,那么正六边形的中心角是60度,半径是a ,边心距是a 23。
12、弧长=180n r π 扇形面积lr r n 213602==π (l 为弧长,n 为所对圆心角,r 为半径) 13、圆柱侧面积=rh π2 圆柱表面积=222r rh ππ+(r 为底面半径,h 为侧面的高)14、圆锥侧面积=rl π 圆锥表面积=2r rl ππ+圆锥侧面展开图圆心角计算 1802l n r ππ= (l 为圆锥母线,r 为底面半径,在圆锥的侧面展开图中,母线l 将为成为扇形半径,底面周长成为扇形弧长)。

初中关于圆的知识点一、圆的基本知识1、相关概念:圆、圆心、半径、弦、直径、弧、半圆、等圆、等弧。
2、垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。
平分弦不是直径的直径垂直于弦,并且平分弦所对的两条弧。
还可以表述为:如果一条直线满足:1过圆心;2垂直于弦;3平分弦:;4平分优弧;5平分劣弧中的任意两个,就可推出其它三个。
3、圆心角定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
还可以表述为:在同圆或等圆中,如果两个圆心角,两条弧,两条弦,或两条弦的弦心距中有一组量相等,那么所对应的其余各组量分别相等。
4、在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对圆心角的一半。
5、半圆或直径所对的圆周角是直角,90°的圆周角所对的弦是直径。
6、圆内接四边形的对角互补。
7、点和圆的位置关系:点P在圆外<=>d>r点P在圆上<=>d=r点P在圆内<=>d8、不在同一直线上的三个点确定一个圆。
9、三角形外接圆圆心是三角形的三边垂直平分线的交点,叫做外心。
10、三角形内切圆圆心是三角形的三条角平分线的交点,叫做内心。
11、直线和圆的位置关系:直线l和圆相离<=>d>r直线l和圆相切<=>d=r直线l和圆相交<=>d12、经过半径的外端并且垂直于这条半径的直线是圆的切线。
13、圆的切线垂直于过切点的半径。
14、证明一条直线是圆的切线的方法:1切点确定,证明直线垂直于半径;2切点不确定,证明圆心到直线的距离等于半径。
15、切线长定理:从圆外一点可以引圆的两条切线,他们的切线长相等,这一点和圆心的连线平分两条切线的夹角。
16、圆和圆的位置关系:外离:d>r1+r2外切:d=r1+r2相交:r1-r2< p="">内切:d=r1-r2内含:d17、正多边形与圆:正多边形外接圆或内切圆的圆心叫做正多边形的中心。

圆的基本概念一、圆的概念平面上一动点以一定点为中心,一定长为距离运动一周的轨迹称为圆周,简称圆。
二、点与圆的位置关系:如果⊙O的半径为r,点P到圆心O的距离为d,那么点P在圆内,d﹤r;点P在圆上,d=r;点P在圆外,d﹥r.三、圆中的有关概念弦:连接圆上任意两点的线段叫做弦。
经过圆心的弦叫做直径。
圆弧:圆上任意两点间的部分叫做圆弧,简称弧。
大于半圆的弧称为优弧,小于半圆的弧称为劣弧。
等弧:在同圆或等圆中,能够互相重合的弧,叫等弧。
同心圆:圆心相同,半径不相等的两个圆叫做同心圆等圆:能够重合的两个圆叫做等圆。
同圆或等圆的半径相等圆心角:顶点在圆心的角叫做圆心角二、例题解析:例1、在Rt△ABC中∠C=90O,AC=4,OC=3,E、F分别为AO、AC的中点,以O为圆心、OC为半径作圆,点E在⊙O的圆_____,点F在⊙O的圆_____.练习题:1.一已知点到圆周上的点的最大距离为m ,最小距离为n .则此圆的半径_____.2.有个长、宽分别为4和3的矩形ABCD,现以点A为圆心,若B、C、D至少有一个点在圆内,且至少有一个点在圆外,则⊙A半径r的范围是_________.3.⊙O的半径为15厘米,点O到直线l的距离OH=9厘米,P,Q,R为l上的三个点,PH=9厘米,QH=12厘米,RH=15厘米,则P,Q,R与⊙O的位置关系分别为 .4.若点A(a,-27)在以点B(-35,-27)为圆心,37为半径的圆上,a= .5.在直角坐标系中,⊙O的半径为5厘米,圆心O的坐标为(-1,-4),点P(3,-1)与圆O的位置关系是 .6.如图,⊙O中,AB、AC是弦,O在∠ABC的内部,∠ABO=a,∠ACO=b,则下列关系中正确的是()A、∠BOC=a+bB、∠BOC=2a+2bC、a+b+∠BOC=180°D、a+b+∠BOC=360°7、如图,在Rt△ABC中,∠ACB=90°,AC=6,AB=10,CD是斜边AB上的中线,以AC为直径作⊙O,设线段CD的中点为P,则点P与⊙O的位置关系是()A、点P在⊙O内 B、点P在⊙O上 C、点P在⊙O外 D、无法确定垂径定理垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧。

24.1.1&24.1.2 圆及垂径定理圆的定义(1)动态:如图,在一个平面内,线段OA 绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫做圆,固定的端点O 叫做圆心,线段OA 叫做半径. 以点O 为圆心的圆,记作“⊙O ”,读作“圆O”.(2)静态:圆心为O,半径为r的圆是平面内到定点O的距离等于定长r的点的集合.注意:①圆心确定圆的位置,半径确定圆的大小;确定一个圆应先确定圆心,再确定半径,二者缺一不可;②圆是一条封闭曲线.题型1:圆的概念1.到圆心的距离不大于半径的点的集合是()A.圆的外部B.圆的内部C.圆D.圆的内部和圆【变式11】下列条件中,能确定一个圆的是()A.以点O为圆心B.以10m长为半径C.以点A为圆心,4cm长为半径D.经过已知点M与圆有关的概念1.弦弦:连结圆上任意两点的线段叫做弦.直径:经过圆心的弦叫做直径.弦心距:圆心到弦的距离叫做弦心距.2. 弧弧:圆上任意两点间的部分叫做圆弧,简称弧.以A、B 为端点的弧记作,读作“圆弧AB”或“弧AB”.半圆:圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆;优弧:大于半圆的弧叫做优弧;劣弧:小于半圆的弧叫做劣弧.圆心相同,半径不等的两个圆叫做同心圆.圆心不同,半径相等的两个圆叫做等圆.同圆或等圆的半径相等.在同圆或等圆中,能够完全重合的弧叫做等弧.题型2:与圆有关的概念2.判断题(对的打√,错的打×,并说明理由)①半圆是弧,但弧不一定是半圆;()②弦是直径;()③长度相等的两段弧是等弧;()④直径是圆中最长的弦. ()【变式21】下列说法:(1)长度相等的弧是等弧,(2)相等的圆心角所对的弧相等,(3)劣弧一定比优弧短,(4)直径是圆中最长的弦.其中正确的有()A.1个B.2个C.3个D.4个【变式22】下列说法:①直径是弦;②弦是直径;③半径相等的两个半圆是等弧;④长度相等的两条弧是等弧;⑤半圆是弧,但弧不一定是半圆.正确的说法有()A.1个B.2个C.3个D.4个题型3:确定圆心和圆3.将图中的破轮子复原,已知弧上三点A,B,C.画出该轮的圆心;【变式31】如图所示,BD,CE是△ABC的高,求证:E,B,C,D四点在同一个圆上.圆的性质①旋转不变性:圆是旋转对称图形,绕圆心旋转任一角度都和原来图形重合;圆是中心对称图形,对称中心是圆心;②圆是轴对称图形:任何一条直径所在直线都是它的对称轴.或者说,经过圆心的任何一条直线都是圆的对称轴.题型4:圆的对称性4.已知:如图,两个以O为圆心的同心圆中,大圆的弦AB交小圆于C,D.求证:AC=BD.【变式41】如图,两个圆都以点O为圆心,大圆的弦AB交小圆于C,D两点,求证:AD=BC.【变式42】如图,在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C、D.(1)求证AC=BD;(2)若AC=3,大圆和小圆的半径分别为6和4,则CD的长度是.垂径定理及推论垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.常见辅助线做法:1)过圆心,作垂线,连半径,造,用勾股,求长度;2)有弧中点,连中点和圆心,得垂直平分.题型5:垂径定理与计算5.如图,AB是⊙O的直径,弦CD⊙AB于点E.若AB=10,BE=2,求弦CD的长.【变式51】如图,AB是⊙O的弦,C为AB的中点,OC的延长线与⊙O交于点D,若CD=2,AB=12,求⊙O的半径.【变式52】如图,AB是⊙O的直径,弦CD⊙AB于点E,OC=10cm,CD=16cm,求AE的长.题型6:垂径定理与证明6.如图,AB是⊙O的弦,C、D为直线AB上两点,OC=OD,求证:AC=BD.【变式61】如图,AB和CD分别是⊙O上的两条弦,过点O分别作ON⊥CD于点N,OM⊥AB于点M,若ON=AB,证明:OM=CD.⌢=BD⌢【变式62】如图,AB、CD都是⊙O的弦,且AB⊙CD,求证:AC题型7:垂径定理分类讨论问题7.在圆柱形油槽内装有一些油,截面如图所示,已知截面⊙O半径为5cm,油面宽AB为6cm,如果再注入一些油后,油面宽变为8cm,则油面AB上升了()cmA.1B.3C.3或4D.1或7题型8:垂径定理翻折问题8.如图,⊙O的半径为4,将⊙O的一部分沿着弦AB翻折,劣弧恰好经过圆心O,则折痕AB的长为.【变式81】如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,求折痕AB的长.【变式82】如图, AB是以点O为圆心的圆形纸片的直径,弦CD⊥AB于点E, AB=10,BE= 3.将阴影部分沿着弦AC翻折压平,翻折后,弧AC对应的弧为G,则点O与弧G所在圆的位置关系为.题型9:垂径定理的应用拱桥问题9.如图所示,某地新建一座石拱桥,桥拱是圆弧形,它的跨度(弧所对的弦的长)为40m,拱高(弧的中点到弦的距离)为8m,求桥拱得半径R.【变式91】如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.(1)求圆弧所在的圆的半径r的长;(2)当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?【变式92】如图,有一拱形公路桥,圆弧形桥拱的水面跨度AB=80m,拱高(弧的中点到弦的距离CD)为20m,求桥拱所在圆的半径.题型10:垂径定理的应用油管问题10.储油罐的截面如图所示,内径1000mm装入一些油后,若油面宽AB=600mm,求油的最大深度.【变式101】在半径为17dm的圆柱形油罐内装进一些油后,横截面如图.(1)若油面宽AB=16dm,求油的最大深度.(2)在(1)的条件下,若油面宽变为CD=30dm,求油的最大深度上升了多少dm?【变式102】在直径为1000毫米的圆柱形油罐内装进一些油.其横截面如图.油面宽AB=600毫米.(1)求油的最大深度;(2)如果再注入一些油后,油面宽变为800毫米,此时油面上升了多少毫米?一、单选题1.已知⊙O中,最长的弦长为16cm,则⊙O的半径是()A.4cm B.8cm C.16cm D.32cm2.如图在⊙O中,弦AB=8,OC⊙AB,垂足为C,且OC=3,则⊙O的半径()A.5B.10C.8D.63.如图,已知⊙O的直径CD=8,AB是⊙O的弦,AB⊥CD,垂足为M,OM=2,则AB的长为()A.2B.2√3C.4D.4√34.下列说法正确的是()A.长度相等的两条弧是等弧B.平分弦的直径垂直于弦C.直径是同一个圆中最长的弦D.过三点能确定一个圆5.如图,AB是⊙O的直径,CD是弦,AB⊙CD,垂足为点E,连接OD、CB、AC,⊙DOB=60°,EB=2,那么CD的长为()A.√3B.2 √3C.3 √3D.4 √36.如图,AB是⊙O的直径,弦CD⊙AB,垂足为E,如果AB=20,CD=16,那么线段OE的长为()A.10B.8C.6D.4二、填空题7.在半径为10的圆中有一条长为16的弦,那么这条弦的弦心距等于.8.如图,在半径为6的⊙O中,劣弧AB⌢的度数是120°,则弦AB的长是.9.如图,平面直角坐标系xOy中,M点的坐标为(3,0),⊙M的半径为2,过M点的直线与⊙M的交点分别为A,B,则⊙AOB的面积的最大值为,此时A,B两点所在直线与x轴的夹角等于°.10.已知⊙O的直径CD=10,AB是⊙O的弦,AB⊙CD,垂足为M,且AB=8,则AC的长为.三、计算题11.如图是一名考古学家发现的一块古代车轮碎片.(1)请你帮他找到这个车轮的圆心(保留作图痕迹);(2)若这个圆的半径为10cm,请求出弦心距为5cm的弦长.四、解答题12.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).求证:AC=BD.13.如图为桥洞的形状,其正视图是由CD⌢和矩形ABCD构成.O点为CD⌢所在⊙O的圆心,点O⌢所又恰好在AB为水面处.若桥洞跨度CD为8米,拱高(OE⊙弦CD于点F )EF为2米.求CD在⊙O的半径DO.14.已知:如图,在⊙O中,弦CD垂直于直径AB,垂足为点E,如果⊙BAD=30°,且BE=2,求弦CD的长.五、综合题15.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图所示).(1)求证:AC=BD;(2)若大圆的半径R=10,小圆的半径r=8,且圆心O到直线AB的距离为6,求AC的长16.《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架.《九章算术》中记载:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,间径几何?”(如图①)阅读完这段文字后,小智画出了一个圆柱截面示意图(如图②),其中BO⊙CD于点A,求间径就是要求⊙O的直径.(1)再次阅读后,发现AB=寸,CD=寸(一尺等于十寸),通过运用有关知识即可解决这个问题.请你补全题目条件.(2)帮助小智求出⊙O的直径.。
圆的概念与垂径定理知识点一、圆的定义1、圆的第一定义:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.这个固定的端点O叫做圆心,线段OA叫做半径.以O点为圆心的圆记作:⊙O,读作圆O.2.战国时期的《墨经》中对圆的定义是:圆,一中同长也.3.圆的第二定义:由圆的定义可知:(1)圆上的各点到圆心的距离都等于定长(即半径r);在一个平面内,到圆心的距离等于半径长的点都在圆上.因此,圆是在一个平面内,所有到一个定点的距离等于定长的点组成的图形.(2)要确定一个圆,需要两个基本条件:一个是圆心,另一个是半径,其中,圆心确定圆的位置,半径确定圆的大小.注意:由圆的概念可知:○1“圆”指的是“圆周”,即一条封闭的曲线,而不是圆面。
○2确定一个圆取决于两个因素:圆心和半径。
例题1:下列说法错误的有()○1经过P点的圆有无数个;○2以P为圆心的圆有无数个;○3半径为3cm且经过P点的圆有无数个;○4以p为圆心,以3cm为半径的圆有无数个。
A、1个B、2个C、3个D、4个知识点二、圆的有关概念1.弦:线段弦直径最长的弦2. 弧:圆上任意两点间的部分叫做圆弧,简称弧,以A,C为端点的弧记作AC,读作圆弧AC或弧AC.3.圆的直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.4.在一个圆中大于半圆的弧叫做优弧;(如图所示ABC叫做优弧)小于半圆的弧叫做劣弧.(如图所示)AC或BC叫做劣弧.5.等圆等弧。
如下图,(1)若点O为⊙O的圆心,则线段__________是圆O的半径;线段________是圆O的弦,其中最长的弦是______;______是劣弧;______是半圆.(2)若∠A=40°,则∠ABO=______,∠C=______,∠ABC=______.综合讲练.讲练1:如图,在同心圆中,大圆的弦AB交小圆于C,D两点.(1)求证:∠AOC=∠BOD;(2)试确定AC与BD两线段之间的大小关系,并证明你的结论.讲练2:如图,已知AB是⊙O的直径,CD是⊙O的弦,AB,CD的延长线交于E,若AB=2DE,∠E=18°,求∠C及∠AOC的度数.知识点三、垂直于弦的直径(垂径定理)1.圆是轴对称图形,其对称轴是任意一条过圆心的直线.说明:①圆的对称轴是直径所在的直线,而不是直径本身. ②圆有无数条对称轴.2.垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.用符号语言描述:∵⊙O 中CD 是直径、AB 是弦,且CD ⊥AB 于M ,∴AM =BM ,AC BC =,AD BD =.你能试着证明吗?说明:①垂径定理中的直径可以是过圆心的的直线或线段;②在有关计算直径或半径、弦长以及圆心到弦的距离等问题中,垂径定理常常和勾股定理结合使用,即:(弦的一半)2+(圆心到弦的距离)2=(半径)2.例1 如图,直线与两个同心圆分别交于图示的各点,则正确的是 A .MP 与RN 的大小关系不定 B.MP=RN C.MP <RN D.MP >RNCD OMBA· AB C DOM第2题图例2 如图,AB 是⊙O 的弦,半径OC ⊥AB 于D 点,且AB =6cm ,OD =4cm ,求DC 的长【课堂操练】1.如图,⊙O 的直径CD ⊥AB ,∠AOC =50°,则∠CDB 大小为( )A 、25°B 、30°C 、40°D 、50°2.如图,在直径AB =12的⊙O 中,弦C D ⊥AB 于M ,且M 是半径OB 的中点,求弦C D 的长(结果保留根号).3.如图,⊙O 的直径CD =10cm ,AB 是⊙O 的弦,AB CD ,垂足为M ,OM :OC =3:5,求AB 的长知识点四、垂径定理的推论推论1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.推论2:平分弦所对的一条弧的直径垂直于弦,并且平分弦所对的另一条弧。
教学目的掌握垂径定理、圆周角和圆心角的关系教学重点垂径定理、圆周角教学内容(一)垂径定理1、圆是轴对称图形,任何一条直径所在直线都是它的对称轴.圆有无数条对称轴。
圆是以圆心为对称中心的中心对称图形;圆具有旋转不变性。
2、垂径定理:垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧。
3、推论:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
圆的两条平行弦所夹的弧相等。
①平分弧的直径必平分弧所对的弦。
( )②平分弦的直线必垂直弦。
( )③垂直于弦的直径平分这条弦。
( )④平分弦的直径垂直于这条弦。
( )⑤弦的垂直平分线是圆的直径。
( )⑥平分弦所对的一条弧的直径必垂直这条弦。
( )⑦在圆中,如果一条直线经过圆心且平分弦,必平分此弦所对的弧。
( )例题赏析如图,在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径.小试牛刀1、如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,求证四边形ADOE是正方形.2、我市某居民区一处圆形地下水管道破裂,修理工人准备更换一段新管道,经测量得到如图所示的数据,修理工人应准备内径多大的管道?若此题只知下面弓形的高和AB的长,你仍然会做吗?60cm10cmA BO3、如图,直径是50cm圆柱形油槽装入油后,油深CD为15cm,求油面宽度ABD OBCA(二)弧、弦、圆心角1、圆心角的概念:顶点在圆心的角ABCDO2、弧、弦与圆心角的关系定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等;所对的弦的弦心距相等。
在同圆或等圆中,满足下面四个条件中的任何一个就能推出另外三个:①两个圆心角相等;②两个圆心角所对的弧相等;③两个圆心角或两条弧所对的弦相等;④两条弦的弦心距相等。
1、相等的圆心角所对的弧相等。
( )2、相等的弧所对的弦相等。
( )3、相等的弦所对的弧相等。
圆知识点汇总(一)一、圆、垂径定理1、圆的定义及表示法(1)圆的定义1:在一个平面内,线段绕它固定的一个端点旋转一周,另一个端点A随之旋转所成的图形叫做圆。
固定的端点O叫做圆心。
线段OA叫做半径(如图1-1)。
(2)圆的表示方法:以点O为圆心的圆,记作“⊙O”,读作“圆O”。
(3)圆的定义2:圆心为O,半径为r的圆可以看成是所有到定点O的距离等于定长r的点组成的图形。
(圆是一条闭合曲线,不包含中间的部分)确定一个圆的要素是圆心和半径。
2、与圆有关的概念(1)弦:连接圆上任意两点的线段叫做弦。
(2)直径:经过圆心的弦是直径。
注意:圆中有无数条弦,其中直径是圆中最长的弦。
(3)圆弧:圆上任意两点间的部分叫做圆弧,简称弧。
(4)半圆弧:圆的任意一条直径的两个端点把圆分成两条弧,每一条弧叫做半圆。
(画图判断带弦的不叫弧,叫弓形)(5)优弧:大于半圆的弧叫做优弧。
优弧CAB,记作“⌒CAB”,如图1-2。
(6)劣弧:小于半圆的弧叫做劣弧。
劣弧表示时只需两个字母。
(7)弓形:由弦及其所对的弧组成的图形叫做弓形。
(8)同心圆:圆心相同,半径不相等的两个圆叫做同心圆。
(9)等圆:能够重合的两个圆叫做等圆。
(10)等弧:在同圆或等圆中,能够互相重合的弧叫做等弧。
判断:长度相等的弧叫做等弧。
(×)3、圆的轴对称性圆是轴对称图形,经过圆心的每一条直线都是它的对称轴。
注意:(1)圆的对称轴有无数条。
(2)错误说法:圆的对称轴是直径。
因为直径是弦,弦是线段,所以直径是线段,而对称轴是直线。
应该说“圆的对称轴是直径所在的直线”。
4、垂径定理垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
5、垂径定理的推论(1)平分弦(不是直径)的直径垂直于弦并且平分弦所对的两条弧。
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
(3)平分弦所对的一条弧的直径,平分弦,并且平分弦所对的另一条弧。
(4)在同圆中,圆的两条平行弦所夹的弧相等。
第13讲圆与垂径定理知识点1:圆的有关概念【例1】(1)圆两种定义方式:(a)在一个平面内线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫做圆,固定的端点O叫做.线段OA叫做.(b)圆是所有点到定点O的距离定长r的点的集合.(2)弦:连接圆上任意两点的叫做弦.(弦不一定是直径,直径一定是弦,直径是圆中最长的弦);(3)弧:圆上任意两点间的部分叫(弧的度数等于这条弧所对的圆心角的度数,等于这条弧所对圆周角的两倍)(4)等弧:在同圆与等圆中,能够的弧叫等弧.(5)等圆:能够的两个圆叫等圆,半径的两个圆也叫等圆.【例2】如图所示,AB是圆的直径,则圆中的弦有条,分别是,劣弧有条,分别是.变式1. 下列说法正确的是()填序号.①半径不等的圆叫做同心圆;②优弧一定大于劣弧;③不同的圆中不可能有相等的弦;④直径是同一个圆中最长的弦.变式2. 如图,在⊙O中,半径有,直径有,弦有,劣弧有,优弧有.知识点2:半径组成的等腰三角形【例3】如图,在⊙O中,AB是O的弦,C、D是直线AB上两点,AC=BD.求证:OC=OD.变式3. 如图,两个圆都以点O为圆心,大圆的弦AB交小圆于C、D两点.求证:AC=BD.【例4】如图,⊙O的直径AB与弦CD的延长线交于点E,若DE=OB,∠AOC=74°,则∠E=.变式4. 如图,AB为⊙O直径,点C、D在⊙O上,已知∠AOD=50°,AD∥OC,则∠BOC=度.知识点3:垂径定理【例5】如图,在⊙O中,MN是直径,AB是弦,且MN⊥AB,垂足为C,下列结论:①AC=BC,②=,③=,④OC=CN上述结论中,正确的有(填序号)【例6】如图,⊙O的弦AB=8,M是AB的中点,且OM=3,则⊙O的半径等于.变式5. 如图,在⊙O中,半径OD垂直于弦AB,垂足为C,OD=13cm,AB=24cm,则CD=cm.变式6. 如图,⊙O的半径为6,OA与弦AB的夹角是30°,则弦AB的长度是.知识点4:垂径定理应用【例7】如图,⊙O的直径CD垂直弦AB于点E,且CE=4,DE=16,则AB的长为.变式7. 如图,在⊙O中,直径AB⊥弦CD于E,若EB=1cm,CD=4cm,则弦心距OE的长是cm.【例8】如图,AB为⊙O的弦,P为AB上一点,且PA=8,PB=6,OP=4,则⊙O的半径为.变式8. 如图,AB为半圆直径,O为圆心,C为半圆上一点,E是弧AC的中点,OE交弦AC于点D,若AC=8cm,DE=2cm,求OD的长.【例9】如图,圆内一条弦CD与直径AB相交成30°角,且分直径成1cm和5cm两部分,则这条弦的弦心距是.变式9. 如图,CD为⊙O的直径,弦AB交CD于E,DE=6cm,CE=2cm,(1)若∠AED=45°,求AB的长;(2)若EB=3cm,求AB的长.【例10】如图,已知在⊙O中,AB,CD两弦互相垂直于点E,AB被分成4cm和10cm两段.(1)求圆心O到CD的距离;(2)若⊙O半径为8cm,求CD的长是多少?变式10. 如图,⊙O的两条弦AB、CD互相垂直,垂足为E,且AB=CD,已知CE=2,ED=6,求⊙O的半径长.【课堂训练】1. 如图,△ABC中,∠ACB=90°,∠A=40°,以C为圆心、CB为半径的圆交AB于点D,则∠ACD=度.2. 如图,AB、AC为⊙O的弦,连接CO、BO并延长分别交弦AB、AC于点E、F,∠B=∠C.求证:CE=BF.3. 把球放在长方体纸盒内,球的一部分露出盒外,其截面如图,已知圆心为O,EF=CD=16厘米,则⊙O 的半径为多少厘米?4. 已知:如图,∠PAC=30°,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP 于E、F两点,求圆心O到AP的距离及EF的长.5. ⊙O的直径AB和弦CD相交于点E,已知AE=1,EB=5,∠DEB=60°,求CD的长.6. 已知:如图,AB是⊙O的弦,半径OC、OD分别交AB于点E、F,且OE=OF.求证:AE=BF.7. 如图,四边形ABCD是矩形,以AD为直径的⊙O交BC边于点E、F,AB=4,AD=12.求线段EF的长.8. 如图,在⊙O中,AD是直径,BC是弦,D为的中点,直径AD交BC于点E,AE=5,ED=1,则BC 的长是m.9. 如图,⊙O中弦AB⊥CD于E,AE=2,EB=6,ED=3,则⊙O的半径为.10. 如图,⊙O的半径为5,弦AB的长为8,点M在线段AB(包括端点A,B)上移动,则OM的取值范围是.【课后训练】1.如图,在⊙O中,MN是直径,AB是弦,且MN⊥AB,垂足为C,下列结论:①AC=BC,②=,③=,④OC=CN,上述结论中,正确的有(填序号)2.如图,AB是⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E.若AB=2DE,∠E=18°,则∠C 的度数为.3.如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB,垂足为D,已知CD=4,OD=3,求AB的长是.4.AB、CD是⊙O的两条弦,∠AOB与∠C互补,∠COD与∠A相等,则∠AOB的度数是.5.如图,△ABC中,∠ACB=90°,∠A=40°,以C为圆心、CB为半径的圆交AB于点D,则∠ACD=度.6.如图所示,⊙O内有折线OABC,其中OA=2,AB=4,∠A=∠B=60°,则BC的长为.7.如图,在△ABC中,∠ACB=90°,以点C为圆心,CB为半径的⊙C与边AB交于点D.若点D为AB的中点,AB=6,则⊙C的半径长为.8.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC,若AB=4,CD=1,则EC的长为.9.一条排水管的截面如图所示,已知排水管的半径OA=1m,水面宽AB=1.2m,某天下雨后,水管水面上升了0.2m,则此时排水管水面宽CD等于m.10.已知:如图,在⊙O中,AB为弦,C、D两点在AB上,且AC=BD.求证:△OAC≌△OBD.11.(2015•东西湖区校级模拟)如图,AB和CD分别是⊙O上的两条弦,过点O分别作ON⊥CD于点N,OM⊥AB于点M,若ON=AB,证明:OM=CD.12.(2015秋•嵊州市校级月考)如图,AB是⊙O的直径,E是弧BC的中点,OE交BC于点D,OD=3,DE=2,求BC和AD.。
圆的基本概念、垂径定理复习一、圆的相关概念知识扫描:1、圆的定义:(1 在同一平面内, 线段 OP 绕它固定的一个端点 O , 另一端点 P 所经过的叫做圆,定点 O 叫做 ,线段 OP 叫做圆的 ,以点 O 为圆心的圆记作 ,读作圆O 。
(2动点到定点等于定长的点的轨迹叫做圆。
2、弦和直径:连接圆上任意叫做弦,其中经过圆心的弦叫做 , 是圆中最长的弦。
3、弧:圆上任意叫做圆弧,简称弧。
圆的任意一条直径的两个端点把圆分成的两条弧,每一条弧都叫做。
小于半圆的弧叫做 , 用弧两端的字母上加上“⌒”就可表示出来,大于半圆的弧叫做 ,用弧两端的字母和中间的字母,再加上“⌒”就可表示出来。
4、等圆:半径相等的两个圆叫做等圆;也可以说能够完全重合的两个圆叫做等圆5、过一点可作过两点可作个圆; 过的三点确定一个圆。
对应练习:1、有下列四个命题:①直径是弦;②经过三个点一定可以作圆;③三角形的外心到三角形各顶点的距离都相等;④长度相等的两段弧是等弧。
其中正确的有(A.4个B.3个C.3个D.2个2、已知矩形 ABCD 的边 AB=3cm, AD=4cm, 若以 A 点为圆心作⊙ A , 使 B 、C 、D 三点中至少有一个点在圆内且至少有一个点在圆外, 则⊙ A 的半径 r 的取值范围是3、如图, AB 为⊙ O 的直径, CD 为⊙ O 的弦, AB 、 CD 的延长线交于点 E ,已知 AB=2DE,∠ E=18°,求∠ AOC 的度数4、已知⊙ O 的半径为 1, 点 P 与圆心 O 的距离为 d , 且方程 x 2-2x+d=0有实数根, 则点 P 在⊙ O 的5、若线段 AB=6,则经过 A 、 B 两点的圆的半径 r 的取值范围是6、在 Rt △ ABC 中,∠ C=90°,两直角边 a 、 b 是方程 x 2-7x+12=0的两根,则△ABC 的外接圆面积为127、如图,点 A 、 D 、 G 、 M 在半圆上,四边形 ABOC , DEOF 、 HMNO 均为矩形, 设 BC=a, EF=b, NH=c,则 a , b , c 的大小关系是二、垂径定理知识扫描:1、轴对称图形:如果一个图形沿着某一条直线直线 , 直线两旁的部分能够 ,那么这个图形就叫做轴对称图形,这条直线就是对称轴。
AODBCAO(一) 圆的相关概念及垂径定理一、知识梳理(一)圆的有关概念1.圆的基本概念:在一个平面内,线段OA 绕它固定的一个端点O 旋转一周,另一个端点A 所形成的图形叫做圆。
固定点O 叫做圆心;线段OA 叫做半径;圆上各点到定点(圆心O )的距离都等于定长(半径r);反之,到定点的距离等于定长的点都在同一个圆上(另一定义); 以O 为圆心的圆,记作“⊙O ”,读作“圆O ”2.圆的对称性及特性:(1)圆是轴对称图形,圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴; (2)圆也是中心对称图形,它的对称中心就是圆心.(3)一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合.这是圆特有的一个性质:圆的旋转不变性 3.弦:连接圆上任意两点的线段叫做弦。
4.弦心距:圆心到弦的距离叫做弦心距. 5.直径:经过圆心的弦叫直径。
注:圆中有无数条直径6.圆弧:(1)圆上任意两点间的部分,也可简称为“弧”以A,B 两点为端点的弧.记作AB ⋂,读作“弧AB”. (2)圆的任意一条直径的两个端点把圆分成两条弧,其中每一条弧都叫半圆。
如弧AD. (3)小于半圆的弧叫做劣弧,如记作AB ⋂(用两个字母). 7.圆心角:顶点在圆心,两边和圆相交的角叫做圆心角。
说明:(1)直径是弦,但弦不一定是直径,直径是圆中最长的弦。
(2)半圆是弧,但弧不一定是半圆。
(3)等弧只能是同圆或等圆中的弧,离开“同圆或等圆”这一条件不存在等弧。
(4)等弧的长度必定相等,但长度相等的弧未必是等弧。
(二)弦、弧、弦心距、圆心角的关系定理:在同圆或等圆中,弦、弧、弦心距、圆心角四组量中只要有一组量相等,则其余三组量也相等。
(三)和圆有关的角:1、圆周角:顶点在圆上,它的两边和圆还有另一个交点的角叫做圆周角。
2、圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半。
推论1:在同圆或等圆中,同弧或等弧所对的圆周角相等。
推论2:圆的两条平行弦所夹的弧相等。
推论3:半圆或直径所对的圆周角是直角。
90°的圆周角所对的弦是直径。
3、弧的度数:一段弧的度数等于它所对的圆心角的度数。
4、圆外角的度数等于它所夹的两段弧的度数的差的一半。
5、圆内角的度数等于它所对的两段弧的度数的和的一半。
(四)垂径定理及推论:如果一条直线具有(1)过圆心,(2)垂直于弦,(3)平分弦,(4)平分弦所对的劣弧,(5)平分弦所对的优弧,这五个性质的任何两个性质,那么这条直线就具有其余三个性质;但“平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧”其中的弦必须是非直径的弦,假若弦是直径,那么这两条直径不一定互相垂直。
(五) 圆的有关性质:1.圆的确定:(1)圆心确定圆的位置半径确定圆的大小。
(2)不在同一直线上的三个点确定一个圆。
(3)三角形的三个顶点确定一个圆,这个圆叫做三角形的外接圆,外接圆的圆心是三角形三边垂直平分线的交点,叫做三角形的外心。
(4)锐角三角形的外心在三角形的内部,钝角三角形的外心在三角形的外部,直角三角形的外心在斜边中点。
2.圆的对称性: (1).圆是轴对称图形,任何一条经过圆心的直线都是它的对称轴。
(2) 圆是中心对称图形,圆心是它的对称中心。
说明:一个圆的对称轴有无数条,对称中心只有一个,一个圆绕圆心旋转任意角度,都能够和原图形重合,即圆还具有旋转不变性。
(六)在解决圆的有关问题时,有以下几种常引用的辅助线:(1)连弦的端点与圆心的半径; (2)作弦心距; (3)作半圆上的圆周角。
(3)连圆心和弦的中点(遇弦的中点时); (4)连圆心和弧的中点(遇弧的中点时);二、典型例题:例1.如图,已知在⊙O 中,直径AB 为10cm ,弦AC 为6cm ,∠ACB 的平分线交⊙O 于D,求BC ,AD 和BD 的长.点评:利用“直径所对的圆周角是直角”构造直角三角形解题。
例2. 如图,AD 是∆ABC 的高,AE 是∆ABC 的外接圆的直径.试说明AB ·AC=AE ·AD .例3. 如图,AB 是⊙O 的直径,C 是⊙O 上一点,连结AC ,过点C 作直线CD ⊥AB ,垂足为点D(AD<DB),点E 是DB 上任意一点(点D 、B 除外),直线CE 交⊙O 于点F ,连结AF ,与直线CD 交于点G .(1)试说明AC 2=AG ·AF ;(2)若点E 是AD(点A 、D 除外)上任意一点,上述结论是否仍然成立?若成立.请画出图形,并给予证明;若不成立,请说明理由.例4.(易错题)在直径为50cm 的圆中,弦AB 为40cm ,弦CD 为48cm ,且AB ∥CD ,求AB•与CD 之间距离.解:如图所示,过O 作OM ⊥AB , ∵AB ∥CD ,∴ON ⊥CD . 在Rt △BMO 中,BO=25cm .由垂径定理得BM=12AB=12×40=20cm , ∴OM=22222520OB BM -=-=15cm . 同理可求ON=22222524OC CN -=-=7cm ,所以MN=OM-ON=15-7=8cm .以上解答有无漏解,漏了什么解,请补上.三、中考链接与创新探究(名校、名书、名题、中考、培优、竞赛)1.(2014温州改编)如图,已知是⊙O 的圆周角,,则圆心角是( )A .B .C .D .2.(2014重庆改编)如图,AB 是⊙O 的直径,点C 在⊙O 上,∠AB C =30°,则∠B AC 的度数为( )A .30°B .45°C .60°D .90°3.(2014台州)下列命题中,正确的是( )①顶点在圆周上的角是圆周角;②圆周角的度数等于圆心角度数的一半;③的圆周角所对的弦是直径;④不在同一条直线上的三个点确定一个圆;⑤同弧所对的圆周角相等 A .①②③B .③④⑤C .①②⑤D .②④⑤4.(2014昆明)AB 是⊙O 的弦,OC 是⊙O 的半径,OC ⊥AB 于点D ,AB =16cm ,OD=6cm ,那么⊙O 的半径是__________cm .5.(2014枣庄)如图,AB 是⊙O 的直径,BC 是弦,OD ⊥BC 于E ,交于D .(1)请写出五个不同类型的正确结论; (2)若BC =8,ED =2,求⊙O 的半径.四、实战演练:1.(2014宜宾)已知:如图,四边形ABCD 是⊙O 的内接正方形,点P 是劣弧⌒CD上不同于点C 的任意一点,则∠BPC 的度数是( )A .45°B .60°C .75°D .90°2.(2014上海)小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是( )A .第①块B .第②块C .第③块D .第④块3.(2014黄石)如图,为⊙O 的直径,点在⊙O 上,,则.4.(2014重庆)已知,如图:AB 为⊙O 的直径,AB =AC ,BC 交⊙O 于点D ,AC 交⊙O 于点E ,∠BAC=450。
给出以下五个结论:①∠EBC =22.50,;②BD =DC ;③AE =2EC ;④劣弧是劣弧的2倍;⑤AE =BC 。
其中正确结论的序号是 .5.(2014湘潭),已知⊙O 半径为5,弦长为8,点为弦上一动点,连结,则线段的最小长度是 . 6.(2014枣庄)如图,△ABC 内接于⊙O ,∠BAC =120°,AB =AC ,BD 为 ⊙O 的直径,AD =6,则BC = 。
7.(2014呼和浩特)已知:如图等边内接于⊙O ,点是劣弧上的一点(端点除外),延长至,使,连结.(1)若过圆心,如图①,请你判断是什么三角形?并说明理由.(2)若不过圆心,如图②,又是什么三角形?为什么?8.(2014沈阳)如图,已知A、B、C、D是⊙O上的四个点,AB=BC,BD交AC于点E,连接CD、AD.(1)求证:DB平分∠ADC;(2)若BE=3,ED=6,求AB的长.五、应用探究:1.(2014烟台)如图,已知AB是半圆O的直径,弦AD、BC相交于点P,若∠DPB=α,那么等于()A.sinαB.COSαC.tanαD.2.(2014兰州)如图,已知是⊙O的直径,把为的直角三角板的一条直角边放在直线上,斜边与⊙O交于点,点与点重合.将三角板沿方向平移,使得点与点重合为止.设,则的取值范围是()A.B. C. D.5.(2014新疆)如图,圆内接四边形ABCD是由四个全等的等腰梯形组成,AD是⊙O的直径,则∠BEC的度数为()A.15°B.30°C.45°D.60°6.6.(2014白银)高速公路的隧道和桥梁最多.图7是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面=10米,净高=7米,则此圆的半径=()A.5B.7C.D.7.(2014贵阳)如图,某机械传动装置在静止状态时,连杆与点运动所形成的⊙O交于点,现测得,.⊙O的半径,此时点到圆心的距离是 cm.8.(2014南通)已知:如图,M是的中点,过点M的弦MN交AB于点C,设⊙O的半径为4cm,MN=4cm.(1)求圆心O到弦MN的距离;(2)求∠ACM的度数.家庭作业第一部分:1.(2014连云港)如图,将半径为的圆形纸片折叠后,圆弧恰好经过圆心,则折痕的长为()A.B.C.D.2.(2014天津)已知,如图与的度数之差为20°,弦AB与CD交于点E,∠CEB=60°,则∠CAB等于()A. 50°B. 45°C. 40°D. 35°第二部分:3.(2010牡丹江)在半径为5cm的圆中,两条平行弦的长度分别为6cm和8cm,则这两条弦之间的距离为。
4.(200龙岩)如图,量角器外沿上有A、B两点,它们的读数分别是70°、40°,则∠1的度数为.第三部分:5.(2014镇江)推理运算:如图,为⊙O直径,为弦,且,垂足为.(1)的平分线交⊙O于,连结.求证:为的中点;(2)如果⊙O的半径为,,①求到弦的距离;②填空:此时圆周上存在个点到直线的距离为.。