C圆的基本知识和垂径定理

圆部分知识点总结垂径定理及其推论垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的弧。

推论1：（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧。

（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧。

（3）平分弦所对的一条弧的直径垂直平分弦，并且平分弦所对的另一条弧。

推论2：圆的两条平行弦所夹的弧相等。

垂径定理及其推论可概括为：过圆心垂直于弦直径平分弦知二推三平分弦所对的优弧平分弦所对的劣弧弧、弦、弦心距、圆心角之间的关系定理1：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦的弦心距相等。

2：在同圆或等圆中，如果两个圆的圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等，那么它们所对应的其余各组量都分别相等。

圆周角定理：一条弧所对的圆周角等于它所对的圆心角的一半。

推论1：同弧或等弧所对的圆周角相等；同圆或等圆中，相等的圆周角所对的弧也相等。

推论2：半圆（或直径）所对的圆周角是直角；90°的圆周角所对的弦是直径。

推论3：如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形。

点和圆的位置关系设⊙O的半径是r，点P到圆心O的距离为d，则有：d<r⇔点P在⊙O内；d=r⇔点P在⊙O上；d>r⇔点P在⊙O外。

过三点的圆1、不在同一直线上的三个点确定一个圆。

2、经过三角形的三个顶点的圆叫做三角形的外接圆。

3、三角形的外接圆的圆心是三角形三条边的垂直平分线的交点，它叫做这个三角形的外心。

直线与圆的位置关系直线和圆有三种位置关系，具体如下：（1）相交：直线和圆有两个公共点时，叫做直线和圆相交，这时直线叫做圆的割线，公共点叫做交点；（2）相切：直线和圆有唯一公共点时，叫做直线和圆相切，这时直线叫做圆的切线， （3）相离：直线和圆没有公共点时，叫做直线和圆相离。

如果⊙O 的半径为r ，圆心O 到直线L 的距离为d,那么：直线L 与⊙O 相交⇔d<r ；直线L 与⊙O 相切⇔d=r ； 直线L 与⊙O 相离⇔d>r ；圆的内接四边形定理：圆的内接四边形的对角互补，外角等于它的内对角。

《圆的基本性质:圆、图形旋转、垂径定理》知识点总结1.圆的定义;在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A随之旋转所形成的封闭曲线叫做圆。

固定的端点O叫做圆心，线段OA叫做半径，以点O为圆心的圆，记作☉O，读作“圆O”2、与圆有关的概念（1）弦和直径（连结圆上任意两点的线段BC叫做弦，经过圆心的弦AB叫做直径）（2）弧和半圆（圆上任意两点间的部分叫做弧，圆的任意一条直径的两个端点分圆成两条弧，每一条弧都叫做半圆），大于半圆的弧叫优弧（优弧用⌒和三个字母表示）、小于半圆的弧叫劣弧（用⌒和两个字母表示）。

（3）等弧：能够互相重合的两段弧（4）等圆（半径相等的两个圆叫做等圆）（5）点和圆的位置关系：如果P是圆所在平面内的一点，d 表示P到圆心的距离，r表示圆的半径，则：（1）d<r → 圆内（2）d=r → 圆上（3）d>r → 圆外（6）不在同一条直线上的三个点确定一个圆。

过不在同一条直线上的三点做圆，能找出圆的圆心（7）三角形的外接圆经过三角形的三个顶点的圆叫做三角形的外接圆，外接圆的圆心叫做三角形的外心，三角形叫做圆的内接三角形。

三角形的外心到各顶点距离相等。

一个三角形有且仅有一个外接圆，但一个圆有无数内接三角形。

3、图形的旋转：原图形上的所有点都绕着一个固定的点，按同一个方向，转动同一个角度，这样的图形运动叫做图形的旋转，这个固定的点叫做旋转中心。

图形经过旋转所得到的图形和原图形全等。

对应点到旋转中心的距离相等，任何一对对应点与旋转中心连线所成的角度等于旋转的角度。

旋转作图基本步骤：1、明确旋转三要素（旋转中心、旋转方向、旋转角度）；2、找出关键点；3、找出关键点的对应点；4、作出新图形；5、写出结论。

4、垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧。

推论：（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；（2）平分弧的直径，垂直平分弧所对的弦。

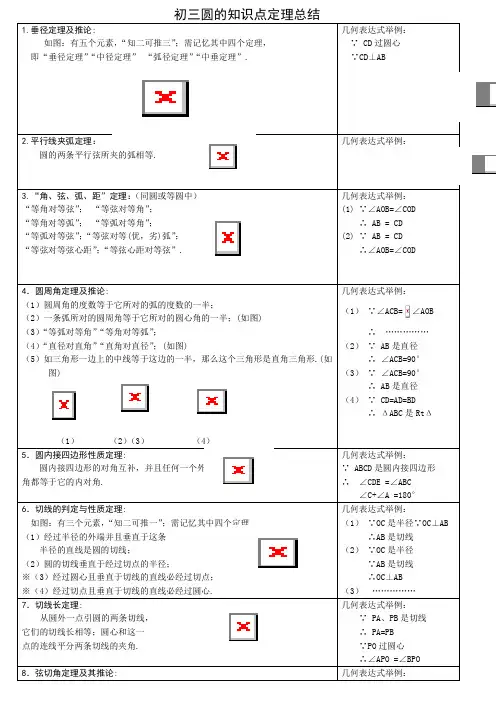
1.垂径定理及推论:如图：有五个元素，“知二可推三”；需记忆其中四个定理，即“垂径定理”“中径定理”“弧径定理”“中垂定理”.几何表达式举例：∵ CD过圆心∵CD⊥AB2.平行线夹弧定理：圆的两条平行弦所夹的弧相等.几何表达式举例：3.“角、弦、弧、距”定理：（同圆或等圆中）“等角对等弦”；“等弦对等角”；“等角对等弧”；“等弧对等角”；“等弧对等弦”；“等弦对等(优，劣)弧”；“等弦对等弦心距”；“等弦心距对等弦”.几何表达式举例：(1) ∵∠AOB=∠COD∴ AB = CD(2) ∵ AB = CD∴∠AOB=∠COD4．圆周角定理及推论:（1）圆周角的度数等于它所对的弧的度数的一半；（2）一条弧所对的圆周角等于它所对的圆心角的一半；(如图)（3）“等弧对等角”“等角对等弧”；（4）“直径对直角”“直角对直径”；(如图)（5）如三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形.(如图)（1）（2）（3）（4）几何表达式举例：（1）∵∠ACB=∠AOB∴……………（2）∵ AB是直径∴∠ACB=90°（3）∵∠ACB=90°∴ AB是直径（4）∵ CD=AD=BD∴ΔABC是RtΔ5．圆内接四边形性质定理:圆内接四边形的对角互补，并且任何一个外角都等于它的内对角.几何表达式举例：∵ ABCD是圆内接四边形∴∠CDE =∠ABC∠C+∠A =180°6．切线的判定与性质定理:如图：有三个元素，“知二可推一”；需记忆其中四个定理.（1）经过半径的外端并且垂直于这条半径的直线是圆的切线；（2）圆的切线垂直于经过切点的半径；※（3）经过圆心且垂直于切线的直线必经过切点；※（4）经过切点且垂直于切线的直线必经过圆心.几何表达式举例：（1）∵OC是半径∵OC⊥AB∴AB是切线（2）∵OC是半径∵AB是切线∴OC⊥AB（3）……………7．切线长定理:从圆外一点引圆的两条切线，它们的切线长相等；圆心和这一点的连线平分两条切线的夹角.几何表达式举例：∵ PA、PB是切线∴ PA=PB∵PO过圆心∴∠APO =∠BPO8．弦切角定理及其推论: 几何表达式举例：（1）弦切角等于它所夹的弧对的圆周角；（2）如果两个弦切角所夹的弧相等，那么这两个弦切角也相等；（3）弦切角的度数等于它所夹的弧的度数的一半.（如图）（1）∵BD是切线，BC是弦∴∠CBD =∠CAB（2）∵ ED，BC是切线∴∠CBA =∠DEF9．相交弦定理及其推论:（1）圆内的两条相交弦，被交点分成的两条线段长的乘积相等；（2）如果弦与直径垂直相交，那么弦的一半是它分直径所成的两条线段长的比例中项. 几何表达式举例：（1）∵PA·PB=PC·PD∴………（2）∵AB是直径∵PC⊥AB∴PC2=PA·PB10．切割线定理及其推论:（1）从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项；（2）从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等.几何表达式举例：（1）∵PC是切线，PB是割线∴PC2=PA·PB （2）∵PB、PD是割线∴PA·PB=PC·PD11．关于两圆的性质定理:（1）相交两圆的连心线垂直平分两圆的公共弦；（2）如果两圆相切，那么切点一定在连心线上.（1）（2）几何表达式举例：（1）∵O1，O2是圆心∴O1O2垂直平分AB （2）∵⊙1 、⊙2相切∴O1 、A、O2三点一线12．正多边形的有关计算:（1）中心角αn ，半径R N ，边心距r n ，边长a n ，内角βn ，边数n；（2）有关计算在RtΔAOC中进行. 公式举例：(1) αn =；(2)几何B级概念：（要求理解、会讲、会用，主要用于填空和选择题）一基本概念：圆的几何定义和集合定义、弦、弦心距、弧、等弧、弓形、弓形高三角形的外接圆、三角形的外心、三角形的内切圆、三角形的内心、圆心角、圆周角、弦切角、圆的切线、圆的割线、两圆的内公切线、两圆的外公切线、两圆的内（外）公切线长、正多边形、正多边形的中心、正多边形的半径、正多边形的边心距、正多边形的中心角.二定理：1．不在一直线上的三个点确定一个圆.2．任何正多边形都有一个外接圆和一个内切圆，这两个圆是同心圆.3．正n边形的半径和边心距把正n边形分为2n个全等的直角三角形.三公式：1.有关的计算：（1）圆的周长C=2πR；（2）弧长L=；（3）圆的面积S=πR2.（4）扇形面积S扇形=；（5）弓形面积S弓形=扇形面积S AOB±ΔAOB的面积.（如图）2.圆柱与圆锥的侧面展开图：（1）圆柱的侧面积：S圆柱侧 =2πrh； (r:底面半径；h:圆柱高)（2）圆锥的侧面积：S圆锥侧 =. （L=2πr，R是圆锥母线长；r是底面半径）四常识：1．圆是轴对称和中心对称图形.2．圆心角的度数等于它所对弧的度数.3．三角形的外心⇔两边中垂线的交点⇔三角形的外接圆的圆心；三角形的内心⇔两内角平分线的交点⇔三角形的内切圆的圆心.4．直线与圆的位置关系：（其中d表示圆心到直线的距离；其中r表示圆的半径）直线与圆相交⇔ d＜r ；直线与圆相切⇔ d=r ；直线与圆相离⇔ d＞r.5．圆与圆的位置关系：（其中d表示圆心到圆心的距离，其中R、r表示两个圆的半径且R≥r）两圆外离⇔ d＞R+r；两圆外切⇔ d=R+r；两圆相交⇔ R-r＜d＜R+r；两圆内切⇔ d=R-r；两圆内含⇔ d＜R-r.6．证直线与圆相切，常利用：“已知交点连半径证垂直”和“不知交点作垂直证半径”的方法加辅助线.7．关于圆的常见辅助线：已知弦构造弦心距.已知弦构造RtΔ. 已知直径构造直角.已知切线连半径，出垂直.圆外角转化为圆周角. 圆内角转化为圆周角. 构造垂径定理. 构造相似形.两圆内切，构造外公切线与垂直.两圆内切，构造外公切线与平行.两圆外切，构造内公切线与垂直.两圆外切，构造内公切线与平行.两圆同心，作弦心距，可证得AC=DB.两圆相交构造公共弦，连结圆心构造中垂线. PA、PB是切线，构造双垂图形和全等.相交弦出相似.一切一割出相似, 并且构造弦切角.两割出相似,并且构造圆周角.双垂出相似,并且构造直角.规则图形折叠出一对全等，一对相似.圆的外切四边形对边和相等. 若AD ∥BC都是切线，连结OA、OB可证∠AOB=180°，即A、O、B三点一线.等腰三角形底边上的的高必过内切圆的圆心和切点,并构造相似形.RtΔABC的内切圆半径：r=.补全半圆.AB=. AB=.PC过圆心，PA是切线，构造双垂、RtΔ.O是圆心，等弧出平行和相似. 作AN⊥BC，可证出:.。

圆的公式1.圆的周长C=2πr=πd2.圆的面积S=πr²3.扇形弧长l=nπr/1804.扇形面积S=nπr²/360=rl/25.圆锥侧面积S=πrl〖圆的定义〗几何说：平面上到定点的距离等于定长的所有点组成的图形叫做圆。

定点称为圆心，定长称为半径。

轨迹说：平面上一动点以一定点为中心，一定长为距离运动一周的轨迹称为圆周，简称圆。

集合说：到定点的距离等于定长的点的集合叫做圆。

〖圆的相关量〗圆周率：圆周长度与圆的直径长度的比叫做圆周率，值是3.14159265358979323846264338327950288419716939937510582097494459230781640628620 89986280348253421170679...，通常用π表示，计算中常取3.14为它的近似值(但奥数常取3或3.1416)。

圆弧和弦：圆上任意两点间的部分叫做圆弧，简称弧。

大于半圆的弧称为优弧，小于半圆的弧称为劣弧。

连接圆上任意两点的线段叫做弦。

经过圆心的弦叫做直径。

圆心角和圆周角：顶点在圆心上的角叫做圆心角。

顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角。

内心和外心：过三角形的三个顶点的圆叫做三角形的外接圆，其圆心叫做三角形的外心。

和三角形三边都相切的圆叫做这个三角形的内切圆，其圆心称为内心。

扇形：在圆上，由两条半径和一段弧围成的图形叫做扇形。

圆锥侧面展开图是一个扇形。

这个扇形的半径成为圆锥的母线。

〖圆和圆的相关量字母表示方法〗圆—⊙半径—r 弧—⌒直径—d 扇形弧长／圆锥母线—l 周长—C 面积—S〖圆和其他图形的位置关系〗圆和点的位置关系：以点P与圆O的为例（设P是一点，则PO是点到圆心的距离），P在⊙O外，PO＞r；P在⊙O上，PO＝r；P在⊙O内，PO＜r。

直线与圆有3种位置关系：无公共点为相离；有两个公共点为相交；圆与直线有唯一公共点为相切，这条直线叫做圆的切线，这个唯一的公共点叫做切点。

圆的垂径定理定理是经过受逻辑限制的证明为真的陈述。

一般来说，在数学中，只有重要或有趣的陈述才叫定理。

证明定理是数学的中心活动。

圆作为数学中常用的图像，有十八个基本定理。

圆的十八个定理1、圆心角定理：在同圆或等圆中，成正比的圆心角所对弧成正比，面元的弦成正比，面元的弦的弦心距成正比。

推论：在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两弦的弦心距中存有一组量成正比那么它们所对应的其余各组量都成正比2、圆周角定理：一条弧所对的圆周角等于它所对的圆心角的一半。

推断1：同弧或等弧所对的圆周角成正比;同圆或等圆中，成正比的圆周角面元的弧也成正比推论2：半圆(或直径)所对的圆周角是直角;90°的圆周角所推断3：如果三角形一边上的中线等同于这边的一半，那么这个三角形就是直角三角形3、垂径定理：垂直弦的直径平分该弦，并且平分这条弦所对的两条弧。

推断1：①平分弦(不是直径)的直径旋转轴弦，并且平分弦所对的两条弧②弦的垂直平分线经过圆心，并且平分弦所对的两条弧推断2 ：圆的两条平行弦所缠的弧成正比4、切线之判定定理：经过半径的外端并且垂直于该半径的直线是圆的切线。

5、切线短定理：从铅直一点引圆的两条切线，他们的切线短成正比，这一点与圆心的连线平分这两条切线的夹角。

6、公切线长定理：如果两圆有两条外公切线或两条内公切线，那么这两条外公切线长相等，两条内公切线长也相等。

如果他们相交，那么交点一定在两圆的连心线上。

7、平行弦定理：圆内两条弦平行，被交点分为的两条线段长的乘积成正比。

8、切割线定理：从圆外一点向圆引一条切线和一条割线，则切线长是这点到割线与圆的两个交点的两条线段长的比例中项。

9、割线短定理：从铅直一点向圆引两条割线，这一点至每条割线与圆的交点的两条线段长的积成正比。

10、切线的性质定理：圆的切线垂直于经过切点的半径推断1 ：经过圆心且旋转轴切线的直线必经过切点推论2：经过切点且垂直于切线的直线必经过圆心11、弦切角定理：弦切角等同于它所缠的弧对的圆周角推论：如果两个弦切角所夹的弧相等，那么这两个弦切角也相等12、定理：平行两圆的连心线垂直平分两圆的公共弦13、定理：把圆分成n(n≥3):⑴依次联结各分点税金的多边形就是这个圆的内arccosn边形⑵经过各分点作圆的切线，以相邻切线的交点为顶点的多边形是这个圆的外切正n边形14、定理：任何正多边形都存有一个外接圆和一个内切圆，这两个圆就是同心圆15、定理：任何正多边形都有一个外接圆和一个内切圆，这两个圆是同心圆16、定理：正n边形的半径和边心距把也已n边形分为2n个全等的直角三角形17、定理：圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角。

垂径定理 相切 1、垂径定理及其推论：定理：垂直于弦的直径，平分弦并且平分弦所对的两条弧.推论：平分弦（不是直径）的直径，垂直于弦并且平分弦所对的两条弧. 2、 基本图形探究：设圆的半径为r ，弦长（AB ）为a ，弦心距（OE ）为d ，弓形的高（CE ）为h .、它们四者满足关系式：①r h d =+；②2222⎪⎭⎫⎝⎛+=a d r .3、定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等.在同圆或等圆中，两个圆心角、两条弧、两条弦、中有一组量相等，那么它们所对应的其余各组量也相等. 4、在同圆或等圆中，同弧或等弧所对的圆周角相等， 5.同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半； 6.半圆（或直径）所对的圆周角是直角； 7.90°的圆周角所对的弦是直径；8如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形. 9、圆内接四边形的性质：圆内接四边形的对角互补；外角等于内对角.基础检测本题型有四类：（1）点在圆内或圆外；（2）点在优弧或劣弧上；（3）圆心在两弦之间或两弦同侧；（4）圆心在三角形内或三角形外．♀例一♀．已知O 的半径为5，弦AB ＝8，P 为直线AB 上一点，PA ＝2，求OP 的长．♂巩固练习♂1．若点P 到O 上的点的最小距离为4，最大距离为8，则该圆的直径是 ．♀例二♀．如图，O 的半径是2，AB 是O 的弦，点P 是弦AB 上的动点，且1≤OP ≤2，则弦AB 所对的圆周角的度数为 ．♂巩固练习♂ 1．已知O 的半径为2，弦BC ＝22，点P 为O 上异于B 、C 的一动点，则∠BPC ＝ ．2．△ABC 内接于O ，OD ⊥AC 于点D ，如果∠COD ＝32°，那么∠B 的度数为 ．♀例三♀．在半径为1的O 中，弦AB 、AC 的长分别为3和2，则∠BAC 的度数为 ．♂巩固练习♂1．在半径为5 cm的圆内有两条互相平行的弦，一条弦长为8 cm，另一条弦长为6 cm，则这两条弦之间的距离为．♀例四♀．已知△ABC内接于O，AB＝AC，O的半径为5，BC＝8，求△ABC的腰长和面积．♂巩固练习♂．已知△ABC内接于O，AB＝AC，O的半径为4，BC＝8，求△ABC的腰长和面积．1．如图，A、B、C在⊙O上，∠OAB＝22.5°，则∠ACB的度数为（）A．115.5°B．112.5°C．122.5°D．135°2一点到圆周上点的最大距离为9，最短距离为1，则这个圆的半径是 .3.过⊙O内一点M的最长的弦长为10㎝，最短弦长为8㎝，则OM的长为 .4．如图，⊙O的半径为3，点P是弦AB延长线上一点，连OP，若OP＝4，∠P＝30°，则弦AB＝_________5．如图，在圆柱形油槽内装有一些油，油槽直径MN为10分米，截面如图，油面宽AB为6分米．如果再注入一些油后，当油面宽变为8分米，则油面AB上升__________分米6．如图，⊙O的半径为5，弦AB＝8，则圆上到弦AB所在的直线距离为2的点有（）个A．1 B．2 C．3 D．07．已知△ABC内接于⊙O，且⊙O的半径为5，若AB＝AC，BC＝8，则△ABC的面积为（）A．8 B．32 C．8或32 D．无法确定4,BC=8，求它的外接圆半径；8..等腰ABC中，AB=AC=59．如图，在⊙O中，弦AB＝1.8 cm，C为⊙O上一点，且∠ACB＝30°，则⊙O的直径为______cm10．如图，△ABC 是⊙O 的内接三角形，AB ＝34，∠C ＝120°，则⊙O 的半径为（ ） A ．32B ．4C ．22D ．3411．如图，在平面直角坐标系中，⊙A 与y 轴相切于原点O ，平行于x 轴的直线⊙A 于M 、N 两点．若点M 的坐标是(－4，－2)，则弦MN 的长为_________12．要测量一个钢板上的小孔的直径，通常采用间接的测量方法．如果用一个直径为10mm 的标准钢珠放在小孔上，测的钢珠顶端与小孔平面的距离h ＝8mm （如图），求此小孔的直径d13．如图，在⊙O 中，AB 是⊙O 的直径，AB ＝8 cm ，弧AC ＝CD ＝BD ，M 是AB 上一动点，CM ＋DM 的最小值为__________圆中的辅助线模型1 连半径构造等腰三角形O A B EC DB1图图2已知AB 是⊙O 的一条弦， 连接OA 、OB ，则∠A=∠B 。

高中圆知识点总结
一、圆的基本概念
定义：圆是平面上到一个定点距离等于定长的所有点的集合。

这个定点叫做圆心，定长叫做半径。

圆心：圆所在平面内到圆内任意点的距离都相等的点。

半径：圆心到圆上任意一点的距离。

直径：通过圆心且两端都在圆上的线段。

二、圆的基本性质
圆的对称性：圆是中心对称图形，也是轴对称图形，其对称轴是任意一条经过圆心的直线。

垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧。

圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半。

三、圆与直线的位置关系
相离：直线与圆没有公共点。

相切：直线与圆有且只有一个公共点，叫做切点。

相交：直线与圆有两个公共点，叫做交点。

四、圆的方程
标准方程：(x - a)^2 + (y - b)^2 = r^2，其中(a, b)为圆心坐标，r为半径。

一般方程：x^2 + y^2 + Dx + Ey + F = 0，其中D^2 + E^2 - 4F > 0。

五、与圆有关的计算
圆的周长：C = 2πr，其中r为圆的半径。

圆的面积：S =
πr^2，其中r为圆的半径。

六、与圆相关的定理和推论
切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角。

割线长定理：从圆外一点引圆的两条割线，它们的割线长满足一定的比例关系。

以上是高中圆的主要知识点总结。

在学习圆的过程中，应注重理解概念、掌握性质、熟悉定理，并结合具体的题目进行练习，以加深对知识点的理解和应用。

初中关于圆的知识点一、圆的基本知识1、相关概念：圆、圆心、半径、弦、直径、弧、半圆、等圆、等弧。

2、垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧。

平分弦不是直径的直径垂直于弦，并且平分弦所对的两条弧。

还可以表述为：如果一条直线满足：1过圆心;2垂直于弦;3平分弦：;4平分优弧;5平分劣弧中的任意两个，就可推出其它三个。

3、圆心角定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等。

还可以表述为：在同圆或等圆中，如果两个圆心角，两条弧，两条弦，或两条弦的弦心距中有一组量相等，那么所对应的其余各组量分别相等。

4、在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对圆心角的一半。

5、半圆或直径所对的圆周角是直角，90°的圆周角所对的弦是直径。

6、圆内接四边形的对角互补。

7、点和圆的位置关系：点P在圆外<=>d>r点P在圆上<=>d=r点P在圆内<=>d8、不在同一直线上的三个点确定一个圆。

9、三角形外接圆圆心是三角形的三边垂直平分线的交点，叫做外心。

10、三角形内切圆圆心是三角形的三条角平分线的交点，叫做内心。

11、直线和圆的位置关系：直线l和圆相离<=>d>r直线l和圆相切<=>d=r直线l和圆相交<=>d12、经过半径的外端并且垂直于这条半径的直线是圆的切线。

13、圆的切线垂直于过切点的半径。

14、证明一条直线是圆的切线的方法：1切点确定，证明直线垂直于半径;2切点不确定，证明圆心到直线的距离等于半径。

15、切线长定理：从圆外一点可以引圆的两条切线，他们的切线长相等，这一点和圆心的连线平分两条切线的夹角。

16、圆和圆的位置关系：外离：d>r1+r2外切：d=r1+r2相交：r1-r2< p="">内切：d=r1-r2内含：d17、正多边形与圆：正多边形外接圆或内切圆的圆心叫做正多边形的中心。