苏州新区二中数学三角形解答题单元综合测试(Word版 含答案)

一、初一数学代数式解答题压轴题精选（难）1．用1块A型钢板可制成2块C型钢板和1块D型钢板；用1块B型钢板可制成1块C 型钢板和3块D型钢板.现购买A、B型钢板共100块，并全部加工成C、D型钢板.设购买A型钢板x块（x为整数）（1）可制成C型钢板块（用含x的代数式表示）；可制成D型钢板块[用含x的代数式表示）.（2）出售C型钢板每块利润为100元，D型钢板每块利润为120元.若将C、D型钢板全部出售，通过计算说明此时获得的总利润.（3）在（2）的条件下，若20≤x≤25，请你设计购买方案使此时获得的总利润最大，并求出最大的总利润.【答案】（1）解：设购买A型钢板x块（x为整数），则购买B型钢板（100﹣x）块，根据题意得：可制成C型钢板2x+（100﹣x）＝（x+100）块，可制成D型钢板x+3（100﹣x）＝（﹣2x+300）块.故答案为：x+100；﹣2x+300（2）解：设获得的总利润为w元，根据题意得：w＝100（x+100）+120（﹣2x+300）＝﹣140x+46000（3）解：∵k＝﹣140＜0，∴w值随x值的增大而减小，又∵20≤x≤25，∴当x＝20时，w取最大值，最大值为43200，∴购买A型钢板20块、B型钢板80块时，可获得的总利润最大，最大的总利润为43200元.【解析】【分析】（1）设购买A型钢板x块（x为整数），则购买B型钢板（100﹣x）块，根据“ 用1块A型钢板可制成2块C型钢板和1块D型钢板；用1块B型钢板可制成1块C型钢板和3块D型钢板”从而用含x的代数式表示出可制成C型钢板及D型钢板的数量.（2）设获得的总利润为w元，根据总利润=100×制成C型钢板的数量+120×制成D型钢板的数量，从而得出结论.（3）利用一次函数的性质求出最大利润及购买方案即可.2．如图，老王开车从A到D，全程共72千米．其中AB段为平地，车速是30千米/小时，BC段为上山路，车速是22.5千米/小时，CD段为下山路，车速是36千米/小时，已知下山路是上山路的2倍．（1）若AB=6千米，老王开车从A到D共需多少时间？（2）当BC的长度在一定范围内变化时，老王开车从A到D所需时间是否会改变？为什么？（给出计算过程）【答案】（1）解：若AB=6千米，则BC=22千米，CD=44千米，从A到D所需时间为：=2.4（小时）（2）解：从A到D所需时间不变，（答案正确不回答不扣分）设BC=d千米，则CD=2d千米，AB=（72﹣3d）千米，t===2.4（小时）【解析】【分析】（1）根据题意可以求出AB,BC,CD的长，然后根据路程除以速度等于时间，即可分别算出老王开车行三段的时间，再求出其和即可；（2）从A到D所需时间不变，设BC=d千米，则CD=2d千米，AB=（72﹣3d）千米，,然后根据路程除以速度等于时间，即可分别表示出老王开车行三段的时间，再根据异分母分式加法法则求出其和，再整体代入即可得出结论；3．如图，阶梯图的每个台阶上都标着一个数，从下到上的第1个至第4个台阶上依次标着-5，-2，1，9，且任意相邻四个台阶上数的和都相等.（1）求前4个台阶上数的和是多少？（2）求第5个台阶上的数是多少？（3）应用求从下到上前31个台阶上数的和．发现试用含k（k为正整数）的式子表示出数“1”所在的台阶数．【答案】（1）解：由题意得前4个台阶上数的和是-5-2+1+9=3（2）解：由题意得-2+1+9+x=3，解得：x=-5，则第5个台阶上的数x是-5（3）解：应用：由题意知台阶上的数字是每4个一循环，∵31÷4=7…3，∴7×3+1-2-5=15，即从下到上前31个台阶上数的和为15；发现：数“1”所在的台阶数为4k-1【解析】【分析】（1）由台阶上的数求出台阶上数的和即可；（2）根据题意和（1）的值，求出第5个台阶上的数x的值；（3）根据题意知台阶上的数字是每4个一循环，得到从下到上前31个台阶上数的和，得到数“1”所在的台阶数为4k-1.4．已知x1， x2， x3，…x2016都是不等于0的有理数，若y1= ，求y1的值．当x1＞0时，y1= = =1；当x1＜0时，y1= = =﹣1，所以y1=±1（1）若y2= + ，求y2的值（2）若y3= + + ，则y3的值为________；（3）由以上探究猜想，y2016= + + +…+ 共有________个不同的值，在y2016这些不同的值中，最大的值和最小的值的差等于________．【答案】（1）解：∵ =±1， =±1，∴y2= + =±2或0（2）±1或±3（3）2017；4032【解析】【解答】解：（2）∵ =±1， =±1， =±1，∴y3= + + =±1或±3．故答案为±1或±3，（ 3 ）由（1）（2）可知，y1有两个值，y2有三个值，y3有四个值，…，由此规律可知，y2016有2017个值，最大值为2016，最小值为﹣2016，最大值与最小值的差为4032．故答案分别为2017，4032．【分析】（1）根据题意先求出=±1，=±1，就可求出y2的3个值。

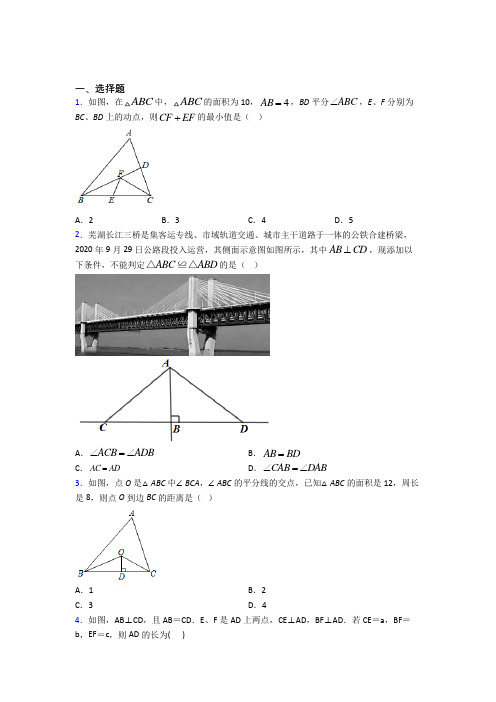
一、选择题1．如图，在ABC 中，ABC 的面积为10，4AB =，BD 平分ABC ∠，E 、F 分别为BC 、BD 上的动点，则CF EF +的最小值是（ ）A ．2B ．3C ．4D ．52．芜湖长江三桥是集客运专线、市域轨道交通、城市主干道路于一体的公铁合建桥梁，2020年9月29日公路段投入运营，其侧面示意图如图所示，其中AB CD ⊥，现添加以下条件，不能判定ABC ABD △≌△的是（ ）A ．ACB ADB ∠=∠B ．AB BD =C ．AC AD =D ．CAB DAB ∠=∠ 3．如图，点O 是△ABC 中∠BCA ，∠ABC 的平分线的交点，已知△ABC 的面积是12，周长是8，则点O 到边BC 的距离是（ ）A ．1B ．2C ．3D ．4 4．如图，AB ⊥CD ，且AB ＝CD ．E 、F 是AD 上两点，CE ⊥AD ，BF ⊥AD ．若CE ＝a ，BF ＝b ，EF ＝c ，则AD 的长为( )A ．a ＋cB ．b ＋cC ．a ＋b －cD ．a －b ＋c5．如图，123,,l l l 是三条两两相交的公路，现需建一个仓库，要求仓库到三条公路距离相等，则仓库的可能地址有（ ）处．A ．1B ．2C ．3D ．46．下列命题中，真命题是（ ）A ．有两边和一角对应相等的两个三角形全等B ．有两边和第三边上的高对应相等的两个三角形全等C ．有两边和其中一边上的高对应相等的两个三角形全等D ．有两边和第三边上的中线对应相等的两个三角形全等7．如图，AB 与CD 相交于点E ，AD=CB ，要使△ADE ≌△CBE ，需添加一个条件，则添加的条件以及相应的判定定理正确的是（ ）A ．AE=CE ；SASB ．DE=BE ；SASC ．∠D=∠B ；AASD ．∠A=∠C ；ASA 8．到ABC 的三条边距离相等的点是ABC 的( )A ．三条中线的交点B ．三条边的垂直平分线的交点C ．三条高的交点D ．三条角平分线的交点 9．对于ABC 与DEF ，已知∠A=∠D ，∠B=∠E ，则下列条件：①AB=DE ；②AC=DF ；③BC=DF ；④AB=EF 中，能判定它们全等的有（ ）A ．①②B ．①③C ．②③D ．③④ 10．如图，在ABC 和△FED 中，AD FC =，AB FE =，下列条件中不能证明F ABC ED ≌△△的是（ ）A ．BC ED =B ．A F ∠=∠C ．B E ∠=∠D ．//AB EF 11．如图，AD 是△ABC 中∠BAC 的角平分线，DE ⊥AB 于点E ，S △ABC =7，DE =2，AB =4，则AC 长是（ ）A ．2.5B ．3C ．3.5D ．412．如图，点C ，D 在线段AB 上，AC DB =，AE //BF ，添加以下哪一个条件仍不能判定△AED ≌△BFC （ ）A ．ED CF =B ．AE BF =C ．E F ∠=∠D ．ED //CF二、填空题13．如图，△ABC 中，∠ACB =90°，点D 在边AC 上，DE ⊥AB 于点E ，DC =DE ，∠A =32°，则∠BDC 的度数为________．14．如图，四边形ABCD 中，AC BC =，90ACB ADC ∠=∠=︒，10CD =，则BCD ∆的面积为______．15．如图，在Rt ABC △中，90C ∠=︒，AD 平分BAC ∠交BC 于点D ．若3BC =，且:5:4BD DC =，5AB =，则ABD △的面积是______．16．如图，D ，E 分别是AB ，AC 上的点，AD=AE ，请添加一个条件，使得ABE ≌ACD ．这个条件可以为_____（只填一个条件即可）．17．如图，ABC ADE ≅，延长BC ，分别交AD ，ED 于点F ，G ，若120EAB ∠=︒，30B ∠=︒，10CAD ∠=︒，则CFD ∠=________︒．18．在Rt △ABC 中，∠C ＝90°，AC ＝15cm ，BC ＝8cm ，AX ⊥AC 于A ，P 、Q 两点分别在边AC 和射线AX 上移动．当PQ ＝AB ，AP ＝_____时，△ABC 和△APQ 全等．19．在ABC 中，48ABC ︒∠=，点D 在BC 边上，且满足18,BAD DC AB ︒∠==，则CAD ∠=________度．20．如图，在Rt ABC 中，90C ∠=︒，AD AC =，DE AB ⊥，交BC 于点E ．若26B ∠=︒，则AEC ∠=______︒．三、解答题21．如图，在△ABC 中，AC ＝BC ，∠ACB ＝90°，点D 在边BC 上（不与点B ，C 重合），过点C 作CE ⊥AD ，垂足为点E ，交AB 于点F ，连接DF ．（1）请直接写出∠CAD 与∠BCF 的数量关系；（2）若点D 是BC 中点，在图2中画出图形，猜想线段AD ，CF ，FD 之间的数量关系，并证明你的猜想．22．作图题：已知∠α，线段m 、n ，请按下列步骤完成作图（不需要写作法，保留作图痕迹）（1）作∠MON ＝∠α（2）在边OM 上截取OA ＝m ，在边ON 上截取OB ＝n ．（3）作直线AB ．23．如图，在ABC 中，按以下步骤作图：①以点B 为圆心，任意长为半径作弧，分别交BA ，BC 于点M ，N ；再以点N 为圆心，MN 长为半径作弧交前面的弧于点F ，作射线BF 交AC 的延长线于点E ．②以点B 为圆心，BA 长为半径作弧交BE 于点D ，连接CD ．请你观察图形，解答下列问题．（1）由尺规作图可证得BMN BFN ≌△△，依据是____________；（2）求证：ABC DBC △≌△；（3）若100BAC ∠=︒，50E ∠=︒，求∠ACB 的度数．24．求证：全等三角形对应边上的中线相等．（根据图形写出已知，求证并完成证明）25．如图，在△ABD 中，∠ABD ＝90°，AB=BD ，点E 在线段BD 上，延长AB 使BC=BE ，连接AE 、CE 、CD ，点M 在线段AE 上，点N 在线段CD 上，BM ⊥BN ，易证△ABE ≌△DBC ；仔细观察，请逐一找出图中其他的全等三角形，并说明理由．26．已知：如图，AC ＝BD ，BD ⊥AD 于点D ，AC ⊥BC 于点C ．求证：∠ABC ＝∠BAD ．【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【分析】过点C 作CM AB ⊥于点M ，交BD 于点'F ，过点'F 作''F E BC ⊥于'E ，则CM 即为CF EF +的最小值，再根据三角形的面积公式求出CM 的长，即为CF EF +的最小值．【详解】解：过点C 作CM AB ⊥于点M ，交BD 于点'F ，过点'F 作''F E BC ⊥于'E ，BD 平分ABC ∠，'MF AB ⊥于点M ，''F E BC ⊥于'E ，'''MF F E ∴=，'''''CM CF MF CF E F ∴=+=+的最小值．三角形ABC 的面积为10，4AB =， ∴14102CM ⨯⋅=，21054CM ⨯∴==． 即CF EF +的最小值为5，故选：D ．【点睛】本题考查的是轴对称-最短路线问题，根据题意作出辅助线是解题的关键．2．B解析：B【分析】根据已知条件可得∠ABC=∠ABD=90°，AB=AB ，结合全等三角形的判定定理依次对各个选项判断．【详解】解：∵AB CD ⊥，∴∠ABC=∠ABD=90°，∵AB=AB ，∴若添加ACB ADB ∠=∠，可借助AAS 证明ABC ABD △≌△，A 选项不符合题意； 若添加AB BD =，无法证明ABC ABD △≌△，B 选项符合题意；若添加AC AD =，可借助HL 证明ABC ABD △≌△，C 选项不符合题意；若添加CAB DAB ∠=∠，可借助ASA 证明ABC ABD △≌△，D 选项不符合题意； 故选：B ．【点睛】本题考查全等三角形的判定．熟练掌握全等三角形的判定定理，并能结合题上已知条件选取合适的定理是解题关键．3．C解析：C【分析】过点O 作OE ⊥AB 于E ，OF ⊥AC 于F ，连接OA ，根据角平分线的性质得：OE ＝OF ＝OD 然后根据△ABC 的面积是12，周长是8，即可得出点O 到边BC 的距离．【详解】如图，过点O 作OE ⊥AB 于E ，OF ⊥AC 于F ，连接OA .∵点O 是∠ABC ，∠ACB 平分线的交点，∴OE ＝OD ，OF ＝OD ，即OE ＝OF ＝OD∴S △ABC ＝S △ABO ＋S △BCO ＋S △ACO ＝12AB ·OE ＋12BC ·OD ＋12AC ·OF ＝12×OD×(AB ＋BC ＋AC )＝12×OD×8＝12 OD=3故选：C【点睛】此题主要考查了角平分线的性质以及三角形面积求法，角的平分线上的点到角的两边的距离相等，正确表示出三角形面积是解题关键．4．C解析：C【分析】由“AAS”可证△ABF≌△CDE，根据全等三角形的性质可得AF＝CE＝a，BF＝DE＝b，则可推出AD＝AF＋DF＝a＋（b−c）＝a＋b−c．【详解】解：∵AB⊥CD，CE⊥AD，BF⊥AD，∴∠AFB＝∠CED＝90°，∠A＋∠D＝90°，∠C＋∠D＝90°，∴∠A＝∠C，∵AB＝CD，∴△ABF≌△CDE（AAS），∴AF＝CE＝a，BF＝DE＝b，∵EF＝c，∴AD＝AF＋DF＝a＋（b−c）＝a＋b−c．故选：C．【点睛】本题考查了全等三角形的判定和性质，解题的关键是掌握全等三角形的判定方法并准确寻找全等三角形解决问题．5．D解析：D【分析】到三条相互交叉的公路距离相等的地点应是三条角平分线的交点，把三条公路的中心部位看作三角形，那么这个三角形两个内角平分线的交点以及三个外角两两平分线的交点都满足要求．【详解】（1）三角形两个内角平分线的交点，共一处（2）三个外角两两平分线的交点，共三处，共四处，故选：D．．【点睛】此题考查角平分线的性质：角平分线上的点到角两边的距离相等，熟记性质是正确解题的关键．6．D解析：D【分析】根据三角形全等的判定方法对A、D进行判断；利用三角形高的位置不同可对B、C进行判断．【详解】A、有两边和它们的夹角对应相等的两个三角形全等，所以A选项错误；B、有两边和第三边上的高对应相等的两个锐角三角形全等，所以B选项错误；C、有两边和其中一边上的高对应相等的两个锐角三角形全等，所以C选错误；D、有两边和第三边上的中线对应相等的两个三角形全等，所以D选项正确；故选：D．【点睛】本题考査了判断命题真假，以及全等三角形的判定，熟练掌握全等三角形的判定，仔细分类讨论是解题关键．7．C解析：C【分析】根据三角形全等的判定方法结合全等的判定方法逐一进行来判断．【详解】解：A.添加AE=CE后，根据已知两边和其中一边的对角对应相等，两个三角形不一定全等；故不符合题意；B.添加DE=BE后，根据已知两边和其中一边的对角对应相等，两个三角形不一定全等；故不符合题意；C.添加∠D=∠B，根据AAS可证明△ADE≌△CBE，故此选项符合题意；D.添加∠A=∠C，根据AAS可证明△ADE≌△CBE，故此选项不符合题意；故选：C【点睛】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、AAS、ASA．关键在于应根据所给的条件判断应证明哪两个三角形全等．8．D解析：D【分析】由于角平分线上的点到角的两边的距离相等，而已知一点到ABC的三条边距离相等，那么这样的点在这个三角形的三条角平分线上，由此即可作出选择.【详解】解:∵到ABC的三条边距离相等，角平分线上的点到角的两边的距离相等，∴这点在这个三角形三条角平分线上，即这点是三条角平分线的交点，故选：D.【点睛】此题主要考查了三角形的角平分线的性质：三条角平分线交于一点，并且这一点到三边的距离相等.9．A解析：A【分析】根据已知条件，已知两角对应相等，所以要证两三角形全等，可以根据角边角、角角边、边角边判定定理添加条件，再根据选项选取答案即可；【详解】题意已知：∠A=∠D ，∠B=∠E ，∴①根据“ASA”可添加AB=DE ，故①正确；②根据“AAS” 可添加AC=DF ，故②正确；③根据“AAS” 可添加BC=EF ，故③错误；④根据“ASA”可添加AB=DE ，故④错误；所以补充①②可判定两三角形全等；故选：A ．【点睛】本题主要考查了三角形全等的判定，根据不同的判定方法可选择不同的条件，所以对三角形全等的判定定理要熟练掌握并归纳总结；10．C解析：C【分析】由AD FC =推出AC=FD ，根据已知AB FE =添加夹角相等或第三边相等即可判定．【详解】∵AD FC =，∴AC=FD ，∵AB FE =，∴当A F ∠=∠（//AB EF 也可得到）或BC ED =时，即可判定F ABC ED ≌△△， 故B E ∠=∠不能判定F ABC ED ≌△△，故选：C ．【点睛】此题考查添加一个条件证明两个三角形全等，熟记全等三角形的判定定理并熟练应用是解题的关键．11．B解析：B【分析】作DH ⊥AC 于H ，如图，利用角平分线的性质得DH=DE=2，根据三角形的面积公式得1 2×2×AC+12×2×4=7，于是可求出AC的值．【详解】解：作DH⊥AC于H，如图，∵AD是△ABC中∠BAC的角平分线，DE⊥AB，DH⊥AC，∴DH=DE=2，∵S△ABC=S△ADC+S△ABD，∴12×2×AC+12×2×4=7，∴AC=3．故选：B．【点睛】本题考查了角平分线的性质：角的平分线上的点到角的两边的距离相等．这里的距离是指点到角的两边垂线段的长．12．A解析：A【分析】欲使△AED≌△BFC，已知AC=DB，AE∥BF，可证明全等三角形判定定理AAS、SAS、ASA添加条件，逐一证明即可；【详解】∵ AC=BD，∴ AD=CE，∵ AE∥BF，∴∠A=∠E，A、如添加ED=CF，不能证明△AED≌△BFC，故该选项符合题意；B、如添加AE=BF，根据SAS，能证明△AED≌△BFC，故该选项不符合题意；C、如添加∠E=∠F，利用AAS即可证明△AED≌△BFC，故该选项不符合题意；D、如添加ED∥CF，得出∠EDC=∠FCE，利用ASA即可证明△AED≌△BFC，故该选项不符合题意；故选：A．【点睛】本题考查了全等三角形的判定定理的理解和掌握，此类添加条件题，要求学生应熟练掌握全等三角形的判定定理；二、填空题13．61°【分析】首先利用直角三角形的性质求得∠ABC的度数然后利用角平分线的判定方法得到BD为∠ABC的平分线再求出∠ABD的度数根据三角形外角的性质进而求得结论【详解】解：∵∠A=32°∠ACB=9解析：61°【分析】首先利用直角三角形的性质求得∠ABC的度数，然后利用角平分线的判定方法得到BD为∠ABC的平分线，再求出∠ABD的度数，根据三角形外角的性质进而求得结论．【详解】解：∵∠A=32°，∠ACB=90°，∴∠CBA=58°，∵DE⊥AB，DC⊥BC，DC=DE，∴BD为∠ABC的平分线，∴∠CBD=∠EBD，∴∠CBD=12∠CBA=12×58°=29°,∴∠BDC=∠A+∠ABD=32°+29°=61°．故答案为：61°．【点睛】本题考查了角平分线的判定与性质，解题的关键是根据已知条件得到BD为∠ABC的平分线，难度不大．14．50【分析】过点B作BE⊥DC交DC的延长线于点E先证明∠CBE=∠ACD从而证明∆ACD≅∆CBE进而即可求解【详解】过点B作BE⊥DC交DC的延长线于点E∵BE⊥CE∴∠BEC=∠CDA=90°解析：50【分析】过点B作BE⊥DC交DC的延长线于点E，先证明∠CBE=∠ACD，从而证明∆ ACD≅∆ CBE，进而即可求解．【详解】过点B作BE⊥DC交DC的延长线于点E，∵BE ⊥CE ，∴∠BEC=∠CDA=90°，∴∠CBE+∠BCE=90°，又∵∠ACB=90°，∴∠BCE+∠ACD=90°，∴∠CBE=∠ACD ，在∆ ACD 与∆ CBE 中，∵CBE ACD CEB ADC BC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴∆ ACD ≅∆ CBE （AAS ），∴BE=CD=10，∴BCD ∆的面积=12CD∙BE=12×10×10=50， 故答案是50．【点睛】本题主要考查全等三角形的判定和性质，等腰直角三角形的性质，添加辅助线，构造“一线三垂直”模型，是解题的关键． 15．【分析】过点D 作DE ⊥AB 利用角平分线的性质可得CD ＝DE 再利用线段的比求得线段DC 的长度进而即可求解【详解】过点D 作DE ⊥AB ∵AD 平分∠BACDE ⊥ABDC ⊥AC ∴CD ＝DE 又∵且BD ：DC ＝5 解析：103【分析】过点D 作DE ⊥AB ，利用角平分线的性质可得CD ＝DE ，再利用线段的比求得线段DC 的长度，进而即可求解．【详解】过点D 作DE ⊥AB ，∵AD 平分∠BAC ，DE ⊥AB ，DC ⊥AC∴CD ＝DE又∵3BC =，且BD ：DC ＝5：4，∴DE ＝DC ＝3÷（5＋4）×4＝43． ∵5AB =，∴ABD △的面积=43×5÷2=103 故答案是：103【点睛】本题考查了角平分线的性质，添加辅助线，是解题的关键． 16．∠B=∠C （或∠ADC=∠AEB 或AB=AC ）【分析】根据已知条件知两个三角形已经具有∠A=∠AAD=AE 两个条件对应相等故再添加一组对应角相等或是AB=AC 即可得到ABE ≌ACD 【详解】∵∠A=∠解析：∠B=∠C （或∠ADC=∠AEB 或AB=AC ）【分析】根据已知条件知两个三角形已经具有∠A=∠A ，AD=AE 两个条件对应相等，故再添加一组对应角相等或是AB=AC 即可得到ABE ≌ACD ． 【详解】∵∠A=∠A ，AD=AE ，∴当∠B=∠C 时，可利用AAS 证明ABE ≌ACD ； 当∠ADC=∠AEB 时，可利用ASA 证明ABE ≌ACD ； 当AB=AC 时，可利用SAS 证明ABE ≌ACD ； 故答案为：∠B=∠C （或∠ADC=∠AEB 或AB=AC ）． 【点睛】此题考查添加一个条件证明三角形全等，熟记三角形全等的判定定理是解题的关键． 17．95【分析】根据全等三角形的性质得∠BAC=∠DAE 结合三角形外角的性质和三角形内角和定理即可求解【详解】解：∵∴∴∴∴故答案为：【点睛】本题主要考查全等三角形的性质三角形外角的性质和三角形内角和定解析：95【分析】根据全等三角形的性质，得∠BAC=∠DAE ，结合三角形外角的性质和三角形内角和定理，即可求解．【详解】解：∵ABC ADE≅，∴()12010255BAC DAE∠=∠=-÷=，∴85ACF BAC B∠=∠+∠=，∴18085CFA ACF CAD∠=-∠-∠=，∴1808595CFD∠=-=．故答案为：95．【点睛】本题主要考查全等三角形的性质，三角形外角的性质和三角形内角和定理，熟练掌握上述定理和性质，是解题的关键．18．8cm或15cm【分析】分情况讨论：①AP＝BC＝8cm时Rt△ABC≌Rt△QPA （HL）；②当P运动到与C点重合时Rt△ABC≌Rt△PQA（HL）此时AP＝AC＝15cm【详解】解：①当P运动解析：8cm或15cm【分析】分情况讨论：①AP＝BC＝8cm时，Rt△ABC≌Rt△QPA（HL）；②当P运动到与C点重合时，Rt△ABC≌Rt△PQA（HL），此时AP＝AC＝15cm．【详解】解：①当P运动到AP＝BC时，如图1所示：在Rt△ABC和Rt△QPA中，AB QP BC PA=⎧⎨=⎩，∴Rt△ABC≌Rt△QPA（HL），即AP＝B＝8cm；②当P运动到与C点重合时，如图2所示：在Rt △ABC 和Rt △PQA 中，AB PQ AC PA =⎧⎨=⎩， ∴Rt △ABC ≌Rt △PQA （HL ），即AP ＝AC ＝15cm ．综上所述，AP 的长度是8cm 或15cm ．故答案为：8cm 或15cm ．【点睛】本题考查了三角形全等的判定与性质，熟练掌握全等三角形的判定与性质是解题的关键，注意分类讨论，以免漏解．19．66【分析】在线段CD 上取点E 使CE=BD 再证明△ADB ≅△AEC 即可求出【详解】在线段DC 取点ECE=BD 连接AE ∵CE=BD ∴BE=CD ∵AB=CD ∴AB=BE ∠BAE=∠BEA=（180°-4解析：66【分析】在线段CD 上取点E 使CE =BD ，再证明△ADB ≅△AEC 即可求出． 【详解】在线段DC 取点E ，CE =BD ，连接AE ，∵CE =BD ，∴BE =CD ，∵AB =CD ，∴AB =BE ，∠BAE =∠BEA =（180°-48°）÷2=66°，∴∠DAE =48° ，∠AED =66°，∴△ADB ≅△AEC ，∴∠BAD =∠CAE =18°，∴∠CAD=∠DAE+∠CAE=66°．故答案为：66．【点睛】本题考察了全等三角形的证明和三角形内角和定理，解题的关键是做出辅助线找到全等三角形．20．58【分析】根据∠C=90°AD=AC证明Rt△CAE≌Rt△DAE∠CAE=∠DAE=∠CAB再由∠C=90°∠B=26°求出∠CAB的度数然后即可求出∠AEC的度数【详解】解：∵在△ABC中∠C解析：58【分析】根据∠C=90°，AD=AC证明Rt△CAE≌Rt△DAE，∠CAE=∠DAE=12∠CAB，再由∠C=90°，∠B=26°，求出∠CAB的度数，然后即可求出∠AEC的度数．【详解】解：∵在△ABC中，∠C=90°，DE⊥AB交BC于点E，∴∠ADE=∠C=90°，在Rt△ACE和Rt△ADE中，∵AC AD AE AE⎧⎨⎩＝＝，∴Rt△CAE≌Rt△DAE，∴∠CAE=∠DAE=12∠CAB，∵∠B+∠CAB=90°，∠B=26°，∴∠CAB=90°-26°=64°，∵∠AEC=90°-12∠CAB=90°-32°=58°．故答案为：58．【点睛】此题主要考查学生对直角三角形全等的判定和三角形内角和定理的理解和掌握，解答此题的关键是求证Rt△CAE≌Rt△DAE．三、解答题21．（1）∠BCF＝∠CAD；（2）AD＝CF+DF，证明见解析【分析】（1）由余角的性质可求解；（2）过点B作BG∥AC交CF的延长线于G，由“ASA”可证△ACD≌△CBG，可得CD＝BG，AD＝CG，由“SAS”可证△BDF≌△BGF，可得DF＝GF，可得结论．【详解】解：（1）∠BCF＝∠CAD，理由如下：∵CE ⊥AD ，∴∠CED ＝∠ACD ＝90°，∴∠CAD +∠ADC ＝90°＝∠ADC +∠BCF ，∴∠CAD ＝∠BCF ；（2）如图所示：猜想：AD ＝CF +DF ，理由如下：过点B 作BG ∥AC 交CF 的延长线于G ，则∠ACB +∠CBG ＝180°，∴∠CBG ＝∠ACD ＝90°，在△ACD 和△CBG 中，∵CAD BCF AC BC ACD CBG ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△ACD ≌△CBG （ASA ），∴CD ＝BG ，AD ＝CG ，∵D 是BC 的中点，∴CD ＝BG ＝BD ，∵AC ＝BC ，∠ACB ＝90°，∴∠CBA ＝∠CAB ，∴∠CBA ＝45°，∴∠FBG ＝∠CBG ﹣∠CBA ＝90°﹣45°＝45°，∴∠FBG ＝∠FBD ，在△BDF 和△BGF 中，BF BF FBD FBG BD BG =⎧⎪∠=∠⎨⎪=⎩∴△BDF ≌△BGF （SAS ），∴DF ＝GF ，∵AD ＝CG ＝CF +FG ，∴AD ＝CF +DF ．【点睛】本题主要考查余角的性质，全等三角形的判定和性质，添加合适的辅助线，构造全等三角形，是解题的关键．22．（1）见解析；（2）见解析；（3）见解析【分析】（1）先画一条射线ON，以∠α的顶点为圆心，任意长度为半径画弧，交∠α的两个边于两个点，这两个点的距离记为a，接着以点O为圆心，同样的长度为半径画弧，交ON于一个点，以这个点为圆心，a为半径画弧，与刚刚画的弧有一个交点，连接这个点和点O，得到射线OM，即可得到∠MON＝∠α；（2）以点O为圆心，m为半径画弧，交OM于点A，以点O为圆心，n为半径画弧，交ON于点B；（3）连接AB，线段AB所在的直线即直线AB．【详解】解：（1）如图所示，（2）如图所示，（3）如图所示，【点睛】本题考查尺规作图，解题的关键是掌握作已知角度的方法，截取线段和画直线的方法．23．（1）SSS ；（2）见解析；（3）65°.【分析】(1)根据同圆的半径相等，BM=BN=BF ，MN=FN ，符合了SSS ；(2)根据(1)知，∠ABC=∠DBC ，BC 是公共边，BA=BD ，符合SAS 原理；(3)△ABE 中，求出∠ABD=30°，从而求得∠ABC=15°，利用三角形外角和定理即可得到答案.【详解】（1）根据基本作图，得BM=BF ，BN=BN ，MN=NF ，符合SSS 原理，故应该填SSS ；（2）由（1）得ABC DBC ∠=∠．∵AB ＝DB ，BC ＝BC ，∴△ABC ≌△DBC （SAS ）；（3）∵∠BAC ＝100°，∠E ＝50°，∴∠ABE ＝30°，∵△MBN ≌△FBN ，∴∠ABC=∠DBC ， ∴1152DBC ABE ∠=∠=︒， ∴∠ACB ＝∠DBC ＋∠E ＝15°＋50°＝65°．【点睛】本题主要考查了基本作图，解答时，清楚同圆半径相等，熟记三角形全等判定的基本原理是解题的关键.24．见解析【分析】利用SAS 证明ABD ≌A B D '''△，即可证得结论．【详解】 解：已知：如图，ABC ≌A B C '''，AD 和A D ''分别是BC 和B C ''上的中线，求证：AD ＝A D ''．证明：∵ABC ≌A B C '''， ∴AB ＝A B ''，∠B ＝∠B '，BC ＝B C ''，∵AD 、A D ''是 BC 和B C ''上的中线，∴BD ＝12BC ，12B D B C ''''=，∴BD ＝B D ''，∴在ABD 与A B D '''△中AB A B B B BD B D =⎧⎪∠=∠⎨⎪=''''⎩' ∴ABD ≌A B D '''△（SAS ），∴AD ＝A D ''．【点睛】本题考查了全等三角形的判定与性质，证明线段相等的问题，基本的思路是转化成三角形全等．25．△ABM ≌△DBN ，△BME ≌△BNC ，理由见解析．【分析】观察图形，可找出△ABM ≌△DBN ，△BME ≌△BNC ．①由△ABE ≌△DBC 可得到∠BAE=∠BDC ，根据BM ⊥BN 可得到∠AMB+∠MBE =∠DBN+∠MBE ，继而得到∠AMB=∠DBN ，AB=BD ，可得△ABM ≌△DBN ；②由△ABM ≌△DBN 可得BM=BN ，根据∠NBE+∠MBE =∠NBE+∠NBC ，可得∠MBE =∠NBC ，继而可证得△BME ≌△BNC ．【详解】解：全等三角形：△ABM ≌△DBN ，△BME ≌△BNC ，理由如下：由题意知△ABE ≌△DBC ，∴∠BAE=∠BDC ，∵BM ⊥BN ，∴∠MNB=90︒，∴∠ABM+∠MBE =∠DBN+∠MBE ，∴∠ABM=∠DBN ，AB=BD ，∴△ABM ≌△DBN ，∴BM=BN,∵∠NBE+∠MBE =∠NBE+∠NBC ，∴∠MBE =∠NBC ，∵BE=BC ，∴△BME ≌△BNC ．【点睛】本题考察全等三角形的判定与性质，熟知全等三角形的判定与性质是解题关键． 26．详见解析【分析】利用HL 证明Rt △ABD ≌Rt △BAC ，即可得到结论．【详解】∵BD ⊥AD ，AC ⊥BC ，∴∠D=∠C=90︒，在Rt △ABD 和Rt △BAC 中，AB BA BD AC=⎧⎨=⎩， ∴Rt △ABD ≌Rt △BAC （HL ），∴∠ABC ＝∠BAD ．【点睛】此题考查全等三角形的判定及性质，根据题中的已知条件确定两个三角形的对应相等的条件，根据全等的判定定理证得这两个三角形全等是解题的关键．。

苏州苏州中学园区校数学三角形填空选择单元测试与练习（word 解析版）一、八年级数学三角形填空题（难）1．如图，Rt △ABC 中，∠C=90°，∠BAC 的角平分线AE 与AC 的中线BD 交于点F ，P 为CE 中点，连结PF ，若CP=2，15BFP S ∆=，则AB 的长度为_______．【答案】15【解析】【分析】作辅助线EH AB ⊥交AB 于H ，再利用等量关系用△BFP 的面积来表示△BEA 的面积，利用三角形的面积公式来求解底边AB 的长度【详解】作EH AB ⊥∵AE 平分∠BACBAE CAE ∴∠=∠EC EH ∴=∵P 为CE 中点4EC EH ==∴∵D 为AC 中点，P 为CE 中点=x =y PEF PCF CDF ADF S S S S ==△△△△∴设，15x BEF S =-△∴15+x+y BCD BDA S S ==△△∴y=15+x+y-y=15+x BFA BDA S S =-△△∴15x+15+x=30BEA BEF BFA S S S =+=-△△△∴1=302BEA S AB EH ⨯=△∵ =15AB ∴【点睛】本题考查了辅助线的运用以及三角形的中线平分三角形的面积，解题的关键在于如何利用△BFP 的面积来表示△BEA 的面积2．如图，ABC ∆的ABC ∠的平分线与ACB ∠的外角平分线相交于点D ，点,E F 分别在线段BD 、CD 上，点G 在EF 的延长线上，EFD ∆与EFH ∆关于直线EF 对称，若60,84,A BEH HFG n ︒︒︒∠=∠=∠=，则n =__________.【答案】78.【解析】【分析】利用ABC ∆的ABC ∠的平分线与ACB ∠的外角平分线相交于点D 得到∠DBC=12∠ABC ，∠ACD=12(∠A+∠ABC)，根据三角形的内角和得到∠D=12∠A=30︒，利用外角定理得到∠DEH=96︒，由EFD ∆与EFH ∆关于直线EF 对称得到∠DEG=∠HEG=48︒，根据外角定理即可得到∠DFG=∠D+∠DEG=78︒.【详解】∵ABC ∆的ABC ∠的平分线与ACB ∠的外角平分线相交于点D∴∠DBC=12∠ABC ，∠ACD=12(∠A+∠ABC)， ∵∠DBC+∠BCD+∠D=180︒，∠A+∠ABC+∠ACB=180︒， ∴∠D=12∠A=30︒， ∵84BEH ︒∠=,∴∠DEH=96︒,∵EFD ∆与EFH ∆关于直线EF 对称，∴∠DEG=∠HEG=48︒，∠DFG=∠HFG n ︒=,∵∠DFG=∠D+∠DEG=78︒，∴n=78.故答案为：78.【点睛】此题考查三角形的内角和定理、外角定理，角平分线性质，轴对称图形的性质，此题中求出∠D=12∠A=30︒是解题的关键.3．如图，ABC 中，点D 在AC 的延长线上，E 、F 分别在边AC 和AB 上，BFE ∠与BCD ∠的平分线相交于点P ，若ABC ∠=70°FEC ∠=80°，则P ∠=______．【答案】85°【解析】【分析】根据四边形内角和等于360°，在四边形FECB 中∠B +∠BFE +∠FEC +∠BCE =360°，结合角平分线的定义计算即可得∠1-∠2=15°；再在四边形EFPC 中求出∠1-∠2+∠P =110°即可解答．【详解】解：∵∠BFE =2∠1，∠BCD =2∠2，又∵∠BFE +∠ABC +∠FEC +∠BCE =360°，ABC ∠=70°，FEC ∠=80°，∴2∠1+（180°-2∠2）+70°+80°=360°，∴∠1-∠2=15°；∵在四边形EFPC 中，∠PFE +∠FEC +∠P +∠PCE =360°，∴∠1+80°+（180°-∠2）+∠P =360°，∴∠1-∠2+∠P =100°，∴∠P =85°，故答案为：85°．【点睛】本题考查的是三角形内角和定理和四边形内角和定理的应用，掌握三角形内角和等于180°和四边形内角和等于360°是解题的关键．4．小明在用计算器计算一个多边形的内角和时，得出的结果为2005°，小芳立即判断他的结构是错误的，小明仔细地复算了一遍，果然发现自己把一个角的度数输入了两遍.你认为正确的内角和应该是________．【答案】1980【解析】【详解】解：设多边形的边数为n ，多加的角度为α，则（n-2）×180°=2005°-α，当n=13时，α=25°，此时（13-2）×180°=1980°，α=25°故答案为1980．5．如图所示，∠1+∠2+∠3+∠4+∠5+∠6=__________度．【答案】360 °【解析】如图所示，根据三角形外角的性质可得，∠1+∠5=∠8，∠4+∠6=∠7，根据四边形的内角和为360°，可得∠2+∠3+∠7+∠8=360°，即可得∠1+∠2+∠3+∠4+∠5+∠6=360°.点睛：本题考查的知识点：（1）三角形的内角和外角之间的关系：三角形的外角等于与它不相邻的两个内角和；（2）四边形内角和定理：四边形内角和为360°．6．一个等腰三角形的两边长分别为4cm和9cm，则它的周长为__cm．【答案】22【解析】【分析】底边可能是4，也可能是9，分类讨论，去掉不合条件的，然后可求周长.【详解】试题解析：①当腰是4cm，底边是9cm时：不满足三角形的三边关系，因此舍去．②当底边是4cm，腰长是9cm时，能构成三角形，则其周长=4+9+9=22cm．故填22．【点睛】本题考查了等腰三角形的性质和三角形的三边关系；已知没有明确腰和底边的题目一定要想到两种情况，分类进行讨论，还应验证各种情况是否能构成三角形进行解答.7．如图，AD是△ABC的中线，CE是△ACD的中线，S△ACE=3cm2，则S△ABC=_____cm2．【答案】12cm2．【解析】【分析】根据三角形的面积公式，得△ACE的面积是△ACD的面积的一半，△ACD的面积是△ABC 的面积的一半．【详解】解：∵CE是△ACD的中线，∴S△ACD=2S△ACE=6cm2．∵AD是△ABC的中线，∴S△ABC=2S△ACD=12cm2．故答案为12cm2．【点睛】此题主要是根据三角形的面积公式，得三角形的中线把三角形的面积分成了相等的两部分．8．一个多边形的内角和与外角和的差是180°，则这个多边形的边数为_____．【答案】5【解析】【分析】根据多边形的内角和公式（n﹣2）•180°与外角和定理列式求解即可【详解】解：设这个多边形的边数是n，则（n﹣2）•180°﹣360°＝180°，解得n＝5．故答案为5．【点睛】本题考查了多边形的内角和与外角和定理，任意多边形的外角和都是360°，与边数无关．9．如图，小亮从A点出发前进5m，向右转15°，再前进5m，又向右转15°…，这样一直走下去，他第一次回到出发点A时，一共走了______m．【答案】120．【解析】【分析】由题意可知小亮所走的路线为正多边形，根据多边形的外角和定理即可求出答案．【详解】解：∵小亮从A 点出发最后回到出发点A 时正好走了一个正多边形，∴该正多边形的边数为n=360°÷15°=24，则一共走了24×5=120米，故答案为：120．【点睛】本题主要考查了多边形的外角和定理．任何一个多边形的外角和都是360°，用外角和求正多边形的边数可直接用360°除以一个外角度数．10．如图所示，请将12A ∠∠∠、、用“＞”排列__________________.【答案】21A ∠∠∠＞＞【解析】【分析】根据三角形的外角的性质判断即可．【详解】解：根据三角形的外角的性质得，∠2＞∠1，∠1＞∠A∴∠2＞∠1＞∠A ，故答案为：∠2＞∠1＞∠A ．【点睛】本题考查了三角形的外角的性质，掌握三角形的一个外角大于和它不相邻的任何一个内角是解题的关键．二、八年级数学三角形选择题（难）11．若△ABC 内有一个点P 1，当P 1、A 、B 、C 没有任何三点在同一直线上时，如图1，可构成3个互不重叠的小三角形；若△ABC 内有两个点P 1、P 2，其它条件不变，如图2，可构成5个互不重叠的小三角形：……若△ABC 内有n 个点，其它条件不变，则构成若干个互不重叠的小三角形，这些小三角形的内角和为（）A．n·180°B．（n+2）·180°C．（2n-1）·180°D．（2n+1）·180°【答案】D【解析】【分析】当△ABC内的点的个数是1时，三角形内互不重叠的小三角形的个数是3；当△ABC内的点的个数是2时，三角形内互不重叠的小三角形的个数是5；依此类推得到当△ABC内的点的个数是3时，三角形内互不重叠的小三角形的个数是7；当△ABC内的点的个数是n 时，三角形内互不重叠的小三角形的个数2n+1，所以这些小三角形的内角和为（2n+1）·180°【详解】】解：图1中，当△ABC内只有1个点时，可分割成3个互不重叠的小三角形；图2中，当△ABC内只有2个点时，可分割成5个互不重叠的小三角形；图3中，当△ABC内只有3个点时，可分割成7个互不重叠的小三角形；根据以上规律，当△ABC内有n个点（P1，P2，…，P n）时，可以把△ABC分割成S=2n+1个互不重叠的三角形，所以这些小三角形的内角和为（2n+1）·180°.【点睛】此题考查了平面图形的有规律变化，要求学生通过观察图形，分析、归纳并发现其中的规律，并应用规律解决问题是解题的关键．12．如图，∠ABC =∠ACB ，BD 、CD 分别平分△ABC 的内角∠ABC 、外角∠ACP ，BE平分外角∠MBC 交 DC 的延长线于点 E ，以下结论：①∠BDE =12∠BAC ；② DB⊥BE ；③∠BDC +∠ACB= 90︒；④∠BAC + 2∠BEC = 180︒ .其中正确的结论有（）A．1 个B．2 个C．3 个D．4 个【答案】D【解析】【分析】根据角平分线的定义、三角形的内角和定理、三角形的外角的性质、判断即可．【详解】① ∵BD、CD分别平分△ABC的内角∠ABC、外角∠ACP，∴∠ACP=2∠DCP，∠ABC=2∠DBC，又∵∠ACP=∠BAC+∠ABC，∠DCP=∠DBC+∠BDC，∴∠BAC=2∠BDE，∴∠BDE =12∠BAC∴①正确；②∵BD、BE分别平分△ABC的内角∠ABC、外角∠MBC，∴∠DBE=∠DBC+∠EBC=12∠ABC+12∠MBC=12×180°=90°，∴EB⊥DB，故②正确，③∵∠DCP=∠BDC+∠CBD，2∠DCP=∠BAC+2∠DBC，∴2(∠BDC+∠CBD)=∠BAC+2∠DBC，∴∠BDC=12∠BAC，∵∠BAC+2∠ACB=180°，∴12∠BAC+∠ACB=90°，∴∠BDC+∠ACB=90°，故③正确，④∵∠BEC=180°−12(∠MBC+∠NCB)=180°−12(∠BAC+∠ACB+∠BAC+∠ABC)=180°−12(180°+∠BAC)∴∠BEC=90°−12∠BAC，∴∠BAC+2∠BEC=180°，故④正确，即正确的有4个，故选D【点睛】此题考查三角形的外角性质，平行线的判定与性质，三角形内角和定理，解题关键在于掌握各性质定理13．马小虎在计算一个多边形的内角和时，由于粗心少算了2个内角，其和等于830，则该多边形的边数是( )A．7B．8C．7或8D．无法确定【答案】C【解析】【分析】n边形的内角和是（n-2）•180°，即为180°的（n-2）倍，多边形的内角一定大于0度，小于180度，因而多边形中，除去2个内角外，其余内角和与180度的商加上2，以后所得的数值，比这个数值大1或2的整数就是多边形的边数．【详解】设少加的2个内角和为x度，边数为n．则（n-2）×180=830+x，即（n-2）×180=4×180+110+x，因此x=70，n=7或x=250，n=8．故该多边形的边数是7或8．故选C．【点睛】本题考查了多边形的内角和定理，正确理解多边形内角的大小的特点，以及多边形的内角和定理是解决本题的关键．14．如图，△ABC中，角平分线AD、BE、CF相交于点H，过H点作HG⊥AC，垂足为G，那么∠AHE和∠CHG的大小关系为（）A．∠AHE＞∠CHG B．∠AHE＜∠CHG C．∠AHE=∠CHG D．不一定【答案】C【解析】【分析】先根据AD、BE、CF为△ABC的角平分线可设∠BAD=∠CAD=x，∠ABE=∠CBE=y，∠BCF=∠ACF=z，由三角形内角和定理可知，2x+2y+2z=180°即x+y+z=90°在△AHB中由三角形外角的性质可知∠AHE=x+y=90°﹣z，在△CHG中，∠CHG=90°﹣z，故可得出结论．【详解】∵AD、BE、CF为△ABC的角平分线∴可设∠BAD=∠CAD=x，∠ABE=∠CBE=y，∠BCF=∠ACF=z，∴2x+2y+2z=180°即x+y+z=90°，∵在△AHB中，∠AHE=x+y=90°﹣z，在△CHG中，∠CHG=90°﹣z，∴∠AHE=∠CHG，故选C．【点睛】本题考查了三角形的内角和定理及三角形外角的性质，熟知三角形的内角和180°，三角形的外角等于和它不相邻的两个内角的和是解答此题的关键．15．如图，在△ABC中，点M、N是∠ABC与∠ACB三等分线的交点．若∠A＝60°，则∠BMN的度数为( )A．45°B．50°C．60°D．65°【答案】B【解析】分析：过点N作NG⊥BC于G，NE⊥BM于E，NF⊥CM于F，根据角平分线上的点到角的两边的距离相等可得NE=NG=NF，再根据到角的两边距离相等的点在角的平分线上判断出MN平分∠BMC，然后根据三角形内角和等于180°求出∠ABC+∠ACB，再根据角的三等分求出∠MBC+∠MCB的度数，然后利用三角形内角和定理求出∠BMC的度数，从而得解．详解：如图，过点N作NG⊥BC于G，NE⊥BM于E，NF⊥CM于F，∵∠ABC的三等分线与∠ACB的三等分线分别交于点M、N，∴BN平分∠MBC，CN平分∠MCB，∴NE=NG，NF=NG，∴NE=NF，∴MN平分∠BMC，∴∠BMN=12∠BMC，∵∠A=60°，∴∠ABC+∠ACB=180°−∠A=180°−60°=120°，根据三等分,∠MBC+∠MCB=23 (∠ABC+∠ACB)=2 3×120°=80°. 在△BMC 中,∠BMC=180°−(∠MBC+∠MCB)=180°−80°=100°. ∴∠BMN=12×100°=50°； 故选：B.点睛：本题考查了三角形的内角和定理：三角形内角和为180°；角平分线的性质：角平分线上的点到角两边的距离相等.熟记性质和定理是解本题的关键.16．如图将直尺与含30°角的三角尺摆放在一起，若120∠=︒，则2∠的度数是（ ）A ．30B ．40︒C ．50︒D ．60︒【答案】C【解析】【分析】 先根据三角形外角的性质求出∠BEF 的度数，再根据平行线的性质得到∠2的度数．【详解】如图，∵∠BEF 是△AEF 的外角，∠1=20︒，∠F=30︒，∴∠BEF=∠1+∠F=50︒，∵AB ∥CD ，∴∠2=∠BEF=50︒，故选：C ．【点睛】本题主要考查了平行线的性质，解题的关键是掌握三角形外角的性质．17．如图，将一张三角形纸片ABC 的一角折叠，使点A 落在ABC ∆处的'A 处，折痕为DE .如果A α∠=，'CEA β∠=，'BDA γ∠=，那么下列式子中正确的是（ ）A ．2γαβ=+B ．2γαβ=+C ．γαβ=+D ．180γαβ=--【答案】A【解析】【分析】【详解】 分析:根据三角形的外角得：∠BDA'=∠A+∠AFD ，∠AFD=∠A'+∠CEA'，代入已知可得结论. 详解:由折叠得：∠A=∠A'，∵∠BDA'=∠A+∠AFD ，∠AFD=∠A'+∠CEA'，∵∠A=α，∠CEA′=β，∠BDA'=γ，∴∠BDA'=γ=α+α+β=2α+β，故选A.点睛：本题考查了三角形外角的性质，熟练掌握三角形的外角等于与它不相邻的两个内角的和是关键.18．已知直线m n ，将一块含45︒角的直角三角板ABC 按如图方式放置，其中斜边BC 与直线n 交于点D .若125∠=︒，则2∠的度数为（ ）A ．60︒B ．65︒C ．70︒D ．75︒【答案】C【分析】先求出∠AED=∠1+∠B=25°+45°=70°，再根据平行线的性质可知∠2=∠AED=70°．【详解】设直线n 与AB 的交点为E 。

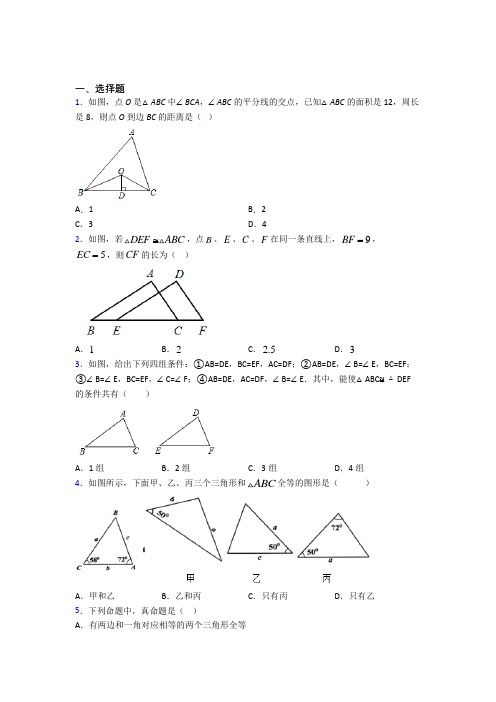
一、选择题1．如图，点O 是△ABC 中∠BCA ，∠ABC 的平分线的交点，已知△ABC 的面积是12，周长是8，则点O 到边BC 的距离是（ ）A ．1B ．2C ．3D ．42．如图，若DEF ABC ≅，点B 、E 、C 、F 在同一条直线上，9BF =，5EC =，则CF 的长为（ ）A ．1B ．2C ．2.5D ．33．如图，给出下列四组条件：①AB=DE ，BC=EF ，AC=DF ；②AB=DE ，∠B=∠E ，BC=EF ；③∠B=∠E ，BC=EF ，∠C=∠F ；④AB=DE ，AC=DF ，∠B=∠E ．其中，能使△ABC ≌△DEF 的条件共有（ ）A ．1组B ．2组C ．3组D ．4组4．如图所示，下面甲、乙、丙三个三角形和ABC 全等的图形是（ ）A ．甲和乙B ．乙和丙C ．只有丙D ．只有乙 5．下列命题中，真命题是（ ）A ．有两边和一角对应相等的两个三角形全等B ．有两边和第三边上的高对应相等的两个三角形全等C ．有两边和其中一边上的高对应相等的两个三角形全等D ．有两边和第三边上的中线对应相等的两个三角形全等6．下列命题的逆命题是假命题的是（ ）A ．直角三角形两锐角互余B ．全等三角形对应角相等C ．两直线平行，同位角相等D ．角平分线上的点到角两边的距离相等 7．如图，在Rt ABC △中，90C ∠=︒，CAB ∠的平分线交BC 于点D ，且DE 所在直线是AB 的垂直平分线，垂足为E ．若3DE =，则BC 的长为（ ）．A ．6B ．7C ．8D ．98．如图，OB 平分∠MON ，A 为OB 的中点，AE ⊥ON ，EA=3，D 为OM 上的一个动点，C 是DA 延长线与BC 的交点，BC //OM ，则CD 的最小值是（ ）A ．6B ．8C ．10D ．129．如图，在ABC 中，B C ∠=∠，E 、D 、 F 分别是AB 、BC 、AC 上的点，且BE CD =，BD CF =，若 104A ∠=︒，则EDF ∠的度数为（ ）A ．24°B ．32°C ．38°D ．52°10．如图，AD 平分∠BAC ，AB=AC ，连接BD ，CD 并延长，分别交AC ，AB 于点F ，E ，则图中全等三角形共有（ ） A ．2对B ．3对C ．4对D ．5对11．如图，△ACB ≌△A 'CB '，∠BCB '=25°，则∠ACA '的度数为（ ）A ．35°B ．30°C ．25°D ．20°12．如图，在四边形ABCD 中，//,AB CD AE 是BAC ∠的平分线，且AE CE ⊥．若,AC a BD b ==，则四边形ABDC 的周长为（ ）A ．1.5()a b +B ．2a b +C ．3a b -D ．2+a b二、填空题13．如图，点D 、E 分别在线段AB 、AC 上，BE 与CD 相交于点O ．若AB AC =，AD AE =，60A ∠=︒，80ADC ∠=︒，则B 的度数为______．14．如图，在Rt ABC △中，90B ∠=︒，12AB =，5BC =，射线AP AB ⊥于点A ，点E 、D 分别在线段AB 和射线AP 上运动，并始终保持DE AC =，要使ABC 和DAE △全等，则AE 的长为______．15．已知点A 、E 、F 、C 在同一条直线l 上，点B 、D 在直线l 的异侧，若AB=CD ，AE=CF ，BF=DE ，则AB 与CD 的位置关系是_______．16．如图，ABC 的面积为215cm ，以顶点A 为圆心，适当长为半径画弧，分别交AC ，AB 于点M ，N ，再分别以点M ，N 为圆心，大于12MN 的长为半径画弧，两弧交于点P ，作射线AP ，过点C 作CD AP ⊥于点D ，连接DB ，则DAB 的面积是______2cm ．17．如图，在ABC 中，点D 是BC 上的一点，已知30DAC ∠=︒，75DAB ∠=︒，CE 平分ACB ∠交AB 于点E ，连接DE ，则DEC ∠=________度．18．如图，AD 为∠CAF 的角平分线，BD=CD ，∠DBC=∠DCB ，∠DCA=∠ABD ，过D 作DE ⊥AC 于E ，DF ⊥AB 交BA 的延长线于F ，则下列结论：①△CDE ≌△BDF ；②CE=AB+AE ；③∠DAF=∠CBD ．其中正确的结论有_____．（填序号）19．已知△ABC ≌△DEF ，△ABC 的三边分别为3，m ，n ，△DEF 的三边分别为5，p ，q ．若△ABC 的三边均为整数，则m+n+p+q 的最大值为________．20．如图，在△ABC 中，∠C =90°，∠A 的平分线交BC 于D ，若20ABD S ∆=cm 2，AB =10cm ，则CD 为__________cm ．三、解答题21．如图所示，△ABC 中，∠ACB=90°，AC=BC ，直线EF 经过点C ，BF ⊥EF 于点F ，AE ⊥EF 于点E ．（1）求证：△ACE ≌△CBF ；（2）如果AE 长12cm ，BF 长5cm ，求EF 的长．22．如图1是一个平分角的仪器，其中OD=OE ，FD=FE ．（1）如图2，将仪器放置在△ABC 上，使点O 与顶点A 重合，D 、E 分别在边AB 、AC 上，沿AF 画一条射线AP ，交BC 于点P ．则AP 就是∠BAC 的平分线吗？请给出判断并说明理由．（2）如图3，在（1）的前提下，过点P 作PQ ⊥AB 于点Q ，已知PQ=4，AC=7，△ABC 的面积是32，求AB 的长．23．如图，在五边形ABCDE 中，AB DE =，AC AD =．（1）请你添加一个与角有关的条件，使得ABC DEA ≌，并说明理由；（2）在（1）的条件下，若65CAD ∠=︒，110B ∠=︒，求BAE ∠的度数． 24．如图，在△ABC 中，∠BAC 的平分线AD 交BC 于点D ，过点D 作DE ⊥AB ，DF ⊥AC ，垂足分别是E ，F ，连接EF ．写出两个结论（∠BAD ＝∠CAD 和DE ＝DF 除外），并选择一个结论进行证明．（1）____________；（2）____________．25．已知ABC 为等腰直角三角形，AB AC =，ADE 为等腰直角三角形，AD AE =，点D 在直线BC 上，连接CE ．（1）若点D 在线段BC 上，如图1，求证：CE BC CD =-；（2）若D 在CB 延长线上，如图2，若D 在BC 延长线上，如图3，其他条件不变，又有怎样的结论？请分别写出你发现的结论，不需要证明；（3）若10CE =，4CD =，则BC 的长为________．26．下面是小芳同学设计的“过直线外一点作这条直线垂线”的尺规作图过程．已知：如图1，直线l 及直线l 外一点P ．求作：直线l 的垂线，使它经过点P ．作法：如图2，① 以P 为圆心，大于P 到直线l 的距离为半径作弧，交直线l 于A 、B 两点；② 连接PA 和PB ；③ 作∠APB 的角平分线PQ ，交直线l 于点Q ．④ 作直线PQ ．∴ 直线PQ 就是所求的直线．根据小芳设计的尺规作图过程，解答下列问题：（1）使用直尺和圆规，补全图2（保留作图痕迹）；（2）补全下面证明过程：证明：∵ PQ 平分∠APB ，∴ ∠APQ=∠QPB ．又∵ PA= ，PQ=PQ ，∴ △APQ ≌△BPQ （ ）（填推理依据）．∴ ∠PQA=∠PQB （ ）（填推理依据）．又∵∠PQA ＋∠PQB ＝ 180°，∴ ∠PQA=∠PQB ＝ 90°．∴ PQ ⊥ l ．【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】过点O作OE⊥AB于E，OF⊥AC于F，连接OA，根据角平分线的性质得：OE＝OF＝OD然后根据△ABC的面积是12，周长是8，即可得出点O到边BC的距离．【详解】如图，过点O作OE⊥AB于E，OF⊥AC于F，连接OA.∵点O是∠ABC，∠ACB平分线的交点，∴OE＝OD，OF＝OD，即OE＝OF＝OD∴S△ABC＝S△ABO＋S△BCO＋S△ACO＝12AB·OE＋12BC·OD＋12AC·OF＝12×OD×(AB＋BC＋AC)＝12×OD×8＝12OD=3故选：C【点睛】此题主要考查了角平分线的性质以及三角形面积求法，角的平分线上的点到角的两边的距离相等，正确表示出三角形面积是解题关键．2．B解析：B【分析】根据全等三角形的对应边相等得到BE=CF，计算即可．【详解】解：∵△DEF≌△ABC，∴BC=EF，∴BE+EC=CF+EC，∴BE=CF，又∵BF=BE+EC+CF=9，EC=5∵CF=12(BF-EC)=12(9-5)=2．故选：B．【点睛】本题考查了全等三角形的性质，掌握全等三角形的对应边相等、全等三角形的对应角相等是解题的关键．3．C解析：C【分析】要使△ABC≌△DEF的条件必须满足SSS、SAS、ASA、AAS，可据此进行判断．【详解】解：第①组满足SSS，能证明△ABC≌△DEF．第②组满足SAS，能证明△ABC≌△DEF．第③组满足ASA，能证明△ABC≌△DEF．第④组只是SSA，不能证明△ABC≌△DEF．所以有3组能证明△ABC≌△DEF．故符合条件的有3组．故选：C．【点睛】本题考查三角形全等的判定方法；判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．添加时注意：AAA、SSA不能判定两个三角形全等，不能添加，根据已知结合图形及判定方法选择条件是正确解答本题的关键．4．B解析：B【分析】甲只有2个已知条件，缺少判定依据；乙可根据SAS判定与△ABC全等；丙可根据AAS判定与△ABC全等，可得答案．【详解】解：甲三角形只知道两条边长无法判断是否与△ABC全等；乙三角形夹50°内角的两边分别与已知三角形对应相等，故乙与△ABC全等；丙三角形72°内角及所对边与△ABC对应相等且均有50°内角，可根据AAS判定乙与△ABC 全等；则与△ABC全等的有乙和丙，故选：B．【点睛】本题主要考查全等三角形的判定定理，熟练掌握并充分理解三角形全等的判定定理，注意对应二字的理解很重要．5．D解析：D【分析】根据三角形全等的判定方法对A、D进行判断；利用三角形高的位置不同可对B、C进行判断．【详解】A、有两边和它们的夹角对应相等的两个三角形全等，所以A选项错误；B、有两边和第三边上的高对应相等的两个锐角三角形全等，所以B选项错误；C、有两边和其中一边上的高对应相等的两个锐角三角形全等，所以C选错误；D、有两边和第三边上的中线对应相等的两个三角形全等，所以D选项正确；故选：D．【点睛】本题考査了判断命题真假，以及全等三角形的判定，熟练掌握全等三角形的判定，仔细分类讨论是解题关键．6．B解析：B【分析】先分别写出这些定理的逆命题，再进行判断即可．【详解】解：A．直角三角形的两锐角互余的逆命题是两锐角互余的三角形是直角三角形，是真命题；B．全等三角形的对应角相等的逆命题是对应角相等的三角形是全等三角形，是假命题；C．两直线平行，同位角相等的逆命题是同位角相等，两直线平行，是真命题；D．角平分线上的点到角两边的距离相等的逆命题是到角两边的距离相等的点在角平分线上，是真命题．故选：B．【点睛】此题考查了命题与定理，两个命题中，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论又是第二个命题的条件，那么这两个命题叫做互逆命题．其中一个命题称为另一个命题的逆命题．7．D解析：D【分析】由角平分线和线段垂直平分线的性质可求得∠B=∠CAD=∠DAB=30°，【详解】解：∵DE 垂直平分AB ，∴DA=DB ，∴∠B=∠DAB ，∵AD 平分∠CAB ，∴∠CAD=∠DAB ，∵∠C=90°，∴3∠EAD=90°，∴∠EAD=30°，∵∠AED=90°，∴DA=BD=2DE ，∵AD 平分∠CAB ，DE ⊥AB ，CD ⊥AC ，∴CD=DE=3，∴DA=BD=6，∴BC=BD+CD=6+3=9，故选：D ．【点睛】本题考查了线段垂直平分线的性质，掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键．8．A解析：A【分析】根据两条平行线之间的距离可知当CD ⊥OM 时，CD 取最小值，先利用角平分线的性质得出AD =AE =3，利用全等三角形的判定和性质得出AC =AD =AE =3，进而解答即可．【详解】解：由题意得，当CD ⊥OM 时，CD 取最小值，∵OB 平分∠MON ，AE ⊥ON 于点E ，CD ⊥OM ，∴AD =AE =3，∵BC ∥OM ，∴∠DOA =∠B ，∵A 为OB 中点，∴AB =AO ，在△ADO 与△ABC 中B DOA AB AO BAC DAO ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△ADO ≌△ABC (SAS ),∴AC =AD =3，∴336CD AC AD =+=+=，故选A ．【点睛】此题考查角平分线的性质、全等三角形的判定和性质、平行线之间的距离，关键是利用全等三角形的判定和性质得出AC =AD =AE =3．9．C解析：C【分析】根据题意可证明BDE CFD ≌，以及求解∠B 的度数，再由三角形的外角性质和全等三角形的性质推出∠EDF=∠B ，从而得出结果．【详解】在BDE 与CFD 中，BE CD B C BD CF =⎧⎪∠=∠⎨⎪=⎩∴()BDE CFD SAS ≌∴∠BED=∠CDF ，又∵∠B+∠BED=∠EDC=∠EDF+∠CDF ，∴∠B=∠EDF ，∵在BAC 中，∠A=104°，∠B=∠C ，∴∠B=（180°-104°）÷2=38°，∴∠EDF=38°，故选：C ．【点睛】本题考查全等三角形的判定与性质，三角形的内角和定理与外角性质，熟练证明全等并利用其性质进行推理演算是解题关键．10．C解析：C【分析】认真观察图形，确定已知条件在图形上的位置，结合全等三角形的判定方法，由易到难，仔细寻找．【详解】解：AD 平分BAC ∠，BAD CAD ∴∠=∠， 在ABD ∆与ACD ∆中，AB AC BAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩，()ABD ACD SAS ∴∆≅∆，BD CD ∴=，B C ∠=∠，ADB ADC ∠=∠，又EDB FDC ∠=∠，ADE ADF ∴∠=∠，AED AFD ，BDE CDF ∆≅∆，∆≅∆ABF ACE ．AED AFD ，ABD ACD ∆≅∆，BDE CDF ∆≅∆，∆≅∆ABF ACE ，共4对． 故选：C ．【点睛】本题考查三角形全等的判定方法和全等三角形的性质，熟悉相关判定定理是解题的关键． 11．C解析：C【分析】利用全等三角形的性质可得∠A′CB′=∠ACB ，再利用等式的性质可得答案．【详解】解：∵△ACB ≌△A′CB′，∴∠A′CB′=∠ACB ，∴∠A′CB′-∠A′CB=∠ACB-∠A′CB ，∴∠ACA′=∠BCB′=25°，故选：C ．【点睛】此题主要考查了全等三角形的性质，关键是掌握全等三角形对应角相等．12．B解析：B【分析】在线段AC 上作AF=AB ，证明△AEF ≌△AEB 可得∠AFE=∠B ，∠AEF=∠AEB ，再证明△CEF ≌△CED 可得CD=CF ，即可求得四边形ABDC 的周长．【详解】解：在线段AC 上作AF=AB ，∵AE 是BAC ∠的平分线，∴∠CAE=∠BAE ，又∵AE=AE ，∴△AEF ≌△AEB （SAS ），∴∠AFE=∠B ，∠AEF=∠AEB ，∵AB ∥CD ，∴∠D+∠B=180°，∵∠AFE+∠CFE=180°，∴∠D=∠CFE ，∵AE CE ⊥，∴∠AEF+∠CEF=90°，∠AEB+∠CED=90°，∴∠CEF=∠CED ，在△CEF 和△CED 中∵D CFE CEF CED CE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△CEF ≌△CED （AAS ）∴CE=CF ，∴四边形ABDC 的周长=AC+AB+BD+CD=AC+AF+CF+BD=2AC+BD=2a b +，故选：B ．【点睛】本题考查全等三角形的性质和判断．能正确作出辅助线构造全等三角形是解题关键．二、填空题13．40°【分析】由全等三角形的判定证得△ABE ≌△ACD （SAS ）由全等三角形的性质可得∠B ＝∠C 根据三角形内角和定理求出∠C 继而即可求解【详解】在△ABE 和△ACD 中∴△ABE ≌△ACD （SAS ）∴解析：40°【分析】由全等三角形的判定证得△ABE ≌△ACD （SAS ），由全等三角形的性质可得∠B ＝∠C ，根据三角形内角和定理求出∠C ，继而即可求解．【详解】在△ABE 和△ACD 中，AB AC AD AE A A ==∠=∠⎧⎪⎨⎪⎩∴△ABE ≌△ACD （SAS ）∴∠B ＝∠C∵60A ∠=︒，80ADC ∠=︒，∴∠C ＝180°－∠A －∠ADC ＝40°，∴∠B=40°故答案为：40°．【点睛】本题考查全等三角形的判定和性质，三角形内角和定理，解题的关键是熟练掌握全等三角形的判定和性质证得∠B ＝∠C ．14．5或12【分析】本题要分情况讨论：①Rt △ABC ≌Rt △DAE 此时AE=BC=5可据此求出E 点的位置②Rt △CBA ≌Rt △DAE 此时AE=AB=12EB 重合【详解】解：①当AE=CB 时∵∠B=∠EA解析：5或12【分析】本题要分情况讨论：①Rt △ABC ≌Rt △DAE ，此时AE=BC=5，可据此求出E 点的位置．②Rt △CBA ≌Rt △DAE ，此时AE=AB=12，E 、B 重合．【详解】解：①当AE=CB 时，∵∠B=∠EAP=90°，在Rt △ABC 与Rt △DAE 中，AE CB DE AC =⎧⎨=⎩， ∴Rt △ABC ≌Rt △DAE （HL ），即AE=BC=5；②当E 运动到与B 点重合时，AE=AB ，在Rt △CBA 与Rt △DAE 中，AE AB DE AC =⎧⎨=⎩， ∴Rt △CBA ≌Rt △DAE （HL ），即AE=AB=12，∴当点E 与点B 重合时，△CBA 才能和△DAE 全等．综上所述，AE=5或12．故答案为：5或12．【点睛】本题考查了三角形全等的判定方法和全等三角形的性质，判定两个三角形全等的一般方法有：SSS 、SAS 、ASA 、AAS 、HL ．由于本题没有说明全等三角形的对应边和对应角，因此要分类讨论，以免漏解．15．AB//CD 【分析】先利用SSS 证明△ABF ≌△CDE 然后根据全等三角形的性质得到∠DCE=∠BAF 最后根据内错角相等两直线平行即可解答【详解】解：∵AE=CF ∴AE+EF=CF+EF 即AF=EC 在解析：AB//CD【分析】先利用SSS 证明△ABF ≌△CDE ，然后根据全等三角形的性质得到∠DCE=∠BAF ，最后根据内错角相等、两直线平行即可解答．【详解】解：∵AE=CF ，∴AE+EF=CF+EF,即AF=EC在△ABF 和△CDE 中，,,,AB CD AF EC BF DE =⎧⎪=⎨⎪=⎩∴△ABF ≌△CDE （SSS ），∴∠DCE=∠BAF ．∴AB//CD ．故答案为：AB//CD ．【点睛】本题主要考查了全等三角形的判定与性质以及平行线的判定，运用全等三角形的知识得到∠DCE=∠BAF 成为解答本题的关键．16．【分析】如图延长CD 交AB 于E 由题意得AP 平分∠CAB 证明△ADC ≌△ADE 得到CD=DE 由此得到推出即可得到答案【详解】如图延长CD 交AB 于E 由题意得AP 平分∠CAB ∴∠CAD=∠EAD ∵CD ⊥A 解析：152【分析】如图，延长CD 交AB 于E ，由题意得AP 平分∠CAB ，证明△ADC ≌△ADE ，得到CD=DE ，由此得到,ACD ADE BCD BED SS S S ==，推出ACD BCD ADE BED S S S S +=+，即可得到答案．【详解】如图，延长CD 交AB 于E ，由题意得AP 平分∠CAB ，∴∠CAD=∠EAD,∵CD ⊥AD ，∴∠ADC=∠ADE ，∵AD=AD ，∴△ADC ≌△ADE ，∴CD=DE ，∴,ACD ADE BCD BED SS S S ==， ∴ACD BCD ADE BED SS S S +=+， ∴12ABD ADE BED ABC S S S S =+==152，故答案为：152． ．【点睛】此题考查三角形角平分线的作图方法，全等三角形的判定及性质，证出CD=DE 得到,ACD ADE BCD BED S S S S ==是解此题的关键．17．15【分析】过点E 作EM ⊥AC 于MEN ⊥AD 于NEF ⊥BC 于H 如图先计算出∠EAM=75°则AE 平分∠EAD 根据角平分线的性质得EM=EN 再由CE 平分∠ACB 得到EM=EH 则EN=EH 于是根据角平分解析：15【分析】过点E 作EM ⊥AC 于M ，EN ⊥AD 于N ，EF ⊥BC 于H ，如图，先计算出∠EAM=75°，则AE 平分∠EAD ，根据角平分线的性质得EM=EN ，再由CE 平分∠ACB 得到EM=EH ，则EN=EH ，于是根据角平分线定理的逆定理可判断DE 平分∠ADB ，则∠1=12∠ADB ，根据三角形外角性质得∠1=∠DEC+∠2，即∠1=∠DEC+12∠ACB ，∠ADB=∠DAC+∠ACB ，所以∠DEC==12∠DAC=15°． 【详解】解：过点E 作EM AC ⊥于M ，EN AD ⊥于N ，EH BC ⊥于H ，如图．∵ 30DAC ∠=，75DAB ∠=，∴ 75EAM ∠=，∴ AE 平分MAD ∠，∴ EM EN =．∵ CE 平分ACB ∠，∴ EM EH =，∴ EN EH =，∴ DE 平分ADB ∠，∴112ADB ∠=∠．∵ 12DEC ∠=∠+∠，而122ACB ∠=∠，∴ 112DEC ACB ∠=∠+∠，而ADB DAC ACB ∠=∠+∠，∴ 11301522DEC DAC ∠=∠=⨯= ．故答案为：15．【点睛】 本题考查了平分线的性质和三角形外角的性质，掌握性质是解题的关键．18．①②③【分析】根据角平分线上的点到角的两边距离相等可得DE ＝DF 再利用HL 证明Rt △CDE 和Rt △BDF 全等根据全等三角形对应边相等可得CE ＝AF 利用HL 证明Rt △ADE 和Rt △ADF 全等根据全等三解析：①②③．【分析】根据角平分线上的点到角的两边距离相等可得DE ＝DF ，再利用“HL”证明Rt △CDE 和Rt △BDF 全等，根据全等三角形对应边相等可得CE ＝AF ，利用“HL”证明Rt △ADE 和Rt △ADF 全等，根据全等三角形对应边相等可得AE ＝AF ，然后求出CE ＝AB ＋AE ；根据全等三角形对应角相等可得∠DBF ＝∠DCE ，利用“8字型”证明∠BDC ＝∠BAC ；根据三角形内角和定理及平角的性质，可得∠DAF ＝∠CBD ．【详解】解：如图∵AD 平分∠CAF ，DE ⊥AC ，DF ⊥AB ，∴DE ＝DF ，在Rt △CDE 和Rt △BDF 中，BD CD DE DF⎧⎨⎩＝＝ ∴Rt △CDE ≌Rt △BDF （HL ），故①正确；∴CE ＝BF ，在Rt △ADE 和Rt △ADF 中，AD AD DE DF＝＝⎧⎨⎩ ，∴Rt△ADE≌Rt△ADF（HL），∴AE＝AF，∴CE＝AB＋AF＝AB＋AE，故②正确；∵Rt△CDE≌Rt△BDF，∴∠DBF＝∠DCE，∵∠AOB＝∠COD，（设AC交BD于O），∴∠BDC＝∠BAC，∵AD平分∠FAE，∴∠DAF＝∠DAE∵BD＝CD∴∠DBC＝∠DCB∵∠BAC＋∠DAF＋∠DAE＝180°，∠BDC＋∠DBC＋∠DCB＝180°，∠BDC＝∠BAC∴∠DAF＋∠DAE＝∠DBC＋∠DCB∴∠DAF＝∠CBD，故③正确综上所述，正确的结论有①②③．【点睛】本题考查了角平分线上的点到角的两边距离相等的性质，全等三角形的判定与性质，熟记性质并准确识图判断出全等的三角形是解题的关键，难点在于需要二次证明三角形全等．19．22【分析】由三角形全等性质可得mn中有一边为5pq中有一边为3mn与pq中剩余两边相等再由三角形三边关系可知mn与pq中剩余两边最大为7如此即可得到m+n+p+q的最大值【详解】∵△ABC≌△DE解析：22【分析】由三角形全等性质可得m、n中有一边为5，p、q中有一边为3，m、n与p、q中剩余两边相等，再由三角形三边关系可知m、n与p、q中剩余两边最大为7，如此即可得到m+n+p+q的最大值．【详解】∵△ABC≌△DEF，∴m、n中有一边为5，p、q中有一边为3，m、n与p、q中剩余两边相等，∵3+5=8，∴两三角形剩余两边最大为7，∴m+n+p+q的最大值为：3+5+7+7=22．【点睛】本题考查三角形全等与三角形三边关系的综合运用，灵活运用三角形全等的性质及三角形三边关系的应用是解题关键．20．4【分析】由角平分线的性质可知D到AB的距离等于DC可得出答案【详解】解：作DE⊥AB于E∵AD平分∠CAB且DC⊥ACDE⊥AB∴DE=DC∵S△ABD=20cm2AB=10cm∴•AB•DE=2解析：4【分析】由角平分线的性质可知D到AB的距离等于DC，可得出答案．【详解】解：作DE⊥AB于E．∵AD平分∠CAB，且DC⊥AC，DE⊥AB，∴DE=DC，∵S△ABD=20cm2，AB=10cm，∴1•AB•DE=20，2∴DE=4cm，∴DC=DE=4cm故答案为：4．【点睛】本题主要考查角平分线的性质，掌握角平分线上的点到角两边的距离相等是解题的关键．三、解答题21．（1）证明见解析；（2）EF=17cm．【分析】（1）根据垂直的定义可得∠AEC=∠CFB=90°，然后求出∠EAC=∠FCB，再利用“角角边”证明即可；（2）由全等三角形的性质可得：AE=CF，CE=BF，再根据线段的和差求解即可．【详解】（1）证明：在Rt△ACB中，∵∠ACB=90°，∴∠ACE+∠BCF=90°∵AE⊥EF，BF⊥EF∴∠ACE+∠EAC=90°∴∠CAE=∠BCF又∵ AC=CB∴△ACE≌△CBF(ASA)(2)由△ACE≌△CBF可得:AE=CF=12cm， EC=BF=5cm，∴EF=EC+CF=12+5=17cm ．【点睛】本题考查了全等三角形的判定与性质，同角的余角相等的性质，熟练掌握三角形全等的判断方法并找出全等的条件是解题的关键．22．（1）AP 是∠BAC 的平分线，理由见解析；（2）AB=9【分析】（1）利用“SSS”证明△ADF ≌△AEF 即可证明AP 是∠BAC 的平分线；（2）利用角平分线的性质得到PG=PQ=4，再根据三角形的面积公式即可求解．【详解】解：（1）AP 是∠BAC 的平分线，理由如下：在△ADF 和△AEF 中，AD AE AF AF DF EF =⎧⎪=⎨⎪=⎩，∴△ADF ≌△AEF （SSS ），∴∠DAF=∠EAF ，即AP 平分∠BAC ；（2）过点P 作PG ⊥AC 于点G ，∵AP 平分∠BAC ，PQ ⊥AB ，PG ⊥AC ，∴PG=PQ=4， ∵11 22ABC ABP APC SS S AB PQ AC PG =+=⋅+⋅ ∴114743222AB ⨯+⨯⨯=， ∴AB=9．【点睛】本题考查了全等三角形的判定及性质，角平分线的判定和性质．熟练掌握确定三角形的判定方法，正确的识别图形是解题的关键．23．（1）添加一个角有关的条件为BAC EDA ∠=∠，使得ABC DEA ≌，理由见解析；（2）BAE ∠的度数为135︒．【分析】(1)根据已知条件，选择SAS 原理，可确定添加的角；(2)利用三角形全等，∠B 的度数，可求∠BAC+∠DAE ，问题可解.【详解】（1）添加一个角方面的条件为BAC EDA ∠=∠，使得ABC DEA ≌.在ABC 和DEA △中∵AB DE =，BAC EDA ∠=∠，AC DA =，∴()SAS ABC DEA ≌△△； （2）在（1）的条件下∵ABC DEA ≌，∴ACB DAE ∠=∠，若65CAD ∠=︒，110B ∠=︒，则18070ACB BAC B ∠+∠=︒-∠=︒，∴70DAE BAC ACB BAC ∠+∠=∠+∠=︒，∴7065135BAE DAE BAC CAD ∠=∠+∠+∠=︒+︒=︒，即BAE ∠的度数为135︒.【点睛】本题考查了三角形全等，熟练掌握全等三角形判定原理和性质是解题的关键.24．（1）∠ADE=∠ADF ；证明见解析；（2）AE=AF ；证明见解析．【分析】（1）∠ADE=∠ADF ，根据DE ⊥AB ，DF ⊥AC 及AD 为∠BAC 的角平分线，即可证得∠ADE=∠ADF ；（2）AE=AF ，根据（1）可知证明△AED ≌△AFD ，即可证得AE=AF ．【详解】（1）结论1：∠ADE=∠ADF ，证明如下：∵DE ⊥AB ，DF ⊥AC ，∴∠AED=∠AFD=90︒，∵AD 为∠BAC 的角平分线，∴∠EAD=∠FAD ，∴∠ADE=∠ADF ；（2）结论2：AE=AF ，证明如下：由（1）可知：△AED ≌△AFD ，∴AE=AF ．【点睛】本题考查全等三角形的性质和判定，解题的关键是灵活运用全等三角形的判定和性质解决问题．25．（1）见解析；（2）图2：CE CD BC =-；图3：CE BC CD =+；（3）14或6【分析】（1）根据等腰直角三角形的性质得到∠ABC=∠BCA=45°，得到∠BAD=∠CAE ，利用SAS 定理证明ABD ACE △≌△，根据全等三角形的性质得到BD=CE ，结合图形证明； （2）同（1）的方法判断出ABD ACE △≌△，得出BD=CE ，即可解决问题；（3）根据（1）（2）得到的结论代入计算即可．【详解】证明：（1）ABC 、ADE 均是等腰直角三角形，AB AC ∴=，AD AE =，BAC DAE ∠=∠．BAC DAC DAE DAC ∴∠-∠=∠-∠．BAD CAE ∴∠=∠，在ABD △和CAE 中 AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩，(SAS)ABD ACE ∴≌，BD CE ∴=．BD BC CD =-，CE BC CD ∴=-．（2）如图2中，CE CD BC =-，理由如下：∵∠BAC=∠DAE=90°，∴∠BAC-∠BAE=∠DAE-∠BAE ，即∠BAD=∠EAC ，在△ABD 和△ACE 中，AB AC BAD CAE AD AE ⎧⎪∠∠⎨⎪⎩＝＝＝ ， ∴△ABD ≌△ACE （SAS ），∴BD=CE ，∴CD=BC+BD=BC+CE即：CE CD BC =-．如图3中，CE=BC+CD ．理由如下：∵∠BAC=∠DAE=90°，∴∠BAC+∠CAD=∠DAE+∠CAD即∠BAD=∠CAE ，∴在△ABD 和△ACE 中，AB AC BAD CAE AD AE ⎧⎪∠∠⎨⎪⎩＝＝＝ ， ∴△ABD ≌△ACE （SAS ），∴BD=CE ，∴BD=BC+CD ，即CE=BC+CD ．综上所述，若D 在CB 延长线上，如图2中，得到结论：CE CD BC =-，如图3，得到结论：CE BC CD =+．（3）∵在图1、图2中：CE CD BC =-（已证），10CE =，4CD =∴=+=10+4=14BC CE CD∵在图3中：CE=BC+CD （已证），10CE =，4CD =∴=-=10-4=6BC CE CD即：14或6．【点睛】本题考查的是全等三角形的判定和性质，掌握全等三角形的判定定理和性质定理是解题的关键．26．（1）见详解；（2）PB ，两边及其夹角相等的两三角形全等，全等三角形对应角相等．【分析】（1）根据尺规作图的步骤先做出PA ，PB ，然后再作出∠APQ 的角平分线PQ 即作出所求图；（2）根据作图过程知PA=PB ，再根据三角形全等的判定定理知所用到的判定定理和性质．【详解】（1）如图：（2）PB；两边及其夹角相等的两三角形全等；全等三角形对应角相等．【点睛】此题考查学生的动手能力——尺规作图中角平分线和垂直平分线的作法，涉及到三角形全等的判定和性质，难度一般．。

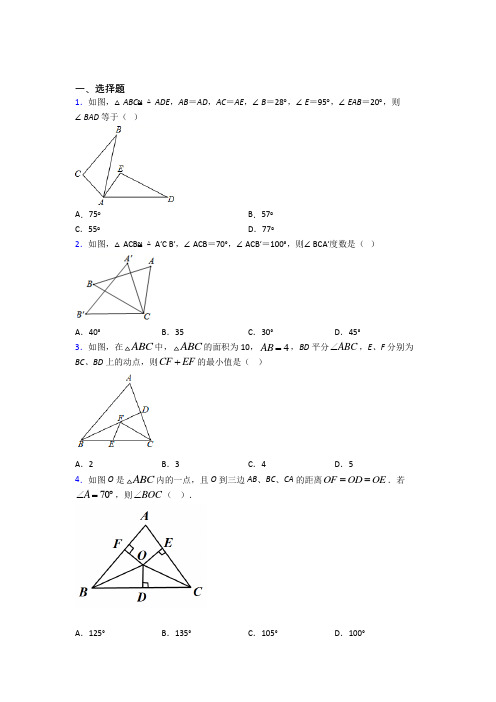
一、选择题1．如图，△ABC ≌△ADE ，AB ＝AD ，AC ＝AE ，∠B ＝28︒，∠E ＝95︒，∠EAB ＝20︒，则∠BAD 等于（ ）A ．75︒B ．57︒C ．55︒D ．77︒2．如图，△ACB ≌△A′C B′，∠ACB ＝70°，∠ACB′＝100°，则∠BCA′度数是（ ）A ．40°B ．35C ．30°D ．45°3．如图，在ABC 中，ABC 的面积为10，4AB =，BD 平分ABC ∠，E 、F 分别为BC 、BD 上的动点，则CF EF +的最小值是（ ）A ．2B ．3C ．4D ．54．如图O 是ABC 内的一点，且O 到三边AB 、BC 、CA 的距离==OF OD OE ．若70A ∠=︒，则BOC ∠（ ）．A ．125°B ．135°C ．105°D ．100°5．如图，在ABC 和DEF 中，,B DEF AB DE ∠=∠=，添加下列一个条件后，仍然不能证明ABC DEF ≌，这个条件是（ ）A ．A D ∠=∠B ．BC EF = C ．ACB F ∠=∠D ．AC DF = 6．下列说法正确的（ ）个．①0.09的算术平方根是0.03；②1的立方根是±1；③3.1＜10＜3.2；④两边及一角分别相等的两个三角形全等．A ．0B ．1C ．2D ．37．如图，在ABC 中，AD BC ⊥于D ，CE AB ⊥于E ，AD 与CE 交于点F ．请你添加一个适当的条件，使AEF ≌CEB △．下列添加的条件不正确的是（ ）A ．EF EB = B ．EA EC = C ．AF CB =D ．AFE B ∠=∠ 8．如图，AB 是线段CD 的垂直平分线，则图中全等三角形的对数有（ ）A ．2对B ．3对C ．4对D ．5对9．如图，AB ＝AC ，AD ＝AE ，∠A ＝105°，∠D ＝25°，则∠ABE 等于（ ）A ．65°B ．60°C ．55°D ．50°10．如图，AP 平分∠BAF ，PD ⊥AB 于点D ，PE ⊥AF 于点E ，则△APD 与△APE 全等的理由是（ ）A ．SSSB ．SASC ．SSAD ．AAS11．下列命题中，真命题是（ ）A ．有两边和一角对应相等的两个三角形全等B ．有两边和第三边上的高对应相等的两个三角形全等C ．有两边和其中一边上的高对应相等的两个三角形全等D ．有两边和第三边上的中线对应相等的两个三角形全等12．如图，AB AC =，AD AE =，55A ︒∠=，35C ︒∠=，则DOE ∠的度数是（ ）A ．105︒B ．115︒C ．125︒D ．130︒13．如图，AB 与CD 相交于点E ，AD=CB ，要使△ADE ≌△CBE ，需添加一个条件，则添加的条件以及相应的判定定理正确的是（ ）A ．AE=CE ；SASB ．DE=BE ；SASC ．∠D=∠B ；AASD ．∠A=∠C ；ASA14．如图，已知∠A=∠D ， AM=DN ，根据下列条件不能够判定△ABN ≅△DCN 的是（ ）A ．BM ∥CNB ．∠M=∠NC ．BM=CND ．AB=CD15．如图，AB＝AC，点D、E分别是AB、AC上一点，AD＝AE，BE、CD相交于点M．若∠BAC＝70°，∠C＝30°，则∠BMD的大小为( )A．50°B．65°C．70°D．80°二、填空题0,3，另16．如图，把等腰直角三角板放平面直角坐标系内，已知直角顶点C的坐标为()8,8，则点A的坐标为____________一个顶点B的坐标为()17．如图，D，E分别是AB，AC上的点，AD=AE，请添加一个条件，使得ABE≌ACD．这个条件可以为_____（只填一个条件即可）．18．已知点A、E、F、C在同一条直线l上，点B、D在直线l的异侧，若AB=CD，AE=CF，BF=DE，则AB与CD的位置关系是_______．≅，延长BC，分别交AD，ED于点F，G，若19．如图，ABC ADE∠=________︒．B∠=︒，10∠=︒，30EAB120CAD∠=︒，则CFD20．如图所示，在ABC 中，AB AC =，AD 是ABC 的角平分线，DE AB ⊥，DF AC ⊥，垂足分别是E ，F ．则下面结论中（1）DA 平分EDF ∠；（2）AE AF =，DE DF =；（3）AD 上的点到B ，C 两点的距离相等；（4）图中共有3对全等三角形．正确的有________ ．21．如图，四边形ABDC 中，对角线AD 平分BAC ∠，136ACD ∠=︒，44BCD ∠=︒，则ADB ∠的度数为_____22．如图，在ABC 中，点D 是BC 上的一点，已知30DAC ∠=︒，75DAB ∠=︒，CE 平分ACB ∠交AB 于点E ，连接DE ，则DEC ∠=________度．23．如图，点D ，E 分别在线段AB ，AC 上，CD 与BE 相交于点P ，已知AD ＝AE ．若△ABE ≌△ACD ，则可添加的条件为_____．24．如图，在四边形ABCD 中，90A ∠=︒，3AD =，连接BD ，BD CD ⊥，ADB C ∠=∠．若P 是BC 边上一动点，则DP 长的最小值为_______．25．如图，在ABC 中，AB CB =，90ABC ∠=︒，AD BD ⊥于点D ，CE BD ⊥于点E ，若7CE =，5AD =，则DE 的长是______．26．如图，ABC 中，90C ∠=，AD 平分BAC ∠，若2DC =，则点D 到线段AB 的距离等于________．三、解答题27．在正方形网格中，网格线的交点叫做格点，三个顶点均在格点上的三角形叫做格点三角形．（1）在图1中计算格点三角形ABC 的面积是__________；（每个小正方形的边长为1） （2）ABC 是格点三角形．①在图2中画出一个与ABC 全等且有一条公共边BC 的格点三角形；②在图3中画出一个与ABC 全等且有一个公共点A 的格点三角形．28．将Rt ABC △的直角顶点C 置于直线l 上，AC BC =，分别过点 A 、B 作直线l 的垂线，垂足分别为点D 、E ，连接AE ．若3BE =， 5DE =．求ACE △的面积．29．如图，,AD BF 相交于点,//,O AB DF AB DF =，点E 与点C 在BF 上，且BE CF =．（1）求证：ABC DFE ∆≅∆；（2）求证：点О为BF 的中点．30．已知矩形ABCD 中，点E 是AD 中点，连接CE ，经过点A ，B ，E 三点作O ，交BC 于点F ，过点F 作FH CE ⊥于H ．（1）求证：直线FH是O的切线；（2）若42AD H恰好为CE中点时，判断此时CE与O的位置关系？说明理由，并求出弧EF，线段EH，FH围成的图形的面积．。

苏科版八年级数学上册 三角形解答题单元综合测试（Word 版 含答案）一、八年级数学三角形解答题压轴题（难）1．如图1，直线MN 与直线AB 、CD 分别交于点E 、F ，1∠与2∠互补.(1)试判断直线AB 与直线CD 的位置关系，并说明理由.(2)如图2，BEF ∠与EFD ∠的角平分线交于点P ，EP 与CD 交于点G ，点H 是MN 上一点，且GH EG ⊥，求证：//PF GH .(3)如图3，在(2)的条件下，连接PH ，K 是GH 上一点使PHK HPK ∠=∠，作PQ 平分EPK ∠，求HPQ ∠的度数.【答案】(1)AB//CD ，理由见解析；(2)证明见解析；(3)45HPQ ∠=. 【解析】 【分析】（1）利用对顶角相等、等量代换可以推知同旁内角∠AEF 、∠CFE 互补，即可证明； （2）利用（1）中平行线的性质、角平分线的性质、三角形内角和定理可得∠EPF=90°，即EG ⊥PF ，再结合GH ⊥EG ，即可证明;（3）利用三角形外角定理、三角形内角和定理求得∠A=90°-∠3=90°-2∠2；然后由邻补角的定义、角平分线的定义推知∠QPK=-12∠EPK=45°+∠2，最后根据角与角间的和差关系即可求解. 【详解】 (1)//AB CD ， 理由如下：如图1，图1∵1∠与2∠互补， ∴12180∠+∠=︒，又∵1AEF ∠=∠，2CFE ∠=∠， ∴180AEF CFE ∠+∠=︒， ∴//AB CD ；(2)如图2，由(1)知，//AB CD ，图2∴180BEF EFD ∠+∠=︒．又∵BEF ∠与EFD ∠的角平分线交于点P ， ∴1(2)90FEP EFP BEF EFD ∠+∠=∠+∠=︒， ∴90EPF ∠=︒，即EG PF ⊥． ∵GH EG ⊥， ∴//PF GH ； (3)如图3，∵PHK HPK ∠=∠，2PKG HPK ∴∠=∠. 又∵GH EG ⊥，∴90902KPG PKG HPK ∠=-∠=-∠． ∴180902EPK KPG HPK ∠=-∠=+∠． ∵PQ 平分EPK ∠， ∴1452QPK EPK HPK ∠=∠=+∠． ∴45HPQ QPK HPK ∠=∠-∠=．【点睛】本题主要考查了平行线的判定与性质、角平分线的性质、三角形内角和定理等知识.解题过程关注中“数形结合”思想是解答本题的关键.2．（1）如图1．在△ABC 中，∠B =60°，∠DAC 和∠ACE 的角平分线交于点O ，则∠O = °，（2）如图2，若∠B =α，其他条件与（1）相同，请用含α的代数式表示∠O 的大小； （3）如图3，若∠B =α，11,PAC DAC PCA E n nAC ∠=∠∠=∠，则∠P = （用含α的代数式表示）．【答案】（1）∠O =60°；（2）90°－12α；（3）11(1)180P n nα∠=-⨯- 【解析】 【分析】（1）由题意利用角平分线的性质和三角形内角和为180°进行分析求解；（2）根据题意设∠BAC=β，∠ACB=γ，则α+β+γ=180°，利用角平分线性质和外角定义找等量关系，用含α的代数式表示∠O 的大小；（3）利用（2）的条件可知n=2时，∠P=111-18022α︒⨯-（），再将2替换成n 即可分析求解. 【详解】解：（1）因为∠DAC 和∠ACE 的角平分线交于点O ，且∠B=60°， 所以18060120OAC OCA οοο∠+∠=-=， 有∠O=180120οο-=60°.（2）设∠BAC=β，∠ACB=γ，则α+β+γ=180° ∵∠ACE 是△ABC 的外角， ∴∠ACE=∠B+∠BAC=α+β ∵CO 平分∠ACE11()22ACO ACE αβ∴∠=∠=+ 同理可得：1()2CAO αγ∠=+ ∵∠O+∠ACO+∠CAO=180°，∴11180180()()22O ACO CAO αβαγ︒︒∠=-∠-∠=-+-+ 1180()2αβαγ︒=-+++111180()1809090222αβααα︒︒︒︒=-++=--=-；（3）∵∠B=α，11,PAC DAC PCA E n nAC ∠=∠∠=∠， 由（2）可知n=2时，有∠P=1180902α︒︒--=111-18022α︒⨯-（），将2替换成n 即可， ∴11(1)180P n nα∠=-⨯-. 【点睛】本题考查用代数式表示角，熟练掌握并综合利用角平分线定义和三角形内角和为180°以及等量替换技巧与数形结合思维分析是解题的关键.3．如图①所示，在三角形纸片ABC 中，70C ∠=︒，65B ∠=︒，将纸片的一角折叠，使点A 落在ABC 内的点A '处. （1）若140∠=︒，2∠=________.（2）如图①，若各个角度不确定，试猜想1∠，2∠，A ∠之间的数量关系，直接写出结论.②当点A 落在四边形BCDE 外部时（如图②），（1）中的猜想是否仍然成立？若成立，请说明理由，若不成立，A ∠，1∠，2∠之间又存在什么关系？请说明．（3）应用：如图③：把一个三角形的三个角向内折叠之后，且三个顶点不重合，那么图中的123456∠+∠+∠+∠+∠+∠和是________. 【答案】(1)50°；(2)①见解析;②见解析;(3)360°. 【解析】 【分析】（1）根据题意，已知70C ∠=︒，65B ∠=︒，可结合三角形内角和定理和折叠变换的性质求解；（2）①先根据折叠得：∠ADE=∠A ′DE ，∠AED=∠A ′ED ，由两个平角∠AEB 和∠ADC 得：∠1+∠2等于360°与四个折叠角的差，化简得结果； ②利用两次外角定理得出结论；（3）由折叠可知∠1+∠2+∠3+∠4+∠5+∠6等于六边形的内角和减去（∠B'GF+∠B'FG）以及（∠C'DE+∠C'ED）和（∠A'HL+∠A'LH），再利用三角形的内角和定理即可求解． 【详解】解：（1）∵70C ∠=︒，65B ∠=︒， ∴∠A ′=∠A=180°-（65°+70°）=45°， ∴∠A ′ED+∠A ′DE =180°-∠A ′=135°，∴∠2=360°-（∠C+∠B+∠1+∠A ′ED+∠A ′DE ）=360°-310°=50°； （2）①122A ∠+∠=∠,理由如下由折叠得：∠ADE=∠A ′DE ，∠AED=∠A ′ED ， ∵∠AEB+∠ADC=360°，∴∠1+∠2=360°-∠ADE-∠A ′DE-∠AED-∠A ′ED=360°-2∠ADE-2∠AED ， ∴∠1+∠2=2（180°-∠ADE-∠AED ）=2∠A ； ②221A ∠=∠+∠，理由如下：∵2∠是ADF 的一个外角 ∴2A AFD ∠=∠+∠. ∵AFD ∠是A EF '△的一个外角 ∴1AFD A '∠=∠+∠ 又∵A A '∠=∠ ∴221A ∠=∠+∠ （3）如图由题意知，∠1+∠2+∠3+∠4+∠5+∠6=720°-（∠B'GF+∠B'FG）-（∠C'DE+∠C'ED）-（∠A'HL+∠A'LH）=720°-（180°-∠B'）-（180°-C'）-（180°-A'）=180°+（∠B'+∠C'+∠A'）又∵∠B=∠B'，∠C=∠C'，∠A=∠A'， ∠A+∠B+∠C=180°，∴∠1+∠2+∠3+∠4+∠5+∠6=360°． 【点睛】题主要考查了折叠变换、三角形、四边形内角和定理．注意折叠前后图形全等；三角形内角和为180°；四边形内角和等于360度．4．探究：（1）如图1，在△ABC中，BP平分∠ABC，CP平分∠ACB．求证：∠P＝90°+12∠A．（2）如图2，在△ABC中，BP平分∠ABC，CP平分外角∠ACE．猜想∠P和∠A有何数量关系，并证明你的结论．（3）如图3，BP平分∠CBF，CP平分∠BCE．猜想∠P和∠A有何数量关系，请直接写出结论．【答案】（1）见解析；（2）12∠A＝∠P，理由见解析；（3）∠P＝90°﹣12∠A，理由见解析【解析】【分析】（1）根据三角形内角和定理以及角平分线的性质进行解答即可：（2）根据角平分线的定义以及一个三角形的外角等于与它不相邻的两个内角和，可求出∠A的度数，根据补角的定义求出∠ACB的度数，根据三角形的内角和即可求出∠P的度数，即可求出结果，（3）根据三角形的外角性质、内角和定理、角平分线的定义探求并证明.【详解】证明：（1）∵△ABC中，∠ABC+∠ACB＝180°﹣∠A．又∵BP平分∠ABC，CP平分∠ACB，∴∠PBC＝12∠ABC，∠PCB＝12∠ACB，∴∠PBC+∠PCB＝12（180°﹣∠A），根据三角形内角和定理可知∠BPC＝180°﹣12（180°﹣∠A）＝90°+12∠A；（2）12∠A＝∠P，理由如下：∵BP是△ABC中∠ABC的平分线，CP是∠ACB的外角的平分线，∴∠PBC＝12∠ABC，∠PCE＝12∠ACE．∵∠ACE是△ABC的外角，∠PCE是△BPC的外角，∴∠ACE＝∠ABC+∠A，∠PCE＝∠PBC+∠P，∴12∠ACP＝12∠ABC+12∠A，∴12∠ABC+12∠A＝∠PBC+∠P，∴12∠A＝∠P．（3）∠P＝90°﹣12∠A，理由如下：∵P点是外角∠CBF和∠BCE的平分线的交点，∠P+∠PBC+∠PCB＝180°∴∠P＝180°﹣（∠PBC+∠PCB）＝180°﹣12（∠FBC+∠ECB）＝180°﹣12（∠A+∠ACB+∠A+∠ABC）＝180°﹣12（∠A+180°）＝90°﹣12∠A．【点睛】本题考查了角平分线的定义，一个三角形的外角等于与它不相邻的两个内角和以及补角的定义以及三角形的内角和为180°，此类题解题的关键是找出角平分线平分的两个角的和的度数，从而利用三角形内角和定理求解.5．如图1，线段AB、CD相交于点O，连结AD、CB，我们把这个图形称为“8字型”根据三角形内角和容易得到：∠A+∠D=∠C+∠B.(1)用“8字型”如图2,∠A+∠B+∠C+∠D+∠E+∠F=___________；(2)造“8字型”如图3,∠A+∠B+∠C+∠D+∠E+∠F+∠G=_____________;(3)发现“8字型”如图4，BE、CD相交于点A，CF为∠BCD的平分线，EF为∠BED的平分线.①图中共有________个“8字型”；②若∠B：∠D：∠F=4：6：x，求x的值.【答案】(1)360°；(2)540；(3)①6；②x=5.【解析】分析：（1）根据题意即可得到结论；（3）①由图形即可得到结论；②根据三角形内角和为180°的性质即可证得关系为∠D+∠B=2∠F，再根据∠B、∠D、∠F的比值，即可求得x的值；详解：（1）∵∠A+∠B=∠GKH+∠GHK，∠C+∠D=∠GHK+∠HGK，∠E+∠F=∠HGK+∠GKH，∠A+∠B+∠C+∠D+∠E+∠F=2（∠GKH+∠GHK+∠HGK）=2×180°=360°，故答案为：360°；（2）如图，连结BC，∵∠E+∠G=∠GCB+∠EBC，∴∠A+∠B+∠C+∠D+∠E+∠F+∠G=五边形FABCD的内角和，即∠A+∠B+∠C+∠D+∠E+∠F+∠G=（5-2）•180°=540°，故答案为：540°；（3）①图中共有6个“8字型”；故答案为：6．②：∵CF平分∠BCD，EF平分∠BED∴∠DEG=∠AEG，∠ACH=∠BCH，∵在△DGE和△FGC中，∠DGE=∠FGC∴∠D+∠DEG=∠F+∠ACH∵在△BHC和△FHE中，∠BHC=∠FHE∴∠B+∠BCH=∠F+∠AEG∴∠D+∠DEG+∠B+∠BCH=∠F+∠ACH+∠F+∠AEG∴∠D+∠B=2∠F；∵∠B：∠D：∠F=4：6：x，∠D+∠B=2∠F，∴x=5．点睛：考查了多边形的内角与外角，三角形的内角和，三角形的外角的性质，正确的识别图形是解题的关键．6．(1)如图①，你知道∠BOC＝∠B＋∠C＋∠A的奥秘吗？请用你学过的知识予以证明；(2)如图②，设x＝∠A＋∠B＋∠C＋∠D＋∠E，运用(1)中的结论填空．x＝____________°；x＝____________°；x＝____________°；(3)如图③，一个六角星，其中∠BOD＝70°，则∠A＋∠B＋∠C＋∠D＋∠E＋∠F＝________°.【答案】（1）证明见解析. (2)180；180；180；(3)140【解析】【分析】（1）首先延长BO交AC于点D，可得BOC=∠BDC+∠C，然后根据∠BDC=∠A+∠B，判断出∠BOC=∠B+∠C+∠A即可．（2）a、首先根据外角的性质，可得∠1=∠A+∠B，∠2=∠C+∠D，然后根据∠1+∠2+∠E=180°，可得x=∠A+∠B+∠C+∠D+∠E=180，据此解答即可．b、首先根据外角的性质，可得∠1=∠A+∠B，∠2=∠C+∠D，然后根据∠1+∠2+∠E=180°，可得x=∠A+∠B+∠C+∠D+∠E=180，据此解答即可．c、首先延长EA交CD于点F，EA和BC交于点G，然后根据外角的性质，可得∠GFC=∠D+∠E，∠FGC=∠A+∠B，再根据∠GFC+∠FGC+∠C=180°，可得x=∠A+∠B+∠C+∠D+∠E=180°，据此解答即可．（3）根据∠BOD=70°，可得∠A+∠C+∠E=70°，∠B+∠D+∠F=70°，据此求出∠A+∠B+∠C+∠D+∠E+∠F的度数是多少即可．【详解】(1)证明：如图，延长BO交AC于点D，则∠BOC＝∠BDC＋∠C，又∵∠BDC＝∠A＋∠B，∴∠BOC＝∠B＋∠C＋∠A.(2)180；180；180(3)140【点睛】（1）此题主要考查了三角形的内角和定理，要熟练掌握，解答此题的关键是要明确：三角形的内角和是180°．（2）此题还考查了三角形的外角的性质和应用，要熟练掌握，解答此题的关键是要明确：①三角形的外角和为360°．②三角形的一个外角等于和它不相邻的两个内角的和．③三角形的一个外角大于和它不相邻的任何一个内角．7．如图①，在△ABC中，AE平分∠BAC，∠C＞∠B，F是AE上一点，且FD⊥BC于D点．(1)试猜想∠EFD，∠B，∠C的关系，并说明理由；(2)如图②，当点F在AE的延长线上时，其余条件不变，(1)中的结论还成立吗？说明理由．①②【答案】(1)∠EFD＝12∠C－12∠B.（）成立，理由见解析.【解析】【分析】先根据AE平分∠BAC推出∠BAE=12∠BAC=12[180°-（∠B+∠C）]，再根据外角的定义求出∠FED=∠B+∠BAE，然后利用直角三角形的性质求出∠EFD=90°-∠FED．【详解】解：(1)∠EFD＝12∠C－12∠B.理由如下：由AE是∠BAC的平分线知∠BAE＝12∠BAC.由三角形外角的性质知∠FED＝∠B＋12∠BAC，故∠B ＋12∠BAC ＋∠EFD ＝90°①. 在△ABC 中，由三角形内角和定理得∠B ＋∠BAC ＋∠C ＝180°， 即12∠C ＋12∠B ＋12∠BAC ＝90°②. ②－①，得∠EFD ＝12∠C －12∠B . (2)成立． 理由如下：由对顶角相等和三角形的外角性质知：∠FED ＝∠AEC ＝∠B ＋12∠BAC ， 故∠B ＋12∠BAC ＋∠EFD ＝90°①. 在△ABC 中，由三角形内角和定理得： ∠B ＋∠BAC ＋∠C ＝180°，即12∠B ＋12∠BAC ＋12∠C ＝90°②.②－①，得∠EFD ＝12∠C －12∠B . 【点睛】 此题主要考查了角平分线的性质、三角形内角和定理和直角三角形的性质，命题时经常将多个知识点联系在一起进行考查，这样更能训练学生的解题能力．8．如图，在△ABC 中，AD ⊥BC ，AE 平分∠BAC ．(1)若∠B ＝72°，∠C ＝30°，①求∠BAE 的度数；②求∠DAE 的度数；(2)探究：如果只知道∠B ＝∠C ＋42°，也能求出∠DAE 的度数吗？若能，请你写出求解过程；若不能，请说明理由．【答案】（1）①39°；②21°；（2）21°.【解析】【分析】()1①先根据三角形内角和定理计算出BAC 78∠=，然后根据角平分线定义得到1BAE BAC 392∠∠==；②根据垂直定义得到ADB 90∠=，则利用互余可计算出BAD 90B 18∠∠=-=，然后利用DAE BAE BAD ∠∠∠=-进行计算即可； ()2由B C BAC 180∠∠∠++=，B C 42∠∠=+可消去C ∠得到BAC 2222B ∠∠=-，则根据角平分线定义得到BAE 111B ∠∠=-，接着在ABD 中利用互余得BAD 90B ∠∠=-，然后利用DAE BAE BAD ∠∠∠=-进行计算即可得到DAE 21∠=．【详解】解：()1B C BAC 180∠∠∠++=①，BAC 180723078∠∴=--=， AE 平分BAC ∠，1BAE BAC 392∠∠∴==； AD BC ⊥②，ADB 90∠∴=，BAD 90B 18∠∠∴=-=，DAE BAE BAD 391821∠∠∠∴=-=-=；()2能．B C BAC 180∠∠∠++=，B C 42∠∠=+，C B 42∠∠∴=-，2B BAC 222∠∠∴+=，BAC 2222B ∠∠∴=-， AE 平分BAC ∠，BAE 111B ∠∠∴=-，在ABD 中，BAD 90B ∠∠=-，()()DAE BAE BAD 111B 90B 21∠∠∠∠∠∴=-=---=．【点睛】本题考查三角形内角和定理：三角形内角和是180.掌握角平分线和高的定义，熟练进行角度的运算．9．动手操作，探究：探究一：三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系．已知：如图（1），在△ADC 中，DP 、CP 分别平分∠ADC 和∠ACD ，试探究∠P 与∠A 的数量关系．并说明理由．探究二：若将△ADC 改为任意四边形ABCD 呢？已知：如图（2），在四边形ABCD 中，DP 、CP 分别平分∠ADC 和∠BCD ，请你利用上述结论探究∠P 与∠A +∠B 的数量关系，并说明理由．探究三：若将上题中的四边形ABCD 改为六边形ABCDEF 如图（3）所示，请你直接写出∠P 与∠A +∠B +∠E +∠F 的数量关系．【答案】探究一： 90°+12∠A；探究二：12（∠A+∠B）；探究三：∠P=12（∠A+∠B+∠E+∠F）﹣180°．【解析】试题分析：探究一：根据角平分线的定义可得∠PDC=12∠ADC，∠PCD=12∠ACD，然后根据三角形内角和定理列式整理即可得解.探究二：根据四边形的内角和定理表示出∠ADC+∠BCD，然后同理探究一解答即可.探究三：根据六边形的内角和公式表示出∠EDC+∠BCD，然后同理探究一解答即可.试题解析：探究一：∵DP、CP分别平分∠AD C和∠ACD，∴∠PDC=12∠ADC，∠PCD=12∠ACD，∴∠DPC=180°-∠PDC-∠PCD，=180°-12∠ADC-12∠ACD，= 180°-12（∠ADC+∠ACD），=180°-12（180°-∠A），=90°+12∠A；探究二：∵DP、CP分别平分∠ADC和∠BCD，∴∠PDC=12∠ADC，∠PCD=12∠BCD，∴∠DPC=180°-∠PDC-∠PCD，=180°-12∠ADC-12∠BCD，=180°-12（∠ADC+∠BCD），=180°-12（360°-∠A -∠B ）， =12（∠A +∠B ）； 探究三：六边形ABCDEF 的内角和为：（6-2）×180°=720°，∵DP 、CP 分别平分∠EDC 和∠BCD ，∴∠PDC =12 ∠EDC ，∠PCD =12∠BCD ， ∴∠P =180°-∠PDC -∠PCD ， =180°-12∠EDC -12∠BCD ， =180°-12（∠EDC +∠BCD ）， =180°-12（720°-∠A -∠B -∠E -∠F ）， =12（∠A +∠B +∠E +∠F ）-180°， 即∠P =12（∠A +∠B +∠E +∠F ）-180°． 点睛：本题考查了三角形的外角性质，三角形的内角和定理，多边形的内角和公式，在此类题目中根据同一个解答思路求解是解题的关键.10．已知：如图，等边三角形ABD 与等边三角形ACE 具有公共顶点A ，连接CD ，BE ，交于点P .（1）观察度量，BPC ∠的度数为＿＿＿＿.（直接写出结果）（2）若绕点A 将△ACE 旋转，使得180BAC ∠=︒，请你画出变化后的图形.（示意图）（3）在（2）的条件下，求出BPC ∠的度数.【答案】（1）120°;（2）作图见解析；（3）∠BPC =120°．【解析】分析：（1）∠BPC 的度数为120°，理由为：由△ABD 与△ACE 都是等边三角形，利用等边三角形的性质得到∠DAB=∠ABD=∠CAE=60°，AD=AB ，AC=AE ，利用等式的性质得到夹角相等，利用SAS 得出三角形DAC 与三角形BAE 全等，由全等三角形的对应角相等得到∠ADC=∠ABE ，利用外角性质，等量代换即可得到所求；（2）作出相应的图形，如图所示；（3）解法同（1），求出∠BPC的度数即可．本题解析：（1）∠BPC的度数为120°，理由为：证明：∵△ABD与△ACE都是等边三角形，∴∠DAB=∠ABD=∠CAE=60°，AD=AB，AC=AE，∴∠DAB+∠BAC=∠CAE+∠BAC，即∠DAC=∠BAE，在△DAC与△BAE中，{AD ABDAC BAE AC AE=∠=∠=，∴△DAC≌△BAE（SAS），∴∠ADC=∠ABE，∵∠ADC+∠CDB=60°，∴∠ABE+∠CDB=60°，∴∠BPC=∠DBP+∠PDB=∠ABE+∠CDB+∠ABC=120°；（2）作出相应的图形，如图所示；（3）∵△ABD与△ACE都是等边三角形，∴∠ADB=∠BAD=∠ABD=∠CAE=60°，AD=AB，AC=AE，∴∠DAB+∠DAE=∠CAE+∠DAE，即∠DAC=∠BAE，在△DAC与△BAE中，{AD ABDAC BAC AC AE=∠=∠=，∴△DAC≌△BAE（SAS），∴∠ADC=∠ABE，∵∠ABE+∠DBP=60°，∴∠ADC+∠DBP=60°，∴∠BPC=∠BDP+∠PBD=∠ADC+∠DBP+∠ADB=120°．点睛：本题考查了等边三角形的性质，外角性质，以及全等三角形的判定与性质，熟练掌握等边三角形的性质是解本题的关键.。

苏州新区二中数学轴对称填空选择单元综合测试（Word版含答案）一、八年级数学全等三角形填空题（难）1．如图，四边形ABCD中，AB＝AD，AC＝5，∠DAB＝∠DCB＝90°，则四边形ABCD的面积为_____．【答案】12.5【解析】【分析】过A作AE⊥AC，交CB的延长线于E，判定△ACD≌△AEB，即可得到△ACE是等腰直角三角形，四边形ABCD的面积与△ACE的面积相等，根据S△ACE=12×5×5=12.5，即可得出结论．【详解】如图，过A作AE⊥AC，交CB的延长线于E，∵∠DAB=∠DCB=90°，∴∠D+∠ABC=180°=∠ABE+∠ABC，∴∠D=∠ABE，又∵∠DAB=∠CAE=90°，∴∠CAD=∠EAB，又∵AD=AB，∴△ACD≌△AEB（ASA），∴AC=AE，即△ACE是等腰直角三角形，∴四边形ABCD的面积与△ACE的面积相等，∵S△ACE=12×5×5=12.5，∴四边形ABCD的面积为12.5，故答案为12.5．【点睛】本题主要考查了全等三角形的判定与性质，解题的关键是学会添加常用辅助线，构造全等三角形解决问题2．如图，已知△ABC为等边三角形，点D，E分别在边BC，AC上，且BD＝CE，若BE交AD于点F，则∠AFE的大小为_____（度）．【答案】60【解析】【分析】根据△ABC为等边三角形得到AB＝BC，∠ABD＝∠BCE＝60°，再利用BD＝CE证得△ABD≌△BCE，得到∠BAD＝∠CBE，再利用内角和外角的关系即可得到∠AFE＝60°.【详解】∵△ABC为等边三角形，点D，E分别在边BC，AC上，且BD＝CE，∴AB＝BC，∠ABD＝∠BCE＝60°，在△ABD和△BCE中，AB BCABD BCEBD CE=⎧⎪∠∠⎨⎪=⎩＝,∴△ABD≌△BCE（SAS），∴∠BAD＝∠CBE，∵∠ABF+∠CBE＝∠ABC＝60°，∴∠ABF+∠BAD＝60°，∵∠AFE＝∠ABF+∠BAD，∴∠AFE＝60°，故答案为：60．【点睛】此题考查三角形全等的判定定理及性质定理，题中证明三角形全等后得到∠BAD＝∠CBE，再利用外角和内角的关系求∠AFE是解题的关键.3．在△ABC中，∠ABC＝60°，∠ACB＝70°，若点O到三边的距离相等，则∠BOC＝_____°．【答案】115或65或22.5【解析】【分析】先画出符合的图形，再根据角平分线的性质和三角形的内角和定理逐个求出即可．【详解】解：①如图，∵点O到三边的距离相等，∴点O是△ABC的三角的平分线的交点，∵∠ABC＝60°，∠ACB＝70°，∴∠OBC＝12∠ABC＝30°，1OCB2∠=∠ACB＝35°，∴∠BOC＝180°﹣∠OBC﹣∠OCB＝115°；②如图，∵∠ABC＝60°，∠ACB＝70°，∴∠EBC＝180°﹣∠ABC＝120°，∠FCB＝180°﹣∠ACB＝110°，∵点O到三边的距离相等，∴O是∠EBC和∠FCB的角平分线的交点，∴∠OBC＝12∠EBC＝60°，1OCB2∠=∠FCB＝55°，∴∠BOC＝180°﹣∠OBC﹣∠OCB＝65°；③如图，∵∠ABC＝60°，∠ACB＝75°，∴∠A＝180°﹣∠ABC﹣∠ACB＝45°，∵点O到三边的距离相等，∴O是∠EBA和∠ACB的角平分线的交点，∴∠OBA＝12∠EBA＝12×（180°﹣60°）＝60°，1OCB2∠=∠ACB＝37.5°，∴∠BOC＝180°﹣（∠OBA+∠ABC+∠OCB）＝180°﹣（60°﹣60°﹣37.5°）＝22.5°；如图，此时∠BOC＝22.5°，故答案为：115或65或22.5．【点睛】此题主要考查三角形的内角和，解题的关键是根据题意分情况讨论.4．如图：已知△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC边上的中点，两边PE，PF分别交AB，AC于点E，F，给出以下四个结论：①AE=CF；②EF=AP；③2S四边形AEPF=S△ABC；④当∠EPF在△ABC内绕顶点P旋转时（点E不与A，B重合）有BE+CF=EF；上述结论中始终正确的序号有__________．【答案】①③【解析】【分析】根据题意，容易证明△AEP≌△CFP，然后能推理得到①③都是正确．【详解】∵AB=AC，∠BAC=90°，点P是BC的中点，∴∠EAP=12∠BAC=45°，AP=12BC=CP．①在△AEP与△CFP中，∵∠EAP=∠C=45°，AP=CP，∠APE=∠CPF=90°-∠APF，∴△AEP≌△CFP，∴AE=CF．正确；②只有当F在AC中点时EF=AP，故不能得出EF=AP，错误；③∵△AEP≌△CFP，同理可证△APF≌△BPE．∴S四边形AEPF=S△AEP+S△APF=S△CPF+S△BPE=12S△ABC，即2S四边形AEPF=S△ABC；正确；④根据等腰直角三角形的性质，2PE，所以，EF随着点E的变化而变化，只有当点E为AB的中点时，2PE=AP，在其它位置时EF≠AP，故④错误；故答案为：①③．【点睛】本题考查了全等三角形的判定与性质，等腰直角三角形的判定与性质，证得△AEP和△CFP 全等是解题的关键，也是本题的突破点．5．已知：四边形ABCD中，AB=AD=CD，∠BAD=90°，三角形ABC的面积为1，则线段AC 的长度是___________.【答案】2【解析】【分析】过B作BE⊥AC于E, 过D作DF⊥AC于F,构造得出BE=AF利用等腰三角形三线合一的性质得出：AF=可得BE=AF=，利用三角形ABC的面积为1进行计算即可.【详解】过B作BE⊥AC于E, 过D作DF⊥AC于F,∴∠BEA=∠AFD=90°∴∠2+∠3=90°∵∠BAD=90°∴∠1+∠2=90°∴∠1=∠3∵AB=AD∴∴BE=AF∵AD=CD，DF⊥AC∴AF=∴BE=AF=∴∴AC=2故答案为：2【点睛】本题考查了利用一线三等角构造全等三角形，以及利用三角形面积公式列方程求线段，熟练掌握辅助线做法构造全等是解题的关键.6．如图，Rt△ABC中，AB＝AC，点D为BC中点．∠MDN＝90°，∠MDN绕点D旋转，DM、DN分别与边AB、AC交于E、F两点．下列结论：①△DEF是等腰直角三角形；②AE＝CF；③△BDE≌△ADF；④BE+CF＝EF；⑤S四边形AEDF＝14AD2，其中正确结论是_____（填序号）【答案】①②③【解析】【分析】先由ASA证明△AED≌△CFD，得出AE＝CF，DE＝FD；再由全等三角形的性质得到BE+CF＝AB，由勾股定理求得EF与AB的值，通过比较它们的大小来判定④的正误；先得出S四边形AEDF＝S△ADC＝12AD2，从而判定⑤的正误．【详解】解：∵Rt△ABC中，AB＝AC，点D为BC中点，∴∠C＝∠BAD＝45°，AD＝BD＝CD，∵∠MDN＝90°，∴∠ADE+∠ADF＝∠ADF+∠CDF＝90°，∴∠ADE＝∠CDF．在△AED与△CFD中，EADC AD CDADE CDF ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△AED ≌△CFD （ASA ），∴AE ＝CF ，ED ＝FD ．故①②正确；又∵△ABD ≌△ACD ，∴△BDE ≌△ADF ．故③正确；∵△AED ≌△CFD ，∴AE ＝CF ，ED ＝FD ，∴BE +CF ＝BE +AE ＝AB ＝2BD ，∵EF ＝2ED ，BD ＞ED ，∴BE +CF ＞EF ．故④错误；∵△AED ≌△CFD ，△BDE ≌△ADF ，∴S 四边形AEDF ＝S △ADC ＝12AD 2．故⑤错误． 综上所述，正确结论是①②③．故答案是：①②③．【点睛】 考查了全等三角形的判定与性质，等腰直角三角形的性质，勾股定理，图形的面积等知识，综合性较强，有一定难度．7．如图,在等腰直角三角形ABC 中,∠C=90 o ，AC=BC=4，点D 是AB 的中点，E ， F 在射线AC 与射线CB 上运动，且满足AE=CF ，∠EDF=90°；当点E 运动到与点C 的距离为1时，则△DEF 的面积为___________.【答案】52或132【解析】 解：①E 在线段AC 上．在△ADE 和△CDF 中，∵AD =CD ，∠A =∠DCF ，AE =CF ，∴△ADE ≌△CDF （SAS ），∴同理△CDE ≌△BDF ，∴四边形CEDF 面积是△ABC 面积的一半．∵CE =1，∴CF =4﹣1=3，∴△CEF 的面积=12CE •CF =32，∴△DEF 的面积=12×2×2﹣32=52． ②E '在AC 延长线上．∵AE '=CF '，AC =BC =4，∠ACB =90°，∴CE '=BF '，∠ACD =∠CBD =45°，CD =AD =BD =22∴∠DCE '=∠DBF '=135°．在△CDE '和△BDF '中，∵CD =BD ，∠DCE ′=DBF ′，CE ′=BF ′，∴△CDE '≌△BDF '（SAS ），∴DE '=DF '，∠CDE '=∠BDF '．∵∠CDE '+∠BDE '=90°，∴∠BDE '+∠BDF '=90°，即∠E 'DF '=90°．∵DE '2=CE '2+CD 2﹣2CD •CE 'cos135°=1+8+2×22×22=13，∴S △E 'DF '=12DE '2=132．故答案为132或52．点睛：本题考查了全等三角形的判定，考查了全等三角形对应边相等的性质，本题中求证△ADE ≌△CDF 和△CDE ≌△BCF 是解题的关键．8．如图，AB ＝BC 且AB ⊥BC ，点P 为线段BC 上一点，PA ⊥PD 且PA ＝PD ，若∠A ＝22°，则∠D 的度数为_________．【答案】23°【解析】解：过D 作DE ⊥PC 于E ．∵PA ⊥PD ，∴∠APB +∠DPE =90°．∵AB ⊥BC ，∴∠A +∠APB =90°，∴∠A =∠DPE =22°．在△ABP 和△PED 中，∵∠A =∠DPE ，∠B =∠E =90°，PA ＝PD ，∴△ABP ≌△PED ，∴AB =PE ，BP =DE ．∵AB =BC ，∴BC =PE ，∴BP =CE ．∵BP =DE ，∴CE =DE ，∴∠DCE =45°，∴∠PDC =∠DCE －∠DPC =45°－22°=23°．故答案为：23°．9．把两个三角板如图甲放置，其中90ACB DEC ∠=∠=︒，45A ∠=︒，30D ∠=︒，斜边12AB =，14CD =，把三角板DCE 绕着点C 顺时针旋转15︒得到△11D CE （如图乙），此时AB 与1CD 交于点O ，则线段1AD 的长度为_________．【答案】10【解析】试题分析：如图所示，∠3=15°，∠1E =90°， ∴∠1=∠2=75°， 又∵∠B=45°，∴∠OF 1E =∠B+∠1=45°+75°=120° ∴∠1D FO=60° ∵∠C 11D E =30°，∴∠5=∠4=90°， 又∵AC=BC ，AB=12， ∴OA=OB=6 ∵∠ACB=90°，∴CO=12AB=6， 又∵C 1D =CD=14， ∴O 1D =C 1D -OC=14-6=8， 在Rt △A 1D O 中，222211A 6810D OA OD =+=+=点睛：本题主要考查的就是旋转的性质、三角形的外角性质、直角三角形的性质及判定以及勾股定理的应用.解决这个问题的关键就是首先根据三角形外角的性质以及旋转图形的性质得出△AO 1D 为直角三角形，然后根据直角三角形的性质得出AO 和O 1D 的长度，最后根据直角三角形的勾股定理得出答案.10．如图，在△ABC 中，∠B ＝∠C ，BD ＝CE ，BE ＝CF .若∠A ＝40°，则∠DEF 的度数为____．【答案】70°【解析】由等腰三角形的性质得出∠B=∠C=70°，再根据SAS证得△BDE≌△CEF，得出∠BDE=∠CEF，运用三角形的外角性质得出∠CEF+∠DEF=∠B+∠BDE，即可得出∠DEF=∠B=70°.点睛：此题主要考查了等腰三角形的性质，解题时，利用等腰三角形的性质和三角形全等的判定证得∠BDE=∠CEF，然后根据三角形外角的性质可求解.二、八年级数学全等三角形选择题（难）11．如图，△ABC的两条外角平分线AP、CP相交于点P，PH⊥AC于H；如果∠ABC=60º，则下列结论：①∠ABP=30º；②∠APC=60º；③PB=2PH；④∠APH=∠BPC；其中正确的结论个数是（）A．1 B．2 C．3 D．4【答案】B【解析】【分析】作PM⊥BC于M，PN⊥BA于N．根据角平分线的性质定理可证得PN=PM，再根据角平分线的判定定理可得PB平分∠ABC，即可判定①；证明△PAN≌△PAH，△PCM≌△PCH，根据全等三角形的性质可得∠APN=∠APH，∠CPM=∠CPH，由此即可判定②；在Rt△PBN 中，∠PBN=30°，根据30°角直角三角形的性质即可判定③；由∠BPN=∠CPA=60°即可判定④.【详解】如图，作PM⊥BC于M，PN⊥BA于N．∵∠PAH=∠PAN，PN⊥AD，PH⊥AC，∴PN=PH ，同理PM=PH ，∴PN=PM ，∴PB 平分∠ABC ，∴∠ABP=12∠ABC=30°，故①正确， ∵在Rt △PAH 和Rt △PAN 中， PA PA PN PH =⎧⎨=⎩， ∴△PAN ≌△PAH ，同理可证，△PCM ≌△PCH ，∴∠APN=∠APH ，∠CPM=∠CPH ，∵∠MPN=180°-∠ABC=120°，∴∠APC=12∠MPN=60°，故②正确， 在Rt △PBN 中，∵∠PBN=30°， ∴PB=2PN=2PH ，故③正确，∵∠BPN=∠CPA=60°，∴∠CPB=∠APN=∠APH ，故④正确．综上，正确的结论为①②③④.故选D.【点睛】本题考查了角平分线的性质定理及判定定理、全等三角形的判定与性质及30°角直角三角形的性质，熟练运用相关知识是解决问题的关键.12．如图,在△ABC 中,∠C=90°,∠B=30°,以A 为圆心,任意长为半径画弧分别交AB,AC 于点M 和N,再分别以M,N 为圆心,大于12MN 的长为半径画弧,两弧交于点P,连结AP 并延长交BC 于点D,则下列说法中正确的个数是( )①AD 平分∠B AC ；②作图依据是S.A ．S ；③∠ADC=60°； ④点D 在AB 的垂直平分线上A ．1个B ．2个C ．3个D ．4个【答案】C【解析】 ①根据作图的过程可以判定AD 是∠BAC 的∠平分线；②根据作图的过程可以判定出AD 的依据；③利用角平分线的定义可以推知∠CAD=30°，则由直角三角形的性质求∠ADC 的度数； ④利用等角对等边可以证得△ADB 的等腰三角形，由等腰三角形的“三合一”的性质可以证明点在AB的中垂线上.解：如图所示，①根据作图的过程可知，AD是∠BAC的∠平分线；故①正确；②根据作图的过程可知，作出AD的依据是SSS；故②错误；③∵在△ABC中，∠C=90°，∠B=30°，∴∠CBA=60°.又∵AD是∠BAC的平分线，∴∠1=∠2=12∠CAB=30°，∴∠3=90°-∠2=60°，即∠ADC=60°.故③正确；④∵∠1=∠B=30°，∴AD=BD，∴点D在AB的中垂线上.故④正确；故选C.“点睛”此题主要考查的是作图-基本作图，涉及到角平分线的作法以及垂直平分线的性质，熟练根据角平分线的性质得出∠A DC的度数是解题的关键.13．如图，在△ABC和△DCB中，AB=DC，AC与BD相交于点E，若不再添加任何字母与辅助线，要使△ABC≌△DCB，则还需增加的一个条件是（）A．AC=BD B．AC=BC C．BE=CE D．AE=DE【答案】A【解析】由AB=DC，BC是公共边，即可得要证△ABC≌△DCB，可利用SSS，即再增加AC=DB即可.故选A.点睛：此题主要考查了全等三角形的判定，解题时利用全等三角形的判定：SSS ，SAS ，ASA ，AAS ，HL ，确定条件即可，此题为开放题，只要答案符合判定定理即可. 14．如图，已知等腰Rt △ABC 和等腰Rt △ADE ，AB=AC=4，∠BAC=∠EAD=90°，D 是射线BC 上任意一点，连接EC ．下列结论：①△AEC △ADB ；② EC ⊥BC ； ③以A 、C 、D 、E 为顶点的四边形面积为8；④当BD=时，四边形AECB 的周长为10524++;⑤ 当BD=32B 时,ED=5AB ；其中正确的有（ ）A ．5个B ．4个C ．3 个D ．2个【答案】B【解析】解：∵∠BAC =∠EAD =90°，∴∠BAD =∠CAE ，∵AB =AC ，AD =AE ，∴△AEC ≌△ADB ，故①正确； ∵△AEC ≌△ADB ，∴∠ACE =∠ABD =45°，∵∠ACB =45°，∴J IAO ECB =90°，∴EC ⊥BC ，故②正确；∵四边形ADCE 的面积=△ADC 的面积+△ACE 的面积=△ADC 的面积+△ABD 的面积=△ABC 的面积=4×4÷2=8．故③正确；∵BD =2，∴EC =2，DC =BC -BD =422-=32，∴DE 2=DC 2+EC 2，=()()22322+=20，∴DE =25，∴AD =AE =252=10.∴AECB 的周长=AB +DC +CE +AE =442210+++=45210++，故④正确；当BD =32BC 时，CD =12BC ，∴DE =221322BC BC ⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭=10BC =5AB ．故⑤错误． 故选B ．点睛：此题是全等三角形的判定与性质的综合运用，熟练掌握等腰直角三角形的性质是解答此题的关键．15．在△ABC 中，∠C=90°，D 为AB 的中点，ED ⊥AB,∠DAE=∠CAE ，则 ∠CAB ＝（ ）A ．30°B ．60°C ．80 °D ．50°【答案】B【解析】试题解析：∵D 为AB 的中点，ED ⊥AB ，∴DE 为线段AB 的垂直平分线， ∴AE =BE ，∴∠DAE =∠DBE ，∴∠DAE =∠DBE =∠CAE ，在Rt △ABC 中，∵∠CAB +∠DBE =90°，∴∠CAE +∠DAE +∠DBE =90°，∴3∠DBE =90°，∴∠DBE =30°，∴∠CAB =90°-∠DBE =90°-30°=60°．故选B ．16．如图所示，在Rt ABC ∆中，E 为斜边AB 的中点，ED AB ⊥，且:1:7CAD BAD ∠∠=，则BAC ∠=( )A ．70B ．45C ．60D ．48【答案】D【解析】 根据线段的垂直平分线，可知∠B=∠BAD ，然后根据直角三角形的两锐角互余，可得∠BAC+∠B=90°，设∠CAD=x ，则∠BAD=7x ，则x+7x+7x=90°，解得x=6°，因此可知∠BAC=∠CDA+∠BAD=6°+42°=48°. 故选：D.点睛：此题主要考查了线段垂直平分线的性质，利用线段垂直平分线的性质和直角三角形的性质求角的关系，根据比例关系设出未知数，然后根据角的关系列方程求解是解题关键.17．如图，点P 、Q 分别是边长为6cm 的等边ABC △边AB 、BC 上的动点，点P 从顶点 A ，点Q 从顶点B 同时出发，且它们的速度都为1cm/s ，下面四个结论：①BQ AM =②ABQ △≌CAP △③CMQ ∠的度数不变，始终等于60︒④当第 2秒或第4秒时，PBQ △为直角三角形，正确的有（ ）个．A ．1B ．2C ．3D ．4【答案】C【解析】 ∵点P 、Q 速度相同，∴AP BQ =．在ACP △和ABQ △中，60AP BQ CAP ABQ AC BA =⎧⎪∠==︒⎨⎪=⎩， ∴ACP △≌BAQ △，故②正确．则AQC CPB ∠=∠．即B BAQ BAQ AMP ∠+∠=∠+∠．∴60AMP B ∠=∠=︒．则60CMQ AMP ∠=∠=︒，故③正确．∵APM ∠不一定等于60︒．∴AP AM ≠．∴BQ AM ≠．故①错误．设时间为t ，则AP=BQ=t ，PB=4-t①当∠PQB =90°时，∵∠B =60°，∴PB =2BQ ，得6-t =2t ，t =2 ；②当∠BPQ =90°时，∵∠B =60°，∴BQ =2BP ，得t =2（6-t ），t =4；∴当第2秒或第4秒时，△PBQ 为直角三角形．∴④正确.故选C.点睛：本题考查了等边三角形的性质、全等三角形的判定与性质、直角三角形的性质等知识点，综合性强，难度较大．18．如图，在△ABC 中，P 是BC 上的点，作PQ ∥AC 交AB 于点Q ，分别作PR ⊥AB ，PS ⊥AC ，垂足分别是R ，S ，若PR=PS ，则下面三个结论：①AS=AR ；②AQ=PQ ；③△PQR ≌△CPS ；④AC ﹣AQ=2SC ，其中正确的是（ ）A ．②③④B ．①②C ．①④D ．①②③④【答案】B【解析】【分析】 连接AP,由已知条件利用角平行线的判定可得∠1 = ∠2,由三角形全等的判定得△APR ≌△APS,得AS=AR,由已知可得∠2 = ∠3,得QP=AQ,答案可得. 【详解】解:如图连接AP,PR=PS,PR ⊥AB,垂足为R,PS ⊥AC,垂足为S,AP 是∠BAC 的平分线,∠1=∠2,△APR ≌△APS.AS=AR,又QP/AR,∠2 = ∠3又∠1 = ∠2，∠1=∠3,AQ=PQ,没有办法证明△PQR ≌△CPS,③不成立,没有办法证明AC-AQ=2SC,④不成立.所以B 选项是正确的.【点睛】本题主要考查三角形全等及三角形全等的性质.19．已知111122,A B C A B C △△的周长相等，现有两个判断：①若21212112,A A B C B A A C ==，则111222A B C A B C △≌△；②若12=A A ∠∠，1122=A C A C ，则111222A B C A B C△≌△，对于上述的两个判断，下列说法正确的是（）A．①，②都正确B．①，②都错误C．①错误，②正确D．①正确，②错误【答案】A【解析】【分析】根据SSS即可推出△111A B C≅△222A B C，判断①正确；根据相似三角形的性质和判定和全等三角形的判定推出即可．【详解】解：①△111A B C，△222A B C的周长相等，1122A B A B=，1122AC A C=，1122B C B C∴=，∴△111A B C≅△222()A B C SSS，∴①正确；②如图，延长11A B到1D，使1111B D B C=，，延长22A B到2D，使2222B D B C=，∴111111A D AB B C=+，222222A D AB B C=+，∵111122,A B C A B C△△的周长相等，1122=A C A C∴1122A D A D=，在△111A B D和△222A B D中1122121122==A D A DA AA C A C=⎧⎪∠∠⎨⎪⎩，∴△111A B D≅△222A B D（SAS）∴12=D D∠∠，∵1111B D B C=，2222B D B C=∴1111=D D C B∠∠，2222=D D C B∠∠，又∵1111111=A B C D D C B∠∠+∠，2222222=A B C D D C B∠∠+∠，∴1112221==2A B C A B C D∠∠∠，在△111A B C和△222A B C中111222121122===A B C A B CA AA C A C∠∠⎧⎪∠∠⎨⎪⎩，∴△111A B C≅△222A B C（AAS），∴②正确；综上所述：①，②都正确．故选：A．【点睛】本题考查了全等三角形的判定、等腰三角形的性质，能构造全等三角形、综合运用定理进行推理是解此题的关键，注意：全等三角形的判定定理有SAS，ASA，AAS，SSS，而AAA和SSA不能判断两三角形全等．20．如图，AC⊥BE于点C ，DF⊥BE于点F，且BC＝EF，如果添上一个条件后，可以直接利用“HL”来证明△ABC≌△DEF，则这个条件应该是()A．AC＝DE B．AB＝DE C．∠B＝∠E D．∠D＝∠A【答案】B【解析】在Rt△ABC与Rt△DEF中，直角边BC＝EF，要利用“HL”判定全等，只需添加条件斜边AB=DE.故选：B.21．如图，已知在正方形ABCD中，点E F、分别在BC CD、上，△AEF是等边三角形，连接AC交EF于G，给出下列结论：①BE DF=； ② 15DAF∠=;③AC垂直平分EF; ④BE DF EF+=．其中结论正确的共有( )．A．1个B．2个C．3个D．4个【答案】C【解析】试题分析：四边形ABCD 是正方形，∴AB=BC=CD=AD ，∠B=∠BCD=∠D=∠BAD=90°．∵△AEF 等边三角形，∴AE=EF=AF ，∠EAF=60°．∴∠BAE+∠DAF=30°．∴Rt △ABE ≌Rt △ADF （HL ），∴BE=DF （故①正确）．∠BAE=∠DAF ，∴∠DAF+∠DAF=30°，即∠DAF=15°（故②正确），∵BC=CD ，∴BC ﹣BE=CD ﹣DF ，即CE=CF ，∵AE=AF ，∴AC 垂直平分EF ．（故③正确）． 设EC=x ，由勾股定理，得EF=x ，CG=x ，AG=AEsin60°=EFsin60°=2×CGsin60°=x ， ∴AC=， ∴AB=， ∴BE=﹣x=， ∴BE+DF=x ﹣x≠x ．（故④错误）．∴综上所述，正确的有3个．考点：正方形的性质；全等三角形的判定与性质；线段垂直平分线的性质；等边三角形的性质．22．如图，在▱ABCD 中，AD =2AB ，F 是AD 的中点，作CE ⊥AB ，垂足E 在线段AB 上，连接EF 、CF ，则下列结论中①∠DCF =123,1x x ==-∠BCD ；②EF =CF ；③S △BEC =2S △CEF ；④∠DFE =3∠AEF ．一定成立的是（ ）A ．①②B ．①③④C ．①②③D ．①②④【答案】D【解析】①∵F 是AD 的中点，∴AF=FD ， ∵在?ABCD 中，AD=2AB ，∴AF=FD=CD ，∴∠DFC=∠DCF ，∵AD ∥BC ，∴∠DFC=∠FCB ，∴∠DCF=∠BCF ，∴∠DCF=12∠BCD ，故此选项正确；延长EF ，交CD 延长线于M ，∵四边形ABCD是平行四边形，∴AB∥CD，∴∠A=∠MDF，∵F为AD中点，∴AF=FD，在△AEF和△DFM中，∠A＝∠FDMAF＝DF∠AFE＝∠DFM，∴△AEF≌△DMF（ASA），∴FE=MF，∠AEF=∠M，∵CE⊥AB，∴∠AEC=90°，∴∠AEC=∠ECD=90°，∵FM=EF，∴FC=FM，故②正确；③∵EF=FM，∴S△EFC=S△CFM，∵MC＞BE，∴S△BEC＜2S△EFC故S△BEC=2S△CEF错误；④设∠FEC=x，则∠FCE=x，∴∠DCF=∠DFC=90°-x，∴∠EFC=180°-2x，∴∠EFD=90°-x+180°-2x=270°-3x，∵∠AEF=90°-x，∴∠DFE=3∠AEF，故此选项正确．故正确的有：①②④．故选D.23．在△ABC与△DEF中，下列各组条件，不能判定这两个三角形全等的是（）A．AB＝DE，∠B＝∠E，∠C＝∠F B．AC＝DE，∠B＝∠E，∠A＝∠FC．AC＝DF，BC＝DE，∠C＝∠D D．AB＝EF，∠A＝∠E，∠B＝∠F【答案】B【解析】利用全等三角形的判定定理，分析可得：A 、AB=DE ，∠B=∠E ，∠C=∠F 可利用AAS 证明△ABC 与△DEF 全等；B 、∠A=∠F ，∠B=∠E ，AC=DE ，对应边不对应，不能证明△ABC 与△DEF 全等； C 、AC=DF ，BC=DE ，∠C=∠D 可利用ASA 证明△ABC 与△DEF 全等；D 、AB=EF ，∠A=∠E ∠B=∠F 可利用SAS 证明△ABC 与△DEF 全等；故选：D ．点睛：本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS 、SAS 、ASA 、AAS 、HL ．注意：AAA 、SSA 不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．24．如图，ABC △是等边三角形，ABD △是等腰直角三角形，∠BAD =90°，AE ⊥BD 于点E ．连CD 分别交AE ，AB 于点F ，G ，过点A 做AH ⊥CD 交BD 于点H ，则下列结论：①∠ADC =15°；②AF =AG ；③AH =DF ；④△ADF ≌△BAH ；⑤DF =2EH .其中正确结论的个数为（ ）A ．5B ．4C ．3D ．2【答案】B【解析】【分析】 ①根据△ABC 为等边三角形，△ABD 为等腰直角三角形，可以得出各角的度数以及DA=AC ，即可作出判断；②分别求出∠AFG 和∠AGD 的度数，即可作出判断；④根据三角形内角和定理求出∠HAB 的度数，求证EHG DFA ∠=∠，利用AAS 即可证出两个三角形全等；③根据④证出的全等即可作出判断；⑤证明∠EAH=30°，即可得到AH=2EH ，又由③可知AH DF =，即可作出判断.【详解】①正确：∵ABC △是等边三角形，∴60BAC ︒∠=，∴CA AB =．∵ABD △是等腰直角三角形，∴DA AB =．又∵90BAD ︒∠=，∴150CAD BAD BAC ︒∠=∠+∠=，∴DA CA =，∴()1180150152ADC ACD ︒︒︒∠=∠=-=； ②错误：∵∠EDF=∠ADB-∠ADC=30°∴∠DFE=90°-∠EDF=90°-30°=60°=∠AFG∵∠AGD=90°-∠ADG=90°-15°=75°∠AFG≠∠AGD∴AF≠AG③，④正确，由题意可得45DAF ABH ︒∠=∠=，DA AB =，∵AE BD ⊥，AH CD ⊥．∴180EHG EFG ︒∠+∠=．又∵180?DFA EFG ∠+∠=，∴EHG DFA ∠=∠，在DAF △和ABH 中()AFD BHA DAF ABHAAS DA AB ∠=∠⎧⎪∠=∠⎨⎪=⎩∴DAF △≌ABH ．∴DF AH =．⑤正确：∵150CAD ︒∠=，AH CD ⊥，∴75DAH ︒∠=，又∵45DAF ︒∠=，∴754530EAH ︒︒︒∠=-=又∵AE DB ⊥，∴2AH EH =，又∵=AH DF ，∴2DF EH =【点睛】本题考查了等边三角形的性质，等腰三角形的性质，三角形的内角和定理，三角形外角的性质，全等三角形的判定与性质，综合性较强，属于较难题目.25．下列两个三角形中,一定全等的是( )A ．两个等边三角形B ．有一个角是40︒,腰相等的两个等腰三角形C ．有一条边相等,有一个内角相等的两个等腰三角形D ．有一个角是100︒,底相等的两个等腰三角形【答案】D【解析】【分析】根据全等三角形的判定方法及等腰三角形的性质对各个选项进行分析,从而得到答案．【详解】解：A 、当两个等边三角形的对应边不相等时,这两个等边三角形也不会全等，故本选项错误；B 、当该角不是对应角时,这两个等腰三角形也不会全等，故本选项错误；C 、当两个等腰三角形的对应边与对应角不相等时,这两个等腰三角形也不会全等，故本选项错误；D 、等腰三角形的100°角只能是顶角,则两个底角是40°,它们对应相等，所以由全等三角形的判定定理ASA 或AAS 证得它们全等，故本选项正确；故选D ．【点睛】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有：SSS 、SAS 、ASA 、AAS 、HL ．注意：AAA 、SSA 不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角．26．如图，点B ，F ，C ，E 在同一条直线上，点A ，D 在直线BE 的两侧，AB ∥DE ，BF ＝CE ，添加一个适当的条件后，仍不能使得△ABC ≌△DEF （ ）A ．AC ＝DFB ．AC ∥DF C ．∠A ＝∠D D ．AB ＝DE【答案】A【解析】【分析】 根据AB ∥DE 证得∠B ＝∠E ，又已知BF ＝CE 证得BC ＝EF ，即已具备两个条件：一边一角，再依次添加选项中的条件即可判断.【详解】∵AB ∥DE ，∴∠B ＝∠E ，∵BF ＝CE ，∴BF +FC ＝CE +FC ，∴BC ＝EF ，若添加AC ＝DF ，则不能判定△ABC ≌△DEF ，故选项A 符合题意；若添加AC ∥DF ，则∠ACB ＝∠DFE ，可以判断△ABC ≌△DEF （ASA ），故选项B 不符合题意；若添加∠A ＝∠D ，可以判断△ABC ≌△DEF （AAS ），故选项C 不符合题意；若添加AB ＝DE ，可以判断△ABC ≌△DEF （SAS ），故选项D 不符合题意；故选：A ．【点睛】此题考查三角形全等的判定定理，熟练掌握定理，并能通过定理去判断条件是否符合全等是解决此题的关键.27．如图，AOB ∆的外角,CAB DBA ∠∠的平分线,AP BP 相交于点P ，PE OC ⊥于E ，PF OD ⊥于F ，下列结论：（1）PE PF =；（2）点P 在COD ∠的平分线上；（3）90APB O ∠=︒-∠，其中正确的有 （ ）A ．0个B ．1个C ．2个D ．3个【答案】C【解析】【分析】 过点P 作PG ⊥AB ，由角平分线的性质定理，得到PE PG PF ==，可判断（1）（2）正确；由12APB EPF ∠=∠，180EPF O ∠+∠=︒，得到1902APB O ∠=︒-∠，可判断（3）错误；即可得到答案．【详解】解：过点P 作PG ⊥AB ，如图：∵AP 平分∠CAB ，BP 平分∠DBA ，PE OC ⊥，PF OD ⊥，PG ⊥AB ，∴PE PG PF ==；故（1）正确；∴点P 在COD ∠的平分线上；故（2）正确；∵12APB APG BPG EPF ∠=∠+∠=∠， 又180EPF O ∠+∠=︒， ∴11(180)9022APB O O ∠=⨯︒-∠=︒-∠；故（3）错误； ∴正确的选项有2个；故选：C ．【点睛】 本题考查了角平分线的判定定理和性质定理，解题的关键是熟练掌握角平分线的判定和性质进行解题．28．如图是由4个相同的小正方形组成的网格图，其中∠1+∠2等于（ ）A ．150°B ．180°C ．210°D ．225°【答案】B【解析】【分析】 根据SAS 可证得ABC ≌EDC ，可得出BAC DEC ∠∠=，继而可得出答案，再根据邻补角的定义求解.【详解】由题意得：AB ED =，BC DC =，D B 90∠∠==， ABC ∴≌EDC ，BAC DEC ∠∠∴=，12180∠∠+=．故选B ．【点睛】 本题考查全等图形的知识，比较简单，解答本题的关键是判断出ABC ≌EDC ．.29．如图，在四边形ABCD 中，对角线AC 平分∠BAD，AB ＞AD ，下列结论中正确的是（ ）A ．AB ﹣AD ＞CB ﹣CDB ．AB ﹣AD=CB ﹣CDC ．AB ﹣AD ＜CB ﹣CDD ．AB ﹣AD 与CB ﹣CD 的大小关系不确定【答案】A【解析】如图，在AB 上截取AE=AD ，连接CE ．∵AC平分∠BAD，∴∠BAC=∠DAC，又AC是公共边，∴△AEC≌△ADC（SAS），∴AE=AD，CE=CD，∴AB-AD=AB-AE=BE，BC-CD=BC-CE，∵在△BCE中，BE＞BC-CE，∴AB-AD＞CB-CD．故选A．30．如图，，，，点D、E为BC边上的两点，且，连接EF、BF则下列结论：≌；≌；；，其中正确的有( )个．A．1B．2C．3D．4【答案】D【解析】【分析】根据∠DAF=90°，∠DAE=45°，得出∠FAE=45°，利用SAS证明△AED≌△AEF，判定①正确；由△AED≌△AEF得AF=AD,由，得∠FAB=∠CAD，又AB=AC, 利用SAS证明≌,判定②正确；先由∠BAC=∠DAF=90°，得出∠CAD=∠BAF，再利用SAS证明△ACD≌△ABF，得出CD=BF，又①知DE=EF，那么在△BEF中根据三角形两边之和大于第三边可得BE+BF＞EF，等量代换后判定③正确；先由△ACD≌△ABF，得出∠C=∠ABF=45°，进而得出∠EBF=90°，判定④正确．【详解】‚解：①∵∠DAF=90°，∠DAE=45°，∴∠FAE=∠DAF-∠DAE=45°．在△AED与△AEF中，，∴△AED≌△AEF（SAS），①正确；②∵△AED≌△AEF,∴AF=AD,∵,∴∠FAB=∠CAD,∵AB=AC，∴≌，②正确；③∵∠BAC=∠DAF=90°，∴∠BAC-∠BAD=∠DAF-∠BAD，即∠CAD=∠BAF．在△ACD与△ABF中，，∴△ACD≌△ABF（SAS），∴CD=BF，由①知△AED≌△AEF，∴DE=EF．在△BEF中，∵BE+BF＞EF，∴BE+DC＞DE，③正确；④由③知△ACD≌△ABF，∴∠C=∠ABF=45°，∵∠ABE=45°，∴∠EBF=∠ABE+∠ABF=90°．④正确．故答案为D．【点睛】本题考查了勾股定理，全等三角形的判定与性质，等腰直角直角三角形的性质，三角形三边关系定理，相似三角形的判定，此题涉及的知识面比较广，解题时要注意仔细分析，有一定难度．。

苏科版数学八年级上册 三角形解答题单元达标训练题（Word 版 含答案）一、八年级数学三角形解答题压轴题（难）1．直线MN 与直线PQ 垂直相交于O ，点A 在直线PQ 上运动，点B 在直线MN 上运动． （1）如图1，已知AE 、BE 分别是∠BAO 和∠ABO 角的平分线，点A 、B 在运动的过程中，∠AEB 的大小是否会发生变化？若发生变化，请说明变化的情况；若不发生变化，试求出∠AEB 的大小．（2）如图2，已知AB 不平行CD ，AD 、BC 分别是∠BAP 和∠ABM 的角平分线，又DE 、CE 分别是∠ADC 和∠BCD 的角平分线，点A 、B 在运动的过程中，∠CED 的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出其值．（3）如图3，延长BA 至G ，已知∠BAO 、∠OAG 的角平分线与∠BOQ 的角平分线及延长线相交于E 、F ，在△AEF 中，如果有一个角是另一个角的3倍，试求∠ABO 的度数．【答案】（1）135°；（2）67.5°；（3）60°， 45°【解析】【分析】（1）根据直线MN 与直线PQ 垂直相交于O 可知∠AOB=90°，再由AE 、BE 分别是∠BAO 和∠ABO 的角平分线得出1BAE OAB 2∠=∠，1ABE ABO 2∠=∠，由三角形内角和定理即可得出结论；（2）延长AD 、BC 交于点F ，根据直线MN 与直线PQ 垂直相交于O 可得出∠AOB=90°，进而得出OAB OBA 90∠+∠=︒ ，故PAB MBA 270∠+∠=︒，再由AD 、BC 分别是∠BAP 和∠ABM 的角平分线，可知1BAD BAP 2∠=∠，1ABC ABM 2∠=∠，由三角形内角和定理可知∠F=45°，再根据DE 、CE 分别是∠ADC 和∠BCD 的角平分线可知CDE DCE 112.5∠+∠=︒，进而得出结论；（3））由∠BAO 与∠BOQ 的角平分线相交于E 可知1EAO BAO 2∠=∠,1EOQ BOQ 2∠=∠ ，进而得出∠E 的度数，由AE 、AF 分别是∠BAO 和∠OAG 的角平分线可知∠EAF=90°，在△AEF 中，由一个角是另一个角的3倍分四种情况进行分类讨论．【详解】（1）∠AEB 的大小不变，∵直线MN 与直线PQ 垂直相交于O ，∴∠AOB=90°， ∴OAB OBA 90∠+∠=︒，∵AE 、BE 分别是∠BAO 和∠ABO 角的平分线，∴1BAE OAB 2∠=∠，1ABE ABO 2∠=∠， ∴()1BAE ABE OAB ABO 452∠+∠=∠+∠=°， ∴∠AEB=135°；（2）∠CED 的大小不变．如图2，延长AD 、BC 交于点F ．∵直线MN 与直线PQ 垂直相交于O ，∴90∠=AOB °，∴OAB OBA 90∠+∠=°，∴PAB MBA 270∠+∠=°，∵AD 、BC 分别是∠BAP 和∠ABM 的角平分线，∴1BAD BAP 2∠=∠，1ABC ABM 2∠=∠， ∴()1BAD ABC PAB ABM 1352∠+∠=∠+∠=°，F 45∠=°， ∴FDC FCD 135∠+∠=°，∴CDA DCB 225∠+∠=°，∵DE 、CE 分别是∠ADC 和∠BCD 的角平分线，∴CDE DCB 112.5∠+∠=°，∴E 67.5∠=°；（3）∵∠BAO 与∠BOQ 的角平分线相交于E ，∴1EAO BAO 2∠=∠,1EOQ BOQ 2∠=∠ ， ∴()11E EOQ EAO BOQ BAQ ABO 22∠=∠-∠=∠-∠=∠， ∵AE 、AF 分别是∠BAO 和∠OAG 的角平分线，∴EAF 90∠=°．在△AEF 中，∵有一个角是另一个角的3倍，故有：①EAF 3E ∠=∠，E 30∠=°，ABO 60∠=°；②EAF 3F ∠=∠，E 60∠=°，ABO 120∠=°；③EAF 3E ∠=∠，E 22.5∠=°，ABO 45∠=°；④EAF 3F ∠=∠，E 67.5∠=°，ABO 135∠=°．∴∠ABO 为60°或45°．【点睛】本题考查的是三角形内角和定理，熟知三角形内角和是180°是解答此题的关键．2．如图，在△ABC 中，已知AD BC ⊥于点D ，AE 平分()BAC C B ∠∠>∠（1）试探究EAD ∠与C B ∠∠、的关系；（2）若F 是AE 上一动点，当F 移动到AE 之间的位置时，FD BD ⊥,如图2所示，此时EFD C B ∠∠∠与、的关系如何？（3）若F 是AE 上一动点，当F 继续移动到AE 的延长线上时，如图3，FD BC ⊥，①中的结论是否还成立？如果成立请说明理由，如果不成立，写出新的结论.【答案】（1）∠EAD=12（∠C-∠B ），理由见解析； （2）∠EFD=12（∠C-∠B ），理由见解析； （3）∠AFD=12（∠C-∠B ）成立，理由见解析. 【解析】【分析】（1）由图不难发现∠EAD=∠EAC-∠DAC ，再根据三角形的内角和定理结合角平分线的定义分别用结论中出现的角替换∠EAC 和∠DAC ；（2）作AG BC ⊥于G 转化为（1）中的情况，利用（1）的结论即可解决；（3）作AH BC ⊥于H 转化为（1）中的情况，利用（1）的结论即可解决．【详解】解：（1）∠EAD=12（∠C-∠B ）.理由如下：∵AE 平分∠BAC ，∴∠BAE=∠CAE=12∠BAC ∵∠BAC=180°-（∠B+∠C ）∴∠EAC=12[180°-（∠B+∠C ）] ∵AD ⊥BC ，∴∠ADC=90°， ∴∠DAC=180°-∠ADC-∠C=90°-∠C ，∵∠EAD=∠EAC-∠DAC∴∠EAD=12 [180°-（∠B+∠C ）]-（90°-∠C ）=12（∠C-∠B ）． （2）∠EFD=12（∠C-∠B ）.理由如下：作AG BC ⊥于G由（1）可知∠EAG=12（∠C-∠B ） ∵FD BD ，AG BC ⊥∴FD ∥AG∴∠EAG=∠EFD ∴∠EFD=12（∠C-∠B ） （3）∠AFD=12（∠C-∠B ）．理由如下：作AH BC ⊥于H由（1）可知∠EAH=12（∠C-∠B ） ∵FD BD ⊥，AH BC ⊥∴FD ∥AH∴∠EAH=∠AFD ∴∠AFD=12（∠C-∠B ） 【点睛】本题主要考查了三角形的内角和定理，综合利用角平分线的定义和三角形内角和定理是解答此题的关键．3．如图, A 为x 轴负半轴上一点, B 为x 轴正半轴上一点, C(0,－2),D(－3,－2).(1)求△BCD 的面积；(2)若AC ⊥BC,作∠CBA 的平分线交CO 于P ,交CA 于Q,判断∠CPQ 与∠CQP 的大小关系, 并证明你的结论.【答案】（1）3；（2）∠CPQ ＝∠CQP ，理由见解析；【解析】【分析】（1）求出CD 的长度，再根据三角形的面积公式列式计算即可得解；（2）根据角平分线的定义可得∠ABQ=∠CBQ ，然后根据等角的余角相等解答；【详解】解：（1）∵点C（0，-2），D（-3，-2），∴CD=3，且CD//x轴∴△BCD面积=12×3×2=3；（2）∠CPQ＝∠CQP，∵AC⊥BC，∴∠ACO＋∠BCO＝90°，又∠ACO＋∠OAC＝90°∴∠OAC＝∠BCO，又BQ平分∠CBA，∴∠ABQ＝∠CBQ，∵∠CQP＝∠OAC＋∠ABQ∠CPQ＝∠CBQ＋∠BCO，∴∠CQP＝∠CPQ（2）∠CPQ＝∠CQP，∵AC⊥BC，∴∠ACO＋∠BCO＝90°，又∠ACO＋∠OAC＝90°∴∠OAC＝∠BCO，又BQ平分∠CBA，∴∠ABQ＝∠CBQ，∵∠CQP＝∠OAC＋∠ABQ∠CPQ＝∠CBQ＋∠BCO，∴∠CQP＝∠CPQ【点睛】本题考查了坐标与图形性质，三角形的角平分线，三角形的面积，三角形的内角和定理，三角形的外角性质，综合题，熟记性质并准确识图是解题的关键.4．如图，四边形ABCD，BE、DF分别平分四边形的外角∠MBC和∠NDC，若∠BAD=α，∠BCD=β（1）如图，若α+β=120°，求∠MBC+∠NDC的度数；（2）如图，若BE与DF相交于点G，∠BGD=30°，请写出α、β所满足的等量关系式；（3）如图，若α=β，判断BE、DF的位置关系，并说明理由．【答案】（1）120°；（2）β﹣α=60° 理由见解析；（3）平行，理由见解析.【解析】【分析】（1）利用四边形的内角和求出∠ABC与∠ADC的和，利用角平分线的定义以及α+β=120°推导即可；（2）由（1）得，∠MBC+∠NDC=α+β，利用角平分线的定义得∠CBG+∠CDG=12(α+β)，在△BCD中利用三角形的内角和定理得∠BDC+∠CDB =180°﹣β，在△BDG中利用三角形的内角和定理得出关于α、β的等式整理即可得出结论；（3）延长BC交DF于H，由（1）得∠MBC+∠NDC=α+β，利用角平分线的定义得∠CBE+∠CDH=12(α+β)，利用三角形的外角的性质得∠CDH=β﹣∠DHB，然后代入∠CBE+∠CDH=12(α+β)计算即可得出一组内错角相等．【详解】（1）解：（1）在四边形ABCD中，∠BAD+∠ABC+∠BCD+∠ADC=360°，∴∠ABC+∠ADC=360°-（α+β），∵∠MBC+∠ABC=180°，∠NDC+∠ADC=180°∴∠MBC+∠NDC=180°-∠ABC+180°-∠ADC=360°-（∠ABC+∠ADC）=360°-[360°-（α+β）]=α+β，∵α+β=120°，∴∠MBC+∠NDC=120°；（2）β﹣α=60°理由：如图1，连接BD，由（1）得，∠MBC+∠NDC=α+β，∵BE、DF分别平分四边形的外角∠MBC和∠NDC，∴∠CBG=12∠MBC，∠CDG=12∠NDC，∴∠CBG+∠CDG=12∠MBC+12∠NDC=12(∠MBC+∠NDC)=12(α+β)，在△BCD中，∠BDC+∠CDB=180°﹣∠BCD=180°﹣β，在△BDG中，∠GBD+∠GDB+∠BGD=180°，∴∠CBG+∠CBD+∠CDG+∠BDC+∠BGD=180°，∴(∠CBG+∠CDG)+(∠BDC+∠CDB)+∠BGD=180°，∴12(α+β)+180°﹣β+30°=180°，∴β﹣α=60°， (3)平行，理由：如图2，延长BC 交DF 于H ，由（1）有，∠MBC +∠NDC =α+β，∵BE 、DF 分别平分四边形的外角∠MBC 和∠NDC ，∴∠CBE =12∠MBC ，∠CDH =12∠NDC ， ∴∠CBE +∠CDH =12∠MBC +12∠NDC =12(∠MBC +∠NDC )=12(α+β)， ∵∠BCD =∠CDH +∠DHB ，∴∠CDH =∠BCD ﹣∠DHB =β﹣∠DHB ， ∴∠CBE +β﹣∠DHB =12(α+β)， ∵α=β，∴∠CBE +β﹣∠DHB =12(β+β)=β， ∴∠CBE =∠DHB ，∴BE ∥DF ．【点睛】此题是三角形综合题，主要考查了平角的意义，四边形的内角和，三角形内角和，三角形的外角的性质，角平分线的意义，用整体代换的思想是解本题的关键，整体思想是初中阶段的一种重要思想，要多加强训练．5．（1）在ABC ∆中，AD BC ⊥，BE AC ⊥，CF AB ⊥，16BC =，3AD =，4BE =，6CF =，则ABC ∆的周长为______.（2）如图①，在ABC ∆中，已知点D ，E ，F 分别为边BC ，BD ，CD 的中点，且4ABC S ∆=2cm ，则AEF S ∆等于______2cm .① ②（3）如②图，三角形ABC 的面积为1，点E 是AC 的中点，点O 是BE 的中点，连接AO 并延长交BC 于点D ，连接CO 并延长交AB 于点F ，则四边形BDOF 的面积为______.【答案】（1）36（2）2（3）16 【解析】【分析】(1)利用三角形面积公式，求出AB 、AC 的长，再计算三角形的周长即可；(2)设ABC ∆在BC 边上的高为h ，则12ABC S BC h ∆=⋅，根据线段中点的定义以及线段的和差得出12EF BC =，继而再根据三角形面积公式进行求解即可； (3)设BOF S x ∆=，BOD S y ∆=，根据三角形中线将三角形分成两个面积相等的三角形可得14AOE COE AOB COB S S S S ∆∆∆∆====，从而得14AOF S x ∆=-，34ACF S x ∆=-，14BCF S x ∆=+，14COD S y ∆=-，34ACD S y ∆=-，14ABD S y ∆=+，利用等高的两三角形面积之比等于底边之比分别列出关于x 、y 的方程，求出x 、y 的值即可求得答案.【详解】 (1)111222ABC S BC AD AC BE AB CF ∆=⋅=⋅=⋅， ∴BC AD AC BE AB CF ⋅=⋅=⋅，即16346AC AB ⨯=⋅=⋅，∴12AC =，8AB =，∴△ABC 的周长=AB+BC+AC=36；(2)设ABC ∆在BC 边上的高为h ， 则12ABC S BC h ∆=⋅， ∵E 为BD 中点，∴12ED BD =， ∵F 为DC 中点，∴12DF DC =， ∴111222EF BD DC BC =+=， ∴211112cm 2222AEF ABC S EF h BC h S ∆∆=⋅=⋅⋅==； (3)设BOF S x ∆=，BOD S y ∆=，∵点E ，O 分别是AC ，BE 的中点，1ABC S ∆=，∴14AOE COE AOB COB S S S S ∆∆∆∆====，∴14AOF S x ∆=-，34ACF S x ∆=-，14BCF S x ∆=+， ∴134414x x x x --=+，即2213164x x x -=-， 解得112x =， 又14COD S y ∆=-，34ACD S y ∆=-，14ABD S y ∆=+， ∴141344y y y y +=--，得112y =， 故11112126BDOF S x y =+=+=四边形. 【点睛】本题考查了三角形面积的应用，三角形的周长，解题关键在于找出等高的两三角形面积与底边的对应关系．6．（1）如图1，有一块直角三角板XYZ （其中∠X=90°）放置在△ABC 上，恰好三角板XYZ 的两条直角边XY ，XZ 分别经过B ，C 两点，且直角顶点X 在△ABC 内部．①若∠A=40°，∠ABC+∠ACB= °；∠XBC+∠XCB= °；②试判断∠A 与∠XBA+∠XCA 之间存在怎样数量关系？并写出证明过程．（2）如图2，如果直角顶点X 在△ABC 外部，试判断∠A 、∠XBA 、∠XCA 之间又存在怎样的数量关系？（只写出答案，无需证明）．【答案】（1）①140，90；②∠A+∠XBA +∠XCA=90°，证明见解析；（2）∠A+（∠XBA －∠XCA ）=90°【解析】试题分析：（1）①根据三角形内角和定理可得∠ABC +∠ACB =180°﹣∠A =140°，∠XBC +∠XCB =180°﹣∠XBC =90°，进而可求出∠ABX +∠ACX 的度数；②根据三角形内角和定义有90°+（∠ABX +∠ACX ）+∠A =180°，则可得出结论．（2）由②的解题思路可得：∠A+（∠XBA －∠XCA ）=90°．（1）①若∠A =40°，∠ABC +∠ACB = 140 °；∠XBC +∠XCB = 90 °；②∠A+∠XBA +∠XCA=90°（或等式的变形也可以）证明：∵∠X=90°∴∠XBC +∠XCB=180°－∠X=90°∵∠A +∠ABC +∠ACB =180°，∴∠A +（∠XBA +∠XCA ）+（∠XBC +∠XCB ）=180°，∴∠A +（∠XBA +∠XCA ）=180°－90°=90°，∴∠A=90°－（∠XBA +∠XCA ）（2） ∠A+（∠XBA －∠XCA ） =90°．点睛：本题考查三角形外角的性质及三角形的内角和定理，解答的关键是熟练掌握三角形的内角和为180°以及沟通外角和内角的关系．7．如图1：ABC 中，AD 是高，AE 是BAC ∠的平分线，=40=70ABC ACB ，∠︒∠︒．（1）求EAD ∠的度数（2）当==ABC ACB αβ∠∠，，请用αβ，表示EAD ∠，并写出推导过程（3）当AE 是BAC ∠的外角FAC ∠的平分线，如图2则此时EAD ∠的度数是多少，用,αβ表示，直接写出结果．【答案】（1）15o ;(2) -2EAD βα∠=;(3) 902EAD αβ-∠=︒+【解析】【分析】 （1）先根据三角形的内角和定理求得∠BAC=180°-∠B-∠C=70°，利用角平分线的定义得∠EAC=12∠BAC=35°，而∠DAC=90°-∠C=20°，通过∠EAD=∠EAC-∠DAC 即可得到结果． （2）猜想∠DAE=12（β-α），重复（1）的过程找出∠BAD 和∠BAE 的度数，二者做差即可得出结论；（3）作∠BAC 的内角平分线AE ′，根据角平分线的性质求出∠EAE′=∠CAE+∠CAE′=12∠CAB+12∠CAF=90°，进而求出∠DAE 的度数. 【详解】解:（1）40,70,ABC ACB ∠=︒∠=︒180704070BAC ∴∠=︒-︒-︒=︒,AE 是BAC ∠的平分线， 1=352BAE CAE BAC ∴∠=∠=∠︒, 在ACD Rt 中，9020CAD C ∠=︒-∠=︒,15EAD EAC CAD ∴∠=∠-∠=︒.（2）,,ABC ACB αβ∠=∠=180BAC αβ∴∠=︒--,AE 是BAC ∠的平分线，1111=180--=90--2222BAE CAE BAC αβαβ∴∠=∠=∠︒︒（）, 在Rt △ACD 中，90CAD β∠=︒-，-=2EAD CAE CAD βα∴∠=∠-∠. （3）902EAD αβ-∠=︒+.如图，作∠CAB 的内角平分线AE′，则∠DAE′=-2βα．因为AE 是∠ACB 的外角平分线，所以∠EAE′=∠CAE+∠CAE′=12∠CAB+12∠CAF=12（∠CAB+∠CAF ）=90°， 所以∠DAE=90°-∠DAE′=90°--2βα=902αβ-︒+． 即∠DAE 的度数为902αβ-︒+. 【点睛】本题考查三角形外角的性质及三角形的内角和定理，解答的关键是沟通外角和内角的关系．解决（3）作辅助线是关键．8．操作示例：如图1，在△ABC中，AD为BC边上的中线，△ABD的面积记为S1，△ADC的面积记为S2．则S1=S2．解决问题：在图2中，点D、E分别是边AB、BC的中点，若△BDE的面积为2，则四边形ADEC的面积为 .拓展延伸：（1）如图3，在△ABC中，点D在边BC上，且BD=2CD，△ABD的面积记为S1，△ADC的面积记为S2．则S1与S2之间的数量关系为．（2）如图4，在△ABC中，点D、E分别在边AB、AC上，连接BE、CD交于点O，且BO=2EO，CO=DO，若△BOC的面积为3，则四边形ADOE的面积为 .【答案】解决问题：6；拓展延伸：（1）S1=2S2（2）10.5【解析】试题分析：解决问题：连接AE，根据操作示例得到S△ADE=S△BDE，S△ABE=S△AEC，从而得到结论；拓展延伸：（1）作△ABD的中线AE，则有BE=ED=DC，从而得到△ABE的面积=△AED的面积=△ADC的面积，由此即可得到结论；（2）连接AO．则可得到△BOD的面积=△BOC的面积，△AOC的面积=△AOD的面积，△EOC的面积=△BOC的面积的一半，△AOB的面积=2△AOE的面积．设△AOD的面积=a，△AOE的面积=b，则a+3=2b，a=b+1.5，求出a、b的值，即可得到结论．试题解析：解：解决问题连接AE．∵点D、E分别是边AB、BC的中点，∴S△ADE=S△BDE，S△ABE=S△AEC．∵S△BDE=2，∴S△ADE =2，∴S△ABE=S△AEC=4，∴四边形ADEC的面积=2+4=6．拓展延伸：解：（1）作△ABD的中线AE，则有BE=ED=DC，∴△ABE的面积=△AED的面积=△ADC的面积= S2，∴S1=2S2．（2）连接AO．∵CO=DO，∴△BOD的面积=△BOC的面积=3，△AOC的面积=△AOD的面积．∵BO=2EO，∴△EOC的面积=△BOC的面积的一半=1.5，△AOB的面积=2△AOE的面积．设△AOD的面积=a，△AOE的面积=b，则a+3=2b，a=b+1.5，解得：a=6，b=4.5，∴四边形ADOE的面积为=a+b=6+4.5=10.5．9．（1）如图①∠1＋∠2与∠B＋∠C有什么关系？为什么？（2）把图①△ABC沿DE折叠，得到图②，填空：∠1＋∠2_______∠B＋∠C(填“＞”“＜”“=”)，当∠A＝40°时，∠B＋∠C＋∠1＋∠2＝______.（3）如图③,是由图①的△ABC沿DE折叠得到的,如果∠A＝30°,则x＋y＝360°－（∠B＋∠C＋∠1＋∠2）＝360°－＝ ,猜想∠BDA＋∠CEA与∠A的关系为【答案】见解析.【解析】【分析】试题分析：（1）根据三角形内角是180度可得出，∠1+∠2=∠B+∠C；（2）△ABC沿DE 折叠，∠1+∠2=∠B+∠C，从而求出当∠A=40°时，∠B+∠C+∠1+∠2=140×2=280°，（3）根据以上计算可归纳出一般规律：∠BDA+∠CEA=2∠A．试题解析：解：（1）∠1+∠2 = ∠B+∠C，理由如下：在△ADE中，∠1+∠2 = 180°- ∠A在△ABC中，∠B+∠C = 180°- ∠A∴∠1+∠2 = ∠B+∠C（2）∵∠1+∠2+∠BDE+∠CED=∠B+∠C+∠BDE+∠CED=360°，∴∠1+∠2=∠B+∠C，当∠A=40°时，∠B+∠C+∠1+∠2=140×2=280°（3）如果∠A=30°，则x+y=360°-（∠B+∠C+∠1+∠2）=360°-300°=60°，所以∠BDA+∠CEA 与∠A的关系为：∠BDA+∠CEA=2∠A.考点：1.翻折变换（折叠问题）；2. 三角形内角和．【详解】请在此输入详解！10．已知:如图1，线段AB、CD相交于点O，连接AD、CB，如图2，在图1的条件下，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N，试解答下列问题：(1)在图1中，请直接写出∠A、∠B、∠C、∠D之间的数量关系:_____________________；(2)在图2中，若∠D=40°，∠B=30°，试求∠P的度数(写出解答过程)；(3)如果图2中，∠D和∠B为任意角，其他条件不变，试写出∠P与∠D、∠B之间的数量关系(直接写出结论即可).【答案】（1）∠A+∠D=∠B+∠C；（2）35°；（3）2∠P=∠B+∠D【解析】【分析】（1）根据三角形的内角和等于180°，易得∠A+∠D=∠B+∠C；（2）仔细观察图2，得到两个关系式∠1+∠D=∠3+∠P，∠2+∠P=∠4+∠B，再由角平分线的性质得∠1=∠2，∠3=∠4，两式相减，即可得结论．（3）参照（2）的解题思路.【详解】解：（1）∠A+∠D=∠B+∠C；（2）由（1）得，∠1+∠D=∠3+∠P，∠2+∠P=∠4+∠B，∴∠1-∠3=∠P-∠D，∠2-∠4=∠B-∠P，又∵AP、CP分别平分∠DAB和∠BCD，∴∠1=∠2，∠3=∠4，∴∠P-∠D=∠B-∠P，即2∠P=∠B+∠D，∴∠P=（40°+30°）÷2=35°．（3）由（2）的解题步骤可知，∠P与∠D、∠B之间的数量关系为：2∠P=∠B+∠D．【点睛】考查三角形内角和定理, 角平分线的定义，掌握三角形的内角和定理是解题的关键.。

苏州新区二中数学三角形填空选择单元综合测试（Word版含答案）一、八年级数学三角形填空题（难）∠=，边AB的垂直平分线交边BC于点D，边AC的垂直平分线1．在ABC中，BACα∠的度数为______.(用含α的代数式表示)交边BC于点E，连结AD，AE，则DAE【答案】2α﹣180°或180°﹣2α【解析】分两种情况进行讨论，先根据线段垂直平分线的性质，得到∠B=∠BAD，∠C=∠CAE，进而得到∠BAD+∠CAE=∠B+∠C=180°－a，再根据角的和差关系进行计算即可．解：有两种情况：①如图所示,当∠BAC⩾90°时，∵DM垂直平分AB，∴DA=DB，∴∠B=∠BAD，同理可得，∠C=∠CAE，∴∠BAD+∠CAE=∠B+∠C=180°−α，∴∠DAE=∠BAC−(∠BAD+∠CAE)=α−(180°−α)=2α−180°；②如图所示,当∠BAC<90°时，∵DM垂直平分AB，∴DA=DB，∴∠B=∠BAD，同理可得，∠C=∠CAE，∴∠BAD+∠CAE=∠B+∠C=180°−α，∴∠DAE=∠BAD+∠CAE−∠BAC=180°−α−α=180°−2α.故答案为2α−180°或180°−2α.点睛：本题主要考查垂直平分线的性质.根据题意准确画出符合题意的两种图形是解题的关键.2．如图，在△ABC中，∠B=50°，三角形的外角∠DAC和∠ACF的平分线交于点E，则∠AEC=_______°.【答案】65【解析】如图，∵AE平分∠DAC，CE平分∠ACF，∴∠1=12∠DAC，∠2=12∠ACF，∴∠1+∠2=12（∠DAC+∠ACF），又∵∠DAC+∠ACF=（180°-∠BAC）+（180°-∠ACB）=360°-（∠BAC+∠ACB），且∠BAC+∠ACB=180°-∠ABC=180°-50°=130°，∴∠1+∠2=12（360°-130°）=115°，∴在△ACE中，∠E=180°-（∠1+∠2）=180°-115°=65°.3．如图，在△ABC中，BD、BE分别是△ABC的高线和角平分线，点F在CA的延长线上，FH⊥BE交BD于点G，交BC于点H．下列结论：①∠DBE=∠F；②∠BEF=1 2（∠BAF+∠C）；③∠FGD=∠ABE+∠C；④∠F=12（∠BAC﹣∠C）；其中正确的是_____．【答案】①②③④【解析】【分析】①根据BD⊥FD，FH⊥BE和∠FGD=∠BGH，证明结论正确；②根据角平分线的定义和三角形外角的性质证明结论正确；③根据垂直的定义和同角的余角相等的性质证明结论正确；④证明∠DBE=∠BAC-∠C，根据①的结论，证明结论正确.【详解】解：①∵BD⊥FD，∴∠FGD+∠F=90°，∵FH⊥BE，∴∠BGH+∠DBE=90°，∵∠FGD=∠BGH，∴∠DBE=∠F，故①正确；②∵BE平分∠ABC，∴∠ABE=∠CBE，∠BEF=∠CBE+∠C，∴2∠BEF=∠ABC+2∠C，∠BAF=∠ABC+∠C，∴2∠BEF=∠BAF+∠C，∴∠BEF=12(∠BAF+∠C)，故②正确；③∵∠AEB=∠EBC+∠C，∵∠ABE=∠EBC，∴∠AEB=∠ABE+∠C，∵BD⊥FC，FH⊥BE，∴∠FGD=90︒-∠DFH，∠AEB=90︒-∠DFH，∴∠FGD=∠AEB∴∠FGD=∠ABE+∠C.故③正确；④∠ABD=90°-∠BAC，∠DBE=∠ABE-∠ABD=∠ABE-90°+∠BAC=∠CBD-∠DBE-90°+∠BAC，∵∠CBD=90°-∠C，∴∠DBE=∠BAC-∠C-∠DBE，由①得，∠DBE=∠F，∴∠F=∠BAC-∠C-∠DBE，∴∠F=12(∠BAC-∠C)；故④正确，故答案为①②③④.【点睛】本题考查的是三角形内角和定理，正确运用三角形的高、中线和角平分线的概念以及三角形外角的性质是解题的关键4．已知a、b、c为△ABC的三边，化简：|a+b﹣c|-|a﹣b﹣c|+|a﹣b+c|=______．--【答案】3a b c【解析】【分析】根据三角形的三边关系判断绝对值内式子的正负，然后利用绝对值的性质去掉绝对值，再去括号合并同类项即可．【详解】解：∵a、b、c为△ABC的三边，∴a+b＞c，a-b＜c，a+c＞b，∴a+b-c＞0，a-b-c＜0，a-b+c＞0，∴|a+b-c|-|a-b-c|+|a-b+c|=(a+b-c)+(a-b- c)+(a-b+c)=a+b-c+a-b- c+a-b+c=3a-b-c．故答案为：3a-b-c．【点睛】本题主要考查了三角形的三边关系定理和利用绝对值的性质进行化简，利用三角形的三边关系得出绝对值内式子的正负是解决此题的关键．5．如果一个n边形的内角和是1440°，那么n=__．【答案】10【解析】∵n边形的内角和是1440°，∴(n−2)×180°=1440°，解得：n=10.故答案为：10.6．两个完全相同的正五边形都有一边在直线l上，且有一个公共顶点O，其摆放方式如图所示，则∠AOB等于 ______ 度．【答案】108°【解析】【分析】如图，易得△OCD 为等腰三角形，根据正五边形内角度数可求出∠OCD ，然后求出顶角∠COD ，再用360°减去∠AOC 、∠BOD 、∠COD 即可【详解】∵五边形是正五边形，∴每一个内角都是108°，∴∠OCD=∠ODC=180°-108°=72°，∴∠COD=36°，∴∠AOB=360°-108°-108°-36°=108°.故答案为108°【点睛】本题考查正多边形的内角计算，分析出△OCD 是等腰三角形，然后求出顶角是关键.7．如图，A 、B 、C 三点在同一条直线上，∠A ＝50°，BD 垂直平分AE ，垂足为D ，则∠EBC 的度数为_____．【答案】100°【解析】【分析】根据线段垂直平分线的性质，得BE BA =，根据等腰三角形的性质，得50E A ∠=∠=︒，再根据三角形外角的性质即可求解．【详解】∵BD 垂直平分AE ，∴BE BA =，∴50E A ∠=∠=︒，∴100EBC E A ∠=∠+∠=︒，故答案为100°．【点睛】考查线段垂直平分线的性质以及三角形外角的性质，掌握线段垂直平分线的性质是解题的关键.8．如图，在△ABC中，∠ABC、∠ACB的平分线BE、CD相交于点F，∠A=60°，则∠BFC=______．【答案】120【解析】【分析】根据角平分线的定义可得出∠CBF=12∠ABC、∠BCF=12∠ACB，再根据内角和定理结合∠A=60°即可求出∠BFC的度数．【详解】∵∠ABC、∠ACB的平分线BE、CD相交于点F，∴∠CBF=12∠ABC，∠BCF=12∠ACB．∵∠A=60°，∴∠ABC+∠ACB=180°﹣∠A=120°，∴∠BFC=180°﹣（∠CBF+BCF）=180°﹣12（∠ABC+∠ACB）=120°．故答案为120°．【点睛】本题考查了三角形内角和定理，根据角平分线的定义结合三角形内角和定理求出角的度数是解题的关键．9．如图，小亮从A点出发前进5m，向右转15°，再前进5m，又向右转15°…，这样一直走下去，他第一次回到出发点A时，一共走了______m．【答案】120．【解析】【分析】由题意可知小亮所走的路线为正多边形，根据多边形的外角和定理即可求出答案．【详解】解：∵小亮从A点出发最后回到出发点A时正好走了一个正多边形，∴该正多边形的边数为n=360°÷15°=24，则一共走了24×5=120米，故答案为：120．【点睛】本题主要考查了多边形的外角和定理．任何一个多边形的外角和都是360°，用外角和求正多边形的边数可直接用360°除以一个外角度数．10．如图，∠1、∠2、∠3、∠4是五边形ABCDE的4个外角，若∠A=100°，则∠1+∠2+∠3+∠4= ．【答案】280°【解析】试题分析：先根据邻补角的定义得出与∠EAB相邻的外角∠5的度数，再根据多边形的外角和定理即可求解．解：如图，∵∠EAB+∠5=180°，∠EAB=100°，∴∠5=80°．∵∠1+∠2+∠3+∠4+∠5=360°，∴∠1+∠2+∠3+∠4=360﹣80°=280°故答案为280°．考点：多边形内角与外角．二、八年级数学三角形选择题（难）11．若△ABC内有一个点P1，当P1、A、B、C没有任何三点在同一直线上时，如图1，可构成3个互不重叠的小三角形；若△ABC内有两个点P1、P2，其它条件不变，如图2，可构成5个互不重叠的小三角形：……若△ABC内有n个点，其它条件不变，则构成若干个互不重叠的小三角形，这些小三角形的内角和为（）A．n·180°B．（n+2）·180°C．（2n-1）·180°D．（2n+1）·180°【答案】D【解析】【分析】当△ABC内的点的个数是1时，三角形内互不重叠的小三角形的个数是3；当△ABC内的点的个数是2时，三角形内互不重叠的小三角形的个数是5；依此类推得到当△ABC内的点的个数是3时，三角形内互不重叠的小三角形的个数是7；当△ABC内的点的个数是n 时，三角形内互不重叠的小三角形的个数2n+1，所以这些小三角形的内角和为（2n+1）·180°【详解】】解：图1中，当△ABC内只有1个点时，可分割成3个互不重叠的小三角形；图2中，当△ABC内只有2个点时，可分割成5个互不重叠的小三角形；图3中，当△ABC内只有3个点时，可分割成7个互不重叠的小三角形；根据以上规律，当△ABC内有n个点（P1，P2，…，P n）时，可以把△ABC分割成S=2n+1个互不重叠的三角形，所以这些小三角形的内角和为（2n+1）·180°.【点睛】此题考查了平面图形的有规律变化，要求学生通过观察图形，分析、归纳并发现其中的规律，并应用规律解决问题是解题的关键．12．如图：∠A+∠B+∠C+∠D+∠E+∠F等于（）A．180°B．360°C．270°D．540°【答案】B【解析】【分析】先根据三角形的外角，用∠AGE表示出∠A，∠B；用∠EMC表示出∠E，∠F；用∠CNA 表示出∠C，∠D，然后再根据对顶角相等的性质解出它们的度数即可【详解】解：如图：∵ ∠AGE 是△ABG 的外角∴∠AGE=∠A+∠B ；同理：∠EMC=∠E+∠F ；∠CNA=∠C+∠D∴∠A+∠B+∠C+∠D+∠E+∠F=∠AGE+∠EMC+∠CNA又∵∠AGE+∠EMC+∠CAN 是△MNG 的三个外角∴∠AGE+∠EMC+∠CAN=360°故选：B ．【点睛】本题主要考查了三角形外角及其外角和，其中找出三角形的外角是解答本题的关键.13．如图，把一张长方形纸条ABCD 沿EF 折叠，C 、D 两点落到'C 、'D 处.已知20DAC ∠=，且''//C D AC ，则AEF ∠的度数为( )A ．20B ．35C ．50D ．70【答案】B【解析】【分析】 依据C'D'//AC ，即可得到∠AHG=∠C′=90°，进而得出AGH 70∠=，由折叠可得，CFE GFE ∠∠=，由AD//BC ，可得CFE GEF ∠∠=，依据三角形外角性质得到1AEF GFE AGH 352∠∠∠===．【详解】如图，C'D'//AC ，，又DAC 20∠=，AGH 70∠∴=，由折叠可得，CFE GFE ∠∠=，由AD//BC ，可得CFE GEF ∠∠=，1AEF GFE AGH 352∠∠∠∴===， 故选：B ．【点睛】本题主要考查了平行线的性质以及三角形外角性质的运用，解题时注意：两直线平行，内错角相等．14．有下列说法：①有一个角为60°的等腰三角形是等边三角形；②三边长为、、3的三角形为直角三角形；③等腰三角形的两边长为3、4，则等腰三角形的周长为10；④一边上的中线等于这边长的一半的三角形是等腰直角三角形．其中正确的个数是（ ）A ．4个B ．3个C ．2个D ．1个【答案】C【解析】试题分析：根据等边三角形的性质可知，有一个角为60°的等腰三角形是等边三角形，故①正确；根据三边可知：，，3²=9，因此可知：，由勾股定理的逆定理可知其是直角三角形，故②正确；由等腰三角形的三边可知其边长为：3，3，4或3，4，4，则周长为10或11，故③不正确； 由一边上的中线等于这边长的一半的直角三角形是等腰直角三角形，故④不正确. 故选：C15．一个多边形的内角和是1260°，这个多边形的边数是（ ）A ．6B ．7C ．8D ．9【答案】D【解析】试题解析：设这个多边形的边数为n ，由题意可得：（n-2）×180°=1260°，解得n=9，∴这个多边形的边数为9，故选D ．16．已知直线m n ，将一块含45︒角的直角三角板ABC 按如图方式放置，其中斜边BC 与直线n 交于点D .若125∠=︒，则2∠的度数为（ ）A ．60︒B ．65︒C ．70︒D ．75︒【答案】C【解析】【分析】 先求出∠AED=∠1+∠B=25°+45°=70°，再根据平行线的性质可知∠2=∠AED=70°．【详解】设直线n 与AB 的交点为E 。