+用户材料子程序实例-Johnson-Cook+金属本构模型
- 格式:pdf
- 大小:395.97 KB
- 文档页数:18


《探寻Johnson-Cook模型参数的深度与广度》1. 引言在材料科学和工程领域中,Johnson-Cook模型是一种常用的材料本构模型,用于描述金属材料在高应变率和高温条件下的本构行为。
该模型的参数对于模拟和预测材料的力学性能至关重要。
本文将围绕Johnson-Cook模型参数展开讨论,深入探究其深度与广度。
2. Johnson-Cook模型简介Johnson-Cook模型是由Johnson和Cook在1983年提出,用于描述金属材料在动态加载和高温条件下的本构行为。
该模型基于实验数据,并考虑了材料的应变率、温度和应变硬化效应。
在Johnson-Cook模型中,参数包括A、B、n、C和m等,它们分别代表了材料的流动应力、应变硬化指数、热软化指数和材料的温度敏感性等重要性质。
3. 参数A的理解和研究3.1 参数A表示了材料的流动应力,在Johnson-Cook模型中具有重要的意义。
对于不同金属材料,参数A的取值不同,反映了材料的强度特征。
通过实验测试和数值模拟,研究人员可以获得不同条件下参数A的数值,从而深入理解材料的力学性能和变形行为。
3.2 个人观点:对于参数A的研究需要综合考虑材料的微观结构和宏观性能,通过建立参数A与其他参数的关联模型,可以更深入地理解材料的强度特征和动态响应。
4. 参数B、n的相关性研究4.1 参数B和n分别代表了材料的应变硬化指数和变形行为。
它们的取值对于描述材料的塑性变形过程至关重要,而且彼此之间存在一定的相关性。
通过实验测试和数值模拟,研究人员可以探究参数B、n 与材料微观结构和塑性变形特征之间的关联,以期深入地理解材料的本构行为。
4.2 个人观点:参数B和n的研究不仅需要考虑材料的单调拉伸试验数据,还需要结合压缩试验、扭转试验等多种试验数据,以全面、深入地评估材料的塑性变形特征和本构行为。
5. 参数C、m的温度敏感性研究5.1 参数C和m代表了材料的热软化指数和温度敏感性。
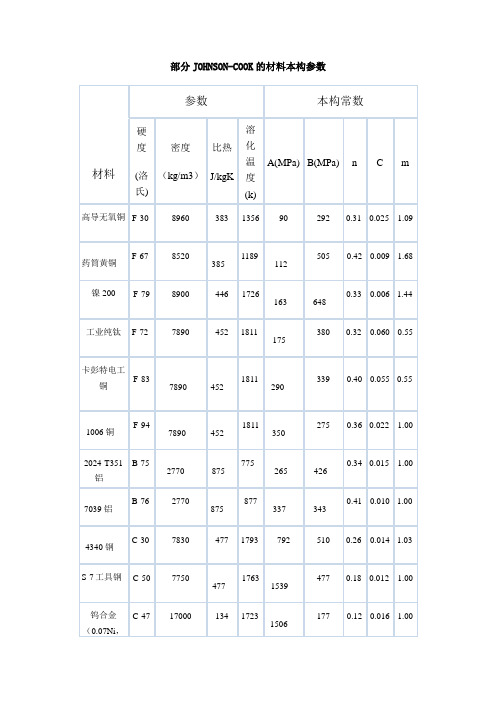
部分JOHNSON-COOK的材料本构参数0.03Fe )DU-75Ti C-45186004471473107911200.250.007 1.00•3#大中小发表于2007-9-24 14:30 只看该作者材料 2024-T3 Aluminum 的本构及失效参数材料2024-T3 AluminumA:369 MPa (53.517 ksi)B:684 MPa (99.202 ksi)n:0.73C:0.0083m:1.7D1:0.112D2:0.123D3:1.500D4:0.007D5:0.0本帖最近评分记录•wswu 贡献积分+1 感谢2007-9-27 07:44yema82811初级会员•个人空间•发短消息4#大中小发表于2007-9-24 14:49 只看该作者一些论文提及的JOHNSON COOK的参数一些论文提及的JOHNSON COOK的参数附件45号钢的动态力学性能研究.pdf (322.69 KB) 2007-9-24 14:49, 下载次数: 126本帖最近评分记录•加为好友•当前离线•wswu 贡献积分+1 感谢2007-9-27 07:45引用使用道具报告回复 TOPyema82811初级会员•个人空间•发短消息•加为好友•当前离线5#大中小发表于2007-9-24 14:51 只看该作者材料 Ti-6Al-4V Titanium材料Ti-6Al-4V TitaniumA:1098 MPa (159.246 ksi)B:1092 MPa (158.376 ksi)n:0.93C:0.014m:1.1D1:-0.090D2:0.270D3:0.480D4:0.014D5:3.870。

johnson-cook力学本构模型约翰逊-库克力学本构模型是一种描述固体材料的非线性变形和失效行为的力学模型,广泛应用于机械工程、材料科学、爆炸动力学等领域。
约翰逊-库克力学本构模型是由美国犹他大学的两位研究人员约翰逊和库克于1983年提出的。
它是一种经验性本构模型,适用于金属等大变形材料的失效特点研究。
该模型的优点是描述了材料的很多失效行为,如塑性、蠕变、断裂等。
缺点是需要较多的材料实验数据,且选取参数较困难。
该本构模型的核心在于使用一个修正的强度函数,该函数可以反映材料的动态增强和动态软化特性。
其中,强度函数表示为:σ=ε[(A+Bεp)(1-Clnεp)+Dln(εp/εp0)](1+ε˙/ε˙0)^n其中,σ为应力,ε为应变,εp为塑性应变,A、B、C、D、n、ε˙0、εp0均为本构模型参数。
该强度函数的特点如下:1.描述了动态增强和动态软化特性。
随着应变率的增加,材料的强度增加,但塑性应变也随之增加,达到一定程度后,材料变脆并出现软化。
2.考虑了材料的压缩和拉伸特性。
A和B参数控制材料在拉伸和压缩下的应力响应。
3.考虑了材料的应变率效应。
n参数表示应变率对材料强度的影响程度。
在该本构模型中,还引入了力学损伤参数D和反应率参数C。
D表示材料的累积剪切变形量对材料强度降低的影响,C则描述了材料在应变程度超过某一界限时出现的软化过程。
该本构模型的参数选择需要依据材料实验数据,通过拟合实验结果来确定,要求较高的实验技术和分析能力。
同时,该本构模型适用于大变形材料的研究,对于其他类型材料的研究需要进一步改进和完善。

abaqus中johnson-cook本构模型理解-回复ABAQUS是一种常用的有限元分析软件,广泛应用于工程领域中的结构和材料分析。
在ABAQUS中,材料模型非常重要,因为它决定了结构或部件的力学行为。
本文将重点介绍ABAQUS中的Johnson-Cook本构模型,解释其原理和应用。
一、Johnson-Cook本构模型的基本原理Johnson-Cook本构模型是一种广泛用于金属材料的本构模型,特别适用于高速冲击、爆炸、冲压等工况下的材料行为分析。
该模型基于强化塑性理论并考虑了材料的塑性变形、热软化和应变速率效应。
1. 强化塑性理论:Johnson-Cook本构模型基于强化塑性理论,该理论假设材料的变形主要由两个独立的部分组成:塑性变形和硬化。
塑性变形是由材料中的晶格滑移和形变所引起的,而硬化则是由位错运动和相互作用引起的。
强化塑性理论提供了描述材料行为的基础。
2. 热软化效应:Johnson-Cook本构模型考虑了材料在高温条件下的热软化效应。
在高温下,材料的塑性变形会导致局部温度升高,从而引起局部软化。
这种软化效应可以通过引入热软化参数来描述。
3. 应变速率效应:Johnson-Cook本构模型还考虑了材料的应变速率效应,即材料的塑性行为会随着应变速率的增加而发生变化。
这是因为在高应变速率下,材料的塑性变形速率超过了晶格中位错的运动速度,从而导致材料的变形行为变得复杂。
二、Johnson-Cook本构模型的参数含义与确定方法Johnson-Cook本构模型的参数包括强度系数、表面硬化系数、形变硬化指数、热软化参数和应变速率敏感指数等。
这些参数的确定非常重要,直接影响着本构模型的准确性和预测能力。
一般来说,可以通过实验测试和数值拟合来确定这些参数。
1. 强度系数和表面硬化系数:强度系数表示材料的杨氏模量和屈服强度之间的关系,是描述材料硬度的参数;表面硬化系数用于描述材料的初始硬化过程。
这两个参数可以通过单轴材料拉伸试验获得,并使用试验数据进行拟合来确定。

abaqus中johnson-cook本构模型理解-回复Abaqus中Johnson-Cook本构模型理解引言:材料的本构模型是描述材料力学行为的数学方程。
在有限元分析中,本构模型可以用于模拟材料的变形和损伤行为,从而预测材料在不同加载条件下的响应。
Johnson-Cook本构模型是一种常用的本构模型,广泛应用于材料科学和工程领域。
本文将从基本原理开始,逐步解释和理解Abaqus 中Johnson-Cook本构模型。
1. 弹塑性本构模型首先需要了解的是,弹塑性本构模型是最基本的材料模型之一。
它基于线弹性理论,假设材料在小应变范围内具有弹性行为,而在大应变范围内表现出塑性行为。
弹塑性本构模型可以描述材料的应力-应变关系,并预测材料的弹性变形和塑性变形。
2. 材料的温度效应在考虑Johnson-Cook本构模型之前,还需要考虑材料的温度效应。
温度对材料力学行为的影响是复杂而重要的。
温度的增加可以引起材料的软化、蠕变和断裂等现象。
因此,在模拟材料行为时,必须考虑材料的温度效应,并选择适当的本构模型来描述。
3. Johnson-Cook本构模型的基本原理Johnson-Cook本构模型是一种经验模型,用于描述材料的塑性行为和温度效应。
它采用以下形式的应力-应变关系:σ= (A + B ε^n) (1 + C ln(ε˙/ε˙_0))^m (1 - T/T_m)^p其中,σ是材料的应力,ε是应变,ε˙是应变速率,T是材料的温度,A、B、C、n、m、p和T_m是需要通过实验来确定的材料参数。
4. 材料参数的确定为了使用Johnson-Cook本构模型,需要通过实验来确定材料参数。
这些参数通常由材料的拉伸实验和冲击实验等得到。
拉伸实验可以提供材料的应力-应变曲线,以及材料的屈服强度和断裂应变等信息。
冲击实验可以提供材料的应变率敏感性和断裂韧性等信息。
根据实验数据,可以使用不同的方法来确定Johnson-Cook本构模型的参数。
JOHNSONCOOK资料及一些材料参数Johnson Cook模型是一种常用的材料本构模型,广泛应用于模拟高速冲击和爆炸等复杂加载条件下的材料行为。
下面将介绍Johnson Cook模型的相关资料和一些材料参数。
Johnson Cook资料:Johnson Cook模型由Johnson、Cook等人在1983年提出,主要用于预测材料在高应变率和高温条件下的本构行为。
该模型可以描述材料的弹塑性行为、变形硬化和动态效应。
材料参数:1. 体积塑性应变(Volumetric Plastic Strain):材料在加载过程中发生塑性变形的体积分数。
2. 动态变形硬化参数(Dynamic Strain Hardening Coefficient):描述材料在动态加载下的硬化行为。
3. 温度变形硬化参数(Temperature Strain Hardening Coefficient):描述材料在高温下的变形硬化行为。
4. 动态变形软化参数(Dynamic Strain Softening Coefficient):描述材料在动态加载下的软化行为。
5. 温度软化参数(Temperature Softening Coefficient):描述材料在高温下的软化行为。
6. 强化系数(Strain-Rate Hardening Exponent):描述材料的强化行为。
7.常数A和B:用于描述材料的流动应力曲线。
以上的材料参数需要通过试验数据或其他可靠途径进行测量或者估算。
一般来说,可以使用高速拉伸、压缩或者冲击试验来获得涉及材料的动态和高应变率加载条件下的数据。
除此之外,还需要在模型中输入材料的温度和应变率等参数,以准确描述材料的行为。
Johnson Cook模型的应用广泛,包括高速碰撞、爆炸冲击、金属成型等领域。
通过合理地选择和确定材料参数,可以准确地模拟材料在复杂加载条件下的变形行为和破坏过程,为工程设计和分析提供参考依据。
johnson-cook本构方程Johnson-Cook本构方程是一种用于描述材料塑性行为的经验模型,在机械材料力学分析中被广泛应用。
本构方程用于描述材料的应力-应变关系,特别适用于高温下变形和失效行为的描述,如金属加工过程中的塑性变形、冲击、爆炸以及动态加载等。
Johnson-Cook方程可以用以下形式表示:$$\sigma = (A + B \cdot \varepsilon^n) \cdot (1 + C \cdot\ln(\dot{\varepsilon_{\text{p}}})) \cdot \left(1 - T^n\right)$$其中,$\sigma$ 是材料的真实应力,$\varepsilon$ 是真实应变,$\dot{\varepsilon_\text{p}}$ 是有效塑性应变速率,$T$ 是材料的温度,$A$、$B$、$C$、$n$ 是方程的参数。
$A$、$B$、$C$是与材料性质相关的常数,可以通过实验测试来确定。
$n$是描述材料的硬化指数,表示应力与应变之间的关系。
$T$是描述温度对材料塑性行为的影响的参数。
在Johnson-Cook方程中,$B \cdot \varepsilon^n$ 部分表示材料的弹性行为,$A$ 是材料的流动应力,$C \cdot\ln(\dot{\varepsilon_{\text{p}}})$ 部分表示材料的动态增强或软化行为,$1 - T^n$ 部分表示材料在高温下的流变特性。
该方程的提出是基于大量试验数据的统计分析,通过拟合实验数据来确定其参数。
Johnson-Cook本构方程具有一定的适用范围,通常适用于金属材料的高速塑性变形行为,并在许多实际应用中取得了良好的结果。
在实际应用中,需要根据具体材料和试验数据来确定Johnson-Cook方程的参数。
可以通过实验测试如拉伸实验、压缩实验和冲击实验来获取材料的应力-应变数据,然后对实验数据进行曲线拟合来确定方程的参数。