普朗克公式普朗克黑体辐射公式为

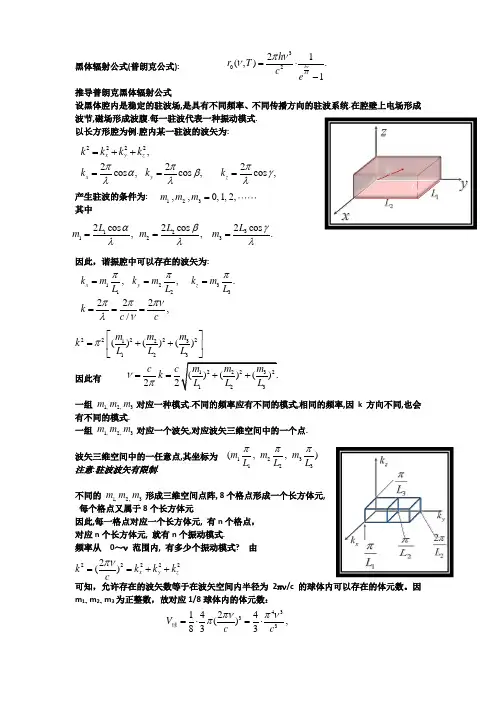
黑体辐射公式(普朗克公式):推导普朗克黑体辐射公式设黑体腔内是稳定的驻波场,是具有不同频率、不同传播方向的驻波系统.在腔壁上电场形成波节,磁场形成波腹.每一驻波代表一种振动模式. 以长方形腔为例.腔内某一驻波的波矢为:产生驻波的条件为: 其中因此，谐振腔中可以存在的波矢为:因此有一组 对应一种模式.不同的频率应有不同的模式,相同的频率,因k 方向不同,也会有不同的模式. 一组 对应一个波矢,对应波矢三维空间中的一个点.波矢三维空间中的一任意点,其坐标为 注意:驻波波矢有限制.不同的 形成三维空间点阵, 8个格点形成一个长方体元, 每个格点又属于8个长方体元因此,每一格点对应一个长方体元, 有n 个格点， 对应n 个长方体元, 就有n 个振动模式.频率从 0～ν 范围内, 有多少个振动模式? 由 可知，允许存在的波矢数等于在波矢空间内半径为2πν/c 的球体内可以存在的体元数。

因m 1、m 2、m 3为正整数，故对应1/8球体内的体元数： 3221(,).1h kTh r T ce νπνν=⋅-2222,x y z k k k k =++2cos ,x k παλ=2cos ,y k πβλ=2cos ,zk πγλ=123,,0,1,2,m m m =112cos ,L m αλ=222cos ,L m βλ=332cos .L m γλ=11,x k m L π=22,y k m L π=33.z k m L π=222,/k c c πππνλν===22222312123()()()m m m k L L L π⎡⎤=++⎢⎥⎣⎦222312123()()().22m mm c c k L L L νπ==++1,2,3m m m 1,2,3m m m 123123(,,)m m m L L L πππ1,2,3m m m 222222()x y z k k k k cπν==++43331424(),833V c cπνπνπ=⋅=⋅球体元的体积:其中，V =L 1L 2L 3为谐振腔的体积 体元数:考虑到两个偏振态:将上式两边除以V 并对ν 微分,得单位体积频率在ν～ d ν 范围内的本征模数. 普朗克认为,黑体腔器壁是不同频率的线性谐振子,由能量子假说,这些谐振子取分立的值,按照玻耳兹曼定理,具有能量 的振动几率有如下关系所以,平均能量为壁上振子分布应与驻波分布相同,因此单位体积内频率范围在 ν ~ d ν 内的能量密度为黑体单色辐出度为二 证明关系式热辐射以光速c 向各个方向辐射，因此，在任意一方向上的立体角d Ω内，频率为ν的辐出度为在小孔外２π立体角空间内总辐射能量为 3123.V L L L Vππππ=⋅⋅=元334,3V V V c πν=⋅球元338.3N V cνπν=⋅238,dn d cπνν=0,h εν=0,m εε=0000,,2,3εεε230001:::kTkTkTeeeενενεν---0000000.11m kTm kT m h kTkTm m eh ee eεεενεενε--∞=∞====--∑∑3381().1h kTh d ceνπνρνν=⋅-30221(,)(,).41h kTc h r T T c eνπννρν==⋅-22001(,)(,)cos sin (,)44cr T c T d d T ππνρνθθθφρνπ==⎰⎰0(,)(,).4cr T T νρν=0(,)(,)cos ,4cdr T T d νρνθπ=Ω。

欢迎阅读普朗克黑体辐射公式的推导所谓的黑体是指能吸收射到其上的全部辐射的物体，这种物体就称为绝对黑体，简称黑体。

黑体辐射：由这样的空腔小孔发出的辐射就称为黑体辐射。

辐射热平衡状态:处于某一温度T 下的腔壁，单位面积所发射出的辐射能量和它所吸收的辐射能量相等时，辐射达到热平衡状态。

实验发现：热平衡时，空腔辐射的能量密度，与辐射的波长的分布曲线，其形状和位置只与黑体的绝对温度T 有关而与黑体的形状和材料无关。

实验得到： 1.Wien 公式从热力学出发加上一些特殊的假设，得到一个分布公式：Wien 公式在短波部分与实验还相符合，长波部分则明显不一致。

2. Rayleigh-Jeans 公式Rayleigh-Jeans 公式在低频区和实验相符，但是在高频区公式与实验不符，并且∞→=⎰∞v v d E E ，既单位体积的能量发散，而实验测得的黑体辐射的能量密度是4T E σ=，该式叫做Stefan-Bolzmann 公式，σ叫做Stefan-Bolzmann 常数。

3. Planck 黑体辐射定律1900年１２月１４日Planck 提出如果空腔内的黑体辐射和腔壁原子处于平衡，那么辐射的能量分布与腔壁原子的能量分布就应有一种对应。

作为辐射原子的模型，Planck 假定：（1）原子的性能和谐振子一样，以给定的频率v 振荡；（2）黑体只能以E=hv 为能量单位不连续的发射和吸收辐射能量，而不是象经典理论所要求的那样可以连续的发射和吸收辐射能量。

得到：νννπνρνd kT h C h d ⎪⎪⎭⎫ ⎝⎛-=1)/exp(1833该式称为Planck 辐射定律 h 为普朗克常数，h=s j .10626.634-⨯4，普朗克的推导过程：把空窖内的电磁波分解为各个频率的简振振动，简振模的形式最后为).(),(wt r K i k k e C t r -=αβψ，为常系数振方向，表示两个互相垂直的偏ααk C 2,1=每一个简振模在力学上等价于一个自由度，记频率在()νννd +,内的自由度数为()ννd g ， 则（0，v ）范围内的总自由度数G(v)与g(v)的关系为()()ννννd g G ⎰=0。

量子力学解释黑体辐射谱黑体辐射谱是指由具有完全吸收和完全发射性质的物体所辐射出的电磁波谱。

在经典物理学中，黑体辐射无法得到很好的解释，而量子力学的发展则提供了更准确的解释和计算方法。

量子力学的基本原理是，微观粒子的能量是量子化的，也就是说，存在一个最小的能量单位，即光子。

光子是电磁波的粒子化表现，其能量与光的频率有关系，由普朗克公式E=hf给出，其中h为普朗克常数，f为光的频率。

在黑体辐射中，物体吸收的能量会导致其内部电子发生激发和跃迁，而发射出的能量会形成辐射光子。

根据量子力学的原理，能量的量子化导致了辐射光子的能量也是离散的。

具体来说，当物体处于较高的温度时，其内部的电子会被激发到较高的能级上，当电子从一个能级跃迁到另一个能级时，能量差可以用一个光子的能量来表示，这个光子的能量对应着一个特定的波长或频率。

根据量子力学的理论，我们可以计算出黑体辐射谱的分布。

普朗克黑体辐射定律给出了黑体辐射功率与波长或频率的关系。

根据定律，黑体辐射功率与波长的关系可以用一个公式来表示，即普朗克公式:B(λ, T) = (2hc^2/λ^5) × (1/(e^(hc/λkT) - 1)其中，B(λ, T)表示单位时间内单位面积的黑体辐射功率，λ表示波长，T表示温度，h为普朗克常数，c为光速，k为玻尔兹曼常数。

根据普朗克公式，我们可以得到黑体辐射谱的分布图像，即黑体辐射谱线。

在低频段（长波段），辐射能量较低，谱线呈现为一个平缓的曲线；随着频率的增加，能量也随之增加，曲线逐渐变得陡峭。

当频率趋近于无穷大时，辐射能量趋于零。

这个分布被称为黑体辐射曲线，也被称为普朗克曲线。

量子力学的解释还提供了对黑体辐射的理论计算。

通过量子力学的数学模型，我们可以计算特定温度下的黑体辐射谱线，并与实验数据进行比较。

这种计算可以更准确地描述和解释黑体辐射的特性。

总的来说，量子力学提供了对黑体辐射谱的解释和计算方法。

通过量子化的能量和光子的概念，我们可以理解和描述黑体辐射谱线的分布规律。

普朗克黑体公式普朗克黑体公式一、什么是普朗克黑体公式？普朗克黑体公式是描述物体辐射能谱特性的公式，由德国物理学家马克斯·普朗克在1900年发现并提出。

它描述了黑体辐射发射的热能随着波长的变化而发生的变化，是理论上探讨电磁波辐射的一个基本理论。

二、普朗克黑体公式的推导普朗克在探讨黑体辐射问题时，通过对辐射器内发射的电磁波的频率与能量的关系进行研究，得出了他 berprzipslichen answer ，即离散的能量量子概念，这就是著名的基本性原理。

在此基础之上，普朗克成功地推导出了描述黑体辐射特性的公式，即普朗克黑体辐射公式。

根据公式，黑体辐射发射的能量谱与温度有关，其随波长λ变化的形状可以用以下公式表示：B(λ, T) = (2hc²/λ⁵) × 1/(ehc/λkT - 1)其中，B(λ, T)表示黑体在特定波长λ和温度T下辐射发射出的能量，h为普朗克常量，c为光速，k为玻尔兹曼常量，e为自然对数。

三、普朗克黑体公式的应用普朗克黑体公式在物理学、工程学、天文学等领域都有广泛的应用。

其中，最为关注的是黑体辐射的特性，因为这关系到很多光学设备的运用。

例如，在卫星辐射成像技术中，黑体的作用是模拟外部环境中的物理状态，通过测量其辐射能够精确计算卫星传感器输出的信号值。

同时，在光电探测、激光测距、夜视设备、光通讯和纳米技术领域等，都有普朗克黑体公式的应用。

四、结语普朗克黑体公式对于描述物体辐射能谱特性提供了重要的理论基础，其成功地解释了许多实验现象，同时也推动了原子物理学、固体物理学和光学等领域的发展。

在现代科技中，普朗克黑体公式的应用将会更加广泛，为科学技术的发展做出更加积极的贡献。

普朗克公式光子能量的公式普朗克公式是描述物体辐射能量的量子化现象的公式，由德国物理学家马克斯·普朗克于1900年提出。

此公式被用来解释黑体辐射的谱线分布，成为量子力学的起点之一，为后来的量子理论打下了基础。

下面将详细介绍普朗克公式以及光子能量的计算公式。

首先，我们来看一下普朗克公式的表达形式。

普朗克公式可以表示为：E=h*ν其中，E表示光子能量，h是普朗克常数，ν表示光子的频率。

普朗克常数h的数值为6.63×10^(-34)J·s。

该常数是量子力学中的基本物理常数之一，与光子的能量密切相关。

光子的频率ν表示的是光的震动次数，是指单位时间内振动的次数。

频率与光子能量之间的关系由普朗克公式给出，可以看出光子的能量与频率成正比。

我们知道，光的波动性与粒子性都是存在的，光的能量可以用光子能量来表示。

光子是光的量子，具有能量、动量等粒子的特性。

光子能量与光子的频率呈正比，频率越高，光子能量越大。

根据普朗克公式，我们可以计算光子的能量。

以可见光为例，可见光的频率范围为4×10^14Hz到8×10^14Hz。

假设光的频率为7×10^14Hz，则根据普朗克公式，计算得到光子的能量为：E=6.63×10^(-34)J·s*7×10^14Hz=4.641×10^(-19)J这就是光子的能量。

这个能量非常微小，对比于常见的物质的能量，可以说是非常微弱的。

根据普朗克公式，我们可以进一步了解光的量子化现象。

根据公式，我们可以看到光子能量和频率之间的关系是线性的，而不是连续的。

这就意味着，光的能量不是连续变化的，而是量子化的。

这一发现对量子力学的发展起到了重要的推动作用。

普朗克公式揭示了能量的离散性，为后来的量子理论奠定了基础。

它也是量子力学中能量量子化的重要证据之一总结起来，普朗克公式是描述物体辐射能量的量子化现象的公式，根据该公式，光子的能量与光子的频率成正比。

二维空间平衡辐射的普朗克公式普朗克公式是物理学中的重要公式之一，它描述了二维空间中的平衡辐射。

平衡辐射是指一个物体既吸收辐射，又发射辐射，且吸收和发射之间达到了平衡状态。

普朗克公式的推导基于黑体辐射的研究。

黑体是一种能够吸收并完全发射所有入射辐射的理想物体。

实际上，没有物体完全符合黑体的特性，但黑体的研究可以为我们提供有关辐射的重要信息。

普朗克公式的表达式为：B(λ, T) = (2hc²/λ⁵) / (exp(hc/λkT) - 1)其中，B(λ, T)代表单位面积单位波长的辐射能量，λ为波长，T为绝对温度，h为普朗克常数，c为光速，k为玻尔兹曼常数。

从公式中可以看出，辐射能量与波长的关系是一个反比关系，即波长越短，辐射能量越大。

这符合我们在日常生活中的观察，例如太阳辐射的能量主要集中在可见光波段，而紫外线和红外线的能量较低。

另外，从公式中还可以看出，辐射能量与温度的关系是一个指数函数。

随着温度的升高，辐射能量呈指数增长。

这也符合热辐射的特性，即温度越高，物体的辐射能力越强。

普朗克公式的应用非常广泛。

它不仅可以用于黑体辐射的研究，还可以用于描述其他类型的辐射，如电磁辐射和热辐射。

在实际应用中，普朗克公式可以用于计算物体的辐射功率和能量分布。

通过测量物体的辐射能量，我们可以了解物体的热特性，如温度和能量分布。

此外，普朗克公式还为研究热辐射的能量转换提供了基础。

热辐射的能量转换是指辐射能量的吸收和发射过程。

根据普朗克公式，我们可以计算辐射能量的吸收率和发射率，进而研究物体的热平衡状态。

总之，普朗克公式是研究二维空间中平衡辐射的重要工具。

它描述了辐射能量与波长和温度的关系，为我们理解辐射现象提供了基础。

通过应用普朗克公式，我们可以计算辐射能量、了解物体的热特性，以及研究热辐射的能量转换过程。

这对于物理学、天文学、材料科学等领域的研究具有重要意义。

描述黑体辐射强度与波长关系全文共四篇示例，供读者参考第一篇示例：黑体辐射是热力学中一种重要的辐射现象，指的是一个物体由于其温度而产生的辐射。

黑体辐射的性质对于理解物质的发光、吸收和辐射具有重要意义，也是研究热辐射和热力学问题的基础。

在黑体辐射中，辐射强度与波长之间存在着一定的关系，这种关系在物理学中被称为黑体辐射定律。

根据普朗克量子理论和玻尔能级理论，黑体辐射的辐射强度与波长的关系可以用普朗克-黑体辐射定律来描述。

根据普朗克-黑体辐射定律，黑体每个频率上的辐射强度与频率成正比，即B_\nu(\nu,T)=\dfrac{\alpha\nu^3}{e^{\dfrac{h\nu}{kT}}-1}。

其中B_\nu(\nu,T)表示频率为\nu时的辐射强度，T表示温度，\alpha为常数，h为普朗克常数，k为玻尔兹曼常数。

根据维恩位移定律，黑体谱线的辐射峰值波长\lambda_{max}与温度成反比，即\lambda_{max}T=\text{常数}。

通过观察黑体辐射谱线的实验数据，科学家们发现，随着温度的升高，黑体辐射谱线的峰值向短波方向移动，即辐射强度峰值对应的波长减小。

这就是所谓的短波红移现象。

这一现象可以由维恩位移定律很好地解释。

维恩位移定律告诉我们，热辐射的波长与其发射温度有直接关系，温度越高，波长越短，辐射强度峰值对应的波长也会随之减小。

除了维恩位移定律外，还有一条与黑体辐射强度与波长关系密切相关的定律，那就是斯特藩-玻尔兹曼定律。

斯特藩-玻尔兹曼定律告诉我们，黑体辐射强度与波长的关系并不仅仅取决于温度，还取决于频率的幂次，即B_\lambda(\lambda,T)=\dfrac{\beta}{\lambda^5(e^{\dfrac{c}{\la mbda T}}-1)}。

其中B_\lambda(\lambda,T)表示波长为\lambda时的辐射强度，\beta为常数，c为光速。

从斯特藩-玻尔兹曼定律可以看出，随着波长的增加，辐射强度会迅速减小，这也是为什么热辐射在可见光谱范围外很难观测到的原因之一。

普朗克黑体辐射公式
普朗克黑体辐射公式是物理学中比较重要的一个重要方程式，由德国
物理学家威廉·黑体（Max Planck）发现于1900年。

它用于解释热辐射，描述在一个热激活的物体和它的环境之间相互作用的过程，以及它们
之间所发生的物理现象。

1. 关于普朗克黑体辐射公式
a. 历史背景
i. 普朗克黑体辐射公式是由德国物理学家威廉·黑体发现于1900年。

ii. 这个公式诞生在热学和热辐射学发展史上，是物理学界为解释热辐射实验结果和理论，解释它们与其它宏观物理现象发生关系而产生的
重要结论。

2. 公式内容
a. 普朗克黑体辐射公式用常量h对辐射能量做出精确的估计：辐射能
量是以频率的平方乘上h的乘积，乘上一个函数表达的常数。

3. 在实际应用中
a. 普朗克黑体辐射公式描述了物体和它的环境之间传热的过程，因此
在热科学中有着最为重要的意义。

b. 这个公式也用于工业应用，可用于估算热导率，对加热过程和发热过程的估算都比较有用。

c. 此外，在这个方程式的帮助下，人们可以计算固态物质的热能容量，从而研究受热的过程，比如冷冻、冷却和加热这些过程。

普朗克常数公式
普朗克常数公式是量子物理学中的一个基本公式，它涉及到微观世界的最小能量单位，即量子。

普朗克常数由德国物理学家马克斯·普朗克于1900 年提出，用以解释黑体辐射现象。

它标志着量子力学的诞生，对现代物理学产生了深远影响。

普朗克常数的定义中包含了量子化的概念，即能量以离散的形式传递。

普朗克公式为E = hf，其中E 表示能量，h 表示普朗克常数，f 表示频率。

这个公式表明，能量与频率成正比，且最小能量单位为普朗克常数。

普朗克常数在物理学中有广泛的应用，如在量子力学中描述电子在原子中的运动；在原子物理学中解释原子光谱现象；在宇宙学中，普朗克常数与宇宙微波背景辐射有关，从而可以推算出宇宙的年龄。

此外，普朗克常数在暗物质与暗能量的研究中也起到了关键作用。

普朗克常数的测量与精度在科学发展中具有重要意义。

历史上，科学家们通过多种方法对普朗克常数进行了测量，如使用热辐射、电子回旋加速器等。

现代测量方法已经达到了极高的精度，如利用激光冷却原子技术等。

在未来科学的发展中，普朗克常数将继续发挥关键作用。

例如，在量子计算、量子通信和量子材料等领域，普朗克常数将作为基本参数推动技术的进步。

普朗克黑体辐射公式的推导所谓的黑体是指能吸收射到其上的全部辐射的物体，这种物体就称为绝对黑体，简称黑体。

黑体辐射：由这样的空腔小孔发出的辐射就称为黑体辐射。

辐射热平衡状态:处于某一温度T 下的腔壁，单位面积所发射出的辐射能量和它所吸收的辐射能量相等时，辐射达到热平衡状态。

实验发现：热平衡时，空腔辐射的能量密度，与辐射的波长的分布曲线，其形状和位置只与黑体的绝对温度T 有关而与黑体的形状和材料无关。

实验得到： 1.Wien 公式从热力学出发加上一些特殊的假设，得到一个分布公式：Wien 公式在短波部分与实验还相符合，长波部分则明显不一致。

2. Rayleigh-Jeans 公式Rayleigh-Jeans 公式在低频区和实验相符，但是在高频区公式与实验不符，并且∞→=⎰∞v v d E E ，既单位体积的能量发散，而实验测得的黑体辐射的能量密度是4T E σ=，该式叫做Stefan-Bolzmann 公式，σ叫做Stefan-Bolzmann 常数。

3. Planck 黑体辐射定律1900年１２月１４日Planck 提出如果空腔内的黑体辐射和腔壁原子处于平衡，那么辐射的能量分布与腔壁原子的能量分布就应有一种对应。

作为辐射原子的模型，Planck 假定：（1）原子的性能和谐振子一样，以给定的频率v 振荡； （2）黑体只能以E=hv 为能量单位不连续的发射和吸收辐射能量，而不是象经典理论所要求的那样可以连续的发射和吸收辐射能量。

得到：νννπνρνd kT h C h d ⎪⎪⎭⎫ ⎝⎛-=1)/exp(1833该式称为Planck 辐射定律 h 为普朗克常数，h=s j .10626.634-⨯4，普朗克的推导过程：把空窖内的电磁波分解为各个频率的简振振动，简振模的形式最后为).(),(wt r K i k k e C t r -=αβψ，为常系数振方向，表示两个互相垂直的偏ααk C 2,1=每一个简振模在力学上等价于一个自由度，记频率在()νννd +,内的自由度数为()ννd g ，则（0，v ）范围内的总自由度数G(v)与g(v)的关系为()()ννννd g G ⎰=0。

普朗克公式-CAL-FENGHAI.-(YICAI)-Company One1普朗克公式的那些事材料科学与工程学院材料物理张培学号：23 19世纪末，经典统计物理学在研究黑体辐射时遇到了巨大的困难：由经典的能量均分定理导出的瑞利-金斯公式在短波方面得出同黑体辐射光谱实验结果相违背的结论。

同时，维恩公式则仅适用于黑体辐射光谱能量分布的短波部分。

也就是说，当时还未能找到一个能够成功描述整个实验曲线的黑体辐射公式。

为了解决经典物理学19世纪末面临的“紫外灾难”，普朗克吸收了维恩公式和瑞利－金斯公式的长处，利用热力学理论和熵能关系，于1900年10月19日“猜测”出了普朗克公式，经鲁本斯实验验证完全正确，很好地解决了前人的黑体辐射理论与实验结果的矛盾。

物理学中，普朗克黑体辐射定律（也简称作普朗克定律或黑体辐射定律）（英文：Planck's law,Blackbody radiation law ）是用于描述在任意温度下，从一个黑体中发射的电磁辐射的辐射率与电磁辐射的频率的关系公式。

这里辐射率是频率的函数：这个函数在时达到峰值。

如果写成波长的函数，在单位立体角内的辐射率为注意这两个函数具有不同的单位：第一个函数是描述单位频率间隔内的辐射率，而第二个则是单位波长间隔内的辐射率。

因而和并不等价。

它们之间存在有如下关系：通过单位频率间隔和单位波长间隔之间的关系，这两个函数可以相互转换：下表中给出了函数中每一个物理量的意义和单位：物理量含义国际单位制厘米-克-秒制辐射率，在单位时间内从单位表面积和单位立体角内以单位频率间隔或单位波长间隔辐射出的能量焦耳·秒-1·米-2·球面度-1·赫兹-1，或焦耳·秒-1·米-2·球面度- 1·米-1尔格·秒-1·厘米-2·赫兹-1·球面度-1频率赫兹(Hz) 赫兹波长米(m)厘米（cm）黑体的温度开尔文(K) 开尔文普朗克常数焦耳·秒 (J·s)尔格·秒（erg·s）光速米/秒(m/s)厘米／秒（cm/s）自然对数的底，...无量纲无量纲玻尔兹曼常数焦耳／开尔文(J/K)尔格／开尔文 (erg/K)在1900年10月19日，在德国物理学会的会议上，普朗克基于一个根据实验数据猜测出来的内插公式,提出了黑体辐射公式:当时对黑体辐射实验测量工作做得较多的有鲁本斯。

第一章1.1 由黑体辐射公式导出维恩位移定律： 能量密度极大值所对应的波长λm 与温度T 成反比，即λm T = b （常量）；并近似计算b 的数值，准确到两位有效数字。

解：黑体辐射的普朗克公式为：)1(833-=kT h e c h νννπρ ∵ v=c/λ∴ dv/dλ= -c/λ²又 ∵ ρv dv= -ρλdλ∴ ρλ=-ρv dv/dλ=8πhc/[λ5(ehc/λkT-1)] 令x=hc/λkT ,则 ρλ=8πhc(kT/hc)5x 5/(e x -1)求ρλ极大值，即令dρλ(x)/dx=0，得：5(e x -1)=xe x可得： x≈4.965∴ b=λm T=hc/kx≈6.626 *10-34*3*108/(4.965*1.381*10-23)≈2.9*10-3（m K ）1.2√. 在0 K 附近，钠的价电子能量约为3电子伏，求其德布罗意波长。

解： h = 6.626×10-34 J ·s , m e = 9.1×10-31 Kg,， 1 eV = 1.6×10-19 J故其德布罗意波长为：07.0727A λ=== 或λ= h/2m E = 6.626×10-34/(2×9.1×10-31×3×1.6×10-19)1/2 ≈ 7.08 Å1.3 √.氦原子的动能是E=32KT （K B 为波尔兹曼常数），求T=1 K 时，氦原子的德布罗意波长。

解：h = 6.626×10-34 J ·s , 氦原子的质量约为=-26-2711.993104=6.641012kg ⨯⨯⨯⨯ , 波尔兹曼常数K B =1.381×10-23 J/K故其德布罗意波长为：λ×10-34/ (2×-276.6410⨯×1.5×1.381×10-23×1)1/2≈01.2706A或λ= 而KT E 23=601.270610A λ-==⨯1.4利用玻尔-索末菲量子化条件，求：a ） 一维谐振子的能量：b ） 在均匀磁场作圆周运动的电子轨道的可能半径。