当前位置：文档之家 › 第14章 刚体定点转动与刚体一般运动——【理论力学课件】

第14章 刚体定点转动与刚体一般运动——【理论力学课件】

  • 格式：pdf
  • 大小：848.61 KB
  • 文档页数：45

下载文档原格式

  / 45

合集下载

刚体的定轴转动及转动定律PPT学习教案

刚体的定轴转动及转动定律PPT学习教案

；（3）t = 6 s 时飞轮边缘上一点的线速度、切向加速度和法
向加速度 .
解：
（1）
5π rads , 1
t = 30 s 时，
0
0.
设 t= 0s
时，
.飞轮做匀减速运动
0 0
0 0 5π rad s1 π rad s2
t
30
6
飞轮 30 s 内rad 2 2 (π 6)
解：
dm dV 2 r h dr
其中：
m m
V r 2 h
所以：
J r 2 dv m
R 2rh r 2dr
0
1 mR2
2
第24页/共28页
第25页/共28页
四 平行轴定理 质量为 的刚体，如果对其质心轴的转动惯量 为 ，则对任一与该轴平行，相距为 的转轴的转动惯量为：
0.105
m s2
an r 2 0.2´ (4 π)2 m ×s2 31.6 m ×s2
第10页/共28页
例2 在高速旋转的微型电机里，有一圆柱形转子可绕垂直其横截
面后通，过其中转心速的达轴到转18动00.0开r·m始in时-1，. 已它知的转角子速的度角加0 速度0与，时经间3成00正s 比
第12页/共28页
一 力矩 刚体上P点的力 对转轴 Z 的力矩为：
大小： 方向：右手定则
例
F
M rF
M
M Fr sin Fd
F
F
Fi 0 , Mi 0
F
F
z
M
r
O
d
F *P
Fi 0 , Mi 0
第13页/共28页
讨论 1）若力 不在转动平面内
则：

《刚体的运动》课件

《刚体的运动》课件

约束的类型与特点
● 约束类型：固定约束、滑动约束、柔性约束 ● 约束特点：限制刚体运动方向、限制刚体运动范围、影响刚体运动状态 约束的类型与特点
• 约束的类型与特点 ● 固定约束：限制刚体在某一方向的移动，使刚体在空间保持相对位置不变。 ● 滑动约束：允许刚体在某一方向上移动，但限制其转动。 ● 柔性约束：通过弹性元件限制刚体的运动，具有非线性特性。 约束的类型与特点
自由度与约束的关系
自由度的定义：刚体在空间中的自由程度，由其质心位置和转动轴决定。
约束的类型：固定约束、滑动约束、柔性约束等，对刚体的自由度产生限制。
自由度与约束的关系：刚体受到约束后，其自由度会相应减少，但仍保持其整体运动状态。
实际应用：在机械设计、航空航天等领域，需要合理考虑刚体的自由度与约束关系，以确保 系统的稳定性和性能。
刚体的平面运动 可以分解为平移 和绕某点的转动
平面运动中，刚 体的形状和大小 保持不变
平面运动中，刚 体的重心轨迹是 平面曲线
平面运动的特点
刚体平面运动定义
刚体平面运动分类
刚体平面运动性质
刚体平面运动实例
平面运动的合成与分解
平面运动的定义与分类 平面运动的合成：矢量法与解析法 平面运动的分解：定轴转动与平移 平面运动的应用实例
定轴转动的特点
刚体绕某一轴线 转动
转动轴固定不动
刚体上任意一点 到转动轴的距离 相等
刚体上任意两点 间的连线在转动 过程中保持不变
定轴转动的角速度和角加速度
角速度定义：刚 体绕定轴转动的 角速度是单位时 间内转过的弧度 （或角度）
角加速度定义： 刚体绕定轴转动 的角加速度是单 位时间内转过的 弧度/秒^2（或 角度/秒^2）

《刚体的定轴转动》课件

《刚体的定轴转动》课件

实例二
陀螺在受到外力矩作用后发生定轴转动。分析过程中应用了转动定 律，解释了陀螺的进动现象。
实例三
电风扇在启动时，叶片的角速度从零逐渐增大到稳定值。分析过程中 应用了转动定律，解释了电风扇叶片角速度的变化规律。
CHAPTER
03
刚体的定轴转动的动能与势能
动能与势能的定义
动能定义
物体由于运动而具有的能量，用 符号E表示，单位是焦耳(J)。
势能定义
物体由于相对位置或压缩状态而 具有的能量，常用符号PE表示， 单位是焦耳(J)。
刚体的定轴转动动能与势能的计算
转动动能计算
刚体的转动动能等于刚体绕定轴转动的动能，等于刚体质量与角速度平方乘积的一半， 即E=1/2Iω^2。
势能计算
刚体的势能等于刚体各质点的势能之和，等于各质点的位置坐标与相应的势能函数的乘 积之和。
01
数学表达式：Iα=M
02
转动惯量的计算：根据刚体的质量和形状，可以计算出其转动
惯量。
角加速度的计算：根据作用在刚体上的外力矩和刚体的转动惯
03
量，可以计算出其角加速度。
转动定律的实例分析
实例一
匀速转动的飞轮在受到阻力矩作用后，角速度逐渐减小，直至停止 转动。分析过程中应用了转动定律，解释了飞轮减速直至停止的原 因。
CHAPTER
02
刚体的定轴转动定律
转动定律的内容
刚体定轴转动定律
对于刚体绕固定轴的转动，其转动惯量与角加速度乘积等于作用 在刚体上的外力矩之和。
转动定律的物理意义
描述了刚体在力矩作用下绕固定轴转动的运动规律。
转动定律的适用范围
适用于刚体在力矩作用下的定轴转动，不适用于质点和弹性体的转 动。

刚体的定点运动与一般运动动力学教学课件

刚体的定点运动与一般运动动力学教学课件
详细描述
根据刚体运动的平面性，一般运动可 以分为平面运动和空间运动。平面运 动是指刚体的所有点在同一平面内运 动，空间运动则涉及刚体的三维空间 运动。一般运动的动力Fra bibliotek方程总结词
一般运动的动力学方程是牛顿第二定律的推广形式。
详细描述
一般运动的动力学方程是描述刚体运动状态变化的数学表达式，它是牛顿第二定律的推广形式。根据 牛顿第二定律，力是质量与加速度的乘积，而在一般运动中，需要考虑刚体的转动惯性，因此动力学 方程中还包括转动惯量。
飞行器控制
航空航天领域的飞行器控制需要 精确的刚体动力学模型来预测飞 行器的姿态、速度和位置等参数 ，以确保安全和稳定的飞行。
卫星姿态调整
卫星在太空中运行时，需要依靠 刚体动力学模型来调整其姿态， 以确保有效载荷的正常工作。
车辆工程
车辆动力学分析
在车辆工程中，刚体动力学被广泛应 用于车辆动力学分析，以优化车辆的 设计和性能，提高行驶的稳定性和安 全性。
自动驾驶技术
自动驾驶技术依赖于精确的刚体动力 学模型来预测车辆的运动状态和行为 ，从而实现安全有效的自动驾驶。
05
总结与展望
刚体动力学的重要性和意义
刚体动力学是研究刚体在力作用下的运动规 律的科学，它在工程、物理、航空航天等领 域有着广泛的应用。
刚体动力学对于理解物体运动规律、设计机 械系统、优化工程结构等方面具有重要意义 ，是工程技术人员必备的基础知识。
03
一般运动的动力学
一般运动的定义
总结词
一般运动是指刚体在空间中的任意运动，其位置和方向随时 间变化。
详细描述
一般运动是相对于定点运动而言的，它描述了刚体在空间中 的任意运动状态，包括平动和转动。刚体的位置和方向随时 间变化，其上任意一点的位置都随时间而改变。

刚体定轴转动定律ppt课件

刚体定轴转动定律ppt课件

6.1 刚体的运动与描述
质点的运动只代表物体的平动，物体实际上是 有形状、大小的，它可以平动、转动，甚至更复杂 的运动。因此，对于机械运动的研究，只限于质点 的情况是不够的。
刚体是一种特殊的质点系，无论在多大外力作 用下，系统内任意两质点间的距离始终保持不变。 即物体的形状、大小都不变的固体称为刚体（rigid body ）。
• 形状和转轴确定后，J 与刚体
Al
的质量有关
Fe
例题2 ：
普通物理学教案
求长为L、质量为 m 的均匀细棒对端点 轴和中垂轴的转动惯量。
解： 取如图坐标 取质量元
A dm
B
L
x
dm dx
A
C
B
J1
L x2 dx mL2 / 3
0
L/2
L/2 x
L
J2
2 L
x2 dx
mL2
/ 12
2
J1 J2
刚体的平动
可用质心运动来代表整体的运动
1。质心的位矢
设N个质点m1,m2,,mN，
定义： 质心的位矢 rc
对应的位矢
miri mi
r1,
r2
rN
xc
1 M
mi
xi
yc
1 M
mi
yi
xc
1 M
xdm
yc
1 M
ydm
zc
1 M
mizi
zc
1 M
zdm
质心 重心
2。质质设质对心心m心所的的i运有受加速动质力速度定点度F：理求i外：和、：Vafcic内dMddM1dMMr则1Vtctc：mddmmdtdmi(tiddiMdai(rd1taiMvit1iiMmF1iFmiMr1ii)ivfmii)imvrificai0i F合外mmirii

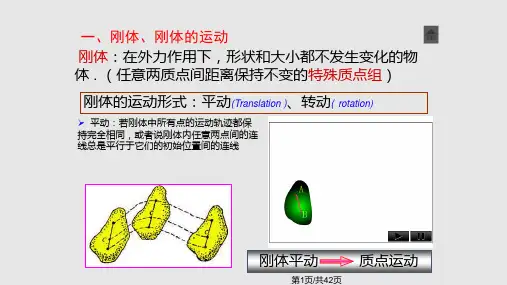
刚体运动学转动惯量定轴转动PPT课件

刚体运动学转动惯量定轴转动PPT课件
2π 2π
（2）t 6s时，飞轮的角速度
0
t
5
π
π 6
6
4
π
rad s1
（3）t 6s时，飞轮边缘上一点的线速度大小
v r 0.2 4π m s2 2.5 m s2
该点的切向加速度和法向加速度
at
r
0.2 (
π) 6
0.105 m s2
an r 2 0.2 (4π2 ) 31.6(m s2 )
面密度： , 面元：dS 体密度： , 体元：dV
注意
刚体对轴的转动惯量 J
与刚体总质量有关 与刚体质量分布有关 与转轴的位置有关
dm dm
dm
只有对于几何形状规则、质量连续且均匀分布 的刚体，才能用积分计算出刚体的转动惯量
第15页/共42页
注意：此
几
处的m是 挖掉后的
种
刚体质量。
常
公式是对 的
见
dr
r
R
角量系统
习题训练
例2 在高速旋转的微型电机里，有一圆柱形转子
可绕垂直其横截面通过中心的轴转动 . 开始时，它的角
速度0 0 ，经300s 后，其转速达到 18000r·min-1 . 已
知转子的角加速度与时间成正比 . 问在这段时间内，转
子转过多少转？
解 由题意，令 ct
d
，即
ct
，积
第11页/共42页
三、定轴转动刚体的角动量
转轴 ，z角速度
刚体上任一质点
转轴与其转动平面交点m
绕 圆周运动半径为
i
O
mi O
ri
z
转动
平面
o ri
vi
mi

《刚体的定轴转动》课件


力矩
总结词
描述刚体转动受到外力矩作用的物理量
详细描述
力矩是描述刚体转动受到外力矩作用的物理量，单位为牛顿·米。它表示力对刚体转动效果的影响，由力和力臂的 乘积得到。力矩可以改变刚体的角动量或使其产生加速度。
动能与势能
总结词
描述刚体转动过程中能量状态的物理量
详细描述
动能和势能是描述刚体转动过程中能量状态的物理量。动能与刚体的质量和速度有关，势能则与刚体 的位置和高度有关。在定轴转动中，动能和势能之间可以相互转化，但总能量保持不变。
03
刚体的定轴转动的动力学规律
转动定律
描述刚体转动时力矩与角加速度关系的定律。
转动定律指出，刚体转动时受到的力矩等于刚体质量与角加速度乘积的两倍。即 M=Jα，其中 M 为力矩，J 为转动惯量，α 为角加速度。
动量矩守恒定律
描述刚体在无外力矩作用时动量矩保持不变的定律。
动量矩守恒定律指出，在没有外力矩作用的情况下，刚体的动量矩是守恒的。即 L=Iw，其中 L 为动 量矩，I 为转动惯量，w 为角速度。
详细描述
进动是指刚体自转轴绕其惯性轴的旋转运动，通常是由于外部力矩的作用引起的。章动 则是自转轴在空间中的摆动，可以看作是进动的补充。这两种运动形式在刚体的动力学
分析中具有重要意义。
刚体的振动与波动
要点一
总结词
振动和波动是描述刚体动态行为的另外两种重要方式，涉 及到刚体的位移、速度和加速度等参数的变化。
刚体上各点绕固定轴线的角速度相同 。
刚体上各点的角速度与转动的角位置 无关，即刚体绕固定轴线的转动是匀 角速度运动。
02
刚体的定轴转动的物理量
角速度
总结词
描述刚体旋转快慢的物理量

刚体运动学和定轴转动PPT学习教案


P
X
参考方向
转轴
第4页/共41页
P X
Q
X
d
dt
d
ddt
d 2
dt 2
dt
v r
角 速 度 方 向 规定为 沿轴方 向，指 向用右 手螺旋 法则确 定。
加速转动
减速转动
r
方向一致
方向相反
v
第5页/共41页
一 、 刚 体 的 转动动 能
E ki
1 2
mivi 2
1 2
miri 2 2
Ep mg
mi hi m
hc
mi yi m
h
mi
PC
hi hC
O
刚 体 的 重 力 势能等 于其重 力与质 心高度 之积.
E p mghC
第32页/共41页
M J
刚 体 定 轴 转 动的转 动定律
与
M J
地位相当
F ma
m反 映 质 点 的 平动 惯性, J反 映刚 体的转 动惯性 .
第18页/共41页
小结
： 研究对象：刚体——理想模型
运动模式 ：刚体 绕定轴 的转动 研究方法 ：
是把质点力学的规律应用到组成刚体
的
质点→质点系→刚体
平动、转 动的类 比：
mg
第21页/共41页
解：
对M：M ＝TR＝J J＝1 MR2
2
对m : mg T ma a R
解方程得：a
m
m M
2
g
mg
4mgh v 2ah
2m M
v 1 4mgh
R R 2m M
第22页/共41页
例2、一个飞轮的质量为69kg，半径 为0.25m,正在以 每分1000转的 转速转 动。现 在要制 动飞轮 ，要求 在5.0秒内使 它均匀 减速而 最后停 下来。 摩擦系 数为0.2。求闸 瓦对轮 子的压 力N为 多大？

理论力学第14章 刚体定点转动与刚体一般运动


v2 = ω × r2
=
−ω1(
j
+
l r
k)
× (ri + lk)
ω
γ
ω2
ζ ωω11
O
γ
α
= −ω1 (li + lj − rk ) x (ξ )
? 方向
a2B = α × r2
? =
−
l2 r
ω
2 1
j
方向
y
a2B
2
xα
a2B
A
z(η)
C*
v2
1
y
36
刚体空间运动
a2N = ω× v2
= ω12[−(
OC*为瞬轴 vC = AC ⋅ ω ω = vC = vC AC r cos β
=
h2 + rh
r2
v C = 常数
25
刚体空间运动
2） 求角加速度
先求牵连角速度和相对角速度。
运动分解： 研究对象：圆锥 动系： Oz轴
牵连运动：Oz轴绕ζ 轴的转动
相对运动：绕Oz轴的自转
ωe = ψ& ωr = ϕ& θ& = 0 θ = 常数 ω = ωe + ωr = ψ& + ϕ& 这种 θ = 常数，ψ& = 常数,ϕ& = 常数 的情况: 规则进动
18
刚体空间运动
§14-4 刚体绕相交轴转动的角速度合成定理
一、 刚体绕相交轴转动的角速度合成定理
框架以ω1绕 z轴转动，同时圆盘又以ω2绕CD轴转动。 ω1 ω2
19
刚体空间运动
动系： 框架 绝对运动： 定点转动 相对运动： 绕CD轴转动 牵连运动： 定轴转动

刚体定点运动-PPT课件

R l t i j R
§2-4 刚体的定点运动
l v OP i j l i R j 2 l k P t R l l 2 j i j k t t R R
§2-4 刚体的定点运动 利用瞬时轴求解 因vQ
0, 为瞬时轴 OQ
2 2 : R : l R t
: R : l
v v k P P
2 2 l R , R R t l
vP t PD
R cos t 2
2 R 2 l
e
§2-4 刚体的定点运动 刚体做定点运动时, 刚体运动状态用 描述 ,运动 状态的变化由 描述 , 的方向随 . 角速度 沿瞬时轴 瞬时轴方位变化而改变, 一般不沿瞬时轴 .

4.定点运动刚体上任一点的速度和加速度
v r r a v r r
瞬时轴永远过定点但其方位可以随时间而变只要除定点外找到刚体上另一个速度为零的点该点与定点的连线即为瞬时轴
§2-4 刚体的定点运动
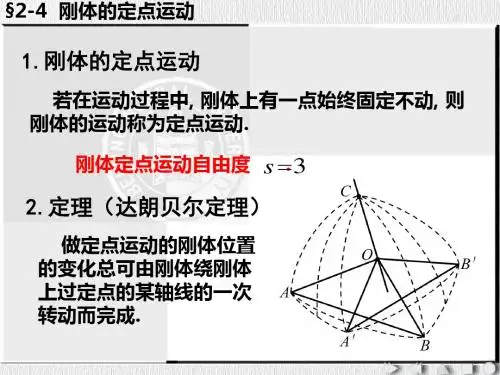
1.刚体的定点运动
若在运动过程中, 刚体上有一点始终固定不动, 则 刚体的运动称为定点运动. 刚体定点运动自由度 s .3
2.定理（达朗贝尔定理）
做定点运动的刚体位置 的变化总可由刚体绕刚体 上过定点的某轴线的一次 转动而完成.
§2-4 刚体的定点运动
3.瞬时转动轴(瞬时轴)
角速度

每一瞬时刚体位置的无限小变化可由刚体绕某转 动轴的无限小转动而完成. 我们把对应每瞬时的无限 小转动的转动轴称为瞬时转动轴, 简称瞬时轴.
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
26
刚体空间运动
27
刚体空间运动
计算角加速度
~
α
=
dω= dt
d ωe dt
+
d ωr dt
+
ωe
× ωr
~
d ωe = 0 d ωr = 0
dt
dt
α = ωe × ωr
由图: ω e = ω ⋅ tan β
α = ω eω r cos β
=
h2 +r2 rh3
vC2
方向？
α
ωe
28
刚体空间运动
( β&
+
γ&)
=
β&&
+
γ&& +
β&
× γ&
在地面上看，其角加速度矢量
ε3
=
d dt
(α&
+
β&
+
γ&)
=
α&&
+
β&&
+
α&
×
β&
+
γ&& +
(α&
+
β&) ×
γ& 22
刚体空间运动
三、用欧拉角速度表示刚体的角速度
23
刚体空间运动
进动角速度 方向沿 z0(ζ) 轴
ωψ = ψ&k 0
章动角速度 方向沿 x1(N) 轴
讨论： 求角速度时可否用
? ω = vC r
α
ω
29
刚体空间运动
§14-5 刚体定点转动时各点的速度与加速度分析
一、速度
已知：刚体绕定点O 转动，
瞬时轴OC*，ω ， rP
C* h
vP
v P = ω × rP vP = ω ⋅ rP sin (ω , rP )
=ωh
P
2
刚体空间运动
§14-1 刚体定点转动力学模型的再简化
一、定义 刚体在运动过程中，其上有一点始终保持不动。
3
刚体空间运动
4
刚体空间运动
5
刚体空间运动
§14-1 刚体定点转动力学模型的再简化
一、定义 二、力学模型的简化
确定作定点转动刚体的位置 球面图形S在球面上的位置 球面图形S上圆弧AB的位置
当△t 趋于零时，OC的极 限位置记为OC*，即
OC * = lim OC Δt→ 0
OC* 即为刚体定点转动 的转动瞬轴，简称为瞬轴。
注意：在不同的瞬时，刚体的瞬轴的位置不同。 ⇔瞬轴在空间的方位是在不断变化的。
14
刚体空间运动
瞬时角速度矢量
大小:
ω = lim Δϕ
Δt→0 Δt
方向： 沿瞬轴
欧拉角： 进动角 ψ ， 章动角 θ，自转角 ϕ 。
8
刚体空间运动
二、运动方程
用欧拉角ψ，θ，ϕ 作为坐标来描述刚体定点转动
的位置，则运动方程为：
ψ = ψ (t)
θ = θ (t)
ϕ = ϕ (t)
9
刚体空间运动
§14-3 欧拉定理
一、欧拉定理 作定点转动的刚体，从某一位置到另一位置的任
何位移，可以由绕过定点的某一轴的一次转动来实现。 ⎯⎯ 达朗贝尔-欧拉位移定理
根据欧拉定理，合成运动是绕瞬轴的转动
ω = ωe + ωr = ω1 + ω2
⎯⎯角速度合成定理
20
刚体空间运动
推广：绕 n个相交轴转动
n
ω = ∑ ωi i =1
二、刚体绕相交轴转动的角加速度合成定理
ω = ωe + ωr
~
α
=
d ω= dt
d ωe dt
+
d ωr dt
+
ωe
×
ωr
α = αe + αr + ωe × ωr
三、自由度
确定S上圆弧AB的位置需要 三个独立的坐标
作定点转动的刚体有 三个自由度
6
刚体空间运动
§14-2 用欧拉角描述刚体定点转动
一、欧拉角 作定点转动的刚体
在空间的位置可以用唯 一的一组欧拉角表示。
定系：Oξηζ
连体坐标系：Oxyz
节线：ON ⎯ Oxy坐标面与Oξη 坐标面的交线
7
刚体空间运动
OC*为瞬轴 vC = AC ⋅ ω ω = vC = vC AC r cos β
=
h2 + rh
r2
v C = 常数
25
刚体空间运动
2） 求角加速度
先求牵连角速度和相对角速度。
运动分解： 研究对象：圆锥 动系： Oz轴
牵连运动：Oz轴绕ζ 轴的转动
相对运动：绕Oz轴的自转
ωe = ψ& ωr = ϕ& θ& = 0 θ = 常数 ω = ωe + ωr = ψ& + ϕ& 这种 θ = 常数，ψ& = 常数,ϕ& = 常数 的情况: 规则进动
18
刚体空间运动
§14-4 刚体绕相交轴转动的角速度合成定理
一、 刚体绕相交轴转动的角速度合成定理
框架以ω1绕 z轴转动，同时圆盘又以ω2绕CD轴转动。 ω1 ω2
19
刚体空间运动
动系： 框架 绝对运动： 定点转动 相对运动： 绕CD轴转动 牵连运动： 定轴转动
ω1
ω
ω2
ωe = ω1 ωr = ω2
指向： 右手法则
瞬时角加速度矢量
α = dω dt
方向：沿角速度矢端曲线的切线方向
15
刚体空间运动
v = dr dt
α = dω dt
v v v vv v vv
r
rr
α α ααα α
ω
ω
O
O
注意：角加速度矢量与角速度矢量一般是不共线的。
16
刚体空间运动
17
刚体空间运动
三、刚体定点转动的运动性质 在每一瞬时都存在一根通过定点的转动瞬轴； 刚体的连续运动为绕一系列的瞬轴以不同的 瞬时角速度作连续的瞬时转动。
α = ωe × ωr
特例 αe = 0 , αr = 0
21
刚体空间运动
第三届江苏省大学生力学竞赛二（4）： α&,α&&
转子的绝对角速度矢量
ω = α& + β& + γ&
在内框上看，其角加
速度矢量
ε1
=
d γ& dt
=
γ&&
β&, β&&
γ&, γ&&
在外框上看，其角加
速度矢量
ε2
=
d dt
说明: 上述的转角可以是有限值(相对于无限小而言)， 称为有限转动。相应地，△t 也可以是有限值。
10
刚体空间运动
11
刚体空间运动
12
刚体空间运动
第四届全国大学生力学竞赛第九题：
z
ቤተ መጻሕፍቲ ባይዱ
z
A
A
O
b x
B a
y
O
b x
C B ay
13
刚体空间运动
二、转动瞬轴、瞬时角速度与角加速度
下面在无限小时间间隔内应用欧拉定理 转动瞬轴
刚体空间运动
专题部分
第 14 章 刚体空间运动
2015年11月21日
1
刚体空间运动
第14章 刚体定点转动与刚体一般运动
§14-1 刚体定点转动力学模型的再简化 §14-2 用欧拉角描述刚体定点转动 §14-3 欧拉定理 §14-4 刚体绕相交轴转动的角速度合成定理 §14-5 刚体定点转动时各点的速度与加速度分析 §14-6 刚体一般运动 §14-7 讨论与小结
ωθ = θ& i1
自转角速度 方向沿 z2(z) 轴
ωϕ = ϕ& k 2
ωϕ ωψ
k2 k0 i1
ωθ
瞬时角速度 ω = ωψ + ωθ + ωϕ
思考：角加速度如何求？
24
刚体空间运动
[例14-1] 正圆锥体
已知： h，r，vC =常数，
圆锥体作纯滚动。
求：圆锥体的角速度
ω
和角加速度。
解： 1） 求角速度