理论力学 刚体平面运动速度分析

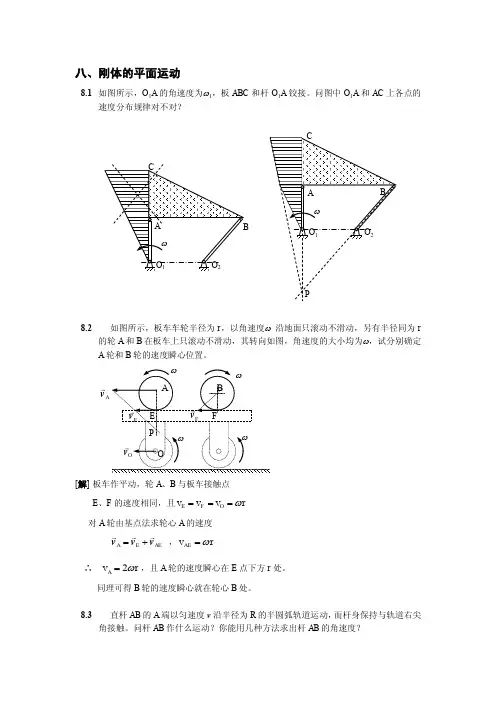
八、刚体的平面运动8.1 如图所示，O 1A 的角速度为ω1，板ABC 和杆O 1A 铰接。

问图中O 1A 和AC 上各点的速度分布规律对不对？8.2如图所示，板车车轮半径为r ，以角速度ω 沿地面只滚动不滑动，另有半径同为r 的轮A 和B 在板车上只滚动不滑动，其转向如图，角速度的大小均为ω，试分别确定A 轮和B 轮的速度瞬心位置。

[解] 板车作平动，轮A 、B 与板车接触点 E 、F 的速度相同，且r v v v O F E ω=== 对A 轮由基点法求轮心A 的速度 A E AE =+v v v ，r v AE ω=∴ r v A ω2=，且A 轮的速度瞬心在E 点下方r 处。

同理可得B 轮的速度瞬心就在轮心B 处。

8.3直杆AB 的A 端以匀速度v 沿半径为R 的半圆弧轨道运动，而杆身保持与轨道右尖角接触。

问杆AB 作什么运动？你能用几种方法求出杆AB 的角速度？E FPOE v Av Fv Ov[解] AB 杆作平面运动。

(一) 瞬心法AB 杆作平面运动，速度瞬心为P 。

Rv AP v AAB2==ω (二)基点法D A DA =+v v v ，DA v v AB A DA ωθ==sin又 DA ＝2R cos(90o －θ)＝2R sin θ ∴ Rv AB 2=ω(三)自然法： d d AB tϕω=，而R S ϕ2= ∴d d 2d d S R v t t ϕ==， d d 2vt R ϕ= ∴ Rv AB 2=ω 8.4如图所示四连杆机构OABO 1中，OA=O 1B=AB/2，曲柄OA 的角速度ω=3rad/s 。

当OA 转到与OO 1垂直时，O 1B 正好在OO 1的延长线上，求该瞬时AB 杆的角速度ωAB 和曲柄O 1B 的角速度ω1。

[解]取AB 为研究对象，AB 作平面运动。

以A 为基点，画B 点速度合成图 由B A BA =+v v v(rad/s)32230sin o==∴⋅=⋅==ωωωωAB OAAB OA v v AB AB ABABBBvvvDAv Dv Dv111cos3022(rad/s)B BAv v OA O Bωωω=︒=⋅=∴=8.5图示曲柄摇机构中，曲柄OA以角速度oω绕O轴转动，带动连杆AC在摇块B内滑动，摇块及与其固结的BD杆绕B铰转动，杆BD长l；求在图示位置时摇块的角速度及D点的速度。

第五章 刚体的平面运动5-1 刚体的平面运动方程一．平面运动的定义二．平面运动的简化刚体的平面运动可以简化为平面图形S 在其自身平面内的运动．三、平面运动分解为平动和转动1.平面运动方程为了确定代表平面运动刚体的平面图形的位置，我们只需确定平面图形内任意一条线段的位置．平面运动方程)(1t f x A = )(2t f y A = )(3t f =ϕ2．平面运动分解为平动和转动刚体平面运动可以看成是平动和转动的合成运动．刚体的平面运动可以分解为随基点的平动和绕基点的转动．3.刚体平面运动的角速度和角加速度平面运动随基点平动的运动规律与基点的选择有关，而绕基点转动的规律与基点选取无关(即在同一瞬间，图形绕任一基点转动的ε ,ω都是相同的）5-2 平面图形内各点的速度一．基点法（合成法）BA A B v v v +=平面图形上任一点的速度等于基点的速度与该点随图形绕基点转动的速度的矢量和二．速度投影法（自：就是基点法的变式） 速度投影定理：[][]AB A AB B v v =平面图形上任意两点的速度在该两点连线上的投影彼此相等三．瞬时速度中心法（速度瞬心法）1. 问题的提出2．速度瞬心的概念即在某一瞬时必唯一存在一点速度等于零，该点称为平面图形在该瞬时的瞬时速度中心，简称速度瞬心．３．几种确定速度瞬心位置的方法 ①已知图形上一点的速度A v 和图形角速度ω，可以确定速度瞬心的位置．（P 点）②已知一平面图形在固定面上作无滑动的滚动, 则图形与固定面的接触点P 为速度瞬心．③已知某瞬间平面图形上A ,B 两点速度B A v v ,的方向，且B A v v 不平行过A , B 两点分别作速度B A v v ,的垂线,交点P 即为该瞬间的速度瞬心.④ 已知某瞬时图形上A ,B 两点速度B A v v ,大小,且AB v AB v B A ⊥⊥ ,⑤已知某瞬时图形上A ,B 两点的速度方向相同，且不与AB 连线垂直．瞬时平动注意：瞬时平动与平动不同瞬时平动构件上各点的速度都相等，但各点的加速度并不相等。

刚体的平面运动-速度分析2面运动图形上速度分布规律？定理：只要 ，任一瞬时平面图形上都唯一存在一个速度等于零的点。

3、速度瞬心法≠ω证明:已知A 点的速度，任一点的速度MAA M v v v +=垂线AL 上点M 的速度大小可表示为MA A M v v v -=ω⋅-=AM v A 因此，在AL 上必存在一点P ，其速度为零。

A v v L 'SAAv MAMLP速度瞬心 某瞬时，平面图形上速度为零点。

ωAv AP =∴0=⋅-=ωAP v v A P唯一性：在某一瞬时，图形只有一个速度瞬心。

瞬时性：在不同瞬时，速度瞬心在平面图形上的位置不同。

注意：速度瞬心的加速度并不为零！S A AvAvMAv ML P特点：速度为零的点P在A点速度的垂线上。

5S 方向： ω⋅=BP v B P选取速度瞬心P 为基点，则平面图形上任一点B 的速度如图所示：BBv AC由此可见，只要已知在某一瞬时平面图形速度瞬心的位置和平面图形的角速度，就可求出该瞬时图形上各点的速度。

BP P B v v v +=大小： ⊥BP ，指向与ω 转向相一致。

Av Cv BPv =S P过速度瞬心P的任一直线上各点的速度分布就速度分布而言，平面图形的运动可视为绕该瞬时的速度瞬心作转动。

—与图形绕定轴转动时的速度分布类似。

有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）672. 已知某瞬间平面图形上A , B 两点速度v A 、v B 的方向几种确定速度瞬心位置的方法1. 已知一平面图形在固定面上作无滑动的滚动已知某瞬时图形上A , B 两点的速度大小相等，方向相同． 各点的加速度是否相等？此时, 图形的瞬心在无穷远处，图形的角速度 =0, 图形上各点速度相等, 这种情况称为 瞬时平动.ABOBv Av MMv例题. 沿直线轨道作纯滚动的车轮，其半径为R ，轮心的速度为v o ，求轮上A 、B 、C 、D 的速度。

第6章 刚体的平面运动分析6－1 图示半径为r 的齿轮由曲柄OA 带动，沿半径为R 的固定齿轮滚动。

曲柄OA 以等角加速度α绕轴O 转动，当运动开始时，角速度0ω= 0，转角0ϕ= 0。

试求动齿轮以圆心A 为基点的平面运动方程。

解：ϕcos )(r R x A += （1） ϕsin )(r R y A +=（2）α为常数，当t = 0时，0ω=0ϕ= 0 221t αϕ=（3）起始位置，P 与P 0重合，即起始位置AP 水平，记θ=∠OAP ，则AP 从起始水平位置至图示AP 位置转过θϕϕ+=A因动齿轮纯滚，故有⋂⋂=CP CP 0，即 θϕr R = ϕθr R =， ϕϕrr R A += （4）将（3）代入（1）、（2）、（4）得动齿轮以A 为基点的平面运动方程为：⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=222212sin )(2cos )(t r r R t r R y t r R x A A A αϕαα6－2 杆AB 斜靠于高为h 的台阶角C 处，一端A 以匀速v 0沿水平向右运动，如图所示。

试以杆与铅垂线的夹角θ 表示杆的角速度。

解：杆AB 作平面运动，点C 的速度v C 沿杆AB 如图所示。

作速度v C 和v 0的垂线交于点P ，点P 即为杆AB 的速度瞬心。

则角速度杆AB 为6－3 图示拖车的车轮A 与垫滚B 的半径均为r 。

试问当拖车以速度v 前进时，轮A 与垫滚B 的角速度A ω与B ω有什么关系？设轮A 和垫滚B 与地面之间以及垫滚B 与拖车之间无滑动。

解：RvR v A A ==ωhv AC v AP v ABθθω2000cos cos ===习题6-1图ABCv 0hθ习题6－2图PωABv CABCv ohθ习题6－2解图习题6-3解图习题6-3图v A = vv B = v ωAωBR vR v B B 22==ω B A ωω2=6－4 直径为360mm 的滚子在水平面上作纯滚动，杆BC 一端与滚子铰接，另一端与滑块C 铰接。

理论力学运动学知识点总结第一篇：理论力学运动学知识点总结运动学重要知识点一、刚体的简单运动知识点总结1.刚体运动的最简单形式为平行移动和绕定轴转动。

2.刚体平行移动。

·刚体内任一直线段在运动过程中，始终与它的最初位置平行，此种运动称为刚体平行移动，或平移。

·刚体作平移时，刚体内各点的轨迹形状完全相同，各点的轨迹可能是直线，也可能是曲线。

·刚体作平移时，在同一瞬时刚体内各点的速度和加速度大小、方向都相同。

3.刚体绕定轴转动。

• 刚体运动时，其中有两点保持不动，此运动称为刚体绕定轴转动，或转动。

• 刚体的转动方程φ=f(t)表示刚体的位置随时间的变化规律。

• 角速度ω表示刚体转动快慢程度和转向，是代数量，以用矢量表示。

，当α与ω。

角速度也可• 角加速度表示角速度对时间的变化率，是代数量，同号时，刚体作匀加速转动；当α 与ω异号时，刚体作匀减速转动。

角加速度也可以用矢量表示。

• 绕定轴转动刚体上点的速度、加速度与角速度、角加速度的关系：。

速度、加速度的代数值为。

• 传动比。

一、点的运动合成知识点总结1.点的绝对运动为点的牵连运动和相对运动的合成结果。

• 绝对运动：动点相对于定参考系的运动；• 相对运动：动点相对于动参考系的运动；• 牵连运动：动参考系相对于定参考系的运动。

2.点的速度合成定理。

• 绝对速度：动点相对于定参考系运动的速度；• 相对速度：动点相对于动参考系运动的速度；• 牵连速度：动参考系上与动点相重合的那一点相对于定参考系运动的速度。

3.点的加速度合成定理。

• 绝对加速度：动点相对于定参考系运动的加速度；• 相对加速度：动点相对于动参考系运动的加速度；• 牵连加速度：动参考系上与动点相重合的那一点相对于定参考系运动的加速度；• 科氏加速度：牵连运动为转动时，牵连运动和相对运动相互影响而出现的一项附加的加速度。

• 当动参考系作平移或 = 0，或与平行时，= 0。

龙源期刊网 刚体平面运动中的速度分析作者：刘战辉张雅男苏静徐飞来源：《科技资讯》2012年第27期摘要：在普通物理教学中，刚体平面运动的纯滚动问题是刚体章节中的重点和难点，对学生而言，也是较为难以掌握的内容。

本文从教学的角度从基本物理概念出发，利用简单的数学知识对刚体平面运动中的速度进行了深入浅出的分析，使学生对这部分知识有更好的理解和掌握。

关键词：刚体平面运动速度分析中图分类号：G64 文献标识码：A 文章编号：1672-3791（2012）09（c）-0249-01刚体平面运动的纯滚动问题中，存在质心C和瞬心P两个特殊点。

其中质心的速度与刚体转动角速度之间满足：vC=Rω。

而瞬心是指刚体任意时刻与接触水平面的接触点，对于刚体平面运动的纯滚动问题，刚体与接触面之间无相对滑动，因此任意时刻瞬心的速度为零，保持静止不动（注：瞬心在不同时刻在刚体上的位置不同，是刚体与水平面的接触点）。

对于解决刚体平面运动的纯滚动问题可以选择任意位置作为基点来讨论刚体的运动，取不同基点，速度形式不同，但是选质心和瞬心为基点最为方便。

综上所述，在刚体平面运动中，其运动可以看作是质心的平动和刚体绕质心的转动的组合，又可以看成绕瞬心作匀速圆周运动，而且选择质心C或瞬心P作为基点可以简单明了认识其运动，但是选择不同的基点运动形式不同。

选择质心C，运动形式比较复杂（圆周运动和直线运动的叠加），但是其物理现象简洁，容易理解。

而选择瞬心P，运动形式简单（圆周运动），但是其物理过程不易理解。

参考文献[1] 刘克哲，张承琚.物理学（上卷）[M].北京：高等教育出版社，2005，6.[2] 刘克哲，张承琚.物理学学习指导[M].北京：高等教育出版社，2006.1.。

刚体平面运动中的速度分析
物体在静止状态下，无论它拥有任何形式的运动，它都可以分解为两个分量，即速度分量和加速度分量。

它们的定义如下：
● 速度：描述物体的实际移动，是物体空间位置的变化量。

● 加速度：速度的变化量。

也就是运动中物体空间位置变化量的变化量。

当物体在空间中运动时，它可以在任何方向上以任意速度移动。

它可以向任
何方向运动，也可以加速或减速。

此外，它的运动受外力的影响。

假定物体的运动是由物理定律所驱动的，那么这种运动就称为平面运动。

在平面运动中，物体速度的变化只受其空间位置的改变影响，并且不受外部力的影响。

因此，在刚体平面运动中，物体的速度由它的空间位置的变化来描述，我们
可以使用下面的方程式来计算：
速度 = 量/时间
加速度 = 速度/时间
例如，让我们考虑一个滑块在水平方向上以一定速度移动的情况。

速度可以
用大写字母V表示，而加速度可以用小写字母a来表示。

因此，这个滑块的速度
可以使用以下方程式来计算：
V = S/t
其中，S表示滑块空间位置的变化，而t表示这个位置变化发生的时间。

这个滑块的加速度可以使用以下方程式来计算：
a = V/t
这里，V表示滑块的速度，而t表示滑块速度发生变化的时间。

刚体的平面运动学分析刚体平面运动学分析是物理学中研究刚体在平面上运动规律的一门学科，它通过分析刚体的位置、速度和加速度等运动参数，揭示刚体的运动规律和运动轨迹。

本文将从三个方面对刚体平面运动学进行详细分析，分别是刚体的位移、速度和加速度。

1. 刚体的位移刚体的位移是指刚体从初始位置到最终位置之间的位移变化。

假设刚体在平面上做平动运动，其初始位置为P1，最终位置为P2。

刚体在平动过程中，可以沿着直线路径移动，也可以绕着某个固定点旋转。

对于直线平动，刚体的位移可以用矢量表示，位移矢量的大小等于两个位置之间的距离，方向沿着直线运动的方向。

对于绕固定点旋转的情况，刚体的位移可以由角位移表示，角位移的大小等于刚体绕固定点旋转的角度。

2. 刚体的速度刚体的速度是指刚体在平面上做运动时，单位时间内位移的变化率，即速度矢量的大小和方向。

刚体在平面上做平动运动时，其速度大小等于位移的变化率，方向沿着位移的方向。

刚体在旋转过程中，速度的大小等于刚体绕固定点旋转的角速度，方向垂直于位于刚体上某一点的矢径方向。

3. 刚体的加速度刚体的加速度是指刚体在平面上做运动时，单位时间内速度的变化率，即加速度矢量的大小和方向。

刚体的加速度可以分为线加速度和角加速度两种情况。

对于平动运动，刚体的线加速度大小等于速度的变化率，方向沿着速度的方向。

对于旋转运动，刚体的角加速度大小等于刚体绕固定点旋转的角度的变化率，方向垂直于位于刚体上某一点的矢径方向。

通过对刚体的位移、速度和加速度的分析，可以得到以下几个重要结论：1) 若刚体的速度和加速度均为零，则刚体处于静止状态；2) 若刚体的速度不为零但加速度为零，则刚体做匀速直线运动；3) 若刚体的速度和加速度均不为零，则刚体做变速直线运动或者曲线运动；4) 若刚体的速度为零但加速度不为零，则刚体处于转动状态。

总之，刚体的平面运动学分析是研究刚体在平面上运动规律的重要学科。

通过对刚体的位移、速度和加速度的分析，可以揭示刚体的运动规律和运动轨迹，为解决实际问题提供理论依据。

刚体平面运动中的速度分析摘要:在普通物理教学中,刚体平面运动的纯滚动问题是刚体章节中的重点和难点,对学生而言,也是较为难以掌握的内容。

本文从教学的角度从基本物理概念出发,利用简单的数学知识对刚体平面运动中的速度进行了深入浅出的分析,使学生对这部分知识有更好的理解和掌握。

关键词:刚体平面运动速度分析刚体平面运动的纯滚动问题中,存在质心C和瞬心P两个特殊点。

其中质心的速度与刚体转动角速度之间满足:vC=Rω。

而瞬心是指刚体任意时刻与接触水平面的接触点,对于刚体平面运动的纯滚动问题,刚体与接触面之间无相对滑动,因此任意时刻瞬心的速度为零,保持静止不动(注:瞬心在不同时刻在刚体上的位置不同,是刚体与水平面的接触点)。

对于解决刚体平面运动的纯滚动问题可以选择任意位置作为基点来讨论刚体的运动,取不同基点,速度形式不同,但是选质心和瞬心为基点最为方便。

现选择半径为R的匀质圆盘在水平面上作纯滚动为例来研究其速度情况。

其中圆盘的质心与圆心重合,瞬心P点为圆盘与水平面的接触点,绕圆心转动的角速度为ω,选择如图1所示坐标系。

在纯滚动过程中,圆盘绕质心转动,而质心始终在作匀速直线运动。

因此对边缘各点的运动可看成绕质心C以角速度为ω,半径为R 作匀速圆周运动和与C以相同速度作匀速直线运动的叠加。

现从基本的物理概念出发对圆盘边缘上四个特殊位置(与坐标轴的交点)的速度进行分析。

对于瞬心P点,,与瞬心的定义任意时刻速度为零保持一致。

其它各点的速度可分别表示为:的方向垂直于PA,其大小可以表示为PA×ω。

因此可知A点的运动可以看成绕瞬心P作以PA长度为半径,角速度为ω作匀速圆周运动。

同理,B点和D点的运动也可以看成分别绕瞬心P作以PB、PD 长度为半径,角速度为ω作匀速圆周运动。

很多教师在教学过程中,推广开来,得到刚体边缘上所有点都可以看成绕瞬心P作匀速圆周运动。

但是,对于学生却很困惑,边缘上其它点的运动是不是这样的呢？下面我们分析边缘上任意点的情况。