初中奥数讲义_直角三角形的再发现附答案

初中数学解直角三角形的应用学习目标一、考点突破1. 弄清俯角、仰角、株距、坡度、坡角、方位角、水平距离、垂直距离、水位等概念的意义，明确各术语与示意图中的什么元素对应。

2. 能够恰当地把实际问题转化为数学问题，从而利用直角三角形的知识解决实际问题。

二、重难点提示重点：将某些实际问题中的数量关系，归结为直角三角形中元素之间的关系，从而解决问题。

难点：如何添作适当的辅助线构造直角三角形。

考点精讲常见应用问题类型1. 仰角和俯角：视线在水平线上方的角叫做仰角；视线在水平线下方的角叫做俯角。

2. 方位角：指北（或指南）方向线与目标方向所成的小于90°的角叫做方位角。

北西南东ABCDO60°70°30°45°3. 坡度和坡角：坡面的铅垂高度h和水平宽度l的比叫做坡面的坡度（或坡比），记作i ＝h∶l。

坡面与水平面的夹角叫做坡角，记作α，且i＝hl＝tanα。

BChlα【核心突破】（1）仰角和俯角是视线相对于水平线而言的，不同位置的仰角和俯角是不同的，可巧记为“上仰下俯”。

（2）实际问题中遇到仰角或俯角时，要放在直角三角形或转化到直角三角形中运用，注意确定水平线。

（3）工程上斜坡的倾斜程度通常用坡度来表示，坡面的铅直高度h与水平宽度l的比为坡度（或坡比），坡度是坡角的正切，坡度越大，坡面越陡。

【重要提示】仰角、俯角、方位角的区别是：三者的参照不同。

仰角与俯角是相对于水平线而言的，而方位角是相对于正北（南）方向而言的。

典例精讲例题1如图1，某超市从一楼到二楼有一自动扶梯，图2是侧面示意图。

已知自动扶梯AB的坡度为1：2.4，AB的长度是13米，MN是二楼楼顶，MN∥PQ，C是MN上处在自动扶梯顶端B点正上方的一点，BC⊥MN，在自动扶梯底端A处测得C点的仰角为42°，则二楼的层高BC约为（精确到0.1米，sin42°≈0.67，tan42°≈0.90）（）A. 10.8米B. 8.9米C. 8.0米D. 5.8米思路分析：延长CB交PQ于点D，根据坡度的定义即可求得BD的长，然后在直角△CDA 中利用三角函数即可求得CD的长，则BC即可得到。

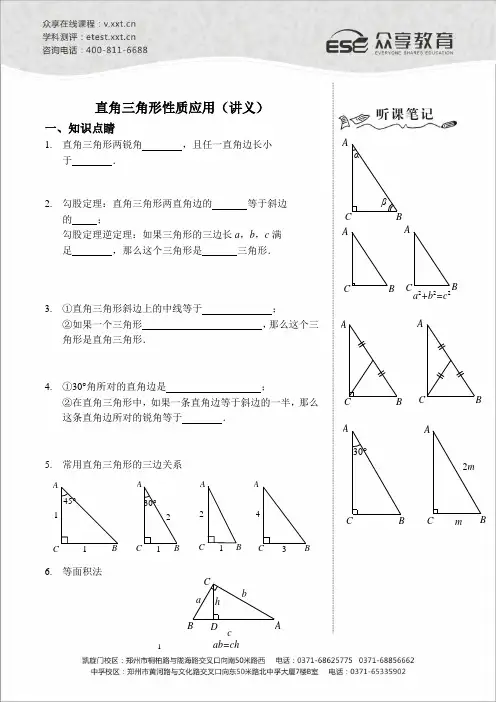
直角三角形性质应用（讲义）一、知识点睛1. 直角三角形两锐角 ，且任一直角边长小于 ．2. 勾股定理：直角三角形两直角边的 等于斜边的 ；勾股定理逆定理：如果三角形的三边长a ，b ，c 满足 ，那么这个三角形是 三角形．3. ①直角三角形斜边上的中线等于 ；②如果一个三角形 ，那么这个三角形是直角三角形．4. ①30°角所对的直角边是 ；②在直角三角形中，如果一条直角边等于斜边的一半，那么这条直角边所对的锐角等于 ．5. 常用直角三角形的三边关系A C B45°1130°234211BCA BCAB CA6. 等面积法ABCC B Aa 2+b 2=c2ABC C BAβαC A B 30°CB A CBA2mmD h C BAc bay x二、精讲精练1. 下图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案，已知大正方形面积为49，小正方形面积为4，若用x ，y 表示直角三角形的两直角边（x ＞y ），下列四个说法：①x 2+y 2=49，②x -y =2，③2xy +4=49，④x +y =9．其中说法正确的是（ ） A ．①③ B ．①②③ C ．②④ D ．①②③④2. 如图，在正方形ABCD 中，E 是DC 的中点，F 为BC 上的一点且BC =4CF ，试说明△AEF 是直角三角形．3. 如图，△ACB 和△ECD 都是等腰直角三角形，∠ACB =∠ECD =90°，D 为AB 边上一点，求证：AD 2+DB 2=DE 2．ABCDE4. 在△ABC 中，AB =15，AC =13，高AD =12，则△ABC 的周长是_______．FE DC B A5.在一张直角三角形纸片的两直角边上各取一点，分别沿斜边中点与这两点的连线剪去两个三角形，剩下的部分是如图所示的直角梯形，其中三边长分别为2、4、3，则原直角三角形纸片的斜边长是（）A．10 B．45C．10或45D．10或2176.直角三角形斜边上的中线长是6.5，一条直角边长是5，则另一直角边长等于（）A．13 B．12 C．10 D．57.如图，在△ABC中，∠ACB=90°，∠ABC=60°，BD平分∠ABC，P点是BD的中点，若AD=6，则CP的长为（）A．3B．3.5C．4D．4.58.△ABC周长是24，M是AB的中点，MC=MA=5，则△ABC的面积是．9.如图，△ABC和△DCE都是边长为4的等边三角形，点B、C、E在同一条直线上，连接BD，则BD的长为（）A．3B．23C．33D．43EDCBAPDCB A23423410. 如图，四边形ABCD 中，∠DAB =∠DCB =90o ，点M 、N 分别是BD 、AC 的中点．MN 、AC 的位置关系如何？证明你的猜想．11. 如图，在Rt △ABC 中，AC ≠AB ，AD 是斜边BC 上的高，DE⊥AC ，DF ⊥AB ，垂足分别为E 、F ，则图中与∠C （除∠C 外）相等的角的个数是（ ） A ．2 B ．3 C ．4 D ．512. 如图，已知DE =m ，BC =n ，∠EBC 与∠DCB 互余，求BD 2+CE 2的值．BCDE13. 在△ABC 中，∠C =90°，AB =6，∠B =30°，点P 是BC 边上的动点，则AP 长不可能是（ ）A ．3.5B ．4.2C ．5.8D ．214. 如图，在Rt △ABC 中，∠A =30°，DE 垂直平分斜边AC ，交AB 于D ，E 是垂足，连接CD ，若BD =1，则AC 的长是（ ） A ．23 B ．2 C ．43 D ．4NMCD BAFEDCB AEDA15. 某市在旧城改造中，计划在一块如图所示的△ABC 空地上种植草皮以美化环境，已知∠A =150°，这种草皮每平方米售价a 元，则购买这种草皮至少需要（ ） A ．300a 元 B ．150a 元 C ．450a 元 D ．225a 元CBA30m20m16. 放风筝是大家喜爱的一种运动．星期天的上午小明在绿城广场上放风筝，如图他在A 处时不小心让风筝挂在了一棵树的树梢上，风筝固定在了D 处，此时风筝线AD 与水平线的夹角为30°．为了便于观察，小明迅速向前边移动边收线到达了离A 处6米的B 处，此时风筝线BD 与水平线的夹角为45°．已知点A 、B 、C 在同一条直线上，∠ACD =90°．求DC 的长度．ABCD30°45°17. 已知，在△ABC 中，∠A =45°，AC =2，AB =3+1，则边BC 的长为 ．CBAP CBA18. 在Rt △ABC 中，∠C =90°，AC =9，BC =12，则点C 到AB 的距离是（ ）A ．365B ．1225C ．94D ．33419. 如图所示，等边△ABC 内一点P 到三边距离分别为h 1，h 2，h 3，且h 1+h 2+h 3=3，其中PD =h 1，PE =h 2，PF =h 3，则△ABC 的面积S △ABC =（ ）A ．23B ．33C ．103D ．12320. 如图，△ABC 中，∠C =90°，两直角边AC =8，BC =6，在三角形内有一点P ，它到各边的距离相等，则这个距离是（ ） A ．1 B ．2 C ．3 D ．无法确定21. 在直线l 上依次摆放着七个正方形(如图所示)．已知斜放置的三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是S 1、S 2、S 3、S 4，则S 1＋S 2＋S 3＋S 4=_______．l321S 4S 3S 2S 1P FEDCBACBA22. 如图，△ABC 中，∠ACB =90°，点E 为AB 的中点，点D 在BC 上，且AD =BD ，AD 、CE 相交于点F ，若∠B =20°，则∠DFE 等于（ ） A ．70° B ．60° C ．50° D ．40°23. 在锐角△ABC 中，∠BAC =60°，BN 、CM 为高，P 为BC 的中点，连接MN 、MP 、NP ，则结论：①NP =MP ；②当∠ABC =60°时，MN ∥BC ；③BN =2AN ；④::AN AB =AM AC ，一定正确的有（ ）A ．1个B ．2个C ．3个D ．4个三、回顾与思考______________________________________________________ ______________________________________________________ ______________________________________________________【参考答案】 一、 知识点睛1.互余，斜边长2.平方和，平方，a 2+b 2=c 2，直角3.斜边的一半，一边上的中线等于这边的一半4.斜边的一半，30°二、精讲精练1．B 2．（略） 3．（略） 4． 42或32 5．C 6．B 7．A 8．24 9．D 10．MN ⊥AC ，证明（略） 11．BABCD EFPNM CBA12．m2+n2，证明（略）13．D14．A15．B 16．8m，求解（略）17．2 18．A19．B20．B 21．4 22．B 23．C。

直角三角形的再发现直角三角形是一类特殊三角形，有着丰富的性质：两锐角互余、斜边的平方是两直角边的平方和、斜边中线等于斜边一半、30°所对的直角边等于斜边一半等，在学习了相似三角形的知识后，我们利用相似三角形法，能得到应用极为广泛的结论．如图，在Rt△ABC中，∠C=90°，CD⊥AB于D，则有：1．同一三角形中三边的平方关系：AB2=AC2+BC2，AC2=AD2+CD2，BC2=CD2+BD2．2．角的相等关系：∠A=∠DCD，∠B=∠ACD．3．线段的等积式：由面积得 AC×BC=AB×CD；由△ACD∽△CBD∽△ABC，得CD2=AD×BD，AC2=AD×AB，BC2=BD×AB．以直角三角形为背景的几何问题，常以下列图形为载体，综合了全等三角形、相似三角形、等腰三角形，特殊四边形等丰富的知识．注直角三角形被斜边上的高分成的3个直角三角形相似，由此导出的等积式的特点是：一线段是两个三角形的公共边，另两条线段在同一直线上，这些等积式广泛应用于与直角三角形问题的计算与证明中．例题求解【例1】等腰三角形ABC的底边长为8cm，腰长5cm，一动点P在底边上从B向C以0．25cm／秒的速度移动，当点P运动到PA与腰垂直的位置时，点P运动的时间为．(江苏省常州市中考题)思路点拨为求BP需作出底边上的高，就得到与直角三角形相关的基本图形，注意动态过程．【例2】如图，在矩形ABCD中，AE⊥BD于E，S矩形ABCD=40cm2，S△ABE：S△DBA=1：5，则AE的长为( ) A．4cm B．5cm C．6cm D．7cm (青岛市中考题)思路点拨 从题设条件及基本图形入手，先建立AB 、AD 的等式．【例3】 如图，在Rt △ABC 中，∠BAC ＝90°，AB ＝AC ，DB 为BC 的中点，E 为AC 上一点，点G 在BE 上，连结DG 并延长交AE 于F ，若∠FGE=45°． (1)求证：BD ×BC ＝BG ×BE ； (2)求证：AG ⊥BE ；(3)若E 为AC 的中点，求EF ：FD 的值．（盐城市中考题）思路点拨 发现图形中特殊三角形、基本图形、线段之间的关系是解本例的基础．(1)证明△GBD ∽△CBE ；(2)证明△ABG ∽EBA ；(3)利用相似三角形，把求FDEF的值转化为求其他线段的比值． 【例4】 如图，H 、Q 分别是正方形ABCD 的边AB 、BC 上的点，且BH=BQ ，过B 作HC 的垂线，垂足为P ．求证：DP ⊥PQ ． (“祖冲之杯”邀请赛试题)思路点拨 因∠BPQ+∠QPC=90°，要证DP ⊥PQ ，即证∠QPC+∠DPC=90°，只需证∠BPQ=∠DPC ，只要证明△BPQ ∽△CPD 即可．注 题设条件有中点，图形中有与直角三角形相关的基本图形，给我们以丰富的联想，单独应用或组合应用可推出许多结论．因此，读者应不拘泥于给出的思路点拨，多角度探索与思考，寻找更多更好的解法，以培养我们发散思的能力．【例5】 已知△ABC 中，BC>AC ，CH 是AB 边上的高，且满足BHAHBC AC22，试探讨∠A 与∠B 的关系，井加以证明． (武汉市选拔赛试题)思路点拨 由题设条件易想到直角三角形中的基本图形、基本结论，可猜想出∠A 与∠B 的关系，解题的关键是综合运用勾股定理、比例线段的性质，推导判定两个三角形相似的条件．注 构造逆命题是提出问题的一个常用方法，本例是在直角三角形被斜边上的高分成的相似三角形得出结论基础上提出的一个逆命题，读者你能提出新的问题吗?并加以证明．学力训练1． 如图，已知正方形ABCD 的边长是1，P 是CD 边的中点，点Q 在线段BC 上， 当BQ= 时，三角形ADP 与三角形QCP 相似． (云南省中考题)2． 如图，Rt △ABC 中，CD 为斜边AB 上的高，DF ⊥CB 于E ，若BE=6，CE=4，则AD= ．3．如图，平行四边形ABCD 中，AB=2，BC=23，AC=4，过AC 的中点O 作EF ⊥AC 交AD 于E ，交BC 于F ，则EF= ． (重庆市竞赛题)4．P 是Rt △ABC 的斜边BC 上异于B 、C 的一点，过点P 作直线截△ABC ，使截得的三角形与△ABC 相似，满足这样条件的直线共有( )A ．1条B ． 2条C ．3条D ．4条 (2001年安徽省中考题)5．在△ABC 中，AD 是高，且AD 2=BD ×CD ，那么∠BAC 的度数是( ) A ．小于90° B ．等于90° C ．大于90° D ．不确定 6．如图，矩形ABCD 中，AB=3，BC=3，AE ⊥BD 于E ，则EC=( )A ．27B ．25C ．215D ．2217．如图，在矩形ABCD 中，E 是CD 的中点，BE ⊥AC 交AC 于F ，过F 作FG ∥AB 交AE 于G ，求证：AG 2＝AF ×FC ．8．如图，在平行四边形ABCD 中，∠DBC ＝45°，DE ⊥BC 于E ，BF ⊥CD 于F ，DE 、BF 相交于H ，BF 、AD 的延长线相交于G ．求证；(1)AB=BH ；(2)AB 2=GA ×HE ． (青岛市中考题)9．如图，在Rt △ABC 中，∠ACB ＝90°，AD 平分∠CAB 交BC 于点D ，过点C 作CE ⊥AD 于E ，CE 的延长线交AB 于点F ，过点E 作EG ∥BC 交AB 于点G ，AE ×AD=16，AB=45 (1)求证：CE=EF ； (2)求EG 的长． (河南省中考题)10．如图，直角梯形ABCD 中，∠A ＝90°，AC ⊥BD ，已知k AD BC ，则BDAC= ． (江苏省竞赛题)11．如图，在Rt △ABC 中，两条直角边AB 、AC 的长分别为l 厘米、2厘米，那么直角的角平分线的长度等12．如图，点D 、E 分别在△ABC 的边AC 和BC 上，∠C ＝90°，DE ∥AB ，且3DE=2AB ，AE=13，BD=9，那么AB 的长为 ．( “我爱数学”初中数学夏令营试题)13．如图，△ABC 为等腰直角三角形，∠C=90°，若AD=31AC ，CE=31BC ，则∠1与∠2的大小关系是( )A ．∠1>∠2B ．∠1<∠2C ．∠1=∠2D ．无法确定 (天津市竞赛题)14．如图，△ABC 中，CD ⊥AB 交AB 于点D ，有下列条件： ①∠A=∠BCD ；②∠A+∠BCD=∠ADC ；③ACBC CD BD =；④BC 2=BD ×BA ． 其中，一定能判断△ABC 是直角三角形的共有( )A ．0个B ．1个C ．2个D ．3个 (2003年河南省竞赛题)15．如图，在直角梯形ABCD 中，AB=7，AD=2，DC=3，如果边AD 上的点P 使得以P ， A 、D 为顶点的三角形和以P 、B 、C 为顶点的三角形相似，那么这样的点P 有( ) A ．1个 B ．2个 C ．3个 D ．4个16．如图，在Rt △ABC 中，∠ACB=90°，CD 是角平分线，DE ∥BC 交AC 于点E ，DF ∥AC 交BC 于点F ． 求证：(1)四边形CEDF 是正方形；(2)CD 2=AE ×BF ． (山东省竞赛题)17．如图，在Rt △ABC 中，∠BCA=90°，CD ⊥AB 于D ，已知Rt △ABC 的三边长都是整数，且BD=113，求Rt △BCD 与Rt △ACD 的周长之比． (全国初中数学联赛题)18．如图，在Rt △ABC 中，∠C=90°，∠A 的平分线AD 交BC 边于D ，求证：BDBCAD AC 222=．19．如图，已知边长为a 的正方形ABCD ，在AB 、AD 上分别取点P 、S ，连结PS ，将Rt △SAP 绕正方形中心O 旋转180°得Rt △QCR ，从而得四边形PQRS ．试判断四边形PQRS 能否变化成矩形?若能，设PA= x ，SA=y ，请说明x 、y 具有什么关系时，四边形PQRS 是矩形；若不能，请说明理由． (山东省济南市中考题)20．如图，在△ABC 中，∠ACB ＝90° (1)当点D 在斜边AB 内时，求证：ABBDAD BC BD CD -=-222； (2)当点D 与点A 重合时，(1)中的等式是否存在?请说明理由； (3)当点D 在BA 的延长线上时，(1)中的等式是否存在?请说明理由．(全国初中数学竞赛题)。

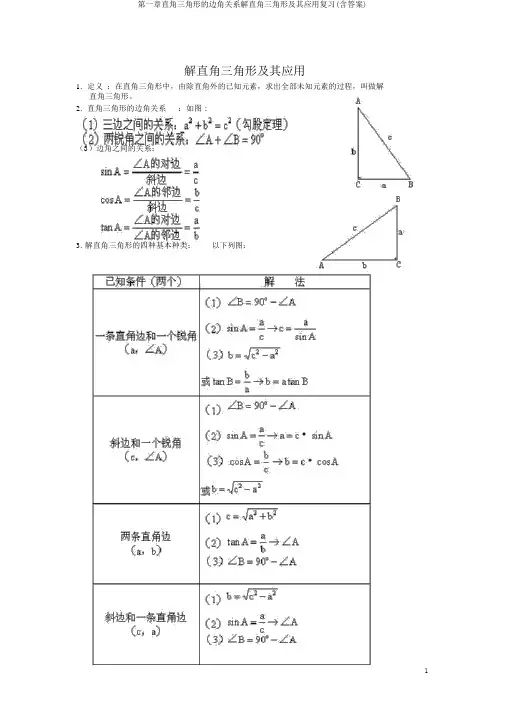
解直角三角形及其应用1.定义：在直角三角形中，由除直角外的已知元素，求出全部未知元素的过程，叫做解直角三角形。

2.直角三角形的边角关系：如图 :（3）边角之间的关系：3. 解直角三角形的四种基本种类：以下列图：已知直角三角形的两个基本元素（起码有一个是边），利用以上关系就能够求出其他的未知元素，此中适合地采用边角关系是重点。

应注意以下原则：（1）有“斜”选“弦”，无“斜”选“切”。

（2）尽量使未知元素在分子的地点上，以便利用乘法运算求未知元素。

（3）尽量使用原始数据：以减少偏差的累积，也可防止因为中间数占有错而产生新的误差。

4.几个常用观点：（1）仰角：在丈量时，从下向上看，视野与水平线的夹角叫仰角。

（2）俯角：在丈量时，从上向下看，视野与水平线的夹角叫俯角。

（3）坡度：（坡比）如图:坡面的铅直高度（h）和水平长度（l ）的比，叫做坡面的坡度。

（4）坡角：坡面与水平面的夹角叫做坡角，记作α。

坡度越大，坡角越大，坡面越陡。

（5）方向角（如图）OA ：北偏东30°OB：东南方（南偏东45°）OC：南偏西70°OD：北偏西60°东西与南北方向线相互垂直。

5.运用解直角三角形的方法解决实质问题：基本思路：要擅长将某些实质问题中的数目关系归纳为直角三角形中的边角关系。

（即建立数学模型：直角三角形），才能运用解直角三角形的方法求解。

一般有以下几个步骤：（1）审题：依据题意画出正确的平面图或截面表示图，在图形中弄清已知和未知。

（2）将已知条件转变为表示图中的边、角关系，把实质问题转变为解直角三角形的问题。

（3）选择适合关系式解直角三角形。

典型例题例 1. 在Rt△ABC中，∠C＝90°，解直角三角形：（1） a＝ 8， b＝ 6（2） c＝ 16，∠ A ＝ 32°剖析：略解：例 2. 如图某公园进口处原有三级台阶，每级台阶高为20cm，深为30cm，为方便残疾人士，能够将台阶改为斜坡，设台阶的起点为 A ，斜坡的起点为 C，现将斜坡的坡角∠ BCA 设计为 12°，求 AC 的长度（精准到 1cm）。

直角三角形一、直角三角形的性质重点：直角三角形的性质定理与其推论：①直角三角形的性质，在直角三角形中，斜边上的中线等于斜边的一半;②推论：（1）在直角三角形中，如果一个锐角等于30°，则它所对的直角边等于斜边的一半;（2）在直角三角形中，如果一条直角边等于斜边的一半，那么这条直角边所对的角为30°.难点：1.性质定理的证明方法.2.性质定理与其推论在解题中的应用.二、直角三角形全等的判断重点：掌握直角三角形全等的判定定理：斜边、直角边公理：斜边和一条直角边对应相等的两个直角三角形全等（）难点：创建全等条件与三角形中各定理联系解综合问题。

三、角平分线的性质定理1.角平分线的性质定理：角平分线上的点到这个角的两边的距离相等.定理的数学表示：如图4，∵是∠的平分线，F是上一点，且⊥于点C，⊥于点D，∴＝.定理的作用：①证明两条线段相等；②用于几何作图问题；角是一个轴对称图形，它的对称轴是角平分线所在的直线.图42.关于三角形三条角平分线的定理：三角形三条角平分线相交于一点，并且这一点到三边的距离相等.定理的数学表示：如图6，如果、、分别是△的内角∠、∠、∠的平分线，那么：①、、相交于一点I；②若、、分别垂直于、、于点D、E、F，则＝＝.定理的作用：①用于证明三角形内的线段相等；②用于实际中的几何作图问题.（2）三角形三条角平分线的交点位置与三角形形状的关系：三角形三个内角角平分线的交点一定在三角形的内部.这个交点叫做三角形的内心（即内切圆的圆心）.3.关于线段的垂直平分线和角平分线的作图：（1）会作已知线段的垂直平分线；（2）会作已知角的角平分线；（3）会作与线段垂直平分线和角平分线有关的简单综合问题的图形.四、勾股定理的证明与应用１．勾股定理内容：直角三角形两直角边的平方和等于斜边的平方；表示方法：如果直角三角形的两直角边分别为a，b，斜边为c，那么222+=a b c勾股定理的由来：勾股定理也叫商高定理，在西方称为毕达哥拉斯定理．我国古代把直角三角形中较短的直角边称为勾，较长的直角边称为股，斜边称为弦．早在三千多年前，周朝数学家商高就提出了“勾三，股四，弦五”形式的勾股定理，后来人们进一步发现并证明了直角三角形的三边关系为：两直角边的平方和等于斜边的平方２.勾股定理的证明勾股定理的证明方法很多，常见的是拼图的方法 用拼图的方法验证勾股定理的思路是①图形进过割补拼接后，只要没有重叠，没有空隙，面积不会改变 ②根据同一种图形的面积不同的表示方法，列出等式，推导出勾股定理 常见方法如下：方法一：4EFGH S S S ∆+=正方形正方形ABCD ，2214()2ab b a c ⨯+-=，化简可证．方法二：四个直角三角形的面积与小正方形面积的和等于大正方形的面积．四个直角三角形的面积与小正方形面积的和为221422S ab c ab c =⨯+=+ 大正方形面积为222()2S a b a ab b =+=++所以222a b c +=方法三：1()()2S a b a b =+⋅+梯形，2112S 222ADE ABE S S ab c ∆∆=+=⋅+梯形，化简得证３.勾股定理的适用范围勾股定理揭示了直角三角形三条边之间所存在的数量关系，它只适用于直角三角形，对于锐角三角形和钝角三角形的三边就不具有这一特征，因而在应用勾股定理时，必须明了所考察的对象是直角三角形４.勾股定理的应用①已知直角三角形的任意两边长，求第三边在ABC ∆中，90C ∠=︒，则c =，b =，a =②知道直角三角形一边，可得另外两边之间的数量关系③可运用勾股定理解决一些实际问题 ５.勾股定理的逆定理如果三角形三边长a ，b ，c 满足222a b c +=，那么这个三角形是直角三角形，其中c 为cbaHG F EDCBAbacbac cabcab a bcc baED CBA斜边①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法，它通过“数转化为形”来确定三角形的可能形状，在运用这一定理时，可用两小边的平方和22a b +与较长边的平方2c 作比较，若它们相等时，以a ，b ，c 为三边的三角形是直角三角形；若222a b c +<，时，以a ，b ，c 为三边的三角形是钝角三角形；若222a b c +>，时，以a ，b ，c 为三边的三角形是锐角三角形；②定理中a ，b ，c 与222a b c +=只是一种表现形式，不可认为是唯一的，如若三角形三边长a ，b ，c 满足222a c b +=，那么以a ，b ，c 为三边的三角形是直角三角形，但是b 为斜边③勾股定理的逆定理在用问题描述时，不能说成：当斜边的平方等于两条直角边的平方和时，这个三角形是直角三角形 ６.勾股数①能够构成直角三角形的三边长的三个正整数称为勾股数，即222a b c +=中，a ，b ，c 为正整数时，称a ，b ，c 为一组勾股数②记住常见的勾股数可以提高解题速度，如3,4,5；6,8,10；5,12,13；7,24,25等 ③用含字母的代数式表示n 组勾股数：221,2,1n n n -+（2,n ≥n 为正整数）；2221,22,221n n n n n ++++（n 为正整数）2222,2,m n mn m n -+（,m n >m ，n 为正整数）７．勾股定理的应用勾股定理能够帮助我们解决直角三角形中的边长的计算或直角三角形中线段之间的关系的证明问题．在使用勾股定理时，必须把握直角三角形的前提条件，了解直角三角形中，斜边和直角边各是什么，以便运用勾股定理进行计算，应设法添加辅助线（通常作垂线），构造直角三角形，以便正确使用勾股定理进行求解． ８.．勾股定理逆定理的应用勾股定理的逆定理能帮助我们通过三角形三边之间的数量关系判断一个三角形是否是直角三角形，在具体推算过程中，应用两短边的平方和与最长边的平方进行比较，切不可不加思考的用两边的平方和与第三边的平方比较而得到错误的结论． ９.勾股定理与其逆定理的应用勾股定理与其逆定理在解决一些实际问题或具体的几何问题中，是密不可分的一个整体．通常既要通过逆定理判定一个三角形是直角三角形，又要用勾股定理求出边的长度，二者相辅相成，完成对问题的解决．常见图形：ABC30°D C BA ADB C10、互逆命题的概念如果一个命题的题设和结论分别是另一个命题的结论和题设，这样的两个命题叫做互逆命题。

第三部分直角三角形一、知识梳理：1.直角三角形的性质：（1）直角三角形两个锐角互余；（2）直角三角形斜边上的中线等于斜边的一半；（3）直角三角形中，30°角所对的直角边等于斜边的一半；（4）勾股定理：在直角三角形中，两直角边的平方和等于斜边的平方，即如果设直角三角形的两条直角边长度分别是a和b，斜边长度是c，那么可以用数学语言表达：222+=a b c （5）勾股数：勾股数就是可以构成一个直角三角形三边的一组正整数．2.直角三角形的判定：（1）有一个角是90°的三角形是直角三角形；（2）有两个角的三角形是直角三角形；（3）如果三角形一边的中线等于这边的一半，那么这个三角形是直角三角形；（4）勾股定理逆定理：如果三角形的三条边长a，b，c满足关系式：222+=a b c，那么这个三角形是直角三角形．二、题型练题型一直角三角形的两锐角互余例1.若直角三角形的一个锐角为15︒，则另一个锐角等于________．75°【分析】根据三角形内角和定理计算即可．【详解】解：∵另一个锐角为15°，∴另一个锐角为180°－90°－15°＝75°，故答案为：75°．【点睛】本题考查了直角三角形的性质，解题的关键是掌握直角三角形两锐角互余．变式11.如图，直线a ∥b ，直线l 与a 、b 分别相交于A 、B 两点，过点A 作直线l 的垂线交直线b 于点C ，若∠1＝60°，则∠2的度数为（）A.30°B.35°C.40°D.60°【答案】A【解析】【分析】由AC l ⊥及160∠=︒，可求得ACB ∠的度数，再由//a b 即可求出2∠的度数．【详解】∵AC l ⊥，160∠=︒∴90130ACB ∠=︒-∠=︒∵//a b∴230ACB ∠=∠=︒故选：A【点睛】本题主要考查了平行线的性质及直角三角形的性质．题型二直角三角形斜边上的中线例2.如图在ABC ∆中，CF AB ⊥于F ，BE AC ⊥于E ，M 为BC 的中点，5EF ＝，EFM ∆的周长为13，则BC 的长是（）A .6B .8C .10D .12B 【解析】【分析】根据直角三角形斜边上的中线等于斜边的一半，求出BC ＝2MF ＝2EM ，所以MF ＝EM ，然后列式整理得到△EFM的周长＝BC＋EF，代入数据进行计算即可．【详解】解：∵在△ABC中，CF⊥AB于F，BE⊥AC于E，M为BC的中点，∴BC＝2MF，BC＝2EM．∴MF＝EM．∴△EFM的周长＝MF＋EM＋EF＝BC＋EF．∵EF＝5，△EFM的周长为13，∴BC＝13－5＝8故选：B．【点睛】本题考查了直角三角形斜边上的中线等于斜边的一半的性质，熟练掌握性质是解题的关键．变式22.如图，在△ABC中，点D，E分别是边AB，AC的中点，点F是线段DE上的一点连接AF，BF，∠AFB=90°，且AB=8，BC=14，则EF的长是（）A.2B.3C.4D.5【答案】B【解析】【分析】根据直角三角形的性质得到DF=4，根据BC=14，由三角形中位线定理得到DE=7，解答即可．【详解】解：∵∠AFB=90°，点D是AB的中点，∴DF=12AB=4，∵BC=14，D、E分别是AB，AC的中点，∴DE=12BC=7，∴EF=DE-DF=3，故选：B【点睛】本题考查了直角三角形的性质和中位线性质，掌握定理是解题的关键．题型三直接考查勾股定理例3.已知直角三角形的两边长分别为3和4，则斜边长为（）A.4B.5C.4或5D.5C【分析】由于此题中直角三角形的斜边不能确定，故应分4是直角三角形的斜边长和直角边长两种情况讨论．【详解】解： 直角三角形的两边长分别为3和4，∴①4是此直角三角形的斜边长；②当45=．综上所述，斜边长为4或5故选：C．【点睛】本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．变式33.如图，在三角形ABC中，∠ACB=90°，AC=3，BC=4，以点A为圆心，AC长为半径画弧，交AB于点D，则BD=（）A. 2.5B.3C.2D.3.5【答案】C【解析】【分析】首先利用勾股定理可以算出AB的长，再根据题意可得到AD=AC，根据BD=AB-AD即可算出答案．【详解】解：∵AC =3，BC =4，∴AB =5，∵以点A 为圆心，AC 长为半径画弧，交AB 于点D ，∴AD =AC ，∴AD =3，∴BD =AB -AD =5-3=2．故选C ．【点睛】此题主要考查了勾股定理，关键是熟练掌握勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．题型四勾股数例4.下列数组是勾股数的是（）A .2、3、4B .0.3、0.4、0.5C .6、8、10D .7、12、15C【分析】根据勾股数的定义：满足222+=a b c 的三个正整数，称为勾股数逐一判断即可．【详解】A ．22223134+=≠，此数组不是勾股数；B ．0.3、0.4、0.5不是整数，此数组不是勾股数；C ．222 6810+=，此数组是勾股数；D ．222 71219315+=≠，此数组不是勾股数；故选：C ．【点睛】本题考查了勾股数的知识，解答此题要用到勾股数的定义，及勾股定理的逆定理：已知△ABC 的三边满足222+=a b c ，则△ABC 是直角三角形．变式44.如图，这是一株美丽的勾股树，所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形A 、B 、C 、D 的边长是3、5、2、3，则最大正方形E 的边长是（）A.13B.C.47D.【答案】B【解析】【分析】设中间两个正方形的边长分别为x 、y ，最大正方形E 的边长为z ，根据勾股定理进行求解．【详解】设中间两个正方形的边长分别为x 、y ，最大正方形E 的边长为z ，由勾股定理得：x 2＝32+52＝34，y 2＝22+32＝13，z 2＝x 2+y 2＝47，即最大正方形E 的面积为：z 2＝47，边长为z 故选B ．【点睛】本题考查勾股定理，掌握以直角三角形斜边为边长的正方形的面积等于两个以直角边为边长的正方形面积之和是解题的关键．题型五勾股定理的证明例5.勾股定理是人类最伟大的十个科学发现之一，在《周髀算经》中就有“若勾三，股四，则弦五”的记载，汉代数学家赵爽为证明勾股定理创制的“赵爽弦图”也流传至今．迄今为止己有400多种证明勾股定理的方法．下面是数学课上创新小组验证过程的一部分．请认真阅读并根据他们的思路将后续的过程补充完整：将两张全等的直角三角形纸片按图所示摆放，其中b a >，点E 在线段AC 上，点B D 、在边AC 两侧，试证明：222+=a b c ．见解析．【分析】首先连结BD ，作DF BC ⊥延长线于F ，则AE b a =-，根据Rt ABC Rt DAE D @D ，易证90DAB ︒∠=，再根据ADE ABC ADFB DFCE S S S S D D =++四边形四边形，ADB DFB ADFB S S S ∆∆=+四边形，两者相等，整理即可得证．【详解】证明：连结BD ，作DF BC ⊥延长线于F ，则AE b a=-ADE ABC ADFB DFCES S S S D D =++四边形四边形()1122ab ab b a b =++-⋅2ab b ab=+-2b =Rt ABC Rt DAE∆≅∆ AB AD c\==ADE BAC∴∠=∠90ADEDAE °??Q 90BAC DAE °\??即90DAB ︒∠=，∴AD AB⊥∴ADB DFBADFB S S S ∆∆=+四边形()()21122c a b b a =++⋅-222111222c b a =+-即有：2222111222b c b a =+-∴222+=a b c 【点睛】本题考查了勾股定理的证明，用两种方法表示出四边形ADFB 的面积是解本题的关键．变式55.勾股定理现约有500种证明方法，是用代数思想解决几何问题的最重要的工具之一．中国古代最早对勾股定理进行证明的是三国时期吴国的数学家赵爽，赵爽创制了如图1所示的“勾股圆方图”，在该图中，以弦c 为边长所得到的正方形ABCD 是由4个全等的直角三角形再加上中间的小正方形EFGH 组成的，其中BF a =，AF b =．（1）请利用面积相等证明勾股定理；（2）在图1中，若大正方形ABCD 的面积是13，2BF =，求小正方形EFGH 的面积；（3）图2是由“勾股圆方图”变化得到的，正方形MNKT 由八个全等的直角三角形和正方形EFGH 拼接而成，记图中正方形MNKT ，正方形ABCD ，正方形EFGH 的面积分别为1S ，2S ，3S ．若12348S S S ++=，求边AB 的长度．【答案】（1）证明见解析；（2）1；（3）4【解析】【分析】（1）根据大正方形的面积=4个全等直角三角形的面积+小正方形的面积证明可得结论；（2）由勾股定理可得AF 的长，从而可得小正方形的边长，进一步可求出小正方形的面积；（3）分别求出正方形MNKT ，正方形ABCD ，正方形EFGH 的边长，求出其面积，代入12348S S S ++=，进一步整理可得解．【详解】解：（1）∵Rt ABF Rt DAE Rt CDH Rt BCG∆≅∆≅∆≅∆∴BF AF DH CG a ====，AF DE CH BG b====∴小正方形EFGH 的边长=b a-又大正方形的边长为c∴正方形ABCD 的面积为2c ，4个全等直角三角形的面积和为2ab ，正方形EFGH 的面积为()2b a -，由“大正方形的面积=4个全等直角三角形的面积+小正方形的面积”得;2214()2c ab b a =⨯+-∴()222c ab b a =+-经过整理可得222c a b =+（2）∵大正方形ABCD 的面积是13，∴213c =∵2BF =，且222BF AF AB +=∴2221349AF AB BE =-=-=∴3AF =(负值舍去)∴321EF =-=∴小正方形EFGH 的面积为1；（3）∵正方形MNKT 由八个全等的直角三角形和正方形EFGH 拼接而成，∴AM AF b ==，MB BF a ==，∴正方形MNKT 的边长为a b +，∴正方形MNKT 的面积为()2a b +．而正方形ABCD 的边长为c ，正方形EFGH 的边长为()b a -，∴正方形ABCD 的面积为2c ，正方形EFGH 的面积为()2b a -，∴()()22248a b c b a +++-=，整理得，2348c =，∴4c =（负值舍去）【点睛】此题考查的是勾股定理的证明和应用，能够准确识图是解答本题的关键．题型六勾股定理的实际应用例6.如图，小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底墙到左墙角的距离为1.5m ，顶端距离地面2m ，如果保持梯子底端位置不动，将梯子斜靠在右墙时，顶端距离地面0.7m ，那么小巷的宽度为（）A .3.2mB .3.5mC .3.9mD .4mC【分析】如图，在Rt △ACB 中，先根据勾股定理求出AB ，然后在Rt △A ′BD 中根据勾股定理求出BD ，进而可得答案．【详解】解：如图，在Rt △ACB 中，∵∠ACB ＝90°，BC ＝1.5米，AC ＝2米，∴AB 2＝1.52＋22＝6.25，∴AB ＝2.5米，在Rt △A ′BD 中，∵∠A ′DB ＝90°，A ′D ＝0.7米，BD 2＋A ′D 2＝A ′B 2，∴BD 2＋0.72＝6.25，∴BD 2＝5.76，∵BD＞0，∴BD＝2.4米，∴CD＝BC＋BD＝1.5＋2.4＝3.9米．故选：C．【点睛】本题考查了勾股定理的应用，正确理解题意、熟练掌握勾股定理是解题的关键．变式66.小明想知道学校旗杆多高，他发现旗杆上的绳子垂到地面还多2m，当他把绳子的下端拉开10m后，发现下端刚好接触地面，则旗杆的高为（）A.16mB.20mC.24mD.28m【答案】C【解析】【分析】根据题意设旗杆的高AB为x米，则绳子AC的长为（x+2）米，再利用勾股定理即可求得AB的长，即旗杆的高．【详解】解：如图：设旗杆的高AB为x米，则绳子AC的长为（x+2）米，在Rt△ABC中，BC=10米，由勾股定理得：AB2+BC2=AC2，∴x2+102=（x+2）2，解得：x=24，∴AB=24．∴旗杆的高24米，故选：C ．【点睛】本题考查学生利用勾股定理解决实际问题的能力，解题关键是构造直角三角形利用勾股定理列出方程．题型七勾股定理的逆定理例7.下列四组数中不能构成直角三角形的一组是（）A .4，5，6B .7，24，25C .5，12，13D .1，2A【分析】分别把选项中的三边平方后，根据勾股定理逆定理即可判断能否构成直角三角形．【详解】解：A 、∵222456+≠，∴三条线段不能组成直角三角形，故A 选项符合题意；B 、∵22272425+=，∴三条线段能组成直角三角形，故B 选项不符合题意；C 、∵22251213+=，∴三条线段能组成直角三角形，故C 选项不符合题意；D 、∵22212+=，∴三条线段能组成直角三角形，故D 选项不符合题意；故选：A ．【点睛】本题考查了勾股定理逆定理，熟悉定理是关键．变式77.在如图的网格中，每个小正方形的边长为1，A 、B 、C 三点均在正方形格点上，若AD 是ABC 的高，则AD 的长为（）A. B. C. D.2【答案】D【解析】【分析】结合格点的特点利用勾股定理求得AB 2，AC 2，BC 2，然后利用勾股定理逆定理判定△ABC 的形状，从而利用三角形面积求解．【详解】解：由题意可得：2222420AB =+=222215AC =+=2223425BC =+=∵222+AB AC BC =∴△ABC 是直角三角形又∵AD 是ABC 的高∴1122AC AB BC AD ⋅=⋅，11522AD ⨯，解得：=2AD 故选：D ．【点睛】本题考查勾股定理及其逆定理，掌握勾股定理，利用网格特点，准确计算是解题关键．题型八勾股定理的逆定理的应用例8.如图所示的网格是正方形网格，ABC ∆是（）三角形．A .锐角B .直角C .钝角D .等腰A【分析】根据勾股定理求出三边的长，再利用勾股定理逆定理可作判断．【详解】解：根据网格图可得：2224117AC =+=，2223110AB =+=，2224325CB =+=，222171025AC AB CB +=+>= ，ABC ∆∴是锐角三角形，故选：A ．【点睛】本题考查了三边的关系，会利用三边关系确定三角形的形状：若三角形的三边分别为a 、b 、c ，①当a 2＋b 2＞c 2时，△ABC 为锐角三角形；②当a 2＋b 2＜c 2时，△ABC 为钝角三角形；③当a 2＋b 2＝c 2时，△ABC 为直角三角形．变式88.甲、乙两艘轮船同时从港口出发，甲以16海里/时的速度向北偏东75︒的方向航行，它们出发1.5小时后，两船相距30海里，若乙以12海里/时的速度航行，则它的航行方向为（）A.北偏西15︒B.南偏西75°C.南偏东15︒或北偏西15︒D.南偏西15︒或北偏东15︒【答案】C【解析】【分析】先求出出发1.5小时后，甲乙两船航行的路程，进而可根据勾股定理的逆定理得出乙船的航行方向与甲船的航行方向垂直，进一步即可得出答案．【详解】解：出发1.5小时后，甲船航行的路程是16×1.5=24海里，乙船航行的路程是12×1.5=18海里；∵222241857632490030+=+==，∴乙船的航行方向与甲船的航行方向垂直，∵甲船的航行方向是北偏东75°，∴乙船的航行方向是南偏东15°或北偏西15°．故选：C ．【点睛】本题考查了勾股定理的逆定理和方位角，属于常考题型，正确理解题意、熟练掌握勾股定理的逆定理是解题的关键．题型九勾股定理与折叠问题例9.如图，矩形纸片ABCD 中，AB ＝CD ＝4，AD ＝BC ＝8，∠BAD ＝∠B ＝∠C ＝∠D ＝90°，将纸片沿EF 折叠，使点C 与点A 重合，使点G 与点D 重合．（1）求证：AE ＝AF ；（2）求GF 的长．（1）详见解析；（2）3【分析】（1）根据翻折的性质可得AEF CEF ∠=∠，根据两直线平行，内错角相等可得∠=∠AFE CEF ，然后求出AEF AFE ∠=∠，根据等角对等边可得AE AF =；（2）根据翻折的性质可得AE CE =，设AE CE x ==，则8BE x =-，再根据勾股定理有：2224(8)x x =+-，于是有5AE AF ==，进而得到3GF FD ==．【详解】解：（1）由翻折的性质得，AEF CEF ∠=∠，矩形ABCD 的对边//AD BC ，AFE CEF ∴∠=∠，AEF AFE ∴∠=∠，AE AF ∴=；（2）由翻折的性质得，AE CE =，设AE CE x ==，则8BE x =-，在Rt ABE ∆中，222AE AB BE =+，2224(8)x x ∴=+-，解得：5x =，5AE ∴=，又由（1）可知，5AF =，853FD AD AF ∴=-=-=，由翻折的性质得，3GF FD ==．【点睛】本题考查了翻折变换的性质，矩形的性质，勾股定理，熟记各性质并作利用勾股定理列方程求出AE 的长度是解题的关键．变式99.如图，在Rt ABC 中，90,5,8ACB AC BC ∠=︒==，点D 是边BC 的中点，点E是边AB 上的任意一点（点E 不与点B 重合），沿DE 翻折DBE 使点B 落在点F 处，连接AF ，则线段AF 长的最小值是（）A.2B.4-C.3D.4-【答案】B【解析】【分析】连接AD ，以D 为圆心，以CD 为半径画圆，交AD 于G ，根据题意可知点F 在D 上，当G 和F 重合时AF 有最小值，然后利用勾股定理计算长度即可．【详解】解：连接AD ，以D 为圆心，以CD 为半径画圆，交AD 于G ，根据题意可知点F 在D 上，当G 和F 重合时AF 有最小值，∵点D 是边BC 的中点，∴142CD GD BC ===,在Rt △ACD 中AD =∴4AG AD GD =-=．故选：B【点睛】本题主要考查圆的性质和勾股定理，能够找到点F 的运动轨迹是解题的关键．题型十最短距离问题例10.如图，台阶A 处的蚂蚁要爬到B 处搬运食物，它爬的最短距离是_____．25【分析】先将图形平面展开，再用勾股定理根据两点之间线段最短进行解答．【详解】解：如图所示：台阶平面展开图为长方形，根据题意得：20AC =，55515BC =++=，则蚂蚁沿台阶面爬行到B 点最短路程是此长方形的对角线长．由勾股定理得：222AB AC BC =+，即2222015AB =+，∴25AB =，故答案为：25【点睛】本题主要考查了平面展开图—最短路径问题，用到台阶的平面展开图，只要根据题意判断出长方形的长和宽即可解答．变式1010.如图，正方形ABCD ，AB 边上有一点E ，3AE =，1EB =，在AC 上有一点P ，使为EP BP +最短．则最短距离EP BP +为_________．【答案】5【解析】【分析】连接DE ，交直线AC 于点P ，根据四边形ABCD 是正方形可知B 、D 关于直线AC 对称，所以DE 的长即为EP+BP 的最短距离，再根据勾股定理即可得出结论．【详解】连接DE，交直线AC于点P，∵四边形ABCD是正方形，∴B、D关于直线AC对称，∴DE的长即为EP+BP的最短距离，∵AE=3，EB=1，∴AD=AB=AE+BE=4，∴5==．故答案为：5．【点睛】本题考查了轴对称－最短路线问题、正方形的性质以及勾股定理的运用，熟知两点之间线段最短是解答此题的关键．实战练11.如图，公路AC，BC互相垂直，公路AB的中点M与点C被湖隔开，若测得AM的长为1.2km，则M、C两点间的距离为（）A0.5km A.0.6km B.0.9km C.1.2km【答案】D【解析】【详解】根据直角三角形斜边上的中线等于斜边的一半即可求得距离为1.2km.故选D视频12.如图，在Rt △ABC 中，∠C ＝90︒，AC ＝4，BC ＝3，把Rt △ABC 绕着点A 逆时针旋转，使点C 落在AB 边的C ′上，C'B 的长度是（）A.1B.32C.2D.52【答案】A【解析】【分析】首先由勾股定理求出AB =5，再由旋转的性质得出4AC AC '==，从而可求出BC '的长．【详解】解：在Rt △ABC 中，∠C ＝90︒，AC ＝4，BC ＝3，∴222AB AC BC =+∴5AB ===由旋转的性质得，4AC AC '==∴541C B AB AC ''=-=-=故选：A ．【点睛】此题主要考查了旋转的性质和勾股定理的运用，运用勾股定理求出AB =5是解答此题的关键．13.下列各组数中不是勾股数的是（）A.3，4．5B.6．8．10C.5，12．13D.4，5，6【答案】D【解析】【分析】欲判断是否为勾股数，必须根据勾股数是正整数，同时还需满足两小边的平方和等于最长边的平方．【详解】解：A 、32+42=25=52，是勾股数，此选项不符合题意；B 、62+82＝100=102，是勾股数，此选项不符合题意；C 、52+122＝169=132，是勾股数，此选项不符合题意；D 、42+52=41≠62，不是勾股数，此选项符合题意．故选：D ．【点睛】此题主要考查了勾股数：满足a 2+b 2＝c 2的三个正整数，称为勾股数．注意：①三个数必须是正整数，例如：2.5、6、6.5满足a 2+b 2＝c 2，但是它们不是正整数，所以它们不是勾股数．②一组勾股数扩大相同的整数倍得到三个数仍是一组勾股数．③记住常用的勾股数再做题可以提高速度．如：3，4，5；6，8，10；5，12，13；…14.满足下列条件的三角形：①三边长之比为3：4：5；②三内角之比为3：4：5；③n 2﹣1，2n ，n 2+1；1+1-，6．其中能组成直角三角形的是（）A.①③B.②④C.①②D.③④【答案】A【解析】【分析】欲求证是否为直角三角形，若已知三边长，只要验证两小边的平方和是否等于最长边的平方；若已知三个角的度数，只要验证是否存在直角即可．【详解】①三边长之比为3:4:5；则有222(3)(4)(5)x x x +=，为直角三角形；②三个内角度数之比为3:4:5，则各角度数分别为31804512︒⨯=︒，41806012︒⨯=︒，51807512︒⨯=︒，不是直角三角形；③22222(1)(2)(1)n n n -+=+ ，∴是直角三角形；④116++=<，∴构不成三角形．故选：A ．【点睛】本题考查勾股定理的逆定理的应用．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．15.《九章算术》是我国古代的数学名著，书中有“折竹抵地”问题：今有竹高一丈，末折抵地，去本三尺．问折者高几何？意思是：一根竹子，原高一丈（一丈10=尺），一阵风将竹子折断，其竹梢恰好抵地，抵地处离竹子底部3尺远，问折断处离地面的高度是多少？设折断处离地面的高度为x 尺，则可列方程为（）A.2223(1)x x -=- B.2223(10)x x -=-C.2223(1)x x +=- D.2223(10x)x +=-【答案】D【解析】【分析】根据勾股定理列方程解答．【详解】解：设折断处离地面的高度为x 尺，则斜边为（10-x ）尺，根据勾股定理得：2223(10x)x +=-，故选：D ．【点睛】此题考查勾股定理的实际应用，正确理解题意得到直角三角形确定三边的关系式是解题的关键．16.如图所示，将一根长为24cm 的筷子，置于底面直径为5cm ，高为12cm 的圆柱形水杯中，设筷子露在外面的长为hcm ，则h 的取值范围是（）A.0＜h ≤11B.11≤h ≤12C.h ≥12D.0＜h ≤12【答案】B【解析】【分析】根据题意画出图形，先找出h的值为最大和最小时筷子的位置，再根据勾股定理解答即可．【详解】解：当筷子与杯底垂直时h最大，h最大＝24﹣12＝12cm．当筷子与杯底及杯高构成直角三角形时h最小，如图所示：此时，AB＝13cm，∴h＝24﹣13＝11cm．∴h的取值范围是11cm≤h≤12cm．故选：B．【点睛】本题考查了勾股定理的实际应用问题，解答此题的关键是根据题意画出图形找出何时h有最大及最小值，同时注意勾股定理的灵活运用，有一定难度．17.某港口P位于东西方向的海岸线上，“远航”号、“海天”号轮船同时离开港口，各自沿一固定方向航行，“远航”号每小时航行16海里，“海天”号每小时航行12海里．它们离开港口一个半小时后分别位于点Q、R处，且相距30海里．如果知道“远航”号沿东北方向航行，则“海天”号沿()方向航行．A.西南B.东北C.西北D.东南【答案】C【解析】【分析】根据路程=速度×时间分别求得PQ、PR的长，再进一步根据勾股定理的逆定理可以证明三角形PQR是直角三角形，从而进行分析求解．【详解】解：根据题意得PQ=16×1.5=24(海里)，PR=12×1.5=18(海里)，QR=30(海里)．∵242+182=302，即PQ2+PR2=QR2，∴∠QPR=90°．由“远航号”沿东北方向航行可知，∠1=45°，则∠2=45°，即“海天”号沿西北方向航行．故选：C．【点睛】本题考查勾股定理的应用，解题的关键是能够根据勾股定理的逆定理发现直角三角形进行解答．18.如图，在 ABC中，AB=8，BC=6，AC=10，D为边AC上一动点，DE⊥AB于点E，DF⊥BC于点F，则EF的最小值为（）A.5B. 4.8C.3D.2.4【答案】B【解析】【分析】根据三个角都是直角的四边形是矩形，得四边形EDFB是矩形，根据矩形的对角线相等，得EF=BD，则EF的最小值即为BD的最小值，根据垂线段最短，知：BD的最小值即等于直角三角形ABC斜边上的高．【详解】如图，连接BD．∵在△ABC中，AB=8，BC=6，AC=10，∴AB 2+BC 2=AC 2，即∠ABC =90°．又∵DE ⊥AB 于点E ，DF ⊥BC 于点F ，∴四边形EDFB 是矩形，∴EF =BD ．∵BD 的最小值即为直角三角形ABC 斜边上的高，即4.8，∴EF 的最小值为4.8，故选：B ．【点睛】此题综合运用了勾股定理的逆定理、矩形的判定及性质、直角三角形的性质，要能够把要求的线段的最小值转换为便于分析其最小值的线段．19.如图，在四边形ABCD 中，1AB BC ==，CD =，AD =，AB BC ⊥，则四边形ABCD 的面积是()A. 2.5B.3C. 3.5D.4【答案】A【解析】【分析】如下图，连接AC ，在Rt △ABC 中先求得AC 的长，从而可判断△ACD 是直角三角形，从而求得△ABC 和△ACD 的面积，进而得出四边形的面积．【详解】如下图，连接AC∵AB=BC=1，AB ⊥BC∴在Rt △ABC 中，，111122ABC S =⨯⨯=∵，又∵(222+=∴三角形ADC 是直角三角形∴122ADC S == ∴四边形ABCD 的面积=12+2=52故选：A ．【点睛】本题考查勾股定理的逆定理，遇到此类题型我们需要敏感一些，首先就猜测△ADC 是直角三角形，然后用勾股定理逆定理验证即可．20.某高速公路的同一侧有A ，B 两个城镇，如图所示，它们到高速公路所在直线MN 的距离分别为2km AE =，3km BF =，12km EF =，要在高速公路上E 、F 之间建一个出口Q ，使A 、B 两城镇到Q 的距离之和最短，在图中画出点Q 所在位置，并求出这个最短距离．【答案】见解析，13km【解析】【分析】作点B 关于MN 的对称点C ，连接AC 交MN 于点Q ，连接QB ，此时QA+QB 的值最小．作AD ⊥BC 于D ，在Rt △ACD 中，利用勾股定理求出AC 即可；【详解】解：作点B 关于MN 的对称点C ，连接AC 交MN 于点Q ，则点Q 为所建的出口；此时A 、B 两城镇到出口Q 的距离之和最短，最短距离为AC 的长．作AD BC ⊥于D ，则90ADC ∠=︒，AE ⊥MN ，BF ⊥MN∴四边形AEFD 为矩形∴12AD EF ==，2DF AE ==在t R ADC 中，12AD =，5DC DF CF =+=，∴由勾股定理得：13AC ===∴这个最短距离为13km ．【点睛】本题考查作图-应用与设计，轴对称-最短问题、勾股定理等知识，解题的关键是学会利用轴对称解决最短问题，学会添加常用辅助线，构造直角三角形解决问题．培优练21.台风是一种自然灾害，它以台风中心为圆心在周围上千米的范围内形成极端气候，有极强的破坏力．如图，有一台风中心沿东西方向AB 由点A 行驶向点B ，已知点C 为一海港，且点C 与直线AB 上两点A ，B 的距离分别为300km 和400km ，又AB=500km ，以台风中心为圆心周围250km 以内为受影响区域．（1）海港C 受台风影响吗？为什么？（2）若台风的速度为20km/h，台风影响该海港持续的时间有小时．【答案】（1）海港C受台风影响，理由见解析；（2）7．【解析】【分析】（1）根据勾股定理的逆定理得出△ABC是直角三角形，利用等面积法得出CD的长，从而可得海港C是否受台风影响；（2）根据勾股定理得出ED以及EF的长，进而得出台风影响该海港持续的时间．【详解】解：（1）海港C受台风影响．理由：如图，过点C作CD⊥AB于D，∵AC＝300km，BC＝400km，AB＝500km，∴AC2＋BC2＝AB2．∴△ABC是直角三角形．∴AC•BC＝CD•AB∴CD＝240（km）∵以台风中心为圆心周围250km以内为受影响区域，∴海港C受到台风影响．（2）当EC＝250km，FC＝250km时，正好影响C港口，∵ED＝70（km）∴EF＝140km∵台风的速度为20km/h，∴140÷20＝7（小时）即台风影响该海港持续的时间为7小时．故答案为：7．【点睛】本题考查了勾股定理及逆定理的应用，解答此类题目的关键掌握勾股定理及其逆定理并构造直角三角形，利用勾股定理解决问题．。

直角三角形一、直角三角形的性质重点：直角三角形的性质定理及其推论：①直角三角形的性质，在直角三角形中，斜边上的中线等于斜边的一半;②推论：（1）在直角三角形中，如果一个锐角等于30°，则它所对的直角边等于斜边的一半;（2）在直角三角形中，如果一条直角边等于斜边的一半，那么这条直角边所对的角为30°.难点：1.性质定理的证明方法.2.性质定理及其推论在解题中的应用.二、直角三角形全等的判断重点：掌握直角三角形全等的判定定理：斜边、直角边公理：斜边和一条直角边对应相等的两个直角三角形全等（HL）难点：创建全等条件与三角形中各定理联系解综合问题。

三、角平分线的性质定理1.角平分线的性质定理：角平分线上的点到这个角的两边的距离相等.定理的数学表示：如图4，∵ OE是∠AOB的平分线，F是OE上一点，且CF⊥OA于点C，DF⊥OB于点D，∴ CF＝DF.定理的作用：①证明两条线段相等；②用于几何作图问题；角是一个轴对称图形，它的对称轴是角平分线所在的直线. 图42.关于三角形三条角平分线的定理：三角形三条角平分线相交于一点，并且这一点到三边的距离相等.定理的数学表示：如图6，如果AP、BQ、CR分别是△ABC 的内角∠BAC、∠ ABC、∠ACB的平分线，那么：① AP、BQ、CR相交于一点I；②若ID、IE、IF分别垂直于BC、CA、AB于点D、E、F，则DI＝EI＝FI.定理的作用：①用于证明三角形内的线段相等；②用于实际中的几何作图问题.（2）三角形三条角平分线的交点位置与三角形形状的关系：三角形三个内角角平分线的交点一定在三角形的内部.这个交点叫做三角形的内心（即内切圆的圆心）.3.关于线段的垂直平分线和角平分线的作图：（1）会作已知线段的垂直平分线；（2）会作已知角的角平分线；（3）会作与线段垂直平分线和角平分线有关的简单综合问题的图形.四、勾股定理的证明及应用１．勾股定理内容：直角三角形两直角边的平方和等于斜边的平方；表示方法：如果直角三角形的两直角边分别为a，b，斜边为c，那么222a b c+=勾股定理的由来：勾股定理也叫商高定理，在西方称为毕达哥拉斯定理．我国古代把直角三角形中较短的直角边称为勾，较长的直角边称为股，斜边称为弦．早在三千多年前，周朝数学家商高就提出了“勾三，股四，弦五”形式的勾股定理，后来人们进一步发现并证明了直角三角形的三边关系为：两直角边的平方和等于斜边的平方２.勾股定理的证明勾股定理的证明方法很多，常见的是拼图的方法 用拼图的方法验证勾股定理的思路是①图形进过割补拼接后，只要没有重叠，没有空隙，面积不会改变 ②根据同一种图形的面积不同的表示方法，列出等式，推导出勾股定理 常见方法如下： 方法一：4EFGH S S S ∆+=正方形正方形ABCD ，2214()2ab b a c ⨯+-=，化简可证．方法二：四个直角三角形的面积与小正方形面积的和等于大正方形的面积．四个直角三角形的面积与小正方形面积的和为221422S ab c ab c =⨯+=+大正方形面积为222()2S a b a ab b=+=++所以222a b c +=方法三：1()()2S a b a b =+⋅+梯形，2112S 222ADE ABE S S ab c ∆∆=+=⋅+梯形，化简得证３.勾股定理的适用范围勾股定理揭示了直角三角形三条边之间所存在的数量关系，它只适用于直角三角形，对于锐角三角形和钝角三角形的三边就不具有这一特征，因而在应用勾股定理时，必须明了所考察的对象是直角三角形４.勾股定理的应用①已知直角三角形的任意两边长，求第三边在ABC ∆中，90C ∠=︒，则c，b =，a ②知道直角三角形一边，可得另外两边之间的数量关系③可运用勾股定理解决一些实际问题 ５.勾股定理的逆定理cba HG F EDCBAbacba ccabcab a bc c baED CBA如果三角形三边长a ，b ，c 满足222a b c +=，那么这个三角形是直角三角形，其中c 为斜边①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法，它通过“数转化为形”来确定三角形的可能形状，在运用这一定理时，可用两小边的平方和22a b +与较长边的平方2c 作比较，若它们相等时，以a ，b ，c 为三边的三角形是直角三角形；若222a b c +<，时，以a ，b ，c 为三边的三角形是钝角三角形；若222a b c +>，时，以a ，b ，c 为三边的三角形是锐角三角形；②定理中a ，b ，c 及222a b c +=只是一种表现形式，不可认为是唯一的，如若三角形三边长a ，b ，c 满足222a c b +=，那么以a ，b ，c 为三边的三角形是直角三角形，但是b 为斜边 ③勾股定理的逆定理在用问题描述时，不能说成：当斜边的平方等于两条直角边的平方和时，这个三角形是直角三角形 ６.勾股数①能够构成直角三角形的三边长的三个正整数称为勾股数，即222a b c +=中，a ，b ，c 为正整数时，称a ，b ，c 为一组勾股数②记住常见的勾股数可以提高解题速度，如3,4,5；6,8,10；5,12,13；7,24,25等 ③用含字母的代数式表示n 组勾股数：221,2,1n n n -+（2,n ≥n 为正整数）；2221,22,221n n n n n ++++（n 为正整数）2222,2,m n mn m n -+（,m n >m ，n 为正整数）７．勾股定理的应用勾股定理能够帮助我们解决直角三角形中的边长的计算或直角三角形中线段之间的关系的证明问题．在使用勾股定理时，必须把握直角三角形的前提条件，了解直角三角形中，斜边和直角边各是什么，以便运用勾股定理进行计算，应设法添加辅助线（通常作垂线），构造直角三角形，以便正确使用勾股定理进行求解． ８.．勾股定理逆定理的应用勾股定理的逆定理能帮助我们通过三角形三边之间的数量关系判断一个三角形是否是直角三角形，在具体推算过程中，应用两短边的平方和与最长边的平方进行比较，切不可不加思考的用两边的平方和与第三边的平方比较而得到错误的结论． ９.勾股定理及其逆定理的应用勾股定理及其逆定理在解决一些实际问题或具体的几何问题中，是密不可分的一个整体．通常既要通过逆定理判定一个三角形是直角三角形，又要用勾股定理求出边的长度，二者相辅相成，完成对问题的解决．常见图形：ABC30°D C BA ADB C10、互逆命题的概念如果一个命题的题设和结论分别是另一个命题的结论和题设，这样的两个命题叫做互逆命题。

中考数学专题复习第十九讲解直角三角形【基础知识回顾】一、锐角三角函数定义：在RE△ABC中，∠C=900, ∠A、∠B、∠C的对边分别为a、b、c，则∠A的正弦可表示为：sinA= ，∠A的余弦可表示为CBA= ∠A的正切：tanA= ，它们弦称为∠A的锐角三角函数【提醒：1、sinA、∠cosA、tanA表示的是一个整体，是两条线段的比，没有，这些比值只与有关，与直角三角形的无关2、取值范围<sinA< cosA< tanA> 】二、特殊角的三角函数值：解的基础上结合表格进行记忆2、当时，正弦和正切值随着角度的增大而余弦值随着角度的增大而3、几个特殊关系：⑴sinA+cos2A= ,tanA=sin A⑵若∠A+∠B=900，则sinA= cosA.tanB= 】三、解直角三角形：1、定义：由直角三角形中除直角外的个已知元素，求出另外个未知元素的过程叫解直角三角形2、解直角三角形的依据：RT∠ABC中，∠C900 三边分别为a、b、c⑴三边关系：⑵两锐角关系⑶边角之间的关系：sinA cosA tanAsinB cosB tanB【提醒：解直角三角形中已知的两个元素应至少有一个是当没有直角三角形时应注意构造直角三角形，再利用相应的边角关系解决】3、解直角三角形应用中的有关概念⑴仰角和俯角：如图：在用上标上仰角和俯角⑵坡度坡角：如图：斜坡AB的垂直度H和水平宽度L的比叫做坡度，用i表示，即i=坡面与水平面得夹角为用字母α表示，则i=h l=⑶方位角：是指南北方向线与目标方向所成的小于900的水平角如图：OA表示OB表示OC表示（也可称西南方向）3、利用解直角三角形知识解决实际问题的一般步骤：⑴把实际问题抓化为数字问题（画出平面图形，转化为解直角三角形的问题）⑵根据条件特点选取合适的锐角三角函数去解直角三角形⑶解数学问题答案，从而得到实际问题的答案【提醒：在解直角三角形实际应用中，先构造符合题意的三角形，解题的关键是弄清在哪个直角三角形中用多少度角的哪种锐角三角函数解决】【重点考点例析】考点一：锐角三角函数的概念例1 （2012•内江）如图所示，△ABC的顶点是正方形网格的格点，则sinA的值为（）A．12B．55C．1010D．255思路分析：利用网格构造直角三角形，根据锐角三角函数的定义解答．解：如图：连接CD交AB于O，根据网格的特点，CD⊥AB，在Rt△AOC中，CO=2211+=2；AC=2213+=10；则sinA=OCAC=25510=．故选B．点评：本题考查了锐角三角函数的定义和勾股定理，作出辅助线CD并利用网格构造直角三角形是解题的关键．对应训练1．（2012•贵港）在平面直角坐标系中，已知点A（2，1）和点B（3，0），则sin∠AOB 的值等于（）A．55B．52C．32D．121．A考点：锐角三角函数的定义；坐标与图形性质；勾股定理．专题：计算题．分析：过A作AC⊥x轴于C，利用A点坐标为（2，1）可得到OC=2，AC=1，利用勾股定理可计算出OA，然后根据正弦的定义即可得到sin∠AOB的值．解答：解：如图过A作AC⊥x轴于C，∵A点坐标为（2，1），∴OC=2，AC=1，∴OA=22OC AC+=5，∴sin∠AOB=1555ACOA==．故选A．点评：本题考查了正弦的定义：在直角三角形中，一个锐角的正弦等于这个角的对边与斜边的比值．也考查了点的坐标与勾股定理．考点二：特殊角的三角函数值例2 （2012•孝感）计算：cos245°+tan30°•sin60°=．思路分析：将cos45°=22，tan30°=33，sin60°=32代入即可得出答案．解：cos245°+tan30°•sin60°=12+33×32=12+12=1．故答案为：1．点评：此题考查了特殊角的三角函数值，属于基础题，熟练记忆一些特殊角的三角函数值是解答本题的关键．对应训练（2012•南昌）计算：sin30°+cos30°•tan60°．思路分析：分别把各特殊角的三角函数代入，再根据二次根式混合运算的法则进行计算即可．解：原式=13322+⨯=1322+=2．点评：本题考查的是特殊角的三角函数值，熟记各特殊角度的三角函数值是解答此题的关键．考点三：化斜三角形为直角三角形例3 （2012•安徽）如图，在△ABC 中，∠A=30°，∠B=45°，AC=23，求AB 的长．6．思路分析：过C 作CD ⊥AB 于D ，求出∠BCD=∠B ，推出BD=CD ，根据含30度角的直角三角形求出CD ，根据勾股定理求出AD ，相加即可求出答案． 解：过C 作CD ⊥AB 于D ， ∴∠ADC=∠BDC=90°， ∵∠B=45°，∴∠BCD=∠B=45°， ∴CD=BD ，∵∠A=30°，AC=23， ∴CD=3， ∴BD=CD=3， 由勾股定理得：AD=22AC CD =3，∴AB=AD+BD=3+3， 答：AB 的长是3+3．点评：本题考查了勾股定理，等腰三角形的性质和判定，含30度角的直角三角形性质等知识点的应用，关键是构造直角三角形，题目具有一定的代表性，是一道比较好的题目． 对应训练3．（2012•重庆）如图，在Rt △ABC 中，∠BAC=90°，点D 在BC 边上，且△ABD 是等边三角形．若AB=2，求△ABC 的周长．（结果保留根号）3．考点：解直角三角形；三角形内角和定理；等边三角形的性质；勾股定理． 专题：计算题．分析：根据等边三角形性质求出∠B=60°，求出∠C=30°，求出BC=4，根据勾股定理求出AC ，相加即可求出答案．解答：解：∵△ABD 是等边三角形， ∴∠B=60°， ∵∠BAC=90°， ∴∠C=180°-90°-60°=30°， ∴BC=2AB=4，在Rt △ABC 中，由勾股定理得：AC=22224223BC AB -=-=， ∴△ABC 的周长是AC+BC+AB=23+4+2=6+23． 答：△ABC 的周长是6+23．点评：本题考查了勾股定理，含30度角的直角三角形，等边三角形性质，三角形的内角和定理等知识点的应用，主要培养学生运用性质进行推理和计算的能力，此题综合性比较强，是一道比较好的题目．考点四：解直角三角形的应用例 4 （2012•张家界）黄岩岛是我国南海上的一个岛屿，其平面图如图甲所示，小明据此构造出该岛的一个数学模型如图乙所示，其中∠B=∠D=90°，AB=BC=15千米，CD=32千米，请据此解答如下问题：（1）求该岛的周长和面积；23≈1.73 6≈2.45） （2）求∠ACD 的余弦值． 考点：解直角三角形的应用．分析：（1）连接AC ，根据AB=BC=15千米，∠B=90°得到∠BAC=∠ACB=45°2千米，再根据∠D=90°利用勾股定理求得AD 的长后即可求周长和面积；（2）直接利用余弦的定义求解即可． 解：（1）连接AC∵AB=BC=15千米，∠B=90° ∴∠BAC=∠ACB=45° AC=152千米 又∵∠D=90°∴AD=22 -AC CD =22(152)(32)123-=（千米）∴周长=AB+BC+CD+DA=30+32+123=30+4.242+20.784≈55（千米） 面积=S △ABC+18 6 ≈157（平方千米）（2）cos ∠ACD=CD 321==AC 5152点评：本题考查了解直角三角形的应用，与时事相结合提高了同学们解题的兴趣，解题的关键是从实际问题中整理出直角三角形并求解． 对应训练 6．（2012•益阳）超速行驶是引发交通事故的主要原因之一．上周末，小明和三位同学尝试用自己所学的知识检测车速．如图，观测点设在A 处，离益阳大道的距离（AC ）为30米．这时，一辆小轿车由西向东匀速行驶，测得此车从B 处行驶到C 处所用的时间为8秒，∠BAC=75°．（1）求B 、C 两点的距离；（2）请判断此车是否超过了益阳大道60千米/小时的限制速度？（计算时距离精确到1米，参考数据：sin75°≈0.9659，cos75°≈0.2588，tan75°≈3.732，3≈1.732，60千米/小时≈16.7米/秒）考点：解直角三角形的应用．专题：计算题．分析：（1）由于A到BC的距离为30米，可见∠C=90°，根据75°角的三角函数值求出BC 的距离；（2）根据速度=路程÷时间即可得到汽车的速度，与60千米/小时进行比较即可．解答：解：（1）法一：在Rt△ABC中，∠ACB=90°，∠BAC=75°，AC=30，∴BC=AC•tan∠BAC=30×tan75°≈30×3.732≈112（米）．法二：在BC上取一点D，连接AD，使∠DAB=∠B，则AD=BD，∵∠BAC=75°，∴∠DAB=∠B=15°，∠CDA=30°，在Rt△ACD中，∠ACD=90°，AC=30，∠CDA=30°，∴AD=60，CD=303，BC=60+303≈112（米）（2）∵此车速度=112÷8=14（米/秒）＜16.7 （米/秒）=60（千米/小时）∴此车没有超过限制速度．点评：本题考查了解直角三角形的应用，理解正切函数的意义是解题的关键．【聚焦山东中考】1．（2012•济南）如图，在8×4的矩形网格中，每格小正方形的边长都是1，若△ABC的三个顶点在图中相应的格点上，则tan∠ACB的值为（）A．13B．12C．22D．31．A考点：锐角三角函数的定义．专题：网格型．分析：结合图形，根据锐角三角函数的定义即可求解．解答：解：由图形知：tan∠ACB=21 63 ，故选A．点评：本题考查了锐角三角函数的定义，属于基础题，关键是掌握锐角三角函数的定义．2．（2012•滨州）把△ABC三边的长度都扩大为原来的3倍，则锐角A的正弦函数值（）A．不变B．缩小为原来的3C．扩大为原来的3倍D．不能确定2．A分析：由于△ABC三边的长度都扩大为原来的3倍所得的三角形与原三角形相似，得到锐角A的大小没改变，根据正弦的定义得到锐角A的正弦函数值也不变．解答：解：因为△ABC三边的长度都扩大为原来的3倍所得的三角形与原三角形相似，所以锐角A的大小没改变，所以锐角A的正弦函数值也不变．故选A．5．（2012•潍坊）校车安全是近几年社会关注的重大问题，安全隐患主要是超速和超载．某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验：先在公路旁边选取一点C，再在笔直的车道l上确定点D，使CD与l垂直，测得CD的长等于21米，在l上点D 的同侧取点A、B，使∠CAD=30°，∠CBD=60°．（1）求AB的长（精确到0.1米，参考数据：=1.73=1.41）；（2）已知本路段对校车限速为40千米/小时，若测得某辆校车从A到B用时2秒，这辆校车是否超速？说明理由．5．考点：解直角三角形的应用．分析：（1）分别在Rt△ADC与Rt△BDC中，利用正切函数，即可求得AD与BD的长，继而求得AB的长；（2）由从A到B用时2秒，即可求得这辆校车的速度，比较与40千米/小时的大小，即可确定这辆校车是否超速．解答：解：（1）由題意得，在Rt△ADC中，AD=CD==21 3tan303=36.33，在Rt△BDC中，BD=CD==7 3tan303=12.11，则AB=AD-BD=36.33-12.11=24.22≈24.2（米）。

第十一讲 解直角三角形趣题引路】台风是一种自然灾害，它以台风中心为圆心在周围数十千米范围内形成气旋风暴，有极强的破坏力，据气象观测，距沿海某城市A 的正南方向220kmB 处有一台风中心，其中心最大风力为12级，每远离台风中心20km ，风力就会减弱一级，该台风中心现正以15km/h 的速度沿北偏东30°方向往C 移动，且台风中心风力不变，若城市所受风力达到或超过四级，则称为受台风影响，若你是该市气象局的首席气象专家，请你对此次台风对该市的影响情况作出预测。

（1）该市是否会受到这次台风的影响？请说明理由；（2）若会受到台风的影响，那么台风影响该城市的持续时间有多长？（3）该城市受到台风影响的最大风力为几级？ABCD E F图11-1解析 （1）作AD BC ⊥于点D ，（如图11-1）， °220,30111.2AD B AD AB km =∠=∴==，由题意知，当A 点距台风中心不超过160km 时，就会受台风影响.由于AD=110＜160，所以A 市会受这次台风影响；（2）在BD 及BD 的延长线上分别取E 、F 两点，使AE=AF=160km ，则当台风中心从到达E 点时起，直到离开F 点，该市都会受到这次台风的影响，),2).DE AE km EF DE km ===∴==∴)h =； （3）当台风中心位于D 时，A 市所受这次这次台风的风力最大，其最大风力为()11012 6.520-=级知识延伸】解三角形，除运用锐角三角函数知识，往往还要用到我们已经学过的勾股定理，以及另两个非常重要的定理：正弦定理和余弦定理.C图11-2如图11-2，在△ABC 中，AC=b ,AB=c ,BC=a .过A 作BC 上的高，长为ha ，则有sin ,ha B c =sin ,ha C b =于是有sin sin ,c B b C ⋅=⋅于是，得sin sin b cB C=，同理可得,sin sin a b A B =因此 ,sin sin sin a b cA B C==这就是正弦定理，推而广之可得一个重要的三角形面积计算公式 111sin sin sin .222ABC S ab C ac B bc A ∆===在上图中，222cos cos ,cos ,BD AB B c B CD BC BD a c B AB BD AD =⋅=⋅=-=-⋅-= ()()222222,cos cos ,AC DC c c B b a c B =-∴-⋅=--⋅得2222cos b a c ac B =+-，同理可得2222cos a b c bc A =+-，2222cos c a b ab C =+-.这就是余弦定理.运用正弦定理和余弦定理可以将三角形的范围由直角三角形扩充到斜三角形.例1 已知，如图11-3，在四边形ABCD 中AD=CD,AB=7,tan 2,A B D =∠=∠=90°，求BC 的长.ABD CE图11-3解析 延长AB 与DC 交于点E ，∠D=90°，tan 2,DEA AD∴==得DE=2AD,CD AD = .EC DC AD ∴==∠BCE=180°-∠BCD=∠A ,tan 2.BEBCE BC∴∠== 设BC=x ，则BE=2x ，因而,又222,AE AD DE =+()))()222127772,1.33x x x BC ∴+=+==-=解得或舍去，故点评：一般图形化为直角三角形，结合方程或二次函数，往往能够简捷地解决问题.例2 在四边形ABCD 中，AB=4,BC=3,CD=12,∠B=90°，36S =四边形ABCD ,求AD 的长.DC图11-4解析 如图11-4，连接AC ，则△ABC 为Rt △，于是AC=5,1136363430.sin 22ACD ABC S S AC CD ACD ∆∆∴=-=-⨯⨯=∴⋅⋅∠=30°， 即1512sin ACD 2⨯⨯⋅∠=30°，sin 1,ACD ACD ∴∠=∴∠=90°. ∴由勾股定理知13.AD ==点评：运用公式1sin 2ABC S ab C ∆=不但可以求三角形的面积，而且可以由面积求边角的大小好题引路】佳题新题品味.例1 如图11-5，河对岸有A 、B 两目标，但不能到达，在河这边沿着与AB 平行的方向取相距40m 的C 、D 两点（点A 、B 、C 、D 在同一平面内），并测得∠ACB=70°，∠BCD=65°，∠ADC=30°，求A 、B 两目标之间的距离.（结果不取近似值，用含有锐角三角函数的式子表示.）DBAC EF图11-5解析 作AE ⊥CD,BF ⊥CD,垂足分别为点E 、F ，∵AB ∥CD,∴四边形ABFE 为矩形，∴AB=EF. ∵∠ACE=180°-∠ACB -∠BCD=180°-70°-65°=45° ∴∠EAC=45°，AE=EC.设EC=x m ， ∵∠ADE=30°，且DE=AE·cot ∠ADE.又∵DE=x +40，∴x +40=x ·cot30°，解得x =20， ∴AE=EC=BF=20,在Rt △BFC 中，cot ∠BCF=CFBF,即CF=BF·cot ∠65°=（20）cot65°，∴AB=EF=EC+CF=(20)+(20)cot ∠65°（m ）点评：本题体现了两种数学方法的应用，①构建数学几何模型，把一般三角形转化为解直角三角形；②通过设未知数，结合几何图形构建方程，将未知量与已知量联系起来.例2 如图11-6，E 是四边形ABCD 的DC 边上一点，CE=,AB=2,BC=1,∠D=90°, ∠B=60°,ABCE S =四边形（1）求AC 的长；（2）求∠ACD 的度数. ABCDEF图11-6解析 （1）过点A 作AF ⊥BC,垂足为F,则AF=AB·sin ∠B=2·sin60°BF=AB·cos ∠B=2·cos60°=1.∴CF=B C －BF=)11-在R t △ACF 中，由勾股定理，得(2)∵ABCE S 四边形=ABC ACE S S ∆∆+而11=,,22ABC ACE S AF BC S CE AD ∆∆⋅=⋅∴)11122+∴又sin ∠ACD=1,2AD AC == 故∠ACD=30°.点评：本题求AC 也可直接利用余弦定理：2222cos ,AC AB BC AB BC B =+-⋅⋅直接求得.中考真题欣赏例1（辽宁省中考）如图，山上有一座铁塔，山脚下有一矩形建筑物ABCD ，建筑物周围没有开阔平整地带.该建筑物顶端宽度AD 和高度DC 都可直接测得.从A 、D 、C 三点可看到塔顶端H,可供使用的测量工具有皮尺、测倾器.(1)请你根据现有条件，充分利用矩形建筑物，设计一个测量塔顶端到地面高度HG 的方案，具体要求如下：①测量数据尽可能少；②在所给图形上，画出你设计的测量平面图，并将应测数据标记在图形（如果测A 、D 间距离，用m 表示；测D 、C 间距离，用n 表示；如果测角，用αβγ、、等表示，测倾器高度不计）.(2)根据你测量的数据，计算塔顶端到地面的高度HG （用字母表示）. 解析 (1)如图11-7，测三个数据：DC 间距离n ，∠HDM ()α,∠HCG ()β； (2)设HG=x .在Rt △CHG 中，CG=cot x β⋅,在Rt △DHM 中，DM=()cot x n α-⋅，∴cotxβ⋅=()cotx nα-⋅. ∴cot.cot cotnxααβ⋅=-点评：本题是一道较为开放的题目，方案很多，但要求抓住题目的要求：“尽可能少”四个字，否则影响得分.例2（南京市）如图11-8，∠POQ=90°，边长为2cm的正方形ABCD的顶点B在OP上，C在OQ上，且∠OBC=30°，分别求点A、D到OP的距离.ABCDFGO图11-8解析过点A、D分别作AE⊥OP,DF⊥OP,DG⊥OQ,垂足分别为E、F、G.在正方形ABCD中,∠ABC=∠BCD=90°.∵∠OBC=30°，∴∠ABE=60°.在Rt△AEB中，AE=AB·sin60°=2·33cm）∵四边形DFOG是矩形，∴DF=GO，∵∠OBC=30°，∴∠BCO=60°，∴∠DCG=30°.在Rt△DCG中，CG=CD·cos30°=2·33cm）在Rt△BOC中，OC=12BC=1（cm）. ∴3∴点A到OP3cm），点D到OP的距离为3点评：本题是一道正方形、矩形与解直角三角形相结合的试题，难度不大，关键是通过作辅助线合理构造直角三角形来解答.竞赛样题展示例1.（1999年全国联赛）如图11-9在正方形ABCD 中，N 是DC 的中点，M 是AD 上异于D 的点，且∠NMB=∠MBC,求tan ∠ABM.ABCDEFMN图11-9解析 延长BC 、MN 交于点E ，作EF ⊥BM 于F.设AB=a ,AM=()x x a <,则MD=a x -，.由正方形ABCD 及N 为DC 的中点，知∠MDN=∠NCE, ∠DNM=∠CNE,ND=CN,故MDN ECN ∆≅∆，可知CE=MD=a x -，BE=2a x -， 由∠NMB=∠MBC,知EB=EM.由EF ⊥BM 知∠FEB=90°-∠FBE=∠ABM,BF=12BM,且∠A=∠BFE.故△AB M ～△FEB .∴BM AMBE BF=,即22BM AM BE =⋅.∴()2222a x x a x +=-.即22340x ax a -+=∴11,.33x a AM AB ==即∴1tan .3AM ABM AB ∠== 点评：本题的解决充分利用了“∠NMB=∠MBC”这个条件来构建等腰三角形，利用等腰三角形的性质及相似三角形列方程求解，本题的解法很多，还可以过点N 作平行线来解决.例2（2000年全国竞赛）如图11-10，四边形EFGH 是正方形ABCD 的内接四边形，两条对角线EG 和FH 所夹得锐角为θ，且∠BEG 与∠CFH 都是锐角.已知EG=k ，FH=l ，四边形EFGH 的面积为S ，求证：sin θ=2S kl. ABCDEFGHMNO图11-10证明 过F 、H 分别作EG 的垂线，垂足分别为M 、N ，EG 和FH 的交点为O .∴sin θ=FM HNFO HO=,即FM=FO·sin θ;HN=HO·sin θ. ∴S=EFG EHG S S ∆∆+=()1111sin sin .2222EG FM EG HN EG FO HO GE FH θθ⋅+⋅=+=⋅∴22sin .S S EG FH klθ==⋅点评：准确使用锐角三角函数的定义是解答本题的关键.过关检测】A 级1.在Rt △ABC 中，∠C=90°，D 为AC 上一点，且AD=BD=5,CD=3,则sinA=______.2.等腰三角形的面积为2，底角为α，则tan α=_______.3.在△ABC ，∠ACB=90°,CD ⊥AB 于D ，CD=1,已知AD 、BD 的长是关于x 的方程20x px q ++=的两个根，且tanA-tanB=2.则_____,_______.p q ==4.已知△ABC 中，∠C=90°，CA=CB ，D 是AC 上一点，且AD:DC=1:2,则tan ∠DBC=________,cos ∠DBC=________.5.如图11-11，在△ABC 中，AB=AC,腰上的高BD=2，底边上的高AE=4，求tanC 的值.ABCDE图11-11B 级1.如图11-12，在△ABC 中，AB=AC ,∠ABN=∠MBC,BM=NM,BN=a ，则点N 到BC 的距离是_______.MNCBAABCD图11-12 图11-132.如图11-13，在Rt △ABC 中，∠C=90°，∠CAB=30°,AD 平分∠CAB ，则_______.AB ACCD CD-=3. △ABC 中，15,17,(a b A θθ==∠=为定值）若满足上述条件的三角形的∠C 唯一存在，则tanC=_______.4.已知菱形ABCD 的两条对角线AC 、BD 的乘积等于菱形的一条边长的平方，则菱形的一个钝角的大小是_______.5.设P 、Q 为线段BC 上两定点，且BP=CQ ，A 为BC 外一动点，当点A 运动到使∠BAP =∠CAQ 时，△ABC 是什么三角形？试证明你的结论.。

第十九讲解直角三角形【基础知识回顾】一、锐角三角函数定义：在Rt△ABC中，∠C=900, ∠A、∠B、∠C的对边分别为a、b、c，则∠A的正弦可表示为：sinA= ，∠A的余弦可表示为cosA= ∠A的正切：tanA= ，它们统称为∠A的锐角三角函数【名师提醒：1、sinA、∠cosA、tanA表示的是一个整体，是两条线段的比，没有单位，这些比值只与有关，与直角三角形的无关2、取值范围<sinA< ，cosA< ，tanA> 】二、特殊角的三角函数值：在理解的基础上结合表格进行记忆2、正弦和正切值随着角度的增大而余弦值随着角度的增大而3、几个特殊关系：⑴sinA+cos2A= ,tanA=sin A（）⑵若∠A+∠B=900，则sinA= ，tanA.tanB= 】三、解直角三角形：1、定义：由直角三角形中除直角外的个已知元素，求出另外个未知元素的过程叫解直角三角形2、解直角三角形的依据：Rt∠ABC中，∠C=900 三边分别为a、b、c⑴三边关系：⑵两锐角关系⑶边角之间的关系：sinA cosA tanAsinBcosB tanB【名师提醒：解直角三角形中已知的两个元素应至少有一个是当没有直角三角形时应注意构造直角三角形，再利用相应的边角关系解决】3、解直角三角形应用中的有关概念⑴仰角和俯角：如图：在图上标上仰角和俯角⑵坡度坡角：如图：斜坡AB的垂直度h和水平宽度l的比叫做坡度，用i表示，即i=坡面与水平面得夹角为用字母α表示，则i=tanα=hl。

铅直水平线⑶方位角：是指南北方向线与目标方向所成的小于900的水平角如图：OA表示OB表示OC表示OD表示（也可称东南方向）3、利用解直角三角形知识解决实际问题的一般步骤：⑴把实际问题抓化为数学问题（画出平面图形，转化为解直角三角形的问题）⑵根据条件特点，选取合适的锐角三角函数去解直角三角形⑶解出数学问题答案，从而得到实际问题的答案【名师提醒：在解直角三角形实际应用中，先构造符合题意的三角形，解题的关键是弄清在哪个直角三角形中用多少度角的哪种锐角三角函数解决】【重点考点例析】考点一：锐角三角函数的概念例1 （2013•贵阳）如图，P是∠α的边OA上一点，点P的坐标为（12，5），则tanα等于（）A．513B．1213C．512D．1251．（2013•宿迁）如图，将∠AOB 放置在5×5的正方形网格中，则tan ∠AOB 的值是（ ）A ．23B ．32C D1．B2．（2013•重庆）计算6tan45°-2cos60°的结果是（）A．B．4 C．D．52．D考点三：化斜三角形为直角三角形3．（2013•陕西）如图，四边形ABCD的对角线AC，BD相交于点O，且BD平分AC．若BD=8，AC=6，∠BOC=120°，则四边形ABCD的面积为．（结果保留根号）3．考点四：解直角三角形的应用例4 （2013•舟山）某学校的校门是伸缩门（如图1），伸缩门中的每一行菱形有20个，每个菱形边长为30厘米．校门关闭时，每个菱形的锐角度数为60°（如图2）；校门打开时，每个菱形的锐角度数从60°缩小为10°（如图3）．问：校门打开了多少米？（结果精确到1米，参考数据：sin5°≈0.0872，cos5°≈0.9962，sin10°≈0.1736，cos10°≈0.9848）．思路分析：先求出校门关闭时，20个菱形的宽即大门的宽；再求出校门打开时，20个菱形的宽即伸缩门的宽；然后将它们相减即可．解：如图，校门关闭时，取其中一个菱形ABCD．根据题意，得∠BAD=60°，AB=0.3米．∵在菱形ABCD中，AB=AD，∴△BAD是等边三角形，∴BD=AB=0.3米，∴大门的宽是：0.3×20≈6（米）；如图，校门打开时，取其中一个菱形A1B1C1D1．根据题意，得∠B1A1D1=10°，A1B1=0.3米．∵在菱形A1B1C1D1中，A1C1⊥B1D1，∠B1A1O1=5°，∴在Rt△A1B1O1中，B1O1=sin∠B1A1O1•A1B1=sin5°×0.3=0.02616（米），∴B1D1=2B1O1=0.05232米，∴伸缩门的宽是：0.05232×20=1.0464米；∴校门打开的宽度为：6-1.0464=4.9536≈5（米）．故校门打开了5米．点评：本题考查了菱形的性质，解直角三角形的应用，难度适中．解题的关键是把实际问题转化为数学问题，只要把实际问题抽象到解直角三角形中，一切将迎刃而解．对应训练【聚焦山东高考】1．2A．12 B．C．米D．米2．A3．（2013•潍坊）一渔船在海岛A南偏东20°方向的B处遇险，测得海岛A与B的距离为20海里，渔船将险情报告给位于A处的救援船后，沿北偏西80°方向向海岛C靠近，同时，从A处出发的救援船沿南偏西10°方向匀速航行，20分钟后，救援船在海岛C处恰好追上渔船，那么救援船航行的速度为（）A．/小时B．30海里/小时C．/小时D．海里/小时3．D4．（2013•东营）某校研究性学习小组测量学校旗杆AB的高度，如图在教学楼一楼C处测得旗杆顶部的仰角为60°，在教学楼三楼D处测得旗杆顶部的仰角为30°，旗杆底部与教学楼一楼在同一水平线上，已知每层楼的高度为3米，则旗杆AB的高度为米．4．9tan11°≈0.19）4【备考真题过关】一、选择题1．（2013•天津）tan60°的值等于（）A．1 B C D．21．C2．（2013•温州）如图，在△ABC中，∠C=90°，AB=5，BC=3，则sinA的值是（）A．34B．43C．35D．452．CA．12B．13C．3D．133．DA．5B．4C．5D．34．AA．B．0 C．D．25．BA．30°B．45°C．60°D．90°6．D7．（2013•宁夏）如图是某水库大坝横断面示意图．其中AB、CD分别表示水库上下底面的水平线，∠ABC=120°，BC的长是50m，则水库大坝的高度h是（）A．B．25m C．m D m7．A8．（2013•山西）如图，某地修建高速公路，要从B地向C地修一座隧道（B、C在同一水平面上）．为了测量B、C两地之间的距离，某工程师乘坐热气球从C地出发，垂直上升100m 到达A处，在A处观察B地的俯角为30°，则B、C两地之间的距离为（）mA． m B． m C．m D．38．A二、填空题10．（2013•淮安）sin30°的值为．110．11．412．（2013•铜仁地区）如图，在直角三角形ABC中，∠C=90°，AC=12，AB=13，则sinB 的值等于．12．1213．14．215．（2013•荆门）如图，在Rt△ABC中，∠ACB=90°，D是AB的中点，过D点作AB的垂线交AC于点E，BC=6，sinA= 35，则DE= ．15．15 416．（2013•成都）如图，某山坡的坡面AB=200米，坡角∠BAC=30°，则该山坡的高BC的长为米．16．10017．（2013•十堰）如图，在小山的东侧A点有一个热气球，由于受西风的影响，以30米/分的速度沿与地面成75°角的方向飞行，25分钟后到达C处，此时热气球上的人测得小山西侧B点的俯角为30°，则小山东西两侧A、B两点间的距离为米．17．18．（2013•荆州）如图，在高度是21米的小山A处没得建筑物CD顶部C处的仰角为30°，底部D处的俯角为何45°，则这个建筑物的高度CD= 米（结果可保留根号）- 21 -。

【例题求解】【例1】如图，已知电线杆AB直立于地面上，它的影子恰好照在土坡的坡面CD和地面BC上，如果CD与地面成45°，∠A＝60°，CD＝4m，BC＝(24-)m，则电线杆AB的长为．26思路点拨延长AD交BC于E，作DF⊥BC于F，为解直角三角形创造条件．【例2】如图，在四边形ABCD中，AB=24-，BC-1，CD=3，∠B=135°，∠C＝90°，则∠D等于( ) A．60° B．67．5° C．75° D．无法确定思路点拨通过对内分割或向外补形，构造直角三角形．注：因直角三角形元素之间有很多关系，故用已知元素与未知元素的途径常不惟一，选择怎样的途径最有效、最合理呢？请记住：有斜用弦，无斜用切，宁乘勿除．在没有直角的条件下，常通过作垂线构造直角三角形；在解由多个直角三角形组合而成的问题时，往往先解已具备条件的直角三角形，使得求解的直角三角形最终可解．【例3】如图，在△ABC中，∠=90°，∠BAC=30°，BC=l，D为BC边上一点，tan∠ADC是方程2)1(5)1(322=+-+x x x x 的一个较大的根?求CD 的长．思路点拨 解方程求出 tan ∠ADC 的值，解Rt △ABC 求出AC 值，为解Rt △ADC 创造条件．【例4】 如图，自卸车车厢的一个侧面是矩形ABCD ，AB=3米，BC=0．5米 ，车厢底部距离地面1．2米，卸货时，车厢倾斜的角度θ=60°．问此时车厢的最高点A 距离地面多少米?(精确到1米) 思路点拨 作辅助线将问题转化为解直角三角形，怎样作辅助线构造基本图形，展开空间想象，就能得到不同的解题寻路【例5】 如图，甲楼楼高16米，乙楼坐落在甲楼的正北面，已知当地冬至中午12时太阳光线与水平面的夹角为30°，此时，求：(1)如果两楼相距20米，那么甲楼的影子落在乙楼上有多高?(2)如果甲楼的影子刚好不落在乙楼上，那么两楼的距离应当是多少米?思路点拨 (1)设甲楼最高处A 点的影子落在乙楼的C 处，则图中CD 的长度就是甲楼的影子在乙楼上的高；(2)设点A 的影子落在地面上某一点C ，求BC 即可．注：在解决一个数学问题后，不能只满足求出问题的答案，同时还应对解题过程进行多方面分析和考察，思考一下有没有多种解题途径，每种途径各有什么优点与缺陷，哪一条途径更合理、更简捷，从中又能给我们带来怎样的启迪等． 若能养成这种良好的思考问题的习惯，则可逐步培养和提高我们分析探索能力．学历训练1．如图，在△ABC 中，∠A=30°，tanB=31，BC=10，则AB 的长为 ．2．如图，在矩形ABCD 中．E 、F 、G 、H 分别为AB 、BC 、CD 、DA 的中点，若tan ∠AEH =34，四边形EFGH 的周长为40cm ，则矩形ABCD 的面积为 ．3．如图，旗杆AB ，在C 处测得旗杆顶A 的仰角为30°，向旗杆前北进10m ，达到D ，在D 处测得A 的仰角为45°，则旗杆的高为 ．4．上午9时，一条船从A 处出发，以每小时40海里的速度向正东方向航行，9时30分到达B 处，从A 、B 两处分别测得小岛M 在北偏东45°和北偏东15°方向，那么B 处船与小岛M 的距离为( )A ．20海里B ．20海里C ．315海里D ．3205．已知a 、b 、c 分别为△ABC 中∠A 、∠B 、∠C 的对边，若关于x 的方程02)(2=-+-+b c ax x c b 有两个相等的实根，且sinB ·cosA —cosB ·sinA ＝0，则△ABC 的形状为( ) A ．直角三角形 B ．等腰三角形 C ．等边三角形 D ．等腰直角三角形6．如图，在四边形ABCD 中，∠A ＝135°，∠B=∠D=90°，BC=32，AD=2，则四边形ABCD 的面积是( )A ．24B ．34C ． 4D ．67．如图，在△ABC 中，∠ACB=90°，CD ⊥AB 于D ，CD=1，已知AD 、BD 的长是关于x 的方程02=++q px x 的两根，且tanA —tanB=2，求p 、q 的值．8．如图，某电信部门计划修建一条连结B 、C 两地的电缆，测量人员在山脚A 点测得B 、C 两地的仰角分别为30°、45°，在B 地测得C 地的仰角为60°．已知C 地比A 地高200米，则电缆BC 至少长多少米?(精确到0.1米)9．如图，在等腰Rt △ABC 中，∠C=90°，∠CBD ＝30，则DCAD= ．10．如图，正方形ABCD 中，N 是DC 的中点．M 是AD 上异于D 的点，且∠NMB=∠MBC ，则tan ∠ABM ＝ ．11．在△ABC 中，AB=26-，BC=2，△ABC 的面积为l ，若∠B 是锐角，则∠C 的度数是 ． 12．已知等腰三角形的三边长为 a 、b 、c ，且c a =，若关于x 的一元二次方程022=+-c bx x 的两根之差为2，则等腰三角形的一个底角是( )A ． 15°B ．30°C ．45°D ．60°13．如图，△ABC 为等腰直角三角形，若AD=31AC ，CE=31BC ，则∠1和∠2的大小关系是( )A ．∠1>∠2B ．∠1<∠2C ．∠1＝∠2D ．无法确定14．如图，在正方形ABCD 中，F 是CD 上一点，AE ⊥AF ，点E 在CB 的延长线上，EF 交AB 于点G ． (1)求证：DF ×FC ＝BG ×EC ；(2)当tan ∠DAF=31时，△AEF 的面积为10，问当tan ∠DAF=32时，△AEF 的面积是多少?15．在一个三角形中，有一边边长为16，这条边上的中线和高线长度分别为10和9，求三角形中此边所对的角的正切值．16．台风是一种自然灾害，它以台风中心为圆心在周围数十千米范围内形成气旋风暴，有极强的破坏力．据气象观测，距沿海某城市A 的正南方向220千米B 处有一台风中心，其中心最大风力为12级，每远离台风中心20千米，风力就会减弱一级，该台风中心现正在以15千米／时的速度沿北偏东30°方向往C 处移动，且台风中心风力不变，若城市所受风力达到或超过四级，则称为受台风影响． (1)该城市是否会受到这次台风的影响?请说明理由．(2)若会受到台风影响，那么台风影响该城市的持续时间有多长? (3)该城市受到台风影响的最大风力为几级?17．如图，山上有一座铁塔，山脚下有一矩形建筑物ABCD ，且建筑物周围没有开阔平整地带．该建筑物顶端宽度AD 和高度DC 都可直接测得，从A 、D 、C 三点可看到塔顶端H ．可供使用的测量工具有皮尺、测角器．(1)请你根据现有条件，充分利用矩形建筑物，设计一个测量塔顶端到地面高度HG 的方案．具体要求如下： ①测量数据尽可能少；②在所给图形上，画出你设计的测量平面图，并将应测数据标记在图形上(如果测A 、D 间距离，用m 表示；如果测D 、C 间距离，用n 表示；如果测角，用α、β、γ等表示．测角器高度不计)． (2)根据你测量的数据，计算塔顶端到地面的高度HG(用字母表示)．参考答案。

中考数学辅导之—解直角三角形Ⅳ从本期开始,我们将学习初三几何第六章解直角三角形.它是继直角三角形中的三边之间的关系,即勾股定理、直角三角形两锐角间的关系、直角三角形两锐角互余后,又一关于直角三角形的知识.本章是三角学的起始部分,对很好的解直角三角形有极大用处.一、本次知识要点及说明的问题1.锐角三角函数是关于直角三角形两直角边及斜边和直角三角形的一个锐角间的关系,设α是直角三角形的一个锐角则围绕三边有六个比值,即①斜边的对边α∠;②斜边的邻边α∠;③的邻边的对边αα∠∠;④的对边的邻边αα∠∠;⑤的对边斜边α∠;⑥的邻边斜边α∠.而①②③④这四个线段的比就是初三所学习的正弦、斜弦、正切、余切函数,这四个函数是角α的变化而变化,而与边长无关.如,设α=30°,无论它的对边和斜边多长21=∠斜边的对边α.2.三角函数定义:我们规定①斜边的对边A ∠叫∠A 的正弦.记作斜边的对边A A ∠=sin②斜边的邻边A ∠叫∠A 的余弦.记作斜边的邻边A A ∠=cosBα∠的对边α∠的邻边BA ∠的对边A ∠的邻边③的邻边的对边A A ∠∠叫∠A 的正切.记作的邻边的对边A A tgA ∠∠=④的对边的邻边A A ∠∠叫∠A 的余切.记作的对边的邻边A A tgA ∠∠=这四个三角函数定义是人们规定的,不能问为什么这样规定?这四个函数定义是本章重点中的重点,要达到①在直角三角形中,给我们一个锐角,我们知道这个角的正弦,余弦,正切,余切是哪两条线段的比.反之②在直角三角形中给我们两条线段的比,我们知道是哪个锐角的什么函数.a b ctgA b a tgA cb Ac a A ====,cos ,sin的什么函数是BDC BDCD∠因为CD 是∠BDC 的邻边,BD 是斜边,BD CD 是∠BDC 的邻边比斜边,所以BDCD是∠BDC 的余弦.3.特殊角的三角函数值①∠A=30°此时,设x AC x AB x BC 3,2,===则则2123030sin sin =====x x AB BC A 斜边的对边οο23233030cos cos =====x x AB AC A 斜边的邻边οο333303030=====xx AC BC tg tgA 的邻边的对边οοο33303030=====x xBCAC ctg tgA 的对边的邻边οοοB②∠A=45°此时,x AB x AC BC 2,=== 则22245sin sin ====x x AB BC A ο 22245cos cos ====xx AB AC A ο 145====x xAC BC tg tgA ο 145====xxBC AC ctg ctgA ο③∠A=60°此时设xBC x AB x AC 3,2,=== 则232360sin sin ====x x AB BC A ο 21260cos cos ====x x AB AC A ο 3360====xxAC BC tg tgA ο 33360====xx BC AC ctg ctgA ο4.互为余角的函数关系式:90°-∠A 与∠A 是互为余角.有A A cos )90sin(=-ο A A sin )90cos(=-ο ctgA A tg =-)90(ο tgA A ctg =-)90(ο通过这四个关系式,可以将正,余弦互化,正切与余切互化. 如οο50cos 40sin = 8451sin 2138cos '='οο οο4842ctg tg = 04540235'='οοtg ctg5.四个三角函数性质当∠A 从30°增长到45°,再增长到60°,它的正弦值从21增到22,再增到23.说明正弦值随着∠A 的增大而增大.即两个锐角,大角的正弦大,反之两个锐角的正弦值比较,正弦值越大,角越大.如οο48sin 50sin >.同理正切函数也具有相同的性质,如tg53°>tg40°,再比如比较tg40°和ctg40°的大小,将ctg40°化成tg50°.∵tg40°<tg50°,∴tg40°<ctg40°.已知βαtg tg >,则一定有βα>的结论.再如?,sin 21)21(sin 2等于多少度ααα-=-解: 21sin ,sin 21|21sin |)21(sin 2≤-=-=-αααα说明οο30,30sin ≤∴≤αα而余弦,余切则是函数值随着角度的增大而减小,即角越大,余弦(切)值越小,反之余弦(切)值越大,它的角越小.如cos40°>cos50° ctg20°>ctg50°若οο60,60cos cos 21cos <∴>>ααα即比较两个函数值的大小,通常化成同名函数,再根据性质比较大小.例1:已知2)cos (sin ,450ααα-<<化简οο 解:|cos sin |)cos (sin 2αααα-=- αααcos sin ,450<∴<<οοΘ 比如αααααcos sin ,23cos ,21sin ,30<==ο. 再如οοοο50sin 40cos cos ,40sin sin ,40====ααα ααcos sin ,40cos 40sin <∴<οοΘ 所以ααααsin cos |cos sin |-=-例2:已知2)cos (sin ,9045ααα-<<化简οο 解:|cos sin |)cos (sin 2αααα-=- αααcos sin ,9045>∴<<οοΘ (在α的取值范围内任取2个角验证即可) ααααcos sin |cos sin |-=-∴ 例3.如已知ααα求,cos 23)23(cos 2-=-的取值范围. 解:αααcos 23|23cos |)23(cos 2-=-=-说明ο30cos cos 23cos ≤≤αα即 ο30≥∴α上述四个函数的性质掌握起来较难,要想法弄懂,多思,多练.6.同角间的三角函数恒等式①平方关系 1cos sin 22=+αα ②倒数关系 1=⋅ααctg tg③比的关系 ααααααsin cos ,cos sin ==ctg tg 在这四个关系中,①②用的最多. 7.正余弦值的取值范围 1cos 0,1sin 0<<<<αα二、本次练习 (一)判断题1.015cos 75sin =-οο.( )2.在Rt ΔABC 中,∠C=90°,a,b,c 分别∠A,∠B,∠C 的对边则c bB c a A ==cos ,sin .( )3.已知βα,是锐角,若βαβα>>则,sin sin .( )4.直角三角形ABC 中,各边都扩大2倍,则正弦值也扩大2倍.( )5.若α是锐角,οο60,30cos sin ==αα则.( )6.当αααααsin cos )cos (sin ,4502-=-<<时οο( ) (二)填空题 1.若ααcos ,23)90sin(则=-ο=______. 2.α是直角三角形的一个锐角,如果方程04cos 3cos 10102=+--ααx x 有两个相等实根,则αsin =______.3.若2)(,9045αααctg tg -<<化简οο的结果是______.4.如果αα则,135)12(=⋅+οοtg tg =______度.5.在Rt ΔABC 中,两直角边分别是2525-+和,则最大锐角的余弦值是______.6.计算οοοοο30sin 43030cos 6045cos 222+-⋅+tg tg 的值是______.7.已知0|3|)1cos 2(,2=-+-βαβαtg 是锐角,则ββαctg tg -⋅sin 的值是______.8.若αα则,033=-ctg =______度.9.在Rt ΔABC 中,∠C=90°,A BC AC sin ,22,24则=== ______.10.βα,是锐角,且23)15cos(,23sin =-=οβα,则3βα+=______. 11.在Rt ΔABC 中,∠C=Rt ∠,则A sin =______,ABAC是∠A 的______函数. 12.若α是锐角,且21cos )21(cos 2-=-αα,则α的取值范围是______.13.化简|154sin |36sin 12-+-οο的结果是______.14.已知等腰三角形的两边分别是10,14.则底角的余弦值是______. 15.已知αα,0sin 2=-m 是锐角,则m 的取值范围是______.(三)选择填空:1.若αααcos ,sin ,450则οο<<的大小关系是:A.ααcos sin >B.ααcos sin <C.ααcos sin =D.大小不确定2.在Rt ΔABC 中,∠C=90°,βcos ,31sin 则=A 等于:A.31B.32C.32D.3223.已知n m n m ,,cos sin ,cos sin 则=⋅=+αααα的关系是: A. m=n B. m=2n+1 C. m 2=2n+1 D. m 2=-2n+14.下列不等式正确的是: A.οοο4848cos 48sin tg << B.οοο48cos 4848sin <<tg C.οοο48cos 48sin 48<<tg D.οοο4848sin 48cos tg <<5.在Rt ΔABC 中,∠C=90°,a,b,c 是∠A,∠B,∠C 的对边.下列关系错误的是: A.B c b cos ⋅= B.tgB a b ⋅= C.A c a sin ⋅= D.ctgB b a ⋅=6.使式子)(31是锐角αα-ctg 有意义的条件是:A.ο30>αB.ο60>αC.ο30<αD.οο6030<<α(四)计算下列各式:1.οοοοοο3852330sin 45cos 30sin 45cos tg tg ⋅++- 2.οοο30cos 160sin 160cos ++ 3.οοοοοο60sin 30sin 45cos 604545sin 2--+tg tg 4.οοοοοοοοο48sin 5842sin 3260sin 32605860222⋅+⋅⋅-⋅-tg ctg ctg ctg tg tg。

第19讲 直角三角形目 录考点一 直角三角形的性质与判定题型01 利用直角三角形的性质求解题型02 根据已知条件判定直角三角形题型03 与直角三角形有关的面积计算考点二 勾股定理题型01 利用勾股定理求线段长题型02 利用勾股定理求面积题型03 已知两点坐标求两点距离题型04 判断勾股数问题题型05 利用勾股定理解决折叠问题题型06 勾股定理与网格问题题型07 勾股定理与无理数题型08 以直角三角形三边为边长的图形面积题型09 利用勾股定理求两条线段的平方和（差）题型10 利用勾股定理证明线段的平方关系题型11 勾股定理的证明方法题型12 以弦图为背景的计算题题型13 利用勾股定理构造图形解决问题题型14 利用勾股定理解决实际问题类型一 求梯子滑落高度类型二 求旗杆高度类型三 大树折断前高度类型四 解决水杯中的筷子问题类型liu 选址到两地距离相等类型六 最短路径类型七 航海问题题型15 勾股定理与规律探究问题考点三 勾股定理逆定理题型01 图形上与已知两地构成直角三角形的点题型02 在网格中判定直角三角形题型03 利用勾股定理逆定理求解题型04 利用勾股定理解决实际生活问题考点一 直角三角形的性质与判定直角三角形的定义：有一个角是直角的三角形叫做直角三角形．直角三角形的性质：1）直角三角形两个锐角互余.2）直角三角形斜边上的中线等于斜边的一半.3）在直角三角形中，30°角所对的直角边等于斜边的一半.直角三角形的判定：1）两个内角互余的三角形是直角三角形.2）三角形一边上的中线等于这条边的一半，那么这个三角形是直角三角形．3）有一个角是直角的三角形叫做直角三角形．4）勾股定理的逆定理：如果三角形的三边长a，b，c有关系a2+b2=c2，那么这个三角形是直角三角形。

面积公式：S=12ab=12cm(其中：c为斜边上的高，m为斜边长)题型01 利用直角三角形的性质求解【例1】（2023·山东聊城·统考二模）如图，直线l1∥l2，AB⊥CD，∠2=68°，那么∠1的度数是（ ）A．68°B．58°C．22°D．32°【答案】C【分析】由两直线平行同位角相等得到∠2=∠3，再由AB与CD垂直，利用垂直的定义得到∠BMC为直角，得到∠1与∠3互余，由∠3的度数求出∠1的度数．【详解】解：∵直线l1∥l2，∴∠2=∠3=68°，∵AB⊥CD，∴∠CMB=90°，∴∠1＋∠3=90°，又∠3=68°，∴∠1=22°，【点拨】此题考查了平行线的性质，垂直定义、直角三角形的两个锐角互余，熟知平行线的性质：两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补．【变式1-1】（2023·广东揭阳点是BD的中点，若CP=A．7B．8【答案】B【分析】由题意推出AD=BD，在【详解】解：∵∠ACB=90°，【答案】30【分析】根据正六边形的性质求出∠B ∠CAF=90°，根据对称性求出∠AFC 【详解】解：在正六边形ABCDEF中，=∠B=∠BAF=∠AFE=180°―360°6【答案】33【分析】根据垂直定义可得∠AEBAE=DE=CE=3，从而得到【详解】解：∵AE⊥BE，题型02 根据已知条件判定直角三角形【点拨】本题主要考查三角形的基本概念和直角三角形，其中在能够组成三角形的条件下，如果满足较小两边平方的和等于最大边的平方是直角三角形；满足较小两边平方的和大于最大边的平方是锐角三角形；满足较小两边平方的和小于最大边的平方是钝角三角形；掌握直角三角形的判断条件是解题的关键．题型03 与直角三角形有关的面积计算A．1B．【答案】A【分析】连接OP，过点P∵AO=BO=BP，∴OP=OB=BP，即△OPB∴∠DPB=30°，设OB=a，则AB=2a，A．48B．54【答案】D【分析】设CD与PQ交于G，连接据全等三角形的性质得到∠PAG∵四边形ABCD和正方形APQR是正方形，∴AB=AP=AD，∠BAD=∠P∵∠BAP=30°，∴∠PAD=60°，【答案】93【分析】根据30°角所对直角边是斜边的一半求出即可得解；【答案】【分析】根据重叠部分的面积求出考点二 勾股定理勾股定理的概念：如果直角三角形的两直角边分别为a ，b ，斜边为c ，那么a 2+b 2=c 2.变式：a 2=c 2―b 2，b 2=c 2―a 2勾股定理的证明方法（常见）：方法一（图一）：4S Δ+S 正方形EFGH =S 正方形ABCD ，4×12a b +(b ―a )2=c 2，化简可证．方法二（图二）：四个直角三角形的面积与小正方形面积的和等于大正方形的面积．四个直角三角形的面积与小正方形面积的和为S =4×12ab +c 2=2ab +c 2大正方形面积为S =(a +b )2=a 2+2ab +b 2，所以a 2+b 2=c 2方法三（图三）：S 梯形=12(a +b )⋅(a +b )，S 梯形=2S ΔADE +S ΔABE =2⋅12ab +12c 2，化简得证a 2+b 2=c 2图一 图二 图三勾股数概念：能够构成直角三角形的三边长的三个正整数称为勾股数，即a 2+b 2=c 2中，a ，b ，c 为正整数时，称a ，b ，c 为一组勾股数.常见的勾股数：如3,4,5；6,8,10；5,12,13；7,24,25等.判断勾股数的方法：1）确定是三个正整数a，b，c；2）确定最大的数c；3）计算较小的两个数的平方a2+b2是否等于c2.1. 勾股定理揭示了直角三角形三条边之间所存在的数量关系，它只适用于直角三角形，因而在应用勾股定理时，必须明了所考察的对象是直角三角形.2. 如果已知的两边没有明确边的类型，那么它们可能都是直角边，也可能是一条直角边、一条斜边，求解时必须进行分类讨论，以免漏解．3. 应用勾股定理时，要分清直角边和斜边，尤其在记忆a2+b2=c2时，斜边只能是c．若b为斜边，则关系式是a2+c2=b2；若a为斜边，则关系式是b2+c2=a2．4. 每组勾股数的相同整数倍也是勾股数.题型01 利用勾股定理求线段长A．5cm【答案】C【分析】本题考查切线的性质、勾股定理，掌握切线性质是关键．先证得解即可．过点A作AD⊥BC，在Rt△ACD中，∵AC=23，∠C=30°，∴AD=3，过点A作AD⊥BC交CB的延长线于点同①可求得：CD=3，BD∴BC=CD―BD=3―1综上，BC的长为2或4，题型02 利用勾股定理求面积，AD则BD=CD=a2∴正三角形的面积为设正六边形的边长同理正六边形的面积为A．64B．48【答案】C【分析】过点P作PD⊥x轴于点的长，继而求得AB的长，继而求得答案．【详解】解：过点P作PD⊥∵点P的坐标为(5,3)，∵⊙P与y轴相切于点C，∴PC=5，PD=3，∴PC=PA=5，DM=PD在Rt△PAD中，AD=PAA．S1=n2S2【答案】B【分析】如图所示，过点BC⋅AD=x，则S1=12【点拨】本题主要考查了等边三角形的性质，勾股定理，正确求出【变式2-3】（2023·山西太原中点，DE⊥AB于点E，则A．1:8B．【答案】A【分析】连接AD，易证△得出BE=12BD，再根据勾股定理得出勾股定理得出AD=32AB，从而得出S△ABC=3BD2，即可得出答案．∵AB=BC=AC∴△ABC为等边三角形∴∠B=60°∵DE⊥AB∴∠BDE=30°∴BE=12 BD题型03 已知两点坐标求两点距离A．13B．【答案】A【分析】首先连接OB，根据两点间距离公式即可求得长．【详解】解：如图：连接OB∵点B的坐标为(2,3)，∴OB=22+32=13，又∵四边形OABC是矩形，∴AC=OB=13，故选：A．【点拨】本题考查了勾股定理，矩形的性质，作出辅助线是解决本题的关键．题型04 判断勾股数问题题型05 利用勾股定理解决折叠问题A．2+3B．2+32【答案】A【分析】设BC=x，求得AB=2BC∠AED=∠BED=∠C=90°，在Rt(23―3)x，根据正切的定义即可得到答案．A．5B【答案】C【分析】由勾股定理得ABCD=C′D=x，利用勾股定理列方程，解得【点拨】本题考查了勾股定理，折叠的性质，解方程，熟练掌握勾股定理和折叠的性质是解题关键．【变式5-2】（2022·广东茂名点B与点A重合，折痕为DE题型06 勾股定理与网格问题13A．1013【答案】D【分析】根据勾股定理计算可．【点拨】本题考查了勾股定理，三角形的面积的计算，掌握勾股定理是解题的关键．题型07 勾股定理与无理数A．2<a<3【答案】B【分析】据勾股定理求出A．2B．【答案】CA．13B．―13【答案】C【分析】先利用勾股定理计算AC，从而得到【详解】∵表示―1的点A.表示2的点∴AB=2―(―1)=3，【答案】＞【分析】依据勾股定理即可得到AD中，AD+BD＞AB，即可得到5+1【详解】∵∠C=90°，BC=3，BD题型08 以直角三角形三边为边长的图形面积A．S1+S2=S3B．S1S2=13【答案】D【分析】如图所示，设AB所在的正五边形的外接圆圆心为出∠AOB=72°，再根据三线合一定理得到求出S3=5AB24t a n36°，同理S1=5BC4t a n36°【详解】解：如图所示，设AB所在的正五边形的外接圆圆心为由正五边形的性质可得∠AOB =∵OA =OB ，OD ⊥AB ，∴BD =12AB ，∠BOD =∠AOD =在Rt △AOD 中，OD =AD t a n ∠AOD =∴S 3=5S △AOB =5×12AB ⋅AB 2t a n36°5BC 25AC 2(1)如图1，是一个重要公式的几何解释，请你写出这个公式：(2)如图2，在RtΔABC中，∠ACB=90°,BC=a,AC=b,AB=c，以RtΔABC的三边长向外作正方形的面积分别为S1,S2,S3，试猜想S1,S2,S3之间存在的等量关系，直接写出结论．(3)如图3，如果以RtΔABC的三边长a,b,c为直径向外作半圆，那么第(2)问的结论由．(4)如图4，在RtΔABC中，∠ACB＝90°，三边分别为5,12,13，分别以它的三边为直【答案】2024【分析】根据勾股定理求出“生长规律解答即可．【详解】解：由题意得，正方形由勾股定理得，正方形B的面积与正方形∴“生长”了1次后形成的图形中所有的正方形的面积和为同理可得，“生长”了2次后形成的图形中所有的正方形的面积和为∴“生长”了3次后形成的图形中所有的正方形的面积和为……∴“生长”了2023次后形成的图形中所有的正方形的面积和为题型09 利用勾股定理求两条线段的平方和（差）【答案】（1）详见解析；（2）①73，②74【分析】（1）利用勾股定理即可得出结论；（2）①根据SAS可证明△PBC≌△ABQ，得∠BPC＝∠BAQ，得∠PDA＝90°②连接PC.AQ交于点D，同①可证△PBC≌△ABQ，则AQ＝PC且AQ⊥PC，43．延长QB作AE⊥QE，求出BE的长，则答案可求出．【详解】解：（1）证明：如图中，∵AC⊥BD，∴∠AOD＝∠AOB＝∠BOC由勾股定理得，AD2+BC2AB2+CD2＝AO2+BO2+CO2∴AB2+CD2＝AD2+BC2；（2）①如图，连接PC.AQ∵△ABP和△CBQ都是等腰直角三角形，∴PB＝AB，CB＝BQ，∠∴∠PBC＝∠ABQ，∴△PBC≌△ABQ（SAS）∴∠BPC＝∠BAQ，又∵∠BPC+∠CPA+∠BAP同①可证△PBC≌△ABQ（∵M、N分别是AC.AP中点，PC，∴MN＝12∵MN＝23，∴AQ＝PC＝43．延长QB作AE⊥QE，题型10 利用勾股定理证明线段的平方关系【例10】（2023·湖北武汉·统考模拟预测）如图，△ACB和△ECD都是等腰直角三角形，CA=CB，CE=CD，△ACB的顶点A在△ECD的斜边DE上．(1)判断∠ACD与∠BCE间的数量关系，并说明理由；(2)直接写出线段AD、AE、AC间满足的数量关系．【答案】(1)见解析(2)AD2+AE2=2AC2，理由见解析【分析】（1）根据已知条件得出∠DCE=∠ACB=90°，即∠DCE=∠ACD+∠ACE,∠ACB=∠BCE+∠ACE，即可得出∠ACD=∠BCE；（2）证明△CAD≌△CBE，得出∠CAD=∠CBE，BE=AD，进而根据四边形内角和为360°，求得∠AEB=90°，进而勾股定理即可得证．【详解】（1）∠ACD=∠BCE理由如下，∵△ACB和△ECD都是等腰直角三角形，∴∠DCE=∠ACB=90°，∵∠DCE=∠ACD+∠ACE,∠ACB=∠BCE+∠ACE，∴∠ACD+∠ACE=∠BCE+∠ACE，∴∠ACD=∠BCE；（2）AD2+AE2=2AC2，如图所示，连接BE，由（1）可得∠ACD=∠BCE∵CA=CB,CD=CE∴△CAD≌△CBE∴∠CAD=∠CBE，BE=AD，∵∠CAD+∠CAE=180°(1)依题意补全图形；(2)求证：∠EMF=∠ACF；(3)判断BM、CM、AC的数量关系，并证明．【答案】(1)见解析(2)见解析(3)AC2+BM2=MC2，见解析【分析】（1）根据题意画出图形即可；（2）根据垂直定义，得出∠DCF+∠DFC=90°，∠EMF+∠EFM=90°，根据等角的余角相等得出结论；（3）延长ME到G使EG=EM，连接AG，CG,根据边角边定理证出△AGE≌△BME，从而证出BM=AG，BM∥AG，根据勾股定理得出AC2+AG2=GC2，再根据线段垂直平分线的性质得出CG=CM，进而得出结论．【详解】（1）解：补全图形，如图所示：（2）∵BD⊥AC，∴∠DCF+∠DFC=90°，∵EM⊥EF，∴∠EMF+∠EFM=90°，∵∠EFM=∠DFC，∴∠EMF=∠DCF；（3）结论：AC2+BM2=MC2；延长ME到G使EG=EM，连接AG，CG，∵∠GEA=∠MEB，EG=EM，AE=BE，∴△AGE≌△BME(SAS)，∴BM=AG，∴∠GAE=∠MBE，∴BM∥AG，∵BD⊥AC，(1)【尝试探究】如图1，若AC=BC，求证AP2+BQ2=PQ2；(2)【深入研究】如图2，试探索（1）中的结论在一般情况下是否仍然成立；(3)【解决问题】如图3，若AC=6，BC=8，点C，P，O，Q在同一个圆上，求【答案】(1)见解析∴AP=CQ，∵AC=BC，∴CP=BQ，∵∠ACB=90°，∴CP2+CQ2=PQ2，∴AP2+BQ2=PQ2；（2）AP2+BQ2=PQ2，仍然成立．证明：延长QO至D，使OD=OQ，连接AD,PD,AQ,BD，∵点O是AB的中点，∴AO=BO，∴AB,DQ互相平分，∴四边形ADBQ是平行四边形，∴AD∥BQ,AD=BQ，∵∠C=90°，∴∠PAD=90°，∴AP2+BQ2=AP2+AD2=PD2，∵∠POQ=90°，∴PO⊥OQ，∴OP垂直平分DQ，∴PQ=PD，∴AP2+BQ2=PQ2；（3）解：∵∠C=90°，点C，P，O，Q在同一个圆上，∴PQ是圆的直径，∴∠POQ=90°，由②知，AP2+BQ2=PQ2，又CP2+CQ2=PQ2，∴AP2+BQ2=CP2+CQ2，设PC=a,CQ=b，则：AP=6―a,BQ=BC―CQ=8―b，题型11 勾股定理的证明方法【例11】（2023·山东济宁·统考二模）勾股定理是人类最伟大的十个科学发现之一，西方国家称之为毕达哥拉斯定理．在我国古书《周髀算经》中就有“若勾三，股四，则弦五”的记载，我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”（如图1），后人称之为“赵爽弦图”，流传至今．勾股定理内容为：如果直角三角形的两条直角边分别为a，b，斜边为c，那么a2+b2=c2．(1)如图2.3.4，以直角三角形的三边为边或直径，分别向外部作正方形、半圆、等边三角形，这三个图形中面积关系满足S1+S2=S3的有______个；(2)如图5所示，分别以直角三角形三边为直径作半圆，设图中两个月形图案（图中阴影部分）的面积分别为S1，S2，直角三角形面积为S3，请判断S1，S2，S3的关系并证明；(3)如果以正方形一边为斜边向外作直角三角形，再以该直角三角形的两直角边分别向外作正方形，重复这一过程就可以得到如图6所示的“勾股树”．在如图7所示的“勾股树”的某部分图形中，设大正方形M的边长为定值m，四个小正方形A，B，C，D的边长分别为a，b，c，d，已知∠1=∠2=∠3=∠α，则当∠α变化时，【点拨】本题考查了求扇形的面积，解直角三角形，勾股定理的证明，以及正方形的性质，掌握勾股定理的内容以及数形结合思想成为解答本题的关键．【变式11-1】（2022·福建龙岩(1)中国古代数学著作《周髀算经》是：“如果直角三角形两直角边长分别为果∠C=90∘，BC=a，AC=b，(3)如图3，把矩形ABCD【答案】(1)a2+b2=c2；(2)(a+b)2；S正方形MNPQ(3)3．【分析】（1）根据勾股定理解答即可；（2）根据题意、结合图形，根据完全平方公式进行计算即可；（3）根据翻折变换的特点、结合勾股定理列出方程，解方程即可．【详解】（1）在Rt△ABC∴a2+b2=c2，故答案为：(a+b)2；S正方形MNPQ；4S△ABC+S正方形ABDE；a2+b2=c2；（3）设BE=x，则EC=8―x，由折叠的性质可知，AE=EC=8―x，在Rt△ABE中，AE2=AB2+BE2，则(8―x)2=42+x2，解得，x=3，则BE的长为3．【点拨】本题考查的是正方形和矩形的性质、勾股定理、翻折变换的性质，正确理解勾股定理、灵活运用数形结合思想是解题的关键【变式11-2】（2021·河北·模拟预测）勾股定理是人类最伟大的十个科学发现之一，西方国家称之为毕达哥拉斯定理．在我国古书《周髀算经》中就有“若勾三，股四，则弦五”的记载，我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”（如图1），后人称之为“赵爽弦图”，流传至今．（1）①请叙述勾股定理；②勾股定理的证明，人们已经找到了400多种方法，请从下列几种常见的证明方法中任选一种来证明该定理；（以下图形均满足证明勾股定理所需的条件）（2）①如图4.5.6，以直角三角形的三边为边或直径，分别向外部作正方形、半圆、等边三角形，这三个图形中面积关系满足S1+S2=S3的有_______个；②如图7所示，分别以直角三角形三边为直径作半圆，设图中两个月形图案（图中阴影部分）的面积分别为S1，S2，直角三角形面积为S3，直接写出S1,S2,S3的关系（无需证明）；。

2
3
精讲精练
1. 已知在△ABC 中，a，b，c 分别为 A，B，C 的对边，请根据 以下条件，解三角形． （1）已知 A 45，C 30，c 10 ，求 B，b，a； （2）已知 B 30，b 4 ，c 4 3 ，求 C，A，a．
2. （1）在△ABC 中， A : B : C 4 :1:1 ，则 a : b : c （ ）
解三角形（讲义）
知识点睛
在本讲中，如没有特别说明，所有△ABC 中角 A，B，C 所对 的边均为 a，b，c，如图．
一、正弦定理、余弦定理
1. 正弦定理
（1） 正弦定理推导
设△ABC 的外接圆是⊙O，半径为 R．我们仅先分析 A 的情
况．
过点 B 作直径 BD，可知 BD=2R．
①如图（1），当 A 为锐角时，连接 CD，则∠BCD=90°， ∴ a 2R sin D ，
（1） S 1 ah (h 为 BC 边上的高)；
2 （2） S 1 ab sin C 1 ac sin B 1 bc sin A ；
2
2
2
（3） S 2R2 sin Asin B sin C (R 为△ABC 外接圆的半径)；
（4） S abc ；
4R （5） S p( p a)( p b)( p c)，其中 p 1 (a b c) ．
∴ | c |2 c c (a b) (a b) a a + b b 2a b
a2 b2 2ab cosC，
∴ c2 a2 b2 2ab cos C ．
同理可证：
（2） 余弦定理 在△ABC 中，任何一边的平方等于其他两边的平方的和减去 这两边与它们的夹角的余弦的积的两倍．即
在△ABC 中，各边和它所对的角的正弦的比相等，即

第九讲直角三角形、锐角三角函数及其应用专项一直角三角形知识清单1. 直角三角形的性质（1）直角三角形的两个锐角；（2）直角三角形斜边上的中线等于斜边的；（3）勾股定理：如果直角三角形的两条直角边长分别为a，b，斜边长为c，那么a，b，c满足；（4）直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的．2. 直角三角形的判定（1）有一个角是直角的三角形是直角三角形；（2）有两个角的三角形是直角三角形；（3）勾股定理的逆定理：如果三角形的三边长a，b，c满足，那么这个三角形是直角三角形；（4）如果一个三角形一边上的中线等于这条边的，那么这个三角形是直角三角形．（这个结论在做填空、选择题时可直接用）3. 勾股数：能够成为的三个正整数，称为勾股数．考点例析例1 如图1，AB∥CD，CE⊥AD，垂足为E．若∠A＝40°，则∠C的度数为（）A．40°B．50°C．60°D．90°图1分析：根据平行线的性质，得∠D＝∠A＝40°，再在Rt△CED中，根据“直角三角形的两个锐角互余”即可求得∠C的度数．例2 如图2，在Rt△ABC中，∠ABC＝90°，BF是AC边上的中线，DE是△ABC的中位线．若DE＝6，则BF的长为（）A．6 B．4 C．3 D．5图2分析：根据三角形的中位线定理可求出AC 的长，再根据“直角三角形斜边上的中线等于斜边的一半”即可求得BF 的长．例3 如图3，在Rt △ABC 中，∠C ＝90°，∠B ＝30°，AB ＝8．若E ，F 是BC 边上的两个动点，以EF 为边的等边三角形EFP 的顶点P 在△ABC 的内部或边上，则等边三角形EFP 的周长的最大值为 ．图3分析：当点F 与点C 重合，点P 落在AB 边上时，△EFP 的边长最长，周长也最长，根据“直角三角形中，30°角所对的直角边等于斜边的一半”可求出AC 的长，再利用三角函数，或求出AP 利用勾股定理均可求得△EFP 边长的最大值，进而得解．例4 如图4，某港口P 位于东西方向的海岸线上，甲、乙轮船同时离开港口，各自沿一固定方向航行，甲、乙轮船每小时分别航行12海里和16海里，1小时后两船分别位于点A ，B 处，且相距20海里．若甲船沿北偏西40°方向航行，则乙船沿 方向航行．图4分析：由题意，知AP ＝12，BP ＝16，AB ＝20，根据勾股定理的逆定理，可推出△APB 是直角三角形，且∠APB ＝90°，结合甲船的航行方向可推出乙船的航行方向．例5 如图5，在Rt △ABC 中，∠ACB ＝90°，以该三角形的三条边为边向外作正方形，正方形的顶点E ，F ，G ，H ，M ，N 都在同一个圆上．记该圆的面积为S 1，△ABC 的面积为S 2，则12S S 的值是（ ） A ．5π2 B ．3π C ．5π D ．11π2图5分析：设Rt △ABC 的三边长为a ，b ，c ，其中c 为斜边，设⊙O 的半径为r ，根据图形的特点找出a ，b ，c，r的等量关系，用含c的式子表示S1和S2，即可求出比值．跟踪训练1.如图，△ABC中，∠ACB＝90°，AC＝8，BC＝6，将△ADE沿DE翻折，使点A与点B重合，则CE的长为（）A．198B．2 C．254D．74第1题图第2题图第3题图2.如图，已知A（8，0），C（-2，0），以点A为圆心，AC长为半径画弧，交y轴正半轴于点B，则点B 的坐标为（）A.（0，5）B.（5，0）C.（6，0）D.（0，6）3.（2021·成都）如图，图中数字代表所在正方形的面积，则A所代表的正方形的面积为．4.（2021·西宁）如图，在Rt△ABC中，∠BAC＝90°，D，E分别是AB，BC的中点，连接AE，DE．若DE＝92，AE＝152，则点A到BC的距离是．第4题图第5题图5.如图，在▱ABCD中，点E在AD上，且EC平分∠BED．若∠EBC＝30°，BE＝10，则▱ABCD的面积为．6.对角线互相垂直的四边形叫做“垂美”四边形，现有如图所示的“垂美”四边形ABCD，对角线AC，BD交于点O．若AD＝2，BC＝4，则AB2+CD2＝．第6题图第7题图7.如图，在四边形ABCD中，AB∥CD，∠ABC＝60°，AD＝BC＝CD＝4．若M是四边形ABCD内的一个动点，满足∠AMD＝90°，则点M到直线BC的距离的最小值为．专项二锐角三角函数知识清单1. 锐角三角函数如图，在Rt△ABC中，∠C＝90°，∠A，∠B，∠C的对边长分别为a，b，c，则∠A的正弦：sin A＝ac；∠A的余弦：cos A＝；∠A的正切：tan A＝．∠A的正弦、余弦、正切都是∠A的锐角三角函数．2. 特殊角的三角函数值考点例析例1如图1，点A，B，C在边长为1的正方形网格格点上，下列结论错误的是（）A．1sin3B=B．25sin C C．1tan2B=D．22sin sin1B C+=图1分析：利用正方形网格的特点，由勾股定理得出AB，AC，BC的长，进而利用勾股定理的逆定理推出△ABC 是直角三角形，最后根据锐角三角函数的定义对选项逐一判断即可．归纳：锐角三角函数使用的前提一定是直角三角形，并能准确地找出某个角的对边、邻边和斜边．例2 如图2，在Rt△ABC中，∠ACB＝90°，CE是斜边AB上的中线，过点E作EF⊥AB交AC于点F．若BC＝4，△AEF的面积为5，则sin∠CEF的值为（）A．35B5C．45D25三角函数α30°45°60°sin αcos αtan α图2分析：根据“直角三角形斜边上的中线等于斜边的一半”，得CE ＝AE ＝BE ，进而得到∠BEC ＝2∠A ，连接BF ，由EF ⊥AB ，得∠BFC ＝2∠A ，所以∠BEC ＝∠BFC ，从而有∠CEF ＝∠CBF ．根据三角形的面积公式求出AF 的长，在Rt △BCF 中，利用勾股定理求出CF ，再根据锐角三角函数的定义求解即可．归纳：一个锐角的三角函数值仅与这个锐角的大小有关，而与这个锐角在何处、在何种三角形中无关（即与三角形三边的长短无关）．当一个锐角的三角函数值求解较烦琐或不易直接求得时，可转化为求与其相等的角的三角函数值．跟踪训练1.tan 30°的值等于（ ）A B C ．1 D ．22.如图，在平面直角坐标系内有一点P （3，4），连接OP ，则OP 与x 轴正方向所夹锐角α的正弦值是（ ）A ．34B ．43C ．35D ．45第2题图 第3题图 第4题图3.如图，在△ABC 中，O 是角平分线AD ，BE 的交点．若AB ＝AC ＝10，BC ＝12，则tan ∠OBD 的值是（ ）A ．12B ．2CD 4.如图，在正方形网格中，每个小正方形的边长都是1，⊙O 是△ABC 的外接圆，点A ，B ，O 在网格线的交点上，则sin ∠ACB 的值是 ．专项三 解直角三角形知识清单解直角三角形的几种常见类型及解法：考点例析例1 在△ABC 中，∠ABC ＝90°．若AC ＝100，sin A ＝35，则AB 的长是（ ） A ．5003 B ．5035 C ．60 D ．80分析：利用锐角三角函数的定义求出BC 的长，然后再利用勾股定理即可求得AB 的长．例2 如图，△ABC 底边BC 上的高为h 1，△PQR 底边QR 上的高为h 2，则有（ ）A ．h 1＝h 2B ．h 1＜h 2C ．h 1＞h 2D ．以上都有可能分析：分别作出△ABC 底边BC 上的高和△PQR 底边QR 上的高，再利用锐角三角函数分别表示出h 1和h 2，即可确定其大小关系．跟踪训练1.如图，在△ABC 中，∠B ＝45°，∠C ＝60°，AD ⊥BC 于点D ，BD 若E ，F 分别为AB ，BC 的中点，则EF 的长为（ ）A B C ．1 D第1题图 第2题图2.如图，△ABC 的顶点B ，C 的坐标分别是（1，0），(，且∠ABC ＝90°，∠A ＝30°，则顶点A 的坐标是 ．3.在△ABC 中，∠A ＝45°，AB ＝BC ＝5，则△ABC 的面积为 ．4.在锐角三角形ABC 中，∠A ，∠B ，∠C 的对边分别为a ，b ，c ，边角总满足关系式：sin sin sin a b c A B C ==． （1）如图①，若a ＝6，∠B ＝45°，∠C ＝75°，求b 的值；（2）某公园准备在园内一个锐角三角形水池ABC 中建一座小型景观桥CD （如图②所示）．若CD ⊥AB ，AC ＝14米，AB ＝10米，sin ∠ACB ，求景观桥CD 的长度．① ②第4题图专项四 锐角三角函数的实际应用知识清单锐角三角函数的实际应用主要是测量物体的高度、测量两点之间的距离等，常用到下面几个概念：1. 仰角、俯角如图1，在视线与水平线所成的锐角中，视线在水平线上方的角叫做 ，视线在水平线下方的角叫做 ．图1 图2 图32. 坡度、坡角如图2，坡面的铅直高度h 和水平宽度l 的比叫做坡面的坡度（或坡比），用字母i 表示；坡面与水平面的夹角α叫做坡角，i ＝ ＝ ，坡度越大，α越 ，坡面越 ．3. 方位角一般是指以观测者的位置为中心，将正北或正南方向作为起始方向，旋转到目标的方向所成的小于90°的角．如图3，点A位于点O的北偏东方向，点B位于点O的60°方向，点C位于点O的（或）方向．考点例析例1 无人机低空遥感技术已广泛应用于农作物监测．如图1，某农业特色品牌示范基地用无人机对一块试验田进行监测作业时，在距地面高度为135 m的A处测得试验田右侧边界N处的俯角为43°，无人机垂直下降40 m至B处，又测得试验田左侧边界M处的俯角为35°，则M，N之间的距离为（参考数据：tan 43°≈0.9，sin 43°≈0.7，cos 35°≈0.8，tan 35°≈0.7）（）A．188 m B．269 m C．286 m D．312 m图1分析：在Rt△AON中，由AO的长和∠N的度数求出ON的长，再在Rt△BOM中，由BO的长和∠M的度数求出MO的长，结合MN＝MO+ON即可求得M，N之间的距离．例2 某商场准备改善原有楼梯的安全性能，把坡角由37°减至30°．已知原楼梯长为5米，调整后的楼梯会加长（参考数据：sin 37°≈0.6，cos 37°≈0.8，tan 37°≈0.75）（）A．6米B．3米C．2米D．1米分析：画出示意图如图2所示，在Rt△BAD中，由AB＝5，∠BAD＝37°，求出BD的长，在Rt△BCD中，根据“直角三角形中，30°角所对的直角边等于斜边的一半”求出BC的长，进而得解．图2例3 如图3，一艘轮船位于灯塔P的南偏东60°方向，距离灯塔50海里的A处，它沿正北方向航行一段时间后，到达位于灯塔P的北偏东45°方向上的B处，此时B处与灯塔P的距离为海里．（结果保留根号）图3分析：过点P作PC⊥AB于点C，在Rt△APC中，由P A的长和∠A的度数求出PC的长，再在Rt△BPC 中，由PC的长和∠B的度数即可求得PB的长．跟踪训练1.如图，在点F处，看建筑物顶端D的仰角为32°，向前走了15米到达点E处，即EF＝15米，在点E处看点D的仰角为64°，则CD的长用三角函数表示为（）A．15sin 32°B．15tan 64°C．15sin 64°D．15tan 32°第1题图第2题图第3题图2.如图，为了测量某建筑物BC的高度，小颖采用了如下的方法：先从与建筑物底端B在同一水平线上的A 点出发，沿斜坡AD行走130米至坡顶D处，再从D处沿水平方向继续前行若干米后至点E处，在E点测得该建筑物顶端C的仰角为60°，建筑物底端B的俯角为45°，点A，B，C，D，E在同一平面内，斜坡AD的坡度i＝1∶2.4．根据小颖的测量数据，计算筑物BC）（）A．136.6米B．86.7米C．186.7米D．86.6米3.某景区A，B两个景点位于湖泊两侧，游客从景点A到景点B必须经过C处才能到达．观测得景点B在景点A的北偏东30°方向，从景点A出发向正北方向步行600米到达C处，测得景点B在C的北偏东75°方向．（1）求景点B和C处之间的距离；（结果保留根号）（2）当地政府为了便捷游客游览，打算修建一条从景点A到景点B的笔直的跨湖大桥．大桥修建后，从景点A到景点B）专项五锐角三角函数中的建模思想知识清单根据实际问题建立数学模型，再通过解决数学问题达到解决实际问题的目的，这种思想被称为建模思想．考点例析例一种可折叠的医疗器械放置在水平地面上，这种医疗器械的侧面结构如图实线所示，底座为△ABC，点B，C，D在同一条直线上，测得∠ACB＝90°，∠ABC＝60°，AB＝32 cm，∠BDE＝75°，其中一段支撑杆CD＝84 cm，另一段支撑杆DE＝70 cm．求支撑杆上的点E到水平地面的距离EF是多少？（结果保留整数；参考数据：sin 15°≈0.26，cos 15°≈0.97，tan 15°≈0.27）分析：过点D作DM⊥EF于点M，DN⊥BA交BA的延长线于点N，解Rt△ABC求出BC的长，再解Rt△BDN 求出DN的长，易得四边形MFND是矩形，利用矩形的性质可得MF＝DN及∠BDM的度数，进而求得∠EDM，最后解Rt△EMD求出EM的长，进而得解．解：归纳：解直角三角形的前提是在直角三角形中进行，对于非直角三角形问题，要注意观察图形特点，作恰当的辅助线，将其转化为直角三角形求解．跟踪训练1.如图①是一台手机支架，图②是其侧面示意图，AB，BC可分别绕点A，B转动，测量知BC＝8 cm，AB ＝16 cm．当AB，BC转动到∠BAE＝60°，∠ABC＝50°时，点C到AE的距离为cm．（结果精确到0.1 cm；参考数据：sin 70°≈0.94）①②①②③第1题图第2题图2.某种落地灯如图①所示，AB为立杆，其高为84 cm；BC为支杆，可绕点B旋转，其中BC长为54 cm；DE为悬杆，滑动悬杆可调节CD的长度．已知支杆BC与悬杆DE之间的夹角∠BCD为60°．（1）如图②，当支杆BC与地面垂直，且CD的长为50 cm时，求灯泡悬挂点D距离地面的高度；（2）在图②所示的状态下，将支杆BC绕点B顺时针旋转20°，同时调节CD的长（如图③），此时测得灯泡悬挂点D到地面的距离为90 cm，求CD的长．（结果精确到1 cm；参考数据：sin 20°≈0.34，cos 20°≈0.94，tan 20°≈0.36，sin 40°≈0.64，cos 40°≈0.77，tan 40°≈0.84）参考答案专项一直角三角形例1 B 例2 A 例3例4 北偏东50°例5 C 解析：如图，取AB的中点O，AC的中点D，连接OC，OD，OE，OG．因为圆心在线段EF和MN的垂直平分线上，所以点O为圆心．设AC＝a，BC＝b，AB＝c，则a2+b2＝c2．在Rt△ABC中，O为AB的中点，所以OA＝OB＝OC．又D为AC的中点，所以OD∥BC．所以OD⊥AC．因为OG，OE为⊙O的半径，所以OD2+DG2＝OB2+BE2，即2222222a cb cb⎛⎫⎛⎫⎛⎫++=+⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭．整理，得a＝b．所以215π4Sc=，224Sc=．所以12SS＝5π．1．D 2．D 3．100 4．3655．50 6．20 7．2专项二锐角三角函数例1 A例2 A 解析：连接BF．在Rt△ABC中，CE是斜边AB上的中线，所以CE＝AE＝BE，所以∠A＝∠ACE．所以∠BEC＝2∠A．因为EF⊥AB，所以EF是AB的垂直平分线．所以S△BEF＝S△AEF＝5，∠FBA＝∠A．所以∠BFC＝2∠A．所以∠BEC＝∠BFC．又∠BEF＝∠BCF＝90°，所以∠CEF＝∠CBF．因为S △AFB ＝2S △AEF ＝10，所以12AF ·BC ＝10．因为BC ＝4，所以AF ＝BF ＝5．所以CF 3． 所以sin ∠CEF ＝sin ∠CBF ＝35CF BF =．1．A 2．D 3．A 4 专项三 解直角三角形例1 D 例2 A1．C 2．( 3．2或144．解：（1）因为∠B ＝45°，∠C ＝75°，所以∠A ＝180°-∠B -∠C ＝60°．所以6sin 60sin 45b =︒︒，解得b ＝（2）因为sin sin AB AC ACB B =∠14sin B =，解得sin B ．所以∠B ＝60°．所以tan B ＝CD BD =BD CD ．在Rt △ACD 中，AC 2＝CD 2+AD 2，即196＝CD 2+210⎛⎫ ⎪ ⎪⎝⎭，解得CD ＝CD ＝-（舍去）． 所以景观桥CD 的长度为专项四 锐角三角函数的实际应用例1 C 例2 D 例3 1．C 2．A3．解：（1）过点C 作CD ⊥AB 于点D ．在Rt △ACD 中，∠A ＝30°，AC ＝600，所以CD ＝12AC ＝300．在Rt △BCD 中，∠B ＝75°-∠A ＝45°，所以BC ＝sin 45CD ︒＝．答：景点B 和C 处之间的距离为m ．（2）在Rt △ACD 中，∠A ＝30°，AC ＝600，所以AD ＝AC ·cos 30°＝．在Rt △BCD 中，∠B ＝45°，所以BD ＝CD ＝300．所以AB ＝AD +BD ＝．所以AC +BC -AB ＝600+-（300+≈205（m ）．答：大桥修建后，从景点A 到景点B 比原来少走约205 m ．专项五 锐角三角函数中的建模思想例 过点D 作DM ⊥EF 于点M ，DN ⊥BA 交BA 的延长线于点N ．在Rt △ABC 中，∠ABC ＝60°，AB ＝32，所以BC ＝AB ·cos 60°＝16．因为CD ＝84，所以BD ＝BC +CD ＝16+84＝100．在Rt △BDN 中，DN ＝BD ·sin 60°＝＝．易得四边形MFND 是矩形，所以MF ＝DN ＝，MD ∥FN ．所以∠BDM ＝∠ABC ＝60°．因为∠BDE ＝75°，所以∠EDM ＝∠BDE -∠BDM ＝75°-60°＝15°．在Rt △EMD 中，DE ＝70，所以EM ＝DE ·sin 15°≈70×0.26＝18.2．所以EF ＝EM +MF ＝18.2+≈105．答：支撑杆上的点E 到水平地面的距离EF 约是105 cm ．1．6.32．解：（1）如图①，过点D 作DF ⊥BC 于点F ．在Rt △DCF 中，CD ＝50，∠FCD ＝60°，所以FC ＝CD ·cos 60°＝25．所以F A ＝AB +BC -FC ＝84+54-25＝113（cm ）．答：灯泡悬挂点D 距离地面的高度为113 cm ．（2）如图②，过点C 作CG 垂直于地面于点G ，过点B 作BN ⊥CG 于点N ，过点D 作DM ⊥CG 于点M ． 在Rt △BCN 中，BC ＝54，∠BCN ＝20°，所以CN ＝BC ·cos 20°≈54×0.94＝50.76．所以CM ＝CN +NG -MG ＝CN +AB -MG ＝50.76+84-90＝44.76．在Rt △DCM 中，∠DCM ＝∠BCD -∠BCN ＝40°，所以CD ＝cos40CM ≈44.760.77≈58（cm ）． 答：CD 的长约为58 cm ．① ②第2题图。

一、考点突破理解直角三角形中五个元素的关系，会运用勾股定理，直角三角形的两个锐角互余及锐角三角函数解直角三角形。

渗透数形结合的数学思想，逐步培养分析问题、解决问题的能力。

二、重难点提示重点：直角三角形的解法。

难点：三角函数在解直角三角形中的灵活运用。

考点精讲解直角三角形2. 解直角三角形时应注意以下问题：（1）在求有关解直角三角形的问题时，要画出图形，以利于分析解决问题；（2）选择关系式时要尽量利用原始数据，以防止“累积错误”；（3）遇到不是直角三角形的图形时，要添加适当的辅助线，将其转化为直角三角形后再求解。

【重要提示】解直角三角形时，选择恰当的边角关系式尤为重要，恰当的边角关系不仅能使问题迅速解决，而且还会使计算简便、过程简捷，达到事半功倍的效果。

解直角三角形的方法遵循“有斜用弦，无斜用切；宁乘勿除，化斜为直”的原则。

注意：直角三角形中的五个元素：两条直角边，一条斜边，两个锐角。

在没有特殊说明的情况下，“解直角三角形”即求出所有的未知元素。

典例精讲例题1如图，在四边形ABCD中，AB＝2，BC＝3－2，CD＝5，∠B＝135°，∠C＝90°，则∠D等于（）AA. 30°B. 60°C. 75°D. 无法确定思路分析：通过对内分割或向外补形，构造直角三角形，通过解直角三角形求出∠D的度数。

答案：如图所示，过A作AE⊥CD于E，过B作BF⊥AE于F。

∵∠B＝135°，∠C＝90°，∴∠BAF＝45°。

∴AF＝BF＝AB·sin∠BAF＝2×＝2，∴AE＝AF＋BC＝2＋3－2＝3，又∵DE＝CD－CE＝5－2＝3，∴tan∠D＝＝，∴∠D＝60°。

选BAE技巧点拨：因直角三角形元素之间有很多关系，故用已知元素与未知元素的途径经常不唯一，选择怎样的途径最有效、最合理呢？请记住：有斜用弦，无斜用切，宁乘勿除。