2016-2017学年高中数学苏教版选修1-2章末综合测评 第2章 Word版含解析

章末检测一、填空题(本大题共14小题，每小题5分，共70分)1．下图是抛物线形拱桥，当水面在l 时，拱顶离水面2米，水面宽4米．水位下降1米后，水面宽________米．答案 2 6解析 建立坐标系如图所示．则抛物线方程为x 2＝－2py (p ＞0)．∵点(2，－2)在抛物线上，∴p ＝1，即抛物线方程为x 2＝－2y .当y ＝－3时，x ＝±6.∴水面下降1米后，水面宽为2 6米．2．双曲线x 2a 2－y 2b2＝1的两条渐近线互相垂直，则双曲线的离心率为__________． 答案 2解析 依题意两条渐近线方程必为y ＝±x ，则a ＝b ，所以c ＝2a ，故双曲线的离心率为 2.3．若抛物线y 2＝2px 的焦点与椭圆x 26＋y 22＝1的右焦点重合，则p 的值为________． 答案 4解析 椭圆x 26＋y 22＝1的右焦点为(2,0)，而抛物线y 2＝2px 的焦点为(p 2，0)，则p 2＝2，故p ＝4. 4．△ABC 的顶点B 、C 在椭圆x 23＋y 2＝1上，顶点A 是椭圆的一个焦点，且椭圆的另外一个焦点在BC 边上，则△ABC 的周长是________．答案 4 3解析 由椭圆的定义椭圆上一点到两焦点的距离之和等于长轴长2a ，可得△ABC 的周长为4a ＝4 3.5．若方程x 225－m ＋y 216＋m ＝1表示焦点在y 轴上的双曲线，则实数m 的取值范围是________．答案 m >25解析 由⎩⎪⎨⎪⎧25－m <0，16＋m >0，解得m 的取值范围是m >25. 6．设双曲线的焦点在x 轴上，两条渐近线为y ＝±12x ，则该双曲线的离心率e 为________． 答案 52 解析 由于焦点在x 轴上，故渐近线方程为y ＝±12x ，可得b a ＝12，又c 2＝a 2＋b 2，可解得e ＝c a 的值为52. 7．抛物线y 2＝2px (p >0)上有一点M 纵坐标为－42，这点到准线的距离为6，则抛物线的方程是____________．答案 y 2＝8x 或y 2＝16x解析 由已知得点M 的横坐标x M ＝(－42)22p ＝16p (p >0)，又x M ＋p 2＝6，即16p ＋p 2＝6，解得p ＝4或p ＝8.故抛物线的方程是y 2＝8x 或y 2＝16x .8．设O 是坐标原点，F 是抛物线y 2＝2px (p >0)的焦点，A 是抛物线上的一点，FA →与x 轴正方向的夹角为60°，则|OA →|＝__________.答案 212p 解析 依题意可设AF 所在直线方程为y －0＝(x －p 2)tan 60°，∴y ＝3(x －p 2)． 联立⎩⎪⎨⎪⎧y ＝3(x －p 2)，y 2＝2px ，解得x ＝p 6或3p 2， ∵FA →与x 轴正向夹角为60°，∴x ＝3p 2，y ＝3p ， ∴|OA →|＝x 2＋y 2＝212p . 9．设抛物线y 2＝8x 的焦点为F ，准线为l ，P 为抛物线上一点，PA ⊥l ，A 为垂足，如果直线AF 斜率为－3，那么PF ＝________.答案 8解析 由题意可知，∠AFO ＝60°，由焦点到准线的距离为4，所以AF ＝8，∵PA ∥FO ，∴∠PAF ＝60°，又由抛物线的定义，知PA ＝PF ，因而△PAF 为正三角形，所以PF ＝AF ＝8.10．在给定椭圆中，过焦点且垂直于长轴的弦长为2，焦点到相应准线的距离为1，则该椭圆的离心率为________．答案 22解析 不妨设椭圆方程为x 2a 2＋y 2b2＝1(a >b >0)， 则有⎩⎨⎧ 2b 2a ＝2，a 2c －c ＝1，即⎩⎨⎧ 2b 2a ＝2， ①b 2c ＝1， ②②÷①得e ＝22. 11．与双曲线x 29－y 23＝1有共同的渐近线，并且经过点(3，－4)的双曲线方程为____________． 答案 y 215－x 245＝1 解析 由题意可设所求双曲线方程为 x 29－y 23＝λ(λ≠0)， ∵双曲线经过点(3，－4)，∴λ＝(3)29－(－4)23＝－5， ∴所求双曲线方程为y 215－x 245＝1. 12．若中心在原点，焦点在坐标轴上的椭圆短轴端点是双曲线y 2－x 2＝1的顶点，且该椭圆的离心率与此双曲线的离心率的乘积为1，则该椭圆的方程为__________．答案 x 22＋y 2＝1 解析 由双曲线y 2－x 2＝1的顶点坐标为(0，±1)，可得椭圆的b ＝1；又双曲线的离心率为 1＋11＝2，从而由已知得椭圆的离心率为22，∴椭圆的a ＝2，∴该椭圆的方程为x 22＋y 2＝1. 13．如图，F 1，F 2是椭圆C 1：x 24＋y 2＝1与双曲线C 2的公共焦点，A ，B 分别是C 1，C 2在第二、四象限的公共点．若四边形AF 1BF 2为矩形，则C 2的离心率是________．答案 62解析 设AF 1＝x ，AF 2＝y ，因为点A 为椭圆C 1：x 24＋y 2＝1上的点， 所以2a ＝4，b ＝1，c ＝3；所以AF 1＋AF 2＝2a ＝4，即x ＋y ＝4；①又四边形AF 1BF 2为矩形，所以AF 21＋AF 22＝F 1F 22，即x 2＋y 2＝(2c )2＝(23)2＝12，②由①②得：⎩⎪⎨⎪⎧ x ＋y ＝4，x 2＋y 2＝12，解得x ＝2－2，y ＝2＋2，设双曲线C 2的实轴长为2a ′，焦距为2c ′，则2a ′＝AF 2－AF 1＝y －x ＝22，2c ′＝222－12＝23， 所以双曲线C 2的离心率e ＝c ′a ′＝32＝62. 14．已知抛物线C 1：y ＝12p x 2(p ＞0)的焦点与双曲线C 2：x 23－y 2＝1的右焦点的连线交C 1于第一象限的点M .若C 1在点M 处的切线平行于C 2的一条渐近线，则p ＝________.答案 433解析 经过第一象限的双曲线的渐近线为y ＝33x .抛物线的焦点为F (0，p 2)，双曲线的右焦点为F 2(2,0)．y ′＝1p x ，所以在M (x 0，x 202p )处的切线斜率为33，即1p x 0＝33，所以x 0＝33p ，即三点F (0，p 2)，F 2(2,0)，M (33p ，p 6)共线，所以p 2－00－2＝p 6－p 233p ，即p ＝433. 二、解答题(本大题共6小题，共90分)15．(14分)如图，在P 处有一堆肥料沿道路PA 或PB 送到矩形的一块田ABCD 中，已知PA ＝100 m ，PB ＝150 m ，BC ＝60 m ，∠APB ＝60°，能否在田中确定一条界线，使位于界线一侧的点沿道路PA 送肥料较近而另一侧的点沿PB 送肥料较近？如果能，说出这条界线是什么曲线？并求出它的方程．解 设M 是界线上任一点，则PA ＋MA ＝PB ＋MB ，MA －MB ＝PA －PB ＝50(常数)，∴界线是以A 、B 为焦点的双曲线一支(右支)．如图建立直角坐标系，设x 2a 2－y 2b2＝1(a >0，b >0)， 由余弦定理得2c ＝AB ＝1002＋1502－2×100×150cos 60°＝507，∴c ＝257，a ＝25，∴b 2＝c 2－a 2＝3 750，∴界线方程：x 2625－y 23 750＝1(x ≥25，y ≥0)． 16．(14分)椭圆x 2a 2＋y 2b 2＝1(a ，b >0)的两个焦点F 1，F 2，点P 在椭圆C 上，且PF 1⊥F 1F 2，PF 1＝43，PF 2＝143； (1)求椭圆C 的方程；(2)若直线l 过圆x 2＋y 2＋4x －2y ＝0的圆心M 交椭圆于A 、B 两点，且A 、B 关于点M 对称，求直线l 的方程．解 (1)因为点P 在椭圆C 上，所以2a ＝PF 1＋PF 2＝6，a ＝3.在Rt △PF 1F 2中，F 1F 2＝PF 22＋PF 21＝25， 故椭圆的半焦距c ＝5，从而b 2＝a 2－c 2＝4，所以椭圆C 的方程为x 29＋y 24＝1. (2)设A 、B 的坐标分别为(x 1，y 1)、(x 2，y 2)．由圆的方程为(x ＋2)2＋(y －1)2＝5，得圆心M 的坐标为(－2,1)．从而可设直线l 的方程为y ＝k (x ＋2)＋1，代入椭圆C 的方程得(4＋9k 2)x 2＋(36k 2＋18k )x ＋36k －27＝0.因为A 、B 关于点M 对称，所以x 1＋x 22＝－18k 2＋9k 4＋9k 2＝－2.解得k ＝89， 所以直线l 的方程为y ＝89(x ＋2)＋1，即8x －9y ＋25＝0(经检验，符合题意)． 17．(14分)如图，直线l ：y ＝x ＋b 与抛物线C ：x 2＝4y 相切于点A .(1)求实数b 的值；(2)求以点A 为圆心，且与抛物线C 的准线相切的圆的方程．解 (1)由⎩⎪⎨⎪⎧y ＝x ＋b ，x 2＝4y 得x 2－4x －4b ＝0，(*) 因为直线l 与抛物线C 相切，所以Δ＝(－4)2－4×(－4b )＝0，解得b ＝－1.(2)由(1)可知b ＝－1，故方程(*)即为x 2－4x ＋4＝0，解得x ＝2，代入x 2＝4y ，得y ＝1.故点A (2,1)，因为圆A 与抛物线C 的准线相切，所以圆A 的半径r 等于圆心A 到抛物线的准线y ＝－1的距离，即r ＝|1－(－1)|＝2，所以圆A 的方程为(x －2)2＋(y －1)2＝4.18．(16分)已知双曲线的中心在原点，焦点F 1，F 2在坐标轴上，离心率为2，且过点(4，－10)．(1)求双曲线方程；(2)若点M (3，m )在双曲线上，求证：点M 在以F 1F 2为直径的圆上；(3)在(2)的条件下求△F 1MF 2的面积．(1)解 ∵离心率e ＝2，∴双曲线为等轴双曲线，可设其方程为x 2－y 2＝λ(λ≠0)，则由点(4，－10)在双曲线上，可得λ＝42－(－10)2＝6，∴双曲线方程为x 2－y 2＝6.(2)证明 ∵点M (3，m )在双曲线上，∴32－m 2＝6，∴m 2＝3，又双曲线x 2－y 2＝6的焦点为F 1(－23，0)，F 2(23，0)，∴MF 1→·MF 2→＝(－23－3，－m )·(23－3，－m )＝(－3)2－(23)2＋m 2＝9－12＋3＝0，∴MF 1⊥MF 2，∴点M 在以F 1F 2为直径的圆上．(3)解 12F MF S ＝12×43×|m |＝6. 19．(16分)已知椭圆G ：x 2a 2＋y 2b 2＝1 (a >b >0)的离心率为63，右焦点为(22，0)，斜率为1的直线l 与椭圆G 交于A 、B 两点，以AB 为底边作等腰三角形，顶点为P (－3,2)．(1)求椭圆G 的方程；(2)求△PAB 的面积．解 (1)由已知得c ＝22，c a ＝63. 解得a ＝23，又b 2＝a 2－c 2＝4.所以椭圆G 的方程为x 212＋y 24＝1. (2)设直线l 的方程为y ＝x ＋m .由⎩⎪⎨⎪⎧y ＝x ＋m x 212＋y 24＝1，得4x 2＋6mx ＋3m 2－12＝0.① 设A 、B 的坐标分别为(x 1，y 1)，(x 2，y 2) (x 1<x 2)，AB 中点为E (x 0，y 0)，则x 0＝x 1＋x 22＝－3m 4，y 0＝x 0＋m ＝m 4； 因为AB 是等腰△PAB 的底边，所以PE ⊥AB .所以PE 的斜率k ＝2－m 4－3＋3m 4＝－1.解得m ＝2. 此时方程①为4x 2＋12x ＝0.解得x 1＝－3，x 2＝0.所以y 1＝－1，y 2＝2.所以AB ＝3 2.此时，点P (－3,2)到直线AB ：x －y ＋2＝0的距离d ＝|－3－2＋2|2＝322，所以△PAB 的面积S ＝12AB ·d ＝92. 20．(16分)椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的左、右焦点分别是F 1，F 2，离心率为32，过F 1且垂直于x 轴的直线被椭圆C 截得的线段长为1.(1)求椭圆C 的方程；(2)点P 是椭圆C 上除长轴端点外的任一点，连结PF 1，PF 2，设∠F 1PF 2的角平分线PM 交C 的长轴于点M (m,0)，求m 的取值范围；(3)在(2)的条件下，过P 点作斜率为k 的直线l ，使得l 与椭圆C 有且只有一个公共点，设直线PF 1，PF 2的斜率分别为k 1，k 2，若k ≠0，试证明1kk 1＋1kk 2为定值，并求出这个定值. 解 (1)由于c 2＝a 2－b 2，将x ＝－c 代入椭圆方程x 2a 2＋y 2b 2＝1得y ＝±b 2a， 由题意知2b 2a＝1，即a ＝2b 2. 又e ＝c a ＝32，所以a ＝2，b ＝1. 所以椭圆方程为x 24＋y 2＝1. (2)由题意可知：PF 1→·PM →|PF 1→||PM →|＝PF 2→·PM →|PF 2→||PM →|，PF 1→·PM →||PF 1→＝PF 2→·PM →||PF 2→，设P (x 0，y 0)其中x 20≠4，将向量坐标代入并化简得：m (4x 20－16)＝3x 30－12x 0，因为x 20≠4, 所以m ＝34x 0，而x 0∈(－2,2)，所以m ∈(－32，32) . (3)由题意可知，l 为椭圆的在p 点处的切线，由导数法可求得，切线方程为x 0x 4＋y 0y ＝1，所以k ＝－x 04y 0，而k 1＝y 0x 0＋3，k 2＝y 0x 0－3，代入1kk 1＋1kk 2中得 1kk 1＋1kk 2＝－4(x 0＋3x 0＋x 0－3x 0)＝－8. 因此，1kk 1＋1kk 2为定值，这个定值为－8.。

章末综合测评（一）（时间120分钟，满分160分）一、填空题(本大题共14小题,每小题5分，共70分,请把答案填写在题中横线上）1。

在直线回归方程y^＝错误!＋错误!x中,错误!表示________.①当x增加一个单位时,y增加错误!的数量;②当y增加一个单位时，x增加错误!的数量；③当x增加一个单位时，y的平均增加量;④当y增加一个单位时,x的平均增加量。

【答案】③2.线性回归方程错误!＝错误!x＋错误!所表示的直线必经过点________。

【答案】（错误!，错误!）3。

经调查某地若干户家庭的年收入x（万元）和年饮食支出y （万元）具有线性相关关系，并得到y关于x的线性回归直线方程:错误!＝0.254x＋0.321，由线性回归直线方程可知，家庭年收入每增加1万元,年饮食支出平均增加________万元。

【解析】∵y关于x的线性回归直线方程：错误!＝0.254x＋0。

321, ①∴年收入增加1万元时,年饮食支出错误!＝0。

254(x＋1）＋0。

321，②②—①可得：年饮食支出平均增加0。

254万元.【答案】0。

2544。

对于线性回归方程错误!＝错误!x＋错误!，下列说法中不正确的序号是________.①直线必经过点(错误!，错误!）；②x增加一个单位时,y平均增加错误!个单位；③样本数据中x＝0时,可能y＝错误!；④样本数据中x＝0时，一定有y＝错误!。

【解析】线性回归方程错误!＝错误!x＋错误!一定过点(错误!，错误!),故①正确；线性回归方程错误!＝错误!x＋错误!中,x增加一个单位时,y平均增加错误!个单位，故②正确;线性回归方程错误!＝错误!x＋错误!中，样本数据中x＝0时,可能有y＝错误!，也可能有y≠错误!，故③正确,④不正确.【答案】④5.已知x,y的取值如下表，如果y与x呈线性相关,且线性回归方程为错误!＝错误!x＋错误!,则错误!＝________.【解析】错误!错误!错误!又∵线性回归方程过样本中心点,且错误!＝错误!＝3，错误!＝错误!＝5,∴回归方程过点（3，5）,∴5＝3错误!＋错误!,∴错误!＝—错误!.【答案】—错误!6。

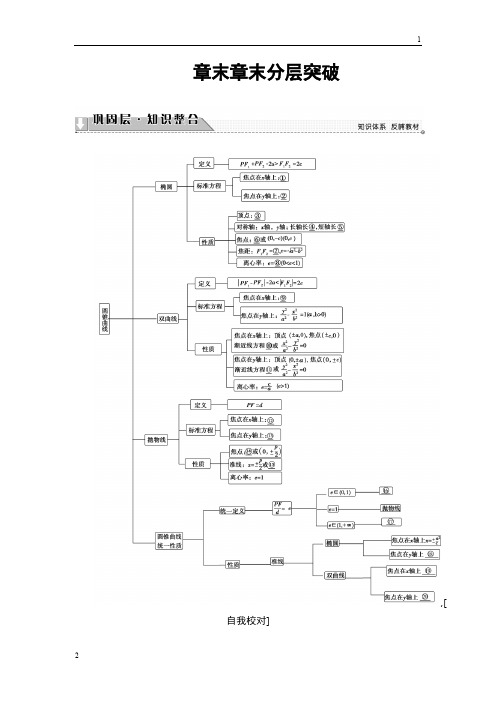
章末章末分层突破,[自我校对]①＋＝1(a >b >0) ②＋＝1(a >b >0) ③(±a,0)，(0，±b )或(0，±a )，x 2a 2y 2b 2y 2a 2x 2b 2(±b,0)④2a ⑤2b⑥(－c,0)，(c,0)⑦2c⑧⑨－＝1(a ，b >0)ca x 2a 2y 2b 2⑩y ＝±xb a ⑪y ＝±x ⑫y 2＝±2px (p >0) ⑬x 2＝±2py (p >0) ⑭(±，0) ⑮y ＝±ab p 2p2⑯椭圆 ⑰双曲线 ⑱y ＝± ⑲x ＝± ⑳y ＝±a 2c a 2c a 2c圆锥曲线的定义的应用圆锥曲线的定义在解题中有着重要作用，要注意灵活运用，可以优化解题过程，圆锥曲线的定义是相对应标准方程和几何性质的“源”，“回归定义”是一种重要的解题策略.运用定义解题主要体现在以下几个方面：(1)在求动点的轨迹方程时，如果动点所满足的几何条件符合某种圆锥曲线的定义，则可直接根据圆锥曲线的方程写出所求的动点的轨迹方程；(2)涉及椭圆或双曲线上的点与两个焦点构成的三角形问题，常常运用圆锥曲线的定义并结合三角形中的正、余弦定理来解决；(3)在求有关抛物线的最值问题时，常利用定义，把抛物线上某一点到焦点的距离转化为到准线的距离，并结合图形的几何意义去解决.　设F 1，F 2是椭圆＋＝1的两个焦点，P 是椭圆上的一x 29y 24点，若·＝0，且PF 1＞PF 2，求的值.PF 1→ PF 2→PF 1|PF 2|【精彩点拨】 ·＝0→PF 1F 2是直角三角形求出PF 1PF 1→ PF 2→――→椭圆的定义 与PF 2【规范解答】　由·＝0，知PF 1⊥PF 2，∴F 1F ＝PF ＋PF ，PF 1→ PF 2→ 2212由椭圆方程＋＝1，知a 2＝9，b 2＝4，x 29y 24∴c ＝＝，F 1F 2＝2.因此PF ＋PF ＝20.①9－455212又由椭圆定义，得PF 1＋PF 2＝6.②由题意知，PF 1＞PF 2，联立①、②得PF 1＝4，PF 2＝2.从而的值为2.PF 1PF 2[再练一题]1.已知双曲线的两个焦点F 1(－，0)，F 2(，0)，P 是双曲线上一点，且55· ＝0，PF 1·PF 2＝2，则双曲线的标准方程为________.PF 1→ PF 2→【解析】　由题意可设双曲线方程为－＝1(a >0，b >0).由· x 2a 2y 2b 2PF 1→ PF 2→ ＝0，得PF 1⊥PF 2.根据勾股定理得PF ＋PF ＝(2c )2，即PF ＋PF ＝20.212212根据双曲线定义有PF 1－PF 2＝2a .两边平方并代入PF 1·PF 2＝2得：20－2×2＝4a 2，解得a 2＝4，从而b 2＝5－4＝1，所以双曲线方程为－y 2＝1.x 24【答案】　－y 2＝1x 24圆锥曲线的方程与性质的应用1.本类问题主要有两种考查类型：(1)已知圆锥曲线的方程研究其几何性质，其中以求椭圆、双曲线的离心率为考查重点；(2)已知圆锥曲线的性质求其方程.2.对于求椭圆和双曲线的离心率，有两种方法：(1)代入法就是代入公式e＝求离心率；ca(2)列方程法就是根据已知条件列出关于a，b，c的关系式，然后把这个关系式整体转化为关于e的方程，解方程即可求出e值.3.求曲线方程的基本方法是待定系数法，其步骤可以概括为“先定位、后定量.”　已知双曲线－＝1(a>0，b>0)的两条渐近线与抛物线x2a2y2b2y2＝2px(p>0)的准线分别交于A，B两点，O为坐标原点.若双曲线的离心率为2，△AOB的面积为，则p＝________.3【精彩点拨】　双曲线的离心率为2→建立a，b的等量关系→求出A，B两点坐标求p――→S△AOB＝3【规范解答】　∵e＝2，∴b2＝3a2，双曲线的两条渐近线方程为y＝±x，3不妨设A＝，B，则AB＝p，又三角形的高为，则S△(－p2，3p2)(－p2，－3p2)3p2 AOB＝××p＝，即p2＝4，又p>0，∴p＝2.12p233【答案】　2[再练一题]2.(2016·徐州高二检测)已知椭圆C：＋＝1(a>b>0)的左焦点为F，C与x2a2y2b2过原点的直线相交于A ，B 两点，连接AF ，BF .若|AB |＝10，|AF |＝6，cos ∠ABF ＝，则C 的离心率e ＝________.45【解析】　在△ABF 中，由余弦定理得，cos ∠ABF ＝，∴BF 2－16BF ＋64＝0，∴BF ＝8，设右焦点为AB 2＋BF 2－AF |22AB ·BFF 1，因为直线过原点，∴BF 1＝AF ＝6，∴2a ＝BF ＋BF 1＝14，∴a ＝7，∵O 为Rt △ABF 斜边AB 的中点，∴OF ＝AB ＝5，∴c ＝5，∴e ＝.1257【答案】　57直线与圆锥曲线的位置关系1.判断直线与二次曲线的位置关系，可把直线方程与二次方程联立，消元后的一元二次方程的判别式大于零，则直线与圆锥曲线有两个交点；等于零，则只有一个交点；小于零，则没有交点.2.涉及直线与圆锥曲线的两个交点坐标问题时，一般不是求出这两个点的坐标，而是设出这两个点的坐标，根据直线方程和曲线方程联立消元后的方程根的情况，使用根与系数的关系进行整体代换，这种设而不求的思想是解析几何中处理直线和二次曲线相交问题的最基本的方法.　设椭圆＋＝1(a >b >0)的左焦点为F ，离心率为，过点x 2a 2y 2b 233F 且与x 轴垂直的直线被椭圆截得的线段长为.433(1)求椭圆的方程；(2)设A ，B 分别为椭圆的左、右顶点，过点F 且斜率为k 的直线与椭圆交于C ，D 两点，若·＋·＝8，求k 的值.AC → DB → AD → CB→ 【精彩点拨】　(1)利用过点F 且与x 轴垂直的直线方程，根据线段的长度求出交点的坐标并代入椭圆方程求出a 和b ，可得椭圆方程；(2)设出直线方程，和椭圆方程联立得到二次方程，利用韦达定理把向量式用点的坐标表示得到关于k 的方程，解方程可得k 的值.【规范解答】 (1)设F (－c,0)，由＝，知a ＝c .过点F 且与x 轴垂直ca 333的直线为x ＝－c ，代入椭圆方程有＋＝1，解得y ＝±，于是＝，解得b ＝－c 2a 2y 2b 26b326b3433.2又a 2－c 2＝b 2，从而a ＝，c ＝1，所以椭圆的方程为＋＝1.3x 23y 22(2)设点C (x 1，y 1)，D (x 2，y 2)，由F (－1,0)得直线CD 的方程为y ＝k (x ＋1)，由方程组Error!消去y ，整理得(2＋3k 2)x 2＋6k 2x ＋3k 2－6＝0.由根与系数的关系可得x 1＋x 2＝－，x 1x 2＝.因为A (－，0)，6k 22＋3k 23k 2－62＋3k 23B (，0)，3所以·＋·＝(x 1＋，y 1)·(－x 2，－y 2)AC → DB → AD → CB→ 33＋(x 2＋，y 2)·(－x 1，－y 1)33＝6－2x 1x 2－2y 1y 2＝6－2x 1x 2－2k 2(x 1＋1)(x 2＋1)＝6－(2＋2k 2)x 1x 2－2k 2(x 1＋x 2)－2k 2＝6＋.由已知得6＋＝8，解得k ＝±.2k 2＋122＋3k 22k 2＋122＋3k 22[再练一题]3.已知抛物线C ：y 2＝4x ，F 是抛物线C 的焦点，过点F 的直线l 与C 相交于A ，B 两点，O 为坐标原点.(1)如果l 的斜率为1，求以AB 为直径的圆的方程；(2)设FA ＝2BF ，求直线l 的方程.【解】　设A (x 1，y 1)，B (x 2，y 2).(1)∵y 2＝4x ，∴F (1,0)，又∵直线l 的斜率为1，∴直线l 的方程为y ＝x －1，代入y 2＝4x ，得x 2－6x ＋1＝0，由根与系数的关系得Error!，易得AB 的中点，即圆心的坐标为(3,2)，又AB ＝x 1＋x 2＋p ＝8，∴圆的半径r ＝4，∴所求的圆的方程为(x －3)2＋(y －2)2＝16.(2)∵FA ＝2BF ，∴＝2，而＝(x 1－1，y 1)，＝(1－x 2，－y 2)，FA → BF → FA → BF→ ∴Error!易知直线l 的斜率存在，设直线l 的斜率为k ，则直线l 的方程为y ＝k (x －1)，代入y 2＝4x ，得k 2x 2－(2k 2＋4)x ＋k 2＝0，由根与系数的关系得Error!∵x 1－1＝2(1－x 2)，∴Error!或Error!，∴k ＝±2，∴直线l 的方程为y ＝±2(x －1).22函数与方程思想圆锥曲线中的许多问题，若能运用函数与方程的思想去分析，则往往能较快地找到解题的突破口.用函数思想求解圆锥曲线中的有关定值、最值问题，最值问题可以说是高中数学中永恒的话题，在圆锥曲线问题中也不例外，而函数思想是解决最值问题最有利的武器.我们通常可用建立目标函数的方法解有关圆锥曲线的最值问题.方程思想是从分析问题的数量关系入手，通过联想与类比，将问题中的条件转化为方程或方程组，然后通过解方程或方程组使问题获解.方程思想是高中数学中的最基本、最重要的思想方法之一，在高考中占有非常重要的地位.在求圆锥曲线方程、直线与圆锥曲线的位置关系的问题中经常利用方程或方程组来解决.　点A 、B 分别是椭圆＋＝1长轴的左、右端点，点F 是x 236y 220椭圆的右焦点，点P 在椭圆上，且位于x 轴上方，PA ⊥PF .(1)求点P 的坐标；(2)设M 是椭圆长轴AB 上的一点，M 到直线AP 的距离等于MB ，求椭圆上的点到点M 的距离d 的最小值.【精彩点拨】　由PA ⊥PF 得P 点的轨迹方程→与椭圆方程联立，求P 点的坐标→由M 到直线AP 的距离等于MB 求出M 点坐标→将距离d 表示成关于椭圆上点的横坐标的函数，转化为函数最值.【规范解答】　(1)由已知可得点A (－6,0)，F (4,0).设点P (x ，y )，则k AP ·k PF ＝－1.由已知可得Error!则2x 2＋9x －18＝0.解得x ＝，或x ＝－6(舍去).32所以x ＝，由于y ＞0，故y ＝.所以点P 的坐标是.32532(32，532)(2)易知直线AP 的方程是x －y ＋6＝0.设点M (m,0)，则M 到直线AP 的距3离是.|m ＋6|2于是＝|m －6|.又－6≤m ≤6，解得m ＝2.椭圆上的点(x ，y )到点M 的|m ＋6|2距离的平方为：d 2＝(x －2)2＋y 2＝x 2－4x ＋4＋20－x 2＝2＋15.5949(x －92)由于－6≤x ≤6，所以当x ＝时，d 取得最小值.9215[再练一题]4.已知过抛物线y 2＝2px (p >0)的焦点，斜率为2的直线交抛物线于2A (x 1，y 1)，B (x 2，y 2)(x 1<x 2)两点，且AB ＝9.(1)求该抛物线的方程；(2)O 为坐标原点，C 为抛物线上一点，若＝＋λ，求λ的值.OC → OA → OB→ 【解】　(1)直线AB 的方程是y ＝2，与y 2＝2px 联立，从而有2(x －p2)4x 2－5px ＋p 2＝0，所以x 1＋x 2＝.5p4由抛物线定义得：AB ＝x 1＋x 2＋p ＝9，所以p ＝4，从而抛物线方程是y 2＝8x .(2)由p ＝4,4x 2－5px ＋p 2＝0可简化为x 2－5x ＋4＝0，从而x 1＝1，x 2＝4，y 1＝－2，y 2＝4，22从而A (1，－2)，B (4,4).22设＝(x 3，y 3)＝(1，－2)＋λ(4,4)＝(4λ＋1，4λ－2)，OC→ 2222又y ＝8x 3，即[2(2λ－1)]2＝8(4λ＋1)，即(2λ－1)2＝4λ＋1，解得λ＝0或232λ＝2.1.(2015·陕西高考改编)已知抛物线y 2＝2px (p ＞0)的准线经过点(－1,1)，则抛物线焦点坐标为________.【解析】　由抛物线y 2＝2px (p ＞0)得准线x ＝－，因为准线经过点(－1,1)，p2所以p ＝2，所以抛物线焦点坐标为(1,0).【答案】　(1,0)2.(2016·天津高考改编)已知双曲线－＝1(a >0，b >0)的焦距为2，且x 2a 2y 2b 25双曲线的一条渐近线与直线2x ＋y ＝0垂直，则双曲线的方程为________.【导学号：24830058】【解析】　由焦距为2得c ＝.因为双曲线的一条渐近线与直线552x ＋y ＝0垂直，所以＝.b a 12又c 2＝a 2＋b 2，解得a ＝2，b ＝1，所以双曲线的方程为－y 2＝1.x 24【答案】　－y 2＝1x 243.(2016·北京高考)已知双曲线－＝1(a ＞0，b ＞0)的一条渐近线为x 2a 2y 2b 22x ＋y ＝0，一个焦点为(，0)，则a ＝________，b ＝________.5【导学号：24830059】【解析】　因为双曲线－＝1(a ＞0，b ＞0)的一条渐近线为2x ＋y ＝0，x 2a 2y 2b 2即y ＝－2x ，所以＝2.①ba 又双曲线的一个焦点为(，0)，所以a 2＋b 2＝5.②5由①②得a ＝1，b ＝2.【答案】　1　24.(2015·福建高考改编)已知椭圆E ：＋＝1(a ＞b ＞0)的右焦点为F .短轴x 2a 2y 2b 2的一个端点为M ，直线l ：3x －4y ＝0交椭圆E 于A ，B 两点.若|AF |＋|BF |＝4，点M 到直线l 的距离不小于，则椭圆E 的离心率的取值范围是________.45【解析】　设左焦点为F 1，连接AF 1，BF 1.则四边形BF 1AF 是平行四边形，故|AF 1|＝|BF |，所以|AF |＋|AF 1|＝4＝2a ，所以a ＝2，设M (0，b )，则≥，故4b545b ≥1，从而a 2－c 2≥1,0＜c 2≤3,0＜c ≤，所以椭圆E 的离心率的取值范围是3.(0，32]【答案】　(0，32]5.(2016·全国甲卷)已知A 是椭圆E ：＋＝1的左顶点，斜率为k (k >0)的x 24y 23直线交E 于A ，M 两点，点N 在E 上，MA ⊥NA .(1)当|AM |＝|AN |时，求△AMN 的面积；(2)当2|AM |＝|AN |时，证明：<k <2.3【解】　(1)设M (x 1，y 1)，则由题意知y 1>0.由已知及椭圆的对称性知，直线AM 的倾斜角为.π4又A (－2,0)，因此直线AM 的方程为y ＝x ＋2.将x ＝y －2代入＋＝1得7y 2－12y ＝0.x 24y 23解得y ＝0或y ＝，所以y 1＝.127127因此△AMN 的面积S △AMN ＝2×××＝.1212712714449(2)证明：设直线AM 的方程为y ＝k (x ＋2)(k ＞0)，代入＋＝1得(3＋4k 2)x 2＋16k 2x ＋16k 2－12＝0.x 24y 23由x 1·(－2)＝得x 1＝，16k 2－123＋4k 22(3－4k 2)3＋4k 2故|AM |＝|x 1＋2|＝.1＋k 2121＋k 23＋4k 2由题意，设直线AN 的方程为y ＝－(x ＋2)，1k故同理可得|AN |＝.12k 1＋k 23k 2＋4由2|AM |＝|AN |得＝，23＋4k 2k3k 2＋4即4k 3－6k 2＋3k －8＝0.设f (t )＝4t 3－6t 2＋3t －8，则k 是f (t )的零点.f ′(t )＝12t 2－12t ＋3＝3(2t －1)2≥0，所以f (t )在(0，＋∞)单调递增.又f ()＝15－26＜0，f (2)＝6＞0，因此33f (t )在(0，＋∞)有唯一的零点，且零点k 在(，2)内，所以＜k ＜2.33章末综合测评(二)　圆锥曲线与方程(时间120分钟，满分160分)一、填空题(本大题共14小题，每小题5分，共70分.请把答案填写在题中横线上.)1.双曲线－＝1的两条渐近线的方程为________.x 216y 29【解析】　由双曲线方程可知a ＝4，b ＝3，所以两条渐近线方程为y ＝±x .34【答案】　y ＝±x342.(2015·上海高考)已知(2,0)是双曲线x 2－＝1(b ＞0)的一个焦点，则y 2b 2b ＝________.【解析】　由题意知c ＝2，a ＝1，b 2＝c 2－a 2＝3，所以b ＝.3【答案】33.若方程＋＝1表示椭圆，则k 的取值范围为________.x 25－k y 2k －3【解析】　由题意可知Error!解得3＜k ＜5且k ≠4.【答案】　(3,4)∪(4,5)4.以y ＝3为准线的抛物线的标准方程为________.【解析】　设抛物线的标准方程为x 2＝2py (p ＞0)，则－＝3，p ＝－6，则p2抛物线方程为x 2＝－12y .【答案】　x 2＝－12y5.(2015·上海高考)抛物线y 2＝2px (p ＞0)上的动点Q 到焦点的距离的最小值为1，则p ＝________.【解析】　依题意，点Q 为坐标原点，所以＝1，即p ＝2.p2【答案】　26.椭圆＋＝1的焦点为F 1，F 2，点P 在椭圆上，若PF 1＝4，则x 29y 22PF 2＝______，∠F 1PF 2的大小为______.【解析】　由椭圆的定义知PF 1＋PF 2＝2a ＝2×3＝6，因为PF 1＝4，所以PF 2＝2.在△PF 1F 2中，cos ∠F 1PF 2＝＝－，∴∠F 1PF 2＝120°.PF 21＋PF 2－F 1F 22PF 1PF 212【答案】　2　120°7.已知A (0，－1)、B (0,1)两点，△ABC 的周长为6，则△ABC 的顶点C 的轨迹方程是________.【解析】　∵2c ＝AB ＝2，∴c ＝1，∴CA ＋CB ＝6－2＝4＝2a ，∴顶点C 的轨迹是以A 、B 为焦点的椭圆(A 、B 、C 不共线).因此，顶点C 的轨迹方程＋y 24＝1(y ≠±2).x 23【答案】　＋＝1(y ≠±2)y 24x 238.(2015·天津高考改编)已知双曲线－＝1(a ＞0，b ＞0)的一个焦点为x 2a 2y 2b 2F (2,0)，且双曲线的渐近线与圆(x －2)2＋y 2＝3相切，则双曲线的方程为________.【导学号：24830061】【解析】　由双曲线的渐近线bx －ay ＝0与圆(x －2)2＋y 2＝3相切得＝，2ba 2＋b 23由c ＝＝2，解得a ＝1，b ＝.a 2＋b 23【答案】　x 2－＝1y 239.已知双曲线中心在原点且一个焦点为F 1(－，0)，点P 位于该双曲线上，5线段PF 1的中点坐标为(0,2)，则双曲线的方程是________.【解析】　∵F 1(－，0)，PF 1的中点坐标为(0,2)，∴P 的坐标为(，4).55又∵双曲线的一个焦点为F 1(－，0)，∴另一个焦点为F 2(，0).55∴2a ＝|PF 1－PF 2|＝－＝2.∴a ＝1.(5＋5)2＋16(5－5)2＋42又∵c ＝，∴b 2＝c 2－a 2＝4.∴双曲线方程为x 2－＝1.5y 24【答案】　x 2－＝1y 2410.已知抛物线C ：x 2＝y ，过点A (0，－1)和点B (t,3)的直线与抛物线C 没12有公共点，则实数t 的取值范围是________.【解析】　显然t ≠0，直线AB 的方程为y ＝x －1，代入抛物线方程得4t 2tx 2－4x ＋t ＝0.由题意Δ＝16－8t 2<0，解得t <－或t >.22【答案】　(－∞，－)∪(，＋∞)2211.若点O 和点F 分别为椭圆＋＝1的中心和左焦点，点P 为椭圆上的x 24y 23任意一点，则·的最大值为________.OP → FP→ 【解析】　椭圆的左焦点F 为(－1,0)，设P (x ，y )，·＝(x ，y )·(x ＋1，y )＝x (x ＋1)＋y 2＝x 2＋x ＋3＝(x ＋2)2＋2OP → FP→1414∵－2≤x ≤2，∴当x ＝2时，·有最大值6.OP → FP→ 【答案】　612.一动圆与两圆：x 2＋y 2＝1和x 2＋y 2－6x ＋5＝0都外切，则动圆圆心的轨迹为________.【解析】　x 2＋y 2＝1是以原点为圆心，半径为1的圆，x 2＋y 2－6x ＋5＝0化为标准方程为(x －3)2＋y 2＝4，是圆心为A (3,0)，半径为2的圆.设所求动圆圆心为P ，动圆半径为r ，如图，则Error!⇒PA －PO ＝1＜AO ＝3，符合双曲线的定义，结合图形可知，动圆圆心的轨迹为双曲线的一支.【答案】　双曲线的一支13.(2015·山东高考)过双曲线C ：－＝1(a >0，b >0)的右焦点作一条与其x 2a 2y 2a 2渐近线平行的直线，交C 于点P ，若点P 的横坐标为2a ，则C 的离心率为________.【解析】　先表示出直线的方程和点P 的坐标，再将点P 的坐标代入直线的方程可得关于a ，b ，c 的方程，化简可以求出离心率.如图所示，不妨设与渐近线平行的直线l 的斜率为，又直线l 过右焦点F (c,0)，则直线l 的方程为y ＝ba (x －c ).因为点P 的横坐标为2a ，代入双曲线方程得－＝1，化简得y ＝－ba 4a 2a 2y 2b 2b 或y ＝b (点P 在x 轴下方，故舍去)，故点P 的坐标为(2a ，－b )，代入333b ＝(2a －c )，化简可得离心率e ＝＝2＋.3ba ca 3【答案】　2314.已知直线y ＝k (x ＋2)(k >0)与抛物线C ：y 2＝8x 相交于A 、B 两点，F 为C 的焦点，若FA＝2FB ，则k ＝________.【解析】　过A 、B 作抛物线准线l 的垂线，垂足分别为A 1、B 1，由抛物线定义可知，AA 1＝AF ，BB 1＝BF ，又∵2FB ＝FA ，∴AA 1＝2BB 1，即B 为AC 的中点.从而y A ＝2y B ，联立方程组Error!⇒消去x 得y 2－y ＋16＝0，8k ∴Error!⇒Error!，消去y B 得k ＝.223【答案】　23二、解答题(本大题共6小题，共90分.解答时应写出文字说明、证明过程或演算步骤.)15.(本小题满分14分)已知抛物线C 1的顶点在坐标原点，它的焦点为双曲线C 2：－＝1(a >0，b >0)的一个焦点F ，若抛物线C 1与双曲线C 2的一个交x 2a 2y 2b 2点是M .(23，263)(1)求抛物线C 1的方程及其焦点F 的坐标；(2)求双曲线C 2的方程及离心率e .【解】　设抛物线C 1的方程为y 2＝2px (p ＞0)，因为图象过点M ，(23，263)则有2＝2p ×，所以p ＝2，则抛物线C 1的方程为y 2＝4x ，焦点F 的(263)23坐标为(1,0).(2)由双曲线C 2过点M 以及焦点为(1,0)和(－1,0)，由双曲线的定义(23，263)可知2a －＝，所以a ＝，b 2＝ ，(23＋1)2＋(263)2(23－1)2＋(263)2231389所以双曲线C 2的方程为9x 2－y 2＝1，离心率e ＝3.9816.(本小题满分14分)椭圆的中心在原点，焦点在坐标轴上，焦距为2.13一双曲线和该椭圆有公共焦点，且双曲线的半实轴长比椭圆的半长轴长小4，双曲线离心率与椭圆离心率之比为7∶3，求椭圆和双曲线的方程.【解】　①焦点在x 轴上，椭圆为＋＝1(a >b >0)，且c ＝.x 2a 2y 2b 213设双曲线为－ ＝1(m >0，n >0)，m ＝a －4.因为＝，所以＝，解x 2m 2y 2n 2e 双e 椭73am 73得a ＝7，m ＝3.，所以b 2＝36，n 2＝4.13所以椭圆方程为＋＝1，双曲线方程为－＝1.x 249y 236x 29y 24②焦点在y 轴上，椭圆方程为＋＝1，双曲线方程为－＝1.x 236y 249y 29x 2417.(本小题满分14分)如图1所示，已知斜率为1的直线l 过椭圆＋y 2＝1的右焦点F ，交椭圆于A 、B 两点，求弦AB 的长.x 24图1【解】　设A 、B 两点的坐标分别为A (x 1，y 1)、B (x 2，y 2)，由椭圆方程知a 2＝4，b 2＝1，c 2＝3，所以F (，0)，直线l 的方程为y ＝x －.将其代入33x 2＋4y 2＝4，化简整理，得5x 2－8x ＋8＝0.所以x 1＋x 2＝，x 1x 2＝.383585所以AB ＝|x 1－x 2| ＝·＝×1＋k 21＋k 2(x 1＋x 2)2－4x 1x 22＝.(83)2－4×5×858518.(本小题满分16分)如图2，已知椭圆＋＝1(a ＞b ＞0)的离心率为，x 2a 2y 2b 222以该椭圆上的点和椭圆的左、右焦点F 1、F 2为顶点的三角形的周长为4(＋1)，2一等轴双曲线的顶点是该椭圆的焦点，设P 为该双曲线上异于顶点的任意一点，直线PF 1和PF 2与椭圆的交点分别为A 、B 和C 、D .图2(1)求椭圆和双曲线的标准方程；(2)设直线PF 1、PF 2的斜率分别为k 1、k 2，求证：k 1k 2＝1.【解】 (1)设椭圆的半焦距为c ，由题意知，＝，2a ＋2c ＝4(＋1)，ca 222所以a ＝2，c ＝2.2又a 2＝b 2＋c 2，因此b ＝2.故椭圆的标准方程为＋＝1.x 28y 24由题意设等轴双曲线的标准方程为－＝1(m ＞0)，因为等轴双曲线的x 2m 2y 2m 2顶点是椭圆的焦点，所以m ＝2，因此双曲线的标准方程为－＝1.x 24y 24(2)证明：设P (x 0，y 0)，则k 1＝，k 2＝.y 0x 0＋2y 0x 0－2因为点P 在双曲线x 2－y 2＝4上，所以x －y ＝4.2020因此k 1k 2＝·＝＝1，即k 1k 2＝1.y 0x 0＋2y 0x 0－2y 20x 20－419.(本小题满分16分)已知直线y ＝－x ＋2和椭圆＋＝1(a ＞b ＞0)相交12x 2a 2y 2b 2于A ，B 两点，M 为AB 的中点，若AB ＝2，直线OM 的斜率为(O 为坐标原512点)，求椭圆的方程.【解】　由Error!消去y ，整理得(a 2＋4b 2)x 2－8a 2x ＋16a 2－4a 2b 2＝0.设A (x 1，y 1)，B (x 2，y 2)，则由根与系数的关系，得x 1＋x 2＝，x 1x 2＝.8a 2a 2＋4b 216a 2－4a 2b 2a 2＋4b 2又设AB 的中点M (x M ，y M )，则x M ＝＝，y M ＝－x M ＋2＝x 1＋x 224a 2a 2＋4b 212.8b 2a 2＋4b 2∵直线OM 的斜率k OM ＝＝，∴＝，∴a 2＝4b 2，yM xM 122b 2a 212从而x 1＋x 2＝＝4，x 1x 2＝＝8－2b 2.8a 2a 2＋4b 216a 2－4a 2b 2a 2＋4b 2又∵AB ＝2，∴ ·＝2，即51＋14(x 1＋x 2)2－4x 1x 25×＝2，5216－4(8－2b )25解得b 2＝4，∴a 2＝4b 2＝16，故所求椭圆的方程为＋＝1.x 216y 2420.(本小题满分16分)(2016·盐城高二检测)设椭圆＋＝1(a >b >0)的左、x 2a 2y 2b 2右焦点分别为F 1，F 2，右顶点为A ，上顶点为B .已知AB ＝F 1F 2.32(1)求椭圆的离心率.(2)设P 为椭圆上异于其顶点的一点，以线段PB 为直径的圆经过点F 1，经过点F 2的直线l 与该圆相切于点M ，MF 2＝2.求椭圆的方程.2【解】　(1)设椭圆右焦点F 2的坐标为(c,0)，由AB ＝F 1F 2，可得32a 2＋b 2＝3c 2，又b 2＝a 2－c 2，则＝.所以椭圆的离心率e ＝.c 2a 21222(2)由(1)知a 2＝2c 2，b 2＝c 2，故椭圆方程为＋＝1.x 22c 2y 2c 2设P (x 0，y 0)，由F 1(－c,0)，B (0，c )，有＝(x 0＋c ，y 0)，＝(c ，c )，F 1P → F 1B→ 由已知，有·＝0，即(x 0＋c )c ＋y 0c ＝0.F 1P → F 1B→ 又c ≠0，故有x 0＋y 0＋c ＝0.①因为点P 在椭圆上，故＋＝1.②x 202c 2y 20c 2由①和②可得3x ＋4cx 0＝0，而点P 不是椭圆的顶点，故x 0＝－，代入204c312①得y 0＝，即点P 的坐标为.设圆的圆心为T (x 1，y 1)，则c 3(－4c 3，c 3)x 1＝＝－c ，y 1＝＝c ，－4c 3＋0223c 3＋c 223进而圆的半径r ＝＝c .由已知，有TF ＝MF ＋r 2，(x 1－0)2＋(y 1－c )25322又MF 2＝2，2故有2＋2＝8＋c 2.解得c 2＝3.所以所求椭圆的方程为(c ＋2c 3)(0－2c 3)59＋＝1.x 26y 23。

章末总结知识点一合情推理归纳和类比是常用的合情推理，都是根据已有的事实，经过观察、分析、比较、联想，再进行归纳类比，然后提出猜想的推理，从推理形式上看，归纳是由部分到整体，个别到一般的推理，类比是由特殊到特殊的推理．例1在平面上有n条直线，任何两条都不平行，并且任何三条都不交于同一点，问这些直线把平面分成多少部分？例2如图所示，在△ABC中，射影定理可表示为a＝b·cos C＋c·cos B，其中a，b，c 分别为角A，B，C的对边，类比上述定理，写出对空间四面体性质的猜想．知识点二 演绎推理合情推理的结论不一定正确，有待进一步证明；演绎推理在前提和推理形式都正确的前提下，得到的结论一定正确．从二者在认识事物的过程中所发挥作用的角度考虑，它们又是紧密联系，相辅相成的．合情推理的结论需要演绎推理的验证，而演绎推理的内容一般是通过合情推理获得，合情推理可以为演绎推理提供方向和思路．演绎推理的一般模式是“三段论”．例3 已知函数f (x )＝ax ＋bx ，其中a >0，b >0，x ∈(0，＋∞)，确定f (x )的单调区间，并证明在每个单调区间上的增减性．知识点三 综合法与分析法综合法和分析法是直接证明中的两种最基本的证明方法，但两种证明方法思路截然相反，分析法既可用于寻找解题思路，也可以是完整的证明过程，分析法和综合法可相互转换，相互渗透，充分利用这一辩证关系，在解题中综合法和分析法联合运用，转换解题思路，增加解题途径．例4 已知a ，b ，c 均为正实数，且a ＋b ＋c ＝1， 求证：⎝⎛⎭⎫1a －1⎝⎛⎭⎫1b －1⎝⎛⎭⎫1c －1≥8.知识点四 反证法反证法是间接证明的一种基本方法，它不去直接证明结论，而是先否定结论，在否定结论的基础上，运用正确的推理，导出矛盾，从而肯定结论的真实性．在证明一些否定性命题、唯一性命题或含有“至多”、“至少”等字句的命题时，正面证明较难，可考虑反证法，即“正难则反”．例5 已知a ，b ，c ∈(0,1)．求证：(1－a )b ，(1－b )c ，(1－c )a 不可能都大于14.例6 如图所示，已知两直线l ∩m ＝O ，l ⊂α，m ⊂α，l ⊄β，m ⊄β，α∩β＝a .求证：l 与m 中至少有一条与β相交．章末总结 答案重点解读例1 解 设n 条直线分平面为S n 部分，先实验观察特例有如下结果：n 与S n n n －1n n －1这是因为在n －1条直线后添加第n 条直线被原(n －1)条直线截得的n 段中的任何一段都将它所在的原平面一分为二，相应地增加n 部分，所以S n ＝S n －1＋n ，即S n －S n －1＝n .从而S 2－S 1＝2，S 3－S 2＝3，S 4－S 3＝4，…，S n －S n －1＝n . 将上面各式相加有S n －S 1＝2＋3＋…＋n ， ∴S n ＝S 1＋2＋3＋…＋n ＝2＋2＋3＋…＋n ＝1＋n (n ＋1)2.例2 解如图所示，在四面体P —ABC 中，设S 1，S 2，S 3，S 分别表示△P AB ，△PBC ，△PCA ，△ABC 的面积，α，β，γ依次表示面P AB ，面PBC ，面PCA 与底面ABC 所成二面角的大小．我们猜想射影定理类比推理到三维空间， 其形式应为：S ＝S 1·cos α＋S 2·cos β＋S 3·cos γ. 例3 解 f (x )的单调区间为⎝⎛⎦⎤0，a b 和⎣⎡⎭⎫a b ，＋∞，证明如下：设0<x 1<x 2，则 f (x 1)－f (x 2)＝⎝⎛⎭⎫a x 1＋bx 1－⎝⎛⎭⎫ax 2＋bx 2 ＝(x 2－x 1)⎝⎛⎭⎫a x 1x 2－b . 当0<x 1<x 2≤ab时， 则x 2－x 1>0,0<x 1x 2<a b ，ax 1x 2>b ，∴f (x 1)－f (x 2)>0，即f (x 1)>f (x 2)， ∴f (x )在⎝⎛⎦⎤0，a b 上是减函数． 当x 2>x 1≥ab时， 则x 2－x 1>0，x 1x 2>a b ，ax 1x 2<b ，∴f (x 1)－f (x 2)<0，即f (x 1)<f (x 2)， ∴f (x )在⎣⎡⎭⎫a b ，＋∞上是增函数． 例4 证明 方法一 (综合法)⎝⎛⎭⎫1a －1⎝⎛⎭⎫1b －1⎝⎛⎭⎫1c －1＝⎝⎛⎭⎫a ＋b ＋c a －1·⎝⎛⎭⎫a ＋b ＋c b －1·⎝⎛⎭⎫a ＋b ＋c c －1 ＝b ＋c a ·a ＋c b ·a ＋b c ＝(b ＋c )(a ＋c )(a ＋b )abc ≥2bc ·2ac ·2ababc＝8，当且仅当a ＝b ＝c 时等号成立，所以不等式成立． 方法二 (分析法)要证⎝⎛⎭⎫1a －1⎝⎛⎭⎫1b －1⎝⎛⎭⎫1c －1≥8成立， 只需证1－a a ·1－b b ·1－c c ≥8成立．因为a ＋b ＋c ＝1，所以只需证(a ＋b ＋c )－a a ·(a ＋b ＋c )－b b ·(a ＋b ＋c )－cc ≥8成立．即b ＋c a ·a ＋c b ·a ＋bc≥8. 只需证b ＋c a ·a ＋c b ·a ＋b c ≥2bc a ·2ac b ·2ab c ≥8成立，而2bc a ·2ac b ·2ab c≥8显然成立， 故⎝⎛⎭⎫1a －1⎝⎛⎭⎫1b －1⎝⎛⎭⎫1c －1≥8成立． 例5 证明 假设三个式子同时大于14，即(1－a )b >14，(1－b )c >14，(1－c )a >14，三式相乘得：(1－a )·a ·(1－b )·b ·(1－c )·c >143，①又因为0<a <1， ∴0<a (1－a )≤⎝⎛⎭⎫a ＋1－a 22＝14，同理0<b (1－b )≤14，0<c (1－c )≤14，所以(1－a)a·(1－b)b·(1－c)c≤143，②①与②矛盾，所以假设不成立，故原命题成立．例6证明假设l，m都不与β相交，∵l⊄β，m⊄β，∴l∥β且m∥β.又∵l⊂α，m⊂α，α∩β＝a，∴l∥a，m∥a，∴l∥m.这与已知l、m是相交直线矛盾．因此l和m至少有一条与β相交．。

第2章 推理与证明(B)(时间：120分钟 满分：160分)一、填空题(本大题共14小题，每小题5分，共70分)1．由代数式的乘法法则类比推导向量的数量积的运算法则：①“mn ＝nm ”类比得到“a ·b ＝b ·a ”；②“(m ＋n )t ＝mt ＋nt ”类比得到“(a ＋b )·c ＝a ·c ＋b ·c ”；③“(m ·n )t ＝m (n ·t )”类比得到“(a ·b )·c ＝a ·(b ·c )”；④“t ≠0，mt ＝xt ⇒m ＝x ”类比得到“p ≠0，a ·p ＝x ·p ⇒a ＝x ”；⑤“|m ·n |＝|m |·|n |”类比得到“|a ·b |＝|a |·|b |”；⑥“ac bc ＝a b ”类比得到“a ·c b ·c ＝a b”． 以上的式子中，类比得到的结论正确的个数是________．2．数列1,1,2,3，x,8,13,21，…中的x 值为________．3．若数列{a n }中，a 1＝1，a 2＝3＋5，a 3＝7＋9＋11，a 4＝13＋15＋17＋19，…，则a 8＝________.4．p ＝ab ＋cd ，q ＝ma ＋nc ·b m ＋d n(m 、n 、a 、b 、c 、d 均为正数)，则p 、q 的大小关系为________．5．凡自然数是整数，4是自然数，所以4是整数．对以上三段论推理下列说法正确的是__________(请填写相应的序号)．①正确；②推理形式不正确；③两个“自然数”概念不一致；④“两个整数”概念不一致．6．观察下列等式：C 15＋C 55＝23－2， C 19＋C 59＋C 99＝27＋23， C 113＋C 513＋C 913＋C 1313＝211－25，C 117＋C 517＋C 917＋C 1317＋C 1717＝215＋27， …由以上等式推测到一个一般的结论：对于n ∈N *，C 14n ＋1＋C 54n ＋1＋C 94n ＋1＋…＋C 4n ＋14n ＋1＝______________.7．对于等差数列{a n }有如下命题：“若{a n }是等差数列，a 1＝0，s 、t 是互不相等的正整数，则有(s －1)a t ＝(t －1)a s ”．类比此命题，给出等比数列{b n }相应的一个正确命题是：“__________________________________________”．8．设f (x )是定义在实数集R 上的函数，且满足f (x ＋2)＝f (x ＋1)－f (x )，如果f (1)＝lg 32，f (2)＝lg 15，则f (2 010)＝__________.9．将杨辉三角中的奇数换成1，偶数换成0，得到如图所示的0～1三角数表．从上往下数，第1次全行的数都为1的是第1行，第2次全行的数都为1的是第3行，…，第n 次全行的数都为1的是第________行；第61行中1的个数是________．第1行 1 1第2行1 0 1第3行1 1 1 1第4行1 0 0 0 1第5行1 1 0 0 1 1…………10．某同学准备用反证法证明如下一个问题：函数f (x )在[0,1]上有意义，且f (0)＝f (1)，如果对于不同的x 1，x 2∈[0,1]，都有|f (x 1)－f (x 2)|<|x 1－x 2|，求证：|f (x 1)－f (x 2)|<12.那么它的反设应该是______________________________．11．凸函数的性质定理为：如果函数f (x )在区间D 上是凸函数，则对于区间D 内的任意x 1，x 2，…，x n ，有f (x 1)＋f (x 2)＋…＋f (x n )n ≤f ⎝⎛⎭⎫x 1＋x 2＋…＋x n n ，已知函数y ＝sin x 在区间(0，π)上是凸函数，则在△ABC 中，sin A ＋sin B ＋sin C 的最大值为_________________________．12．若不等式(－1)n a <2＋(－1)n ＋1n对任意正整数n 恒成立，则实数a 的取值范围是________． 13．由“等腰三角形的两底角相等，两腰相等”可以类比推出正棱锥的类似属性是__________________________________________________．14．船在流水中在甲地和乙地间来回行驶一次的平均速度v 1和在静水中的速度v 2的大小关系为_____________________________________________________________________．二、解答题(本大题共6小题，共90分)15．(14分)已知a 、b 、c 是互不相等的正数，且abc ＝1， 求证：a ＋b ＋c <1a ＋1b ＋1c.16．(14分)把下面在平面内成立的结论类比地推广到空间，并判断类比的结论是否成立．(1)如果一条直线和两条平行线中的一条相交，则必和另一条相交；(2)如果两条直线同时垂直于第三条直线，则这两条直线互相平行．17．(14分)已知a >0，求证： a 2＋1a 2－2≥a ＋1a－2.18．(16分)在不等边△ABC 中，A 是最小角，求证：A <60°.19．(16分)先解答(1)，再通过类比解答(2)．(1)求证：tan ⎝⎛⎭⎫x ＋π4＝1＋tan x 1－tan x ；(2)设x ∈R 且f (x ＋1)＝1＋f (x )1－f (x )，试问f (x )是周期函数吗？证明你的结论．20．(16分)等差数列{a n }的前n 项和为S n ，a 1＝1＋2，S 3＝9＋3 2.(1)求数列{a n }的通项a n 与前n 项和S n ；(2)设b n ＝S n n(n ∈N *)，求证：数列{b n }中任意不同的三项都不可能成为等比数列．第2章 推理与证明(B)答案1．2解析 只有①②对，其余错误．2．5解析 每相邻两数相加等于后面的数．3．512解析 由a 1，a 2，a 3，a 4的形式可归纳，∵1＋2＋3＋4＋…＋7＝7×(1＋7)2＝28， ∴a 8的首项应为第29个正奇数，即2×29－1＝57.∴a 8＝57＋59＋61＋63＋65＋67＋69＋71＝8×(57＋71)2＝512. 4．p ≤q 解析 q ＝ab ＋mad n ＋nbc m＋cd ≥ab ＋2abcd ＋cd ＝ab ＋cd ＝p .5．①解析 三段论中的大前提、小前提及推理形式都是正确的．6．24n －1＋(－1)n 22n －17．若{b n }是等比数列，b 1＝1，s ，t 是互不相等的正整数，则有b s －1t ＝b t －1s解析 由类比推理可得．8．－1解析 由f (1)＝lg 32＝lg 15－1，f (2)＝lg 15， f (3)＝f (2)－f (1)＝1，f (4)＝f (3)－f (2)＝1－lg 15，f (5)＝f (4)－f (3)＝－lg 15，f (6)＝f (5)－f (4)＝－1，f (7)＝f (6)－f (5)＝lg 15－1，f (8)＝f (7)－f (6)＝lg 15，…，可以猜想到，从f (7)开始，又重复了上述数值，即f (x ＋6)＝f (x )，∴f (2 010)＝f (335×6)＝f (6)＝－1.9．2n －1 32解析 (1)第一次全行的数都是1的是第1行，第二次全行的数都是1的是第3行，第三次全行的数都是1的是第7行，第n 次全行的数都是1的是第2n －1行．(2)1 1 0 0 ... 0 0 1 1 (61)1 0 1 0 ... 0 1 0 1 (62)1 1 1 1 ... 1 1 1 1 (63)由图可知第61行的数的特点是两个1两个0交替出现，最后两个数为1，所以在第61行的62个数中有32个1.10．“∃x 1，x 2∈[0,1]，使得|f (x 1)－f (x 2)|<|x 1－x 2|且|f (x 1)－f (x 2)|≥12” 11．332解析 ∵f (x )＝sin x 在区间(0，π)上是凸函数，且A 、B 、C ∈(0，π)，∴f (A )＋f (B )＋f (C )3≤f ⎝ ⎛⎭⎪⎫A ＋B ＋C 3＝f ⎝⎛⎭⎫π3， 即sin A ＋sin B ＋sin C ≤3sin π3＝332， 所以sin A ＋sin B ＋sin C 的最大值为332. 12．－2≤a <32解析 当n 为偶数时，a <2－1n， 而2－1n ≥2－12＝32，∴a <32. 当n 为奇数时，a >－2－1n， 而－2－1n<－2，∴a ≥－2. 综上可得－2≤a <32. 13．正棱锥各侧面与底面所成二面角相等，各侧面都是全等的三角形或各侧棱相等 解析 等腰三角形的底与腰可分别与正棱锥的底面与侧面类比．14．v 1<v 2解析 设甲地到乙地的距离为S ，船在静水中的速度为v 2，水流速度为v (v 2>v >0)，则船在流水中在甲、乙间来回行驶一次的时间t ＝S v 2＋v ＋S v 2－v ＝2v 2S v 22－v2，平均速度v 1＝2S t ＝v 22－v 2v 2.∵v 1－v 2＝v 22－v 2v 2－v 2＝－v 2v 2<0， ∴v 1<v 2.15．证明 ∵a 、b 、c 是不等正数，且abc ＝1， ∴a ＋b ＋c ＝1bc ＋1ca ＋1ab<1b ＋1c 2＋1c ＋1a 2＋1a ＋1b 2＝1a ＋1b ＋1c . 故a ＋b ＋c <1a ＋1b ＋1c. 16．解 (1)类比为：如果一个平面和两个平行平面中的一个相交，则必和另一个相交． 结论是正确的：证明如下：设α∥β，且γ∩α＝a ，则必有γ∩β＝b ，若γ与β不相交，则必有γ∥β，又α∥β，∴α∥γ，与γ∩α＝a 矛盾，∴必有γ∩β＝b .(2)类比为：如果两个平面同时垂直于第三个平面，则这两个平面互相平行，结论是错误的，这两个平面也可能相交．17．证明 要证a 2＋1a 2－2≥a ＋1a －2， 只要证a 2＋1a 2＋2≥a ＋1a＋ 2. ∵a >0，故只要证⎝⎛⎭⎫a 2＋1a 2＋22≥⎝⎛⎭⎫a ＋1a＋22， 即a 2＋1a 2＋4a 2＋1a2＋4 ≥a 2＋2＋1a2＋22⎝⎛⎭⎫a ＋1a ＋2， 从而只要证2a 2＋1a2≥2⎝⎛⎭⎫a ＋1a ， 只要证4⎝⎛⎭⎫a 2＋1a 2≥2⎝⎛⎭⎫a 2＋2＋1a 2， 即a 2＋1a 2≥2， 而上述不等式显然成立，故原不等式成立．18．证明 假设A ≥60°，∵A 是不等边三角形ABC 的最小角，∵B >A ≥60°，C >A ≥60°， ∴A ＋B ＋C >180°，与三角形内角和等于180°矛盾，∴假设错误，原结论成立，即A <60°.19．(1)证明 tan ⎝⎛⎭⎫x ＋π4＝tan x ＋tan π41－tan x tan π4＝1＋tan x 1－tan x； (2)解 f (x )是以4为一个周期的周期函数．证明如下：∵f (x ＋2)＝f ((x ＋1)＋1)＝1＋f (x ＋1)1－f (x ＋1)＝1＋1＋f (x )1－f (x )1－1＋f (x )1－f (x )＝－1f (x )， ∴f (x ＋4)＝f ((x ＋2)＋2)＝－1f (x ＋2)＝f (x )， ∴f (x )是周期函数．20．(1)解 由已知得⎩⎪⎨⎪⎧a 1＝2＋1，3a 1＋3d ＝9＋32， ∴d ＝2，故a n ＝2n －1＋2，S n ＝n (n ＋2)．(2)证明 由(1)得b n ＝S n n＝n ＋ 2. 假设数列{b n }中存在三项b p 、b q 、b r (p 、q 、r ∈N *且互不相等)成等比数列，则b 2q ＝b p b r ， 即(q ＋2)2＝(p ＋2)(r ＋2)，∴(q 2－pr )＋2(2q －p －r )＝0. ∵p 、q 、r ∈N *，∴⎩⎪⎨⎪⎧ q 2－pr ＝0，2q －p －r ＝0， ∴⎝ ⎛⎭⎪⎫p ＋r 22＝pr ，(p －r )2＝0， ∴p ＝r ，这与p ≠r 矛盾．∴数列{b n }中任意不同的三项都不可能成为等比数列．。

章末综合测评(二) 圆锥曲线与方程(时间120分钟，满分160分)一、填空题(本大题共14小题，每小题5分，共70分.请把答案填写在题中横线上.)1.双曲线x 216－y 29＝1的两条渐近线的方程为________.【解析】 由双曲线方程可知a ＝4，b ＝3，所以两条渐近线方程为y ＝±34x . 【答案】 y ＝±34x2.(2015·上海高考)已知(2,0)是双曲线x 2－y 2b 2＝1(b ＞0)的一个焦点，则b ＝________.【解析】 由题意知c ＝2，a ＝1，b 2＝c 2－a 2＝3，所以b ＝ 3. 【答案】33.若方程x 25－k ＋y 2k －3＝1表示椭圆，则k 的取值范围为________.【解析】由题意可知⎩⎪⎨⎪⎧5－k ＞0，k －3＞0，5－k ≠k －3，解得3＜k ＜5且k ≠4.【答案】 (3,4)∪(4,5)4.以y ＝3为准线的抛物线的标准方程为________.【解析】 设抛物线的标准方程为x 2＝2py (p ＞0)，则－p2＝3，p ＝－6，则抛物线方程为x 2＝－12y .【答案】 x 2＝－12y5.(2015·上海高考)抛物线y 2＝2px (p ＞0)上的动点Q 到焦点的距离的最小值为1，则p ＝________.【解析】 依题意，点Q 为坐标原点，所以p2＝1，即p ＝2.【答案】 26.椭圆x 29＋y 22＝1的焦点为F 1，F 2，点P 在椭圆上，若PF 1＝4，则PF 2＝______，∠F 1PF 2的大小为______.【解析】 由椭圆的定义知PF 1＋PF 2＝2a ＝2×3＝6，因为PF 1＝4，所以PF 2＝2.在△PF 1F 2中，cos ∠F 1PF 2＝PF 21＋PF 22－F 1F 222PF 1PF 2＝－12，∴∠F 1PF 2＝120°.【答案】 2 120°7.已知A (0，－1)、B (0,1)两点，△ABC 的周长为6，则△ABC 的顶点C 的轨迹方程是________.【解析】 ∵2c ＝AB ＝2，∴c ＝1，∴CA ＋CB ＝6－2＝4＝2a ，∴顶点C 的轨迹是以A 、B 为焦点的椭圆(A 、B 、C 不共线).因此，顶点C 的轨迹方程y 24＋x 23＝1(y ≠±2).【答案】 y 24＋x 23＝1(y ≠±2)8.(2015·天津高考改编)已知双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的一个焦点为F (2,0)，且双曲线的渐近线与圆(x －2)2＋y 2＝3相切，则双曲线的方程为________.【导学号：24830061】【解析】 由双曲线的渐近线bx －ay ＝0与圆(x －2)2＋y 2＝3相切得2b a 2＋b 2＝3，由c ＝a 2＋b 2＝2，解得a ＝1，b ＝ 3.【答案】 x 2－y 23＝19.已知双曲线中心在原点且一个焦点为F 1(－5，0)，点P 位于该双曲线上，线段PF 1的中点坐标为(0,2)，则双曲线的方程是________.【解析】 ∵F 1(－5，0)，PF 1的中点坐标为(0,2)，∴P 的坐标为(5，4). 又∵双曲线的一个焦点为F 1(－5，0)，∴另一个焦点为F 2(5，0).∴2a ＝|PF 1－PF 2|＝(5＋5)2＋16－(5－5)2＋42＝2.∴a ＝1.又∵c ＝5，∴b 2＝c 2－a 2＝4.∴双曲线方程为x 2－y 24＝1. 【答案】 x 2－y 24＝110.已知抛物线C ：x 2＝12y ，过点A (0，－1)和点B (t,3)的直线与抛物线C 没有公共点，则实数t 的取值范围是________.【解析】 显然t ≠0，直线AB 的方程为y ＝4t x －1，代入抛物线方程得2tx 2－4x ＋t ＝0.由题意Δ＝16－8t 2<0，解得t <－2或t > 2. 【答案】 (－∞，－2)∪(2，＋∞)11.若点O 和点F 分别为椭圆x 24＋y 23＝1的中心和左焦点，点P 为椭圆上的任意一点，则OP →·FP →的最大值为________.【解析】 椭圆的左焦点F 为(－1,0)，设P (x ，y )，OP →·FP →＝(x ，y )·(x ＋1，y )＝x (x ＋1)＋y 2＝14x 2＋x ＋3＝14(x ＋2)2＋2 ∵－2≤x ≤2，∴当x ＝2时，OP →·FP →有最大值6. 【答案】 612.一动圆与两圆：x 2＋y 2＝1和x 2＋y 2－6x ＋5＝0都外切，则动圆圆心的轨迹为________.【解析】 x 2＋y 2＝1是以原点为圆心，半径为1的圆，x 2＋y 2－6x ＋5＝0化为标准方程为(x －3)2＋y 2＝4，是圆心为A (3,0)，半径为2的圆.设所求动圆圆心为P ，动圆半径为r ，如图，则⎭⎪⎬⎪⎫PO ＝r ＋1P A ＝r ＋2⇒P A －PO ＝1＜AO ＝3，符合双曲线的定义，结合图形可知，动圆圆心的轨迹为双曲线的一支. 【答案】 双曲线的一支13.(2015·山东高考)过双曲线C ：x 2a 2－y 2a 2＝1(a >0，b >0)的右焦点作一条与其渐近线平行的直线，交C 于点P ，若点P 的横坐标为2a ，则C 的离心率为________.【解析】 先表示出直线的方程和点P 的坐标，再将点P 的坐标代入直线的方程可得关于a ，b ，c 的方程，化简可以求出离心率.如图所示，不妨设与渐近线平行的直线l 的斜率为b a ，又直线l 过右焦点F (c,0)，则直线l 的方程为y ＝b a (x －c ).因为点P 的横坐标为2a ，代入双曲线方程得4a 2a 2－y 2b 2＝1，化简得y ＝－3b 或y ＝3b (点P 在x 轴下方，故舍去)，故点P 的坐标为(2a ，－3b )，代入直线方程得－3b ＝b a (2a －c )，化简可得离心率e ＝ca ＝2＋ 3.【答案】 2＋ 314.已知直线y ＝k (x ＋2)(k >0)与抛物线C ：y 2＝8x 相交于A 、B 两点，F 为C 的焦点，若F A ＝2FB ，则k ＝________.【解析】 过A 、B 作抛物线准线l 的垂线，垂足分别为A 1、B 1，由抛物线定义可知，AA 1＝AF ，BB 1＝BF ，又∵2FB ＝F A ，∴AA 1＝2BB 1，即B 为AC 的中点.从而y A ＝2y B ，联立方程组⎩⎪⎨⎪⎧y ＝k (x ＋2)，y 2＝8x ，⇒消去x 得y 2－8k y ＋16＝0，∴⎩⎨⎧y A ＋y B ＝8k ，y A ·y B ＝16⇒⎩⎨⎧3y B ＝8k ，2y 2B ＝16，，消去y B 得k ＝223.【答案】223二、解答题(本大题共6小题，共90分.解答时应写出文字说明、证明过程或演算步骤.)15.(本小题满分14分)已知抛物线C 1的顶点在坐标原点，它的焦点为双曲线C 2：x 2a 2－y 2b 2＝1(a >0，b >0)的一个焦点F ，若抛物线C 1与双曲线C 2的一个交点是M ⎝ ⎛⎭⎪⎫23，263. (1)求抛物线C 1的方程及其焦点F 的坐标； (2)求双曲线C 2的方程及离心率e .【解】 设抛物线C 1的方程为y 2＝2px (p ＞0)，因为图象过点M ⎝ ⎛⎭⎪⎫23，263， 则有⎝⎛⎭⎪⎫2632＝2p ×23，所以p ＝2，则抛物线C 1的方程为y 2＝4x ，焦点F 的坐标为(1,0).(2)由双曲线C 2过点M ⎝ ⎛⎭⎪⎫23，263以及焦点为(1,0)和(－1,0)，由双曲线的定义可知2a ＝⎝ ⎛⎭⎪⎫23＋12＋⎝ ⎛⎭⎪⎫2632－⎝ ⎛⎭⎪⎫23－12＋⎝ ⎛⎭⎪⎫2632＝23，所以a ＝13，b 2＝89 ，所以双曲线C 2的方程为9x 2－98y 2＝1，离心率e ＝3.16.(本小题满分14分)椭圆的中心在原点，焦点在坐标轴上，焦距为213.一双曲线和该椭圆有公共焦点，且双曲线的半实轴长比椭圆的半长轴长小4，双曲线离心率与椭圆离心率之比为7∶3，求椭圆和双曲线的方程.【解】 ①焦点在x 轴上，椭圆为x 2a 2＋y 2b 2＝1(a >b >0)，且c ＝13.设双曲线为x 2m 2－y 2n 2 ＝1(m >0，n >0)，m ＝a －4.因为e 双e 椭＝73，所以a m ＝73，解得a ＝7，m ＝3.因为椭圆和双曲线的焦半距为13，所以b 2＝36，n 2＝4. 所以椭圆方程为x 249＋y 236＝1，双曲线方程为x 29－y 24＝1.②焦点在y 轴上，椭圆方程为x 236＋y 249＝1，双曲线方程为y 29－x 24＝1. 17.(本小题满分14分)如图1所示，已知斜率为1的直线l 过椭圆x 24＋y 2＝1的右焦点F ，交椭圆于A 、B 两点，求弦AB 的长.图1【解】 设A 、B 两点的坐标分别为A (x 1，y 1)、B (x 2，y 2)，由椭圆方程知a 2＝4，b 2＝1，c 2＝3，所以F (3，0)，直线l 的方程为y ＝x － 3.将其代入x 2＋4y 2＝4，化简整理，得5x 2－83x ＋8＝0.所以x 1＋x 2＝835，x 1x 2＝85.所以AB ＝1＋k 2|x 1－x 2| ＝1＋k 2·(x 1＋x 2)2－4x 1x 2＝2×(83)2－4×5×85＝85.18.(本小题满分16分)如图2，已知椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)的离心率为22，以该椭圆上的点和椭圆的左、右焦点F 1、F 2为顶点的三角形的周长为4(2＋1)，一等轴双曲线的顶点是该椭圆的焦点，设P 为该双曲线上异于顶点的任意一点，直线PF 1和PF 2与椭圆的交点分别为A 、B 和C 、D .图2(1)求椭圆和双曲线的标准方程；(2)设直线PF 1、PF 2的斜率分别为k 1、k 2，求证：k 1k 2＝1.【解】 (1)设椭圆的半焦距为c ，由题意知，c a ＝22，2a ＋2c ＝4(2＋1)，所以a ＝22，c ＝2.又a 2＝b 2＋c 2，因此b ＝2.故椭圆的标准方程为x 28＋y 24＝1.由题意设等轴双曲线的标准方程为x 2m 2－y 2m 2＝1(m ＞0)，因为等轴双曲线的顶点是椭圆的焦点，所以m ＝2，因此双曲线的标准方程为x 24－y 24＝1.(2)证明：设P (x 0，y 0)，则k 1＝y 0x 0＋2，k 2＝y 0x 0－2. 因为点P 在双曲线x 2－y 2＝4上，所以x 20－y 20＝4.因此k 1k 2＝y 0x 0＋2·y 0x 0－2＝y 20x 20－4＝1，即k 1k 2＝1.19.(本小题满分16分)已知直线y ＝－12x ＋2和椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)相交于A ，B 两点，M 为AB 的中点，若AB ＝25，直线OM 的斜率为12(O 为坐标原点)，求椭圆的方程.【解】由⎩⎪⎨⎪⎧y ＝－12x ＋2，x 2a 2＋y 2b 2＝1，消去y ，整理得(a 2＋4b 2)x 2－8a 2x ＋16a 2－4a 2b 2＝0.设A (x 1，y 1)，B (x 2，y 2)，则由根与系数的关系，得x 1＋x 2＝8a 2a 2＋4b 2，x 1x 2＝16a 2－4a 2b 2a 2＋4b2. 又设AB 的中点M (x M ，y M )，则x M ＝x 1＋x 22＝4a 2a 2＋4b 2，y M ＝－12x M ＋2＝8b 2a 2＋4b 2. ∵直线OM 的斜率k OM ＝y M x M ＝12，∴2b 2a 2＝12，∴a 2＝4b 2，从而x 1＋x 2＝8a 2a 2＋4b 2＝4，x 1x 2＝16a 2－4a 2b 2a 2＋4b 2＝8－2b 2. 又∵AB ＝25，∴ 1＋14·(x 1＋x 2)2－4x 1x 2＝25，即52×16－4(8－2b )2＝25，解得b 2＝4，∴a 2＝4b 2＝16，故所求椭圆的方程为x 216＋y 24＝1.20.(本小题满分16分)(2016·盐城高二检测)设椭圆x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点分别为F 1，F 2，右顶点为A ，上顶点为B .已知AB ＝32F 1F 2. (1)求椭圆的离心率.(2)设P 为椭圆上异于其顶点的一点，以线段PB 为直径的圆经过点F 1，经过点F 2的直线l 与该圆相切于点M ，MF 2＝2 2.求椭圆的方程.【解】 (1)设椭圆右焦点F 2的坐标为(c,0)，由AB ＝32F 1F 2，可得a 2＋b 2＝3c 2，又b 2＝a 2－c 2，则c 2a 2＝12.所以椭圆的离心率e ＝22.(2)由(1)知a 2＝2c 2，b 2＝c 2，故椭圆方程为x 22c 2＋y 2c 2＝1.设P (x 0，y 0)，由F 1(－c,0)，B (0，c )，有F 1P →＝(x 0＋c ，y 0)，F 1B →＝(c ，c )， 由已知，有F 1P →·F 1B →＝0，即(x 0＋c )c ＋y 0c ＝0. 又c ≠0，故有x 0＋y 0＋c ＝0.① 因为点P 在椭圆上，故x 202c 2＋y 20c 2＝1.②由①和②可得3x 20＋4cx 0＝0，而点P 不是椭圆的顶点，故x 0＝－4c 3，代入①得y 0＝c 3，即点P 的坐标为⎝ ⎛⎭⎪⎫ －4c 3，c 3.设圆的圆心为T (x 1，y 1)，则x 1＝－4c3＋02＝－23c ，y 1＝c3＋c 2＝23c ，进而圆的半径r ＝(x 1－0)2＋(y 1－c )2＝53c .由已知，有TF 22＝MF 22＋r 2，又MF 2＝22，故有⎝ ⎛⎭⎪⎫c ＋2c 32＋⎝ ⎛⎭⎪⎫0－2c 32＝8＋59c 2.解得c 2＝3.所以所求椭圆的方程为x 26＋y 23＝1.。

章末综合测评(二）（时间120分钟，满分160分）一、填空题（本大题共14小题,每小题5分，共70分，请把答案填写在题中横线上)1.有一段“三段论"推理是这样的：对于可导函数f（x），若f（x0)＝0,则x＝x0是函数f(x）的极值点。

因为f(x)＝x3在x＝0处的导数值f′（0）＝0，所以x＝0是f（x）＝x3的极值点。

以上推理中________错误。

【解析】大前提是错误的，若f′（x0)＝0,x＝x0不一定是函数f（x)的极值点.【答案】大前提2。

下列四个图形中,着色三角形的个数依次构成一个数列的前4项，则这个数列的一个通项公式为________。

图1【解析】由图形可知,着色三角形的个数依次为:1,3，9，27,…,故a n＝3n—1。

【答案】3n-13.（2016·日照联考)已知f(n）＝1＋错误!＋错误!＋…＋错误!（n∈N ＊）,计算得f(22）＞2，f(23)＞错误!，f（24)＞3，f(25)＞错误!,由此推测，当n≥2时，有________.【解析】因为f（22)＞错误!,f（23)＞错误!，f(24）＞错误!，f（25）＞错误!，所以推测，当n≥2时，f（2n）＞错误!。

【答案】f(2n）＞错误!4.已知圆x2＋y2＝r2（r＞0）的面积为S＝πr2，由此类比椭圆错误!＋错误!＝1(a＞b＞0）的面积最有可能是________。

【解析】将圆看作椭圆的极端情况，即a＝b情形。

∴类比S圆＝πr2,得椭圆面积S＝πab。

【答案】πab5.已知a＞0，b＞0，m＝lg错误!，n＝lg错误!，则m与n的大小关系为________。

【解析】∵（错误!＋错误!）2＝a＋b＋2错误!＞a＋b＞0,∴错误!＋错误!＞错误!＞0，则错误!＞错误!。

∴lg错误!＞lg错误!，则m＞n。

【答案】m＞n6.已知数列｛a n}为等差数列，数列{b n｝是各项均为正数的等比数列，且公比q＞1，若a1＝b1，a2 013＝b2 013,则a1 007与b1 007的大小关系是________。

章末综合测评(二)圆锥曲线与方程（时间120分钟，满分160分）一、填空题（本大题共14小题，每小题5分，共70分．请把答案填在题中横线上）1．抛物线y＝－错误!x2的准线方程是________．【解析】把抛物线方程化为标准形式得x2＝－8y，所以抛物线的准线方程为y＝2.【答案】y＝22．如果方程错误!＋错误!＝1表示焦点在x轴上的椭圆,则实数a的取值范围是________．【解析】焦点在x轴上,则标准方程中a2>a＋6，解得a〉3或a<－2.又a2〉0,a＋6>0，所以a>3或－6<a〈－2.【答案】a>3或－6〈a〈－23．双曲线错误!－错误!＝1的渐近线与圆(x－3）2＋y2＝r2(r>0）相切，则r等于________．【解析】双曲线错误!－错误!＝1的渐近线方程为y＝±错误!x，与圆（x－3）2＋y2＝r2(r〉0)相切，得r＝错误!。

【答案】34．若F1，F2是双曲线错误!－错误!＝1（a＞0，b＞0）与椭圆错误!＋y2＝1的共同的左、右焦点，点P是两曲线的一个交点，且△PF1F2 9为等腰三角形，则该双曲线的渐近线方程是________。

【导学号:09390068】【解析】不妨设PF1＞PF2，则PF1＝F1F2＝8,由双曲线及椭圆的定义,可知错误!即错误!得2a＝6，a＝3。

又a2＋b2＝16，所以b2＝7，故双曲线的渐近线方程为y＝±错误! x。

【答案】y＝±错误!x5．设抛物线y2＝8x的准线与x轴交于点Q，若过点Q的直线l 与抛物线有公共点，则直线l的斜率的取值范围是________．【解析】易知抛物线y2＝8x的准线x＝－2与x轴的交点为Q(－2，0),于是，可设过点Q(－2，0）的直线l的方程为y＝k（x＋2）(由题可知k是存在的），联立错误!⇒k2x2＋(4k2－8)x＋4k2＝0。

当k＝0时,易知符合题意;当k≠0时，其判别式为Δ＝(4k2－8）2－16k4＝－64k2＋64≥0，可解得－1≤k≤1，且k≠0,综上可知，－1≤k≤1。

1.2 回归分析1.会作出两个有关联变量的散点图，并利用散点图认识变量间的相关关系.2.了解线性回归模型，能根据给出的线性回归方程系数公式建立线性回归方程.(重点、难点)3.了解回归分析的基本思想、方法及简单应用.[基础·初探]教材整理1 线性回归模型 阅读教材P 13～P 14，完成下列问题1.线性回归模型的概念：将y ＝a ＋bx ＋ε称为线性回归模型，其中a ＋bx 是确定性函数，ε称为随机误差.2.线性回归方程：直线y ^＝a ^＋b ^x 称为线性回归方程，其中a ^称为回归截距，b ^称为回归系数，y ^称为回归值，其中⎩⎪⎨⎪⎧b ^＝∑ni ＝1x i y i -n x - y-∑n i ＝1x 2i-n (x -)2，a ^＝y --b ^x -.其中x -＝1n ∑n i ＝1x i ，y -＝1n ∑ni ＝1y i.设某大学生的女生体重y (单位：kg)与身高x (单位：cm)具有线性相关关系.根据一组样本数据(x i ，y i )(i ＝1,2，…，n )，用最小二乘法建立的回归方程为y ^＝0.85x -85.71，则下列结论中正确的是________(填序号).【导学号：97220003】(1)y 与x 具有正的线性相关关系(2)回归直线过样本点的中心(x，y)(3)若该大学某女生身高增加1 cm，则其体重约增加0.85 kg(4)若该大学某女生身高为170 cm，则可断定其体重必为58.79 kg【解析】回归方程中x的系数为0.85>0，因此y与x具有正的线性相关关系，(1)正确；由回归方程系数的意义可知回归直线过样本点的中心(x，y)，(2)正确；∵回归方程y^＝0.85x-85.71，∴该大学某女生身高增加1 cm，则其体重约增加0.85 kg，(3)正确；用回归方程对总体进行估计不能得到肯定结论，故(4)不正确.【答案】(1)(2)(3)教材整理2相关关系阅读教材P16～P17“例2”以上部分完成下列问题1.相关系数是精确刻画线性相关关系的量.2.相关系数r＝∑ni＝1(x i-x-)(y i-y-)∑ni＝1(x i-x-)2∑ni＝1(y i-y-)2＝∑ni＝1x i y i-n x-y-⎝⎛⎭⎪⎫∑ni＝1x2i-n(x-)2⎝⎛⎭⎪⎫∑ni＝1y2i-n(y-)2.3.相关系数r具有的性质：(1)|r|≤1；(2)|r|越接近于1，x，y的线性相关程度越强；(3)|r|越接近于0，x，y的线性相关程度越弱.4.相关性检验的步骤：(1)提出统计假设H0：变量x，y不具有线性相关关系；(2)如果以95%的把握作出推断，那么可以根据1-0.95＝0.05与n-2在附录1中查出一个r的临界值r0.05(其中1-0.95＝0.05称为检验水平).(3)计算样本相关系数r ；(4)作统计推断：若|r |>r 0.05，则否定H 0，表明有95%的把握认为x 与y 之间具有线性相关关系；若|r |≤r 0.05，则没有理由拒绝原来的假设H 0，即就目前数据而言，没有充分理由认为y 与x 之间有线性相关关系.判断正误：(1)求回归直线方程前必须进行相关性检验.( )(2)两个变量的相关系数越大，它们的相关程度越强.( ) (3)若相关系数r ＝0，则两变量x ，y 之间没有关系.( ) 【答案】 (1)√ (2)× (3)√[质疑·手记]预习完成后，请将你的疑问记录，并与“小伙伴们”探讨交流：疑问1： 解惑： 疑问2： 解惑： 疑问3： 解惑：[小组合作型](1)①线性回归分析就是由样本点去寻找一条直线，使之贴近这些样本点的数学方法；②利用样本点的散点图可以直观判断两个变量的关系是否可以用线性关系表示；③通过回归方程y ^＝b ^x ＋a ^，可以估计和观测变量的取值和变化趋势；④因为由任何一组观测值都可以求得一个线性回归方程，所以没有必要进行相关性检验.其中正确命题是__________(填序号).(2)如果某地的财政收入x 与支出y 满足线性回归方程y ^＝b ^x ＋a ^＋e (单位：亿元)，其中b ^＝0.8，a ^＝2，|e |≤0.5，如果今年该地区财政收入10亿元，则今年支出预计不会超过________亿.【自主解答】 (1)①反映的正是最小二乘法思想，故正确.②反映的是画散点图的作用，也正确.③解释的是回归方程y ^＝b ^x ＋a ^的作用，故也正确.④在求回归方程之前必须进行相关性检验，以体现两变量的关系，故不正确.(2)由题意可得：y ^＝0.8x ＋2＋e ，当x ＝10时，y ^＝0.8×10＋2＋e ＝10＋e ，又|e |≤0.5，∴9.5≤y ^≤10.5.故今年支出预计不会超过10.5亿. 【答案】 (1)①②③ (2)10.51.在分析两个变量的相关关系时，可根据样本数据散点图确定两个变量之间是否存在相关关系，然后利用最小二乘法求出回归直线方程.2.由线性回归方程给出的是一个预报值而非精确值.3.随机误差的主要来源(1)线性回归模型与真实情况引起的误差； (2)省略了一些因素的影响产生的误差； (3)观测与计算产生的误差. 4.残差分析是回归分析的一种方法.[再练一题]1.下列有关线性回归的说法，不正确的是________(填序号).①自变量取值一定时，因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系；②在平面直角坐标系中用描点的方法得到表示具有相关关系的两个量的一组数据的图形叫做散点图；③线性回归方程最能代表观测值x ，y 之间的关系； ④任何一组观测值都能得到具有代表意义的回归直线方程.【解析】 只有具有线性相关的两个观测值才能得到具有代表意义的回归直线方程.【答案】 ④某班5(2)求物理成绩y 对数学成绩x 的回归直线方程； (3)一名学生的数学成绩是96，试预测他的物理成绩.【精彩点拨】 先画散点图，分析物理与数学成绩是否有线性相关关系，若相关，再利用线性回归模型求解.【自主解答】 (1)散点图如图所示.(2)由散点图可知y 与x 之间具有线性相关关系. 因为x -＝15×(88＋76＋73＋66＋63)＝73.2，y -＝15×(78＋65＋71＋64＋61)＝67.8，∑5i ＝1x i y i ＝88×78＋76×65＋73×71＋66×64＋63×61＝25 054， ∑5i ＝1x 2i ＝882＋762＋732＋662＋632＝27 174.所以b ^＝∑5i ＝1x i y i -5 x - y-∑5i ＝1x 2i -5(x -)2＝25 054-5×73.2×67.827 174-5×73.22≈0.625，a ^＝y --b ^x -≈67.8-0.625×73.2＝22.05.所以y 对x 的回归直线方程是y ^＝0.625x ＋22.05.(3)当x ＝96时，y ^＝0.625×96＋22.05≈82，即可以预测他的物理成绩是82.1.求线性回归方程的基本步骤：2.需特别注意的是，只有在散点图大致呈直线时，求出的线性回归方程才有实际意义，否则求出的回归方程毫无意义.[再练一题]2.某商场经营一批进价是30元/台的小商品，在市场调查中发现，此商品的销售单价x (x 取整数)元与日销售量y 台之间有如下关系：(1)y 与x 求出回归直线方程.(方程的回归系数保留一位有效数字)(2)设经营此商品的日销售利润为P 元，根据(1)写出P 关于x 的函数关系式，并预测当销售单价x 为多少元时，才能获得最大日销售利润.【解】 (1)散点图如图所示，从图中可以看出这些点大致分布在一条直线附近，因此两个变量线性相关.设回归直线为y ^＝b ^x ＋a ^，由题知x -＝42.5，y -＝34，则求得b ^＝∑4i ＝1x i y i -4x - y-∑4i ＝1x 2i -4(x -)2＝-370125≈-3. a ^＝y --b ^x -＝34-(-3)×42.5＝161.5. ∴y ^＝-3x ＋161.5.(2)依题意有P ＝(-3x ＋161.5)(x -30)＝-3x 2＋251.5x -4 845＝-3⎝ ⎛⎭⎪⎫x -251.562＋251.5212-4 845.∴当x ＝251.56≈42时，P 有最大值，约为426. 即预测销售单价为42元时，能获得最大日销售利润.[探究共研型]探究1 【提示】 直观分析数据是否存在线性相关关系.探究2 下表显示出变量y 随变量x 变化的一组数据，由此判断表示y 与x 之间的关系最可能的是________.(填序号).【解析】画出散点图(图略)，可以得到这些样本点在一条直线附近，故最可能是线性函数模型.【答案】①10名同学在高一和高二的数学成绩如下表：(1)y与x是否具有相关关系？(2)如果y与x具有线性相关关系，求回归直线方程.【精彩点拨】可先计算线性相关系数r的值，然后与r0.05比较，进而对x 与y的相关性做出判断.【自主解答】(1)由已知表格中的数据，求得x＝71，y＝72.3，r＝∑i＝110(x i-x)(y i-y)∑i＝110(x i-x)2∑i＝110(y i-y)2≈0.78.由检验水平0.05及n-2＝8，在课本附录1中查得r0.05＝0.632，因为0.78>0.632，所以y与x之间具有很强的线性相关关系.(2)y与x具有线性相关关系，设回归直线方程为y ^＝a ^＋b ^x ，则有b ^＝∑i ＝110(x i -x )(y i -y )∑i ＝110(x i -x )2≈1.22，a ^＝y --b ^x -＝72.3-1.22×71＝-14.32.所以y 关于x 的回归直线方程为y ^＝1.22x -14.32.1.线性回归分析必须进行相关性检验；若忽略，则所求回归方程没有实际意义.2.|r |越接近于1，两变量相关性越强，|r |越接近于0，两变量相关性越弱.[再练一题]3.关于两个变量x 和y 的7组数据如下表所示：【解】 x -＝17×(21＋23＋25＋27＋29＋32＋35)≈27.4， y -＝17×(7＋11＋21＋24＋66＋115＋325)≈81.3， ∑7i ＝1x 2i ＝212＋232＋252＋272＋292＋322＋352＝5 414，∑7i ＝1x i y i ＝21×7＋23×11＋25×21＋27×24＋29×66＋32×115＋35×325＝18 542，∑7i ＝1y 2i ＝72＋112＋212＋242＋662＋1152＋3252＝124 393，∴r＝∑7i＝1x i y i-7 x-y-(∑7i＝1x2i-7(x-)2)(∑7i＝1y2i-7(y-)2)＝18 542-7×27.4×81.3(5 414-7×27.42)(124 393-7×81.32)≈0.837 5.∵0.837 5>0.755，∴x与y之间具有线性相关关系.[构建·体系]1.在下列各量之间，存在相关关系的是：①正方体的体积与棱长之间的关系；②一块农田的水稻产量与施肥量之间的关系；③人的身高与年龄之间的关系；④家庭的支出与收入之间的关系；⑤某户家庭用电量与电价之间的关系.【答案】②③④2.根据如下样本数据得到的回归方程为y＝bx＋a，则下列说法正确的是__________.(填序号)①a>0，b>0 ②a>0，b<0③a<0，b>0 ④a<0，b<0【解析】由表中数据画出散点图，如图，由散点图可知b<0，a>0，故②正确.【答案】 ②3.设有一个回归方程为y ^＝2-2.5x ，则变量x 每增加一个单位时，y ＝__________.【导学号：97220004】【解析】 由回归系数的意义可知当变量x 增加一个单位时，y ^的平均改变量为b ^，由题目回归方程y ^＝2-2.5x ，可得当变量x 增加一个单位时，y ^平均减少2.5个单位. 【答案】 平均减少2.5个单位4.对具有线性相关关系的变量x 和y ，由测得的一组数据求得回归直线的斜率为6.5，且恒过(2,3)点，则这条回归直线的方程为________.【解析】 由题意知x ＝2，y ＝3，b ^＝6.5，所以a ^＝y -b ^x ＝3-6.5×2＝-10，即回归直线的方程为y ^＝-10＋6.5x .【答案】 y ^＝-10＋6.5x5.某工厂为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如下数据：(1)求回归直线方程y ＝b x ＋a ，其中b ＝-20，a ＝y -b x ；(2)预计在今后的销售中，销量与单价仍然服从(1)中的关系，且该产品的成本是4元/件，为使工厂获得最大利润，该产品的单价应定为多少元？(利润＝销售收入-成本)【解】 (1)x ＝16(8＋8.2＋8.4＋8.6＋8.8＋9)＝8.5， y ＝16(90＋84＋83＋80＋75＋68)＝80， ∵b ^＝-20，a ^＝y -b ^x ，∴a ^＝80＋20×8.5＝250， ∴回归直线方程为y ^＝-20x ＋250.(2)设工厂获得的利润为L 元，则L ＝x (-20x ＋250)-4(-20x ＋250)＝-20⎝ ⎛⎭⎪⎫x -3342＋361.25，∴该产品的单价应定为334元时，工厂获得的利润最大.我还有这些不足：(1) (2) 我的课下提升方案：(1) (2)。