直接离散化控制器设计方法-2015.04.27
- 格式:pptx
- 大小:512.66 KB
- 文档页数:43


离散控制系统中的控制器设计方法离散控制系统是一种应用广泛的控制系统形式,它对于许多工程领域都具有重要的意义。
而在离散控制系统的设计中,控制器的选择和设计是至关重要的一步。
本文将介绍几种常用的离散控制系统中控制器设计的方法。
一、比例控制器比例控制器是最简单的一种控制器设计方法之一。
它基于一个简单的原理:输出信号与输入信号的乘积成正比。
比例控制器的数学模型可以表示为:u(k) = Kp * e(k)其中,u(k)是控制器的输出信号,Kp是比例增益,e(k)是当前时刻的误差信号。
比例控制器的设计方法相对简单,但其对系统的调节性能有一定的限制。
在一些简单的离散控制系统中,比例控制器已经能够满足需求。
但在一些复杂的系统中,需要使用更加先进的控制器设计方法。
二、积分控制器积分控制器是比例控制器的一种改进方法,它可以有效降低系统的稳态误差。
积分控制器的数学模型可以表示为:u(k) = Ki * ∑e(i)其中,u(k)是控制器的输出信号,Ki是积分增益,e(i)是当前时刻之前的误差信号。
通过积分控制器的使用,系统的稳态误差可以被消除或者减小到一个可接受的范围内。
积分控制器在一些要求较高的离散控制系统中得到了广泛应用。
三、微分控制器微分控制器是在比例控制器的基础上引入了微分项的一种控制器设计方法。
它可以增强系统的动态响应,并提高控制系统的稳定性。
微分控制器的数学模型可以表示为:u(k) = Kd * [e(k) - e(k-1)]其中,u(k)是控制器的输出信号,Kd是微分增益,e(k)是当前时刻的误差信号,e(k-1)是上一时刻的误差信号。
微分控制器的引入可以抑制系统的超调和振荡现象,提高系统的控制性能。
在一些快速响应要求较高的离散控制系统中,微分控制器是一种常用的设计方法。
四、PID控制器PID控制器是由比例控制器、积分控制器和微分控制器组成的一种复合控制器设计方法。
PID控制器综合了比例、积分和微分三个方面的调节策略,可以更加精确地控制系统的性能。



离散控制系统中的控制器设计与实现离散控制系统在现代自动化领域中扮演着至关重要的角色。
而其中的控制器设计与实现是整个系统运行的核心。
在本文中,我们将讨论离散控制系统中的控制器设计与实现的一些关键要素。
1. 控制器设计的基本原则在离散控制系统中,控制器的设计目标是实现系统的稳定性和性能。
为了达到这个目标,我们需要考虑以下几个基本原则:1.1 控制器结构的选择控制器的结构选择应该根据控制系统的特点和要求来确定。
常见的控制器结构包括比例-积分-微分(PID)控制器、模糊控制器和模型预测控制器等。
根据系统的复杂程度和工作环境的特点,选择适合的结构非常重要。
1.2 控制器参数的确定控制器的参数对系统的响应速度、稳定性和鲁棒性等性能指标有着直接的影响。
参数的确定可以通过实验或者理论分析等方式进行。
其中,经典的PID控制器参数调整方法包括Ziegler-Nichols方法和世界经验公式法等。
1.3 控制器输出的动态限制在实际的控制系统中,控制器的输出通常存在着动态限制。
例如,电机控制系统中,控制器的输出通常受到电流限制或者电压限制等约束。
在设计控制器时,需要考虑这些限制条件,以避免系统无法正常工作或者损坏。
2. 控制器设计的方法与工具现代离散控制系统设计过程中,许多方法和工具可用于辅助控制器的设计与实现。
下面介绍一些常用的方法与工具:2.1 系统建模与仿真在控制器设计之前,需要对系统进行建模与仿真,以了解系统的动态行为和性能。
常见的建模与仿真工具包括MATLAB/Simulink、LabVIEW等,通过这些工具可以方便地进行系统参数的调整和性能的评估。
2.2 控制器参数优化控制器参数的优化是一个非常重要的任务,可以通过各种优化算法来实现。
例如,可以使用遗传算法、粒子群优化算法等来自动搜索最优的参数组合,以达到最佳的控制效果。
2.3 控制器实现与调试一旦完成了控制器设计,需要将其实现到实际系统中,并进行调试和验证。

第五章数字控制器的离散化设计⽅法第五章数字控制器的离散化设计⽅法数字控制器的连续化设计是按照连续控制系统的理论在S 域内设计模拟调节器,然后再⽤计算机进⾏数字模拟,通过软件编程实现的。
这种⽅法要求采样周期⾜够⼩才能得到满意的设计结果,因此只能实现⽐较简单的控制算法。
当控制回路⽐较多或者控制规律⽐较复杂时,系统的采样周期不可能太⼩,数字控制器的连续化设计⽅法往往得不到满意的控制效果。
这时要考虑信号采样的影响,从被控对象的实际特性出发,直接根据采样控制理论进⾏分析和综合,在Z 平⾯设计数字控制器,最后通过软件编程实现,这种⽅法称为数字控制器的离散化设计⽅法,也称为数字控制器的直接设计法。
数字控制器的离散化设计完全根据采样系统的特点进⾏分析和设计,不论采样周期的⼤⼩,这种⽅法都适合,因此它更具有⼀般的意义,⽽且它可以实现⽐较复杂的控制规律。
5.1 数字控制器的离散化设计步骤数字控制器的连续化设计是把计算机控制系统近似看作连续系统,所⽤的数学⼯具是微分⽅程和拉⽒变换;⽽离散化设计是把计算机控制系统近似看作离散系统,所⽤的数学⼯具是差分⽅程和Z 变换,完全采⽤离散控制系统理论进⾏分析,直接设计数字控制器。
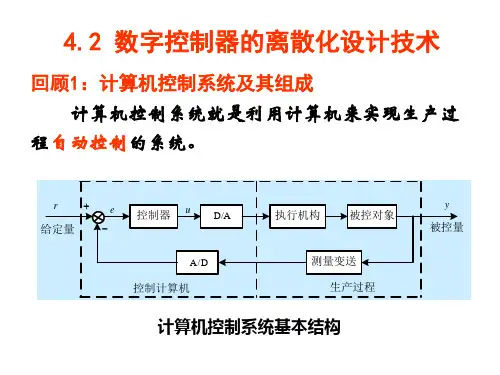
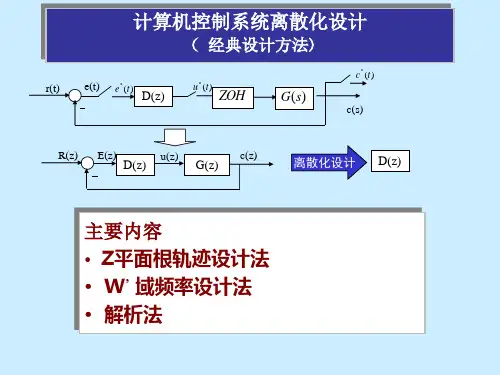
计算机采样控制系统基本结构如图5.1所⽰。
图中G 0(s)是被控对象的传递函数,H(s)是零阶保持器的传递函数,G(z)是⼴义被控对象的脉冲传递函数,D(z)是数字控制器的脉冲传递函数, R(z)是系统的给定输⼊,C(z)是闭环系统的输出,φ(z)是闭环系统的脉冲传递函数。
零阶保持器的传递函数为:se s H Ts--=1)( (5-1)⼴义被控对象的脉冲传递函数为:[])()()(0s G s H Z z G = (5-2)由图可以求出开环系统的脉冲传递函数为:图5.1 计算机采样控制系统基本结构图)()()()()(z G z D z E z C z W == (5-3)闭环系统的脉冲传递函数为:()()()()()1()()C zD z G z z R z D z G z Φ==+ (5-4)误差的脉冲传递函数为:()1()()1()()e E z z R z D z G z Φ==+ (5-5)显然 )(1)(z z e Φ-=Φ(5-6)由式(5-4)可以求出数字控制器的脉冲传递函数为:)](1)[()()(z z G z z D Φ-Φ= (5-7)如果已知被控对象的传递函数G 0(s),并且可以根据控制系统的性能指标确定闭环系统的脉冲传递函数φ(z),由上式可以得到离散化⽅法设计数字控制器的步骤:(1)根据式(5-2)求出⼴义被控对象的脉冲传递函数G(z)。



8. 离散控制系统的设计流程是怎样的?离散控制系统的设计可不像做一顿简单的饭菜,它需要一系列严谨又巧妙的步骤。
咱们先来说说第一步,那就是明确设计要求。
这就好比你决定出门旅行,得先搞清楚自己想去哪儿、想怎么玩。
比如说,你是想要系统响应速度快得像火箭,还是想要系统稳定得像泰山?是对精度要求极高,还是对成本控制很严格?举个例子哈,就像有一家工厂要设计一个控制机器人搬运货物的离散控制系统。
他们的要求就是机器人搬运货物的速度得快,而且不能出错,否则货物摔坏了损失可就大了。
接下来第二步,就是建立数学模型啦。
这就像是给系统画一幅“肖像画”,把它的特点和行为都用数学公式表现出来。
这个过程可不简单,得考虑各种因素,像系统的延迟、噪声干扰等等。
比如说,还是那个工厂的例子,要考虑机器人的机械结构、电机的性能、传感器的精度等等,把这些都转化成数学语言。
然后是第三步,选择控制算法。
这就像是给系统选一件合适的“衣服”,得合身又好看。
常见的控制算法有 PID 控制、模糊控制、最优控制等等。
还是拿工厂举例,经过分析,如果对系统的精度要求很高,可能就会选择 PID 控制算法。
第四步是进行仿真分析。
这就像是在虚拟世界里先让系统“跑一跑”,看看效果怎么样。
可以通过计算机软件来模拟系统的运行,看看是不是达到了设计要求。
比如说,在仿真中发现机器人搬运货物的速度不够快,那就得回去调整控制算法的参数。
再往后,第五步就是硬件实现啦。
这就像是把虚拟的梦想变成现实的存在。
要选择合适的控制器、传感器、执行器等等。
比如说,为了让机器人能准确感知货物的位置,就得选高精度的传感器。
第六步,系统调试。
这就像是给新做好的衣服修修改改,让它更合身。
在实际运行中,不断调整参数,优化系统性能。
比如说,可能会发现机器人在某些特殊情况下会出现卡顿,那就得赶紧查找原因,进行调试。
最后一步,系统评估。
这就像是给系统来一场“考试”,看看它到底合不合格。
离散控制系统的设计流程虽然听起来复杂,但每一步都至关重要。
离散控制系统中的PID控制器设计PID控制器是一种常用的控制器,广泛应用于离散控制系统中。
它是由比例项(P项)、积分项(I项)和微分项(D项)三个部分组成的,通过对系统的反馈信号进行处理,以使得系统响应更加稳定和准确。
在离散控制系统中,PID控制器的设计十分关键。
合理地设置PID 参数是实现良好控制效果的关键。
下面将基于离散控制系统中的PID 控制器设计,详细讨论PID参数的选择方法与调整策略。
一、PID参数的选择方法PID控制器的性能取决于其参数的选择,而PID参数的选择可以采用以下几种常用的方法:1. 经验法:根据经验公式或者实际应用中的调试经验,直接选取PID参数。
由于经验法灵活性较大,但不够科学,容易导致控制效果不理想。
2. Ziegler-Nichols方法:该方法基于系统的频域特性进行参数的调整,步骤较为简单。
首先,将控制器的I、D项参数设为0,只保留P 项;然后逐步增加P项增益,直至系统产生持续性振荡;最后按照振荡周期调整P、I、D项参数。
3. 优化算法:如遗传算法、粒子群算法等,通过优化算法求解PID 参数的最优取值。
该方法需要有系统的数学模型作为基础,且需要足够多的计算资源支持。
以上是几种常用的PID参数选择方法,不同的方法适用于不同的情况。
在具体选择过程中,需要从实际需求和系统特点出发,综合考虑,选择适合的方法。
二、PID参数的调整策略PID参数的调整是为了使得控制系统更加稳定和准确,常用的调整策略包括参数整定法和自整定法两种:1. 参数整定法:该方法是根据系统的动态性能指标,通过试探和修正的方式进行PID参数的调整。
常用的动态性能指标包括超调量、调整时间、稳态误差等。
根据实验结果,逐步修正PID参数,直至满足系统的性能要求。
2. 自整定法:自整定法是指采用自适应控制算法,通过系统自身的响应来动态调整PID参数。
常用的自整定算法有基于模型的自整定方法、经验模型自调整控制(EMC)方法等。
离散控制系统中的控制器设计离散控制系统(Discrete Control System)是指具有离散时间特性的控制系统,其输入、输出和状态变量仅在离散时间点上进行采样和处理。
而控制器则是离散控制系统中的关键组成部分,起着决定系统性能、稳定性和可靠性的重要作用。
本文将介绍离散控制系统中的控制器设计方法及其相关技术。
一、控制器设计的目标在离散控制系统中,设计一个合适的控制器是保证系统良好性能的关键。
通常,控制器设计的目标包括以下几个方面:1. 系统稳定性:控制器应当能够使系统在给定运行条件下达到稳定状态,避免出现震荡、振荡等不稳定现象。
2. 快速响应:控制器应当具备快速响应的能力,能够在系统发生变化时迅速调整,使系统在最短的时间内达到期望状态。
3. 抗干扰能力:控制器应当具备较高的抗干扰能力,能够有效地抵消或减小来自外界的各种扰动对系统的影响。
4. 误差补偿:控制器应当能够对系统误差进行准确补偿,使系统输出能够与期望输出尽量接近。
二、传统控制器设计方法在传统的离散控制系统中,常用的控制器设计方法主要包括比例控制器(Proportional Controller)、积分控制器(Integral Controller)和比例积分控制器(Proportional-Integral Controller)。
1. 比例控制器(P控制器)比例控制器是最简单的控制器之一,其输出信号与误差信号成比例关系。
比例控制器的数学表达式为:\[u(t) = K_p \cdot e(t)\]其中,\(u(t)\)是控制器的输出信号,\(K_p\)为比例增益,\(e(t)\)为误差信号。
比例控制器的特点是具有简单的结构和快速的响应速度,但其无法消除系统的稳态误差,较难应对复杂的系统动态特性。
2. 积分控制器(I控制器)积分控制器是在比例控制器的基础上引入了积分环节,可以消除系统的稳态误差,提高系统的稳定性。
积分控制器的数学表达式为:\[u(t) = K_i \cdot \int_{0}^{t} e(\tau) d\tau\]其中,\(u(t)\)是控制器的输出信号,\(K_i\)为积分增益,\(e(t)\)为误差信号。