5.1连续域设计离散化方法

第八章 连续域-离散化设计8.1设计的基本原理7.4)(109z 811实现：章、：域设计控制器（离散）章）连续域离散化（章）现代控制理论（反馈控制理论：域设计控制器（连续）z D s ⎪⎭⎪⎬⎫→⎩⎨⎧连续域－离散化设计方法：D(s)→ D(z)控制器软件的实现过程：1）根据被控对象的传递函数)(s G ，按连续系统的分析与设计方法设计)(s D稳（稳定性）：稳定裕度（幅值裕度和相角裕度） 准（稳态误差）：位置、速度和加速度误差系数 快（动态性能指标）：谐振峰值、谐振频率、通频带、阻尼比最小拍：在离散系统中，调节时间的长短以采样周期个数表示，一个采样周期称一拍，调节时间最短的系统称最小拍2）根据系统特性和要求选T （9章） 3）D(s)→ D(z)4）标准)(s D 与)(z D 性能对比 5）由)(z D 求差分方程，编软件程序 6）系统调试8.2冲击响应不变法（Z 变换）一、定义：○1)()]([z D s D Z =； 二、特性：1频率坐标变换是线性（T ωω→）变换 说线性不妥，有超越函数e∑+∞-∞=±==±==n s jn j s e z jn j D T s D z D sT j )(1)(*)(ωωωωω s ω太小易混叠，应提高s ω2若)(s D 稳定，则)(z D 稳定3)(s D 与)(z D 的冲击响应相同冲击响应为)(t δ，其拉氏变换为1)]([=t L δ，若输入为冲击响应，则1)]([)(==t L s R δ)]([)]()([)(s D Z s R s D Z z D ==若不为冲击响应，则)]([)]()([)(s D Z s R s D Z z D ≠=4无串联性)]([)]([)]()([2121s D Z s D Z s D s D Z ≠注意：若保持增益不变，根据∑+∞-∞=±==±==n s jn j s e z jn j D T s D z D sT j )(1)(*)(ωωωωω 则)]([)(*s D TZ z D = 三、例题例：已知23)(+=s s D ，T=0.01s ，求)(z D 解：101.02113]23[)(-⨯--⨯=+=z e s Z z D 例：已知2)1()(+=s ss D ，T=1s ，求)(z D解：])1([)(2+=s sZ z D21211222212111)()()()(][d d ])1()1[(d d ])1()1[(d d lim ])()[(d d lim )!1(1T T T s sT sT sT s sTs sT sT s sTq i q q p s i e z TZe e z e z sZTe e z e z zs s e z zs s s s e z zs s s s e z zs F p s s q R i ----=-=-=--→--→---=-+-=-=-++=-++=---=8.3阶跃响应不变法一、定义（1） （2） （3）这种方法的思想是先将模拟控制器)(s D 近似为加零阶保持器的系统，再将该系统用Z 变换方法离散化为数字控制器)(z D 。

将连续型数据进行离散化处理是为了将其划分为若干个离散的区间或类别，这样有助于简化数据分析、模型建立和可视化。

离散化可以通过分箱（binning）等方法来实现。

以下是一些常见的连续型数据离散化的方法：
等宽离散化：
将数据的值范围划分为等宽的区间，每个区间的宽度相同。

这样可以简化数据，但可能无法很好地捕捉数据的分布特征。

等频离散化：
将数据划分为每个区间包含近似相同数量的数据点的区间。

这有助于保持每个区间中数据点的均衡性，但可能导致一些区间的宽度不一致。

聚类离散化：
使用聚类算法（如K均值聚类）将数据点划分为若干个簇，每个簇对应一个离散化的类别。

这种方法可以更好地捕捉数据的分布特征，但需要选择合适的聚类数。

自定义分位数离散化：
根据数据的分位数（如四分位数）将数据划分为多个类别。

这种方法能够较好地反映数据的整体分布，并且可以根据具体需求调整分位数的数量。

决策树离散化：
使用决策树算法对连续型数据进行离散化。

决策树的分裂点可以被用作离散化的边界，将数据划分为不同的类别。

离散化的选择通常取决于具体问题的要求以及对数据的理解。

在进行离散化处理时，需要注意选择合适的方法，并确保离散化后的数据仍然能够保持原始数据的主要特征。

离散化后的数据可以用于构建分类模型、降低计算复杂度、提高模型的可解释性等方面。

连续离散化方法离散化是将连续数据转换为离散数据的过程。

在实际应用中，离散化可以用于数据预处理、数据分析、特征工程等领域。

下面将介绍几种常见的离散化方法。

1. 等宽离散化（等距离散化）：等宽离散化是将连续数据按照固定的宽度划分成若干个区间，使得每个区间中的数据数量大致相等。

具体步骤如下：a. 确定划分的区间个数，可以根据经验或统计方法确定。

b. 计算最大值和最小值之间的距离（width）。

c. 根据区间个数和width计算每个区间的宽度，即划分的区间宽度。

d. 根据宽度将数据进行划分，并将每个数据映射到对应的区间。

等宽离散化的优点是简单易懂，适用于数据范围较小且不太关注具体分布的情况。

但缺点是可能导致数据量不均匀，对于数据分布不均匀的情况效果较差。

2. 等频离散化：等频离散化是将连续数据按照固定的数量划分为若干个区间，使得每个区间中的数据数量相等。

具体步骤如下：a. 确定划分的区间个数，可以根据经验或统计方法确定。

b. 计算每个区间应包含的数据数量，即总数据样本数量除以区间个数，得到每个区间应包含的数据数量。

c. 将数据按照从小到大的顺序进行排序。

d. 按照每个区间应包含的数据数量将数据进行划分，并将每个数据映射到对应的区间。

等频离散化的优点是对数据分布不均匀的情况有较好的表现，同时能保证每个区间中的数据数量相对平均。

但缺点是对于数据总量较少的情况可能会导致区间过小，不够有意义。

3. KMeans离散化：KMeans离散化是根据KMeans聚类算法将连续数据聚类为若干个簇，每个簇内的数据属于同一离散化区间。

具体步骤如下：a. 确定划分的区间个数，即聚类的簇个数。

b. 使用KMeans算法对数据进行聚类，将数据分配到不同的簇中。

c. 根据每个簇的数据计算簇的中心点或代表点作为离散化的分割点。

d. 将数据通过计算与分割点的距离将其映射到对应的离散化区间。

KMeans离散化的优点是能够较好地反映数据的分布情况，同时根据簇的中心点进行划分可以保证区间的连续性。

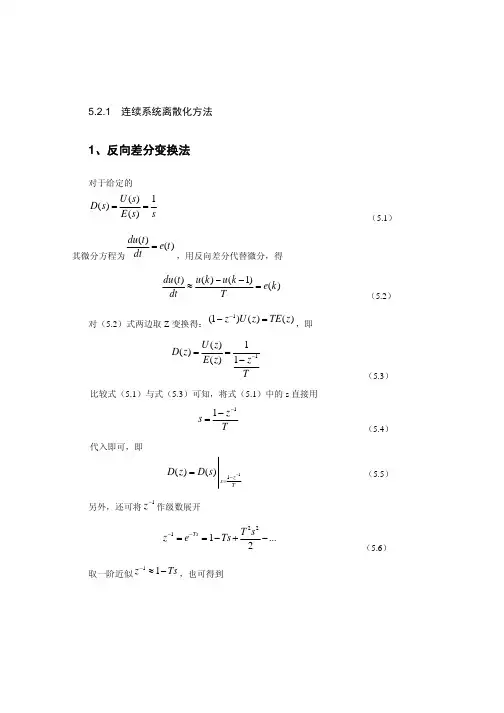
连续系统离散化方法连续系统离散化方法是一种常用的数值计算方法，它将连续系统转化为离散系统，从而使得计算机可以进行处理。

本文将从离散化方法的定义、应用、实现以及优缺点等方面进行介绍。

一、离散化方法的定义离散化方法是指将连续系统转化为离散系统的过程。

在计算机中，所有的数值都是离散的，而实际上很多系统是连续的，比如电路、机械系统、化学反应等等。

离散化方法就是将这些连续系统转化为可以在计算机中处理的离散系统。

离散化方法可以通过采样和量化来实现。

二、离散化方法的应用离散化方法在很多领域都有应用，比如电路设计、控制系统设计、信号处理等等。

在电路设计中，离散化方法可以将连续电路转化为数字电路，从而实现数字信号的处理。

在控制系统设计中，离散化方法可以将连续控制器转化为数字控制器，从而实现数字化自动控制。

在信号处理中，离散化方法可以将连续信号转化为数字信号，从而实现对信号的数字处理。

三、离散化方法的实现离散化方法的实现可以通过采样和量化来实现。

采样是指对连续信号进行离散化，将其转化为一系列的采样值。

量化是指对采样值进行离散化，将其转化为一系列的离散数值。

采样和量化的具体实现方式包括正弦采样、脉冲采样、最大值采样、平均值采样等等。

量化的具体实现方式包括线性量化、对数量化、非线性量化等等。

四、离散化方法的优缺点离散化方法的优点是可以将连续系统转化为离散系统，从而可以在计算机中进行处理。

离散系统具有稳定性、可控性、可观性等优点。

离散化方法的缺点是会引入误差，因为离散化过程中会丢失一些信息。

此外，离散化方法需要选取适当的采样周期和量化精度，否则会影响系统的性能。

离散化方法是一种常用的数值计算方法，它将连续系统转化为离散系统，从而使得计算机可以进行处理。

离散化方法的应用广泛，包括电路设计、控制系统设计、信号处理等等。

离散化方法的实现可以通过采样和量化来实现。

离散化方法既有优点，又有缺点，需要在具体应用中对其进行合理的选择和设计。

连续系统离散化方法一、概述连续系统离散化方法是一种将连续系统转化为离散系统的方法，常用于控制系统的设计和分析。

该方法可以将一个无限维度的连续系统转化为有限维度的离散系统，使得控制器设计和分析变得更加简单和可行。

二、连续系统模型在开始进行连续系统离散化的过程中，需要先建立一个连续系统模型。

通常情况下，这个模型可以由微分方程或者差分方程来表示。

三、离散化方法1. 时域离散化方法时域离散化方法是最基本的离散化方法之一。

它通过将时间轴上的信号进行采样，从而将一个连续时间信号转换为一个离散时间信号。

这个过程中需要确定采样周期以及采样点数目等参数。

2. 频域离散化方法频域离散化方法是一种利用傅里叶变换将一个连续时间信号转换为一个频域信号，然后再对该频域信号进行采样得到一个离散时间信号的方法。

这个过程中需要确定采样频率以及采样点数目等参数。

3. 模拟器法模拟器法是一种将连续系统转化为离散系统的方法。

这个方法的核心思想是利用一个数字模拟器来模拟连续系统的行为，从而得到一个离散时间信号。

4. 差分方程法差分方程法是一种将连续系统转化为离散系统的方法。

这个方法的核心思想是利用微分方程在离散时间点上进行近似，从而得到一个差分方程。

四、误差分析在进行离散化过程中，会产生一定的误差。

因此，需要对误差进行分析和评估，以确保离散化后的结果与原始连续系统相近。

五、应用实例1. 机械控制系统机械控制系统中通常需要对连续时间信号进行采样和处理。

通过使用离散化方法，可以将连续信号转换为数字信号，并且可以在数字域上进行控制器设计和分析。

2. 电力电子控制系统电力电子控制系统中通常需要对高频信号进行处理。

通过使用频域离散化方法，可以将高频信号转换为数字信号，并且可以在数字域上进行控制器设计和分析。

六、总结连续系统离散化方法是一种将连续系统转化为离散系统的方法。

通过使用不同的离散化方法，可以将连续时间信号转换为数字信号，并且可以在数字域上进行控制器设计和分析。

连续状态方程离散化方法
连续状态方程离散化方法是一种将连续状态方程在离散空间上进行求解的
方法,它有助于简化数学模型的复杂性,加速计算的速度,并且能够更好地理解模型的工作原理。

连续状态方程是指描述化学反应或物理过程的数学方程,它通常包含在化学或物理手册中,用于描述反应或物理过程在不同条件下的动力学行为。

然而,由于连续状态方程通常包含大量参数,因此很难通过直接数值求解得到准确的解,需
要进行离散化处理。

离散化方法可以将连续状态方程转化为一组离散变量的线性方程,这些方程在离散空间上进行求解,从而得到数值解。

这种方法通常用于计算化学反应的速率、能量代谢率、热力学问题等领域。

离散化方法的基本思想是将连续状态方程转化为离散变量方程,然后通过数值求解的方法得到数值解。

离散化方法的具体方法包括差分法、插值法、拟牛顿法等。

其中,差分法是最常用的方法之一,它通过将连续状态方程离散化为一组离散变量方程,然后通过求解离散变量方程得到数值解。

除了差分法外,还有其他离散化方法,例如基于迭代法的插值法,以及基于有限元方法的拟牛顿法。

这些方法的选择取决于具体的应用场景和求解要求。

连续状态方程离散化方法的应用范围非常广泛,例如用于计算化学反应速率、热力学问题、生物分子的运动等。

此外,离散化方法还可以与其他数值方法相结合,例如有限差分法、有限元法等,用于解决更加复杂的问题。

在实际应用中,需要根据具体问题的特点选择合适的离散化方法,并进行合
理的参数设定和模型修正,才能得到准确的数值解。

因此,连续状态方程离散化方
法在实际应用中具有广泛的应用前景。