边界层 - 射流分析
- 格式:ppt
- 大小:389.00 KB
- 文档页数:36


高压氢气小孔泄漏射流分层流动模型与验证摘要:高压氢气泄漏射流是氢安全研究的重要内容,而在一定实验测量的基础上进行数值模拟是该领域的重要研究手段。
目前高压氢气射流完整数值模拟存在计算效率低、不稳定和难收敛的问题,而现有的简化模拟方法存在模型假设不合理和计算结果不准确的问题。
本文在定量激波结构测量的基础上,结合气体状态方程和守恒方程构建了分层流动模型,综合考虑了实际的射流核心区和边界层内不同的流动情况,且无需计算气流参数变化剧烈的激波区,从而简化了数值模拟计算。
采用分层流动模型模拟的速度场和浓度场计算结果与完整模拟的计算值和实验测量值一致,优于采用传统虚喷管模型模拟的结果。
该研究为高压氢气泄漏研究提供了一种在保证计算结果准确性基础上提高计算效率的模拟方法,对进一步推动氢安全研究具有一定意义。
作为一种极具潜力的可再生能源,氢气具有清洁、高效、单位质量能量密度高和来源广泛等优点。
以氢燃料电池汽车为代表的氢能研究和应用越来越受到关注[1]。
然而,在氢能的大规模商业化应用之前,必须全面系统地研究氢安全问题,以推动相关安全标准和技术规范的制定[2]。
典型的氢安全事故序列往往包括意外泄漏、扩散、点燃、爆燃或爆炸等过程[3]。
其中,氢气泄漏和扩散阶段的特性对于后续事故现象的发展和事故应急处理都具有决定性的作用。
氢气泄漏一般通过等效直径非常小的裂口(毫米级),以高速射流的形式发生,因此属于小孔泄漏的范畴,目前已有许多针对高压氢气射流的理论和实验研究[4-6],但是理论模型仅适用于自由空间射流分析,难以用于限制空间或有障碍物存在时的情况;实验研究测试工况有限,很难同时测量射流的流场和浓度场,且氢气射流实验所需的安全保障成本较高。
因此,在一定的实验验证的基础上进行数值模拟研究就成为完善氢安全研究的重要途径和必然选择。
高压氢气泄漏射流的数值模拟存在两个主要的难点:一是泄漏点外剧烈变化气流参数使得数值计算难以稳定和收敛;二是泄漏点的尺度(毫米级)与整个计算域的尺度(米级)之间的差距较大,且泄漏点附近需要特别精细的网格以捕捉气流参数剧烈变化的激波区域,从而导致整个计算域网格单元数目巨大。

射流jet从管口、孔口、狭缝射出,或靠机械推动,并同周围流体掺混的一股流体流动。
经常遇到的大雷诺数射流一般是无固壁约束的自由湍流。
这种湍性射流通过边界上活跃的湍流混合将周围流体卷吸进来而不断扩大,并流向下游。
射流在水泵、蒸汽泵、通风机、化工设备和喷气式飞机等许多技术领域得到广泛应用。
距射流源足够远处,湍性射流可以用边界层理论进行分析。
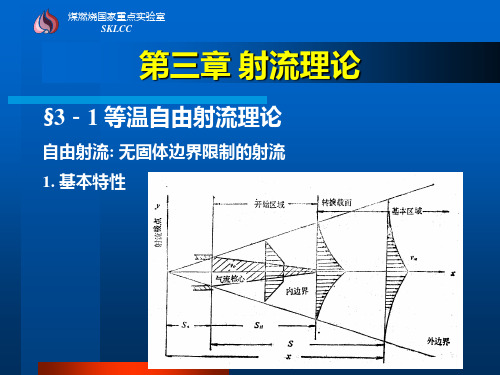
下面以不可压缩流体的平面湍性射流(见图)为例来说明,并设周围流体处于静止状态。
纵向平均速度ū(x,y)不等于零的射流区是以中心线为界的上下两个“边界层”的组合。
图中虚线是通常边界层理论意义下的边界。
在整个射流区内压力几乎不变。
因此,对于定常平面湍性射流,以下湍流边界层方程组(见湍流理论)近似成立:式中ū、尌为x、y方向的平均速度;ρ为流体密度;τ为湍流剪应力。
为求解以上方程组,首先必须写出湍流剪应力表达式。
根据涡粘性假设,,式中ετ为涡粘性系数,它是湍流的一个重要特征参数。
此系数可用L.普朗特提出的混合长l表示,即,并假定混合长沿射流宽度保持不变,且l(x)~b(x),这里b(x)为射流宽度的一半。
为了简化分析,进一步假定射流各横截面上的速度分布具有相似性,即。
根据以上方程和假定,H.赖夏特等对不可压缩流体的平面湍性射流进行了完整的理论分析,求得与实验相吻合的结果。
其主要结果如下:①射流宽度同到射流源的距离成正比,即平面湍性射流的边界是一条从射流源发出的直线,如果忽略雷诺数的影响,此射流大约以13°半角向后扩张;②射流速度分布为;③射流中心线上最大速度同到射流源的距离的平方根成反比,因此,随着此距离增大,射流最大速度越来越小。
轴对称湍性射流的分析方法同平面湍性射流类似。
不同的是,基本方程必须采用轴对称边界层方程,而且在结果中~x-1,即射流中心线上最大速度比平面射流衰减得更快。
上面仅讨论了不可压缩流体的常压自由射流。
各种工程技术中遇到的射流要比这种射流复杂。


南京航空航天大学硕士学位论文微尺度射流、平板边界层及叶栅流动实验研究姓名:***申请学位级别:硕士专业:航空宇航推进理论与工程指导教师:梁德旺;黄国平20060101南京航空航天大学硕士学位论文摘要本文以某型微型涡轮喷气发动机研制为背景,以认识微尺度下粘性流体流动状态及其机理和微涡轮叶栅通道内部流动特性为目的,设计并搭建了除本实验外还可供其他流体力学实验使用的微型风洞,并在该微型风洞基础上进行了微尺度射流实验、微尺度壁面边界层实验和微尺度涡轮叶栅实验。
微射流实验在出口宽度固定为20mm情况下,选取了3种不同出口高度:2mm,3mm和5mm,并通过改变速度使出口高度雷诺数在约20000到约55000之间改变,实验得到了流动图谱和微射流数学模型。
实验发现微射流中内外层流体微团之间的动量交换较常规大尺度下减弱,掺混变得相对缓慢,射流特征半厚度相对减小,从而初始段扩张角和基本段极角都有所减小。
该实验还同时研究了下游较远处射流流动情形,发现其掺混强度在微尺度二维平面射流和常规三维射流之间。
微尺度平板边界层实验选取从总长度为15mm的微平板前缘8mm到14mm之间的7个站位,4种马赫数,13个不同雷诺数(从35000到150000)的实验状态,发现了该尺度下边界层流动的一些新的特点,如形状因子比常规大尺寸下充分发展湍流状态的形状因子更小等。
微尺度叶栅实验使用弦长5.64mm的VKI-1叶型,选取了4种安装角度,3种叶尖间隙,4种出口主流马赫数状态的实验,得到了叶栅出口的总损失分布云图,发现微尺度叶栅栅后高损失区域与栅距的比例较常规大尺度下明显增大;同时对叶栅出口流动损失进行了分析,发现为了提高涡轮的效率,需要尽可能减小叶尖间隙并选择合适的安装角度(针对本实验中叶栅,最佳安装角为45~50度)。
关键词微流动微射流平板边界层流动涡轮叶栅Experimental Research on Micro Jet Flow , Flat Plate Boundary Layer Flow & Turbine Cascades FlowAbstractThis dissertation has on the research and design of a Micro Turbine Engine as background and it is for the purpose of comprehending viscous flow behaviors in micro scaled conditions and that in the mini-turbine cascades. A mini wind tunnel is designed and set up which also can be used in other micro flow experiments. On the basis of this mini wind tunnel, three mini flow experiments, including micro jet experiment, micro boundary layer experiment and mini-turbine cascades experiment, have been carried out.The micro jet experiment is under conditions of 3 different heights, 2mm, 3mm and 5mm of 2D (2 dimensional) rectangle jet outlet and the width of each is same, 20mm. 5 Reynolds numbers vary from 20,000 to 55,000.The experiment characters tell that compared with that of the normal scaled jet flow, the dilution power of this micro jet becomes weaker. Furthermore, the flow in the far down stream are also researched. The diluting power of the flow within this area is between that of 2D micro jets and normal scale 3D jets.The micro boundary layer experiment is carried out from 8mm to 14mm of a 15mm-long micro plane. Re numbers vary from 35,000 to 150,000 and 4 different Mach numbers are selected. Some new characters are discovered, such as velocity curve factor is smaller than that of well developed normal scale turbulence Boundary Layer.VKI-1 cascade with 5.64mm chord is adopted in mini-turbine cascades experiment. 4 assembly angles, 3 different blade tip clearances and 4 Mach number statuses are chosed as status variables. From 12 total pressure distribution maps, a conclusion is formed that ratio of high-loss area to full width of cascades period is large that that of normal scaled cascedes. Based on effiociency analysis,it has been found that narrower blade tip clearance and right assembly angle lead to utmost efficience. (e.g. 45~50 degree for this micro VKI-1 cascades)Keywords: Micro Flow, Micro Fluid, Micro jet(s), Flat Plate Boundary Layer Flow, Turbinary Cascades.承诺书本人郑重声明:所呈交的学位论文,是本人在导师的指导下,独立进行研究工作所取得的成果。
由于航发燃烧室中的流动特性极其复杂,要想提高数值计算的预测能力,必须要慎重选择湍流模型。
用四种不同的湍流模型对带双径向旋流杯的下游流场进行数值模拟,将计算结果与实验结果作对比,比较各湍流模型的原理与物理基础,优劣,并分析流场速度分布与回流区特性。
涉及的湍流模型:标准k-ε湍流模型(SKE)1标准k-ε湍流模型有较高的稳定性,经济性与计算精度,应用广泛,适合高雷诺数湍流,但不适合旋流等各向异性较强的流动。
2简单的湍流模型是两个方程的模型,需要解两个变量,即速度与长度。
在fluent中,标准k-ε湍流模型自从被Launder and Spalding 提出之后,就变成流场计算中的主要工具。
其在工业上被普遍应用,其计算收敛性与准确性都非常符合工程计算的要求。
3但其也有某些限制,如ε方程包含不能在壁面计算的项,因此必须使用壁面函数。
另外,其预测强分离流,包含大曲率的流动与强压力梯度流动的结果较弱。
它是个半经验的公式,是从实验现象中总结出来的。
动能输运方程是通过精确的方程推导得到,耗散率方程是通过物理推理,数学上模拟相似原型方程得到的。
应用范围:该模型假设流动为完全湍流,分子粘性的影响可以忽略,此标准κ-ε模型只适合完全湍流的流动过程模拟。
可实现的k-ε模型是才出现的,比起标准k-ε模型来有两个主要的不同点:·可实现的k-ε模型为湍流粘性增加了一个公式。
·为耗散率增加了新的传输方程,这个方程来源于一个为层流速度波动而作的精确方程。
术语“realizable”,意味着模型要确保在雷诺压力中要有数学约束,湍流的连续性。
应用范围:可实现的k-ε模型直接的好处是对于平板与圆柱射流的发散比率的更精确的预测。
而且它对于旋转流动、强逆压梯度的边界层流动、流动分离与二次流有很好的表现。
可实现的k-ε模型与RNG k-ε模型都显现出比标准k-ε模型在强流线弯曲、漩涡与旋转有更好的表现。
由于带旋流修正的k-ε模型是新出现的模型,所以还没有确凿的证据表明它比RNG k-ε模型有更好的表现。