正截面受弯承载力计算的基本规定

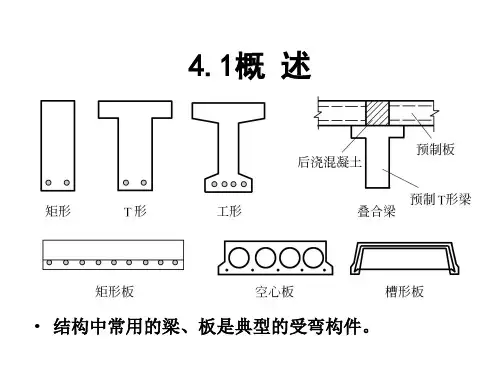
正截面抗弯承载力计算公式弯曲方向上的抗弯矩可以通过以下公式计算：M=σ*y*S其中，M为弯矩，单位为N·mm；σ为截面的应力，单位为N/mm²；y为截面的离心距，即截面中心到受拉纤维的距离，单位为mm；S为截面的抵抗矩，单位为mm³。

剪切方向上的抗剪力可以通过以下公式计算：V=τ*A其中，V为剪力，单位为N；τ为截面中剪应力，单位为N/mm²；A为截面的剪切面积，单位为mm²。

综合考虑两种方向上的抗弯承载力，可以得到正截面抗弯承载力的计算公式：W = Min(M/b , V/yc)其中，W为正截面的抗弯承载力，单位为N；M为弯矩，单位为N·mm；b为截面的宽度，单位为mm；V为剪力，单位为N；yc为截面的离心距，即截面中心到受拉纤维的距离，单位为mm。

在实际设计中，为了保证结构的安全性，通常需要根据材料的强度参数和结构的要求来确定截面的尺寸和形状。

在正截面抗弯承载力的计算过程中，需要注意以下几个要点：1.材料的强度参数：计算前需要明确截面所采用的材料的强度参数，如屈服强度和抗拉强度等。

2.截面形状的选择：根据结构的要求和截面的受力条件，选择适当的截面形状，如矩形、圆形、梯形等。

3.弯矩和剪力的确定：根据结构的受力分析，确定截面上的弯矩和剪力大小。

4.抵抗矩和剪切面积的计算：根据截面形状的不同，采用相应的计算方法计算抵抗矩和剪切面积。

5.安全系数的考虑：为了保证结构的安全性，在计算过程中通常会引入相应的安全系数，以考虑不同因素对结构性能的影响。

总之，正截面抗弯承载力的计算需要考虑弯曲方向上的抗弯矩和剪切方向上的抗剪力，通过综合考虑两者，可以得到正截面的抗弯承载力的计算公式。

在使用公式进行计算时，需要明确材料的强度参数，选择适当的截面形状，并考虑安全系数的影响，以确保结构的安全性。

受弯构件正截面受弯承载力计算
在进行受弯构件正截面受弯承载力计算时，首先需要了解构件的几何尺寸和材料特性。

几何尺寸包括构件的宽度、高度和长度，材料特性包括材料的抗弯强度和弹性模量等。

在进行受弯构件正截面受弯承载力计算时，一般采用等效应力法。

根据等效应力法，构件的正截面受弯承载力可以通过以下公式计算：M=σ×S
其中，M是受弯构件所受弯矩，σ是构件截面上的应力，S是截面的抵抗矩。

在计算截面上的应力时，可以使用以下公式：
σ=M×y/I
其中，M是受弯构件所受弯矩，y是距离截面中性轴距离，I是截面的惯性矩。

在计算截面的抵抗矩时，可以使用以下公式：
S=y×A×f
其中，y是距离截面中性轴距离，A是截面的面积，f是材料的抗弯强度。

综合以上公式，可以得到受弯构件的正截面受弯承载力公式：
N=σ×S=(M×y/I)×(y×A×f)
根据构件的几何尺寸和材料特性，可以计算出受弯构件的正截面受弯
承载力。

需要注意的是，在实际工程中，受弯构件的应力和截面的抵抗矩常常
不是均匀分布的，需要进行更加详细的计算和分析。

此外，由于材料的塑
性变形和结构的不完美性等因素的存在，实际承载能力可能小于理论计算值。

综上所述，受弯构件正截面受弯承载力计算是结构工程中的重要任务，它通过等效应力法来确定构件在受弯状态下的承载能力。

在实际工程中，
应该考虑到材料和结构的各种因素，进行更加精细的分析和计算。

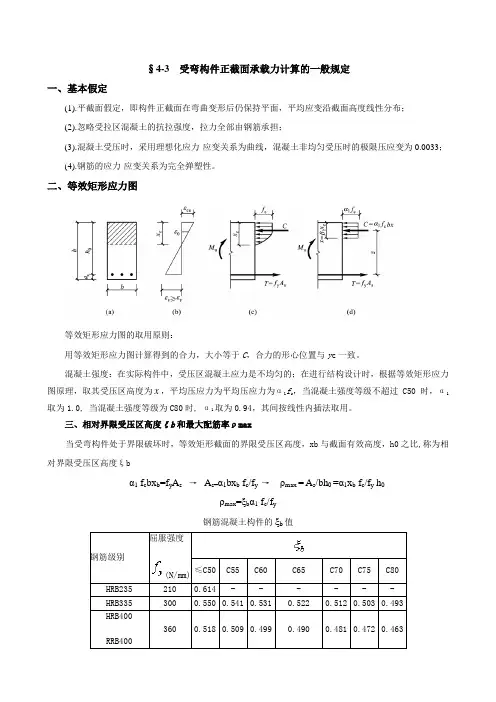
§4-3 受弯构件正截面承载力计算的一般规定一、基本假定(1).平截面假定，即构件正截面在弯曲变形后仍保持平面，平均应变沿截面高度线性分布；(2).忽略受拉区混凝土的抗拉强度，拉力全部由钢筋承担；(3).混凝土受压时，采用理想化应力-应变关系为曲线，混凝土非均匀受压时的极限压应变为0.0033；(4).钢筋的应力-应变关系为完全弹塑性。

二、等效矩形应力图等效矩形应力图的取用原则：用等效矩形应力图计算得到的合力，大小等于C，合力的形心位置与y c一致。

混凝土强度：在实际构件中，受压区混凝土应力是不均匀的；在进行结构设计时，根据等效矩形应力图原理，取其受压区高度为x，平均压应力为平均压应力为α1f c，当混凝土强度等级不超过C50时，α1取为1.0, 当混凝土强度等级为C80时, α1取为0.94，其间按线性内插法取用。

三、相对界限受压区高度ξb和最大配筋率ρmax当受弯构件处于界限破坏时，等效矩形截面的界限受压区高度，xb与截面有效高度，h0之比,称为相对界限受压区高度ξ bα1 f c bx b=f y A s →A s=α1bx b f c/f y →ρmax =A s/bh0 =α1x b f c/f y h0ρmax=ξbα1 f c/f y钢筋混凝土构件的ξb值四、最小配筋率ρmin最小配筋率ρmin 是适筋梁与少筋梁的界限，《规范》规定的纵向受力钢筋最小配筋百分率见附表B.3。

受弯构件：ρmin=max（0.2% ，0.45f t /f y）§4-4 单筋矩形截面正截面承载力计算仅在受拉区配置纵向受拉钢筋的矩形截面, 称为单筋矩形截面。

一、基本公式及适用条件1、基本公式：f y A s= α1 f c bx(4.9)(4.10)(4.11)2、适用条件（1）为防止超筋破坏：；或；或当时，（2）为防止少筋破坏：；或二、基本公式的应用受弯构件正截面承载力计算分截面设计和截面复核两类问题。

受弯构件正截面承载力计算有哪些基本假定受弯构件正截面承载力计算是工程力学中的重要内容，是评估和设计结构承载能力的关键步骤。

在进行这一计算时，工程师们通常会基于一系列基本假定进行分析。

下面我将深入探讨受弯构件正截面承载力计算的基本假定，并结合具体的工程实例进行解析。

1. 材料的弹性本构假定在进行受弯构件正截面承载力计算时，通常假定材料具有线弹性本构，即在应力和应变之间存在线性关系。

这意味着材料在弹性阶段的变形行为可以通过弹性模量来描述，这一假定为后续的承载力计算提供了基础。

2. 平面截面的假定在受弯构件的正截面承载力计算中，通常假定截面仍然是平面的。

这意味着截面内部的应力沿纵向和横向均保持平衡，从而简化了截面内部应力和变形的分析。

3. 材料的等强度假定受弯构件正截面承载力计算通常基于等强度假定，即假定截面内各点的材料强度相同。

这一假定在实际工程中虽然存在一定的误差，但在设计阶段可以简化材料强度的考虑，从而便于工程师进行承载力的评估和设计。

4. 截面平面仍然保持平面的假定在受弯构件正截面承载力计算中，通常假定截面在弯曲后仍然保持平面的。

虽然在弯曲过程中会产生一定的截面扭转变形，但这一假定可以简化截面内部应力和变形的分析，为后续的计算提供了便利。

受弯构件正截面承载力计算涉及了多项基本假定，这些假定在一定程度上简化了工程设计过程，便于工程师进行承载能力的评估和设计。

然而，在实际工程中，这些假定可能会与实际情况存在一定差异，因此在进行设计时需要综合考虑各种因素，以确保结构的安全可靠性。

在工程实践中，正确理解和应用这些基本假定对于进行承载能力计算是非常重要的。

工程师需要根据具体的工程要求和实际情况，合理应用这些假定，并结合实际数据和分析结果进行准确的承载能力评估和设计。

【总结】本文通过对受弯构件正截面承载力计算的基本假定进行深入探讨，并结合实际工程实例进行解析，阐述了这些基本假定在工程设计中的重要性和应用。

3.2-正截面承载力计算3.2 正截面承载力计算钢筋混凝土受弯构件通常承受弯矩和剪力共同作用，其破坏有两种可能：一种是由弯矩引起的，破坏截面与构件的纵轴线垂直，称为沿正截面破坏；另一种是由弯矩和剪力共同作用引起的，破坏截面是倾斜的，称为沿斜截面破坏。

所以，设计受弯构件时，需进行正截面承载力和斜截面承载力计算。

一、单筋矩形截面1.单筋截面受弯构件沿正截面的破坏特征钢筋混凝土受弯构件正截面的破坏形式与钢筋和混凝土的强度以及纵向受拉钢筋配筋率ρ有关。

ρ用纵向受拉钢筋的截面面积与正截面的有效面积的比值来表示，即ρ＝As/(bh0)，其中A s为受拉钢筋截面面积；b为梁的截面宽度；h0为梁的截面有效高度。

根据梁纵向钢筋配筋率的不同，钢筋混凝土梁可分为适筋梁、超筋梁和少筋梁三种类型，不同类型梁的具有不同破坏特征。

①适筋梁配置适量纵向受力钢筋的梁称为适筋梁。

适筋梁从开始加载到完全破坏，其应力变化经历了三个阶段，如图3.2.1。

第I阶段（弹性工作阶段）：荷载很小时，混凝土的压应力及拉应力都很小，应力和应变几乎成直线关系，如图3.2.1a。

当弯矩增大时，受拉区混凝土表现出明显的塑性特征，应力和应变不再呈直线关系，应力分布呈曲线。

当受拉边缘纤维的应变达到混凝土的极限拉应变εtu时，截面处于将裂未裂的极限状态，即第Ⅰ阶段末，用Ⅰa表示，此时截面所能承担的弯矩称抗裂弯矩M cr，如图3.2.1b。

Ⅰa阶段的应力状态是抗裂验算的依据。

第Ⅱ阶段（带裂缝工作阶段）：当弯矩继续增加时，受拉区混凝土的拉应变超过其极限拉应变εtu，受拉区出现裂缝，截面即进入第Ⅱ阶段。

裂缝出现后，在裂缝截面处，受拉区混凝土大部分退出工作，拉力几乎全部由受拉钢筋承担。

随着弯矩的不断增加，裂缝逐渐向上扩展，中和轴逐渐上移，受压区混凝土呈现出一定的塑性特征，应力图形呈曲线形，如图3.2.1c。

第Ⅱ阶段的应力状态是裂缝宽度和变形验算的依据。

当弯矩继续增加，钢筋应力达到屈服强度f y，这时截面所能承担的弯矩称为屈服弯矩M y。

受弯构件正截面承载力计算的依据受弯构件的正截面承载力计算是基于材料的力学性能以及力学原理的基础上进行的。

这里将从材料力学性能、截面形状、状态及应力分布、截面性质以及计算方法等几个方面进行详细介绍。

首先，材料力学性能是正截面承载力计算的基础。

通常考虑的主要性能有弹性模量、屈服强度、抗拉强度、断裂强度等。

这些性能参数与所用材料的力学性能有关，对于计算来说是重要的参考标准，需要通过实验和测试得到准确的数值。

在计算中，这些参数用来确定截面的强度和刚度，从而计算出承载力。

其次，截面形状、状态及应力分布也是计算的重要依据。

一般来说，正截面承载力计算通常假设构件是线弹性的，也就是说所考虑的材料在加载时仍然服从胡克定律。

以钢结构为例，正截面承载力计算时会采用弹性理论，并通过计算应力、应变和应力分布来确定构件的承载能力。

在计算过程中，需要考虑截面的几何形状，如矩形、圆形、梯形等，并根据截面的状态和加载情况来确定应力分布，进而计算出承载力。

截面性质也是计算的依据之一、例如，正截面承载力计算中常常采用矩形截面，因为矩形截面具有分布均匀的应力情况，方便计算和确定承载能力。

另外，截面的其他性质，如面积、惯性矩、截面模量等也是计算的重要参数，需要根据具体截面的尺寸和形状来确定。

最后，计算方法也是正截面承载力计算的依据之一、目前，常用的计算方法有弯矩引起的应力法、轴力引起的应力法和切力引起的应力法等。

这些方法根据构件的不同受力状态和截面形状，采用不同的计算公式和理论模型来确定构件的承载能力。

总而言之，受弯构件正截面承载力计算的依据主要包括材料的力学性能、截面形状、状态及应力分布、截面性质以及计算方法等。

这些依据之间相互关联，通过计算公式和理论模型来确定构件的承载能力，为结构设计和工程实践提供了重要的理论支持。