具有年龄结构的种群增长模型模拟(生态学实验报告)

问题陈述：一群动物最高年龄为15岁(年)，繁殖周期为5年，因此每5岁一组分成3个年龄组，各组繁殖率为0, 4, 3，存活率为1/2,1/4。

建立种群增长模型。

(1)开始每组各有1000只，求30年内每5年各组动物数量; 并确定种群的固有增长率和稳定分布。

(2)如果饲养者每5年出售一次动物，出售量为龄组i在这5年的增量，记出售量与该龄组存量之比为本时段收获系数H，即hi(n)ai (n)=ai (n)-ai (n-1)，H(n)=diag(h1(n), h2 (n), h3(n)) 。

建立稳定收获模型。

(3)如果饲养者只出售幼龄组动物，即h2 =h3 =0。

求稳定收获的收获系数h1，该种群的稳定分布和收获量。

（所谓稳定收获指收获量不变，这时收获系数和收获后的种群数量与时间n无关）问题（1）分析：问题（1）蕴含着三个平衡关系：第k个5年的幼年=第k-1个5年的中年和老年所繁殖之和；第k个5年的中年=第K-1个5年的存活下来的幼年；第k个5年的老年=第K-1个5年的存活下来的中年；于是可以依此给出LESLIE矩阵，建立模型，求出30年内每5年各组的数量。

至于固有增长率和稳定分布，归结为求矩阵的特征值特征向量的问题。

问题假设：幼年经过5年存活下来的就成长为中年，中年经过5年存活下来的就成长为老年，老年经过5年全部死亡。

变量：幼年在第K个5年的数量a1(k)中年在第K个5年的数量a2(k)老年在第K个5年的数量a3(k)LESLIE矩阵A建立模型：根据平衡关系可以列出方程：[a1(k) a2(k) a3(k) ]’=A*[ a1(k-1) a2(k-1) a3(k-1)] ’;其中A=[0 4 3;0.5 0 0 ;0 0.25 0];初始条件为:[a1(1) a2(1) a3(1) ]’=[1000 1000 1000]’1按照这个递推关系求出30年内各个年龄组的数量为第个5年0 1 2 3 4 5 6 幼年1000 7000 2750 14375 8125 29781 21641中年1000 500 3500 1375 7188 4063 14891老年1000 250 125 875 344 1797 10162 画出各个年龄组数量随时间变化图像如下蓝色代表幼年，绿色代表中年，红色代表老年。

种群的逻辑斯蒂增长实验报告本次实验所研究的是种群的逻辑斯蒂增长。

逻辑斯蒂增长模型是指在一定环境条件下，种群数量进行上升的模型。

该模型的增长速率受到环境资源的限制，并且在达到极限后，随着资源的减少而逐渐趋于平缓或停滞。

为了更加深入地了解逻辑斯蒂增长的规律和特性，我们进行了一次实验。

实验方法：我们将实验用的种群分成两个组，一组在充足资源的条件下生长，另一组在缺少资源的条件下生长。

充足资源组在适宜的温度、光照强度和氧气含量下生长。

缺乏资源组则在低温、弱光照和高二氧化碳含量的环境下生长。

在实验过程中我们记录每组种群数量的变化情况，直到达到最终的平衡状态。

实验结果：根据实验数据，我们得出以下结论：1. 种群数量增长的速度在充足资源组中更快，而在缺乏资源组中较慢。

2. 在初期，两个组的种群数量增长速度都很快。

但随着种群数量的增长，增长速度逐渐减缓。

3. 在达到最大数量后，充足资源组的种群数量呈现平缓状态，而缺乏资源组的种群数量则停滞。

分析和结论：我们将以上实验数据分析进行如下解释：1. 种群数量增长的速度受到环境资源的限制。

当资源充足时，种群数量增长快；但资源不足时，种群数量增长缓慢。

2. 因为环境资源是有限的，种群数量增加后，需要更多的资源来支撑更多的生命。

因此，增长速度会逐渐减缓，直到达到最大数量。

综上所述，逻辑斯蒂增长模型可以很好地解释种群数量增长的规律。

在自然界中，种群增长也受到各种限制，如食物、栖息地、气候等。

这些因素的作用机制类似于上述的实验结果。

通过这次实验，我们更加深入地理解了逻辑斯蒂增长模型的规律，以及资源限制对种群数量和生存的影响。

实验报告种群增长极环境的影响一、实验目的和要求1.了解Logistic 模型,并能运用模型进行种群增长的研究分析。

2.了解小球藻的培养过程,掌握Logistic 增长曲线绘制的一般方法。

3.了解环境对种群增长的影响。

二、实验内容和原理在自然条件下，因受空间，食物等必需资源的限制，在有限的条件下,开始时因数量少而增长缓慢,随后逐渐加快；但是随着环境阻力逐渐增加,增长速度又开始下降。

当种群数量达到其环境资源所能维持的最大数量,即环境容纳量时,种群停止增长并维持下去。

种群的个体出生率和死亡率都随着种群密度变化而变化。

动物种群不可能持续呈“J ”型增长。

随着数量的上升，个体间为资源的竞争相应增加，以至影响种群的出生率和存活率，种群增长率下降，种群数量停止增加甚至下降。

逻辑斯谛 (Logistic) 方程是描述在资源有限条件下种群增长规律的一个最佳数学模型。

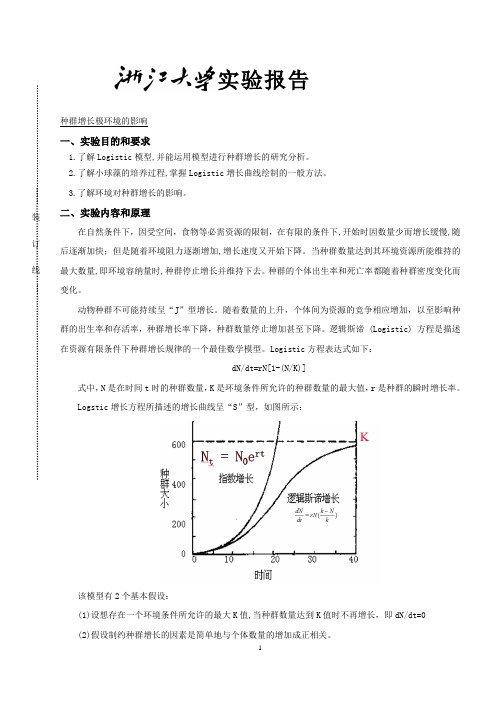
Logistic 方程表达式如下：dN/dt=rN[1-(N/K)]式中，N 是在时间t 时的种群数量，K 是环境条件所允许的种群数量的最大值，r 是种群的瞬时增长率。

Logstic 增长方程所描述的增长曲线呈“S ”型，如图所示：该模型有2个基本假设：(1)设想存在一个环境条件所允许的最大K 值,当种群数量达到K 值时不再增长，即dN/dt=0 (2)假设制约种群增长的因素是简单地与个体数量的增加成正相关。

装 订线三、主要仪器设备光照培养箱、三角瓶、分光光度计，移液管；小球藻、小球藻培养液。

四、操作方法和实验步骤1.取10mL藻种培养液转移至250mL三角瓶中,加入100mL培养液(空白对照组加入110mL培养液),震荡均匀测定OD650值(以培养液作为空白对照)，重复2次，取其平均值作为起始浓度；每组四瓶。

2.帖上标签，日期、组名等。

3.三角瓶置于光温培养箱中，分别在20℃和30℃、12小时光照条件下连续培养一周，每天定时观测一次(测定前振荡均匀，每次测定用同一仪器和比色皿)，记录OD650值。

华南师范大学实验报告学生姓名 学 号 专 业 年级、班级 课程名称生态学实验 实验项目 种群的逻辑斯蒂增长模型 实验类型 验证 □设计□综合 实验时间 年 月 日 实验指导老师 实验评分种群的逻辑斯蒂增长模型1 实验目的1.1 了解种群在有限环境中的增长方式，理解环境对种群增长的限制作用；1.2 学习种群密度的检测，种群增长模型的建立，参数的估计以及种群增长曲线的拟合等实验技术； 1.3 加深对逻辑斯蒂增长模型的特征及其模型中两个参数r 、k 的理解。

2 材料与方法2.1 材料与试剂草履虫、干稻草、鲁哥氏固定液2.2 实验仪器六孔培养皿、量筒、解剖镜、锥形瓶、烧杯、锥形瓶2.3 实验方法2.3.1 配制人工海水 按表1配制30‰人工海水的人工海水，再将30‰人工海水加矿泉水稀释为20‰的人工海水。

表1 30‰人工海水配方（1升水） 药品 含量 NaCL 28.000g KCL 0.800g MgCl 2·6H 2O 25.000g CaCl 2·H 2O1.200g2.3.2 接种红色伪角毛虫 在六孔平板中的两个孔滴加5ml20‰人工海水，两个孔滴加5ml30‰人工海水→做好标记→每孔分别放两粒米粒→分别在解剖镜中吸取50只红色伪角毛虫→常温下培养→实验开始的7天内，每天定时对培养液中的草履虫密度进行检测。

（每次计数至少重复3次）2.3.3 Logistic 增长模型的拟合 种群在有限环境中的连续增长表现为Logistic 增长，其增长曲线呈S 型。

Logistic 增长数学模型为：）（K N K N N -r dt d =或）（KNN N -1r dt d = 式中：dtd N为种群的增长；N 为种群大小；t 为时间；r 为种群的瞬时增长率；K 为环境容纳量； ）（KN-1为“剩余空间”。

因此，Logistic 模型的积分公式为：rt-a e 1+=KN式中：a 与初始数量0N 有关的常数；e 为自然对数的底。

第五章 种群增长种群数量大小和增长速度是种群生态学中的重要问题，也是社会极为关切的问题。

种群增长模型即是以数学模型定量描述种群数量的动态变化，重点是探讨哪些因素决定种群大小，哪些参数决定种群对自然和人为干扰的反应速度。

§1. 非密度制约的种群增长种群在“无限”的环境中，即假定环境中空间、食物等资源是无限的，因而种群数量的增长不受种群密度的限制，即非密度制约性增长（density-independent growth ），这类种群的增长呈指数增长（exponential growth ）。

在数学表达上，指数增长又与世代重叠与否有关，世代不重叠的种群增长为离散型增长，以差分方程描述，而世代重叠的种群增长为连续型增长，以微分方程描述。

一、世代不重叠种群的离散型指数增长模型假设：①种群增长是无限的；②世代不重叠；③没有迁出与迁入；④不具年龄结构，即各年龄组的出生率与死亡率均视为相等。

以N 表示种群数目（大小、密度），t 表示世代时间，λ表示周限增长率（即指种群在一个世代时间内的增长率）。

则 N t+1=λN 或 N t = N 0λt当λ>1时, N t+1 > N t , 种群增长；λ=1时，N t+1 = N t , 种群稳定；0<λ<1时，N t+1 < N t , 种群下降；λ= 0时，N t+1= 0，下一代灭绝。

二、世代重叠种群的连续型指数增长模型假设：①种群增长是无限的；②世代重叠；③没有迁入和迁出；④不具年龄结构（各年龄组出生率、死亡率均相等）。

r 为瞬时增长率（每员增长率或内禀自然增长率）：既不随时间而变化，又不受种群密度的影响，其最大值r m 是物种固有的受遗传特性控制的生殖潜能。

则：,1r d t dN N =即⎰⎰+=c r d t dN N 1当 t = 0 时，N o = e c ·c r · o = e c所以 N t = N o e r t当 r > 0时，N t > N o ，种群增长； ,ln c rt N rN dtdN t +==rtc c rt t e e eN ⋅==+r = 0时，N t = N o ，种群稳定；r < 0时，N t < N o ，种群下降。

实验22 按年龄分组的种群增长模型实验目的1、利用常差分方程建立实际问题的数学；2、学会用MATLAB 软件计算出模型的相关问题。

实验内容1、用常差分方程建立按年龄分组的种群增长模型；2、用MATLAB 软件求按年龄分组的种群模型的一些问题。

实验步骤问题 野生或饲养的动物因繁殖而增加，因自然死亡和人为屠杀而减少，不同年龄动物的繁殖率、死亡率有较大差别，因此在研究某一种群数量的变化时，需要考虑按年龄分组的种群增长。

将种群按年龄等间隔地分成若干个年龄组，时间也离散化为时段，给定各年龄组种群的繁殖率和死亡率（在稳定环境下不妨假定它们与时段无关），建立按年龄分组的种群增长模型，预测未来各年龄组的种群数量，并讨论时间充分长以后的变化趋势。

模型及其求解 设种群按年龄等间隔地分成n 个年龄组，记0,1,2,...,i n =，时段记作0,1,2,...k =，且年龄组区间与时段长度相等（若5岁为一个年龄组，则5年为一个时段）。

以雌性个体为研究对象比较方便，以下种群数量均指其中的雌性。

记第i 年龄组在时段k 的数量为()x k i ；第i 年龄组的繁殖率为i b ，表示每个（雌性）个体在一个时段内繁殖的数量；第i 年龄组的死亡率为i d ，表示一个时段内死亡数与总数的比。

1i i s d =-是存活率。

为建立()i x k 的变化规律，我们注意到:第1年龄组在时候1k +的数量为各年龄组在第k 时段繁殖的数量之和，即11(1)()0,1,ni i i x k b x k k =+==∑(22.1)而第1i +年龄组在时段1k +的数量是第i 年龄组在时段k 存活的数量，即 1(1)()1,2,,1,0,1,i i i x k s x k i n k ++==-=(22.2) 记在时段k 种群各年龄组的数量为12()((),(),,())T n x k x k x k x k = 。

(22.3)这样，有1(1)(),0,1,k x k Lx k k ++== (22.4)将()x k 归一化后的向量记做()xk ,称种群按年龄的分布向量。