高一数学春季讲义 第6讲 常见不等式通用解法 教师版

主 题一元二次不等式的解法教学内容1. 掌握一元二次不等式的解法；2. 学会用区间表示集合；3. 通过利用二次函数的图像来求解一元二次不等式的解集，培养数形结合的数学思想。

一、一元二次不等式的解法：探究：我们来考察它与其所对的二次函数25y x x =-及二次方程250x x -=的关系：（1）当0x <或5x >时，0y >，即在x 轴上方； （2）当0x =或5x =时，0y =，即在x 轴上； （3）当05x <<时，0y <，即在x 轴下方.其中0x =，5x =是二次函数25y x x =-与x 轴的交点，是二次方程250x x -=的两根.探究得出：结合图像知不等式250x x -≤的解集是 {}05x x ≤≤ 那么对于一般的不等式 20ax bx c ++>或()200ax bx c a ++<>又怎样去寻求解集呢？请同学们思考下列问题：如果相应的一元二次方程02=++c bx ax 分别有两实根、惟一实根，无实根的话，其对应的二次函数)0(2>++=a c bx ax y 的图像与x 轴的位置关系如何？可以提问程度较好的学生【答】二次函数c bx ax y ++=2的图像开口向上且分别与x 轴交于两点，一点及无交点。

现在请同学们观察表中的二次函数图，并写出相应一元二次不等式的解集。

ac b 42-=∆ 0>∆ 0=∆ 0<∆二次函数)0(2>++=a c bx ax y 的图像02=++c bx ax 的根 ab x 22,1∆±-=ab x x 221-== ∅02>++c bx ax 的解集 02<++c bx ax 的解集【答】02>++c bx ax 的解集依次是{}.R ;2R ;21⎭⎬⎫⎩⎨⎧-≠∈><a b x x x x x x x x 但或 02<++c bx ax 的解集依次是{}.;;21∅∅<<x x x x它是我们今后求解一元二次不等式的主要工具。

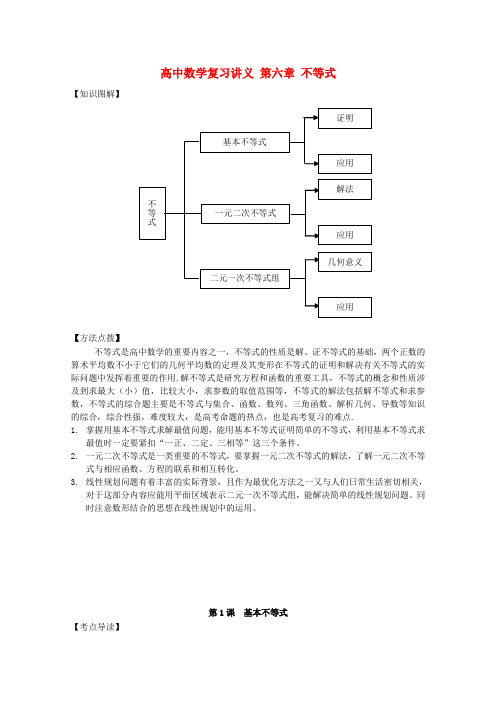
高中数学复习讲义第六章不等式【知识图解】【方法点拨】不等式是高中数学的重要内容之一，不等式的性质是解、证不等式的基础，两个正数的算术平均数不小于它们的几何平均数的定理及其变形在不等式的证明和解决有关不等式的实际问题中发挥着重要的作用.解不等式是研究方程和函数的重要工具，不等式的概念和性质涉及到求最大（小）值，比较大小，求参数的取值范围等，不等式的解法包括解不等式和求参数，不等式的综合题主要是不等式与集合、函数、数列、三角函数、解析几何、导数等知识的综合，综合性强，难度较大，是高考命题的热点，也是高考复习的难点.1.掌握用基本不等式求解最值问题，能用基本不等式证明简单的不等式，利用基本不等式求最值时一定要紧扣“一正、二定、三相等”这三个条件。

2.一元二次不等式是一类重要的不等式，要掌握一元二次不等式的解法，了解一元二次不等式与相应函数、方程的联系和相互转化。

3.线性规划问题有着丰富的实际背景，且作为最优化方法之一又与人们日常生活密切相关，对于这部分内容应能用平面区域表示二元一次不等式组，能解决简单的线性规划问题。

同时注意数形结合的思想在线性规划中的运用。

第1课基本不等式【考点导读】1. 能用基本不等式证明其他的不等式，能用基本不等式求解简单的最值问题。

2. 能用基本不等式解决综合形较强的问题。

【基础练习】1.“a >b >0”是“ab <222a b +”的充分而不必要条件(填写充分而不必要条件、必要而不充分条件、充分必要条件、既不充分也不必要条件)2.ca bc ab a c c b b a ++=+=+=+则,2,2,1222222的最小值为12-3.已知,x y R +∈，且41x y +=，则x y ⋅的最大值为161 4.已知lg lg 1x y +=，则52x y+的最小值是2 【范例导析】 例1.已知54x <，求函数14245y x x =-+-的最大值. 分析：由于450x -<，所以首先要调整符号. 解：∵54x <∴540x -> ∴y=4x-2+145x -=154354x x ⎛⎫--++ ⎪-⎝⎭≤-2+3=1 当且仅当15454x x-=-，即x=1时，上式成立，故当x=1时，max 1y =. 例2.（1）已知a ，b 为正常数，x 、y 为正实数，且1a b+=x y，求x+y 的最小值。

高一数学复习考点题型专题讲解第6讲等式与不等式性质一、单选题1．下列运用等式的性质，变形不正确的是（）A．若x=y，则x+5=y+5B．若a=b，则ac=bcC．若a bc c=，则a=bD．若x=y，则x ya a=【答案】D【分析】利用等式的性质分别对各选项逐一分析判断并作答.【解析】对于选项A，由等式的性质知，若x=y，则x+5=y+5，A正确；对于选项B，由等式的性质知，若a=b，则ac=bc，B正确；对于选项C，由等式的性质知，若a bc c=，则a=b，C正确；对于选项D，由等式的性质知，若x=y，则x ya a=的前提条件为a≠0，D错误．故选：D2．已知0a b c>>>，则以下不等式不正确的是（）A．22ac bc>B．c a c b a b ++>C ．22a ab b >>D ．b a a b> 【答案】D【分析】利用不等式的性质逐项判断即得.【解析】∵0a b c >>>，∴2220,c ac bc >>，故A 正确； ∵0a b c >>>，∴1110,ab a b ><，∴,11c c c c a b a b >+>+，即c a c b a b++>，故B 正确； 由0a b >>可得，22,a ab ab b >>，∴22a ab b >>，故C 正确； 因为0a b >>，所以22a b >，10ab >，所以2211a b ab ab ⨯>⨯，即a b b a>．故D 错误. 故选：D ．3．下列命题正确的是（ ） A ．若ac bc >，则a b > B ．若ac bc =，则a b = C ．若a b >，则11ab< D ．若22ac bc >，则a b > 【答案】D【分析】由不等式性质依次判断各个选项即可.【解析】对于A ，若0c <，由ac bc >可得：a b <，A 错误； 对于B ，若0c =，则0ac bc ==，此时a b =未必成立，B 错误； 对于C ，当0a b >>时，110ab>>，C 错误；对于D ，当22ac bc >时，由不等式性质知：a b >，D 正确. 故选：D.4．已知a ，b 为实数，则“1a b >>”是“1111a b <--”的（ ） A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 【答案】A【分析】根据不等式的性质可判断. 【解析】由11111011a b a b a b >>⇒->->⇒<--． 当0a =，2b =时，11111a b a b <>>--¿， 故“1a b >>”是“1111a b <--”的充分不必要条件. 故选：A ．5．已知22t a b =+，221s a b =++，则（ ） A ．t s >B ．t s ≥C ．t s ≤D ．t s < 【答案】C【分析】作差法即可比较大小.【解析】()()()22222110t s a b a b a -=+-++=--≤，故t s ≤，当1a =时，t s =. 故选：C.6．已知2x ≠，1y ≠-，2242M x y x y =+-+，5N =-，则M 与N 的大小关系是（ ） A ．M N >B ．M N <C ．M N =D ．不能确定 【答案】A【分析】采用作差法计算M N -与0的大小关系，由此判断出,M N 的大小关系. 【解析】因为()()222242521x y x y M N x y +-++=-++-=，且2x ≠，1y ≠-，所以0M N ->，所以M N >， 故选：A.7．若a ，b ，c ，d 均为实数，则下列不等关系中一定成立的是（ ） A ．若,a b c d ><，则a c b d +>+B ．若,a b c d >>，则ac bd > C ．若0,0c d bc ad ab ->->，则0ab <D ．若0,0a bcd >>>>>【答案】D【分析】举特例说明并判断选项A ，B ，利用不等式性质推理判断选项C ，D 即可作答. 【解析】对于A ，如3>2，-3<0，显然3+(-3)<2+0，A 不正确； 对于B ，如3>2，-4>-5，显然3(4)2(5)⨯-<⨯-，B 不正确； 对于C ，因0bc ad ->，而0c d bc adabab--=>，则0ab >，C 不正确； 对于D ，因0c d >>，则110d c >>，又0a b >>，于是得0a b d c >>D 正确. 故选：D8．已知1a 、()21,a ∈+∞，设1211P a a =+，1211Q a a =+，则P 与Q 的大小关系为（ ）A ．P Q >B ．P Q <C ．P Q =D ．不确定 【答案】B【分析】利用作差法可得出P 与Q 的大小关系.【解析】解析：()()()121121212121212121212111111111a a a a a a a a a P Q a a a a a a a a a a a a -+---⎛⎫⎛⎫++-=+-+=-== ⎪ ⎪⎝⎭⎝⎭． 因为1a 、()21,a ∈+∞，所以110a ->，210a -<，120a a >，所以()()1212110a a P Q a a ---=<，所以P Q <．故选：B．9．设n*∈NAC．不能确定【答案】B【分析】把两个代数式进行分子有理化，比较分母的大小可以比较出大小关系．22-==.22-==.*n N∈42,31n n n n+>++>+根据不等式的开方性质可以得出再根据不等式相加性质可以得出成立，因此本题选B．【点睛】对于二次根式的加減运算，分母有理化是常见的运算要求，但是有时分子有理化会起到意想不到的作用，尤其是在比较二个二次根式减法算式之间的大小关系时，经常会用到分子有理化这个方法．当然不等式的性质也是很重要的．10．已知14a b≤+≤，12a b-≤-≤，则42a b-的取值范围是（）A．[]4,10-B．[]3,6-C．[]2,14-D．[]2,10-【答案】D【分析】利用待定系数法得出()()423a b a b a b -=++-，并计算出()3a b -的取值范围，利用不等式的性质可得出42a b -的取值范围.【解析】设()()()()42a b x a b y a b x y a x y b -=++-=++-，42x y x y +=⎧∴⎨-=-⎩，解得13x y =⎧⎨=⎩， ()()423a b a b a b ∴-=++-，14a b ≤+≤Q ，12a b -≤-≤，()336a b ∴-≤-≤，由不等式的性质可得()()2310a b a b -≤++-≤，即24210a b -≤-≤， 因此，42a b -的取值范围是[]2,10-，故选D.【点睛】本题考查求代数式的取值范围，解题的关键就是将所求代数式用已知的代数式加以表示，在求解可充分利用待定系数法，考查运算求解能力，属于中等题. 11．已知ABC 的三边长分别为a 、b 、c ，有以下4个命题：（1 （2）以2a 、2b 、2c 为边长的三角形一定存在； （3）以2a b +、2b c +、2c a+为边长的三角形一定存在；（4）以ab 、bc 、ca 为边长的三角形一定存在；其中正确命题的个数为（ ） A ．1个B ．2个C ．3个D ．4个 【答案】B【分析】ABC 的三边长分别为a 、b 、c ，不妨设a b c ≥≥，则b c a +>，通过平方作差判断（1）正确，直接作差判断（2）（3），举反例判断（4），进而可得正确答案. 【解析】ABC 的三边长分别为a 、b 、c ，不妨设a b c ≥≥，则b c a +>，对于（1）：220b c a -=+-+1）正确；对于（2）：()2222220b c a b c bc a +-=+-->不一定成立，因此以2a 、2b 、2c 为边长的三角形不一定存在；故（2）不正确； 对于（3）：0222b c c a a b c ++++-=>，因此以2a b +、2b c +、2c a+为边长的三角形一定存在；故（3）正确；对于（4）： 取5,4,2a b c ===，b c a +>，因此a 、b 、c ，能构成一个三角形的三边，而ac bc ab +<，因此以ab 、bc 、ca 为边长的三角形不一定存在，故（4）不正确， 所以正确的命题有2个， 故选：B【点睛】关键点点睛：本题关键是设不妨设a b c ≥≥，则b c a +>，然后（1）中带根号，所以平方后作差满足两边之和大于第三边，对于（2）（3）直接作差，利用两个小编之和大于第三边，即可求解.12．已知,αβ满足11123αβαβ-≤+≤⎧⎨≤+≤⎩，，则3αβ+的取值范围是A ．137αβ≤+≤B ．313αβ+-5≤≤C ．37αβ+-5≤≤D ．1313αβ+≤≤ 【答案】A【分析】首先利用待定系数法用,2αβαβ++表示出3αβ+，然后利用不等式的性质结合题意确定其取值范围即可.【解析】设()()()()322.αβλαβυαβλυαλυβ+=+++=+++ 比较,αβ的系数，得1,23,λυλυ+=⎧⎨+=⎩从而解得1,2,λυ=-⎧⎨=⎩ 即()()322αβαβαβ+=-+++， 由题得()()11,226αβαβ-++≤-≤≤2≤，两式相加，得137αβ≤+≤. 故选A.【点睛】本题主要考查不等式的性质，函数与方程的思想，待定系数法的应用等知识，意在考查学生的转化能力和计算求解能力.二、多选题13．已知a ，b ，c ，d 均为实数，则下列命题正确的是（ ） A ．若a >b ，c >d ，则a -d >b -c B ．若a >b ，c >d 则ac >bd C ．若ab >0，bc -ad >0，则c da b >D ．若a >b ，c >d >0，则a b d c> 【答案】AC【分析】根据不等式的性质和特殊值法逐项分析可求得答案. 【解析】解：由不等式性质逐项分析：A 选项：由c d >，故c d -<-，根据不等式同向相加的原则a d b c ->-，故A 正确B 选项：若0a b >>，0c d >>则ac bd <，故B 错误；C 选项：0ab >，0bc ad ->，则0bc adab ->，化简得0c d a b->，故C 正确； D 选项：1a =-，2b =-，2c =，1d =则1a bd c==-，故D 错误. 故选：AC14．下列命题正确的是（ ）A ．2,,2(1)0a b R a b ∃∈-++≤B ．a ∀∈R ，x R ∃∈，使得ax ＞2C ．ab =0是220a b +=的充要条件D ．a ≥b ＞－1，则11a b a b ≥++【答案】AD【分析】举出一例判断存在命题是否正确，判断A ，举反例判断BC ，由不等式的性质判断D ．【解析】对A ，2,1a b ==-时，22(2)(1)0a b -++=，A 正确； 对B ，0a =时，对任意x ∈R ，0ax =，2>ax 不成立，B 错； 对C ，1,0a b ==时满足0ab =，但此时2210a b +=≠，C 错； 对D ，1a b >-≥，则110a b +≥+>，(1)(1)a b a ab b ab b a +=+≥+=+，则11a b a b≥++，D 正确．故选：AD ．15．设a 、b 为正实数下列命题正确的是（ ） A ．若221a b -=，则1a b -< B ．若111ba-=，则1a b -<C 1=，则1a b -<D ．若1a ≤，1b ≤，则1a b ab -≤-E ．若a b >，则a c b c > 【答案】AD【解析】利用不等式的性质以及反证法证明1a b -<成立即可判断A 选项； 取5a =，56b =判断B 选项； 取4a =，1b =判断C 选项；利用不等式的性质以及作差法判断D 选项； 取0c =，判断E 选项；【解析】对于A ，若a ，b 为正实数，则221100a b a b a b a b a b-=⇒-=⇒->⇒>>+，故0a b a b +>->，若1a b -≥，则111a b a b≥⇒+≤+，这与0a b a b +>->矛盾，故1a b -<成立，所以A 正确；对于B ，取5a =，56b =，则111b a -=，但5516a b -=->，所以B 不正确；对于C ，取4a =，1b =1=，但31a b -=<不成立，所以C 不正确；对于D ，()()()()2222222211110a b ab a b a b a b ---=+--=--≤，即1a b ab -≤-，所以D 正确；对于E ，取0c =，则a c b c =，所以E 不正确.故选AD.【点睛】本题主要考查了由已知条件判断所给不等式是否正确，属于中档题. 16．已知ABC 的角,,A B C 所对边长分别为()(),,,,0,40a b c A B a b c b b c bc >--<+-=，则（ ） A ．a c >B ．59a << C ．5b >D ．5c > 【答案】AC【分析】利用大角对大边及符号法则可得c b a <<，结合条件利用特值法及不等式的性质即得.【解析】在ABC 中，A B >，a b ∴>，又()()0a b c b --<， ∴c b a <<，故A 正确；40b c bc +-=，即411b c+=， 当8b =时，2c =，此时810a <<，故B 错误；又414141411,1b b b c c c b c+<+=+>+=，5,5b c ∴><，故C 正确，D 错误. 故选：AC.17．甲、乙两个项目组完成一项工程，甲项目组在做工程的前一半时间内用速率u 工作，后一半用速率v 工作；乙项目组在完成工程量的前一半中用速率u 工作，在后一半用速率v 工作，则（ ）A ．如果u v =，则两个项目组同时完工B ．如果u v =，则甲项目组先完工C ．如果u v ≠，则甲项目组先完工D ．如果u v ≠，则乙项目组先完工【答案】AC【分析】设总工程量为1，计算出甲、乙两个项目组做工程的时间，利用作差法可得出结论.【解析】设总工程量为1，甲项目组在做工程的前一半时间内用速率u 工作，后一半用速率v 工作，122t t u v ∴⋅+⋅=甲甲，2t u v ∴=+甲， 乙项目组在完成工程量的前一半中用速率u 工作，在后一半用速率v 工作，11222u v t u v uv+∴=+=乙， 当u v =时，212t u u ==甲，2212u t u u ==乙，t t ∴=乙甲，即甲、乙项目组同时完工； 当u v ≠时， 2t u v =+甲，2u v t uv+=乙， ()()()()22 4202uv u v u v u v v t t u v uv u u v uv u v -+--+∴-==<+-=++甲乙，t t ∴<甲乙，即甲项目组先完工，故选：AC.【点睛】方法点睛：比较法是不等式性质证明的理论依据，是不等式证明的主要方法之一，作差法的主要步骤为：作差——变形——判断正负．在所给不等式是积、商、幂的形式时，可考虑比商.18．已知a ，b ，R c ∈，若2221a b c ++=，且(1)(1)(1)a b c abc ---=，则下列结论正确的是（ ）A ．1a b c ++=B ．1ab bc ca ++<C ．c 的最大值为1D ．a 的最小值为-1【答案】ABC【解析】由题可得1ab bc ca a b c ++=++-，设a b c x ++=，则可得22(1)1x x --=，即可解出1a b c ++=，0ab bc ca ++=，判断AB 正确；将条件转化为22(1)0b a b a a +-+-=，利用判别式可求出a 的范围，同理求出c 的范围.【解析】由(1)(1)(1)a b c abc ---=，得1abc ab bc ca a b c abc ---+++-=，1ab bc ca a b c ∴++=++-，设a b c x ++=，则1ab bc ca x ++=-.2222()2()1a b c a b c ab bc ca ++=++-++=，22(1)1x x ∴--=，解得1x =，即1a b c ++=，0ab bc ca ++=，故AB 正确；()0ab a b c ∴++=，即()(1)0ab a b a b ++--=.220a b ab a b ∴++--=，即22(1)0b a b a a +-+-=.由a ，b R ∈知，()()22140a a a ∆=---≥. ∴23210a a --?，解得113a -≤≤，同理可得113c -≤≤，故C 正确，D 错误.故选：ABC.【点睛】关键点睛：本题考查根据已知等量关系求范围，解题的关键是根据条件令a b c x ++=，转化出22(1)1x x --=，即可求出1a b c ++=，进一步利用判别式可求出,a c 范围.三、填空题19．用“>”或“<”填空：（1）5x +________2x +；（2）3a b a <⇒_____3b ；（3）5a b a <⇒-______5b -；（4）当c _______0时，a b ac bc >⇒<；（5）1a b a >⇒-______2b -；（6）0,0a b c d ac >><<⇒_______bd .【答案】 > < > < > <【解析】由不等式的性质及推论逐一判断即可得解.【解析】解：（1）∵52>，∴52x x +>+；（2）∵,30a b <>， ∴33a b <；（3）∵,50a b <-<，∴55a b ->-；（4）当0c <时，a b ac bc >⇒<；（5）∵,12a b >->-，∴12a b ->-；（6）∵0,0a b c d >><<，∴0c d ->->，则ac bd ->-，即ac bd <.故答案为：（1）>（2）<（3）>（4）<（5）>（6）<.【点睛】本题考查了不等式的性质及推论，属基础题.20．“a c b d +<+”是“a b <且c d <”的______条件．【答案】必要非充分【分析】根据不等式的性质可知若“a b <且c d <”，则必有“a c b d +<+”成立，通过反例可以说明前者的逆命题不成立.【解析】若“a b <且c d <”，则a c b c b d +<+<+，故“a c b d +<+”成立；若10,100,20,60a c b d ==-=-=-，则9080a c b d +=-<+=-，但,a b c d ><，所以“a c b d +<+”是“a b <且c d <”成立的必要不充分条件.故填必要非充分.【点睛】充分性与必要性的判断，可以依据命题的真假来判断，若“若p 则q ”是真命题，“若q 则p ”是假命题，则p 是q 的充分不必要条件；若“若p 则q ”是真命题，“若q 则p ”是真命题，则p 是q 的充分必要条件；若“若p 则q ”是假命题，“若q 则p ”是真命题，则p 是q 的必要不充分条件；若“若p 则q ”是假命题，“若q 则p ”是假命题，则p 是q 的既不充分也不必要条件.21．已知|a |<1，则11a +与1－a 的大小关系为________. 【答案】111a a≥-+ 【分析】利用不等式的基本性质求解.【解析】由|a |<1，得－1<a <1，∴1＋a >0,1－a >0，∴0<1－a 2≤1， ∴2111a ≥-， 111∴≥-+a a， 故答案为：111a a ≥-+ 【点睛】本题主要考查不等式的基本性质，属于基础题.22．若,,x a b R ∈，下列4个命题：①232x x +>；②553223a b a b a b +>+；③()2221a b a b +≥+-；④2b a a b+≥，其中正确的序号是_____ 【答案】①③【分析】利用作差、配方可判断①、②、③；根据基本不等式适用的条件可判断④.【解析】对于①，作差可得()2232120x x x +-=-+>，即232x x +>，正确；对于②作差并因式分解()()5532232233a b a b a b a b a b +--=-- ()()()222a b a b a ab b =-+-+，因,a b 符号而变，错误； 对于③，作差配方可得()()()222221110a b a b a b +-+-=-+-≥，正确；对于④，由于符号不定，显然当,a b 小于0不成立.故答案为：①③23．若实数,αβ满足11αβ-≤+≤，123αβ≤+≤，则3αβ+的取值范围为________．【答案】[]1,7【分析】设()3(2)αβλαβμαβ+++=+，解得1λ=-，2μ=，再由不等式的性质即可求解.【解析】设()3(2)αβλαβμαβ+++=+，解得1λ=-，2μ=所以()(322)αβαβαβ++-+=+．又11αβ-≤+≤，123αβ≤+≤，()11αβ∴-≤-+≤，()2226αβ≤+≤所以137αβ≤+≤.故答案为：[]1,7．【点睛】关键点点睛：本题考查利用不等式的性质求取值范围，变形()(322)αβαβαβ++-+=+是解题的关键，考查学生的运算求解能力，属于基础题. 24．已知a +b +c ＝0，a ＞b ＞c ，则ca的取值范围是_______.【答案】12,2⎛⎫-- ⎪⎝⎭ 【解析】首先将a +b +c ＝0变形为b ＝﹣a ﹣c .再将b ＝﹣a ﹣c 代入不等式a ＞b ，b ＞c ，解这两个不等式，即可求得a 与c 的比值关系，联立求得c a 的取值范围.【解析】解：∵a +b +c ＝0，∴a ＞0，c ＜0 ①∴b ＝﹣a ﹣c ，且a ＞0，c ＜0∵a ＞b ＞c∴﹣a ﹣c ＜a ，即2a ＞﹣c ② 解得2c a >-，将b ＝﹣a ﹣c 代入b ＞c ，得﹣a ﹣c ＞c ，即a ＜﹣2c ③ 解得12c a <-， ∴122c a -<<-. 故答案为：12,2⎛⎫-- ⎪⎝⎭. 【点睛】本题考查不等式性质的应用.解决本题的关键是将a +b +c ＝0变形为b ＝﹣a ﹣c ，代入后消去b ，进而求得a 、c 的关系.四、解答题25．下列结论是否成立？若成立，试说明理由；若不成立，试举出反例．(1)如果c a c b ->-，那么a b <；(2)若ab c >，0b >，则ca b>；(3)若ac bc >，则a b >；(4)若a b >，c d >，则a c b d ->-．【答案】(1)成立，理由见解析；(2)成立，理由见解析；(3)不成立，理由见解析；(4)不成立，理由见解析；【分析】由不等式的性质判断（1）（2）成立，取特殊值判断（3）（4）不成立.(1)c a c b ->-，a b ∴->-，a b ∴<，故成立.(2)ab c >，0b >,11ab c b b ⋅>⋅∴, 即ca b >.(3)取1,2,1a b c ===-时，满足ac bc >，但是a b >不成立.(4)取1,0,3,1a b c d ====-，满足a b >，c d >，但是a c b d ->-不成立.26．（1）已知,a b c d ><，求证：a c b d ->-；（2）已知,0a b ab >>，求证：11a b<；（3）已知0,0a b c d >><<，求证：ab c d >. 【答案】（1）证明见解析；（2）证明见解析；（3）证明见解析.【分析】（1）根据c d <不等号左右两边同时乘以一个负数,不等号方向改变得到 c d ->-, 再用同向可加性法则即可得出结果.（2）根据正数的倒数大于0可得10ab>,再用同向同正可乘性得出结果. （3）因为0c d <<，根据（2）的结论，得110c d>>,再用同向同正可乘性得出结果. 【解析】证明：（1）因为,a b c d ><，所以,a b c d >->-.则a c b d ->-.（2）因为0ab >，所以10ab >. 又因为a b >，所以1a b ab ab1⋅>⋅， 即11b a >，因此11a b<.（3）因为0c d <<，根据（2）的结论，得110c d >>. 又因为0a b >>，则 11a b c d ⋅>⋅， 即ab c d >. 【点睛】本题考查不等式的基本性质与不等关系,是基础题.27．一般认为，民用住宅的窗户面积必须小于地板面积，但窗户面积与地板面积的比应不小于10%，而且这个比值越大，采光效果越好．设某所公寓的窗户面积为2m a ，地板面积为2m b ，(1)若这所公寓窗户面积与地板面积的总和为2330m ，则这所公寓的窗户面积至少为多少平方米？(2)若同时增加相同的窗户面积和地板面积，设增加的面积为2m t ，则公寓的采光效果是变好了还是变坏了？请说明理由．【答案】(1)30平方米(2)变好了【分析】（1）根据题意列出关于,a b 的等量关系和不等量关系，化简求解即可（2）分式的分子分母同时增加t ，通过作差法比较新的分式与原来分式的大小，从而判断采光效果变好了还是变坏了(1) 根据题意可得：33010%a b a b+=⎧⎪⎨≥⎪⎩ ，则330b a =-，所以10%330a a ≥-，解得：30a ≥，所以这所公寓的窗户面积至少为30平方米(2) 同时增加窗户面积和地板面积后，比值为a t b t++，则()()()t b a a t a ab tb ab at b t b b b t b b t -++---==+++，因为0,0,b t b a >>>，所以()()0t b a a t a b t b b b t -+-=>++，所以a t a b t b +>+，所以同时增加相同的窗户面积和地板面积后，公寓的采光效果变好了28．1.已知m n ≠，43x m m n =-，34y n m n =-，比较x 与y 的大小．【答案】x y >【分析】运用作差法，进而分解因式，讨论每个因式的符号，最后得到答案.【解析】()()()()()()43343333x y m m n n m n m m n n m n m n m n -=---=---=--()()222m n m mn n =-++． 因为m n ≠，所以()20m n ->，22223024n n m mn n m ⎛⎫++=++> ⎪⎝⎭， 所以()()2220m n m mn n -++>，所以0x y ->，所以x y >． 29．比较下列各题中两个代数式值的大小：(1))21与)21；(2)()()2211x x ++与()()2211x x x x ++-+．【答案】(1)221)1)≤(2)()()2211x x ++()()2211x x x x ≤++-+【分析】利用作差法得出大小关系. (1)))()()221111m m -=--+=-因为0m ≥，所以221)1)0-≤，当且仅当0m =时，取等号.即221)1)≤ (2)()()2211x x ++()()2211x x x x -++-+ ()()2222222121x x x x x ⎡⎤⎡⎤=+--+-=-⎢⎥⎢⎥⎣⎦⎣⎦因为0x ≥，所以()()2222221210x x x x ⎡⎤⎡⎤+--+-≤⎢⎥⎢⎥⎣⎦⎣⎦，当且仅当0x =时，取等号.故()()2211x x ++()()2211x x x x ≤++-+.30．（1）设0xy <，试比较()22()x y x y +-与()22()x y x y -+的大小；（2）已知13a b <+<，22a b -<-<，求23a b +的取值范围．【答案】（1）答案见解析；（2）3172322a b <+<. 【分析】（1）通过作差化简原式等价于()2xy x y --，通过分为 x y >和x y <两种情形得结果；（2）将23a b +用a b +，-a b 线性表示，结合不等式的性质即可得结果.【解析】（1）()()2222()()x y x y x y x y +---+222()()x y x y x y ⎡⎤=-+-+⎣⎦2()xy x y =--．∵0xy <，∴当 x y >时，0x y ->，2()0xy x y -->，得()()2222()()x y x y x y x y +->-+；当x y <时，0x y -<，2()0xy x y --<，得()()2222()()x y x y x y x y +-<-+．（2）设23()()a b m a b n a b +=++-，则2,3,m n m n +=⎧⎨-=⎩解得52m =，12n =-． 则5123()()22a b a b a b +=+--．∵13a b <+<，22a b -<-<， ∴5515()222a b <+<，11()12a b -<--<． ∴35117()()2222a b a b <+--<． 即3172322a b <+<． 31．若实数x ，y ，m 满足||||x m y m ->-，则称x 比y 远离m .(1)若x 比12远离1，求实数x 的取值范围；(2)若1m £，2x y +=，试问：x 与22x y +哪一个更远离m ，并说明理由.【答案】(1)13(,)(,)22-∞+∞； (2)22x y +比x 更远离m ，理由见解析.【分析】（1）由绝对值的几何意义可得112x ->，即可求x 的取值范围；（2）只需比较22||,||x y m x m +--的大小，讨论x m <、x m ≥分别判断代数式的大小关系，即知x 与22x y +哪一个更远离m . (1)由x 比12远离1，则1112x ->-，即112x ->. ∴112x ->或112x -<-，得：12x <或32x >.∴x 的取值范围是13(,)(,)22-∞+∞. (2)因为222()22x y x y m ++=≥≥，有2222||x y m x y m +-=+-，因为2x y +=，所以222244x x y x =-++．从而222||||244||x y m x m x x m x m +---=-+---，①当x m ≥时，22||||x y m x m +---2425x x -+=2572()048x =-+>2244()x x m x m =-+---，即22||||x y m x m +->-；②当x m <时，22||||x y m x m +---2244()x x m x m =-+-+-23242x m x =-+-23232()248x m =-+-， 又1m £，则23208m ->． ∴23232()2048x m -+->，即22||||x y m x m +->-． 综上，22||||x y m x m +->-，即22x y +比x 更远离m ．32．对在直角坐标系的第一象限内的任意两点作如下定义：若ac b d>，那么称点（a ，b ）是点（c ，d ）的“上位点”，同时点（c ，d ）是点（a ，b ）的“下位点”(1)试写出点（3，5）的一个“上位点”坐标和一个“下位点”坐标；(2)已知点（a ，b ）是点（c ，d ）的“上位点”，判断是否一定存在点P ，满足既是点（c ，d ）的“上位点，又是点（a ，b ）的“下位点”，若存在，写出一个点P 坐标，并证明；若不存在，则说明理由；【答案】(1)点（3，5）的一个“上位点”坐标是（3，4）和一个“下位点”坐标是（3，6）（答案不唯一）；(2)存在，证明详见解析.【分析】（1）利用“上位点”和一个“下位点”的定义求解；（2）利用“上位点”和一个“下位点”的定义证明；(1)解：因为对在直角坐标系的第一象限内的任意两点作如下定义： 若ac b d>，那么称点（a ，b ）是点（c ，d ）的“上位点”，同时点（c ，d ）是点（a ，b ）的“下位点”，所以点（3，5）的一个“上位点”坐标是（3，4）和一个“下位点”坐标是（3，6）；(2)因为点（a ，b ）是点（c ，d ）的“上位点”，所以一定存在点P （a +c ，b +d ）满足既是点（c ，d ）的“上位点，又是点（a ，b ）的“下位点”，证明如下：因为点（a ，b ）是点（c ，d ）的“上位点”， 所以ac b d>，即ad >bc ， 所以220a c c ad cd bc dc ad bc b d dbd d bd d ++----==>+++， 即 a c c b c d +>+，所以点P （a +c ，b +d ）是点（c ，d ）的“上位点， 所以220a c a ab cb ab ad bc ad b d b bd b bd d ++----==<+++， 即 a c a b d b+<+，所以点P （a +c ，b +d ）是点（a ，b ）的“下位点， 综上：点P （a +c ，b +d ）满足既是点（c ，d ）的“上位点，又是点（a ，b ）的“下位点”.。

一．不等式的性质：1．同向不等式可以相加；异向不等式可以相减：若,a bc d >>，则a c b d +>+（若,a b c d ><，则a c b d ->-），但异向不等式不可以相加；同向不等式不可以相减；2．左右同正不等式：同向的不等式可以相乘，但不能相除；异向不等式可以相除，但不能相乘：若0,0a b c d >>>>，则ac bd >（若0,0a b c d >><<，则a b c d>）；3．左右同正不等式：两边可以同时乘方或开方：若0a b >>，则n n a b >或nn a b >；4．若0ab >，a b >，则11a b<；若0ab <，a b >，则11ab>。

如（1）对于实数c b a ,,中，给出下列命题：①22,bc ac b a >>则若； ②b a bc ac >>则若,22； ③22,0b ab a b a >><<则若； ④ba b a 11,0<<<则若；⑤ba ab b a ><<则若,0； ⑥b a b a ><<则若,0；⑦bc b ac ab ac ->->>>则若,0； ⑧11,a b ab>>若，则0,0a b ><。

其中正确的命题是______（答：②③⑥⑦⑧）；（2）已知11x y -≤+≤，13x y ≤-≤，则3x y -的取值范围是______（答：137x y ≤-≤）； （3）已知c b a >>，且,0=++c b a 则ac 的取值范围是______（答：12,2⎛⎫-- ⎪⎝⎭）二．不等式大小比较的常用方法：1．作差：作差后通过分解因式、配方等手段判断差的符号得出结果； 2．作商（常用于分数指数幂的代数式）； 3．分析法； 4．平方法；5．分子（或分母）有理化； 6．利用函数的单调性； 7．寻找中间量或放缩法 ；8．图象法。

第3讲简单不等式的解法知识点1、一元一次不等式1、解法：ax b +0>0<0a >b x a >-b x a <-a <b x a <-b x a >-2、步骤：①利用不等式性质1，去分母移项整理；②利用不等式性质3，去系数（注意系数为负，不等号一定要变号）；③写结果。

3、注意：一次项系数是否为0的情况，即讨论0a =，此时解集无解或恒成立。

如：0ax b ax b+>⇒>-当0,0a b =>时：解集为任意实数；当0,0a b =<时：解集为无解。

1、解法：2(0)ax bx c a ++>24b ac∆=-0∆>0∆=0∆<图像20ax bx c ++=12,x x x x ==12x x x ==无解20ax bx c ++>2x x >或1x x <1x x ≠所有实数20ax bx c ++≥2x x ≥或1x x ≤所有实数所有实数20ax bx c ++<12x x x <<无解无解20ax bx c ++≤12x x x ≤≤12x x x ==无解2、步骤：（1）首正：整理成一般形式化二次项系数为正。

若为负，不等号一定变号；（2）求根：检验判别式，若0∆≥，计算一元二次方程的两根。

①首选因式分解法求出12,x x （其中12x x <）；②无法因式分解的用求根公式；③若0∆<，对二次三项式进行配方变形成2224()24b ac b ax bx c a x a a-++=++，再结合完全平方式为非负数的性质求解。

（3）根据不等号方向确定解集“0>”型的解为12x x x x <>或(“两根之外”)；“0<”型的解为12x x x <<(“两根之间”)；有等号，一律取等。

知识点3、分式不等式1、解分式不等式的基本思路：将分式不等式转化为整式不等式，利用符号法则进行求解。

6.1不等式的概念和性质〖考纲要求〗掌握不等式的性质及其证明，能正确使用这些概念解决一些简单问题.〖复习建议〗不等式的性质是解、证不等式的基础，对于这些性质，关键是正确理解和熟练运用，要弄清每一个条件和结论，学会对不等式进行条件的放宽和加强。

〖双基回顾〗常见的性质有8条： 1、反身性（也叫对称性）：a ＞b ⇔b ＜a 2、传递性：a ＞b ，b ＞c ⇔a ＞c 3、平移性：a ＞b ⇔a +c ＞b +c 4、伸缩性：⎩⎨⎧>>0c b a ⇔ac ＞bc ；⎩⎨⎧<>0c ba ⇔ac ＜bc5、乘方性：a ＞b ≥0⇔a n ＞b n （n ∈N ，n ≥2）6、开方性：a ＞b ≥0⇔na ＞nb （n ∈N ，n ≥2）7、叠加性：a ＞b ，c ＞d ⇔a +c ＞b +d 8、叠乘性：a ＞b ≥0，c ＞d ≥0⇔a ·c ＞b ·d一、知识点训练：1、ba b a 11〈⇔〉成立的充要条件为2、用“＞”“＜”“＝”填空：(1)a <b <c <0则ac bc ；a c bc； (2) 0<a <b <c <1，则a c b c ；a b a c ；log c a log c b ；a lg c b lg c ；a r c si na a r c si nb .二、典型例题分析：1、比较下面各小题中a 与b 的大小：(1)a =m 3－m 2n －3mn 2 与 b =2m 2n －6mn 2＋n 3 (2)a =3x 2－x ＋1与b =2x 2＋x －1 (3)10231=-=b a 与 .2、bxax x f -=)(，1≤)1(f ≤2，13≤)2(f ≤20，求)3(f 的取值范围. 三、课堂练习：1、若b a 〉，则下列不等式成立的是………………………………………………………………… （ ） (A )ba 11〈 (B ))0(22≠〉c bc ac (C ) 0)lg(〉-b a (D ) b a lg lg 〉 2、设d c b a ≥〉,，那么下列不等式成立的是……………………………………………………… （ ） (A )22)()(c b d a -〈- (B ) 22)()(c b d a -≥- (C ) 22)()(c b d a -≤- (D ) 以上都不对四、课堂小结：1、不等式的基本性质是解不等式与证明不等式的理论依据，必须透彻理解，特别要注意同向不等式可相加，也可相乘，但相乘时，两个不等式都需大于零.2、处理分式不等式时不要随便将不等式两边乘以含有字母的分式，如果需要去分母，一定要考虑所乘的代数式的正负.3、作差法是证明不等式的最基本也是很重要的方法，应引起高度注意.五、能力测试： 姓名 得分1、下列命题中正确的是……………………………………………………………………………… ( )(A )22,b a b a 〉〉则若 (B ) b a b a 〉〉则若,22(C ) 22,b a b a 〉〉则若 (D ) 22,b a b a 〉〉则若2、设011〈〈ba ，则有 …………………………………………………………………………………（ ） (A ) 22b a 〉 (B ) ab b a 2〉+ (C ) 2b ab 〈 (D ) b a b a +〉+223、若0,=++〉〉c b a c b a ,则有…………………………………………………………………… ( ) (A ) ac ab 〉 (B ) bc ac 〉 (C ) bc ab 〉 (D )以上皆错4、若0,〉〉〉b a bd ac ,则 ………………………………………………………………………………( ) (A ) 0〉〉d c (B ) d c 〉 (C ) d c 〈 (D )c 、d 大小不确定5、以下命题：⑴a >b ⇒|a |>b ⑵a >b ⇒a 2>b 2 ⑶|a |>b ⇒ a >b ⑷a >|b | ⇒ a >b 正确的个数有………………………………………………………………………………………（ ） (A ) 1个 (B ) 2个 (C ) 3个 (D )4个6、已知a ＞2,比较12++=a ab 与2的大小.7、比较下列各数的大小： (1))11(log ),1(log an a m a a +=+= （提示：分a ＞1，a ＜1讨论） (2)n n a -+=1与1--=n n b （提示：分子有理化后再比较）8、如果二次函数)(x f y =的图象过原点，并且1≤)1(-f ≤2,3≤)1(f ≤4,求)2(-f 的取值范围.6.2不等式的解法——分式与高次〖考纲要求〗在熟练掌握一元一次与一元二次不等式的解法的基础上初步分式与高次不等式的解法. 〖复习建议〗分式与高次不等式的一般解法：序轴标根法，能注意到其中的一些特殊点与解集的关系，能注意到区间端点与解集的关系.一、知识点训练：1、下列不等式与012≤+x x同解的是……………………………………………………………（ ） (A) 01≤+xx (B)0)1(≤+x x(C)0)1lg(≤+x (D)21|1|≤+x x2、不等式(x －2)2·(x －1)>0的解集为 .3、不等式(x ＋1) ·(x －1)2≤0的解集为 .4、不等式x x<1的解集为 . 二、典型例题分析：1、解不等式：(x －1)·(x －2)·(x －3)·(x －4)>1202、解不等式：0)5)(1)(3()2(2>-+++x x x x 3、解不等式：232532≥-+-x x x 4、若不等式6163922<+--+<-x x mx x 对一切x 恒成立,求实数m 的范围 5、求适合不等式11)1(02<+-<x x 的整数x 的值. 6、解关于x 的不等式a x x-<-11三、课堂练习：1、不等式1213≥--x x 的解集为……………………………………………………………………（ ） (A){x |43≤x ≤2} (B) {x |43≤x <2}(C) {x |x >2或者x ≤43} (D){x |x ＜2}2、不等式21≥+x x的解集为 . 3、如果不等式1122+-->++-x x b x x x a x 的解集为（21，1），则b a ⋅= .四、课堂小结：分式与高次不等式的解题基础是一元二次不等式的解法，常用方法是序轴标根法，但是要注意标根时的起点位置.五、能力测试：1、与不等式023≥--xx 同解的不等式是……………………………………………………………（ ）(A)(x －3)(2－x )≥0 (B)lg(x －2)≤0 (C) 032≥--x x(D)(x －3)(2－x )>02、如果x 1<x 2<…<x n ，n ≥2,并且{x |(x －x 1)(x －x 2)…(x －x n )>0}⊃{x |x 2－(x 1＋x 2)x ＋x 1x 2<0}，那么自然数n …………………………………………………………………………………………………（ ） (A)等于2 (B)是大于2的奇数(C) 是大于2的偶数 (D)是大于1的任意自然数 3、不等式(x －1)(x ＋2)(3－x )>0的解集为 .4、不等式01)3()4)(1(2≤+---x x x x 的解集为 . 5、a >0,b >0，那么不等式a xb <<-1的解集为 . 6、已知不等式11<-x ax的解集为{x |x <1或x >2}，那么a = . 7、解不等式：x xx x x <-+-+222322（提示：)1)(2(2223++-=---x x x x x x ）8、不等式)(122322N n n x x x x ∈>++++对一切x 都成立，求n 的值.9、解关于x 的不等式)0( 12)1(>>--a x x a6.3不等式的证明—比较法〖考纲要求〗掌握不等式的性质及其证明，能正确使用这些性质解决一些简单问题. 〖复习建议〗掌握求差法与求商法比较两个数的大小。