当前位置：文档之家 › 《工程力学》第 3 章 力矩与平面力偶系

《工程力学》第 3 章 力矩与平面力偶系

  • 格式：ppt
  • 大小：641.50 KB
  • 文档页数：31

下载文档原格式

  / 31

合集下载

工程力学(静力学与材料力学)第三章力偶系详解

工程力学(静力学与材料力学)第三章力偶系详解

FB
r M2 0 ∑ M = 0 ， FA sin
M 2 2r FA
M2 = 4M1 = 8kNm
2M 1 FO FB FA 8kN r
• 作业3-1,3-4,3-8
考虑CB部分为二力构件，得：
FC FA FB FC
例3-4
图示机构自重不记。圆轮上的销子 A 放在 摇杆 BC上的光滑导槽内。M 1 = 2kNm，OA = r = 0.5m 。图示位置OA⊥OB，α = 30°，且系统平衡。 求作用于摇杆 BC 上力偶的矩 M 2 及 O、B 支座的反 力。 解：受力分析
M1
R
F1
M
F2
2
M1 + M2 = rBA×F1 + rBA×F2 = rBA×( F1 + F2 ) = rBA×R = M
如有n个力偶，按上法依次合成, 最后得一力偶,合力偶矩矢为 M = M1 +M2 + … +Mn = ∑M I
B
rBA
A
F2
F1
任意个力偶可以合成为一个 合力偶，这个合力偶矩矢等于各 分力偶矩矢的矢量和。 M = M 1+ M 2+ … + M n = ∑M i
性质三
证：
力偶没有合力
仍用反证法，即假定力偶有合力，那么总可 找到一个与此力大小相等，方向相反而作用线 共线的力与此力平衡，即力与力偶相平衡。与 性质二矛盾。
性质一、二和三告诉我们力偶只能与力偶等 效而不能与单个力等效。
•力偶只能与力偶相平衡 力偶只能与力偶相平衡
§3-4 力偶系的合成
设有两个力偶，由性质一,将 力偶中两力分别移到两力偶作用面 交线上的两点 A 和 B,可得到两个 汇交力系，其合力分别为R 、 R ’ 。

工程力学I-第3章 力矩与平面力偶系

工程力学I-第3章 力矩与平面力偶系

D
x
§3-2 关于力偶的概念

力偶：一对等值、反向而不共线的平行力，用 符号（F ,F′）表示。

力偶臂：两个力作用
线之间的垂直距离d。

F’
F
力偶的作用面：两个 力作用线所决定的平 面
§3-2 关于力偶的概念
F F
d
d
F
d
F
F
F
转动游戏方向盘
拧水龙头
扳手拧螺母
§3-2 关于力偶的概念

Q AABD AABC 显然， 并注意到力偶矩的转向也相同， 则有M ( F , F ) M ( P, P) P
M (P 1, P 1 ) M ( P, P ) 显然， 1, P 1) 从而有M ，( F , F ) M ( P
P1
力偶等效
M ( F , F ) M ( P 1, P 1)
（1）力对点之矩，不仅取决于力的大小，还与矩心的位置有关。
（2）力对任一点之矩，不因该力的作用点沿其作用线移动而改变。 *（3）力的大小等于零或其作用线通过矩心时，力矩等于零。 （4）互成平衡的两个力对同一点之矩的代数和为零。
Mo(F)＝±Fd
§3-1 关于力矩的概念及其计算

合力矩定理：
y Fy
(3)将力P和P’沿各自的作用 线移至任意点A’，B’，根 据力的可传性原理，有 (P,P’) =(P1,P1’) 。
§3-2 关于力偶的概念
(4) A′
P1′ b F′ A A F B Q′ D P′ B′ C
M (F , F ) AB BD 2 AABD ,
M（P, P'） AB BC 2 AABC

第三章 力偶与平面力偶理论)

第三章 力偶与平面力偶理论)

M 0 F F h
力对点之矩（力矩）是一个代数量，它的绝 对值等于力的大小与力臂的乘积；
它的正负：力使物体绕矩心逆时针转向时为正，反之为负。 常用单位为 N· m 或 kN· m。 注意：力矩在下列几种情况下等于零 （1）力的大小等于零；
（2）力的作用线通过矩心，即力臂等于零；
（3） 互成平衡的二力对同一点之矩为零。
78.93N m
按合力矩定理 M O F M O Ft M O Fr



F cos θ r 78.93N m
例3-2 已知：q,l； 求： 合力及合力作用线位置. 解： 取微元如图
x q q l l x 1 P q dx ql 0 l 2
M Mi Mi
i 1 n
平面力偶系平衡的充要条件 M = 0，有如下平衡方程
Mi
0
平面力偶系平衡的必要和充分条件是：所有各力 偶矩的代数和等于零。
例3-1
已知: F=1400N, θ 20 , r 60mm
求: M O F .
解:直接按定义
MO

F F h F r cos θ
M1 F1 d M2 F2 d
M1 F1d
M 2 F2d
Mn Fn d
M n Fnd
=
=
FR F1 F2 Fn
F1 F2 Fn FR
=
=
=
M FRd F1d F2d Fnd M1 M 2 M n
定理：同平面内的两个力偶，如果力偶矩相等，则两力偶 彼此等效。 推论： 任一力偶可在它的作用面内任意转移，而不改变它对刚体 的作用。因此力偶对刚体的作用与力偶在其作用面内的位置无 关。 只要保持力偶矩不变，可以同时改变力偶中力的大小与 力偶臂的长短，对刚体的作用效果不变.

工程力学 第3章 力偶系

工程力学 第3章 力偶系

M 2 F2 , F2'
M F1'
r1
F F1 F2 F ' F1' F2'
F2' MR F, F '
F2
F1 F
M2
MR r F ' r (F1'F2 ') r F1'r F2 '
M1 M2
结论：两个力偶的合成仍然为力偶，且
第三章 力偶系
§1 力对点之矩矢 一、 平面力对点之矩（回顾）
力使物体绕某点转动的力学效应，称为力对该点之矩。 例如扳手旋转螺母。
BF
dA L
O
力F对O点之矩定义为： Mo(F)＝±Fd
通常规定：力使物体绕矩心逆时针方向转动时，力矩 为正，反之为负。
第三章 力偶系
二、力对点之矩矢量 1、空间力矩三个要素：
一、力偶 在日常生活和工程实际中经常见到物体受动两个大小相等、 方向相反，但不在同一直线上的两个平行力作用的情况。例如
第三章 力偶系
B d
F’
F A
M
B
F
rBA
F’ d A
1. 定义：在力学中把这样一对等值、反向而不共线的平行力 称为力偶，用符号 ( F , F′)表示。
两个力作用线之间的垂直距离 d 称为力偶臂， 两个力作用线所决定的平面称为力偶的作用面。
x (F ) y (F )

yFz zFx

zFy xFz

M
z
(F
)

xFy

yFx

力对点之矩在各坐标轴上的投影
MO z
O xr

工程力学(第三章)

工程力学(第三章)

MR
y
MR Mz cos MR
§3-6
力偶系的平衡条件
M 0
平衡： 力偶系平衡的充要条件是 其合力偶矩矢为零。
即：力偶系平衡
一、平面力偶系的平衡条件
M R M（代数和） i
M 0
平面力偶系的平衡方程
§3-6
力偶系的平衡条件
M 0
平衡： 力偶系平衡的充要条件是 其合力偶矩矢为零。
力对点之矩矢
作用： 用来度量力使物体绕某点转动效应的量。
（代数量） 一、平面中力对点之矩（力矩）
F
O
h
定义：M O

F Fh
正负号规定： 力使物体绕矩心逆转为正，顺转为负。
作用： 用来度量力使物体绕某点转动效应的量。 1、平面问题
（代数量） 力矩作用面
矩心 O h
力臂
定义： M O F Fh
A
O x

y
Fx
z
y
Fy
x
A x, y, z ,
F Fx , Fy , Fz


（一）、力对点的矩
1、平面问题
MO

F Fh
MO F
O
h
z
F
F
2、空间问题
MO F r F


x
（二）、力对轴的矩
空间： 力偶对空间任一点的矩矢恒等于力偶矩矢， 而与矩心位置无关。
性质二 力偶可在其作用面内任意移转，或移到另
一平行平面，而不改变对刚体的作用效应。
= =
F
F
F
F

工程力学(静力学与材料力学)(第2版)教学课件第3章 力偶系

工程力学(静力学与材料力学)(第2版)教学课件第3章 力偶系

6
力偶的等效条件
作用于刚体上的两个力偶等效的条件是力偶矩矢相等， 即两个力偶矩矢相等的力偶等效。
力偶的性质
性质一 力偶不能与一个力等效,也不能与一个力平衡。 性质二 力偶可在其作用面或平行平面内任意移动,而 不改变力偶对刚体的作用效应。
性质三 只要力偶矩矢的大小与方向不变,即使改变力 与力偶臂的大小，均不改变力偶对刚体的作用效应。
工程力学（静力学与材料力学）
4
§2 力偶矩矢与力偶的性质
力偶
力偶-等值、反向、作用线平行的力F与F’组成的力系, 并用（F,F’）表示。
力偶作用面-两力作用线所在平面
力偶臂-两力作用线间垂直距离d
力偶系-作用于刚体上的一组力偶
平面力偶系-各力偶作用面的方位 相同的力偶系
空间力偶系-各力偶作用面的方位
工程力学（静力学与材料力学）
7
§3 力偶系的合成与平衡条件
力偶系的合成
刚体上两个力偶,力偶矩矢 M1与M2，转换至A与B点,得
M1rF1 M2 rF2
F F1F2 形成M
M rF r(F1F2) rF1rF2
M M1M2 MR
n
MR Mi
i1
空间力偶系可合成为一合力偶，其力偶矩矢等于
系内各分力偶矩矢的矢量和 。
MO (F )Fd
MO (F ) 2ABO
平面力对点之矩是代数量，使刚体绕矩心沿逆时针
方向转动者为正，反之为负。
工程力学（静力学与材料力学）
2
力对点之矩矢
空间力系各力，使刚体绕同一点转动的转轴方位不 同, 力对点之矩应该用矢量表示，即力对点之矩矢。
MO (F ) r F
r-A点对于O点的矢径 rF Frsin Fd

第3章力矩与力偶

第3章力矩与力偶

第3章力矩与平面力偶系教学提示：本章主要研究力矩、力偶和平面力偶系的理论。

这都是有关力的转动效应的基本知识，在理论研究和工程实际应用中都有重要的意义。

教学要求：本章让学生掌握力矩、力偶和平面力偶系的概念，掌握力对点之矩的两种求解方法，即直接作力臂的方法与利用合力矩定理求解的方法，掌握平面力偶的性质及平面力偶系的合成与平衡条件，会利用平衡条件求解约束反力。

力对点之矩1.力矩的概念力不仅可以改变物体的移动状态，而且还能改变物体的转动状态。

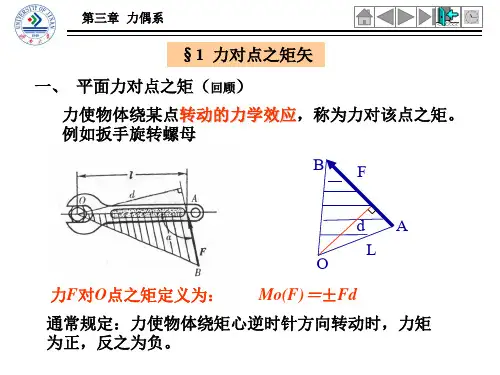
力使物体绕某点转动的力学效应，称为力对该点之矩。

以扳手旋转螺母为例，如图3－1所示，设螺母能绕点O转动。

由经验可知，螺母能否旋动，不仅取决于作用在扳手上的力F的大小，而且还与点O到F的作用线的垂直距离d有关。

因此，用F与d的乘积作为力F 使螺母绕点O转动效应的量度。

其中距离d称为F对O点的力臂，点O称为矩心。

由于转动有逆时针和顺时针两个转向，则力F对O点之矩定义为：力的大小F与力臂d 的乘积冠以适当的正负号，以符号m o(F)表示，记为m o(F)＝±Fh（3－1）通常规定：力使物体绕矩心逆时针方向转动时，力矩为正，反之为负。

图由图3－1可见，力F对O点之矩的大小，也可以用三角形OAB的面积的两倍表示，即m o(F)＝±2ΔABC（3－2）在国际单位制中，力矩的单位是牛顿•米（N•m）或千牛顿•米（kN•m）。

由上述分析可得力矩的性质：（1）力对点之矩，不仅取决于力的大小，还与矩心的位置有关。

力矩随矩心的位置变化而变化。

（2）力对任一点之矩，不因该力的作用点沿其作用线移动而改变，再次说明力是滑移矢量。

（3）力的大小等于零或其作用线通过矩心时，力矩等于零。

2.合力矩定理定理：平面汇交力系的合力对其平面内任一点的矩等于所有各分力对同一点之矩的代数和。

m o(F R)＝m o(F1)＋m o(F2)＋…＋m o(F n)即m o(F R)＝Σm o(F)（3－3）上式称为合力矩定理。

工程力学第3章(力偶系)

工程力学第3章(力偶系)
工程力学
Engineering Mechanics
中南大学土木建筑学院力学系
Department of Mechanics of School of Civil Engineering and Architecture of Central South University
第三章 力偶系 §3-1 力对点之矩矢
力偶臂d 力偶臂 1=200mm， ，
，力偶臂d ， F2 = F2' = 120N，力偶臂 2=300mm ， F3 = F3' = 80 N，
M 1 = 100 × 0.2 = 20
N.m N.m
M 2 = 120 × 0.3 = 36
M 3 = 80 × 0.18 = 14.4 N.m
M Rx M Ry = ∑ M y = M 1 = 20 N.m
二、力对轴之矩的 解析表达式
M x ( F ) = M x ( Fy ) + M x ( Fz ) = -zFy + yFz M y ( F ) = M y ( Fz ) + M y ( Fx ) = -xFz + zFx M z ( F ) = M z ( Fx ) + M z ( Fy ) = -yFx + xFy
M R = M1 + M 2 + ⋅ ⋅ ⋅ + M n = ∑ M
M R = M1 + M 2 + ⋅ ⋅ ⋅ + M n = ∑ M
合力偶矩矢的大小 M R = ( ∑ M x ) 2 + ( ∑ M y )2 + ( ∑ M z )2 合力偶矩矢的方向
R
∑M cos( M ，i ) =
cos( M R，j ) = MR

工程力学(人民交通出版社)第3章 第2节力偶系

工程力学(人民交通出版社)第3章 第2节力偶系

Fy
F

C
B D
b
Fx x
a
MA( F ) MA( Fx ) MA( Fy ) Fx b Fy a F cos b F sin a Fa sin Fb cos
F Fx Fy
Fx F cos Fy F sin
Mo (F , F ' ) Mo (F ) Mo (F ' ) F (d x ) F ' x F d
⑦正负规定：逆时针为正 ⑧单位量纲：N m 或 kN m
二、力偶与力偶矩
2、力偶的特点 ⑨力偶的三要素： 力偶矩的大小、力偶的转向、力偶的作用面 ⑩力偶矩矢 用一个矢量表达三要素：力偶矩矢。
§3-2
力矩与力偶理论
一、力对点之矩 二、力偶与力偶矩 三、力偶系的合成与平衡
一、力对点之矩
1、平面中力矩的概念
力对物体可产生运动效应，在一般情况下，既可能产生移动（平动）效应， 也可能产生转动效应，或者同时产生这两种运动效应。力的移动效应取决于 力的大小和方向，而力使物体绕某点的转动效应，则用力对该点的矩来度量， 简称力矩。
2）合力矩定理 将力Fn分解为切由合力矩定理得：
M o (Fn ) M o (Ft ) M o (Fr ) Fn r cos 0 Fn r cos
小结力偶和力偶矩
1. 力矩是力学中的一个基本概念。度量力对物体的转动 效应：
即有： Mx mx My my Mz mz 同理： M Mx 2 My 2 Mz 2
( Mx ) ( My ) ( Mz )
2 2 2
z
MZ

力矩与平面力偶系

力矩与平面力偶系

工程力学与建筑结构
1.4 力偶的合成 作用在同一物体上的若干个力偶组成一个力偶系，若
力偶系中各力偶均作用在同一平面，则称为平面力偶系。 平面力偶系合成的结果为一合力偶，其合力偶矩等于
各分力偶矩的代数和。即 M =M1＋M2＋…＋Mn=∑M
1.5力偶系的平衡条件 平面力偶系平衡的必要和充分条件是：力偶系中各力
偶矩的代数和为零。即 ∑M=0
工程力学与建筑结构
工程力学与建筑结构
工程力学与建筑结构
力矩与平面力偶系 1.1力矩的概念
用力的大小F与d的乘积度量力F使扳手绕O点的转动 效示应。，即称为力F对O点之矩，简称力矩，用符号MO（F）表
MO（F）=±Fd 式中，O点称为“矩心”，d称为“力臂”。 力矩的正负规定为：力使物体绕矩心逆时针方向转动时， 力矩为正；反之为负。
M=±Fd
力偶矩的正负规定与力矩正负规定一致，即：使物体 逆时针方向转动的力偶矩为正；反之为负。
F
F
B
h
铰杠
丝锥
F'
F d
F'

A
(a)
F' (b)
(c)
工程力学与建筑结构
在平面问题中，力偶矩也是代数量。力偶矩的单位与力矩 单位相同，即N•m。 根据力偶的概念可以证明，力偶具有以下性质： （1）力偶在其作用面上任一轴的投影为零。 （2）力偶对其作用面上任一点之矩，与矩心位置无关，恒 等于力偶矩。
系中所有分力对同一点之矩的代数和。
MO（FR）=MO（F1）＋ MO （F2）＋…＋ MO （Fn）=∑ MO （F）
F1 y
A
FR
F2
O x
工程力学与建筑结构
1.3 力偶的概念

力矩与平面力偶系

力矩与平面力偶系
4.力偶没有合力，力偶只能由力偶来平衡.
5.力偶对物体不产生移动效应，只产生转动效应。
力偶的三要素： 力偶对物体的转动效应，取决于下列三个因素： 1.力偶矩的大小 2.力偶的转向 3.力偶的作用面
1 8
§3-3平面力偶系的合成和平衡条件
平面力偶系：作用在物体上同一平面内的若干力偶。
已知：M1, M2 ,Mn;
FAl M1 M 2 M3 0
解得
FA
FB
M1
M2 l
M3
200N
2 2
综合例题
已知 M 2kN m,OA r 0.5m,θ 30 ; 1
求：平衡时的 M 2及铰链O，B处的约束力.
解：取轮,由力偶只能由力偶平衡的性质,画受力图.
M 0 M1 FA r sin 0
解得 FO FA 8kN
cos
AB
r2
r1
cos
d
AB
cos
r2
cos
r1
mA (F ) Fd F (r1 r2 cos )
1 0
§3-2 平面力偶理论
一.力偶和力偶矩
1.力偶
由两个等值、反向、作用线平行的力组成的力系称为力偶，
记作
F
,
F
1
1
2.力偶矩 力偶中两力所在平面称为力偶作用面
力偶两力之间的垂直距离称为力偶臂
:逆时针转动为正,反之为负.
力对点之矩是一个代数量，它的绝对值等于力的大小与力臂
的乘积，它的正负：力使物体绕矩心逆时针转向时为证，反之为
负.常用单位Nm或kNm
4
例:F=50N,d=0.3m. 求F力对O点之矩. 解:Mo(F)= Fd = … = 15Nm (1)当F=0,或d=0（力作用线通过矩心）时，力矩为零。 (2)当力沿其作用线 滑移时，力矩不变。 (3)力矩与矩心有关。 在平面问题中，力对点之矩实际上指力使物体绕通过矩心的 某一轴转动效果的度量，该轴垂直于由力的作用线和矩心所 决定的平面。

理论力学03力矩力偶与平面力偶系

理论力学03力矩力偶与平面力偶系

本章讨论平面力偶系的合成与平衡问题
一、平面力偶系的合成 平面力偶系可合成为一个合力偶； 合力偶矩等于各分力偶矩的代数和，即
M1
M2 M3
M4
M Mi
二、平面力偶系的平衡方程
Mi 0
M
说明：根据平面力偶系的平衡方程，可解 一个未知量。
ቤተ መጻሕፍቲ ባይዱ
[例2] 已知梁长 l = 5 m，M = 100 kN·m ；若不计梁的自重，试求 铰支座 A 、B 处的约束力。
2. 力偶中的两个力对任一点的矩的代数和 恒等于力偶矩，与矩心位置无关。
dF F
3. 作用于刚体同一平面内两个力偶等效的充要条件为其力偶矩 相等。
结论：力偶矩唯一决定了力偶对刚体的作用效应。
◆ 通常用力偶矩符号来代表力偶：
F
d
M Fd
F
M 或M
第三节 平面力偶系
平面力偶系：由位于同一平面内的一群力偶所组成的力系
构平衡。试求作用于摆杆 BO1上的力偶矩 M2 （各构件的自重不计）
解： 1）首先研究曲柄 AO与套筒A 的组合 画受力图 列平衡方程
Mi 0, M1 FA r sin 30 0
解得
FA
FO
2M1 r
M1
O
FO
FA
FA
FO
2M1 r
2）再选取摆杆 BO1 为研究对象
画受力图
列平衡方程
Mi 0, M 2 FA AO1 0
的平行力称为一个力偶，记作 F, F。
dF F
二、力偶矩 定义
M Fd
为平面内力偶 F, F 的矩，简称力偶矩。
说明： 1）平面内力偶矩为代数量，其正负号表转向，一般规定 逆时针转向为正，反之为负。

力矩与平面力偶系课件

力矩与平面力偶系课件
- F22d ＝M2
FR＝F11-F22
d2F1有作偶个一力设用两平同内成系偶合力平的一.
FR' ＝ F11 '-F22 '
MR = FR d= ( F11- F22 )d
=F1 1d- F22 d= M 1 - M2
F1
F
d1
2
d2
F1'
F'
2
F2
2
F11'
d
F11
F22
'
FR' d
F
R
? MR为合力F R ，F R '组成的力偶(F R ，F R ' ) (称 为合力偶)的力偶矩， 称为合力偶矩； 也是原来两个力 偶的力偶矩的和。
作偶对该力用面)内偶力的‘，F物体有作偶臂一力设用为(
力偶对作用面内任一点的矩之大小恒等于力偶中 一力的大小和力偶臂的乘积，而与矩心的位置无关。
力偶对物体的转动效应可用力与力偶臂的乘积Fd 及转向来度量，该物理量称为力偶矩。
?力偶矩用符号M (F ，F')或M表示；即 M (F ，F') = ±Fd 规定：逆时针转动时，力偶矩取正号；
?力的作用线如通过矩心，则力矩为零； 反之，如一个大小不为零的力对一点之 矩为零，则此力的作用线必通过该点。
?互成平衡的二力对同一点的力矩之和为 零
虽然力矩概念由力对物体上固定点的 作用引出。实际上，作用于物体上的力 可以对任意点取矩，即矩心可是空间中 的任意点。
二．力对轴的矩
力对轴的矩用来度量力对 所作用的刚体绕某一固定轴转 动的效应。
a
，力偶矩为 -
4
3
Fa F1y与F2y组成一个力偶，力偶臂为1

工程力学第三章力矩力偶系

工程力学第三章力矩力偶系

M ( F ) r F sin O
定理：如果力系存在合力,则合力对某一点的矩等于力 系中各分力对同一点的矩的矢量和。
即：若作用在刚体上 { F , F , , F } { F } 1 2 n R
则：
M ( F ) M ( F O R O i)
i 1
n
例 水平梁 AB 受按三角形分布的载荷作用。载荷的最 大值为 q ，梁长为 l 。试求合力作用线的位置。
0
将 Q 和 q(x) 的数值代入可得
xC
2 l 3
§3-2 力偶理论
一.力偶和力偶矩
1、力偶 · 力偶的作用 效果 ·力偶的第一性质
力偶的定义：由大小相等，方 向相反且不共线的两个平行力 所组成的力系，称为力偶。记 之为： ( F, F ' )
F
hபைடு நூலகம்
F
'
h——力偶臂
力与力偶的作用效果比较：
FA
第三章 力矩 力偶系理论
§3-1 力对点之矩（力矩） 力对刚体的移动效应用力矢量来度量 力对刚体的转动效应用力矩来度量 一、力对点之矩
B F O
定义：
r
h
A
M r F oF

矢量积形式
M r F oF
二、 合力矩定理

大小： r F F h 2 OAB 方向： 由右手定则判定
25 N 0.4 m
M=10 Nm
25 N
§3-3 力偶系的合成与平衡
力偶系合成的结果为一合力偶
{ M , M , , M } { M } 1 2 n R
n
即：
M R Mi
i 1
力偶平衡的充分必要条件:

第三章 平面力偶系

第三章 平面力偶系

FA
AM
D
解: 1）分析BD杆
C
450 E
M = 0, M1 - FE ·a = 0 FB = FE = M1 / a
M1
B FB FB B
D
E FE
M1
2）分析整体 FA = FB = M1 / a M = 0, M1 - M = 0 M = M1
27
作业：习题 P54 3—1
3—4 3—7(F ) Fd A 225N m M C (F ) Fd C
F AD F CD
sin 30 sin 30
B
75 N m
2）由合力矩定理 M B (F ) Fx AB Fy AD
求对B点的矩 F cos 30 AB F sin 30 AD
144N
FB FA 144N
(2)取CD杆
M 0, M 0 FC CD cos 0
cos
0.24
0.182 0.242
FC

5M 0 4 0.32m

5 40N m 4 0.32m
156N
FE FD FD FC 156N
FNB可知由力偶概念可知FNA FNB
F’NA
Fy 0, FT W
24
课上练习3
B M C
l
已知：结构中AB为r的圆弧，l=2r，M已知。 求：A和C处的反力。
解：1）分析AB：
可知是二力构件，受力如图
A
F'B
FB
r
M
2）分析BC：受力如图
FA
M 0, M FBd 0

大学工科工程力学第三章 力偶系

大学工科工程力学第三章 力偶系
= F3 d − F4 d
= M1 − M 2
结论：
在同平面内的任意个力偶可合成 一个合力偶，其合力偶矩等于各 个力偶矩的代数和。
M =
∑M
i =1
n
i
b、平面力偶系的平衡条件 充要条件：
∑M
i =1
n
i
=0
即：所有力偶的合力偶矩的代数和等于零。
根据力偶理论，一个力偶与一个力是不可能平衡的。
M
r O
第三章
力偶系
本章主要内容
力对点之矩矢 力对轴之矩 力偶矩矢 力偶的等效条件和性质 力偶系的合成和平衡条件
力偶的定义
A
F′
B
F
大小相等,方向相 反,不共线的两个力所 组成的力系。
力 偶 实 例
§3-1 力对点之矩矢
一、平面中力对点之矩（力矩） 力对物体可以产生： 移动效应--取决于力的大小、方向 转动效应--取决于力矩的大小、方向
§3-3 力偶矩矢
一、平面力偶矩 用以衡量力偶对刚体的转动效应
B A
O
x
d
F´
平面有一个力偶，将它们对O 点取矩 根据力对点之矩，力偶对O 之矩为：
F
M = mo ( F ) + mo ( F ′) = − Fx + F ′( x + d ) = Fd = F ′d
M = ± Fd
力偶矩与矩心的位置无关。
M ∑ cos α = M
xi
M ∑ , cos β = M
yi
M ∑ , cos γ = M
zi
空间力偶系的平衡条件是：合力偶矩矢为零
∑M ∑M ∑M
x y z
=0 =0 =0

工程力学——力矩和平面

工程力学——力矩和平面
力偶矩的大小也可以通过力与力偶臂组成的三角
形面积的2倍来表示，如图3.5所表示。即 M=±2△OAB
图3.5
力偶对物体的转动效应，取决于下列三要素： ① 力偶矩的大小； ② 力偶的转向； ③ 力偶作用面的方位。
3.3 力偶的性质
一、力偶无合力，力偶不能用一个力来代替 由于组成力偶的两个力是等值、反向的，它们在任 一坐标轴上的投影的代数和恒等于零(如图3.6所示)，因此， 力偶对物体只有转动效应而没有移动效应。
力偶不能合成一个力， 它不能用一个力来平衡而只能 和力偶相平衡。所以力偶和力 是组成力系的两个基本物理量。 或者说，力偶和力是静力学的 两个基本要素。
图3.6
二、力偶对其作用面上任意点之矩，恒等于力偶 矩，而与矩心的位置无关
证明：设有一力偶(F，F′)作用在物体上其力偶矩 M= F·d (见图3.7)。在力偶的作用平面内任取一点O为矩 心，设O点至F′的垂直距离为a。显然，力偶使物体绕O 点转动的效应，等于组成力偶的两个力使物体绕O点转 动的效应之和，即
从式(3-1)可知： (1) 力沿作用线移动时，不会改变力对某一矩心的力 矩，因为此时并未改变力、力臂的大小及力矩的转向。 (2) 当力的作用线通过矩心时，力矩为零。 合力矩定理 平面汇交力系的合力对平面内任一点之矩，等于力 系中各力对同一点力矩的代数和。即：
MO(F)= MO(F1)+ MO(F2)+…+MO(Fn)= MO(Fi) (3-3) 合力矩定理不仅适用于平面汇交力系，也同样适用于任 何力系。
各分力偶矩的代数和。
3.4.2 平面力偶系的平衡
由于平面力偶系合成的结果为一合力偶，当其合 力偶矩等于零时，表明使物体顺时针方向转动的力偶矩 与使物体逆时针方向转动的力偶矩相等，作用效果相互 抵消，物体保持平衡状态。即平面力偶系的平衡条件为
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
A′ P1 D Q A a P B′ C P′ B Q′ b P1′
M ( F , F ) 2 S ABD , M ( P , P ) 2 S ABC S ABD S ABC M ( F , F ) M ( P , P ) M ( P , P ) M ( P1 , P1) M ( F , F ) M ( P1 , P1)
F1
F1 F2
′
F2
F1
′
F2′
F2
F1′
图3-17
工程力学电子教案
力矩与平面力偶系
28
思考题 3-3
图3-18所示圆盘由O点处的轴承支持，在力偶 M 和力F 的作用下处于平衡。能不能说力偶被力F 所平衡？为什么？ 思考题3-4
力矩和力偶有什么联 系？又有什么区别？
M
O
图3-18
F
工程力学电子教案
力矩与平面力偶系
29
思考题 3-5 两轮半径同为 r ，一轮在轮缘上受一大小为F 的力作用，另一轮在轮缘上受两个方向相反、大小 都是F/2 的力作用，各轮上的力对轮心的矩是否相 同？两轮上的力对轮的外效应是否相同？
F/2 r O1 O2 r
F/2 F (a)
图3-19
(b)
工程力学电子教案
力矩与平面力偶系
工程力学电子教案
力矩与平面力偶系
20
两力偶作用在板上，尺寸如图，已 知 F1 = F2=1.5 kN , F3 =F4 = 1 kN, 求作用在板上 的合力偶矩。 解：由式
F1 180mm F
例 题 3- 1
2
F4
则 M =-F1 · 0.18 –F3 · 0.08 = -350 N· m
M = M1 + M2
F 力偶臂 d F′ 力偶作用面
图3-6
x
工程力学电子教案
力矩与平面力偶系
12
(3) 力偶矩 其转动效应——力对点之矩，即用力偶中 的两个力对其作用面内任一点之矩的代数和来 度量。
M ( F , F ) F d 或 M F d
例如：
M O ( F ) M O ( F ) - F x - F (d - x ) -F d
这样得到新的力偶(FR , FR′),则
M= FRd= (F11 - F22)d=F11d - F22 d=M1+M2 (2) 任意个力偶的情况 M=M1 + M2 + … + Mn , 或 M=∑Mi
Mn M1
M2
图3-13
工程力学电子教案
力矩与平面力偶系
19
2. 平衡条件 平面力偶系平衡的必要和充分条件是：力偶 系中各力偶矩的代数和等于零，即 ∑Mi=0 利用这个平衡条件，可以求解一个未知量。
F11′ d
F2
d2
F2′
=
F11
=
F22′
d FR FR′
M 1 F1 d 1 , M 2 - F2 d 2
M 1 F11 d , M 2 - F22 d
FR F11 - F22 , FR F11 - F22
工程力学电子教案
力矩与平面力偶系
18
q
M1 M2 D
O
工程力学电子教案
力矩与平面力偶系
25
写出杆OA和DB的平衡方程： ∑M = 0
FBA A M1 FO O FAB B
M 1 - FAB rcos a 0 - M 2 2 FBA rcos a 0
因为
M2
D
FAB FBA M 2 2M 1
所以求得
FD
工程力学电子教案
F
x
d O
F
图3-7
工程力学电子教案
力矩与平面力偶系
13
(4) 力偶的三要素 (a) 力偶矩的大小； (b) 力偶的转向； (c) 力偶作用面在空间的方位。
2. 平面力偶等效定理 定理：在同一平面内（或两平行平面）的两 个力偶，如它们的力偶矩的大小相等，而且转向 相同，则此两力偶等效。 F1 F′
30
思考题 3-6 图中所示两轮在图示主动力作用下能否处于平 衡？为什么？若不能平衡，可否再在轮上加一个力 使之平衡？如何加？
r
F/2
O2
r
O1 F
(a)
F/2
图3-20
(b)
工程力学电子教案
力矩与平面力偶系
31
d
a-q
图 3-3
工程力学电子教案
力矩与平面力偶系
9
则
MO (F) xA Fy - yA Fx
(a)
若作用在 A点上的是一个汇交力系（F1 、F2 、… Fn） 则可将每个力对O点之矩相加，有
M
O
(F) xA Fy - yA Fx
(b)
该汇交力系的合力FR=∑F，由式(a)，它对O点的矩 为：
例如：方向盘
C A D F
B
F1′
图3-8
工程力学电子教案
力矩与平面力偶系
14
证明：设有一力偶 (F, F ′),如图所示 . 运用加减平 衡力系的公理并注意到：
( F , F ) ~ ( F , F , Q , Q ) ~ ( P , P ) ( F , F ) ~ ( P1 , P1)
M O ( F ) F d F r sin(a - q ) F r (sin a cos q - sin q cos a ) F r sin a cos q
而
O x r Fy F
A
a
y Fx x
q
- F r sin q cos a
F cos a Fx , F sin a Fy r cos q xA , r sin q y A
MO (FR ) xA FR y - yA FR x xA F y - yA F x (c)
比较(b)、(c)两式有
M O ( FR ) M O ( F )
证毕。
工程力学电子教案
力矩与平面力偶系
10
§3-2 力偶的概念
1. 力偶和力偶矩
(1) 力偶的概念 把大小相等、方向相反、作用线平行的 两个力叫做力偶。并记作（F，F′）。可用 图3-4表示, 例如：方向盘等
F d F′ 力偶作用面 F 力偶臂 F1 A D B F1′ C F′
图 3-4
图3-5
工程力学电子教案
力矩与平面力偶系
11
(2) 力偶的性质 (a) 力偶在任何坐标轴上的投影等于零； (b)力偶不能合成为一力，或者说力偶没有合力， 即它不能与一个力等效，因而也不能被一个力平 衡； (c) 力偶对物体不产生移动效应，只产生转动效 应，即它可以也只能改变物体的转动状态。
力矩与平面力偶系
7
(2) 力的作用线如通过矩心，则力矩为零；反之，如 果一 个力其大小不为零，而它对某点之矩为零， 则此力的作用线必通过该点； (3) 互成平衡的二力对同一点之矩的代数和为零。
F2 F O F1
o 图 3-2 (b)
图 3-2 (c)
工程力学电子教案
力矩与平面力偶系
8
2. 合力矩定理 表达式： M O ( FR ) M O ( F ) 证明：由图得 y
F3
80mm
负号表明转向为顺时针。
图3- 4 m的简支梁的两端A、B 处作 例 题 3- 2 用有二个力偶，大小各为M1 =16 N· m，M2 = 4 N· m， 转向如图。试求A、B支座的约束力。
M1 M1
A
4m (a) M2
B
60
A
FA
B FB d M2
力矩与平面力偶系
26
思考题 3-1 一力偶(F1,F1′)作用在Oxy平面内,另一力偶(F2 ， F2′)作用在Oyz平面内,它们的力偶矩大小相等(如图)。 试问此两力偶是否等效，为什么？
z
F2 F2′
y
O F1
x F1′
图3-16
工程力学电子教案
力矩与平面力偶系
27
思考题 3-2 如图所示，在物体上作用有两力偶(F1,F1′)和 (F2,F2′)其力多边形封闭。问该物体是否平衡？为 什么？
(b)
M2
d
解得
故
FA、FB为正值，说明图中所示FA、FB的指向正确。
工程力学电子教案
力矩与平面力偶系
23
例 题 3- 3 如图所示的铰接四连杆机构OABD，在杆OA 和BD上分别作用着矩为M1和M2的力偶，而使机 构在图示位置处于平衡。已知OA=r，DB=2r，θ =30°，不计各杆自重，试求M1和M2间的关系。
工程力学电子教案
力矩与平面力偶系
4
§3-1 力矩的概念和计算
1. 力对点之矩
l F A
(1) 用扳手拧螺母； (2) 开门，关门。
d
O
图3-1
由上图知，力F 使物体绕O点转动的效应，不仅与 力的大小，而且与O点到力的作用线的垂直距离d 有关，故用乘积F· 来度量力的转动效应。该乘积 d
工程力学电子教案
工程力学电子教案
力矩与平面力偶系
3
谁曾经想过用杠杆来移动地球？ 古希腊科学家阿基米德曾说过“如果给我一个支点，我就能
撬起地球”。这句名言从理论上讲是完全正确的，
因为杠杆能使力变大，只要杠杆足够长，就 能产生足够大的力来“搬动”地球。
动力臂越长，施力的一方经过的距离越
长，力省了，可增加了距离。如果真有一个支 点，要撬动地球，恐怕撬棍的动力臂长得你 无法想象，比阻力臂要长1000万万亿倍，要 把地球撬起1厘米，如果按每秒移动1米计算， 要花3万亿年的时间，这比地球的历史还要长。 ——来自中国科普网