当前位置：文档之家 › 建筑力学力矩与平面力偶系讲课稿

建筑力学力矩与平面力偶系讲课稿

  • 格式：ppt
  • 大小：720.00 KB
  • 文档页数：16

下载文档原格式

  / 16

合集下载

力对点的矩与平面力偶系—平面力偶系的合成与平衡(建筑力学)

力对点的矩与平面力偶系—平面力偶系的合成与平衡(建筑力学)


平面力偶系
例3-4 如图示的梁AB，受一力偶的作用，已知力偶， M=20kNm，梁长l=4m,梁自重不计，求A、B支座处反力。
解 取梁AB为研究对象。
梁在力偶和A、B两处支座反力作用下平衡。
M 0
FByl M 0
FBy
M l
20 kN 5kN 4FAyLeabharlann FBy 5kN平面力偶系
第三节 平面力偶系的合成与平衡
作用在物体上的两个或两个以上的力偶，称为力偶系。 作用在同一平面内的力偶系称为平面力偶系。 一、平面力偶系的合成
平面力偶系可以合成为一个合力偶，其合力偶矩等于各个 力偶矩的代数和。即
M R M1 M 2 M n M
式中MR表示合力偶矩, M 、M … … Mn表示原力偶系中各 力偶的力偶矩。
合力偶矩大小为
M M1 M 2 M 3 (64 60 24)N m 28N m （ ）
平面力偶系
二、平面力偶系的平衡条件 平面力偶系合成的结果为一个合力偶，力偶系的平衡就
要求合力偶矩等于零。 平面力偶系平衡的必要和充分条件是：力偶系中所有各
力偶矩的代数和等于零。
M 0
上式又称为平面力偶系的平衡方程。利用其可以求解一 个未知量。
平面力偶系
例3-3 如图示有三个力偶同时作用在物体某平面内。已知 F1=80N，d1=0.8m，F2=100N ，d2=0.6m，M3=24N.m ，求其合 成的结果。
解 三个共面力偶合成的结果是一个合力偶。各力偶矩为
M1 F1d1 80 0.8 64N m M 3 24N m
M 2 F2d2 100 0.6 60N m
第三章 力偶与平面力偶理论)

第三章 力偶与平面力偶理论)


M 0 F F h
力对点之矩（力矩）是一个代数量，它的绝 对值等于力的大小与力臂的乘积；
它的正负：力使物体绕矩心逆时针转向时为正，反之为负。 常用单位为 N· m 或 kN· m。 注意：力矩在下列几种情况下等于零 （1）力的大小等于零；
（2）力的作用线通过矩心，即力臂等于零；
（3） 互成平衡的二力对同一点之矩为零。
78.93N m
按合力矩定理 M O F M O Ft M O Fr



F cos θ r 78.93N m
例3-2 已知：q,l； 求： 合力及合力作用线位置. 解： 取微元如图
x q q l l x 1 P q dx ql 0 l 2
M Mi Mi
i 1 n
平面力偶系平衡的充要条件 M = 0，有如下平衡方程
Mi
0
平面力偶系平衡的必要和充分条件是：所有各力 偶矩的代数和等于零。
例3-1
已知: F=1400N, θ 20 , r 60mm
求: M O F .
解:直接按定义
MO

F F h F r cos θ
M1 F1 d M2 F2 d
M1 F1d
M 2 F2d
Mn Fn d
M n Fnd
=
=
FR F1 F2 Fn
F1 F2 Fn FR
=
=
=
M FRd F1d F2d Fnd M1 M 2 M n
定理：同平面内的两个力偶，如果力偶矩相等，则两力偶 彼此等效。 推论： 任一力偶可在它的作用面内任意转移，而不改变它对刚体 的作用。因此力偶对刚体的作用与力偶在其作用面内的位置无 关。 只要保持力偶矩不变，可以同时改变力偶中力的大小与 力偶臂的长短，对刚体的作用效果不变.
力矩与平面力偶系 ppt课件

力矩与平面力偶系 ppt课件


Ａ
Ｏ
d
即力对Ｏ点的矩的大小
等于△OAB面积的２倍。
ppt课件
7
力对任一已知点的矩，不会因该力沿作 用线移动而改变。
力的作用线如通过矩心，则力矩为零； 反之，如一个大小不为零的力对一点之 矩为零，则此力的作用线必通过该点。
互成平衡的二力对同一点的力矩之和为 零
虽然力矩概念由力对物体上固定点的 作用引出。实际上，作用于物体上的力 可以对任意点取矩，即矩心可是空间中 的任意点。
第三章: 力矩与平面力偶系
ppt课件
1
本章研究力矩和力偶的概念、力偶的 性质、平面力偶系的合成与平衡。本 章与第二章的理论是研究平面一般力 系的基础。
ppt课件
2
§3-1 力矩的概念和计算
一般情况下，力对物体作用时可以产 生移动和转动两种外效应。力的移动 效应取决于力的大小和方向。为了度 量力的转动效应，需要引入力矩的概 念。
力偶对物体产生转动的效应怎样度 量？
力对物体转动的效应用力矩来度量， 因此力偶对物体转动的效应可用力偶 中的两个力对其作用面内任一点之矩 的代数和来度量。
ppt课件
18
设物体上作用有一 力偶臂为d的力偶 （Ｆ，Ｆ‘）
该力偶对作用面内任 一点Ｏ之矩为：
Ｏ x
F
F’ d
Ｍo(F)+Mo(F’)=F(x+d)-Fx=Fd
ppt课件
3
一. 力对点之矩
用扳手拧一螺母，
扳手连同螺母绕一
定点Ｏ转动。由经
验可知，力越大， 螺母拧得越紧；力
F d
的作用线离螺母中
心愈远，拧紧螺母
O
愈省力。
ppt课件
4
工程力学第三章力矩与平面力偶系

工程力学第三章力矩与平面力偶系


x
o r
d
A
y

Fx
x
而 F cos Fx , F sin Fy
r cos x, r sin y
则
mo (F ) xFy yFx
( a)
第三章力矩与平面力偶系
湖南工业大学土木工程学院
§3-1力矩的概念和计算
mo (F ) xFy yFx
y
(a)
Fy
的半径 r = 60 mm，试计算力 Fn 对 于轴心O的力矩。
第三章力矩与平面力偶系
湖南工业大学土木工程学院 18
例题
力对点之矩
r O
h

解： 解法一
计算力Fn对轴心O的矩，按力矩的定义得
MO (Fn ) Fn h Fnr cos
78.93 N m
解法二
r
或根据合力矩定理，将
0
0l
2
湖南工业大学土木工程学院 27
例题
力对点之矩
F
q A
dx x
h l
设合力F 的作用线距A端的距
离为h，根据合力矩定理，有
q Bx
l
Fh 0 qxdx
将q' 和 F 的值代入上式，得
h 2l 3
第三章力矩与平面力偶系
湖南工业大学土木工程学院 28
§3-2力偶的概念
第三章力矩与平面力偶系
3、合力的作用线通过荷载图的形心。
第三章力矩与平面力偶系
湖南工业大学土木工程学院
平行分布线荷载的简化
1、均布荷载 Q ql
2、三角形荷载
Q 1 ql 2
3、梯形荷载
Q
q
工程力学第三章力矩与平面力偶系_图文

工程力学第三章力矩与平面力偶系_图文

反力也必须组成一个同平面的力偶 （ ， ）与 之平衡。
例题讲解
【解】作 AB 梁的受力图，如图（ b ）所示。AB梁上作用 有二个力偶组成的平面力偶系，在 A 、B 处的约束
反力也必须组成一个同平面的力偶 （ ， ） 与之平衡。 由平衡方程
() RA 、RB为正值，说明图中所示RA 、RB 的指向正确。
力臂d
=
1m
×
sinα
=
1m
×
。 sin45 =
m
MB(F)=+F×d= +15kN×0.5 m = +7.5 kN ·m
注意：负号必须标注，正号可标也可不标。一般不标注。
§3-1力矩的概念和计算
（二）合力矩定理
表达式： 证明： 由图得
而 则
Fy
F
A
Fx
()
§3-1力矩的概念和计算
()
若作用在 A 点上的是一个汇交力系（ 、 、 ），则可将每个力对 o 点之矩相加，有
2. 力偶的三要素 （2）力偶的方向； （3）力偶的作用面。
3. 力偶的性质 （1）力偶在任何坐标轴上的投影等于零；
（2）力偶不能合成为一力，或者说力 偶没有合 力，即它不能与一个力等效， y
因而也不能被一个力平衡；
（3）力偶对物体不产生移动效应，只 产生转动 效应，既它可以也只能改变物
体的转动状 态。
例题讲解
【例题5】在一钻床上水平放置工件,在工件上同时钻四个等 直径的孔,每个钻头的力偶矩为 求工件的总切削力偶矩和A 、B端水平反力?
解: 各力偶的合力偶距为
根据平面力偶系平衡方程有:
由力偶只能与力偶平衡的性质 ，力NA与力NB组成一力偶。
例题讲解
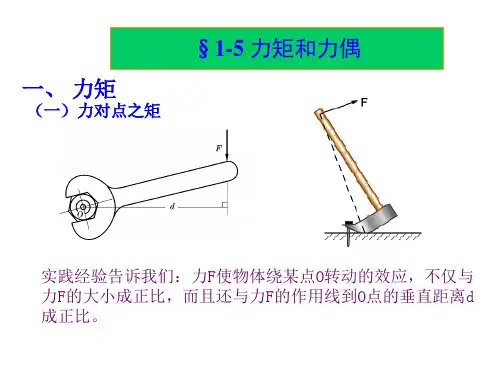
建筑力学_力矩和力偶讲诉

建筑力学_力矩和力偶讲诉


M A Fxdx Fyd y
由于 dx = 0 ，所以：
M A Fyd y 20
2 2 28.28kN m 2
二、力偶
1. 相反但不共线的 一对平行力组成的力系称为力偶，记作（F,F`）
Fd F'
力偶臂
力偶作用面
2. 力偶矩
在力偶作用面内，力偶对物体的转动效应取决于力偶中力和力 臂乘积的大小以及力偶的转向。因此，在力学中用力的大小F与力 偶臂d的乘积Fd加上正负号作为度量力偶对物体的转动效应的物理 量，称为力偶矩。
二力偶力偶作用面力偶臂力偶的概念把作用在同一物体上大小相等方向相反但不共线的一对平行力组成的力系称为力偶记作ff在力偶作用面内力偶对物体的转动效应取决于力偶中力和力臂乘积的大小以及力偶的转向
一、 力矩
（一）力对点之矩
§1-5 力矩和力偶
实践经验告诉我们：力F使物体绕某点O转动的效应，不仅与 力F的大小成正比，而且还与力F的作用线到O点的垂直距离d 成正比。
M
M
说明：
① 力矩是一个代数量；
② 力矩的大小与矩心的位置有关，同一个力对于不同 的矩心，力矩是不相同的。
③力的作用线如通过矩心，则力矩为零；反之，如果 一个力其大小不为零，而它对某点之矩为零，则此力 的作用线必通过该点。
（二）合力矩定理
y
Fx
F
合力对平面内任意一点之矩， 等于所有分力对同一点之矩的代数 和。
位置无关。
（3）力偶的等效性。在同一平面内的两个力偶，如果它们的力偶
矩大小相等，力偶的转向相同，则这两个力偶是等效的。
4. 力偶的平移定理 根据力偶的等效性，可以得出以下两个推论：
推论1：力偶可以在其作用面内任意移转而不改变它对物体的 转动效应。
建筑力学力矩(课堂PPT)

建筑力学力矩(课堂PPT)

解：Mo(F1)F1d11000.220N.m
0.2 Mo(F2)F2d2100co3s023.1N.m Mo(F3)F3d310000N.m
16
3.均布线荷载力矩的计算
均布线荷载力矩的计算公式： Mo(q)=Mo(FR)=± FR.d
17
均布线荷载力矩计算举例
例：试计算下图(a)、（c）所示均布线荷载 q 分别对点O、A 之矩。
1、P61 2-9 （d） （c） （e）
23
LOGO
很高兴与大家共度一段美好的时光!
24
6
力矩平面力偶系的合成与平衡（一）
请一位同学转动用扳手拧螺母。 在这些物体绕某点的转动中,瞧（如上图），
它的绕哪点转动的？转动能力的大小与 哪些因素有关？
7
二、新课讲解 1、力矩
a、力矩的概念 （1）导入：如上图，力F使扳手绕螺母中心O转动，实践
经验告诉我们，转动效果不仅与力的大小成正比，而 且还与该力作用线到O点的垂直距离d成正比。 （2）分析：当改变F的指向时，扳手的转向也随之改变。 力F使物体绕O点的转动效应用什么来度量呢？
单位制中常用单位是牛顿•米（N•m）或
千牛顿•米(kN•m）。
10
力矩性质
➢ 力矩为零的情况：力等于零或力的作用线通过矩心。 ➢ 力矩不变的情况：若将力F沿其作用线移动，则因为
力的大小、方向和力臂都没有改变，所以不会改变该 力对某一矩心的力矩。
11
二、 力矩的计算
1. 荷载的分类 荷载按作用的范围不同可分为集中荷载和分布荷载。 如果荷载作用在结构上的面积与结构的尺寸相比很小， 就称为集中荷载。用F表示，其常用单位为牛（N）、 千牛（kN）。例如梁对柱子或墙的压力属于集中荷载。 如果荷载连续地作用在整个结构上或结构的一部分 （不能看成集中荷载时），就称为分布荷载。例如水 压力属于分布荷载，还有风荷载、雪荷载等。
力矩与平面力偶系 PPT课件

力矩与平面力偶系 PPT课件

F1 d A F 1 B A F2 D ABD , M ( P , P ) 2 S ABC S ABD S ABC M ( F , F ) M ( P , P ) M ( P , P ) M ( P1 , P1) M ( F , F ) M ( P1 , P1)
F′ F
F2 F O F1
o 图 3-2 (b)
图 3-2 (c)
2. 合力矩定理 表达式： M O ( FR ) M O ( F ) 证明：由图得 y
M O ( F ) F d F r sin( ) F r (sin cos sin cos ) F r sin cos
图 3-4
图3-5
(2) 力偶的性质 (a) 力偶在任何坐标轴上的投影等于零； (b)力偶不能合成为一力，或者说力偶没有合力， 即它不能与一个力等效，因而也不能被一个力平 衡； (c) 力偶对物体不产生移动效应，只产生转动效 应，即它可以也只能改变物体的转动状态。
F d F′ 力偶作用面 力偶臂
图3-6
而
O x r Fy F
A

y Fx x

F r sin cos
F cos Fx , F sin Fy r cos x A , r sin y A
d
M

图 3-3
则
MO (F) xA Fy yA Fx
(a)
MO (F) xA Fy yA Fx
谁曾经想过用杠杆来移动地球？ 古希腊科学家阿基米德曾说过“如果给我一个支点，我就能
撬起地球”。这句名言从理论上讲是完全正确的，
因为杠杆能使力变大，只要杠杆足够长，就 能产生足够大的力来“搬动”地球。
工程力学力矩与平面力偶系课件

工程力学力矩与平面力偶系课件

总结词
吊桥的受力分析
详细描述
吊桥在风力和车辆负载的作用下保持平衡。通过分析吊 桥的受力，可以了解平面力系中力的平衡条件。
平面力系的实例三
总结词
旋转门的工作原理
详细描述
旋转门在开启和关闭过程中受到推力和拉力作用。这 些力产生力矩，使门旋转。这个例子展示了力矩在平 面力系中的作用。
谢谢聆听
04
验证解的合理性
通过代入原始数据或进行实物实 验验证解的合理性。
05 平面力系的实例分析
平面力系的实例一
要点一
总结词
平衡状态下的斜面
要点二
详细描述
一个斜面上的物体在重力作用下处于平衡状态，重力可分 解为两个力，一个沿斜面向下，另一个垂直于斜面。这个 例子展示了平面力系中力的合成与分解。
平面力系的实例二
VS
详细描述
力偶是工程力学中一个基本概念，它由两 个力组成，这两个力大小相等、方向相反 ，且作用线相互平行但不在同一直线上。 力偶在平面或空间中都可以存在，但在平 面问题中更为常见。
力偶的性质
总结词
力偶具有方向性、大小不变性和作用点无关性。
详细描述
力偶具有三个重要的性质。首先，力偶具有方向性，它只能沿其所在的平面转动，不能在平面内移动 。其次，力偶的大小是恒定的，不会因为改变作用点而改变。最后，力偶的作用点无关性意味着力偶 可以在其作用线上任意移动，只要保持两个力的大小和方向不变，其效果就不会改变。
平面力的合成
总结词
平面力的合成是指将两个或多个在同一平面内的力合成为一 个力的过程。
详细描述
平面力的合成可以通过平行四边形法则或三角形法则进行。 具体来说，两个在同一平面内的力可以合成一个力，这个力 的方向和大小可以通过平行四边形法则或三角形法则确定。
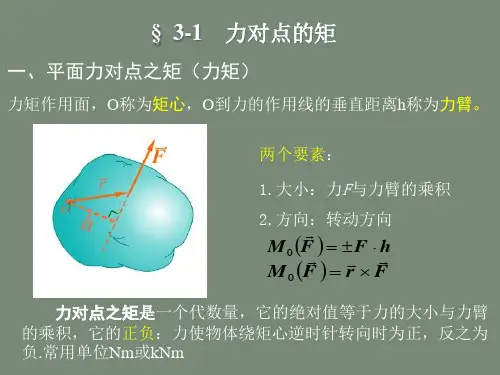
力矩和平面力偶理论课件

力矩和平面力偶理论课件


FO
FB
FA
M1 r sin 30
8
kN
作业：P49~P53 3－5、3－10、3－11
FA
A
O
M1
FO
C
M2
A
FA
FB
B
解：先取圆轮为研究对象，因为力偶只
能与力偶平衡，所以，力FA 与FO 构成一 力偶，故FA= –FO。
M 0, M1 FAr sin 0
解得
FA
M1 r sin 30
再取摇杆BC为研究对象。
M 0,
M2
FA
r
sin
0
其中 FA FA
解得 M 2 4M1 8 kN m
M 0, M FA l cos 45 0
解得
FA
FB
M l cos 45
2M l
例3-7 ：
如图所示的铰接四连杆机构OABD，在杆OA和BD上分 别作用着矩为M1和M2的力偶，而使机构在图示位置处于 平衡。已知OA=r，DB=2r，α=30°，不计杆重，试求M1和 M2间的关系。
Aα
M1
O
=
=
=
M FRd F1d F2d Fnd M1 M2 Mn
n
M Mi Mi
i 1
平面力偶系平衡的充要条件 M = 0，有如下平衡方程
Mi 0
平面力偶系平衡的必要和充分条件是：所有各力偶 矩的代数和等于零。
例3-1
已知: F=1400N, θ 20 , r 60mm 求: MO F .
所以求得
M2
1 2
M1
例3-8 ：
C
M2
Ar O
M1
B
如图所示机构的自重不计。圆轮 上的销子A放在摇杆BC上的光滑导槽 内。圆轮上作用一力偶，其力偶矩为 M1=2 kN·m ， OA = r =0.5 m。图示位 置时OA与OB垂直，角α=30o , 且系统 平衡。求作用于摇杆BC上的力偶的矩 M2 及铰链O，B处的约束反力。
理论力学精品课程 第三章 力矩与平面力偶理论

理论力学精品课程 第三章 力矩与平面力偶理论


一,平面中力矩的概念
3.1 力 矩 的 概
y
二),平面汇交力系的合力矩定理 ),平面汇交力系的合力矩定理 定理: 定理:平面汇交力系的合力对平面内任意 一点的矩等于各个分力对同一点之矩的代 数和. 数和.即
mo ( R ) = ∑ mo ( Fi )
Y
y
F
X
A
o
x
x
利用合力矩定理, 利用合力矩定理,可以 写出力对坐标原点的矩的解 析表达式, 析表达式,即
B
C
E B
ND
∑ m = 0 : M N A AD = 0
M
D
A AD = (2 R) 2 R 2 = 3R NA M M 3M 所以: N A = = = = ND 3R AD 3R
例6
3.3 平 面 力 偶 系 的 合 成 与 平 衡 再以轮C为研究对象,受力 如图,建立如图坐标.
′ ND
及
由此可见, 由此可见,两力偶的等效条件是力偶矩 相等. 相等. 在平面问题中, 在平面问题中,决定力偶作用效果的因 素为:矩的大小和转向. 素为:矩的大小和转向.所以力偶矩是代数 量. 力偶可表示为: 力偶可表示为:
m
m
一,力偶的性质
3.2 力 偶 及 其
3,力偶在作用面内任一轴上的投 , 影均为零. 4,力偶对其作用面内任一点之矩 , 与矩心的位置无关, 与矩心的位置无关,恒等于力偶矩.
mo (F ) = mo (Y ) + mo ( X ) = Y x X y
例1
3.1 力 矩 的 概
dA
支架如图所示,已知F=100N, AB=AC=30cm,CD=15cm, α = 30
dC
A

【建筑】建筑力学力矩与平面力偶系ppt模版课件共17页文档


M=±F×· d
注：力偶逆时针转动时取正， 反之取负。
d F′
力偶矩的单位：N m 、kN m
F
F= F ′ d：力偶臂
二、力偶的基本性质
d偶没有合力。一个力偶不能用一个力代替，也不 能与一个力平衡。力偶在任一轴上的投影为零。
• ⑵力偶对作用面内任一点之矩恒等于力偶矩，而与矩 心位置无关。两个力偶等效的条件是力偶矩相等。
• ⑶只要力偶矩保持不变，力偶可在其作用面内任意移 转，或者可以同时改变力偶中力的大小和力偶臂的长 短，力偶对物体的效应不变。
• 力偶的三要素：力偶矩的大小、力偶的转向，作 用面。
力偶的简化表示符号：
§3-3 平面力偶系的合成与平衡
一、平面力偶系的合成
• 平面力偶系的合成结果为一个合力偶，合力偶 的力偶矩等于各分力偶的力偶矩的代数和。
• 平面力偶系平衡的充要条件：各力偶的力偶矩代数 和等于零。 mi =0
简答
（1）力偶不能和一个力平衡，为什么图中的轮子又 能平衡？
M=P r
r
O
P M=P r
O
P
P
力偶只能和力偶平衡，P、O两点的力应构成 力偶，所以，这个力偶与M平衡。
简答
(2)图中梁AB处于平衡，如何确定支座A、B处反力的方向？
SUMMER TEMPLATE
【建筑】建筑力学力矩与平面力偶系 ppt模版课件
第三章 力矩与平面力偶系
§3-1 力对点之矩与合力矩定理 §3-2 力偶及其基本性质 §3-3 平面力偶系的合成与平衡
§3-1 力对点之矩与合力矩定理 一、力F对O点的矩
d为O点到力F作用线的（垂直）距离。
记为 mO（F）=±F*d，单位：N·m（牛顿·米）

建筑力学课件 第四章 力矩与平面力偶系

力矩的概念可以推广到普遍的情形。在具 体应用时，对于矩心的选择无任何限制， 作用于物体上的力可以对平面内任一点取 矩。
4.1力对点之矩、合力矩定理
3.力矩的性质 综上所述，得出如下力矩性质：
（1）力F对点O的矩，不仅决定于力的大 小，同时与矩心的位置有关。矩心的位 置不同，力矩随之而异。
（2）力F对任一点的矩，不因为F的作用 点沿其作用线移动而改变，因为力和力 臂的大小均未改变。
2.力矩的计算
在平面问题中,我们把乘积Fd加上适当的正负号,
作为力F使物体绕点O转动效应的度量,并称为
力F对点O的矩,简称力矩,用Mo(F) 或MO表示
即 MO (F)=± Fd
（4-1）
点O称为矩心，力作用线到矩心的垂直距离d称
为力臂。正负号通常用来区别力使物体矩心
转动的方向，并规定：若力使物体绕矩心作
4.1力对点之矩、合力矩定理
（3）力的大小等于零或力的作用线通过 矩心，即公式（4-1）中的F=0或者d = 0,则 力矩等于零。
（4）相互平衡的两个力对同一点的矩的 代数和等于零。（相互抵消）
4.关于力矩的量纲单位：
在国际单位制中，力矩的单位是牛·米（ N·m）或千牛·米（kN·m）。
4.1力对点之矩、合力矩定理
M1 = F1 d1 M2 = F2 d2 M3 = －F3d3
4.3 平面力偶系
在力偶作用面内取任意线段AB = d，在保持力偶 矩不改变的条件下将各力偶的臂都化为d，于是 各力偶的力的大小应改变为
4.3 平面力偶系
然后移转各力偶,使它们的臂都 与AB重合,则原平面力偶系变换 为作用在点A及B的两个共线力 系。
在同一平面内的两个力偶，只要两力 偶的力偶矩（包括大小和转向）相等 ，则此两力偶的效应相等。这就是平 面力偶的等效条件。

力对点的矩与平面力偶系—力偶及其基本性质(建筑力学)


力偶
第二节 力偶及其基本性质
一、力偶和力偶矩 . 力偶
力学中，把作用于物体上的一对 等值、反向、平行的力组成的力系称 为力偶，记作（F，F′）。
力偶中，二力作用线间的垂直距离d称为力偶臂，二力 所在的平面称为力偶的作用面。
力偶
力偶与单个力一样，是构成力的基本元素。 2. 力偶矩
力偶对物体的转动效应由组成力偶的力的大小与力偶臂 的乘积，即力偶矩确定。记作：记作M（F，F′）或M，即
3）在同一平面内的两个力偶，如果它们的力偶矩大小 相等，转向相同，则这两个力偶是等效的。
力偶
推论1 力偶可以在其作用平面内任意移动或转动，只要 不改变力偶的三要素，就不会改变它对物体的转动效应。即 力偶对刚体的转动效应与它在作用平面内的位置无关。
力偶
推论2 只要保持力偶矩的大小和力偶的转向不变，可 同时改变组成力偶的力的大小和力偶臂的长度，而不改变 它对物体的转动效应。
M（F，F′）= M =±Fd
在平面力系中，力偶矩为代数 量，力偶使物体做逆时针转动时， 力偶矩为正；反之为负。
单位：KN.m或N.m
力偶
力偶对物体的转动效应完全取决于力偶的三要素，即力偶 矩的大小、力偶的转向和力偶作用平面。
改变其中任何一个要素，都将改变这个力偶的作用效应。 力偶在其作用面内除可用两个力表示外，通常还可用一 带箭头的弧来表示，其中箭头表示力偶的转向，M表示力 偶矩的大小。
力偶
二、力偶的基本性质
）力偶不能合成为一个合力，所以不能用一个力来代替。 由力偶的定义和力的合力投影定理可以得出，力偶在任一 轴上的投影恒为零。由此可知，力偶不会使物体移动，只会 使物体转动。力偶和力对物体作用的效应不同。 力偶不能和一个力平衡，力偶只能和力偶平衡。

理论力学课件-力矩力偶与平面力偶系.ppt

1
第三章 力矩、力偶与平面力偶系
本章内容: 1 力对点的矩 2 力偶与力偶矩 的概念 3 力偶的性质 4 平面力偶系的合成 5 平面力偶系的平衡
2
第一节 力对点的矩
一、平面力对点的矩（力矩）
力矩是度量力对物体的转动效应的物理量。
BF
1、力矩的定义
MO (F ) Fd
A O —— 矩心 d —— 力臂
d
MO (F ) 2A OAB
“＋ ”—— 使物体逆时针转时力矩为正； MO（F）——代数量 “－” —— 使物体顺时针转时力矩为负。
力矩的单位为 N （m牛顿·米）。
3
2、力矩的性质 （1）力沿作用线移动时，对某点的矩不变; （2）力作用过线矩心时，此力对矩心之矩等于零; （３）互成平衡的力对同一点的矩之和等于零。
合力偶矩等于零即力偶系各力偶矩的代数和等于零二平面力偶系的平衡和平衡方程前牙反颌和开颌的原因多由于不良喂养方式和吮指等不良习惯造成也可因多颗乳磨牙过早缺失迫使儿童用前牙咀嚼下颌逐渐前伸移位造成
思考题2-2
构件自重不计，忽略摩擦。Θ=60度。如B处作用有相同 的水平力F。问A处的约束力是否相同，请作图表示其大小 和方向
3、力矩的两个要素 （1）大小：力与力臂的乘积 （2）方向：转动方向
注意：说明力矩时，要指明是哪个力对哪个点的
力矩
4
例 3-1 如图所示，F1 50 kN ，F2 100 kN，AB 6 m 。
试分别求F1 、F2 对 A 点的矩。
F1
B
解：力F1使杆 AB 绕 A 点逆时针转动
M A(F1) F1 AB
平面力偶系—— 作用在物体同一平面内的若干个 力偶所组成的力系。
一、平面力偶系的合成 平面力偶系可合成为一个合力偶，合力偶矩等于 各分力偶矩的代数和，即
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
• ⑶只要力偶矩保持不变，力偶可在其作用面内任意移 转，或者可以同时改变力偶中力的大小和力偶臂的长 短，力偶对物体的效应不变。
• 力偶的三要素：力偶矩的大小、力偶的转向，作 用面。
力偶的简化表示符号：
§3-3 平面力偶系的合成与平衡
一、平面力偶系的合成
• 平面力偶系的合成结果为一个合力偶，合力偶 的力偶矩等于各分力偶的力偶矩的代数和。
A
M1 M2
B A M1 M2 B
l
FA
FB
力偶只能和力偶平衡，A、B两点的力 应构 成力偶，所以，这两个力大小相等、方向相反。 即A点的水平分力为零，可以不画。
此课件下载可自行编辑修改，仅供参考！ 感谢您的支持，我们努力做得更好！谢谢
F
α
Fy
Fx
A
B a
b
解：用定义计算，力臂不 易确定，所以，用合 力矩定理。
Fx=Fcosα Fy=Fsin α MA(F) = －Fx ·b=－ b·Fcosα
MB(F)= MB(Fx) +MB(Fy) = － b ·Fcosα+ a ·Fsin α
• 力偶系平衡条件与汇交力系平衡相类似，力偶系的 平衡即为力偶系的作用不能使物体发生变速转动， 物体处于平衡状态，其合力偶矩等于零，即力偶系 中各力偶的代数和等于零。m=mi =0
• 平面力偶系平衡的充要条件：各力偶的力偶矩代数 和等于零。 mi =0
简答
（1）力偶不能和一个力平衡，为什么图中的轮子又 能平衡？
M=P r
r
O
P M=P r
O
P
P
力偶只能和力偶平衡，P、O两点的力应构成 力偶，所以，这个力偶与M平衡。
精品课件！
精品课件！
简答
(2)图中梁AB处于平衡，如何确定支座A、B处反力的方向？
建筑力学力矩与平面力偶系
二、平面力系的合力矩定理
如果R是平面力系F1、F2、….FN的合力，由于合 力R与力系等效，则合力对其平面内任一点O之矩
等于力系中各分力对同一点之矩的代数和，即：
Mo(FR)=Mo(F1) + Mo(F2)+ ······+ Mo(Fn)+ = ΣMo(F)
F1 F2
O
B
O
Mn
M1
M2
=
M
M = M1+M2+······+Mn = ΣM
简答
车间内有一矩形钢板，要使钢板转动，加力F, F′如图 示。试问应如何加才能使所要的力最小？
F
b
b
a
a F′
当力偶一定时，只有力偶臂最长所用的力才最小。
计算
• 刚架上作用着力F,分别计算力F对A点和B点的力矩。 F、α、a、b为已知。
一、力偶及力偶矩
由大小相等、方向相反、不共线的两个力组 成的力系称为力偶。 力偶对物体的效应：只产生转动效应，而无移动效应。
• 力偶矩：力偶的两个力所在的平面称为力偶的作用 面，两个力作用线间的垂直距离称为力偶臂，用d 表示。力学中，用力偶的任一力的大小F与力偶臂d 的乘积在冠以相应的正、负号，作为力偶使物体转 动效应的度量，称为力偶矩，用M表示。
M=±F×· d
注：力偶逆时针转动时取正， 反之取负。
d F′
力偶矩的单位：N m 、kN m
F
F= F ′ d：力偶臂
二、力偶的基本性质
偶没有合力。一个力偶不能用一个力代替，也不 能与一个力平衡。力偶在任一轴上的投影为零。
• ⑵力偶对作用面内任一点之矩恒等于力偶矩，而与矩 心位置无关。两个力偶等效的条件是力偶矩相等。
F4
R d
计算
图中所示的拉力实验机上的摆锤重 G，悬挂点到摆锤 重心C的距离为l ,摆锤在图示三个位置时，求重力G对 O点之矩各为多少？
l
3 o
θ
2
C
1
G
解: MO(F) = Fd
位置1: MO(F) = Gd = 0 位置2: MO(F) = Glsinθ
位置3: MO(F) = －Gl
§3-2 力偶及其基本性质