数字电子技术基础(第四版)课后习题答案_第四章
- 格式:doc
- 大小:211.50 KB
- 文档页数:12


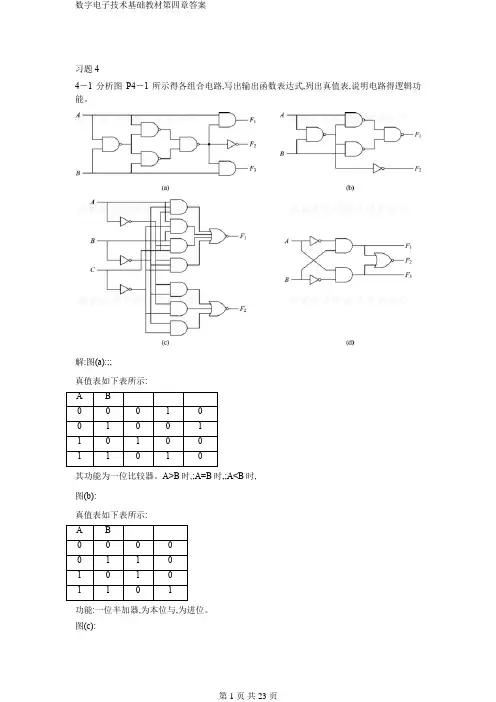
习题44-1 分析图P4-1所示得各组合电路,写出输出函数表达式,列出真值表,说明电路得逻辑功能。
解:图(a):;;真值表如下表所示:其功能为一位比较器。
A>B时,;A=B时,;A<B时,图(b):真值表如下表所示:功能:一位半加器,为本位与,为进位。
图(c):真值表如下表所示:功能:一位全加器,为本位与,为本位向高位得进位。
图(d):;;功能:为一位比较器,A<B时,=1;A=B时,=1;A>B时,=14-2 分析图P4-2所示得组合电路,写出输出函数表达式,列出真值表,指出该电路完成得逻辑功能。
解:该电路得输出逻辑函数表达式为:因此该电路就是一个四选一数据选择器,其真值表如下表所示:,当M=1时,完成4为二进制码至格雷码得转换;当M=0时,完成4为格雷码至二进制得转换。
试分别写出,,,得逻辑函数得表达式,并列出真值表,说明该电路得工作原理。
解:该电路得输入为,输出为。
真值表如下:由此可得:完成二进制至格雷码得转换。
完成格雷码至二进制得转换。
4-4 图P4-4就是一个多功能逻辑运算电路,图中,,,为控制输入端。
试列表说明电路在,,,得各种取值组合下F与A,B得逻辑关系。
解:,功能如下表所示,两个变量有四个最小项,最多可构造种不同得组合,因此该电路就是一个能产生十六种函数得多功能逻辑运算器电路。
4-5 已知某组合电路得输出波形如图P4-5所示,试用最少得或非门实现之。
解:电路图如下:4-6 用逻辑门设计一个受光,声与触摸控制得电灯开关逻辑电路,分别用A,B,C表示光,声与触摸信号,用F表示电灯。
灯亮得条件就是:无论有无光,声信号,只要有人触摸开关,灯就亮;当无人触摸开关时,只有当无关,有声音时灯才亮。
试列出真值表,写出输出函数表达式,并画出最简逻辑电路图。
解:根据题意,列出真值表如下:由真值表可以作出卡诺图,如下图:C AB 00 10 11 100 1由卡诺图得到它得逻辑表达式为: 由此得到逻辑电路为:4-7 用逻辑门设计一个多输出逻辑电路,输入为8421BCD 码,输出为3个检测信号。
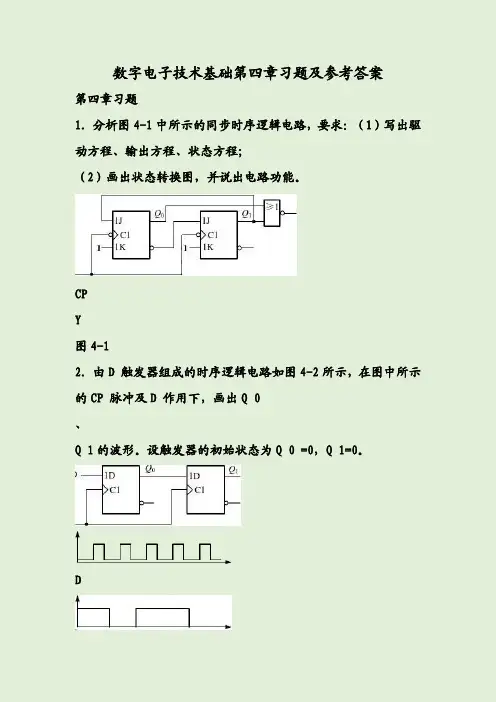
数字电子技术基础第四章习题及参考答案第四章习题1.分析图4-1中所示的同步时序逻辑电路,要求:(1)写出驱动方程、输出方程、状态方程;(2)画出状态转换图,并说出电路功能。
CPY图4-12.由D触发器组成的时序逻辑电路如图4-2所示,在图中所示的CP脉冲及D作用下,画出Q0、Q1的波形。
设触发器的初始状态为Q0=0,Q1=0。
D图4-23.试分析图4-3所示同步时序逻辑电路,要求:写出驱动方程、状态方程,列出状态真值表,画出状态图。
CP图4-34.一同步时序逻辑电路如图4-4所示,设各触发器的起始状态均为0态。
(1)作出电路的状态转换表;(2)画出电路的状态图;(3)画出CP作用下Q0、Q1、Q2的波形图;(4)说明电路的逻辑功能。
图4-45.试画出如图4-5所示电路在CP波形作用下的输出波形Q1及Q0,并说明它的功能(假设初态Q0Q1=00)。
CPQ1Q0CP图4-56.分析如图4-6所示同步时序逻辑电路的功能,写出分析过程。
Y图4-67.分析图4-7所示电路的逻辑功能。
(1)写出驱动方程、状态方程;(2)作出状态转移表、状态转移图;(3)指出电路的逻辑功能,并说明能否自启动;(4)画出在时钟作用下的各触发器输出波形。
CP图4-78.时序逻辑电路分析。
电路如图4-8所示:(1)列出方程式、状态表;(2)画出状态图、时序图。
并说明电路的功能。
1C图4-89.试分析图4-9下面时序逻辑电路:(1)写出该电路的驱动方程,状态方程和输出方程;(2)画出Q1Q0的状态转换图;(3)根据状态图分析其功能;1B图4-910.分析如图4-10所示同步时序逻辑电路,具体要求:写出它的激励方程组、状态方程组和输出方程,画出状态图并描述功能。
1Z图4-1011.已知某同步时序逻辑电路如图4-11所示,试:(1)分析电路的状态转移图,并要求给出详细分析过程。
(2)电路逻辑功能是什么,能否自启动?(3)若计数脉冲f CP频率等于700Hz,从Q2端输出时的脉冲频率是多少?CP图4-1112.分析图4-12所示同步时序逻辑电路,写出它的激励方程组、状态方程组,并画出状态转换图。

第一章1.1二进制到十六进制、十进制(1)(10010111)2=(97)16=(151)10 (2)(1101101)2=(6D)16=(109)10(3)(0.01011111)2=(0.5F)16=(0.37109375)10 (4)(11.001)2=(3.2)16=(3.125)10 1.2十进制到二进制、十六进制(1)(17)10=(10001)2=(11)16 (2)(127)10=(1111111)2=(7F)161621016210)3.19()1010 1(11001.101(25.7)(4))A D7030.6()0101 0000 0111 1101 0110 (0.0110(0.39)(3) B ====1.8用公式化简逻辑函数(1)Y=A+B (3)Y=1)=+(解:1A A 1)2(=+++=+++=+++=C B A C C B A C B Y CB AC B A Y ADC C B AD C B C B AD DC A ABD CD B A Y =++=++=++=)()(Y )4(解:(5)Y=0 (7)Y=A+CDE ABCD E C ABCD CE AD B BC CE AD B BC Y CE AD B BC B A D C AC Y =+=⋅+=+⋅=++++=)()()()()()6(解:CB AC B C B A A C B A C B A C B A C B C B A A C B A C B A C B A Y C B A C B A C B A Y +=++=+++=++++=++++⋅+=++++++=)())(())()(())()((8解:)(D A D A C B Y ++=)9(E BD E D BF E A AD AC Y ++++=)10(1.9 (a) C B C B A Y += (b) C B A ABC Y +=(c) ACD D C A D C A B A Y D AC B A Y +++=+=21,(d) C B A ABC C B A C B A Y BC AC AB Y +++=++=21, 1.10 求下列函数的反函数并化简为最简与或式(1)C B C A Y += (2)DC A Y++=CB C B AC C B AC B A BC AC C A B A BC AC C A B A Y BCAC C A B A Y +=++++=⋅+++=+++=+++=))((]))([())(())(()3(解: (4)C B A Y ++=DC ABD C B D C A D C B D A C A C D C B C A D A Y CD C B C A D A Y =++=+++=++++=+++=)())(())()(()5(解: (6)0=Y1.11 将函数化简为最小项之和的形式CB AC B A ABC BC A C B A C B A C B A ABC BC A CB A AC B B A BC A C B AC BC A Y CB AC BC A Y +++=++++=++++=++=++=)()()1(解:D C B A CD B A D C B A ABCD BCD A D C B A Y +++++=)(2)13()()()(3CD B A BCD A D BC A D C B A D C B A ABCD D ABC D C AB D C AB CD B A D C B A D C B A D C B A CD AB B A B A B A ACD D AC D C A D C A CD A D C A D C A D C A B BCD D BC D C B D C B CD B D C B D C B D C B A Y CDB A Y ++++++++++++=+++++++++++++++++++=++=解:)((4)CD B A D ABC D BC A D C AB D C AB CD B A ABCD BCD A Y +++++++= (5)MN L N M L N LM N M L N M L N M L Y +++++=1.12 将下列各函数式化为最大项之积的形式(1)))()((C B A C B A C B A Y ++++++= (2)))()((C B A C B A C B A Y ++++++= (3)76430M M M M M Y ⋅⋅⋅⋅= (4)13129640M M M M M M Y ⋅⋅⋅⋅⋅= (5)530M M M Y ⋅⋅=1.13 用卡诺图化简法将下列函数化为最简与或形式:(1)D A Y +=(3)1=Y (2)D C BC C A B A Y +++= (4)B AC B A Y ++=B A DC Y ++=AC B A Y +=(5)D C B Y ++= (6)C B AC B A Y ++=(7)C Y = (9)D C A C B D A D B Y +++=(8))14,11,10,9,8,6,4,3,2,1,0(),,,(m D C B A Y ∑= (10)),,(),,(741m m m C B A Y ∑=D A D C B Y ++=ABC C B A C B A Y ++=1.14化简下列逻辑函数(1)D C B A Y +++= (2)D C A D C Y += (3)C A D AB Y ++= (4)D B C B Y += (5)E D C A D A E BD CE E D B A Y +++++=1.20将下列函数化为最简与或式(1)AD D C B D C A Y ++= (2)AC D A B Y ++= (3)C B A Y ++= (4)D B A Y +=第二章2.1解:Vv v V V v T I mA I mA Vv T V v a o B o B BS B o B 10T 3.0~0(2.017.0230103.0207.101.57.05I V 5v 1021.5201.510V 0v )(i i ≈≈∴<=×≈=−≈∴−=×+−=截止,负值,悬空时,都行)饱和-=时,=当截止时,=当都行)=饱和,,-=悬空时,都行)饱和。

习题44-1 分析图P4-1所示的各组合电路,写出输出函数表达式,列出真值表,说明电路的逻辑功能。
解:图(a ):1F AB =;2FA B =;3F AB =真值表如下表所示:AB 1F 2F 3F0 0 0 1 0 0 1 0 0 1 1 0 1111其功能为一位比较器。
A>B 时,11F =;A=B 时,21F =;A<B 时,31F = 图(b ):12F AB AB F AB =+=; 真值表如下表所示:功能:一位半加器,1F 为本位和,2F 为进位。
图(c ):1(0,3,5,6)(1,2,4,7)F M m ==∑∏2(0,1,2,4)(3,5,6,7)F M m ==∑∏真值表如下表所示:功能:一位全加器,1F 为本位和,2F 为本位向高位的进位。
图(d ):1F AB =;2F A B =;3F AB =功能:为一位比较器,A<B 时,1F =1;A=B 时,2F =1;A>B 时,3F =14-2 分析图P4-2所示的组合电路,写出输出函数表达式,列出真值表,指出该电路完成的逻辑功能。
解:该电路的输出逻辑函数表达式为:100101102103F A A x A A x A A x A A x =+++因此该电路是一个四选一数据选择器,其真值表如下表所示:1A0AF0 0 0x 0 1 1x1 0 2x 1 13x4-3 图P4-3是一个受M 控制的代码转换电路,当M =1时,完成4为二进制码至格雷码的转换;当M =0时,完成4为格雷码至二进制的转换。
试分别写出0Y ,1Y ,2Y ,3Y 的逻辑函数的表达式,并列出真值表,说明该电路的工作原理。
解:该电路的输入为3x 2x 1x 0x ,输出为3Y 2Y 1Y 0Y 。
真值表如下: 3x2x1x0x3Y2Y1Y0YM=10 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 1 0 0 0 1 1 0 0 1 1 0 0 1 0 0 1 0 0 0 1 1 0 0 1 0 1 0 1 1 1 0 1 1 0 0 1 0 1 01 1 0 0 1 0 0 M=0 1 0 0 0 1 1 1 1 1 0 0 1 1 1 1 0 1 0 1 0 1 1 0 0 1 0 1 1 1 1 0 1 1 1 0 0 1 0 0 0 1 1 0 1 1 0 0 1 1111111 1 1 1 1 0 1 0由此可得:1M =当时,33232121010Y x Y x x Y x x Y x x =⎧⎪=⊕⎪⎨=⊕⎪⎪=⊕⎩ 完成二进制至格雷码的转换。


第1章习题与参考答案【题1-1】将下列十进制数转换为二进制数、八进制数、十六进制数。
(1)25;(2)43;(3)56;(4)78解:(1)25=(11001)2=(31)8=(19)16(2)43=(101011)2=(53)8=(2B)16(3)56=(111000)2=(70)8=(38)16(4)(1001110)2、(116)8、(4E)16【题1-2】将下列二进制数转换为十进制数。
(1)10110001;(2)10101010;(3)11110001;(4)10001000 解:(1)10110001=177(2)10101010=170(3)11110001=241(4)10001000=136【题1-3】将下列十六进制数转换为十进制数。
(1)FF;(2)3FF;(3)AB;(4)13FF解:(1)(FF)16=255(2)(3FF)16=1023(3)(AB)16=171(4)(13FF)16=5119【题1-4】将下列十六进制数转换为二进制数。
(1)11;(2)9C;(3)B1;(4)AF解:(1)(11)16=(00010001)2(2)(9C)16=(10011100)2(3)(B1)16=(1011 0001)2(4)(AF)16=(10101111)2【题1-5】将下列二进制数转换为十进制数。
(1)1110.01;(2)1010.11;(3)1100.101;(4)1001.0101解:(1)(1110.01)2=14.25(2)(1010.11)2=10.75(3)(1001.0101)2=9.3125【题1-6】将下列十进制数转换为二进制数。
(1)20.7;(2)10.2;(3)5.8;(4)101.71解:(1)20.7=(10100.1011)2(2)10.2=(1010.0011)2(3)5.8=(101.1100)2(4)101.71=(1100101.1011)2【题1-7】写出下列二进制数的反码与补码(最高位为符号位)。

思考题与习题4-1 触发器的主要性能是什么?它有哪几种结构形式?其触发方式有什么不同?触发器是一种存储电路,具有记忆功能。
在数字电路系统中起着重要作用。
依据不同的标准,触发器可以划分为多种不同类型。
从结构上来分,触发器分为基本触发器,时钟触发器,主从触发器以及边沿触发器。
基本触发器为异步(或直接)触发,时钟触发器为CP电平触发,主从和边沿触发器为边沿触发。
4-2 试分别写出RS触发器、JK触发器、D触发器、T触发器和T′触发器的状态转换表和特性方程。
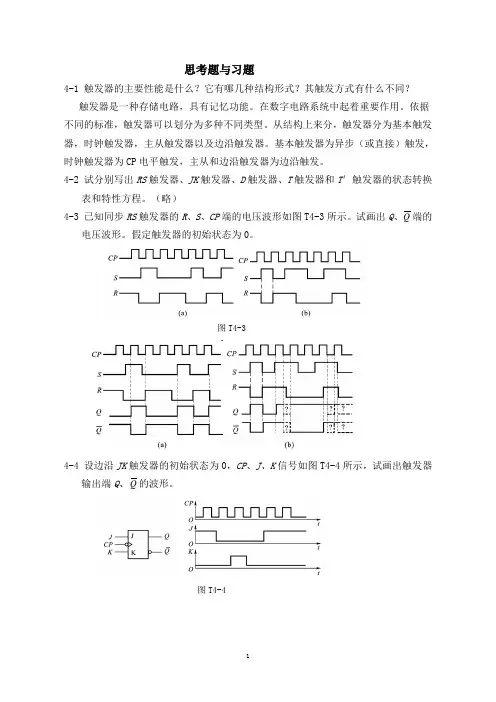
(略)4-3 已知同步RS触发器的R、S、CP端的电压波形如图T4-3所示。
试画出Q、Q端的电压波形。
假定触发器的初始状态为0。
图T4-34-4 设边沿JK触发器的初始状态为0,CP、J、K信号如图T4-4所示,试画出触发器输出端Q、Q的波形。
图T4-44-5电路如图T4-5(a)所示,输入波形如图T4-5(b)所示,试画出该电路输出端G的波形,设触发器的初始状态为0。
图T5-24-6 试画出图T4-6所示波形加在以下两种触发器上时,触发器输出Q的波形:(1)下降沿触发的触发器(2)上升沿触发的触发器图T4-64-7 已知A、B为输入信号,试写出图T4-7所示各触发器的次态逻辑表达式。
图T4-7nn n n n n n n nn n )b (n )a (Q B Q B Q Q B AQ Q Q B AQ Q K Q J Q B A D Q ⋅=+=++=⋅+=+=⊕==++11 4-8 设图T4-8所示中各TTL 触发器的初始状态皆为0,试画出在CP 信号作用下各触发的输出端Q 1-Q 6的波形。
图T4-84-9 试对应画出图T4-9所示电路中Q 1、Q 2波形。
(初始状态均为0)图T4-94-10 一逻辑电路如图T4-10所示,试画出在CP 作用下3210Y Y Y Y 、、、的波形。
(CT74LS139为2线—4线译码器。
)图T4-104-11由边沿D触发器和边沿JK触发器组成图T4-11(a)所示的电路。
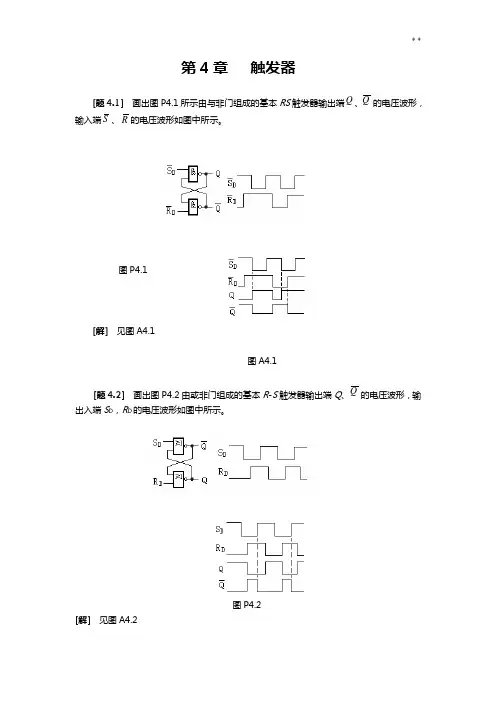
第4章触发器[题4.1]画出图P4.1所示由与非门组成的基本RS触发器输出端Q、Q的电压波形,输入端S、R的电压波形如图中所示。
图P4.1[解]见图A4.1图A4.1[题4.2]画出图P4.2由或非门组成的基本R-S触发器输出端Q、Q的电压波形,输出入端S D,R D的电压波形如图中所示。
图P4.2[解]见图A4.2[题4.3] 试分析图P4.3所示电路的逻辑功能,列出真值表写出逻辑函数式。
图P4.3[解]S R Q n Q n+1 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 1 1 0 1 1 1 1 0 0* 1 110*由真值表得逻辑函数式 01=+=+SR Q R S Q nn[题4.4] 图P4.4所示为一个防抖动输出的开关电路。
当拨动开关S 时,由于开关触点接触瞬间发生振颤,D S 和D R 的电压波形如图中所示,试画出Q 、Q 端对应的电压波形。
图P4.4[解]见图A4.4图A4.4[题4.5]在图P4.5电路中,若CP、S、R的电压波形如图中所示,试画出Q和Q端与之对应的电压波形。
假定触发器的初始状态为Q=0。
图P4.5[解]见图A4.5图A4.5[题4.6]若将同步RS触发器的Q与R、Q与S相连如图P4.6所示,试画出在CP 信号作用下Q和Q端的电压波形。
己知CP信号的宽度t w = 4 t Pd 。
t Pd为门电路的平均传输延迟时间,假定t Pd≈t PHL≈t PLH,设触发器的初始状态为Q=0。
图P4.6图A4.6[解]见图A4.6[题4.7]若主从结构RS触发器各输入端的电压波形如图P4.7中所给出,试画Q、Q 端对应的电压波形。
设触发器的初始状态为Q=0。
图P4.7[解] 见图A4.7图A4.7[题4.8]若主从结构RS触发器的CP、S、R、D R各输入端的电压波形如图P4.8所S。
试画出Q、Q端对应的电压波形。
示,1D图P4.8[解] 见图A4.8图A4.8[题4.9]已知主从结构JK触发器输入端J、K和CP的电压波形如图P4.9所示,试画出Q、Q端对应的电压波形。
习题44-1 分析图P4-1所示的各组合电路,写出输出函数表达式,列出真值表,说明电路的逻辑功能。
解:图(a ):1F AB =;2F A B =e ;3F AB = 真值表如下表所示: A B 1F2F3F0 0 0 1 0 0 1 0 0 1 1 0 1 0 0 111其功能为一位比较器。
A>B 时,11F =;A=B 时,21F =;A<B 时,31F = 图(b ):12F AB AB F AB =+=; 真值表如下表所示: A B 1F2F功能:一位半加器,1F 为本位和,2F 为进位。
图(c ):1(0,3,5,6)(1,2,4,7)F M m ==∑∏2(0,1,2,4)(3,5,6,7)F M m ==∑∏真值表如下表所示:功能:一位全加器,1F 为本位和,2F 为本位向高位的进位。
图(d ):1F AB =;2F A B =e ;3F AB =功能:为一位比较器,A<B 时,1F =1;A=B 时,2F =1;A>B 时,3F =14-2 分析图P4-2所示的组合电路,写出输出函数表达式,列出真值表,指出该电路完成的逻辑功能。
解:该电路的输出逻辑函数表达式为:100101102103F A A x A A x A A x A A x =+++因此该电路是一个四选一数据选择器,其真值表如下表所示:1A0AF0 0 0x 0 1 1x 1 0 2x 1 13x4-3 图P4-3是一个受M 控制的代码转换电路,当M =1时,完成4为二进制码至格雷码的转换;当M =0时,完成4为格雷码至二进制的转换。
试分别写出0Y ,1Y ,2Y ,3Y 的逻辑函数的表达式,并列出真值表,说明该电路的工作原理。
解:该电路的输入为3x 2x 1x 0x ,输出为3Y 2Y 1Y 0Y 。
真值表如下: 3x2x1x0x3Y2Y1Y0YM=10 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 1 0 0 0 1 1 0 0 1 1 0 0 1 0 0 1 0 0 0 1 1 0 0 1 0 1 0 1 1 1 0 1 1 0 0 1 0 1 01 1 0 0 1 0 0 M=0 1 0 0 0 1 1 1 1 1 0 0 1 1 1 1 0 1 0 1 0 1 1 0 0 1 0 1 1 1 1 0 1 1 1 0 0 1 0 0 0 1 1 0 1 1 0 0 1 1 1 1 0 1 0 1 1 111111由此可得:1M =当时,33232121010Y x Y x x Y x x Y x x =⎧⎪=⊕⎪⎨=⊕⎪⎪=⊕⎩ 完成二进制至格雷码的转换。
第4章习题解答4-1 写出图T4-1电路的输出函数式,证明a 、b 有相同的逻辑功能。
B(a)A(b)BA 图T4-1 习题4-1的图解4-1 Y 1= A B ' +A ' B ' ; Y 2=( A+B)(A ' +B ' )= AB ' +A ' B ' =Y 14-2 试写出图T4-2所示逻辑电路的输出函数式并化简,指出电路的逻辑功能。
A BMBA图T4-2习题4-2的图图T4-3习题4-3的图解4-2 由图T4-2写电路的输出函数式并化简得AB B A B A AB Y +''='''''=))()(( (JT4-2)由JT4-2式可知,电路实现的是二变量同或功能。
4-3 图T4-3是一个选通电路。
M 为控制信号,通过M 电平的高低来选择让A 还是让B 从输出端送出。
试写逻辑电路的输出函数式并化简,分析电路能否实现上述要求。
解4-3 由图T4-3写电路的输出函数式并化简得M B AM M B M A Y '+='''=)((( (JT4-3)由JT4-3式可知,电路能够实现选通要求,当M=1时,Y=A ;当M=0时,Y=B 。
4-4.用与非门设计一个四人表决逻辑电路,结果按“少数服从多数”的原则决定。
解4-4(1)列真值表设四个人的意见为变量A 、B 、C 、D ,表决结果为函数Y 。
按正逻辑给变量赋值:同意为“1”,不同意为“0”;提案通过为“1”,没通过为“0”,所列真值表如表JT4-4所示。
表JT4-4输 入输 出A B C D 0 0 0 0 0 00 0 0 1 0 1 0 1 0 10 0 0 1 1 0 1 1 0 0 0 1 1 01 1 Y000000001 0 1 0 1 0 1 01 1 1 1 1 11 1 0 0 0 1 1 0 1 1 0 00 1 1 0 1 100000000输 入输 出A B C D Y(2)写输出逻辑函数式由表JT4-4可写输出逻辑函数式ABCD D ABC D C AB CD B A BCD A Y +'+'+'+'= (JT4-4a)(3)化简填卡诺图,如图JT 4-4(a)所示合并最小项,得最简与—或式BCD ACD ABD ABC Y +++= (JT4-4b)(4)画逻辑电路图将式JT4-4(b)转换成与非—与非式)()()()(('''''=D BC ACD ABD ABC Y (JT4-4c)按式JT4-4(c)用与非门画逻辑电路图,如图JT4-4(b)所示。
第4章触发器
[题4.1]画出图P4.1所示由与非门组成的根本RS触发器输出端Q、Q的电压波形,输入端S、R的电压波形如图中所示。
图P4.1
[解]见图A4.1
图A4.1
[题4.2]画出图P4.2由或非门组成的根本R-S触发器输出端Q、Q的电压波形,输出入端S D,R D的电压波形如图中所示。
图P4.2
[解]见图A4.2
[题4.3]试分析图P4.3所示电路的逻辑功能,列出真值表写
出逻辑函数式。
图P4.3 [解]:图P4.3所示电路的真值表
S R Q n Q n+1 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 1 1 0 1 1 1 1 0 0* 1 1
1
0*
由真值表得逻辑函数式 01=+=+SR Q R S Q n
n
[题4.4] 图P4.4所示为一个防抖动输出的开关电路。
当拨动开关S 时,由于开关触点接触瞬间发生振颤,D S 和D R 的电压波形如图中所示,试画出Q 、Q 端对应的电压波形。
图P4.4
[解] 见图A4.4
图A4.4
[题4.5] 在图P4.5电路中,假设CP 、S 、R 的电压波形如图中所示,试画出Q 和Q 端与之对应的电压波形。
假定触发器的初始状态为Q =0。
图P4.5
[解]见图A4.5
图A4.5
[题4.6]假设将同步RS触发器的Q与R、Q与S相连如图P4.6所示,试画出在CP 信号作用下Q和Q端的电压波形。
己知CP信号的宽度t w = 4 t Pd 。
t Pd为门电路的平均传输延迟时间,假定t Pd≈t PHL≈t PLH,设触发器的初始状态为Q=0。
图P4.6
图A4.6
[解]见图A4.6
[题4.7]假设主从结构RS触发器各输入端的电压波形如图P4.7中所给出,试画Q、Q端对应的电压波形。
设触发器的初始状态为Q=0。
图P4.7
[解] 见图A4.7
图A4.7
[题4.8]假设主从结构RS触发器的CP、S、R、D
R各输入端的电压波形如图P4.8
所示,
1
D
S。
试画出Q、Q端对应的电压波形。
图P4.8
[解] 见图A4.8
图A4.8
[题4.9] 主从结构JK 触发器输入端J 、K 和CP 的电压波形如图P4.9所示,试画出Q 、
Q 端对应的电压波形。
设触发器的初始状态为Q = 0。
图P4.9
[解]见图A4.9
图A4.9
[题4.10] 假设主从结构JK 触发器CP 、D R 、D S 、J 、K 端的电压波形如图P4.10所
示,试画出Q 、Q 端对应的电压波形。
图P4.10
[解] 见图A4.10
图A4.10
[题4.11]己知维持阻塞结构D触发器输入端的电压波形如图P4.11所示,试画出Q、Q端对应的电压波形。
图P4.11
[解] 见图A4.11
图A4.11
[题4.12]CMOS边沿触发结构JK触发器各输入端的电压波形如图P4.12所示,试画Q端对应的电压波形。
出Q、
图P4.12
[解] 见图A4.12
图A4.12
[题4.13]设图P4.13中各触发器的初始状态皆为Q=0,试画出在CP信号连续作用下各触发器输出端的电压波形。
图P4.13 [解] 见图A4.13
图A4.13
[题4.14]试写出图P4.14〔a〕中各电路的次态函数〔即
1
1
+
n
Q、1
2
+
n
Q、13+n
Q、1
4
+
n
Q〕
与现态和输入变量之间的函数式,并画出在图P4.14〔b〕给定信号的作用下Q1、Q2、、、Q3、、Q4的电压波形。
假定各触发器的初始状态均为Q=0。
[解]
电路驱动方程为:
A Q A AQ J n n =+=11,
B Q B BQ K n
n =+=11;
AB S =,B A R +=;B A T ⊕=;B A D ⊕=
代入特性方程,得状态方程:
n n n n n BQ Q A Q K Q J Q 111111 +=+=+
n n n Q B A AB Q R S Q 2
212)(++=+=+
n n n Q B A Q T Q 3313⊕⊕=⊕=+ B A D Q n ⊕==+14
根据状态方程画波形,见图A4.14。
图A4.14
[题4.15] 在图P4.15所示主从结构JK 触发器电路中,己知CP 和输入信号T 的电压波形如下图,试画出触发器输出端Q 和Q 的电压波形,设触发器的起始状态为Q =0。
图P4.15
[解] 见图A4.15
图A4.15
[题4.16] 在图P4.16电路中,输入信号I v 的电压波形如下图,试画出与之对应的输出电压O v 的波形。
触发器为维持阻塞结构,初始状态为Q =0。
〔提示:应考虑触发器和异或门的传输延迟时间。
〕
图P4.16
[解] 见图A4.16
图A4.16
[题4.17] 在图P4.17的主从JK 触发电路中,CP 和A 的电压波形如图中所示,试画出Q 端对应的电压波形。
设触发器的初始状态为Q = 0。
图P4.17
[解] 见图A4.17
图A4.17
[题4.18] 图P4.18所示是用CMOS边沿触发器和或非门组成的脉冲分频电路。
试画出在一系列CP脉冲作用下,Q1、Q2和Z端对应的输出电压波形。
设触发器的初始状态皆为Q = 0。
图P4.18
[解] 见图A4.18
图A4.18
[题4.19] 图P4.19所示是用维持阻塞结构D触发器组成的脉冲分频电路。
试画出在一系列CP脉冲作用下输出端Y对应的电压波形。
设触发器的初始状态均为Q = 0。
图P4.19
[解] 见图A4.19
图A4.19
[题4.20] 试画出图P4.20电路输出Y 、Z 的电压波形,输入信号A 和时钟CP 的电压波形如图中所示,设触发器的初始状态均为Q = 0。
图P4.20
[解]
2121Q Q Q Q Y +==
2121Q Q Q Q Z +==
A Q n =+11; 11
2n n Q Q =+
波形见图A4.20。
图
A4.20
[题4.21] 试画出图P4.21电路输出端Q 2的电
压波形。
输入信号A 和CP 的电压波形与上题相同,假定触发器为主从结构,初始状态均为Q = 0。
图P4.21
[解]
) (1111A CP Q Q n n ==+;
21Q R D =;
) ( 22112CP CP Q Q Q n n n ==+ 波形见图A4.21。
图
A4.21
[题4.22] 试画出图P4.22电路在一系列CP 信号作用下Q 1、Q 2、Q 3端输出电压的波形,触发器为边沿触发结构,初始状态为Q = 0。
图P4.22
[解]
)(CP CP Q Q n n ==+1111 ) 12212Q CP Q Q n n ==+( )( 133213Q CP Q Q Q n n n =⊕=+
波形见图A4.22。
图A4.22
[题4.23] 试画出图P4.23电路在图中所示CP 、D R 信号作用下Q 1、Q 2、Q 3的输出电压波形,并说明Q 1、Q 2、Q 3输出信号的频率与CP 信号频率之间的关系。
图P4.23
[解]
)(CP CP Q Q n n ==+1111
)(12212 Q CP Q Q n n ==+
)(23313 Q CP Q Q n n ==+
波形见图A4.23。
图A4.23
假设CP 的频率为0f ,那么Q 1、Q 2、Q 3的频率分别为021f 、041f 、081
f 。