结构力学——力法对称性的利用

第7章　力　法
7.1　复习笔记【知识框架】
【重点难点归纳】
一、概述（见表7-1-1）　★★
表7-1-1　概述
二、超静定次数的确定（见表7-1-2）　★★★★
表7-1-2　超静定次数的确定
三、力法的基本概念（见表7-1-3）　★★★
力法的基本概念，包括基本未知量、基本体系、基本结构以及基本方程见表7-1-3，此外，表中还归纳了超静定结构的力法分析步骤。

表7-1-3　力法的基本未知量、基本体系和基本方程
四、力法的典型方程（见表7-1-4）　★★★
表7-1-4　力法的典型方程
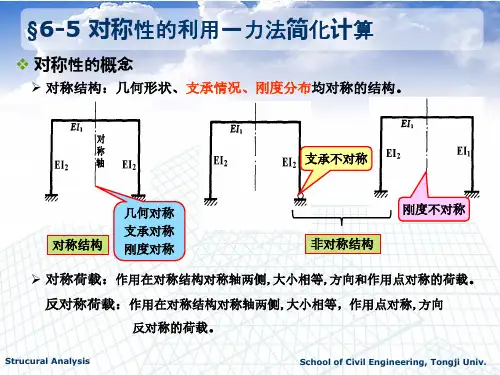
五、对称性的利用　★★★★
1．对称结构及作用荷载的对称性（表7-1-5）
表7-1-5　对称结构及作用荷载的对称性
2．非对称荷载的处理（表7-1-6）
表7-1-6　非对称荷载的处理。

考研结构⼒学知识点梳理1.瞬变体系：本来是⼏何可变，经微⼩位移后，⼜成为⼏何不变的体系，成为瞬变体系。

瞬变体系⾄少有⼀个多余约束。

2.两根链杆只有同时连接两个相同的刚⽚，才能看成是瞬铰。

3.关于⽆穷远处的瞬铰：（1）每个⽅向都有且只有⼀个⽆穷远点，（即该⽅向各平⾏线的交点），不同⽅向有不同的⽆穷远点。

（2）各个⽅向的⽆穷远点都在同⼀条直线上（⼴义）。

（3）有限点都不在⽆穷线上。

4.结构及和分析中的灵活处理：（1）去⽀座去⼆元体。

体系与⼤地通过三个约束相连时，应去⽀座去⼆元体；体系与⼤地相连的约束多于4个时，考虑将⼤地视为⼀个刚⽚。

（2）需要时，链杆可以看成刚⽚，刚⽚也可以看成链杆，且⼀种形状的刚⽚可以转化成另⼀种形状的刚⽚。

5.关于计算⾃由度：（基本不会考）（1）,则体系中缺乏必要约束，是⼏何常变的。

（2）若，则体系具有保证⼏何不变所需的最少约束，若体系⽆多余约束，则为⼏何不变，若有多余约束，则为⼏何可变。

（3），则体系具有多与约束。

是保证体系为⼏何不变的必要条件，⽽⾮充分条件。

若分析的体系没有与基础相连，应将计算出的W减去3.1.静定结构的⼀般性质：（1）静定结构是⽆多余约束的⼏何不变体系，⽤静⼒平衡条件可以唯⼀的求得全部内⼒和反⼒。

（2）静定结构只在荷载作⽤下产⽣内⼒，其他因素作⽤时，只引起位移和变形。

（3）静定结构的内⼒与杆件的刚度⽆关。

（4）在荷载作⽤下，如果仅靠静定结构的某⼀局部就可以与荷载维持平衡，则只有这部分受⼒，其余部分不受⼒。

（5）当静定结构的⼀个内部⼏何不变部分上的荷载或构造做等效变换时，其余部分的内⼒不变。

（6）静定结构有弹性⽀座或弹性结点时，内⼒与刚性⽀座或刚性节点时⼀样。

解放思想：计算内⼒和位移时，任何因素都可以分别作⽤，分别求解，再线性叠加，以将复杂问题拆解为简单情况处理。

2.叠加院⾥的应⽤条件是：⽤于静定结构内⼒计算时应满⾜⼩变形，⽤于位移计算和超静定结构的内⼒计算时材料还应服从胡克定律，即材料是线弹性的。

五．力法一.超静定结构概念和超静定次数的确定1.超静定结构的概念：有多余约束存在，支座反力和内力不能仅靠静力平衡方程确定的几何不变体系；2.超静定结构的性质：（1）多余约束反力的确定，除使用静力平衡条件外，还需考虑变形；（2）受力情况与材料的物理性质、截面几何性质有关系；（刚度）（3）去掉一些约束后，体系仍可以保持几何不变；（4）制造误差、支座移动、温度等原因能使结构产生内力；2.超静定次数的确定：（1）超静定次数=未知力个数-平衡方程的个数=多余未知力的个数=多余约束的个数=把结构变成静定结构时所需撤除的约束个数（2）将超静定结构变成静定结构的几种基本方法：A.去掉支座的一根链杆或切断一根链杆，相当于去掉一个约束；B.去掉一个单铰，相当于去掉两个约束；C.将刚性连接改成单铰连接，相当于去掉一个约束；D.刚性连接处切断，相当于去掉三个约束；（3）需要注意的几个问题：A去掉的约束必须是保证体系几何不变的多余约束；B.多余约束必须都拆除；C.去多余约束的办法不仅只有一种，只是要保证去掉约束后保证其几何不变性；D.去掉多余约束后的静定结构称该超静定结构的基本结构，由上知基本结构不唯一；二.计算超静定结构的基本方法（1）计算超静定结构的方法很多，但基本方法只有两种：力法、位移法；（2）力法：多余约束力为基本未知量，位移谐调建立平衡方程（3）位移法：位移为基本未知量，节点受力平衡建立平衡方程（4）力法位移法基本思路：把不会算的结构通过未知量转换成会算的结构即基本结构（5）力法与位移法计算步骤：A.选取基本结构、基本未知量；B.用关于力的或位移的代数方程组求解未知量；三.力法思想（1）取图b为基本结构，则相应的基本体系为图e，这种情况下，图a中C处可动铰支座被视为多余约束，X1为基本未知量；（2）图a为一次超静定；（3）力法方程的概念（以图b所示的基本结构为例）：图a中，在F P作用下，体系将产生变形，但支座C处竖向位移为零（约束边界条件决定），想要静力等效，在基本体系1中（图e），基本结构在F P和基本未知量X1的作用下，C点的竖向位移为零；力法中，体系必须为线性体系，内力和位移才可以使用叠加原理，在图e 中，使用叠加原理保证C点的竖向位移为零是力法的基本思想；在F P作用下，基本结构C 点将发生竖向的位移分量Δ1P，同样，在基本未知量X1作用下，C点将产生竖向位移分量Δ11，Δ1P和Δ11必须保证C点竖向位移分量为零，则有Δ1P+Δ11=0由图乘法可以求得Δ1P和Δ11（X1的函数），然后通过C点位移为零建立方程，最终求得X1；（4）力法典型方程：⎪⎭⎪⎬⎫=∆+++=∆=∆+++=∆=∆+++=∆0X X X 0X X X 0X X X P 33332321313P 23232221212P 131********δδδδδδδδδ相同道理，如果是n 次超静定，力法方程可表示成为⎪⎪⎭⎪⎪⎬⎫=∆++++=∆++++=∆++++0X X X 0X X X 0X X X nF n nn 22n 11n F 2n n 2222121F 1n n 1212111δδδδδδδδδ矩阵表达式：0X X X nF F2F 1n 21nn 1n 1n n 22121n 11211=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∆∆∆+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⋅⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡δδδδδδδδδ 柔度系数：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡nn 22n1n22212n 11211δδδδδδδδδ自由项：{}iF ∆根据位移互等定理，柔度矩阵是一个对称矩阵，主对角线元素ii δ称为主系数，主系数均为正值且不等于零。

结构力学——力法对称性的利用力法对称性是结构力学中常用的一种方法，可以有效简化结构分析的复杂性。

它基于结构的几何和物理特性，通过利用结构的对称性来减少需要考虑的自由度，从而简化结构力学问题。

力法对称性的利用可以在两个方面发挥作用：减少计算自由度和简化载荷分析。

首先，力法对称性可以减少计算自由度。

结构力学问题的求解通常需要计算结构的内力和变形。

结构的自由度越多，计算所需的计算量就越大，求解也就越复杂。

通过利用结构的对称性，我们可以将结构分为若干对称部分，仅对其中一个部分进行力学分析，然后通过对称性来得到其他部分的结果。

这样可以大大减少计算自由度，简化结构力学问题的求解过程。

具体来说，力法对称性可以应用于不同的结构部分，如杆件、板和壳体等。

例如，在杆件问题中，结构的对称性可以体现为几何对称性，如轴对称、平面对称等。

通过建立合适的坐标系和选择适当的参考点，可以简化结构的力学分析。

力法对称性还可以应用于简化载荷分析。

结构在受力时，通常存在很多不同的载荷情况，如重力、集中力、分布力等。

利用力法对称性可以简化对这些载荷的分析。

通过找到适当的对称轴或对称面，可以使得一些载荷分布具有对称性，从而简化分析。

通过减少载荷分布的复杂程度，可以更方便地计算结构的内力和变形。

需要注意的是，力法对称性在实际应用中需要满足一定的条件。

首先，结构必须存在对称性，即具有一定的几何和物理特性。

其次，结构的对称性必须与载荷情况相匹配。

如果对称性不满足这些条件，力法对称性可能无法有效地简化结构力学问题。

总之，力法对称性在结构力学中的应用可以大大简化力学分析的困难。

通过减少计算自由度和简化载荷分析，可以提高结构力学问题的求解效率。

利用力法对称性，结构工程师可以更加方便地进行结构设计和分析，提高工作效率和设计质量。

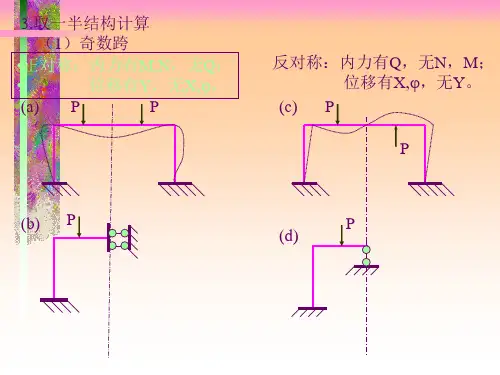
第四章 力法4-1 利用对称与反对称条件，简化图4-15所示各平面刚架结构，要求画出简化图及其位移边界条件。

(a)(a)解：对称结构，在对称载荷作用下，在对称轴上反对称内力为零。

由静力平衡条件∑=0X可得23PN =再由两个静力平衡条件，剩余4个未知力，为二次静不定。

本题中通过对称性条件的使用，将6次静不定的问题转化为2次静不定。

PP(b)(b)解：对称结构，在反对称载荷作用下，在对称轴上对称的内力为零。

受力分析如图所示有2根对称轴，结合平衡方程，剩下三个未知数，为3次静不定。

本题中通过对称性条件的使用，将6次静不定问题转化为3次静不定。

(c)(c)解：对称结构，在对称载荷作用下，在对称轴上反对称内力为零。

有一根对称轴，减少了两个静不定度本题中通过对称性条件的使用，将3次静不定问题转化为1次静不定。

4-2图4-16所示桁架各杆的EA均相同，求桁架各杆的内力。

(a)(a)解：1、分析结构静不定次数。

结构有4个结点8个自由度，6根杆6个约束，3个外部约束。

因此结构静不定次数为1，f=1。

2、取基本状态。

切开2-4杆，取<P>,<1>状态，各杆内力如图。

1234P-P √2P<P>1234P<1>11√22√22√22√22计算影响系数∑=∆EAl N N i p P 11()2422222+=⎪⎪⎭⎫ ⎝⎛⨯+⨯=EA Pa P P EA a ∑=EAl N i1211δ()22222142222+=⎪⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯=EA a EA a 列正则方程：()()02242221=+++P X解之()P X 42321-=3、由11N X N N P +=，得()P X N 423220112-=⎪⎪⎭⎫ ⎝⎛-⋅+= ()P X P N 42212113+=⋅+=()P X N 423220114-=⎪⎪⎭⎫ ⎝⎛-⋅+=()P X N 423220123-=⎪⎪⎭⎫ ⎝⎛-⋅+=()P X N 423210124-=⋅+=()P X P N 42122134+-=⎪⎪⎭⎫ ⎝⎛-⋅+-=4、校核。

结构力学第20次课 力法6-5 位移法7-6结构的对称性 foxscarlet12012-5-17 《结构力学》第20次课 第6章力法6-5P225与第7章位移法7-6P302内容6-5 7-6 对称性利用1 对称性（1）结构的对称性：对称结构是指几何形状、支座情况、刚度都关于某轴对称。

（2）荷载的对称性： 对称荷载 反对称荷载 任何荷载都可以分解成对称荷载+反对称荷载两部分。

2 取对称的基本体系计算： 不论在何种外因作用下，对称结构应考虑采用对称的基本体系计算。

沿对称轴将梁切开，三对多余未知力中，弯矩X 1和轴力X 2是 未知力，剪力X 3是 未知力。

对称未知力产生的单位弯矩图和变形图是对称的；反对称未知力产生的单位弯矩图和变形图是反对称的。

如果荷载对称，M P 对称，Δ3P =0，X 3=0， 未知力为零；如果荷载反对称，M P 反对称，Δ1P =0， Δ2P =0， X 1= X 2 =0， 未知力为零。

3 取等代结构计算对称结构的变形特点，针对切开对称轴处是刚结点。

注意，如果对称轴上是铰结点有所不同。

（1）对称结构在对称荷载作用下位于对称轴上的截面，水平位移和转角为零，只有竖向位移。

（2）对称结构在反对称荷载作用下位于对称轴上的截面，竖向位移为零，水平位移和转角不为零。

① 奇数跨（无中柱）对称结构在对称荷载作用下的等代结构 §7-6 对称结构的计算奇数跨刚架受对称荷载A. 奇数跨结构（无中柱对称结构）F PF P(1) 对称荷载F P半边结构对称轴截面内力结构与荷载3 取等代结构计算1扩展练习 奇数跨结构受对称荷载作用llqllAB例2. 图示结构EI = 常数。

对称性只有竖向荷载作用1X 3=3X 2X 1X 2=【例题】利用对称性计算图示结构,绘制弯矩图。

（EI=常l↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓ql/2l/2l/2l/2（a ）ldbFPFP4 无弯矩状态判定对称结构正对称荷载。