结构力学——力法对称性的利用学习资料
- 格式:ppt
- 大小:739.00 KB
- 文档页数:21


对称性在结构力学中的应用土木工程系土木5班徐亚飞20080420529 在工程实际中,有很多结构具有对称性,而结构力学研究的就是结构的杆系模型,因此对称性在结构力学中有着广泛的应用。
现在业已学完了结构力学,现就对称性在结构力学中的应用做一简单的总结。
所谓结构的对称性,需要满足以下两个方面的要求:(1)结构的几何形状和支撑情况对某一轴线对称;(2)杆件截面和材料的性质也对此轴对称。
结构上力的对称性有正对称和反对称两种类型,非对称的力都可以化为正对称力与反对称力的叠加。
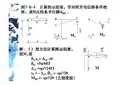
一、对称性在求解结构内力中的应用因为对称结构在对称荷载作用下,其对称的内力(弯矩和轴力)是正对称的,其反对称的内力(剪力)是反对称的;在反对称荷载作用下,其对称的内力(弯矩和轴力)是反对称的,其反对称的内力(剪力)是正对称的。
因此,只要我们做出半边结构的内力图,也就知道了整个结构的内力图。
据此,我们在对对称结构进行内力分析时,就可以取半边结构进行分析。
取半边结构进行分析,可以减少超静定次数,减少基本未知量,为解题提供了很大的方便。
二、对称性在体系自由振动中的应用我们知道,结构的频率、主振型及主振型的正交性是结构本身的固有特性,与外界因素无关。
只要结构本身和质量分布都是对称的,其振型或为正对称,或为反对称,因此,我们可以选取半边结构计算其相应的自振频率。
但其只能应用于两个自由度的振动体系,且自振频率小的为第一振型,较大的为第二振型。
运用对称性求解结构的自振频率,避免了求解复杂的频率方程,使得计算大大简化。
三、对称性在结构稳定性分析中的应用结构的稳定性分析,就是为了确定在新的平衡形式的荷载,即临界荷载。
通常的解法是假设新的平衡形式,运用静力平衡法或能量法通过稳定方程求的临界荷载,进而确定新的平衡形式。
但,对于对称的体系,其新的平衡形式不是正对称的就是反对称的。
因此,我们就可以利用对称性,取半边结构进行分析。
但此法只能应用于只有两个自由度的体系的结构稳定性分析。



7-7 对称性的利用1位移法中对称性的利用关键是半结构的选取(1)对称荷载1Z 2Z 12Z Z =?12Z Z =−1Z 位移法中对称性的利用关键是半结构的选取Z 14在对称轴上的结点B 和A 均无转角及水平线位移,但可发生竖向线位移且两点相等,中央竖杆AB 不发生挠曲。
截取半结构时,可将杆AB 看作刚性杆而保留,并在结点B 、A 分别加上水平链杆支承。
EI =∞偶数跨对称结构1Z 2Z 3Z 结点转角为零(2)反对称荷载在对称轴上的截面C 没有竖向位移,但可有转角和水平位移。
2Z 1Z在对称轴上,柱CD没有轴力和轴向位移,但有弯矩和弯曲变形。
可将中间柱分成两根柱,分柱的抗弯刚度为原柱的一半。
因为忽略轴向变形的影响,C处的竖向支杆可取消。
对称轴上的结点A 和B 均有转角和侧移,但无竖向线位移,中央竖杆AB 发生挠曲变形。
在截取半结构计算时,除了取竖杆AB 刚度之半(EI /2)外,还应在A 处加一竖向链杆支承。
1Z 2Z 3Z 4Z 5Z 6Z81Z 2Z 3Z 最少未知量1Z 2Z M1Z 讨论:M1Z 01111=+P R Z r M M/2M PM1Z 2Z 3Z 2Z 1Z 3Z PM111Z 2Z 2Z 1Z 3Z 2Z 1Z 3Z12列出用位移法并利用对称性计算图示刚架的基本结构及典型方程。
(各杆的EI =常数)a a a a aq qm2a 例取半结构13mq qZ 1q典型方程:01212111=++P R Z r Z r 02222121=++P R Z r Z r Z 1q2Z 2Z典型方程:3434333=++P R Z r Z r r Z r Z R P 43344440++=2Z 1Z取半结构示例16mq qZ1Z117例1利用对称性简化图a 所示的对称结构,取出最简的计算简图、基本体系,并作出M 图。
1111=+P R Z r183511EI r =mkN R P ⋅−=301EIZ 5901=最简的基本体系及M 图PM Z M M +=11例219图示结构,设E I=常数,P=10kN,试画出刚架的M图。


对称性应用在工程问题中,有很多结构都具有对称性。
我们对这些结构进行受力分析的时候,常常将结构简化为杆系模型,而结构力学研究的就是结构的杆系模型,因此对称性在结构力学中有着广泛的应用。
现在就对称性在结构力学中的应用做一简单的总结。
结构的对称性是指结构的几何形状和支座形式均对称于某一几何轴线。
而荷载的对称则分为正对称荷载和反对称荷载。
另外需要注意的是杆件截面和材料的性质也要对于此轴对称。
在对称荷载作用下,结构内力呈对称分布。
在反对称荷载作用下,结构内力呈反对称分布。
如下图所示:对称性在求解结构内力中的应用:对称结构在正对称荷载作用下,其对称的内力(弯矩和轴力)和位移是正对称的,其反对称的内力(剪力)是反对称的;在反对称荷载作用下,其对称的内力(弯矩和轴力)和位移是反对称的,其反对称的内力(剪力)是正对称的。
因此,只要我们做出半边结构的内力图,也就知道了整个结构的内力图。
据此,我们在对对称结构进行内力分析时,就可以取半边结构进行分析。
取半边结构进行分析,可以减少超静定次数,减少基本未知量,为解题提供了很大的方便。
在用力法解决超静定问题时,对于对称的结构,可利用对称性简化计算。
简化步骤如下:1、选取对称的基本结构。
2、将未知力及荷载分组。
3、取半结构进行计算。
对于对称结构承受一般非对称荷载时,利用荷载分组,将荷载分解为正、反对称的两组,并将他们分别作用于结构上求解内力,然后将计算结果叠加。
反对称正对称在计算对称结构时,根据对称结构特性,可以选取半个结构计算。
选取半结构的原则:1、在对称轴的截面或位于对称轴的节点处2、按原结构的静力和位移条件设置相应的支撑,使半结构与原结构的内力和变形完全等效奇数跨对称结构:偶数跨对称结构:在用位移法求解超静定结构的时候,同样可以利用对称性简化计算。
分析可知,在正对称荷载时用位移法求解只有一个基本未知量;但在反对称荷载时若用位移法求解将有两个基本未知量,而用力法求解则只有一个未知量。
结构力学第20次课 力法6-5 位移法7-6结构的对称性 foxscarlet12012-5-17 《结构力学》第20次课 第6章力法6-5P225与第7章位移法7-6P302内容6-5 7-6 对称性利用1 对称性(1)结构的对称性:对称结构是指几何形状、支座情况、刚度都关于某轴对称。
(2)荷载的对称性: 对称荷载 反对称荷载 任何荷载都可以分解成对称荷载+反对称荷载两部分。
2 取对称的基本体系计算: 不论在何种外因作用下,对称结构应考虑采用对称的基本体系计算。
沿对称轴将梁切开,三对多余未知力中,弯矩X 1和轴力X 2是 未知力,剪力X 3是 未知力。
对称未知力产生的单位弯矩图和变形图是对称的;反对称未知力产生的单位弯矩图和变形图是反对称的。
如果荷载对称,M P 对称,Δ3P =0,X 3=0, 未知力为零;如果荷载反对称,M P 反对称,Δ1P =0, Δ2P =0, X 1= X 2 =0, 未知力为零。
3 取等代结构计算对称结构的变形特点,针对切开对称轴处是刚结点。
注意,如果对称轴上是铰结点有所不同。
(1)对称结构在对称荷载作用下位于对称轴上的截面,水平位移和转角为零,只有竖向位移。
(2)对称结构在反对称荷载作用下位于对称轴上的截面,竖向位移为零,水平位移和转角不为零。
① 奇数跨(无中柱)对称结构在对称荷载作用下的等代结构 §7-6 对称结构的计算奇数跨刚架受对称荷载A. 奇数跨结构(无中柱对称结构)F PF P(1) 对称荷载F P半边结构对称轴截面内力结构与荷载3 取等代结构计算1扩展练习 奇数跨结构受对称荷载作用llqllAB例2. 图示结构EI = 常数。
对称性只有竖向荷载作用1X 3=3X 2X 1X 2=【例题】利用对称性计算图示结构,绘制弯矩图。
(EI=常l↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓ql/2l/2l/2l/2(a )ldbFPFP4 无弯矩状态判定对称结构正对称荷载。
结构对称性的概念
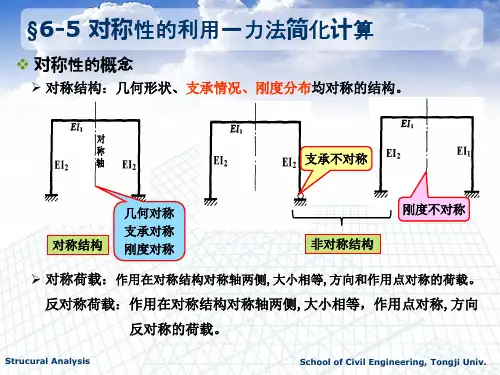
(1)对称结构:几何尺寸、支承情况、刚度分布对称的结构。
(2)荷载的对称性,如图1
正对称荷载:作用在对称结构对称轴两侧,大小相等,方向和作用点对称的荷载。
反对称荷载:作用在对称结构对称轴两侧,大小相等,作用点对称,方向反对称的荷载。
(3)对称结构在正对称、反对称荷载作用下的内力和变形,如图2
基本受力特点:
正对称荷载作用下,结构的内力和变形都是正对称的;
反对称荷载作用下,结构的内力和变形都是反对称的。
(4)特殊截面——对称轴通过的截面,如图3
对称结构,正对称荷载下,对称轴处切开,反对称的剪力为0,内力与位移分布均正对称;
对称结构,反对称荷载下,对称轴处切开,正对称的弯矩与轴力为0,内力与位移分布均反对称。
要使半结构能等效代替原结构的受力和变形状态。
关键在于被截开处应按原结构上的位移条件及相应的静力条件设置相应合适的支撑
例:用力法计算图示结构。
EI=常数。
图1
图2
图3。