量子力学讲义第4章
- 格式:doc
- 大小:612.00 KB
- 文档页数:15





第四章 量子力学的表述形式(本章对初学者来讲是难点)表象:量子力学中态和力学量的具体表示形式。
为了便于理解本章内容,我们先进行一下类比:矢量(欧几里德空间) 量子力学的态(希尔伯特空间) 基矢),,(321e e e~三维 本征函数,...),...,,(21n ψψψ~无限维任意矢展开∑=ii i e A A任意态展开 ∑=nn n a ψψ),,(z y x e e e),...)(),...,(),((21x x x n ψψψ 取不同坐标系 ),,(ϕθe e e r取不同表象 ),...)(),...,(),((21p C p C p C n ………. ………. 不同坐标之间可以进行变换 不同表象之间可以进行变换由此可见,可以类似于矢量A,将量子力学“几何化”→在矢量空间中建立它的一般形式。
为此,我们将① 引进量子力学的矢量空间~希尔伯特空间; ② 给出态和力学量算符在该空间的表示; ③ 建立各种不同表示之间的变换关系。
最后介绍一个典型应用(谐振子的粒子数表象)和量子力学的三种绘景。
4.1希尔伯特空间 狄拉克符号狄拉克符号“”~类比:),,(z y x A A A欧氏空间的矢量 A→坐标系中的分量 ),,(ϕθA A A r……….)(rψ →表象下的表示)(p C……….引入狄拉克符号的优点:①运算简洁;②勿需采用具体表象讨论。
一、 希尔伯特空间的矢量定义:希尔伯特空间是定义在复数域上的、完备的、线性内积空间,并且一般是无限维的。
1、线性:①c b a =+;②a b λ=。
2、完备性:∑=nn n a a 。
3、内积空间:引入与右矢空间相互共轭的左矢空间∑==↔+nn n a a a a *;)(:。
定义内积:==*ab b a 复数,0≥a a 。
1=a a ~归一化;b a b a ,~0=正交;m n n m δ=~正交归一;)(x x x x '-='δ~连续谱的正交归一。
第四章 量子力学的表述形式(本章对初学者来讲是难点)表象:量子力学中态和力学量的具体表示形式。
为了便于理解本章内容,我们先进行一下类比:矢量(欧几里德空间) 量子力学的态(希尔伯特空间) 基矢),,(321e e e~三维 本征函数,...),...,,(21n ψψψ~无限维任意矢展开∑=ii i e A A任意态展开 ∑=nn n a ψψ),,(z y x e e e),...)(),...,(),((21x x x n ψψψ 取不同坐标系 ),,(ϕθe e e r取不同表象 ),...)(),...,(),((21p C p C p C n ………. ………. 不同坐标之间可以进行变换 不同表象之间可以进行变换由此可见,可以类似于矢量A,将量子力学“几何化”→在矢量空间中建立它的一般形式。
为此,我们将① 引进量子力学的矢量空间~希尔伯特空间; ② 给出态和力学量算符在该空间的表示; ③ 建立各种不同表示之间的变换关系。
最后介绍一个典型应用(谐振子的粒子数表象)和量子力学的三种绘景。
4.1希尔伯特空间 狄拉克符号狄拉克符号“”~类比:),,(z y x A A A欧氏空间的矢量 A→坐标系中的分量 ),,(ϕθA A A r……….)(rψ →表象下的表示)(p C……….引入狄拉克符号的优点:①运算简洁;②勿需采用具体表象讨论。
一、 希尔伯特空间的矢量定义:希尔伯特空间是定义在复数域上的、完备的、线性内积空间,并且一般是无限维的。
1、线性:①c b a =+;②a b λ=。
2、完备性:∑=nn n a a 。
3、内积空间:引入与右矢空间相互共轭的左矢空间∑==↔+nn n a a a a *;)(:。
定义内积:==*ab b a 复数,0≥a a 。
1=a a ~归一化;b a b a ,~0=正交;m n n m δ=~正交归一;)(x x x x '-='δ~连续谱的正交归一。
二、 量子体系的态用希尔伯特空间的矢量表示(此属“符号问题”,仅作简要介绍,主要由学生自己通过练习来熟悉符号)1、态矢符合线性空间的要求:ϕλψψψψ=+=21。
2、任意态矢可用一组完备的基矢展开:nm m n n nn f f f a δψ==∑,。
∑∑=→====nnn n m mn n n m n m n f a a a f f a f a ψδψ?。
3、态可以求内积:⎰⎰==dx x x dx x x )(,)(ϕϕψψ ~ 以}{x 为基,其中 ϕϕψψx x x x ==)()(。
取ψ的左矢:⎰=dx x x )(*ψψ,有内积⎰⎰⎰⎰='''='''=dx x x dx x d x x x x x d x x dx x x )()()()()()(***ϕψϕψϕψϕψ 上式已利用了连续谱的正交归一性)(x x x x '-='δ。
三、 希尔伯特空间的算符算符 ψϕF F =:1、算符对左矢的作用: F b 存在,其意义(定义)为 )()(a F b a F a F==。
2、厄米共轭算符:B A A ψψψ=−→−++)(,称 A B A B ==++,,即 ++=A A ψψ)(。
有 +++=A B B A )((自证)。
若 A A =+ 则厄米算符。
3、矢量的外积:内积b a ~b ~ 是一个线性算符(并矢)。
作用于ac b c →~(右)态矢;作用于a c b c →~(左)态矢。
4、取乘积的厄米共轭规则(反序):+++++→→→A B B A a a a a )(,,*例:F为厄米算符,试计算?*=bF a解:注意到,对于复数,“*”=“+”,故a Fb a F b b F a b F a +++++=== *,。
~ 这也可作为用狄拉克符号写出的厄米算符的定义。
5、投影算符:n n n f f P =n P作用于任意态矢n f →ψ的分量:n n n n n f a f f P ==ψψ 。
6、基矢的完备性(这是非常有用的性质):ψψψψψn nnnn n n n n nn f f f f f a f a ∑∑∑==→==由单位算符I的定义:ψψI = 知对连续谱,有7、本征值方程:(分立谱)或(连续谱)。
8、可见,力学量算符由它的本征值谱}{n f 和本征矢完全集}{n f 完全确定。
作业:习题4.1、1[原题有误,应为证(13)式和(16)式],2,4,5。
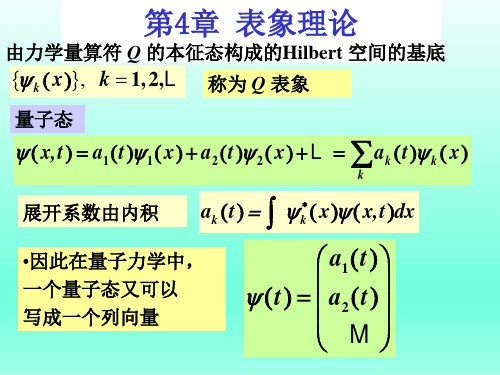
4.2 态和力学量的表象表示(本节可主要由学生自学,只列出要点)在具体计算时,要取“坐标系” --- 表象。
取力学量Q(也可以代表一个力学量完全集):以Q 的正交归一本征态完备系为基矢}{n q ,则称为一、 态的表象表示 Q-表象:基{n q ,本征值谱}{n q ,有∑==nn nmn n m I q qq q ,δ我们以分立谱为例讨论(请自学连续谱)。
任意态: ∑∑==nnn n n n q t a t q q t )()()(ψψ,)()(t q t a n n ψ=, )(t ψ在Q-表象中的表示。
(}{n a 表示态与)(t ψ表示态完全等价)矩阵形式: ()...,...,,,......**2*121n n a a a a a a =⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=+ψψ。
特别地,m q t =)(ψ 体系处于Q的本征态:mn n a δ=。
请同学们认真研究教材P136-139的各表,归纳态的表示的规律。
二、 算符的表象表示 Q -表象:由 ψϕψϕn nn m m n nn q q F q q I q q F ∑∑=→==,即 ∑=nn mn m a F b :ψn n q a =为ψ在Q-表象的表示(“投影”),ϕm m qb =为ϕ在Q-表象的表示(“投影”), n m m n q F q F =为F在Q -表象的表示(“投影”)。
矩阵形式:⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=............................................................,.................................... (21212222111211)21212222111211n nn n n n n n nn n n n n a a a F F F F F F F F F b b b F F F F F F F F F F ,或简写成 ψϕF =。
(注意,教材P141排版有误,见我在教材中的注。
)4.3 量子力学公式的表象表示(我们以分立谱为例,主要讲要点和思路,具体细节可由学生自学。
)一、归一化条件: 1)()(=t t ψψQ -表象: 1*====∑∑+ψψψψψψnn nn nn a a q q 。
二、平均值: )()(t F t F ψψ= Q -表象:∑∑+====nm n m n mn n nm m m F a F a q q F q q t F t F ,*,)()(ψψψψψψ 。
三、本征值方程 矩阵形式下本征值方程的求解(重点讲解)k k k f f f F =Q -表象:∑=nk m k k n n m f q f f q q F q,记∑∑∑=⇒==→=nnk mk k n mn n k n nk n n k k n k n a f a F q a f q q f f q a )()()()(, 即有0)()(=-∑nk n mn k mn a f F δ。
写成矩阵形式:0......................................................)()(2)(1212222111211=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛---k n k k k nn n n nkn k a a a f F F F F f F F F F f F ,这是关于}{)(k n a 的齐次线性方程组,具有非零解的条件是:即0................................................212222111211=---knn n n n kn kf F F F F f F F F F f F 。
求解方法:① 由久期方程→k f ;②代入方程组→}{)(k n a ;③由此得本征矢∑=nn k nk q a f )(。
例:(见教材P149)在(z L L ,2)的共同表象中,x L的矩阵表示为⎪⎪⎪⎭⎫⎝⎛=010******* x L ,求它的本征值和归一化本征矢。
解:矩阵方程为 λψψ=x L设 ⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛⇒⎪⎪⎪⎭⎫ ⎝⎛=3213213210101010102a a a a a a a a a λψ (1) 令 2λλ=',有010*******=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛'-'-'-a a a λλλ。
其久期方程为⎪⎩⎪⎨⎧⎪⎩⎪⎨⎧-===⇒-='='='='+'-→='-'-'- 32132130********1101λλλλλλλλλλλ ① 将 =1λ代入(1)式可得 12132,a a a a ==,即⎪⎪⎪⎭⎫⎝⎛=+1211a ψ。
由归一化条件()211412112112121=→=⋅=⎪⎪⎪⎭⎫⎝⎛=+++a a a ψψ(取实数),⎪⎪⎪⎭⎫ ⎝⎛=∴+12121ψ。
② 将02=λ代入(1)式可得 ⎪⎪⎪⎪⎭⎫⎝⎛-=202210ψ。
③ 将 -=3λ代入(1)式可得 ⎪⎪⎪⎭⎫⎝⎛-=-12121ψ。
四、S-方程)()(t H t ti ψψ=∂∂Q-表象:ψψH t i a a H H H H a a t i t a H t a t i nn mn m =∂∂⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛∂∂⇒=∂∂∑ ~.....................)()(212221121121。
作业:习题4.2、1,8;习题4.3、1,2,3。
4.4 表象变换问题:A-表象←→B 表象一、 表象变换是么正变换A- 表象:n n n n a a a A a ={B-表象:n n n n b b b B b =},{ ①考虑A →B :?==U a U b n n由 nk k n a a δ=→。
k nk nn k n nn k b b a a b a U ===∑∑δ。
②I U U U U==++ 这是保证本征矢正交归一性的必然要求: Ia a a a ab b a a b a b U U n nnnk k kn n kn kk n n k kk n nn=====∑∑∑∑∑++δ,,)(同理 I b b b a a b a b a b U U n nn kn k k n n k kk n nn ====∑∑∑∑++,)(。