电阻星角转换的计算

星形电阻三角形电阻等效变换形（△形）电阻网络。

星形电阻网络与三角形电阻网络可以根据需要进行等效变换。

（1）、由三角形电阻网络变为等效星形电阻网络星形网络中①、②两端间的端口等效电阻（③端开路）由与串联组成，三角形网络中①、②两端间的等效电阻（③端开路）由与串联后再与并联组成。

令此两等效电阻相等，即得（③端开路）（2-2-1）同理（①端开路）（2-2-2）（②端开路）（2-2-3）由式（2-2-1）至（2-2-3）联立得（2-2-4）（2-2-5）（2-2-6）以上三式是由三角形电阻网络变为等效星形电阻网络时计算星形网络电阻的公式。

这三个公式的结构规律可以概括为：星形网络中的一个电阻，等于三角形网络中联接到对应端点的两邻边电阻之积除以三边电阻之和。

（2）、由星形电阻网络变为等效三角形电阻网络可将式（2-2-4）、（2-2-5）、（2-2-6）对、和联立求解得（2-2-7）（2-2-8）（2-2-9）这是由星形电阻网络变换为等效三角形电阻网络时计算三角形网络电阻的公式。

这三个公式的结构规律可以概括为：三角形网络中一边的电阻，等于星形网络中联接到两个对应端点的电阻之和再加上这两个电阻之积除以另一电阻。

（3）、对称三端网络（symmetricalthree –terminal resistance network）三个电阻相等的三端网络称为对称三端网络。

对称三端电阻网络的等效变换：已知三角形网络电阻为变换为等效星形电阻网络的等效电阻为相反的变换是就是说：对称三角形电阻网络变换为等效星形电阻网络时，这个等效星形电阻网络也是对称的，其中每个电阻等于原对称三角形网络每边电阻的。

对称星形电阻网络变换为等效三角形电阻网络时，这个等效三角形电阻网络也是对称的，其中每边的电阻等于原对称星形网络每个电阻的3倍。

阻抗星三角变换公式好的，以下是为您生成的文章：咱今天来聊聊阻抗星三角变换公式，这玩意儿在电学里可有着重要的地位呢！还记得我当年在学校学习这个公式的时候，那可真是费了一番功夫。

当时我们的电学老师，是一个特别严谨又有点小幽默的人。

有一次上课，他为了让我们更清楚地理解这个公式，特意带来了一堆电线、电阻啥的，就在讲台上摆弄起来。

他一边接线路，一边给我们讲解：“同学们，你们看，这就好比是一个电路的迷宫，而阻抗星三角变换公式就是我们走出这个迷宫的钥匙。

” 我们都瞪大了眼睛，盯着老师的操作。

老师接着说：“星型连接的时候，三个阻抗分别是 Z1、Z2、Z3，而三角型连接的时候，对应的阻抗就是 Z12、Z23、Z31。

它们之间的关系，就像是一场巧妙的变形秀。

”咱们先来说说星型连接到三角型连接的变换公式。

Z12 = (Z1 * Z2 +Z2 * Z3 + Z3 * Z1) / Z3 ，Z23 = (Z1 * Z2 + Z2 * Z3 + Z3 * Z1) / Z1 ，Z31 = (Z1 * Z2 + Z2 * Z3 + Z3 * Z1) / Z2 。

这看起来是不是有点复杂？别着急，咱们来举个例子。

假设 Z1 =3Ω，Z2 = 4Ω，Z3 = 5Ω ，那咱们算算 Z12 是多少。

先把数值代入公式，Z12 = (3×4 + 4×5 + 5×3) / 5 = 8.2Ω 。

再来说说三角型连接到星型连接的变换公式。

Z1 = Z12 * Z31 / (Z12 + Z23 + Z31) ，Z2 = Z12 * Z23 / (Z12 + Z23 + Z31) ，Z3 = Z23 * Z31 /(Z12 + Z23 + Z31) 。

咱们还是用刚才的数值来算一下，Z1 = 8.2×7.5 / (8.2 + 10 + 7.5) ≈2.5Ω 。

在实际的电路分析中，这个阻抗星三角变换公式用处可大了。

比如说，我们要计算复杂电路中的电流和电压，如果直接计算很困难，这时候通过变换连接方式，用这个公式就能让问题变得简单许多。

复杂电路中的电阻计算口诀1、口诀复杂电路变简单，可将星角来变换。

变时一点要牢记，外接三点不能变。

星变角时求某边，两两积和除对面。

角变星时求某枝，两臂之积除和三。

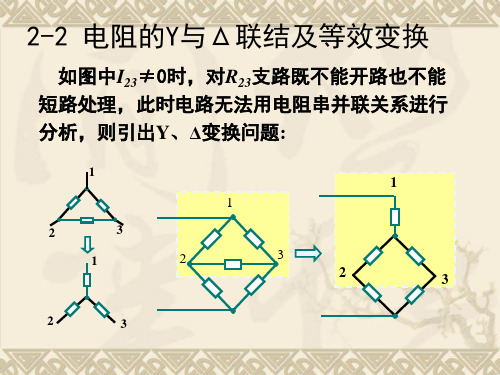
2、说明1. 概述不能使用串并联的关系进行电阻计算的电路被称为复杂电路，最简单的复杂电路是图1所示的桥式电路。

图1 最简单的复杂电路——桥式电路对于复杂电路，可先将其中连成星形（三个电阻有一个公共的连接点时，称为星形联结）的三个电阻（图1中的R1、R2和R3）转化成三角形电路（三个电阻依次连接成为一个闭合回路时，称为三角形联结），或将其中连成三角形的三个电阻（图1中的R1、R3和R4）转化成星形电路，这就是所谓的电阻星-三角变换问题。

进行上述变换后，原有的复杂电路就会转变为简单电路，就可以用串并联的计算方法求出总电阻值。

电阻星-三角变换的理论推导相对较复杂，在此不准备给出。

下面只给出转换方法口诀和使用方法举例。

2. 口诀说明设星形联结的三个电阻分别是R1、R2和R3，三角形联结的三个电阻分别是R12（对应星形连接的R1和R2）、R23（对应星形连接的R2和R3）和R31（对应星形连接的R3和R1），参照图2说明转换口诀的使用方法。

图2 电阻的星-三角变换电路（1）当由星形联结转换成三角形联结时，口诀为“星变角时求某边，两两积和除对面”。

这里的“两两”是指星形联结时的每两个电阻，“两两积和”即为（R1R2+ R2R3+ R3R1）；“对面”是指与转换成三角形联结后的一个电阻相对的原星形联结的那个电阻，如图2中R12的“对面”应是R3。

由此可得到由星形联结转换成三角形联结时的三个电阻计算公式为R12＝（R1R2+ R2R3+ R3R1）/R3R23＝（R1R2+ R2R3+ R3R1）/R1R31＝（R1R2+ R2R3+ R3R1）/R2（2）当由三角形联结转换成星形联结时，口诀为“角变星时求某枝，两臂之积除和三”。

这里的“两臂”是指与转换成星形联结的一个电阻（后面称为“一枝”，例如R1）同一个顶点的三角形联结时的两个电阻（例如对应R1的两臂是R12和R31），“和三”即为三角形联结时三个电阻之和，即（R12+ R23+ R31）。

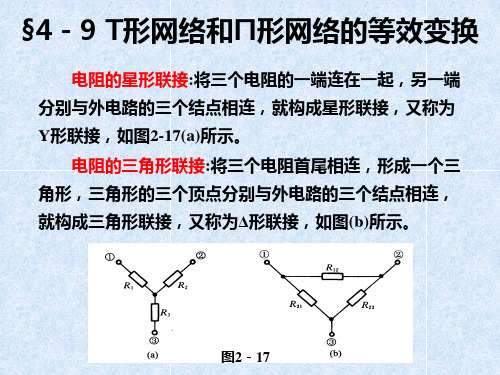
电阻的星形与三角形的等效变换
电阻的星形与三角形等效变换是指将一个电阻网络的星形连接转化为相应的等效三角形连接，或者将一个电阻网络的三角形连接转化为相应的等效星形连接。

这种变换可以使电阻网络更易于分析和计算。

将星形电阻连接转化为等效三角形电阻连接的方法如下：
1. 将三个电阻连接在一起，形成一个三角形。

2. 对于每一个电阻，通过连接其两个端点和三角形的第三个顶点来连接它们。

3. 删除原来的星形连接。

这样得到的等效三角形电阻网络与原来的星形电阻网络在电阻值等效的情况下具有相同的电流分布和电压分布。

将三角形电阻连接转化为等效星形电阻连接的方法如下：
1. 将三个电阻的一个共享节点连接在一起，形成一个星形。

2. 对于每一个电阻，通过连接其两个端点和星形的共享节点来连接它们。

3. 删除原来的三角形连接。

这样得到的等效星形电阻网络与原来的三角形电阻网络在电阻值等效的情况下具有相同的电流分布和电压分布。

通过这种等效变换，我们可以简化复杂的电阻网络，使得分析和计算更加容易和方便。

电阻星型连接和三角型连接的转换关系的推导以电阻星型连接和三角型连接的转换关系的推导为标题，我们将探讨这两种连接方式之间的关系，并推导出它们之间的转换公式。

让我们来了解一下电阻星型连接和三角型连接的基本概念。

在电路中，电阻星型连接和三角型连接是两种常见的电阻网络连接方式。

在电阻星型连接中，三个电阻分别连接在一个中心点上，形成一个星型。

这种连接方式常用于需要将多个电阻连接到一个共同节点的情况下。

而在电阻三角型连接中，三个电阻形成一个三角形，每个电阻的两个端点连接在一起。

这种连接方式常用于需要将电阻连接成一个闭合回路的情况下。

接下来，我们将推导出电阻星型连接和三角型连接之间的转换关系。

假设电阻星型连接中的三个电阻分别为R1、R2和R3，它们的连接关系可以表示为：R1和R2连接在一起，并与R3的一端连接在一起；R2和R3连接在一起，并与R1的一端连接在一起；R3和R1连接在一起，并与R2的一端连接在一起。

我们可以通过观察电路图，利用欧姆定律来推导出电阻星型连接和三角型连接之间的转换关系。

假设电流I流经电阻R1，根据欧姆定律可得：U1 = R1 * I其中，U1表示R1两端的电压。

接着，根据电流的分配规律，我们可以得到：I1 = I - I23其中，I1表示流经R1的电流，I23表示流经R2和R3的电流。

根据电流的串联规律，我们可以得到：I23 = I2 = I3即流经R2和R3的电流相等。

再根据欧姆定律，我们可以得到：U23 = (R2 + R3) * I23其中，U23表示R2和R3两端的电压。

根据电压的串联规律，我们可以得到：U2 = U3 = U23即R2和R3两端的电压相等。

将上述推导结果代入欧姆定律的公式中，我们可以得到：U2 = (R2 + R3) * I23U3 = (R2 + R3) * I23将U2和U3带入到R2和R3的欧姆定律公式中，我们可以得到：R2 * I2 + R2 * I3 = (R2 + R3) * I23R3 * I2 + R3 * I3 = (R2 + R3) * I23整理上述方程，我们可以得到：R2 * (I2 - I23) = R3 * I23R3 * (I3 - I23) = R2 * I23根据之前的推导结果，我们可以得到：I1 = I - I23将I1的表达式代入到上述方程中，我们可以得到：R2 * (I - I23 - I + I23) = R3 * I23R3 * (I - I23 - I + I23) = R2 * I23化简上述方程，我们可以得到：R2 * I = R3 * I23R3 * I = R2 * I23将上述方程整理，可以得到电阻星型连接和三角型连接之间的转换关系：R1 = R23 / (R2 + R3)R2 = R13 / (R1 + R3)R3 = R12 / (R1 + R2)其中，R12表示R1和R2两个电阻的串联电阻，R13表示R1和R3两个电阻的串联电阻，R23表示R2和R3两个电阻的串联电阻。

三角形电阻计算公式在我们的电学世界里，三角形电阻可是个有点让人头疼但又十分有趣的家伙。

先来说说啥是三角形电阻。

简单来讲，就是电阻在电路中连接成了三角形的样子。

这时候要计算它们的总电阻，可就不能像算简单串联或并联电阻那样轻松啦。

那三角形电阻的计算公式是啥呢？咱们得引入一个叫“星三角变换”的方法。

这就好比是一把神奇的钥匙，能帮咱们打开计算三角形电阻的大门。

假设我们有一个三角形连接的电阻网络，三个电阻分别是 R1、R2和 R3。

要把它变成星型连接，也就是三个电阻的一端连接在一起，另一端分别连接到电路的不同位置。

经过一系列复杂但又有趣的推导（这里咱就不详细说啦，不然脑袋得晕乎），咱们能得出星型电阻的值。

比如说，星型电阻 R1' = R1×R2 / (R1 + R2 + R3) ，R2' 和 R3' 也类似。

然后再根据星型电阻的计算方法，就能算出等效电阻啦。

我记得有一次，我在给学生们讲这个知识点的时候，有个小同学眼睛瞪得大大的，一脸迷茫地问我：“老师，这咋这么复杂呀，生活里真能用得着吗？”我笑着跟他说：“孩子呀，你想想看，咱们家里的各种电器，电路可复杂着呢，要是工程师们不懂这些知识，咱们的电器说不定一会儿就坏啦。

”这孩子似懂非懂地点点头，继续认真听我讲。

其实呀，三角形电阻的计算在实际生活中的应用还真不少。

比如在一些大型的电力设备中，还有复杂的电子电路里，都得靠准确计算电阻来保证设备正常运行，不出现故障。

学习三角形电阻计算公式虽然有点难，但只要咱们多琢磨，多练习，就一定能掌握它。

就像咱们学走路一样，一开始摇摇晃晃，但坚持下去就能走得稳稳当当。

总之，三角形电阻计算公式虽然有点小麻烦，但只要咱们用心去学，就能在电学的世界里畅游无阻，解决一个又一个的难题！。